Flash Attention是怎么做到又快又省显存的？

转自：https://zhuanlan.zhihu.com/p/721973285

Flash Attention 并没有减少 Attention 的计算量，也不影响精度，但是却比标准的Attention运算快 2~4 倍的运行速度，减少了 5~20 倍的内存使用量。究竟是怎么实现的呢？

Attention 为什么慢？

此处的“快慢”是相对而言的。严格意义上来说，相比于传统的 RNN，Transformer中的Attention可以并行地处理序列所有位置的信息（RNN 只能串行处理），因此计算效率并不低，但是仍然有可以进一步改进的空间。

众所周知，科学计算通常分为计算密集型 (compute-bound) 和内存密集型 (memory-bound) 两类。其中，计算密集型运算的时间瓶颈主要在于算数计算，比如大型矩阵的相乘等，而内存密集型运算的时间瓶颈主要在于内存的读写时间，比如批归一化、层归一化等等。

时间复杂度：Attention 需要对矩阵 $Q 和矩阵 K 的转置做乘法来得到注意力权重矩阵。不考虑 batch 维度，假设矩阵 Q、K 的尺寸都为 $(n, dim)$，那么两个维度为 $(n, dim)$ 的矩阵相乘的时间复杂度是序列长度 n 的平方级 $O(n^2)$；在计算完注意力权重矩阵后，还需要对其进行 softmax 操作，这个算法需要分成三次迭代来执行 $O(n^3)$。$
空间复杂度：Attention 的计算过程需要存储 $$S = QK^T$ 和 $P = \text{softmax}(S)$ 这两个尺寸均为 $(n, n)$ 的矩阵。$

$为了对 Attention 的内存读取时间有更清晰的感知，这里简单介绍 GPU 的内存层级。$

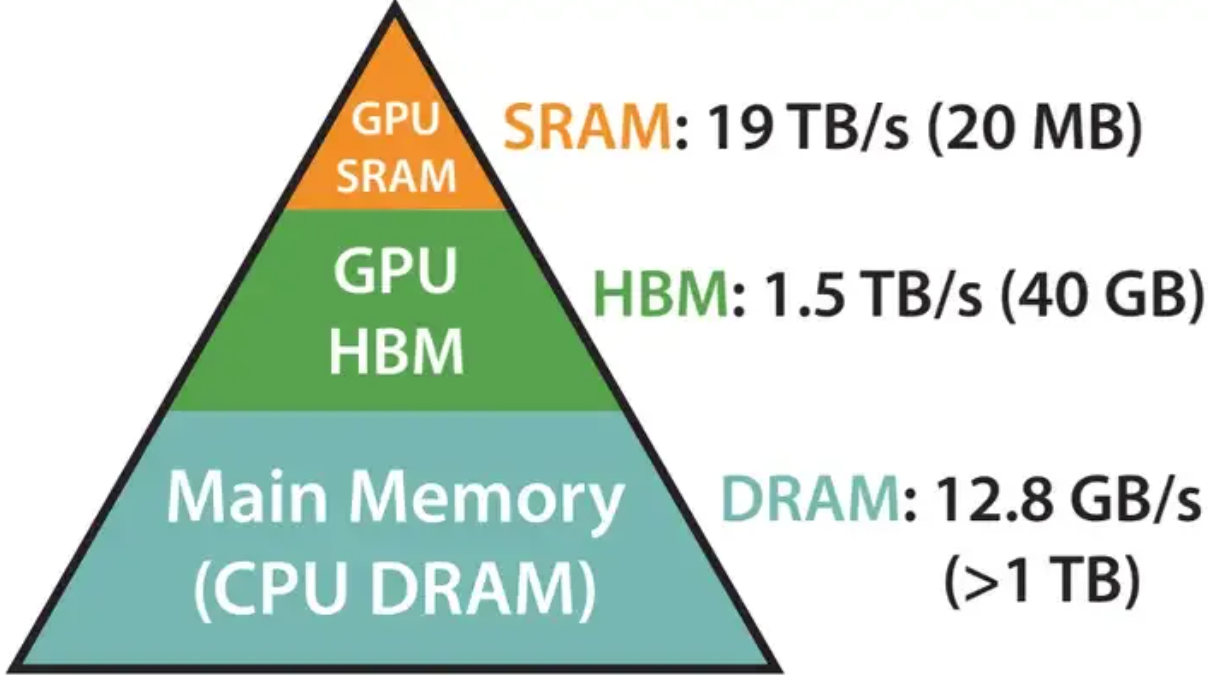
GPU 的内存可以分为 HBM 和 SRAM 两部分。例如，A100 GPU具有40-80 GB的高带宽内存（上图中的 HBM，即我们平时说的“显存”），带宽为 1.5TB/s，并且108个流式多核处理器都有 192 KB 的片上 SRAM，带宽约为 19 TB/s。片上 SRAM 比 HBM 快一个数量级，但容量要小很多个数量级。

在 GPU 运算之前，数据和模型先从 CPU 的内存（上图中的DRAM）移动到 GPU 的 HBM，然后再从 HBM 移动到 GPU 的 SRAM，CUDA kernel 在 SRAM 中对这些数据进行运算，运算完毕后将运算结果再从 SRAM 移动到 HBM。

所以提高Attention运算效率，需要从降低attention的时间和空间复杂度入手。

时间复杂度

在$S = QK^T$

性能比不上原始 attention。不论是稀疏估计、低秩估计还是其他，这些方法都采用了某种近似算法来估算注意力权重矩阵，难免会丢失信息。目前主流的还是原始的attention
无法减少内存读取的时间消耗。这些方法只能降低 attention 的计算复杂度，但是无法对 attention 运算过程中的空间复杂度等进行控制，无法减少内存读写带来的时间损耗

所以在时间复杂度方向的优化主要在softmax的计算过程中：

$ \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{k=1}^{N} e^{x_k}} $

Native softmax算法分二次迭代：

计算 softmax 分母

　　　　$ \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad d_i = d_{i-1} + e^{x_i} \end{aligned} $

求对应位置的softmax

　　　　$ \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad a_i = \frac{e^{x_i}}{d_N} \end{aligned} $

softmax 有个问题，那就是很容易溢出。比如float16的最大值为65504，所以只要 $x ≥ 11$的话softmax就溢出了。好在 exp 有这么一个性质，那就是$e^{x - y} = \frac{e^x}{e^y}$，根据这个性质，可以在分子分母上同时除以一个数，这样可以将的范围都缩放到范围内，保证计算 softmax 时的数值稳定性。Safe Softmax 的数学公式是：

$ \text{SafeSoftmax}(x_i) = \frac{e^{x_i - m}}{\sum_{k=1}^{N} e^{x_k - m}} \quad \text{其中 } m = \max(x_1, x_2, ..., x_N) $

这个算法可以分成三次迭代来执行：

遍历所有数，求 x 中的最大值m

　　　　$ \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad m_i = \max(m_i, x_i) \end{aligned} $

计算 softmax 分母，并根据m对其进行缩放

　　　　$ \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad d_i = d_{i-1} + e^{x_i - m_N} \end{aligned} $

求对应位置的 softmax

　　　　$ \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad a_i = \frac{e^{x_i - m_N}}{d_N} \end{aligned} $

分析以上步骤可以发现，如果是不做任何优化的话，至少要进行和 GPU 进行6次通信（3次写入，3次写出），如果对每一步的for循环进行一些并行切分的的话，还要加上 reduce_sum 和 reduce_max 之类的通信成本。所以2018年 Nvidia 提出了《Online normalizer calculation for softmax》，核心改进是去掉第二步中$ d_i = d_{i-1} + e^{x_i - m_N} $对$ m_N $的依赖，设$ d_i' = \sum_{j}^{i} e^{x_j - m_i} $（这里的全局最大值变成了当前最大值），这个式子有如下的性质：

$ \begin{aligned} d_i' &= \sum_{j}^{i} e^{x_j - m_i} \\ &= \sum_{j}^{i-1} e^{x_j - m_i} + e^{x_i - m_i} \\ &= \sum_{j}^{i-1} e^{x_j - m_{i-1} + m_{i-1} - m_i} + e^{x_i - m_i} \\ &= \left( \sum_{j}^{i-1} e^{x_j - m_{i-1}} \right) e^{m_{i-1} - m_i} + e^{x_i - m_i} \\ &= d_{i-1}' e^{m_{i-1} - m_i} + e^{x_i - m_i} \end{aligned} $

这个式子依赖于$ d_{i-1}' $，$ m_i $，$ m_{i-1} $。那么就可以将softmax前两步合并到一起：

求 x 的最大值 m, 计算 softmax 的分母

　　　　$ \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad m_i = \max(m_i, x_i) \\ &\quad d_i' = d_{i-1}' e^{m_{i-1} - m_i} + e^{x_i - m_i} \end{aligned} $

求对应位置的 softmax

　　　　$ \begin{aligned} &\text{for } i \leftarrow 1, N \text{ do} \\ &\quad a_i = \frac{e^{x_i - m_N}}{d_N} \end{aligned} $

以上的算法优化可以将3步合并变成2步，将softmax的时间复杂度降为\$O(n^2)$。

Python代码实现

下面是一个简单的 Python 实现，展示了如何用 Online Softmax 处理数据流：

import math

def online_softmax(x):
    """
    在线计算 Softmax，单次遍历，适合流式数据处理
    参数:
        x: 可迭代对象，输入的数值序列
    返回:
        Softmax 输出列表
    """
    m = float('-inf')  # 当前最大值
    d = 0.0           # 当前分母
    exp_values = []   # 存储 e^{x_i - m}，用于最终归一化
    
    # 单次遍历：更新最大值和分母
    for xi in x:
        m_new = max(m, xi)
        d = d * math.exp(m - m_new) + math.exp(xi - m_new)
        exp_values.append(math.exp(xi - m_new))
        m = m_new
    
    # 计算 Softmax 输出
    result = [v / d for v in exp_values]
    return result

# 示例用法
if __name__ == "__main__":
    x = [1.0, 2.0, 3.0, 4.0, 5.0]
    result = online_softmax(x)
    print("输入:", x)
    print("Softmax 输出:", result)
    print("和:", sum(result))  # 验证和为 1

空间复杂度

在将3步合成2步的同时：

借助GPU的share memory来存储中间结果，将上面的两步只用一个 kernel 实现，这样就只需要与 global memory 通信两次（一次写入数据，一次读取结果）
还可以减少 Reduce_max 和 Reduce_sum 之类的通信成本

空间复杂度方面优化的基本思路是降低Attention对于显存的需求，减少HBM和SRAM之间的换入换出，充分利用 GPU 的并行优势，进而减少Attention运算的时间消耗。

总结

Flash Attention的动机是尽可能避免大尺寸的注意力权重矩阵在 HBM 和 SRAM 之间的换入换出。论文中具体方法包含两个部分：tiling 和 recomputation。

tiling 的基本思路：不直接对整个输入序列计算注意力，而是将其分为多个较小的块，逐个对这些块进行计算，增量式地进行 softmax 的规约。规约过程中只需要更新某些中间变量，不需要计算整个注意力权重矩阵，就是以上介绍的将三步合并成两步的过程。

recomputation 的基本思路：基于 tiling 技巧，在反向传播过程中不保留整个注意力权重矩阵，而是只保留前向过程中 tiling 的某些中间变量，然后在反向传播过程中重新计算注意力权重矩阵。recomputation 可以看作是一种基于 tiling 的特殊的 gradient checkpointing，想进一步了解 recomputation 的读者可以翻阅Flash Attention原文。

得益于上述技巧，Flash Attention 可以同时做到又快（运算速度快）又省（节省显存）。

posted @ 2025-09-17 13:31 有何m不可阅读(171) 评论(0) 收藏举报

刷新页面返回顶部

gongzb

Flash Attention是怎么做到又快又省显存的？

Attention 为什么慢？

时间复杂度

空间复杂度

总结

公告