大模型基础｜位置编码｜RoPE｜ALiBi

转自：https://zhuanlan.zhihu.com/p/650469278

Transformer 模型在处理序列数据时，其自注意力机制使得模型能够全局地捕捉不同元素之间的依赖关系，但这样做的代价是丧失了序列中的元素顺序信息。由于自注意力机制并不考虑元素在序列中的位置，所以在输入序列的任何置换下都是不变的，这就意味着模型无法区分序列中元素的相对位置。在许多自然语言处理任务中，词语之间的顺序是至关重要的，所以需要一种方法来让模型捕获这一信息。

这就是位置编码（Positional Encoding）的角色所在。本文主要介绍常见的绝对位置编码（sinusoidal），旋转位置编码（RoPE），以及相对位置编码ALiBi。

sinusoidal位置编码

绝对位置编码是直接将序列中每个位置的信息编码进模型的，从而使模型能够了解每个元素在序列中的具体位置。原始Transformer提出时采用了sinusoidal位置编码，通过正弦和余弦的函数结构使得模型捕获位置之间的复杂关系，且这些编码与序列中每个位置的绝对值有关。

$PE_{(pos,2i)} = sin(pos / 10000^{2i / d_{model}}), PE_{(pos,2i + 1)} = cos(pos / 10000^{2i / d_{model}})$

其中，$pos$表示位置，$d_{model}$代表$embedding$的维度，$2i$，$2i + 1$代表的是$embedding$不同位置的索引。

原始 Transformer 的位置编码虽然是基于绝对位置的，但其数学结构使其能够捕获一些相对位置信息。使用正弦和余弦函数的组合为每个位置创建编码，波长呈几何级数排列，意味着每个位置的编码都是独特的。然而，正弦和余弦函数的周期性特性确保了不同位置之间的编码关系是连续且平滑的。

比如：

对于相邻位置，位置编码的差异较小，与两者之间的距离成正比。
对于相隔较远的位置，位置编码的差异较大，与两者之间的距离成正比。

这种连续和平滑的关系允许模型学习位置之间的相对关系，而不仅仅是各自的绝对位置。考虑两个位置

代码实现如下：

import math
import torch
import torch.nn as nn
import numpy as np

class PositionalEncoding(nn.Module):
    def __init__(self, d_model: int, dropout_prob: float, max_len: int = 5000):
        super().__init__()
        self.dropout = nn.Dropout(dropout_prob)
        encodings = self.get_positional_encoding(d_model, max_len)
        self.register_buffer('positional_encodings', encodings, False)

    @staticmethod
    def get_positional_encoding(d_model: int, max_len: int):
        position = torch.arange(0, max_len, dtype=torch.float32).unsqueeze(1)
        two_i = torch.arange(0, d_model, 2, dtype=torch.float32)
        div_term = torch.exp(two_i * -(math.log(10000.0) / d_model))
        encodings = torch.zeros(max_len, d_model)
        encodings[:, 0::2] = torch.sin(position * div_term)
        encodings[:, 1::2] = torch.cos(position * div_term)
        return encodings.unsqueeze(0).requires_grad_(False)

    def forward(self, x: torch.Tensor):
        pe = self.positional_encodings[:x.shape[1]].detach().requires_grad_(False)
        return self.dropout(x + pe)

def _test_positional_encoding():
    import matplotlib.pyplot as plt
    plt.figure(figsize=(15, 5))
    pe = PositionalEncoding.get_positional_encoding(20, 100)
    print(pe.shape)
    plt.plot(np.arange(100), pe[:, 0, 4:8].numpy())
    plt.legend(["dim %d" % p for p in [4, 5, 6, 7]])
    plt.title("Positional encoding")
    plt.show()

if __name__ == '__main__':
    _test_positional_encoding()

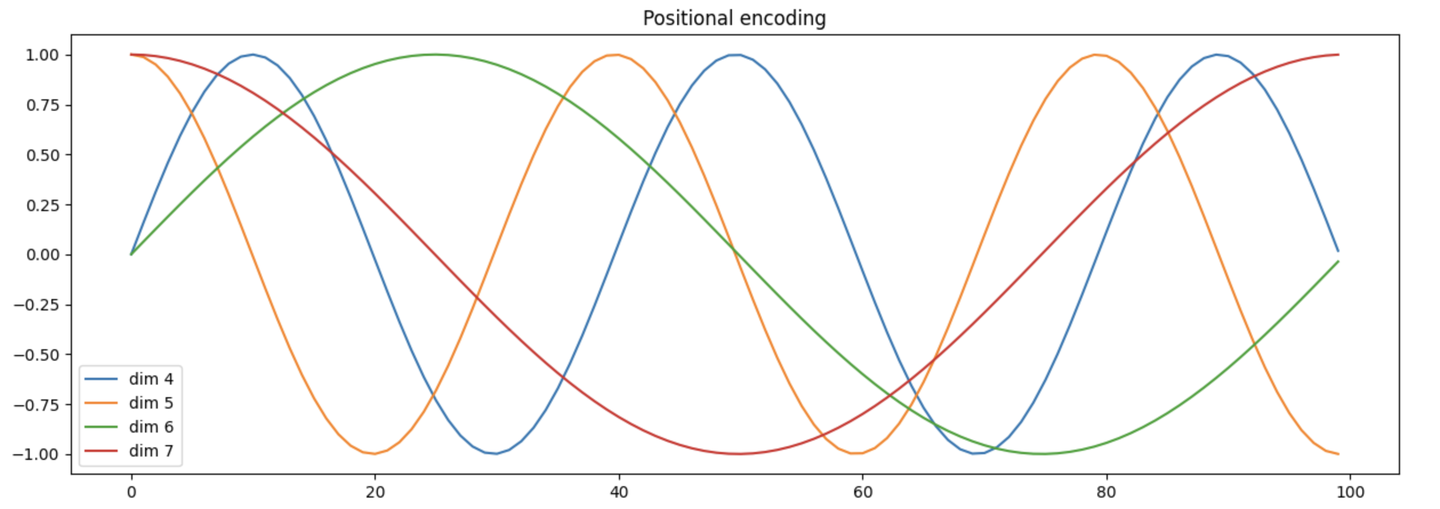
可以看到不同维度沿着序列方向的位置编码变化如下：

Rotary Position Embedding

sinusoidal位置编码对相对位置关系的表示还是比较间接的，那有没有办法更直接的表示相对位置关系呢？那肯定是有的，而且有许多不同的方法，旋转位置编码（Rotary Position Embedding，RoPE）是一种用绝对位置编码来表征相对位置编码的方法，并被用在了很多大语言模型的设计中。

RoPE的设计思路可以这么来理解：我们通常会通过向量内积来计算注意力系数，如果能够对

假设$$\langle f(q,m),f(k,n)\rangle = g(q,k,m-n)$$

RoPE这一研究就是为上面这个等式找到了一组解答，也就是 $$f(q,m) = q e^{im\theta}$$

此时就能够使得两个向量的内积包含它们的相对位置关系$m - n$了(在复数域，转为共轭内积后取实部)

$$\langle f(q,m),f(k,n)\rangle = Re\left[q e^{im\theta} \cdot k e^{-in\theta}\right] = Re\left[q \cdot k e^{i(m-n)\theta}\right]$$

由于这里$f$函数的定义其实对应着向量的旋转，所以这种位置编码也就叫做“旋转位置编码”。基于$f$函数的矩阵形式以及内积的线性叠加性，可以得到下面形式（具体推导感兴趣的可以看苏剑林老师的博客，本文主要介绍思想）

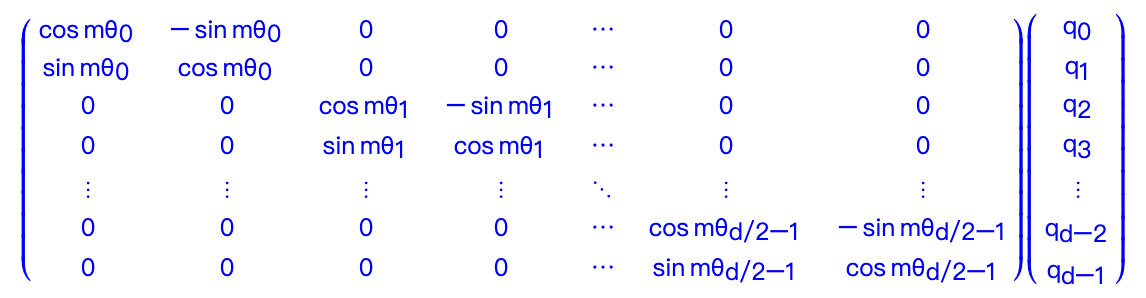
有了这一形式后，具体实现有两种方式：

转到复数域，对两个向量进行旋转，再转回实数域
直接在实数域通过向量和正余弦函数的乘法进行运算，也就是下面这个公式

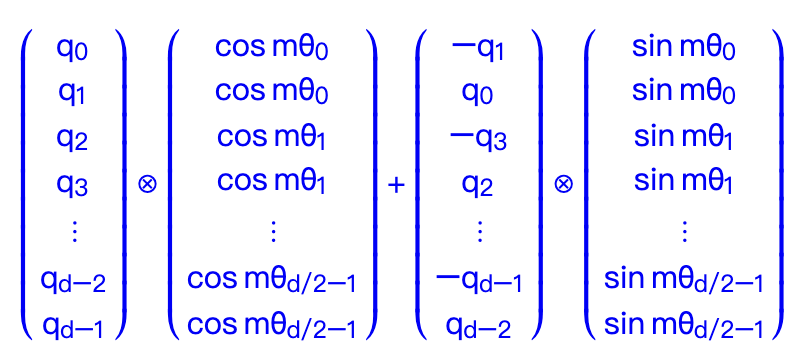
llama的代码实现就是采用了第一种形式，如下

def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    t = torch.arange(end, device=freqs.device)  # type: ignore
    freqs = torch.outer(t, freqs).float()  # type: ignore
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis

def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    ndim = x.ndim
    assert 0 <= 1 < ndim
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    return freqs_cis.view(*shape)

def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)

第二种方式的实现会更加易懂一点，就是把前面那个公式中的四个向量凑出来，然后照着公式算一下就可以了，示例代码如下：

import torch
import math

def rotary_position_embedding(q, k):
    """
    Rotary Position Embedding (RoPE) for queries and keys.
    
    Args:
        q: tensor for queries of shape (batch_size, num_heads, seq_len, dim)
        k: tensor for keys of shape (batch_size, num_heads, seq_len, dim)
        
    Returns:
        Rotated queries and keys
    """
    batch_size, num_heads, seq_len, dim = q.size()
    
    # Begin of sinusoidal_position_embedding content
    position = torch.arange(seq_len, dtype=torch.float).unsqueeze(-1).to(q.device)
    div_term = torch.exp(torch.arange(0, dim, 2, dtype=torch.float) * -(math.log(10000.0) / dim)).to(q.device)
    
    pos_emb = position * div_term
    pos_emb = torch.stack([torch.sin(pos_emb), torch.cos(pos_emb)], dim=-1).flatten(-2, -1)
    pos_emb = pos_emb.unsqueeze(0).unsqueeze(1)
    pos_emb = pos_emb.expand(batch_size, num_heads, -1, -1)
    # End of sinusoidal_position_embedding content

    # Extract and duplicate cosine and sine embeddings
    cos_emb = pos_emb[..., 1::2].repeat_interleave(2, dim=-1)
    sin_emb = pos_emb[..., ::2].repeat_interleave(2, dim=-1)

    # Create alternate versions of q and k
    q_alternate = torch.stack([-q[..., 1::2], q[..., ::2]], dim=-1).reshape(q.size())
    k_alternate = torch.stack([-k[..., 1::2], k[..., ::2]], dim=-1).reshape(k.size())

    # Rotate queries and keys
    q_rotated = q * cos_emb + q_alternate * sin_emb
    k_rotated = k * cos_emb + k_alternate * sin_emb

    return q_rotated, k_rotated

ALiBi

使用正弦位置编码的transformer的外推能力非常弱。虽然旋转位置编码比正弦方法有所改进，但仍未达到令人满意的结果。

为了有效地实现外推，作者引入了一种称为"注意力线性偏置 (ALiBi)"的方法。与传统方法不同，ALiBi不向单词embedding中添加位置embedding，而是根据token之间的距离给 attention score 加上一个预设好的偏置矩阵，比如

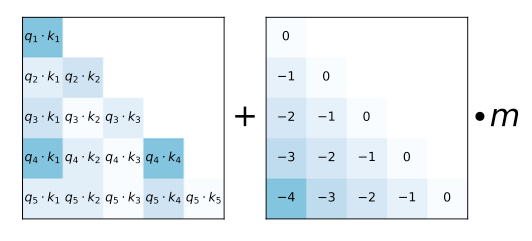
左侧的矩阵展示了每一对query-key的注意力得分。右侧的矩阵展示了每一对query-key之间的距离。m是固定的参数，每个注意头对应一个标量。

import math
import torch
from torch import nn

def get_slopes(n_heads: int):
    
    n = 2 ** math.floor(math.log2(n_heads))
    m_0 = 2.0 ** (-8.0 / n)
    m = torch.pow(m_0, torch.arange(1, 1 + n))

    if n < n_heads:
        m_hat_0 = 2.0 ** (-4.0 / n)
        m_hat = torch.pow(m_hat_0, torch.arange(1, 1 + 2 * (n_heads - n), 2))
        m = torch.cat([m, m_hat])
        
    return m


@torch.no_grad()
def get_alibi_biases(n_heads: int, mask: torch.Tensor):

    m = get_slopes(n_heads).to(mask.device)
    seq_len = mask.size(0)
    distance = torch.tril(torch.arange(0, -seq_len, -1).view(-1, 1).expand(seq_len, seq_len))
    print(distance)

    return distance[:, :, None] * m[None, None, :]

seq_len = 10
n_heads = 8

m = get_slopes(n_heads)
print(m)

alibi_biases = torch.zeros(seq_len,seq_len)
for j in range(1,seq_len):
    for i in range(j, seq_len):
        alibi_biases[i, i - j] = -j
print(alibi_biases)

print(alibi_biases[:, :, None].shape, m[None, None, :].shape)

alibi_biases[:, :, None] * m[None, None, :]

可以看到下面打印出来的第一行就是给不同head的系数

ALiBi方法不需要对原始网络进行改动，允许在较短的输入序列上训练模型，同时在推理时能够有效地外推到较长的序列，从而实现了更高的效率和性能。

posted @ 2025-09-13 14:17 有何m不可阅读(75) 评论(0) 收藏举报

刷新页面返回顶部

gongzb

大模型基础｜位置编码｜RoPE｜ALiBi

sinusoidal位置编码

Rotary Position Embedding

ALiBi

公告