基于Transformer的预训练大语言模型，如何区分文本位置？

 一、Transformer位置编码问题

Transformer的自注意力机制本质上是一种基于内容相似度的匹配操作，其核心计算过程与词序无关。给定输入序列中任意两个词元 token，其注意力分数仅依赖于它们的语义相关性，而与它们在序列中的绝对或相对位置无关。具体表现为：

1. 查询-键相关性计算：

通过投影矩阵将输入向量转换为查询（Query）和键（Key），计算二者的点积相似度：

$$\text{Score}(q_i, k_j) = q_i^\top k_j$$

其中 \( W_q, W_k \) 为可学习参数，\( d_k \) 为键向量的维度。若交换 \( q_i \) 和 \( q_j \) 的位置，计算结果不变，即：

$$\text{Score}(q_i, k_j) = \text{Score}(q_j, k_i)$$

2. 注意力权重生成：

对分数矩阵进行 Softmax 归一化，得到注意力权重分布：

$$\alpha_{ij} = \frac{\exp(\text{Score}(q_i, k_j))}{\sum_k \exp(\text{Score}(q_i, k_k))}$$

此时权重仅反映词元间的语义关联强度，缺乏位置信息编码。

---

二、Transformer位置编码的重要性

在自然语言处理中，词序通常对语义理解起关键作用。以关系分类任务为例，模型需要根据文本中两个实体的顺序和上下文关系，准确判断它们之间的语义关联。若词序信息丢失或错乱，可能导致模型误判关系类型。

示例说明

• 句子1："公司收购了竞争对手"
• 句子2："竞争对手收购了公司"

虽然两句话包含相同的词汇，但词序反转导致实体关系完全相反：

• 句子1中，“公司”是收购方（主体），“竞争对手”是被收购方（客体），关系为“收购”；
• 句子2中，主客体对调，关系变为“被收购”。

⚠️ 若模型忽略词序，将无法区分这两种截然不同的语义。

---

三、Transformer如何做位置编码？

向Transformer模型中加入位置编码是必不可少的操作。位置编码可以分为绝对位置编码和相对位置编码两大类。

📌 外推能力对比：
绝对位置编码外推能力较差。推理时如果输入文本长度超过训练阶段的最大长度，模型表现会显著下降。
因此，主流大语言模型普遍采用相对位置编码，以增强长序列外推能力。

目前主要有两种典型的位置编码方法：

1. 可训练绝对位置编码（如 BERT）

• 将位置信息表示为可训练的参数矩阵 \( P \in \mathbb{R}^{L \times d} \)，其中：
• \( L \)：预设的最大序列长度（如512）
•  \( d \)：隐藏层维度
• 对于第 \( i \) 个位置的 token，其位置编码为 \( P_i \)，并与词嵌入相加作为输入： $$\text{Input}_i = E_i + P_i$$
• 优点：简单直接，易于训练。
• 缺点：无法外推 —— 当测试序列长度 \( > L \)  时，无法生成有效的位置编码。

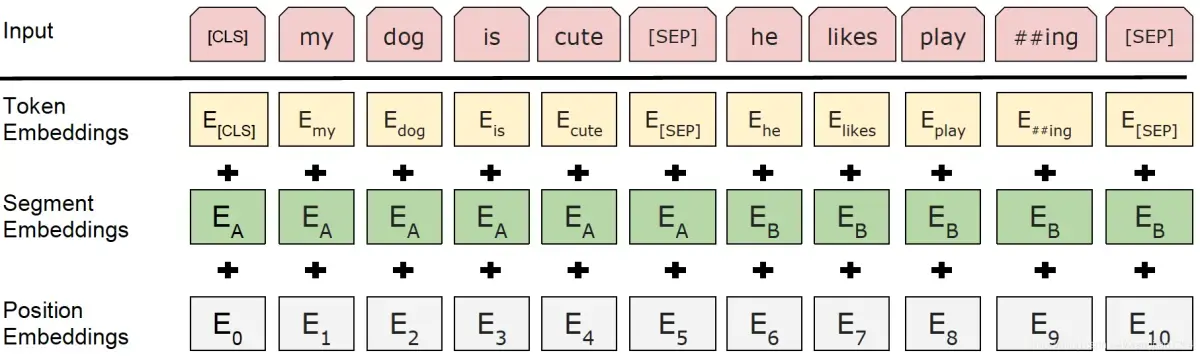
代码实现

import torch
import torch.nn as nn

class BertStyleEmbedding(nn.Module):
    """
    包含词嵌入 + 可训练位置编码 + 段嵌入
    """
    def __init__(self, vocab_size, hidden_size, max_seq_len, num_segments=2):
        super().__init__()
        # 词嵌入
        self.word_embedding = nn.Embedding(vocab_size, hidden_size, padding_idx=0)
        # 可训练位置编码
        self.pos_embedding = nn.Embedding(max_seq_len, hidden_size)
        # 段嵌入（句子A / 句子B）
        self.seg_embedding = nn.Embedding(num_segments, hidden_size)
        
        # 层归一化和dropout
        self.layer_norm = nn.LayerNorm(hidden_size)
        self.dropout = nn.Dropout(0.1)
        
    def forward(self, input_ids, segment_ids=None):
        """
        input_ids: [batch_size, seq_len]
        segment_ids: [batch_size, seq_len] （可选，默认为0）
        """
        batch_size, seq_len = input_ids.size()
        
        # 生成位置索引: [0, 1, 2, ..., seq_len-1]
        position_ids = torch.arange(seq_len, dtype=torch.long, device=input_ids.device)
        position_ids = position_ids.unsqueeze(0).repeat(batch_size, 1)  # [batch_size, seq_len]
        
        if segment_ids is None:
            segment_ids = torch.zeros_like(input_ids)
            
        # 三种嵌入相加
        word_emb = self.word_embedding(input_ids)           # [B, L, H]
        pos_emb = self.pos_embedding(position_ids)          # [B, L, H]
        seg_emb = self.seg_embedding(segment_ids)           # [B, L, H]
        
        embeddings = word_emb + pos_emb + seg_emb           # [B, L, H]
        embeddings = self.layer_norm(embeddings)            # 层归一化
        embeddings = self.dropout(embeddings)               # dropout
        
        return embeddings

2. 正弦位置编码（如原始 Transformer）

• 使用预定义的三角函数生成位置编码： $$PE_{(pos, 2j)} = \sin\left( \frac{pos}{10000^{2j/d}} \right), \quad PE_{(pos, 2j + 1)} = \cos\left( \frac{pos}{10000^{2j/d}} \right)$$
• 优点：
• 具有相对位置敏感性
• 理论上支持任意长度外推（可计算任意 pos 的编码）
• 缺点：不如 RoPE 灵活，表达能力有限

代码实现

class PositionalEncoding(nn.Module):
    """位置编码"""
    def __init__(self, num_hiddens, dropout, max_len=1000):
        super().__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P
        self.P = torch.zeros((1, max_len, num_hiddens))
        X = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1) / torch.pow(10000, torch.arange(0, num_hiddens, 2, dtype=torch.torch.float32) / num_hiddens)
        # X.shape torch.Size([1000, 16])
        # P.shape torch.Size([1，1000, 32])
        # 第三维 隔一个取
        self.P[:, :, 0::2] = torch.sin(X)
        self.P[:, :, 1::2] = torch.cos(X)
        print(f"P的均值为{self.P.mean()},方差为{self.P.var()}")
    
    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)

---

四、RoPE：旋转位置编码（Rotary Position Embedding）

旋转位置编码（Rotary Position Embedding, RoPE）是一种创新的相对位置编码方法，其核心思想是：

✅ 通过旋转矩阵将绝对位置信息融入注意力机制，同时保留词向量的相对位置关系。

核心思想

• 对查询向量  和键向量  施加与位置相关的旋转变换。
• 利用正弦/余弦函数的“和差化积”性质，将绝对位置  的旋转转化为相对位置  的相位差。

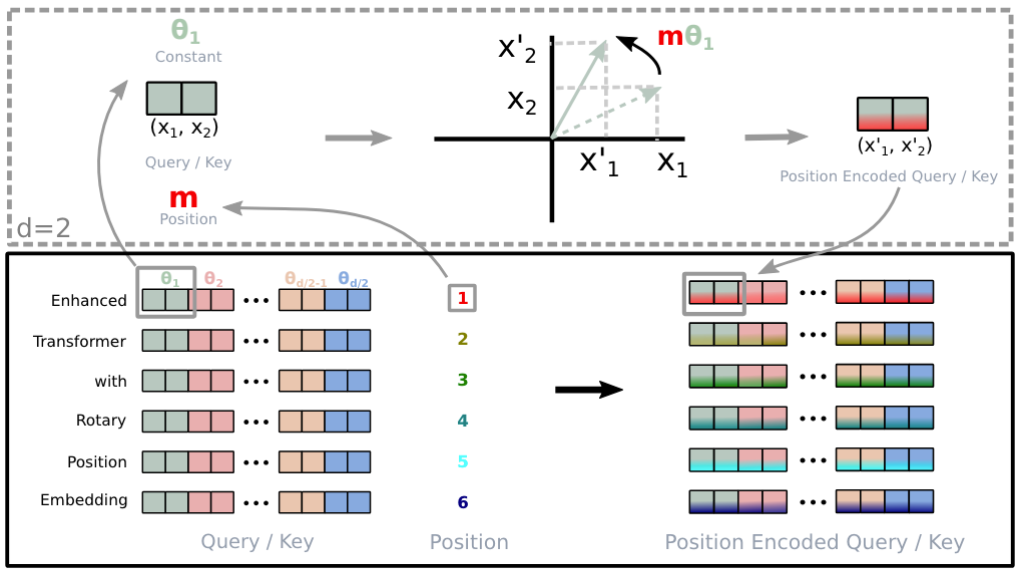
旋转操作定义

定义二维旋转矩阵： $$R_m = \begin{bmatrix} \cos\theta_m & -\sin\theta_m \\ \sin\theta_m & \cos\theta_m \end{bmatrix}, \quad \theta_m = m \cdot \alpha / d^{2j/d}$$

其中：

• \( m \)：当前位置（如第 \( m \) 个词）
•  \( d \)：位置编码总维度
• \( \alpha \)：调节因子（控制频率衰减速度）
• \( \theta_m \)：随位置变化的旋转角度

旋转特性

当向量乘以  \( R_m \) 时，其幅值不变，仅在二维平面上旋转角度 \( \theta_m \)。

原因在于：

•  \( R_m \) 是标准的正交矩阵：\( R_m^\top R_m = I \) 
• 行列式为 1：\( \det(R_m) = \cos^2\theta + \sin^2\theta = 1 \to \) 无缩放，纯旋转

注意力分数引入相对位置

令旋转后的查询和键为： $$q'_m = R_m q_m, \quad k'_n = R_n k_n$$

则注意力内积为： $$\langle q'_m, k'_n \rangle = \langle R_m q_m, R_n k_n \rangle$$

利用三角恒等式，最终可推导出该内积依赖于相对位置 ，从而实现相对位置编码。

代码实现

具体实现有两种方式：

1.转到复数域，对两个向量进行旋转，再转回实数域

# llama的代码实现就是采用了第一种形式
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    t = torch.arange(end, device=freqs.device)  # type: ignore
    freqs = torch.outer(t, freqs).float()  # type: ignore
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis

def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    ndim = x.ndim
    assert 0 <= 1 < ndim
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    return freqs_cis.view(*shape)

def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)

2.直接在实数域通过向量和正余弦函数的乘法进行运算，也就是下面这个公式

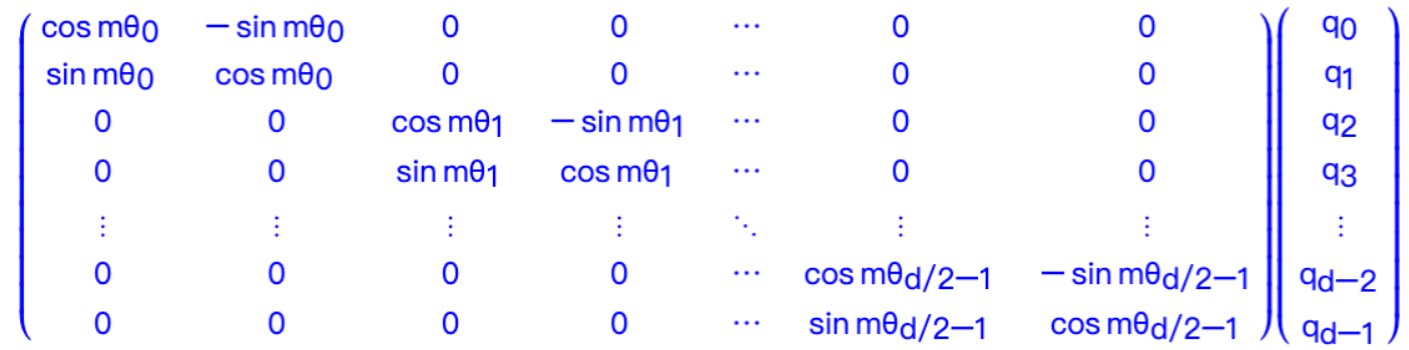
由于的稀疏性，所以直接用矩阵乘法来实现会很浪费算力，推荐通过下述方式来实现 RoPE：

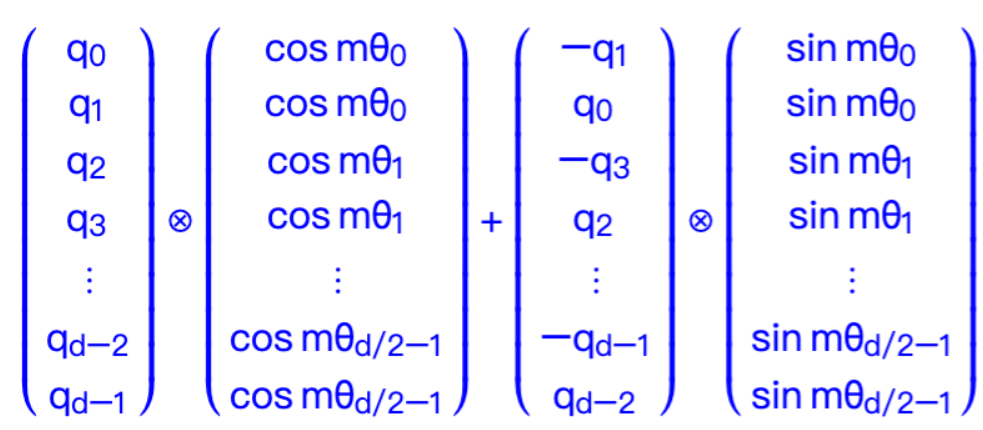
其中是逐位对应相乘，即计算框架中的运算。从这个实现也可以看到，RoPE 可以视为是乘性位置编码的变体。

import torch
import math

def rotary_position_embedding(q, k):
    """
    Rotary Position Embedding (RoPE) for queries and keys.
    
    Args:
        q: tensor for queries of shape (batch_size, num_heads, seq_len, dim)
        k: tensor for keys of shape (batch_size, num_heads, seq_len, dim)
        
    Returns:
        Rotated queries and keys
    """
    batch_size, num_heads, seq_len, dim = q.size()
    
    # Begin of sinusoidal_position_embedding content
    position = torch.arange(seq_len, dtype=torch.float).unsqueeze(-1).to(q.device)
    div_term = torch.exp(torch.arange(0, dim, 2, dtype=torch.float) * -(math.log(10000.0) / dim)).to(q.device)
    
    pos_emb = position * div_term
    pos_emb = torch.stack([torch.sin(pos_emb), torch.cos(pos_emb)], dim=-1).flatten(-2, -1)
    pos_emb = pos_emb.unsqueeze(0).unsqueeze(1)
    pos_emb = pos_emb.expand(batch_size, num_heads, -1, -1)
    # End of sinusoidal_position_embedding content

    # Extract and duplicate cosine and sine embeddings
    cos_emb = pos_emb[..., 1::2].repeat_interleave(2, dim=-1)
    sin_emb = pos_emb[..., ::2].repeat_interleave(2, dim=-1)

    # Create alternate versions of q and k
    q_alternate = torch.stack([-q[..., 1::2], q[..., ::2]], dim=-1).reshape(q.size())
    k_alternate = torch.stack([-k[..., 1::2], k[..., ::2]], dim=-1).reshape(k.size())

    # Rotate queries and keys
    q_rotated = q * cos_emb + q_alternate * sin_emb
    k_rotated = k * cos_emb + k_alternate * sin_emb

    return q_rotated, k_rotated

💡 类比：想象一个时钟指针

• 原始向量是时针的初始方向
• RoPE 根据位置  把时针旋转一个角度（长度不变）
• 两个“旋转后”的指针夹角（内积）反映它们的相对位置差

 

---

五、YaRN：弥补RoPE的缺陷

尽管 RoPE 具有良好的外推能力，但仍受限于周期性函数的震荡特性。

问题描述

由于旋转角度使用正弦/余弦函数计算，具有周期性：

• 每词旋转 30°，则位置 12（360°）与位置 0 的向量方向完全一致
• 模型无法区分位置 0 和位置 12 → 位置混淆

YaRN 的解决方案：VTK-by-parts 分段函数调整

YaRN 提出结合“by-parts”机制，动态调整周期性参数，提升外推性能。

核心概念

• 周期 \( T_i \)：参数 \( \theta_i \)  完成一个完整循环所需的时间或步数
• 圈数 \( r_i = \frac{L_{\text{train}}}{T_i} \)：训练阶段完成的周期数
• 阈值\( \tau \) ：判断是否“充分训练”的临界值

分三阶段处理（by-parts）

情况	条件	处理方式
充分训练	\( r_i \geq \tau \)	保留原周期，无需调整
未充分训练	\( r_i < 1 \)	将周期缩放为 \( T'_i = L_{\text{test}} / r_i \)，确保测试阶段至少完成一个完整周期
中间过渡	\( 1 \leq r_i < \tau \)	线性插值平滑过渡

✅ 优势：动态适应训练充分度，提升训练与测试阶段的一致性，尤其适用于长序列外推。

---

六、ALiBi：另一种相对位置编码视角

ALiBi（Attention with Linear Biases）提供了一种全新的位置编码思路：不显式编码位置，而是直接在注意力分数中加入基于相对距离的线性偏置。

三大核心组件

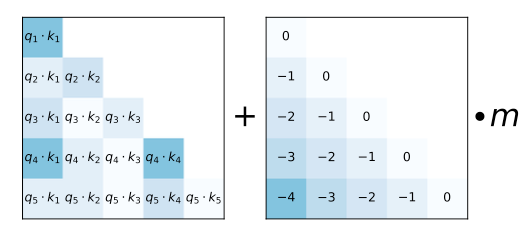
1. 注意力分数矩阵（左图）
   传统 $Q \cdot K$ 点积结果，反映语义相关性。

2. 偏置矩阵（右图）
   设计为线性衰减形式：$$B_{ij} = -m \cdot |i - j|$$ 

   例如：\( q_3 \) 与 \( k_1 \)距离为 2，则偏置为  \( -2m \)

   📉 设计哲学：距离越远，负偏置越大，抑制长程依赖，鼓励局部关注

3. 斜率项 m

• 与“注意力头数”相关
• 多头时， 序列呈几何级数下降（如 \(m_h = 2^{-8h/H}\) ）
• 实现多尺度位置感知

最终注意力计算

\(\text{Attention}(Q, K, V) = \text{Softmax} \left( Q K^\top + B \right) V\)

其中 \(B_{ij} = -m \cdot |i - j|\)

优势

• ✅ 天然支持任意长度序列
• ✅ 不依赖绝对位置，无外推限制
• ✅ 计算高效，无需额外位置嵌入

代码实现

import math
import torch
from torch import nn

def get_slopes(n_heads: int):
    
    n = 2 ** math.floor(math.log2(n_heads))
    m_0 = 2.0 ** (-8.0 / n)
    m = torch.pow(m_0, torch.arange(1, 1 + n))

    if n < n_heads:
        m_hat_0 = 2.0 ** (-4.0 / n)
        m_hat = torch.pow(m_hat_0, torch.arange(1, 1 + 2 * (n_heads - n), 2))
        m = torch.cat([m, m_hat])
        
    return m


@torch.no_grad()
def get_alibi_biases(n_heads: int, mask: torch.Tensor):

    m = get_slopes(n_heads).to(mask.device)
    seq_len = mask.size(0)
    distance = torch.tril(torch.arange(0, -seq_len, -1).view(-1, 1).expand(seq_len, seq_len))
    print(distance)

    return distance[:, :, None] * m[None, None, :]

seq_len = 10
n_heads = 8

m = get_slopes(n_heads)
print(m)

alibi_biases = torch.zeros(seq_len,seq_len)
for j in range(1,seq_len):
    for i in range(j, seq_len):
        alibi_biases[i, i - j] = -j
print(alibi_biases)

print(alibi_biases[:, :, None].shape, m[None, None, :].shape)

alibi_biases[:, :, None] * m[None, None, :]

 

🆚 对比 RoPE：
RoPE 外推能力较强（约可外推200 token），但仍受周期性限制；
ALiBi 更简单、更稳定，适合超长文本建模。

---

🔚 总结：

现代大语言模型普遍采用相对位置编码（如 RoPE、ALiBi）来克服绝对位置编码的外推瓶颈。其中：

• RoPE 通过旋转向量建模相对位置，表达能力强；
• YaRN 改进 RoPE 的周期性缺陷，提升外推精度；
• ALiBi 以线性偏置方式建模距离，简洁高效，适合超长序列。

这些技术共同推动了大模型在长文本理解、代码生成等任务中的突破。 

转自：https://mp.weixin.qq.com/s/hF1MmdOpxPae0wVTSbFr4A