卷积的原理

一、点乘

　　卷积的底层逻辑就是点乘，点对点的相乘之后再相加

 

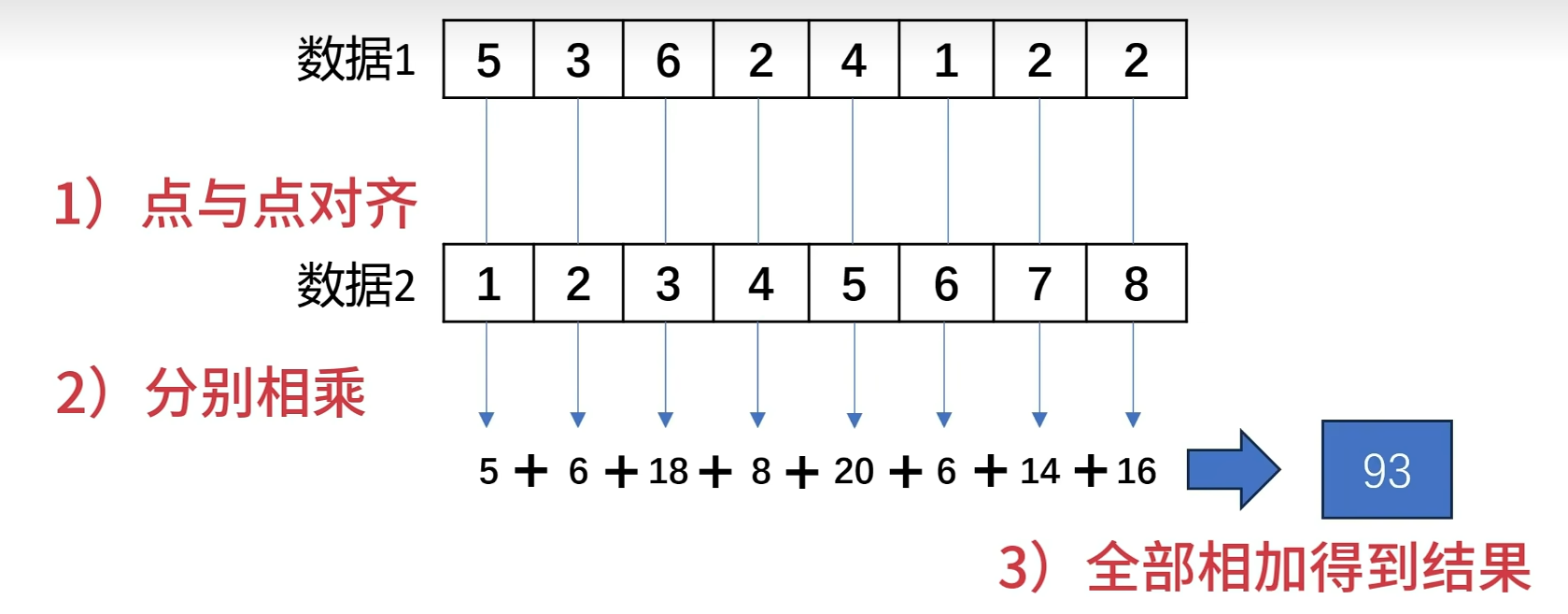
二、点乘的功效

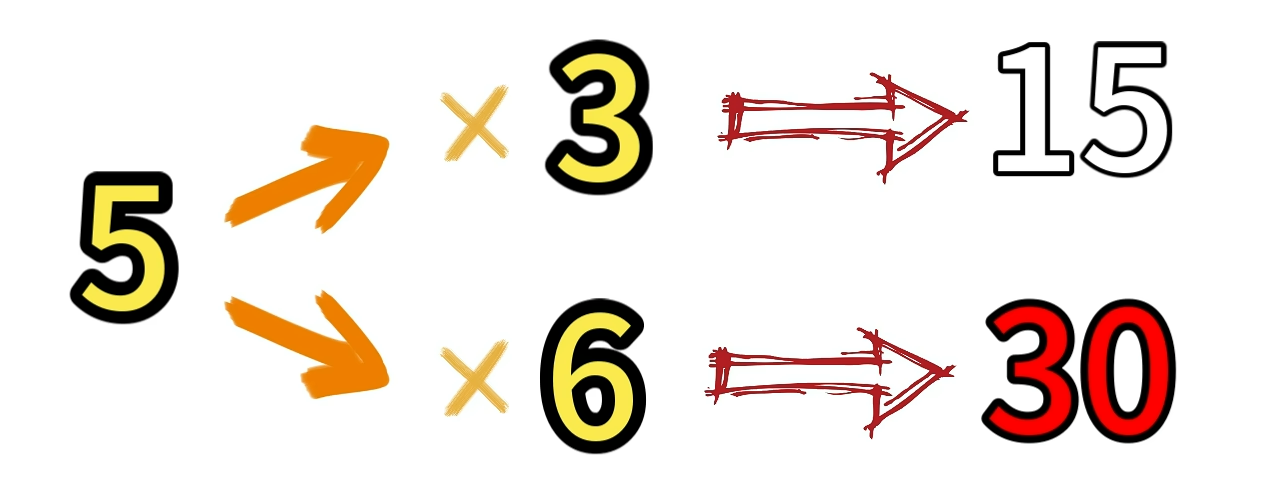
　　1.衡量相似程度和影响程度，例如：5 * 3 = 15,  5 * 6 =30 所以 6对5的影响更大一些。

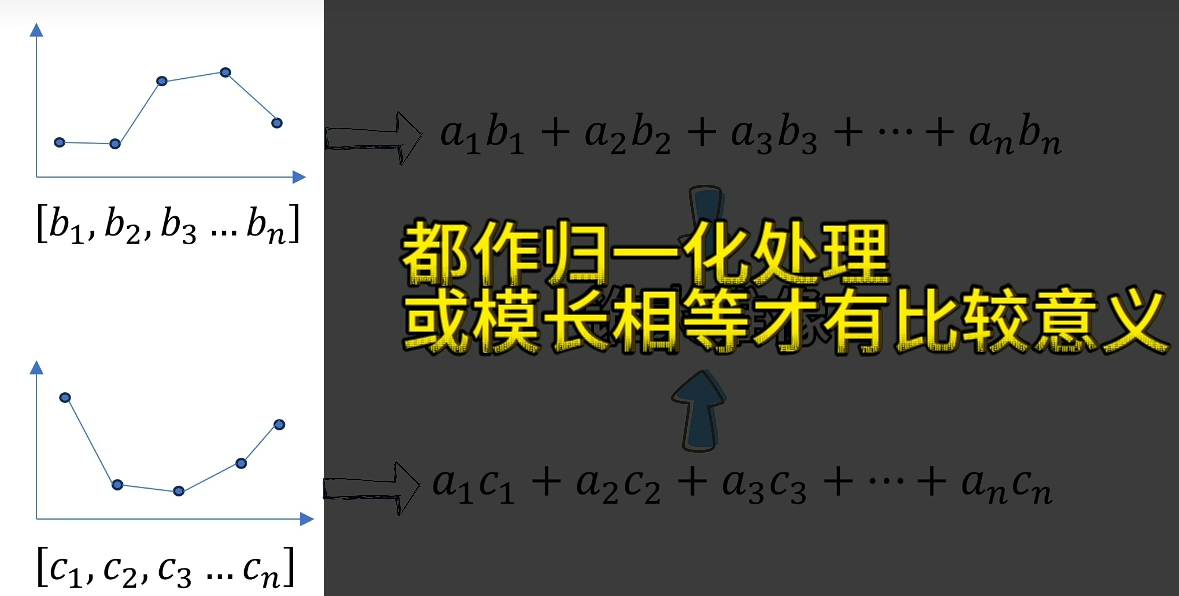
如果相比较数组A与 数组B、数组C哪个更相似

A序列	B序列	C序列

先做归一化处理或模长相等才有比较意义

 

 举一个简单的例子：

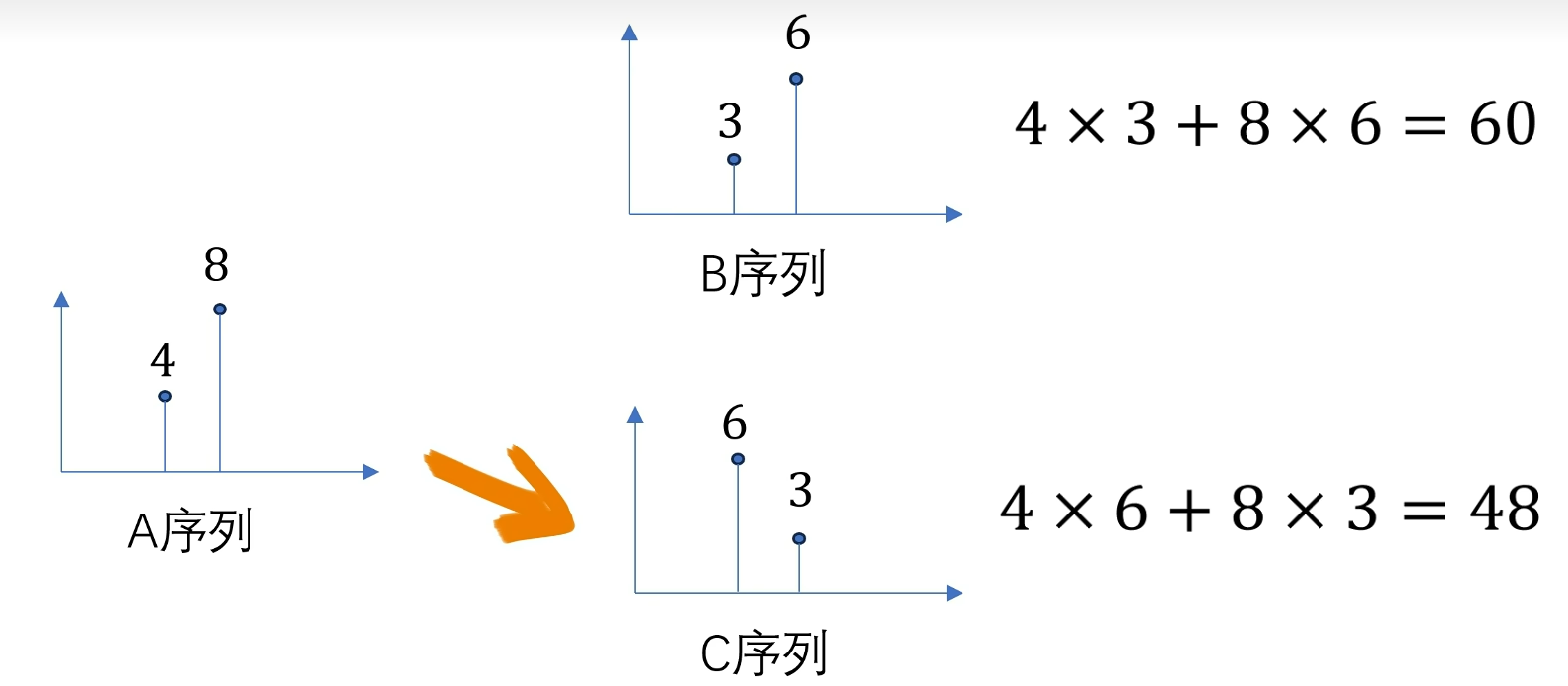
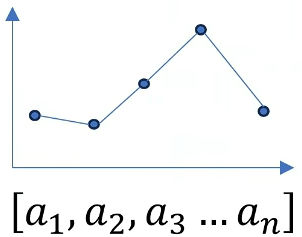
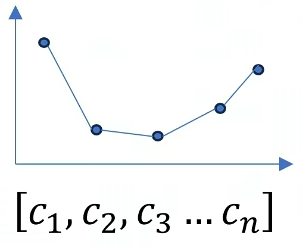
再举一个复杂一点的例子：定义一个A序列  然后把B序列打乱顺序后得到C序列（这样可以保证B，C序列模长一致），通过观察 图形 可以得到B序列和A序列更像。

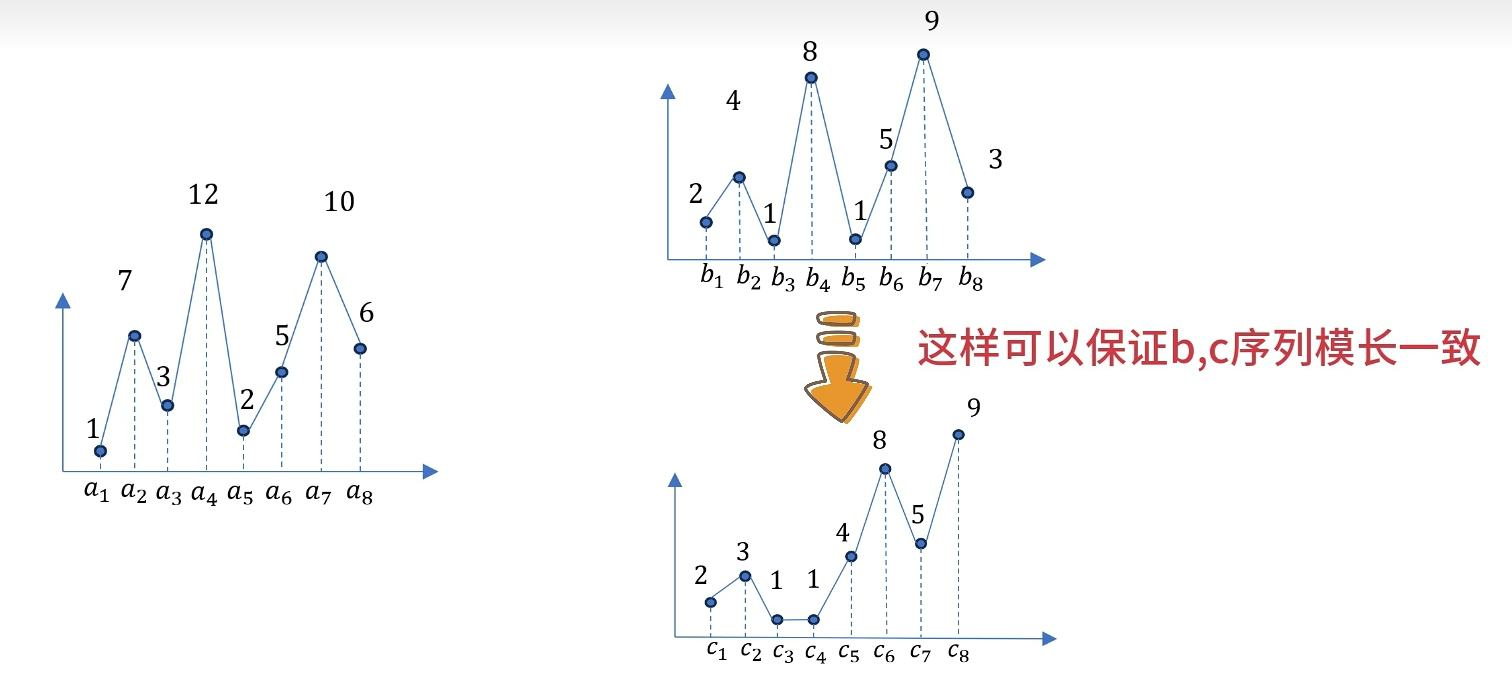
计算AB的点乘是264，AC的点乘是190，越相似点乘的结果也就越大。

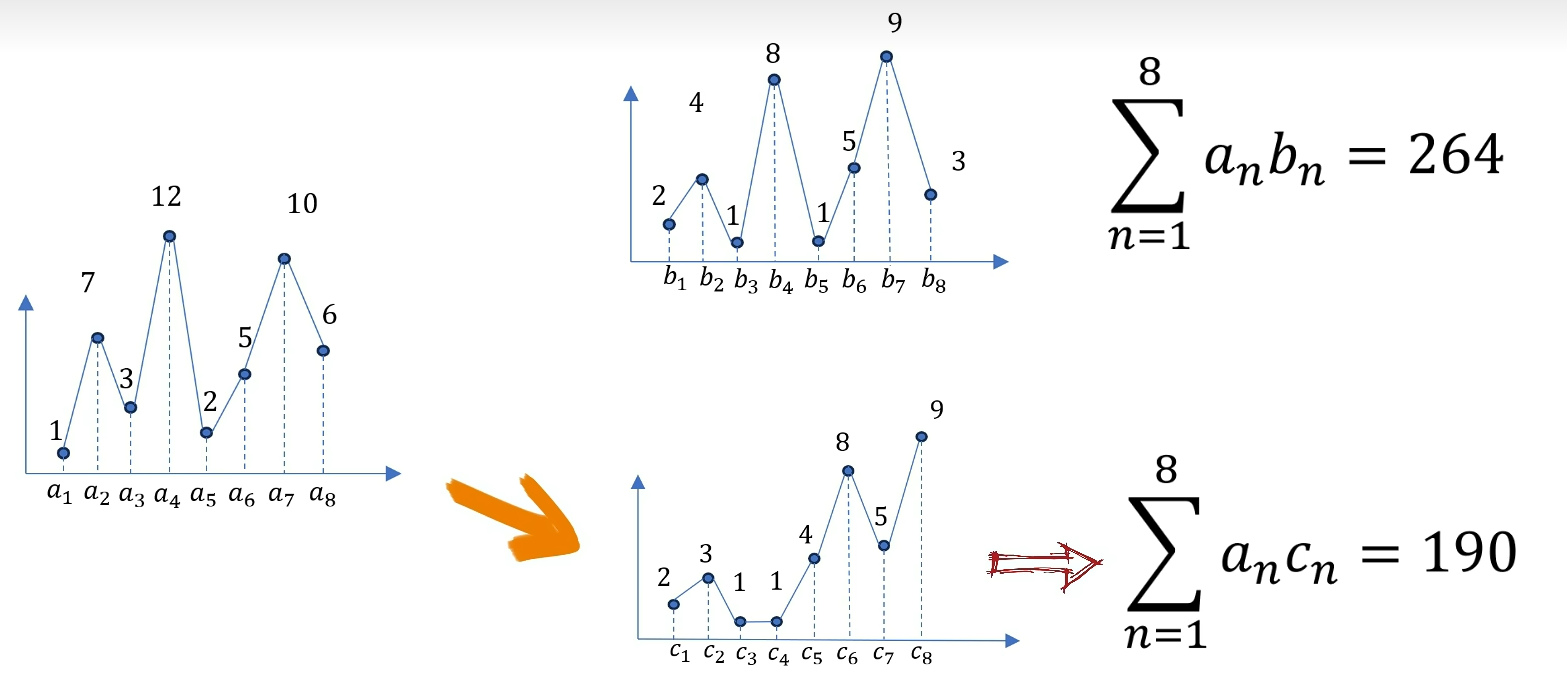
假如你用各个不同频率的正余弦信号与原信号进行点乘

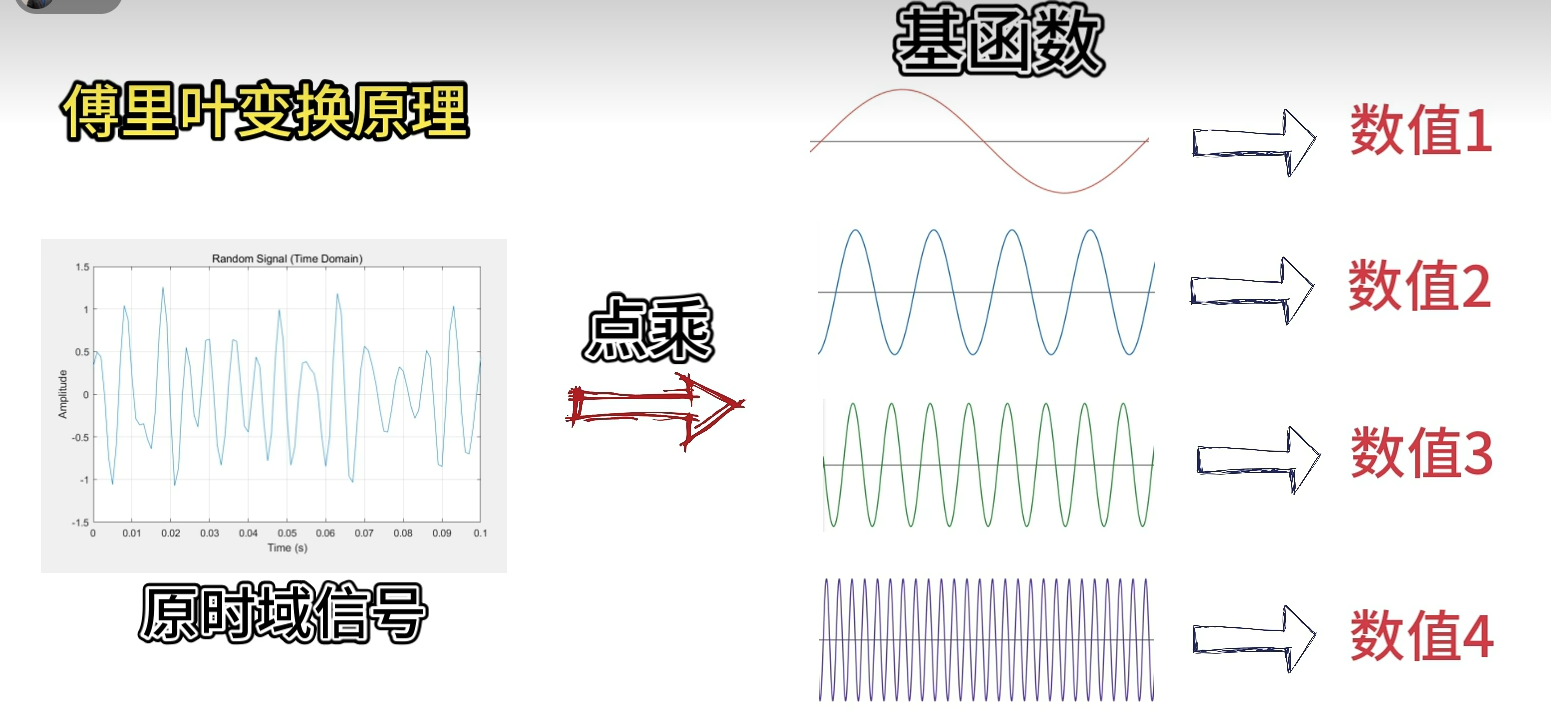
 发现100到200Hz的正余弦信号，点乘出来的数值比较大，那就证明了原信号的能量是集中在100到200Hz这个波段的，而且这些点乘的绝对值是可以直接反映该频率成分在原信号的占比。在加上正余弦函数的正交性，甚至你还能根据这个占比重构出原信号来。

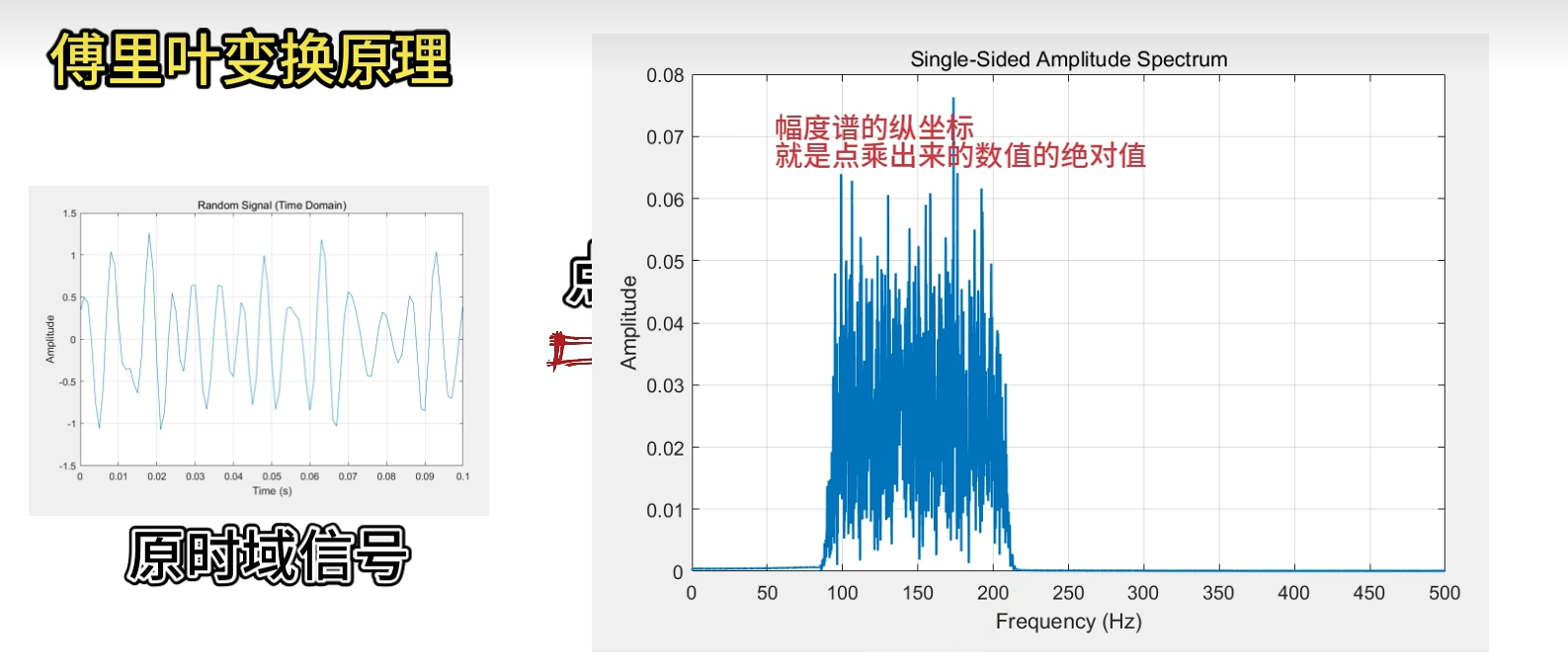
 2.点乘的第二个作用：滤波

滤波，顾名思义就是对一个信号的波形进行过滤。

 

 

 

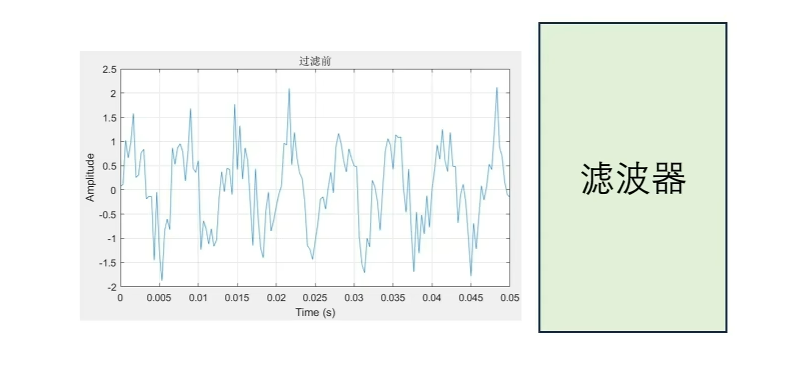
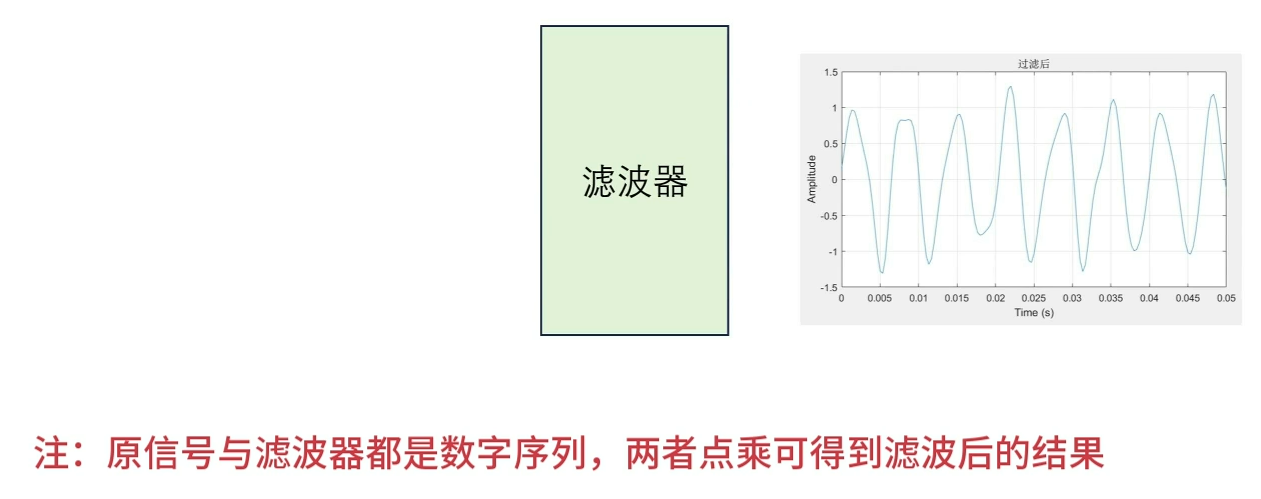
 两个序列点乘不剩一个数了吗？这还怎么形成波形呢？关键就是得动起来。一般来讲，你要滤波，其中一个序列就得短一些

 

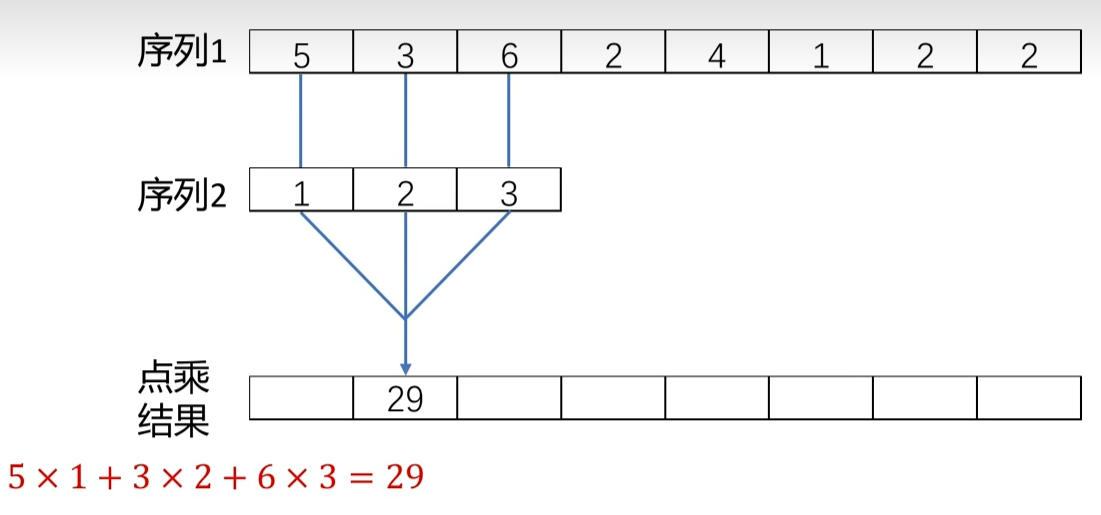
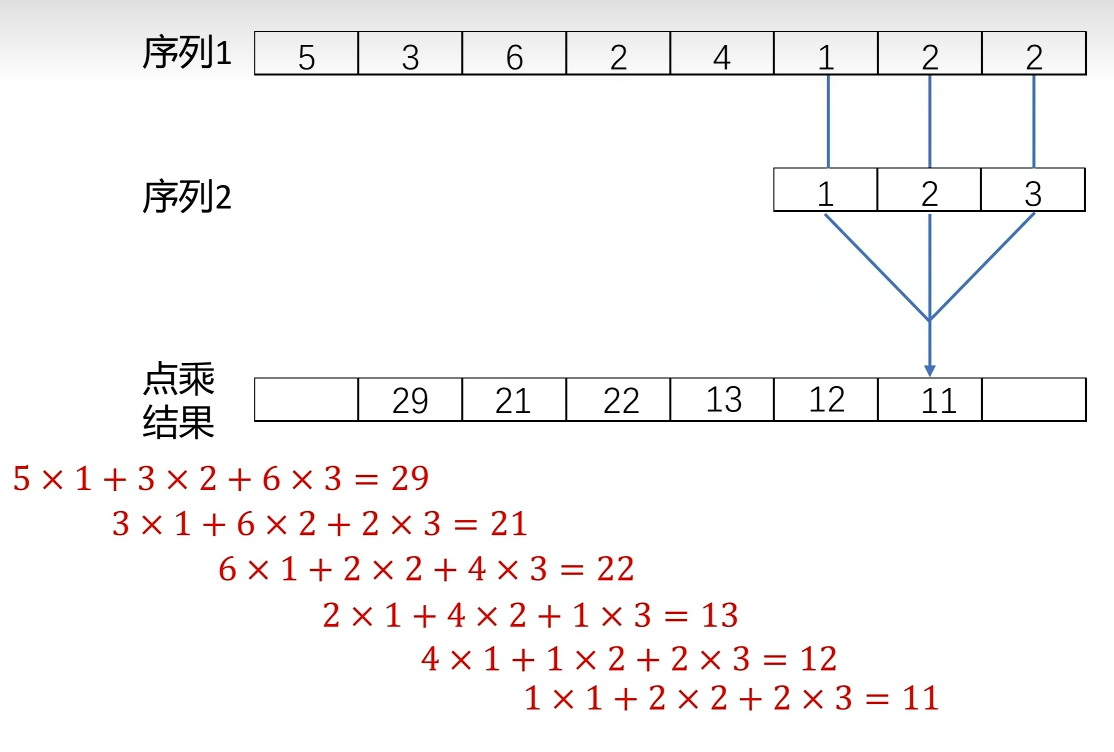
3. 点乘的第三个作用 加权求和。

　　加权是可以有选择性的加的，就看你想把那部分抑制、哪部分增强而已。而滤波的结果就是原信号分段加权求和之后的拼接结果。当然你用前面的相似度的理论去理解也是可以的，因为这些短序列本身也是有频率和相位的，所以你有不同的需求，就得用不同的权重。

这种不同的权重，也可以称为滤波器或者卷积核。

在图像处理中，图像可以化为数字矩阵，分别对图像不同区域的数字做加权求和，再拼接起来就可以得到过滤后的图像了。

以上的种种行为就一个数学本质就是，点乘。只不过放到不同领域、不同的应用，手法也就稍微有点不同，也就有了不同的称谓而已。例如：傅里叶变换，拉普拉斯变换、小波变换等等。

 

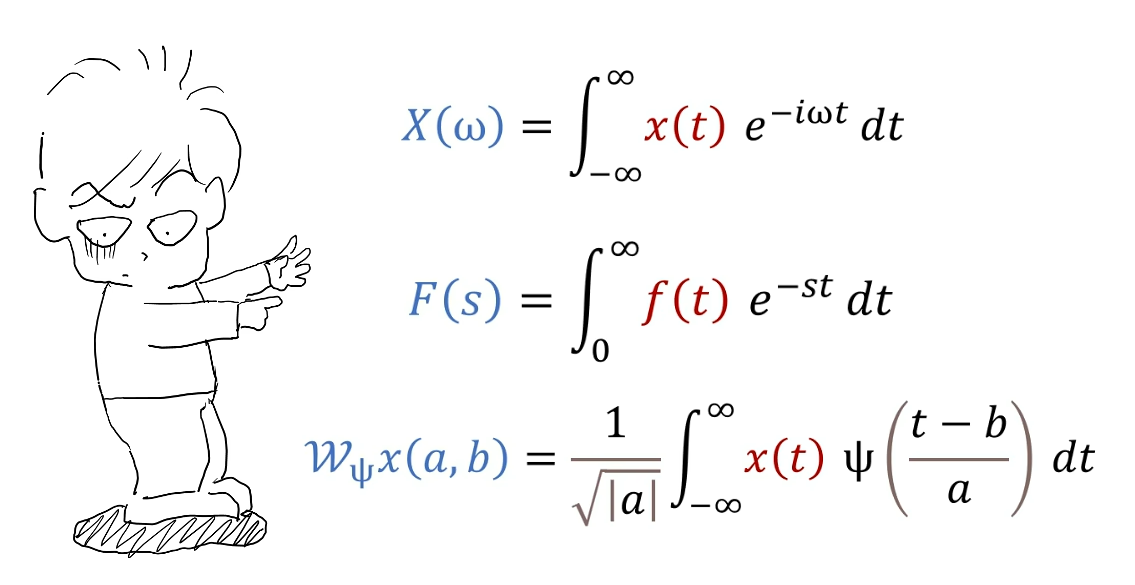
也包括今天的主题卷积，它的底层本质就是滑动点乘。也就是前面所说的滤波。

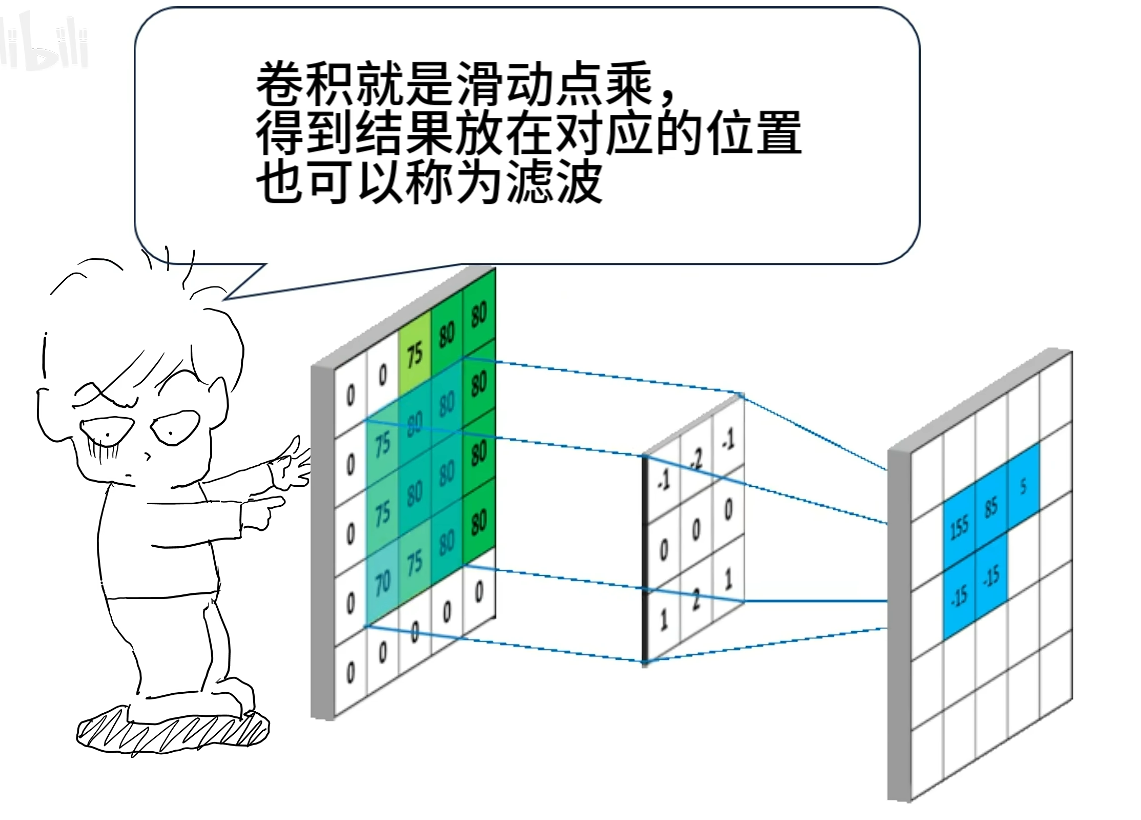
 它跟普通的滤波有什么区别呢？谜底就在米面上， 区别在于“卷”！不卷的那个叫互相关。

 

 举个栗子： 

原信号：X[n] = [1, 2, 3, 4] 

卷积核：H[n]=[1, 2, 3]

现在要对X[n]进行卷积，那么你就得把卷积核给卷过来。变成[3, 2, 1], 然后再去滑动点乘。

 

 

 

 

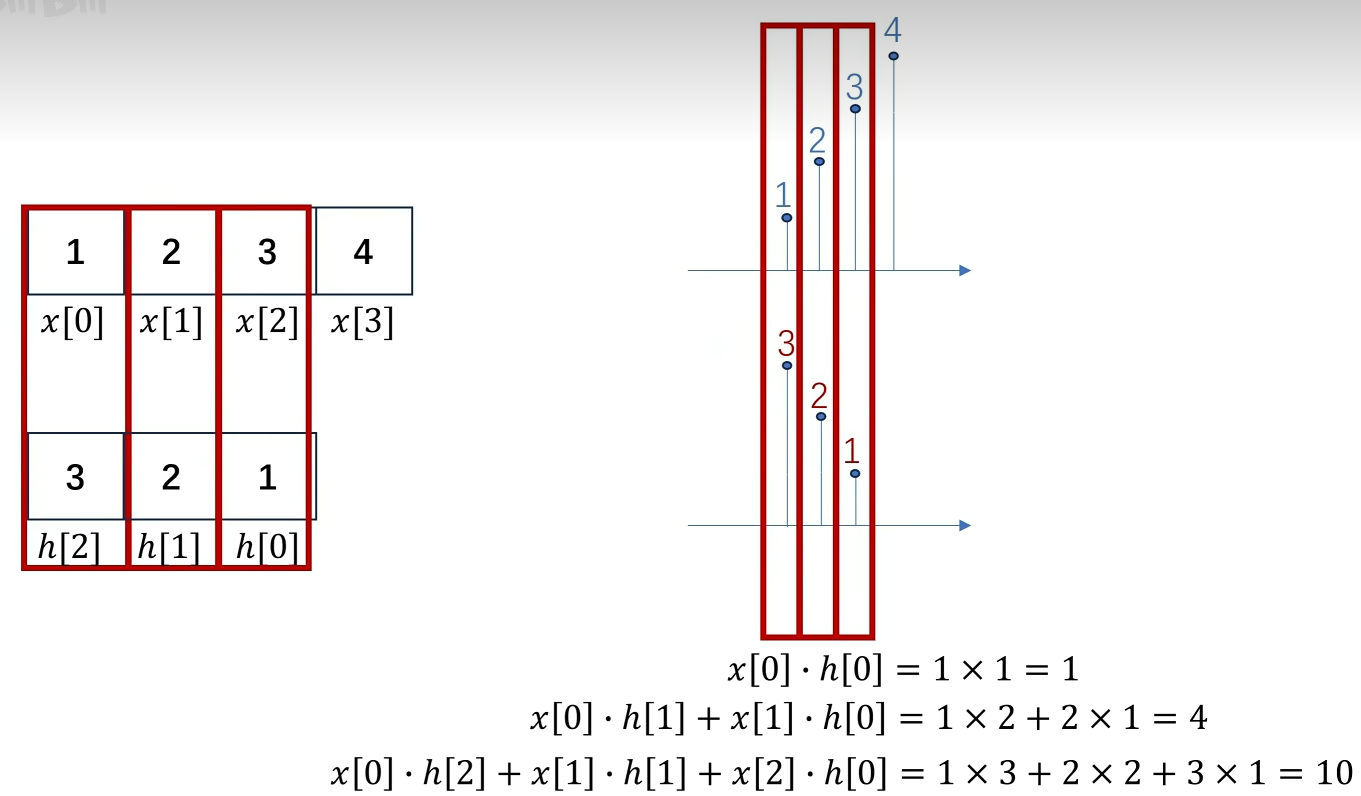
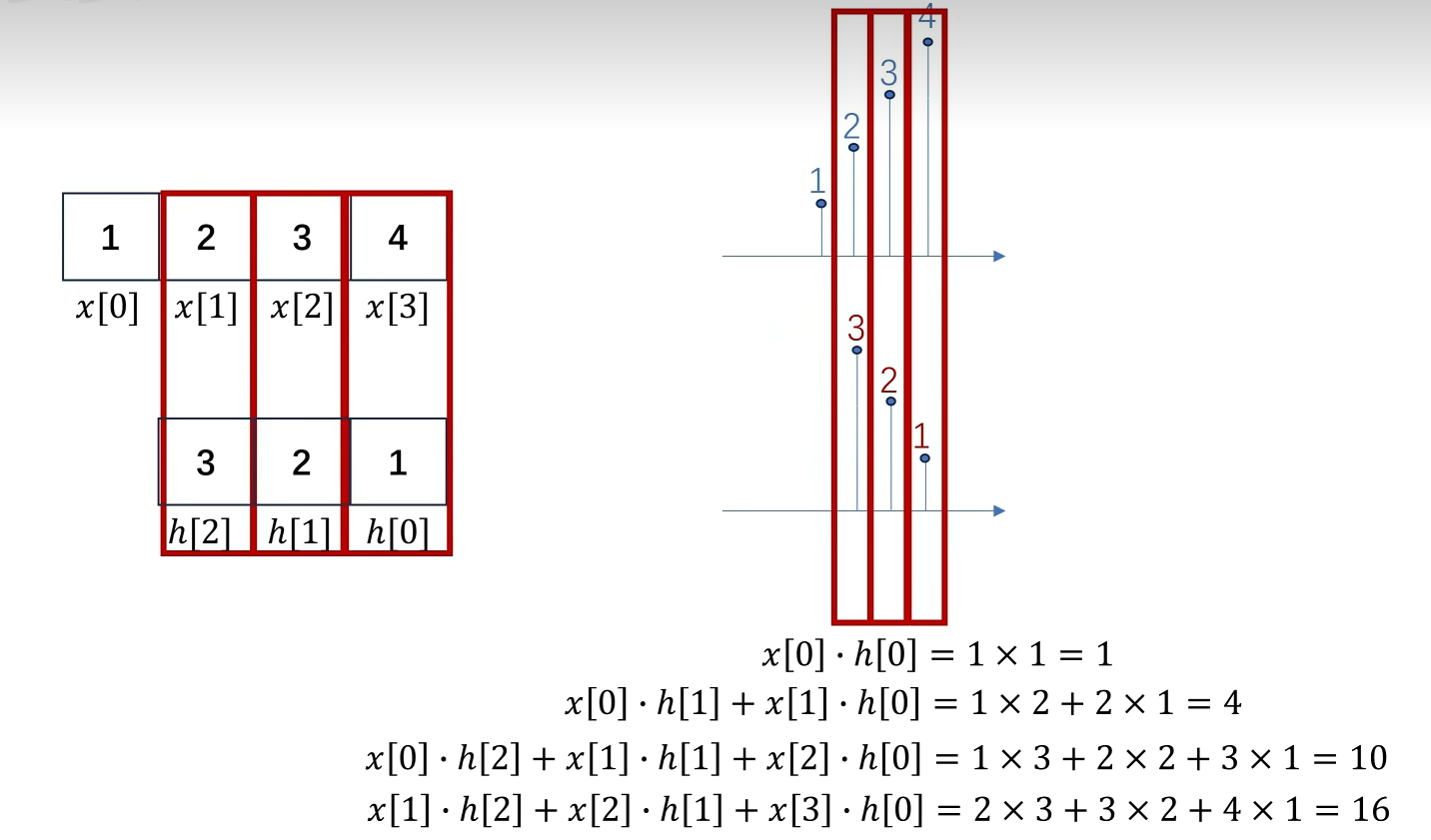
 但是为什么要卷那么一下呢？

首先你这个卷积核，也是有时间依赖的，从时间采样上来讲，先采的1，再采的2，最后是3。

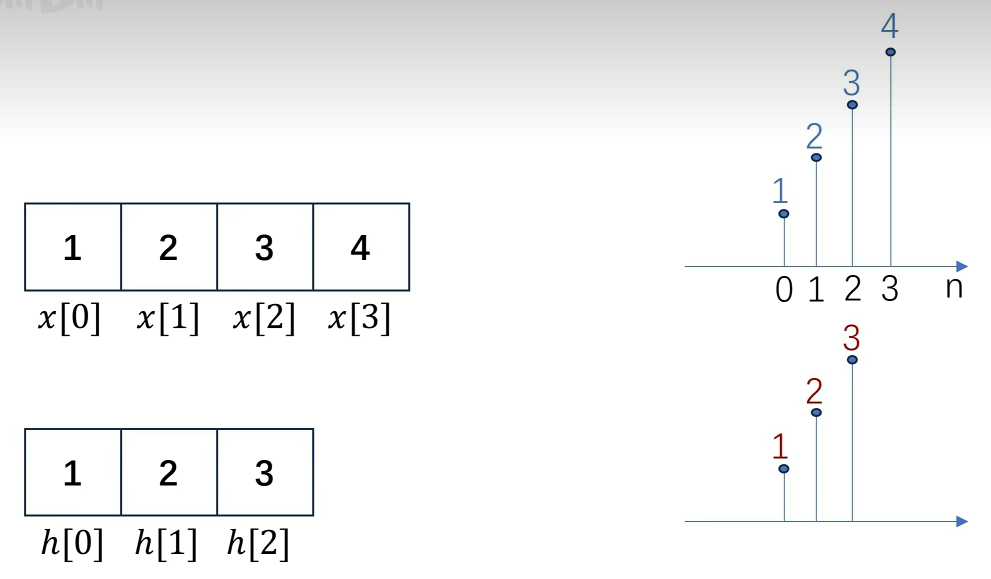
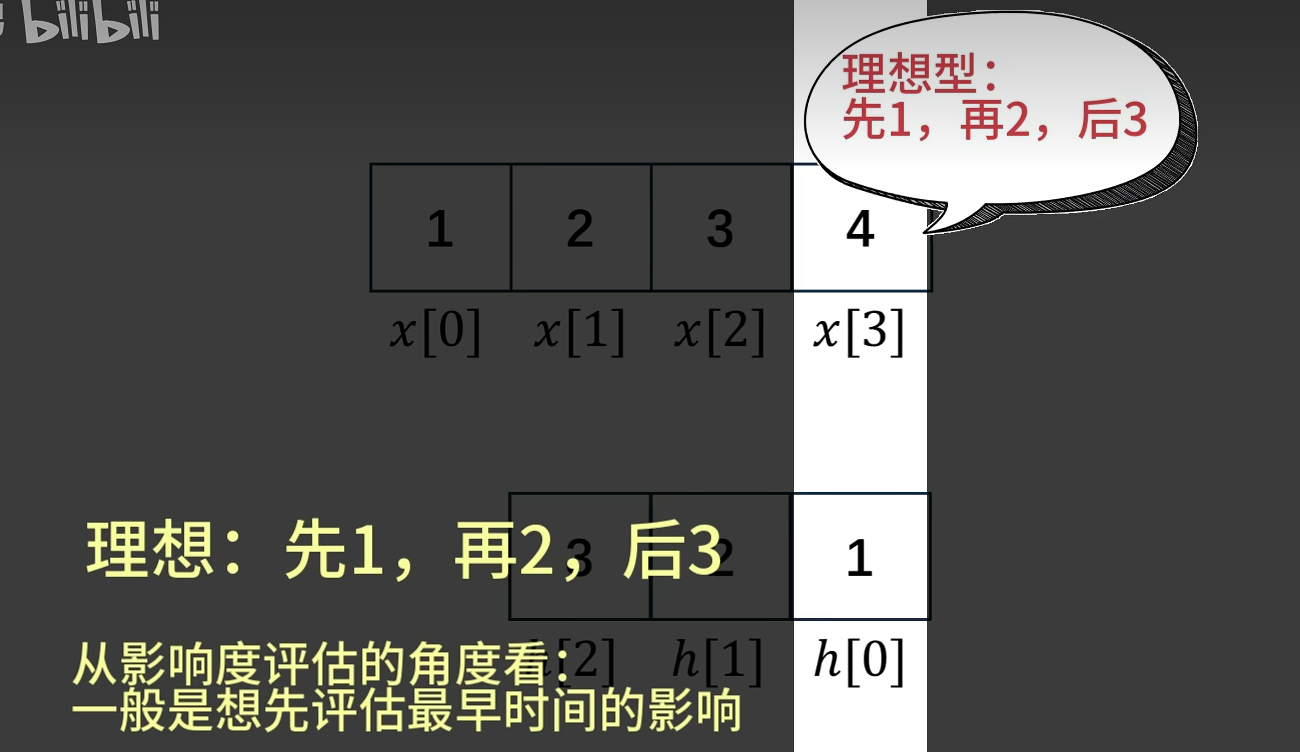
 我们切换到原信号中某个位置信号点的视角来看一下，例如x[3] =4这个点，对于它来说，反正卷积核里面的数字都得过来跟它乘一乘的，

 从时间的先后关系来看，它肯定是想先和1乘，再到2，最后到3，这样子才有了一个时间上的先后对应，为了实现这种对应，那你是不是就得要把它先卷一下呢？

有的同学会这样子想，万一滤波器太长而步子太短，那原序列有些店不就被重复计算了吗？

像刚刚的例子：滤波器长度是3，前进的步长是1，以结果中这三个位置y[1], y[2], y[3]的数值来说明，原信号的这个点x[1]都参与了计算,本来原信号这些相邻的数据点就不是孤立的，它被重复计算，就相当于把它对相邻点的影响或关联也考虑进去了。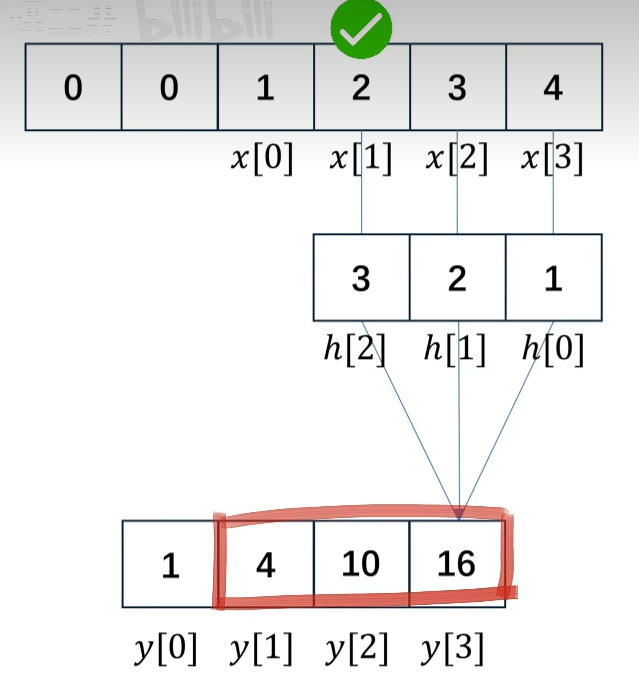

就好比图像处理，如果你要做模糊或者是锐化滤波，你要不要考虑相邻点的影响，那肯定是要的。又好比声波，它也是有从弱到强的过渡的，所以你把相邻点的影响或关联考虑进去就对了。

 离散卷积公式

 

 一般卷积的输出长度 要比 原序列输入的长度要长，因为等于 输出的长度 = 原函数的长度 + 卷积核的长度  - 1

卷那一下 会在数学上带来哪些好处呢？

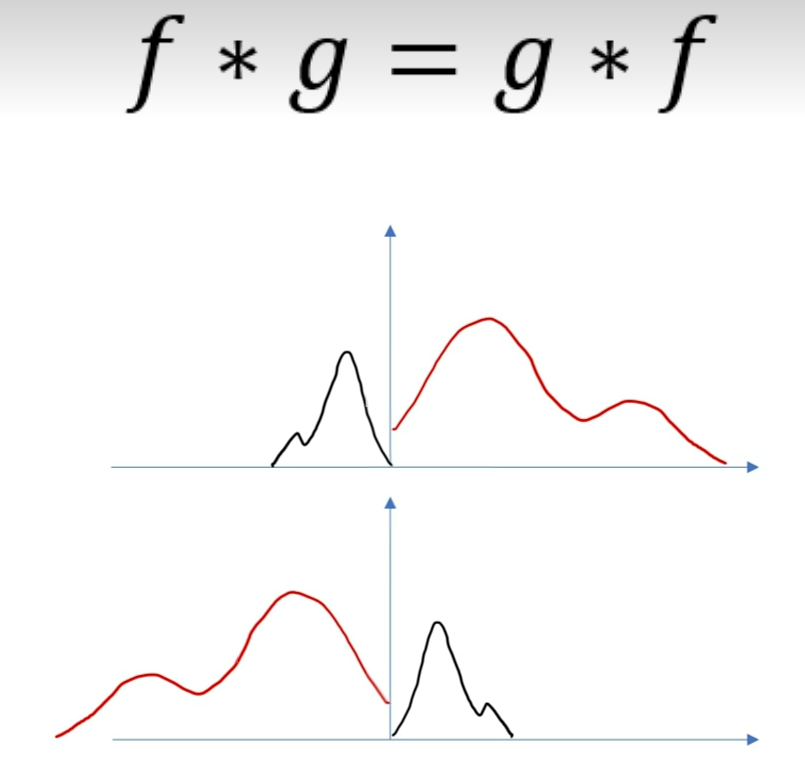
1.满足交换率 f * g = g * f

因为有了翻转这个动作，滑动点乘实际上就是两个函数的背对背的相对运动。无论是f卷g还是g卷f，结果都是一样。

 2.卷积定理  

如果我要求新的时域函数y(t)的频率情况 需要对 y(t) 求傅里叶变换，如果我知道了f(t)和g(t)的频域函数F(w)  G(w)，就不用去求y(t)的傅里叶变换了，直接使用Y(w) =F(w) * G(w)

 是不是非卷不可呢？

也不一定。因为卷那一下是从纯数学语境继承下来的，有些应用你卷与不卷区别不大，例如：卷积神经网络的应用，你卷不卷，最后都会通过自我学习区修正的。

视频笔记：https://www.bilibili.com/video/BV16yjdzmE3W