大模型高效微调-LoRA原理详解和训练过程深入分析

一、LoRA原理

转自：https://zhuanlan.zhihu.com/p/702629428

LoRA(Low-Rank Adaptation of LLMs)，即LLMs的低秩适应，是参数高效微调最常用的方法。

LoRA的本质就是用更少的训练参数来近似LLM全参数微调所得的增量参数，从而达到使用更少显存占用的高效微调。

Ps: 参与训练的参数都变少很多，优化器状态和梯度自然大大减少，从而节约了很多显存。这是自然而然的道理了，也是PEFT的核心思路

1.1 问题定义

LoRA与训练目标是解耦的，但本文设定就是语言模型建模。

以下将给出语言建模（可自然推广到序列建模）的基本符号定义，即最大化给定提示的条件概率（极大似然估计）。

The maximization of conditional probabilities given a task-specific prompt

给定一个参数为𝛷预训练的自回归语言模型 𝑃Φ(𝑦|𝑥) 。

𝑥为输入，𝑦为输出

note: 为与原文符号一致，下文𝛷、𝛩、𝑊均表示模型参数

全参数微调

每次full fine-tuning训练，学一个 Δ𝛷 ，， |Δ𝛷| 参数量大hold不住

语言模型的条件概率分布建模目标

高效微调

Δ𝛷 是特定于下游任务的增量参数

LoRA将 Δ𝛷=Δ𝛷(Θ) ，用参数量更少的 𝛩 来编码（低秩降维表示来近似）, |𝛷|<<|𝛩|

LoRA训练目标

Transformer架构参数

  • Transformer层的输入和输出维度大小 𝑑𝑚𝑜𝑑𝑒𝑙
  • 𝑊𝑞、𝑊𝑘、𝑊𝑣,和𝑊𝑜分别代表自注意力的query、key、value和output投影矩阵
  • 𝑊或𝑊0代表预训练的权重矩阵
  • ∆𝑊是微调后得到的增量参数矩阵（训练后，优化算法在参数上的累计更新量）
  • 𝑟代表LoRA的低秩适应参数的秩

1.2 LoRA简介

LoRA的核心思想是，在冻结预训练模型权重后，将可训练的低秩分解矩阵注入到的Transformer架构的每一层中，从而大大减少了在下游任务上的可训练参数量。

LoRA结构
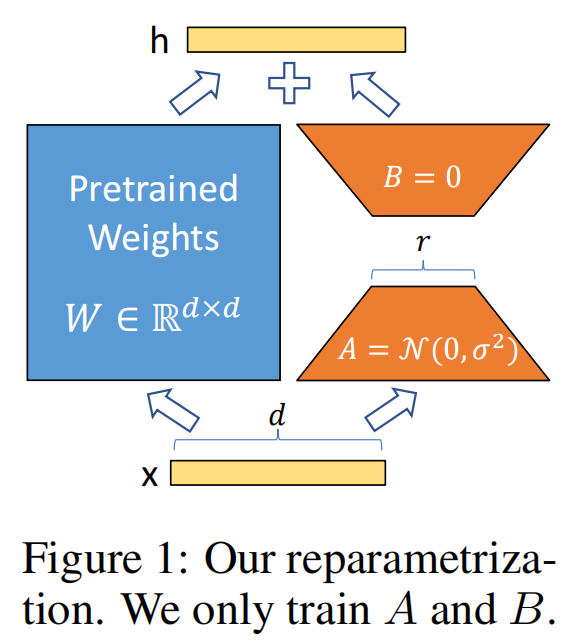
We propose Low-Rank Adaptation(LoRA), which freezes the pre trained model weights and injects trainable rank decomposition matrices into each layer of the Transformer architecture, greatly reducing the number of trainable parameters for downstream tasks.

在推理时，对于使用LoRA的模型来说，可直接将原预训练模型权重与训练好的LoRA权重合并，因此在推理时不存在额外开销。

1.3 为什么要LoRA

背景

通常，冻结预训练模型权重，再额外插入可训练的权重是常规做法，例如Adapter。可训练的权重学习的就是微调数据的知识。

推理性能比较

但它们的问题在于，不仅额外增加了参数，而且还改变了模型结构。因为它们往往把新的参数，插到模型内部。

这会导致模型训练、推理的计算成本和内存占用急剧增加，尤其在模型参数需在多GPU上分布式推理时（这越来越常见）。

动机

深度网络由大量Dense层构成，这些参数矩阵通常是满秩的。

相关工作表明，When adapting to a specific task, 训练学到的过度参数化的模型实际上存在于一个较低的内在维度上（高维数据实际是在低维子空间中）

We take inspiration from Li et al. (2018a); Aghajanyan et al. (2020) which show that the learned over-parametrized models in fact reside on a low intrinsic dimension.
低秩矩阵

LoRA就假设LLM在下游任务上微调得到的增量参数矩阵Δ𝑊是低秩的（肯定不是满秩），即存在冗余参数或高度相关的参数矩阵，但实际有效参数是更低维度的。

We hypothesize that the change in weights during model adaptation also has a low “intrinsic rank”, leading to our proposed Low-Rank Adaptation (LoRA) approach.

LoRA遂设想，对全参数微调的增量参数矩阵Δ𝑊进行低秩分解近似表示（即对参数做降维）。

PCA降维示意图，源于https://lightning.ai/pages/community/tutorial/lora-llm/

这样训练Δ𝑊的低秩分解近似参数矩阵，效果上相比其他PEFT方法不会打什么折扣，而且还能在推理时不增加额外开销。

LoRA allows us to train some dense layers in a neural network indirectly by optimizing rank decomposition matrices of the dense layers’change during adaptation instead, while keeping the pre-trained weights frozen

LoRA的大体思路就是这样，具体的矩阵分解也是靠微调过程学习的。

接下来，介绍LoRA的具体方案。

1.4 LoRA实现

LoRA就是低秩矩阵适应，在冻结原有LLM参数时，用参数量更小的矩阵进行低秩近似训练。

对于预训练权重矩阵𝑊0∈𝑅𝑑×𝑑，LoRa限制了其更新方式，即将全参微调的增量参数矩阵Δ𝑊表示为两个参数量更小的矩阵 𝐵 和 𝐴 的低秩近似：

𝑊0+Δ𝑊=𝑊0+𝐵𝐴

其中，𝐵∈𝑅𝑑×𝑟和𝐴∈𝑅𝑟×𝑑为LoRA低秩适应的权重矩阵，秩𝑟远小于𝑑。

此时，微调的参数量从原来Δ𝑊的𝑑∗𝑑，变成了𝐵 和 𝐴的2∗𝑟∗𝑑。可知，2∗𝑟∗𝑑<𝑑∗𝑑（有2𝑟<𝑑）

全参微调 v.s. LoRA微调

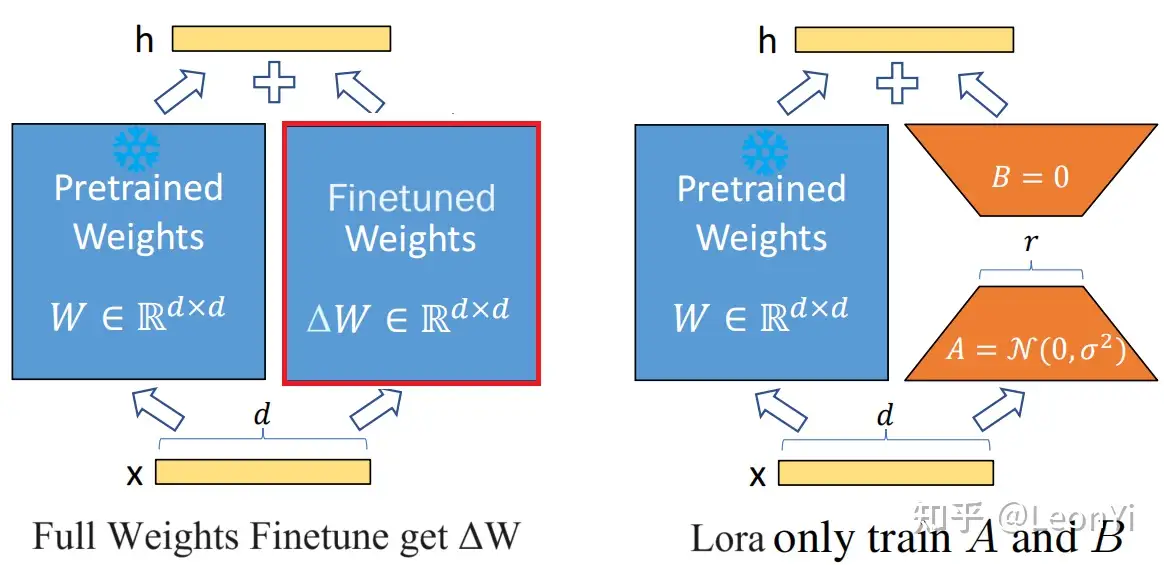
给定输入𝑥∈𝑅𝑑，添加LoRA后的输出ℎ∈𝑅𝑑：

ℎ=(𝑊0+Δ𝑊)𝑥=𝑊0𝑥+𝐵𝐴𝑥

这里，将Δℎ=𝐵𝐴𝑥，便于后续求导计算。

在训练时，原始参数𝑊0被冻结，意味着𝑊0虽然会参与前向传播和反向传播，但是不会计算其对应梯度∂𝐿∂𝑊0，更不会更新其参数。

在推理时，直接按上面的式子将𝐵𝐴合并到𝑊0中，因此相比原始LLM不存在推理延时。

1.5 LoRA参数初始化

在开始训练时：

矩阵 𝐵 为全零初始化，𝑏𝑖=0

矩阵 𝐴 通过高斯函数初始化，𝑎𝑖∼𝑁(0,𝜎𝑎2)

这使得训练开始前，LoRA的旁路𝐵𝐴=0，那么微调就能从预训练权重𝑊0开始。

这样就能和全参数微调时一样，能有相同的开始。

这个策略要求，至少𝐵 和 𝐴中有一个被初始化为全0项。

但如果，全被初始化为0，𝐵 和 𝐴就训不动了。因为，𝐵 和 𝐴全0时，处于鞍点，两个权重的梯度也全为0

𝐵 的梯度 ∂𝐿∂𝐵依赖𝐴，𝐴 的梯度∂𝐿∂𝐴依赖𝐵，如果仅一项为0训练是可以启动的。

为什么，因为按当前的设定， 𝐵的梯度 ∂𝐿∂𝐵依赖于非0矩阵𝐴，使得其第一步训练的梯度值实际不是0，自然更新后𝐵不在是0矩阵了。具体推导如下：

假设在训练第一步，𝐵=0使得𝐴 的梯度项 ∂𝐿∂𝐴=∂𝐿∂ℎ∂ℎ∂Δℎ∂Δℎ∂𝐴=𝐵𝑇∂𝐿∂ℎ𝑥𝑇 为0矩阵，但𝐴 是高斯初始化，使得𝐵 的梯度项∂𝐿∂𝐵=∂𝐿∂ℎ∂ℎ∂Δℎ∂Δℎ∂𝐵=∂𝐿∂ℎ(𝐴𝑥)𝑇 不为0。

那么假设经过一次SGD的optimizer.step()更新后。𝐴 没任何变化，但是由于非0的 ∂𝐿∂𝐵反而使得初始为全0的矩阵𝐵变成了非0矩阵𝜂∂𝐿∂𝐵=𝜂∂𝐿∂ℎ(𝐴𝑥)𝑇(令 𝜂 为SGD的学习率)。

参数第一步更新后，之后的训练就不存在阻碍了。

可以看到这确实是一个反直觉的结果。而且怎么初始化其实还有其他变体（本文就不详细阐述了，具体可看LoRA-GA）

1.6 LoRA参数合并系数

实际实现时，Δ𝑊=𝐵𝐴会乘以系数𝛼𝑟与原始预训练权重合并𝑊0，𝛼是一个超参：

ℎ=(𝑊0+𝛼𝑟Δ𝑊)𝑥

直观来看，系数𝛼𝑟决定了在下游任务上微调得到的LoRA低秩适应的权重矩阵𝐵𝐴占最终模型参数的比例。

给定一个或多个下游任务数据，进行LoRA微调：

  • 系数𝛼𝑟越大，LoRA微调权重的影响就越大，在下游任务上越容易过拟合
  • 系数𝛼𝑟越小，LoRA微调权重的影响就越小（微调的效果不明显，原始模型参数受到的影响也较少）

一般来说，在给定任务上LoRA微调，让𝛼为𝑟的2倍数。（太大学过头了，太小学不动。）

根据经验，LoRA训练大概很难注入新的知识，更多是修改LLM的指令尊随的能力，例如输出风格和格式。原始的LLM能力，是在预训练是获得的（取决于参数量、数据规模X数据质量）。

LoRA的秩𝑟决定，LoRA的低秩近似矩阵的拟合能力，实际任务需要调参挑选合适的秩𝑟维度。系数𝛼𝑟中𝛼决定新老权重的占比。

1.7 LoRA的秩如何选择

和推荐系统中的评分矩阵分解、文本的非负矩阵分解，以及奇异值分解一样。LoRA的低秩分解近似矩阵𝐵 和 𝐴的秩𝑟的大小，决定了其拟合能力。

理想的情况是找到一个秩𝑟，使得LoRA的低秩近似结构𝐵𝐴能具备全参数微调的增量矩阵Δ𝑊 的表达能力，能越接近越好。

秩𝑟成为了LoRA的超参数，随着秩𝑟维度的不断增加，参与训练的参数量也随之增加，LoRA的低秩适应能力将逐渐提高甚至过拟合。

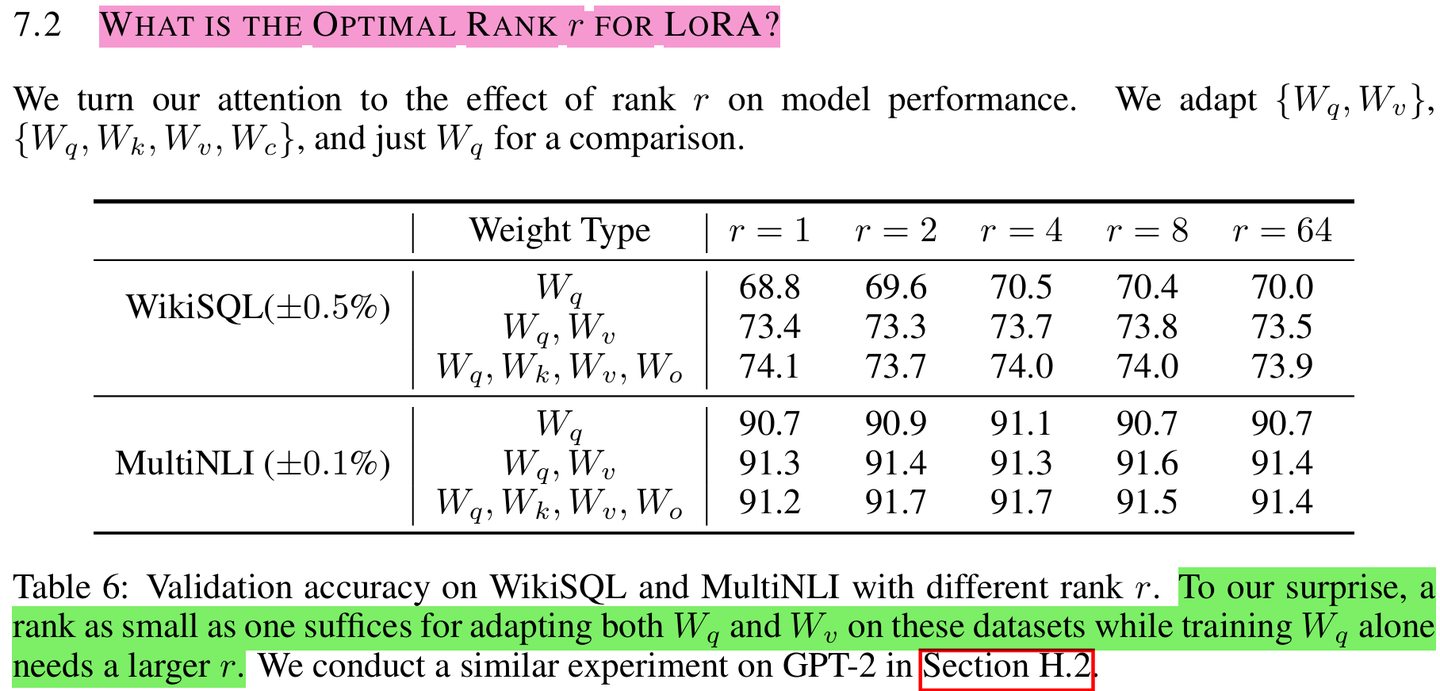
论文基于GPT-3 175B，WikiSQL和MultiNLI数据上，进行了关于LoRA秩$r$选取的实验分析

Weight Type指明对Attention的那部分参数做了低秩适应。可以发现，在这个2个数据集上，𝑟=4,8时基本上要略优于𝑟=64的效果。更高的𝑟不一定带来更好的效果。

作者指出，增加𝑟并不能涵盖更有意义的子空间，这表明低秩适应矩阵就足够了。但是，并不可能期望一个小的𝑟适用于每个任务或数据集

一些秩𝑟选取经验：

微调的下游任务：
简单任务所需的秩𝑟不大，任务越难/多任务混合的情况，需要更大的秩𝑟

  • 基座能力：
    越强的基座，所需的秩𝑟应该更小。例如Qwen2-72B-Instruct对比Qwen2-7B-Instruct。

越强的基座在处理同等任务时，需要微调的样本数也通常会更少些。

数据规模：
数据规模越大，需要更大的秩𝑟

1.8 LoRA微调的模型参数选取

LoRA原始论文只研究了注意力参数𝑊𝑞、𝑊𝑘、𝑊𝑣,和𝑊𝑜。

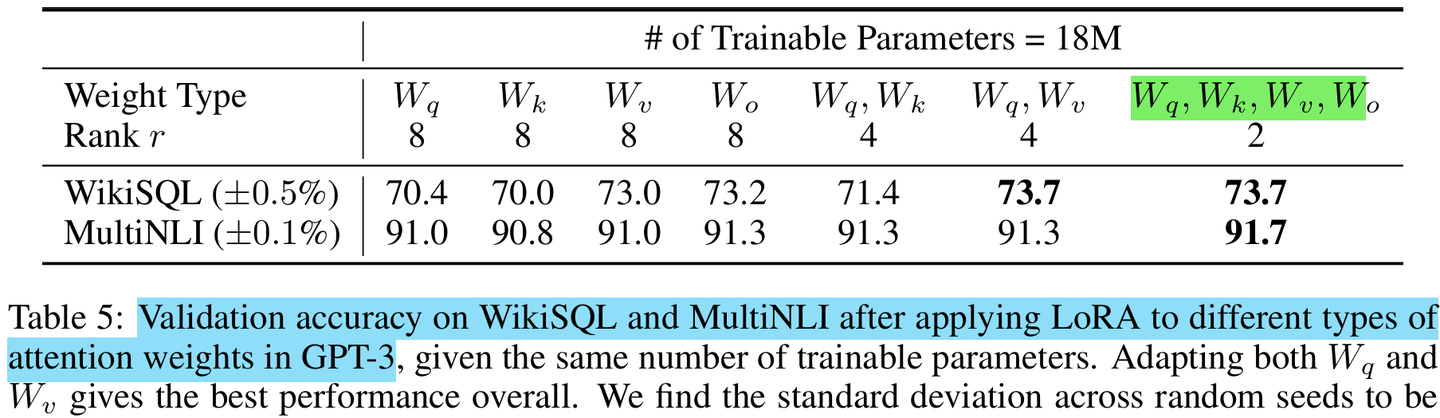
论文基于GPT-3 175B，对比分析了训练预算有限时，关于LoRA的微调注意力参数的选择

在训练预算为18M时 (roughly 35MB if stored
in FP16) on GPT-3 175B，注意力权重全部选择时的效果最佳。

这表明，即使全部的注意力参数即使秩更小时（𝑟=2），相比秩更大的（𝑟=8）部分注意力参数，具有更强的建模能力。

在实际中，一般会把FFN的参数也考虑进来。

二、LoRA训练

LoRA反向传播的过程

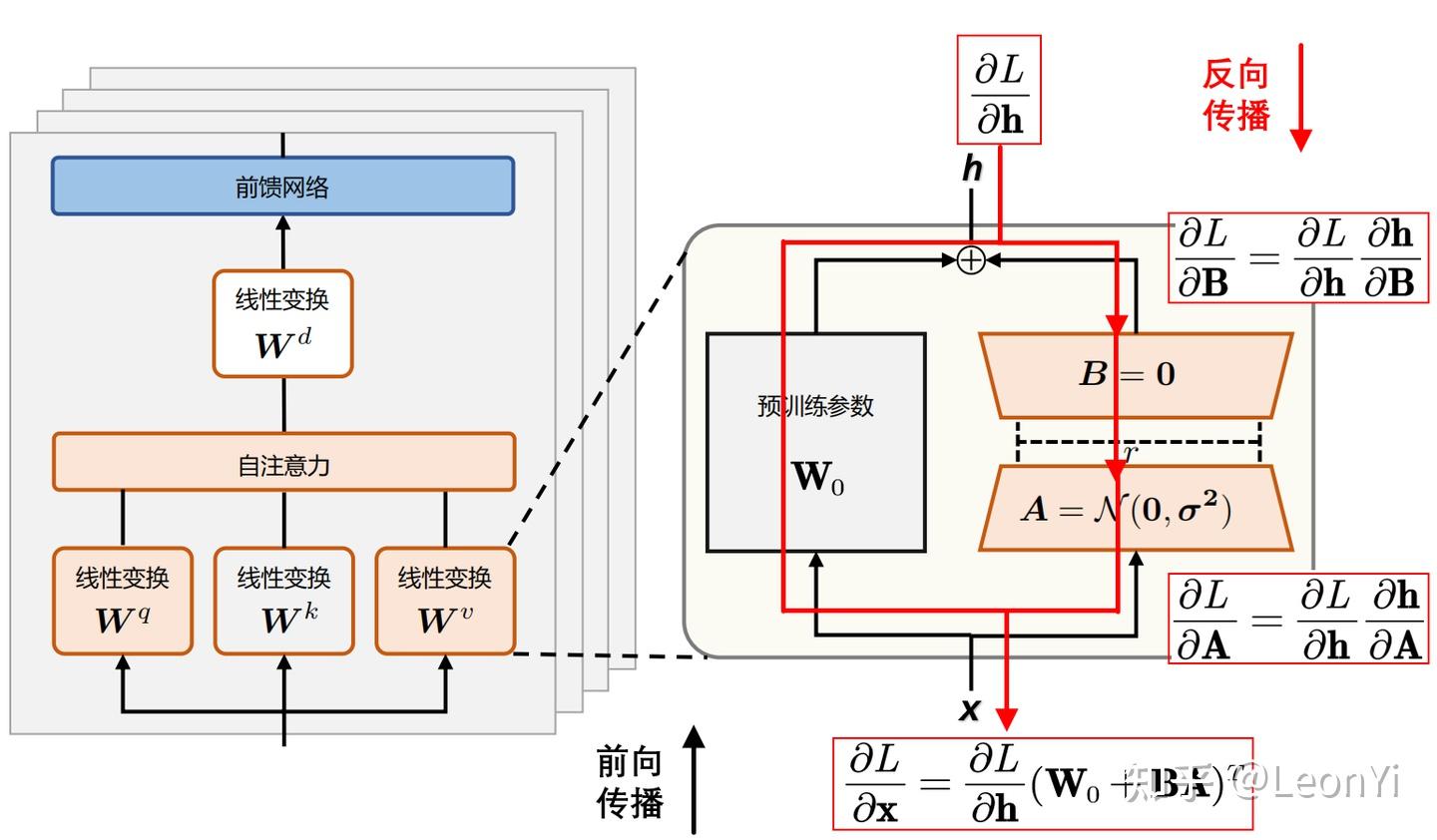
LoRA训练时，将冻结预训练权重 𝑊0，只优化低秩矩阵 𝐵和𝐴。

LoRA训练后，只需保存低秩矩阵的𝐵和𝐴参数。

2.1 LoRA训练的梯度计算

LoRA的计算图和梯度计算


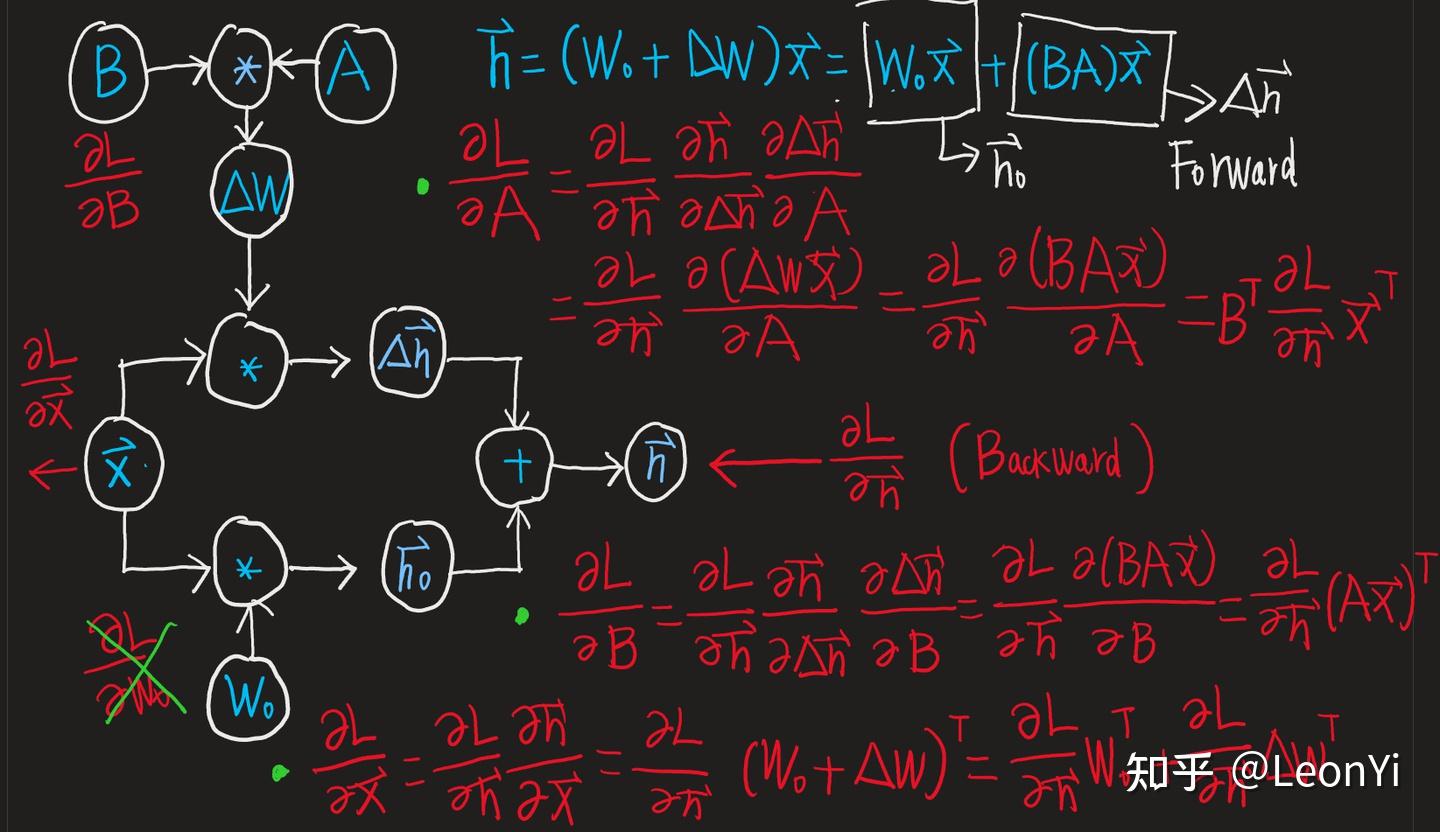
𝐵 和 𝐴的梯度计算, 𝑊0不参与计算。

∂𝐿∂𝐵=∂𝐿∂ℎ∂ℎ∂Δℎ∂Δℎ∂𝐵=∂𝐿∂ℎ(𝐴𝑥)𝑇∈𝑅𝑑×𝑟

∂𝐿∂𝐴=∂𝐿∂ℎ∂ℎ∂Δℎ∂Δℎ∂𝐴=𝐵𝑇∂𝐿∂ℎ𝑥𝑇∈𝑅𝑟×𝑑

继续回传的梯度，包括𝑊0这一路：

∂𝐿∂𝑥=∂𝐿∂ℎ∂ℎ∂𝑥=∂𝐿∂ℎ(𝑊0+𝐵𝐴)𝑇

2.2 反向传播计算量

全量微调前向计算： ℎ=𝑊0𝑥

全量微调反向计算：

∂𝐿∂𝑊0=∂𝐿∂ℎ∂ℎ∂𝑊0=∂𝐿∂ℎ𝑥𝑇∈𝑅𝑑×𝑑

∂𝐿∂𝑥=∂𝐿∂ℎ∂ℎ∂𝑥=∂𝐿∂ℎ𝑊0𝑇

LoRA微调计算： ℎ=𝑊0𝑥+𝐵𝐴𝑥

此时，微调的参数量从原来Δ𝑊的𝑑∗𝑑，变成了𝐵 和 𝐴的2∗𝑟∗𝑑。

可知，2∗𝑟∗𝑑<<𝑑∗𝑑（有2𝑟<<𝑑）

不考虑pytorch或如llm.c的训练优化实现。可以看到，光梯度计算的话，实际计算量是增加了的。

2.3 LoRA在哪里减少了显存占用

𝐵和𝐴的参数、梯度和优化器状态是小头，暂时忽略。

预训练权重 𝑊0的梯度和优化器状态存储开销，实际就是LoRA能大大减少了显存占用的关键。

在LoRA训练时，𝑊0仍然会参与前向传播和反向传播，但是不会计算其对应梯度∂𝐿∂𝑊0，更不会更新其参数。

因此，这一步不再需要计算和保存梯度∂𝐿∂𝑊0，以及更新𝑊0，也就不需要维护其优化器状态了。

以𝑑=4096,𝑟=16为例，这部分减少的梯度显存占用粗略估计为：𝑑∗𝑑−2∗𝑑∗𝑟=1−2𝑟𝑑, 减少了99.2187%。

若以混合精度训练的视角来看，梯度为半精度bfl6，以Adaw optimizer为例，所有参与了LoRA训练的原始参数，其优化器状态Optimizer states（梯度的一阶矩（均值） + 二阶原始矩（有偏方差）+ 参数备份，均为全精度float32），是参数的3倍空间，也成比例减少了。

Adaw优化器

也就是说，加入LoRA训练的参数，对应的模型状态中的模型参数+梯度+优化器状态，节约了训练过程中优化器状态这部分的大头，引入了2个低秩矩阵的模型状态，这就是LoRA高效微调节约显存的原因。

2.4 LoRA Pytorch仿真

import torch

d = 4 # 模型维度为4
r = 2 # LoRA秩为2

x = torch.ones(d, requires_grad=True)   # 输入tensor
y = torch.zeros(d)                      # 模拟计算损失的标签

# h = W0x + BAx LoRA计算
W_0 = torch.randn(d, d, requires_grad=False) # 预训练权重
B = torch.randn(d, r, requires_grad=True)    
A = torch.randn(r, d, requires_grad=True)
delta_W = torch.matmul(B, A)
delta_h = torch.matmul(x, delta_W)
delta_h.retain_grad()
h = torch.matmul(x, W_0) + delta_h
h.retain_grad()
loss = torch.nn.functional.binary_cross_entropy_with_logits(h, y)
loss

损失：tensor(1.8470, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)

print(f"Gradient function for h = {h.grad_fn}")
print(f"Gradient function for loss = {loss.grad_fn}")

梯度函数：

Gradient function for h = <AddBackward0 object at 0x000002D6DE7D0D00>
Gradient function for loss = <BinaryCrossEntropyWithLogitsBackward0 object at 0x000002D6DE7D1DB0>

反向传播

loss.backward()
print(B.grad, (B.grad).shape)
print(A.grad, (A.grad).shape)

梯度值

tensor([[0.1928, 0.2755],
        [0.1928, 0.2755],
        [0.1928, 0.2755],
        [0.1928, 0.2755]]) torch.Size([4, 2])
tensor([[-0.0582, -0.2058, -0.2852, -0.0059],
        [ 0.0909,  0.3217,  0.4458,  0.0093]]) torch.Size([2, 4])

x.grad即 ∂𝐿∂𝑥

tensor([-0.1980, -0.1575,  0.4884,  0.5149])

计算值 ∂𝐿∂𝑥=∂𝐿∂ℎ(𝑊0+𝐵𝐴)𝑇

torch.matmul(h.grad, (W_0 + delta_W).T)

可以看到梯度值和torch计算梯度一样

tensor([-0.1980, -0.1575,  0.4884,  0.5149], grad_fn=<SqueezeBackward4>)

三、LoRA显存占用

按照LoRA论文报告的结果，LoRA微调使得在训练GPT3 175B时的，显存消耗从1.2TB降至350GB；

当𝑟=4时，最终保存的模型从350GB降至35MB，极大降低了训练的开销。

下表，来源于LlamaFactory Github展示的微调LLM的最小硬件依赖估算值。

AMP为fp16混合精度训练，默认模型和梯度为fp16，优化器状态为fp32全精度。那么全参微调时，显存占用不考虑和序列长度相关的激活值，就至少为参数规模的16倍

半精度存储的10亿参数，占据空间1G * 2B=2GB , 以字节Byte为单位，模型参数2+梯度2+优化器状态12=16倍系数

例如7B参数，全参微调，默认占用7B *16 = 112B， 预估至少就要120GB空间了

方法精度7B13B30B70B8x7B8x22B
Full AMP 120GB 240GB 600GB 1200GB 900GB 2400GB
Full 16 60GB 120GB 300GB 600GB 400GB 1200GB
Freeze 16 20GB 40GB 80GB 200GB 160GB 400GB
LoRA/GaLore/BAdam 16 16GB 32GB 64GB 160GB 120GB 320GB
QLoRA 8 10GB 20GB 40GB 80GB 60GB 160GB
QLoRA 4 6GB 12GB 24GB 48GB 30GB 96GB
QLoRA 2 4GB 8GB 16GB 24GB 18GB 48GB

实际的使用情况：

  • 一张16GB显存 T4，仅够6B或7B的模型在batchsize为1时，进行int4 QLoRA，这还只是考虑输入输出有限时。
  • 一张32GB显存 V100，大致够6B或7B的模型在batchsize为1时，进行LoRA微调。
  • 一张80GB显存 A800，Qwen1.5 72B 进行int4 QLoRA，以及例如Baichuan13B / Qwen14B的LoRA微调
  • 2张A800 80GB显存，可以进行全参SFT或增量SFT

四、实验分析

4.1 BERT系列

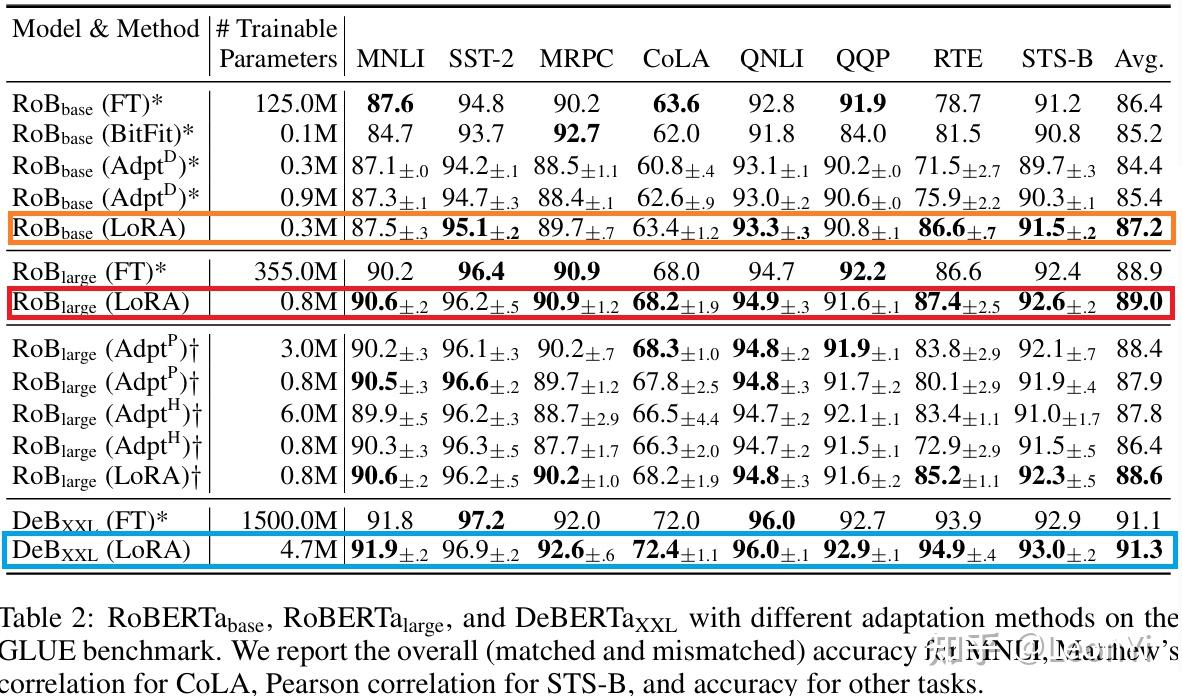
对比了RoRERTa-base, RoRERTa-large和DeRERTa-XXL

判别任务实验可以发现，LoRA相比BitFit和Adpater（D,H,P三种），基本上都更好。

和全参微调FT对比，LoRA基本上是旗鼓相当甚至更好（不过我怀疑是可能是LoRA相比全参微调可以使劲调参）

当然，一般还是参数量越大的预训练模型微调效果越好。

调参的超参数

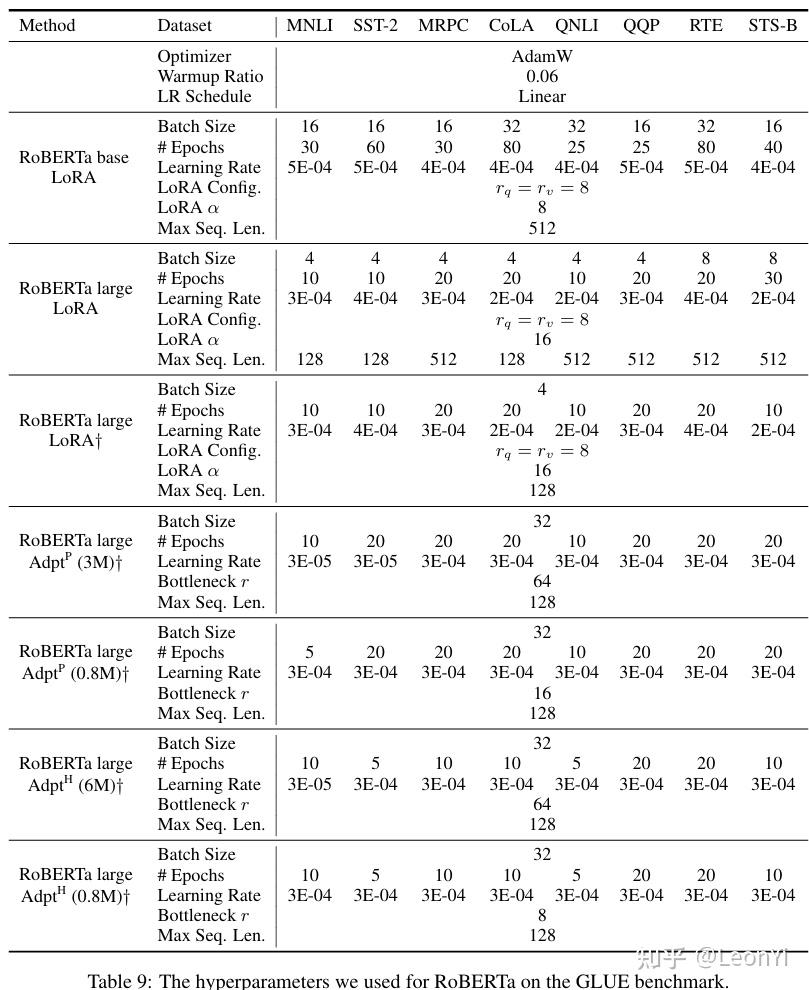
4.2 GPT2系列

对比了GPT-2 M和 GPT-2 L

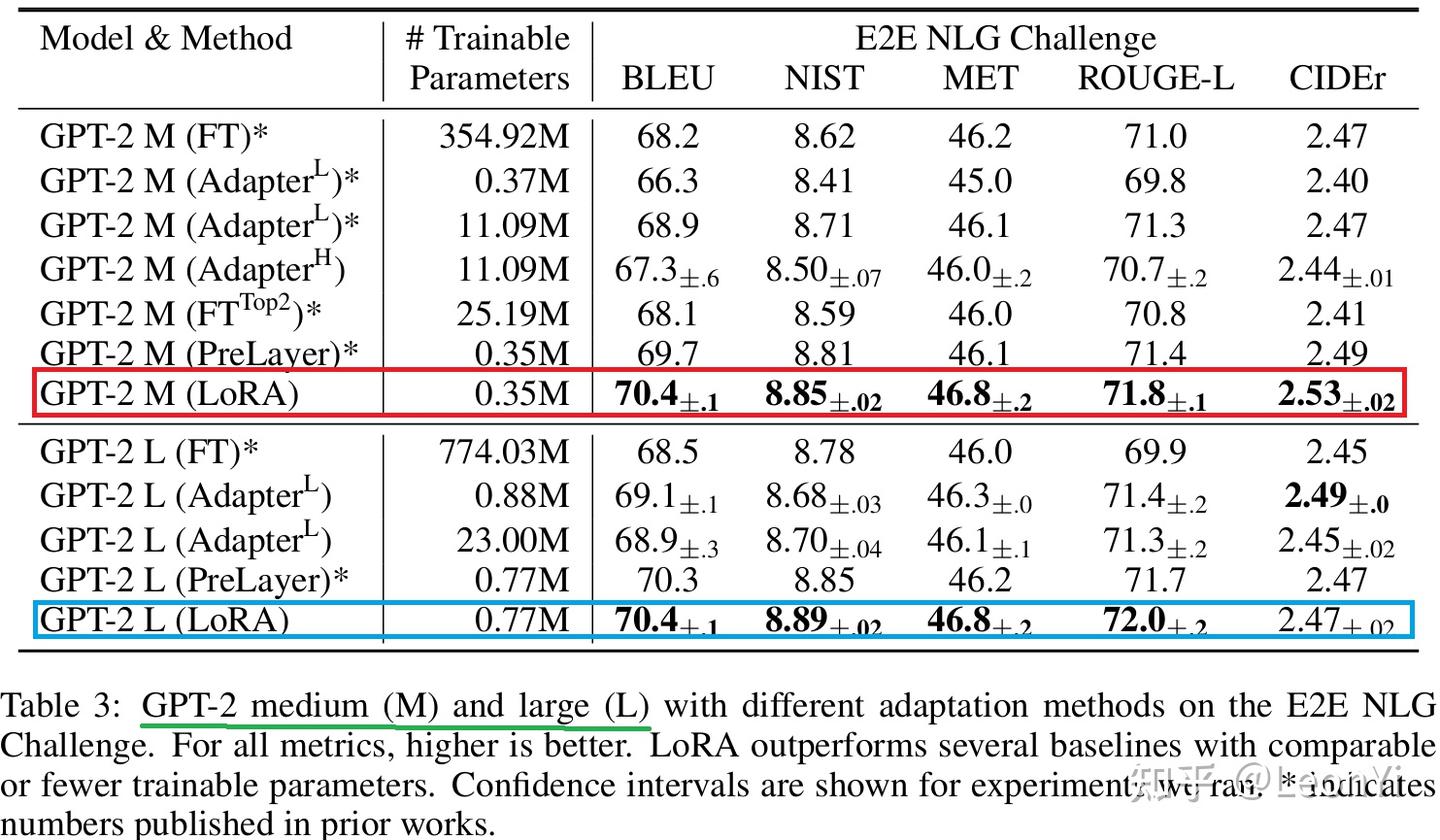
在生成任务上。LoRa以更少或相当的参数，效果打败了PreLayer (即Prefix-layer tuning) 和Adpater（L,H）

4.3 GPT3规模

GPT3 175B参数

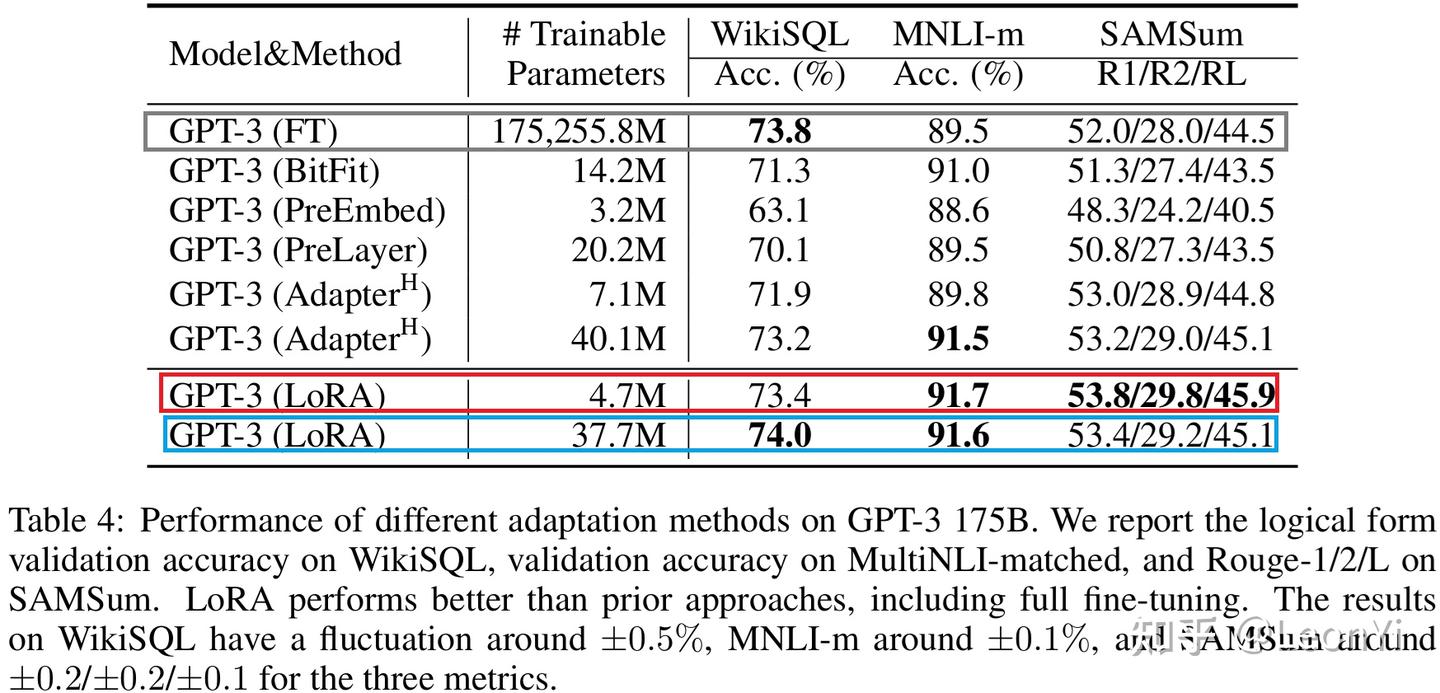
LoRA matches or exceeds the fine-tuning baseline on all three datasets

1、WikiSQL是NL2SQL任务，56355/8421 training/validation， 给定x = {table schema，query} ，预测 y ={ SQL}
2、SAMSum是对话摘要任务（2人），14732/819 training/test examples

LoRA微调，参数不是越多越好。甚至LoRA的效果还要优于FT。论文没有解释原因

不是所有的方法都随着微调参数增加，其效果也呈单调递增

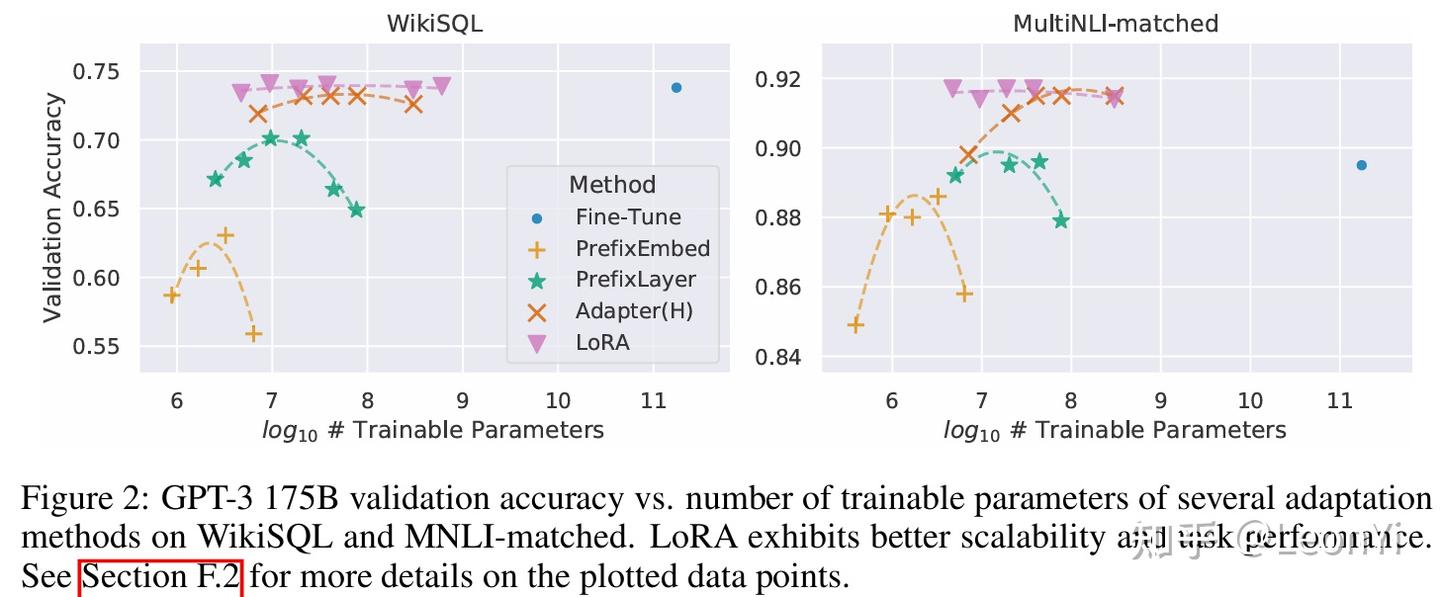
4.4 GPT3规模是否要微调

当只有少数训练样本时，少样本学习或提示工程是非常有利的。

然而，在实践中，我们通常有能力为性能敏感型应用程序策划几千个或更多的训练示例。

GPT3 Few-shot和微调的对比结果

如上所示，与小样本上下文学习相比，对大规模或小规模的数据集微调都显著提升了效果。

对于几百亿参数如Qwen2-72B这种规模的开源LLM，写得比较好的提示词（CoStar目标+COT）+少量样本，可能媲美几十亿Qwen2-7B微调的效果。要想进一步提升效果，微调更大规模的LLM还是有用的（尽管有部署难度和推理时延）。

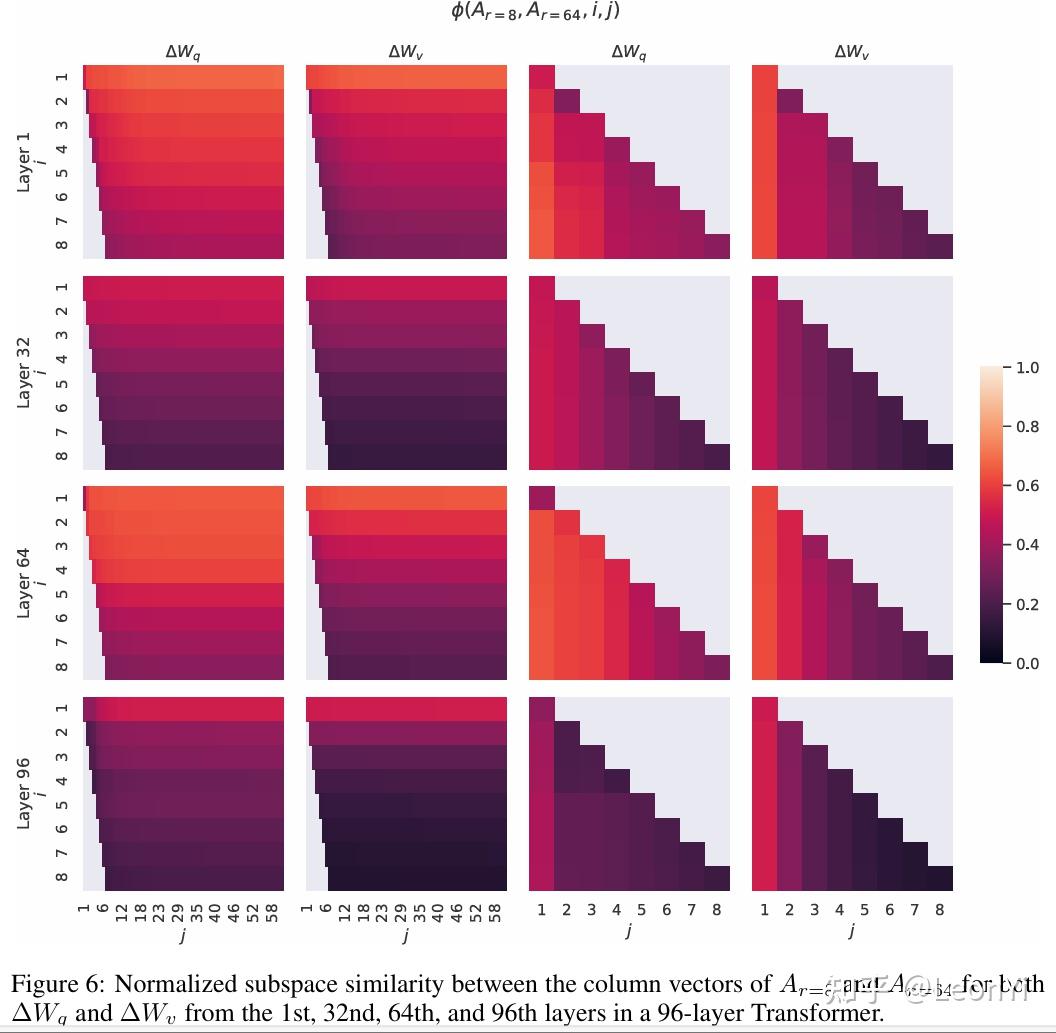
4.5 预训练参数和LoRA低秩适应参数的联系

∆ 和 在不同维度r上的归一化子空间的相似度比较
posted @ 2025-07-10 12:10  有何m不可  阅读(2400)  评论(0)    收藏  举报