强化学习之图解PPO算法和TD3算法

转自：https://zhuanlan.zhihu.com/p/384497349

关于on-policy和off-policy的定义，网上有很多不同的讨论，比较常见的说法是看behavior policy（行为策略，即与环境进行交互的策略）和target policy（目标策略，即学习准确地评估Q值的策略）是否为同一个，如果为同一个，那么就为on-policy，反之为off-policy。我认为， 更加通俗一点的理解是，on-policy和off-policy的差异 在于 训练目标策略 所用到的数据 (𝑠,𝑎,𝑟,𝑠′) （有时候也表现为数据 (𝑠,𝑎,𝑟,𝑠′,𝑎′) ）是不是当前目标策略（此时还没开始训练）得到的 ，如果是目标策略得到的，那么就是on-policy，如果不是，那么就是off-policy。

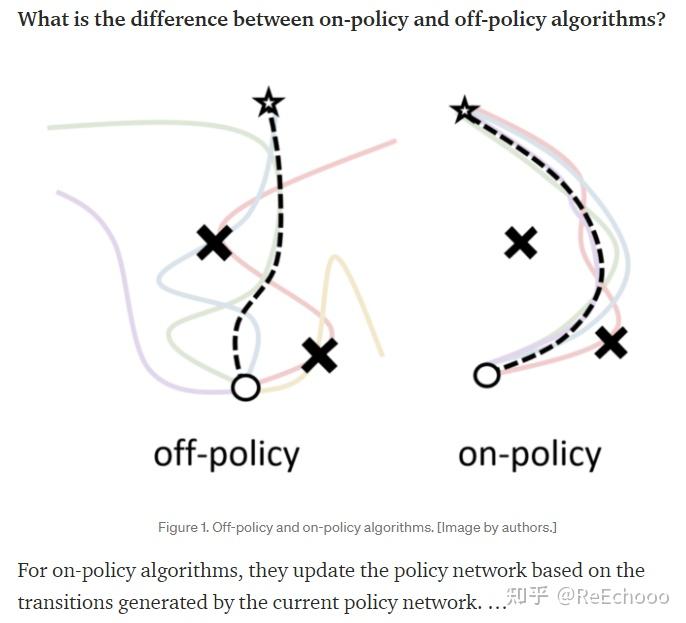
图片摘自：https://elegantrl.medium.com/

 

比如在 SARSA算法 中，目标策略（target policy）是基于Q表的 𝜖 -贪婪策略，基于目标策略采取的动作会成为当前数据 (𝑠,𝑎,𝑟,𝑠′,𝑎′) 的 𝑎′（并且是下一条数据 (𝑠,𝑎,𝑟,𝑠′,𝑎′) 的 𝑎），用采集到的数据更新Q表，因此训练目标策略的数据是由当前目标策略得到的，故为 on-policy算法 。

 

在 Q-learning算法 中，目标策略是基于Q表的完全贪婪策略，更新Q表的数据(𝑠,𝑎,𝑟,𝑠′)并不是由完全贪婪策略得到，而是由𝜖 -贪婪策略得到（因为 𝑎 是由𝜖 -贪婪策略得到），因此训练目标策略的数据不是由当前目标策略（完全贪婪策略）得到的，因此为 off-policy算法 。

 

（注：以上两张截图摘自：https://www.zhihu.com/question/57159315）

PPO算法 因为在buffer里使用的数据都是由目标策略 𝜋𝜃𝑜𝑙𝑑 得到，只是会多更新几次 𝜋𝜃𝑜𝑙𝑑 ，将 𝜃𝑜𝑙𝑑 更新之后得到 𝜃 ，那么buffer里的数据都不能再用了，需要清空buffer，因此是 on-policy算法 .（其实因为PPO存在一个buffer多更新几次的情况，所以说它的off-policy也有一定道理，但它总体上还是on-policy）

 

 

DDPG算法 和 TD3算法 思路相同，就放在一起讲了，如下图所示，可以看到目标策略更新之后，buffer里的数据并不会清空，会夹杂着旧的数据一起采样训练，所以他们都是 off-policy算法 。

 

 

1. PPO算法

邻近策略优化（Proximal Policy Optimization，PPO）算法的网络结构有两个。PPO算法解决的问题是 离散动作空间和连续动作空间 的强化学习问题，是 on-policy 的强化学习算法。论文原文见《Proximal Policy Optimization Algorithms》。

1.1 网络结构

 

 

一个actor网络，一个critic网络。

actor网络的输入为状态，输出为动作概率 𝜋(𝑎𝑡|𝑠𝑡) （对于离散动作空间而言）或者动作概率分布参数（对于连续动作空间而言）

critic网络的输入为状态，输出为状态的价值。

显然，如果actor网络输出的动作越能够使优势（优势的定义等下给出）变大，那么就越好。如果critic网络输出的状态价值越准确，那么就越好。

1.2 产生experience的过程

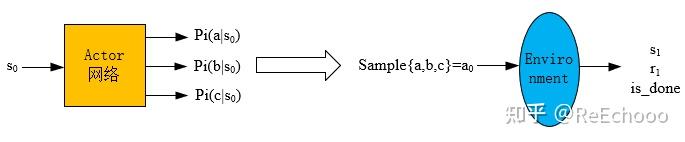
已知一个状态 𝑠0 ，通过 actor网络 得到所有动作的概率（图中以三个动作：a,b,c为例），然后依概率采样得到动作 𝑎0 ，然后将 𝑎0 输入到环境中，得到 𝑠1 和 𝑟1 。状态价值 𝑣(𝑠0) 是通过critic网络输出得到的，这样就得到一个experience: (𝑠0,𝑎0,𝑟1,𝑣(𝑠0),𝑙𝑜𝑔𝑃(𝑎0|𝑠0)) ，然后将experience放入经验池中（当然之后还会计算 𝐴(𝑠0,𝑎0) 以及 𝐺0 ，经验池中也存了这两个信息）。

（注：虽然 𝑣(𝑠0) 可以用一条轨迹的折扣回报得到，即： 𝑣(𝑠0)=𝑟1+𝛾𝑟2+⋯+𝛾𝑇𝑟𝑇+1+𝛾𝑇+1𝑣(𝑠𝑇+1) ，但是轨迹末状态的下一状态 𝑠𝑇+1 的 𝑣(𝑠𝑇+1) 还是需要critic网络来估计，当然如果 𝑠𝑇+1 是正常游戏结束，而不是达到了最大步长，那么令 𝑣(𝑠𝑇+1)=0 。与其这样，还不如用critic网络直接估计 𝑣(𝑠0) ，而且值得注意的是， 𝑣(𝑠0)=𝑟1+𝛾𝑟2+⋯+𝛾𝑇𝑟𝑇+1+𝛾𝑇+1𝑣(𝑠𝑇+1) 正是我们critic网络作为监督学习的真值）

以上是离散动作的情况，如果是连续动作，就输出概率分布的参数（比如高斯分布的均值和方差），然后按照概率分布去采样得到动作 𝑎0 .

经验池 存在的意义是为了，更加方便地计算，一条轨迹上状态的累积折扣回报 𝑣(𝑠𝑡) 以及优势 𝐴(𝑠𝑡,𝑎𝑡) ，而不是消除experience的相关性。

 

 

1.3 Actor网络的更新流程

首先来看优势函数 𝐴 的定义（论文中使用的符号为 𝐴𝑡^ ，注：论文中的 𝑟𝑡 为笔者文章的 𝑟𝑡+1 ）：

 

 

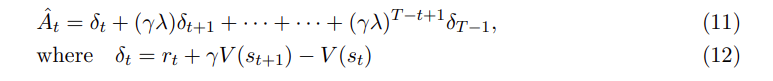
因为Actor网络需要输出的动作优势尽可能地大，所以它的训练需要用以下表达式作为Loss函数

 

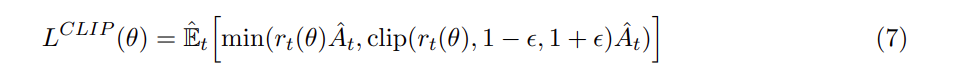
其中：

 

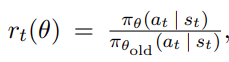
值得注意的是： 和TD3算法的单步TD不同，PPO算法使用多步TD，因此它需要跑完一条轨迹后，才开始计算各个状态的累积回报和动作的优势。具体而言，状态价值 ，𝑣(𝑠0)，𝑣(𝑠1) 是通过critic网络输出得到的，动作优势 𝐴(𝑠0,𝑎0) 是通过首先计算 𝛿0=𝑟1+𝑣(𝑠1)−𝑣(𝑠0) ，然后用 𝛾𝜆 作为折扣因子去计算动作优势 𝐴(𝑠0,𝑎0) ，具体可以看公式（11）。

因此训练actor网络的时候需要，将经验池中的所有数据都拿出来，计算loss，然后用梯度上升法，多更新几步梯度。更新完成后即将经验池清空，等待下一个新的actor网络与环境互动去收集数据。

pytorch代码如下：

# train actor net
        all_pi_tensor = self.actor_net(state_tensor)
        pi_tensor = all_pi_tensor.gather(1, action_tensor.unsqueeze(1)).squeeze(1)
        surrogate_advantage_tensor = (pi_tensor / old_pi_tensor) *                 advantage_tensor
        clip_times_advantage_tensor = 0.1 * surrogate_advantage_tensor
        max_surrogate_advantage_tensor = advantage_tensor +                 torch.where(advantage_tensor > 0.,
                clip_times_advantage_tensor, -clip_times_advantage_tensor)
        clipped_surrogate_advantage_tensor = torch.min(
                surrogate_advantage_tensor, max_surrogate_advantage_tensor)
        actor_loss_tensor = -clipped_surrogate_advantage_tensor.mean()
        self.actor_optimizer.zero_grad()
        actor_loss_tensor.backward()
        self.actor_optimizer.step()

 

1.4 Critic网络的更新流程

Actor网络更新后，接着拿从经验池buffer中采出的数据进行Critic网络的更新（数据已经计算了状态价值，折扣回报 𝐺𝑡 的计算是基于多步TD的方法，从那个状态开始，用每一步环境返回的奖励 𝑅 与折扣因子相乘后累加，即： 𝐺𝑡=𝑟𝑡+1+𝛾𝑟𝑡+2+⋅⋅⋅+𝛾𝑇−𝑡𝑟𝑇+1+𝛾𝑇+1−𝑡𝑣(𝑠𝑇+1) ），其中 𝑣(𝑠𝑇+1) 为网络的估计值，更新方式即为：计算好的折扣回报 𝐺𝑡 与Critic网络预测当前状态价值 𝑣(𝑠𝑡) 做差，用MSEloss作为Loss函数，对神经网络进行训练。

pytorch代码如下：

# train critic net
        pred_tensor = self.critic_net(state_tensor)
        critic_loss_tensor = self.critic_loss(pred_tensor, return_tensor)
        self.critic_optimizer.zero_grad()
        critic_loss_tensor.backward()
        self.critic_optimizer.step()

2. TD3算法

双重延迟深度确定性策略梯度（Twin Delayed Deep Deterministic Policy Gradient，TD3）算法的网络结构有六个。TD3算法解决的问题是 连续动作空间 的强化学习问题，是 off-policy 的强化学习算法。论文原文见《Addressing Function Approximation Error in Actor-Critic Methods》。

2.1 网络结构

作为对比，首先来看深度确定性策略梯度（DDPG）的网络结构，有四个，分别如下所示：

 

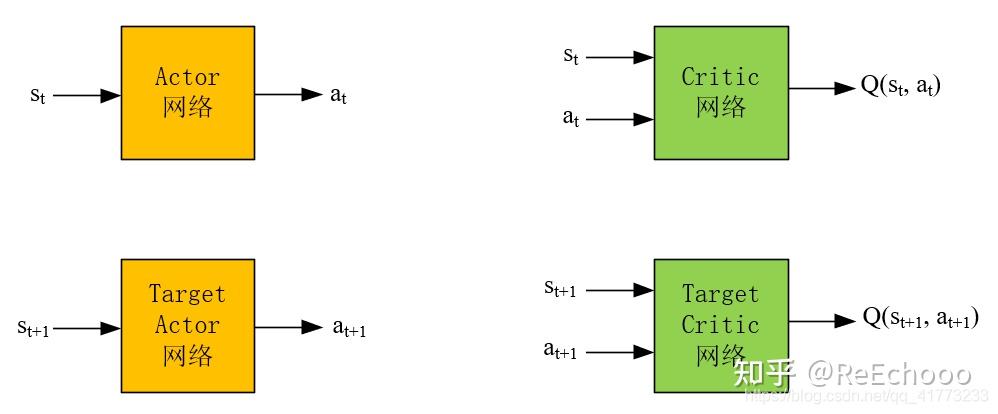
TD3算法的网络结构为以下六个：

 

 

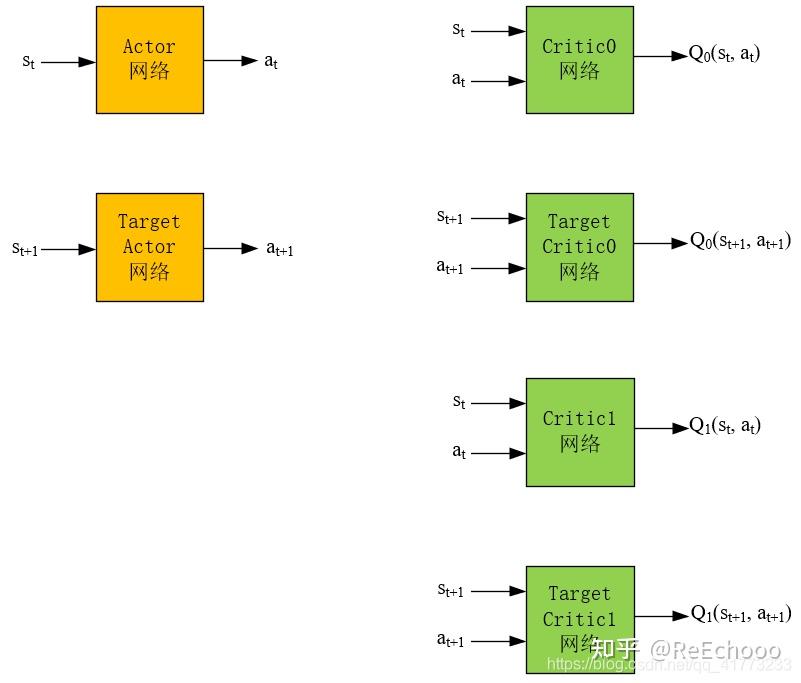
Actor网络和Critic网络的作用和DDPG完全一致（DDPG的内容可以参考：图解DQN，DDQN，DDPG网络），即：

Actor网络输入是状态，输出是动作。Critic网络输入是状态和动作，输出是对应的Q值。

Actor网络的目的是根据状态 𝑠𝑡 ，能够输出使得 𝑄(𝑠𝑡,𝑎𝑡) 最大的动作 𝑎𝑡 ，这个 𝑎𝑡 越能使 𝑄(𝑠𝑡,𝑎𝑡) 大，就说明网络训练地越好。

Critic网络的目的是根据状态动作对 (𝑠𝑡,𝑎𝑡) 能够输出其action value 𝑄(𝑠𝑡,𝑎𝑡) ，这个 𝑄 值越精确，就说明网络训练地越好。

Actor网络和Target Actor网络的区别是，Actor网络是每步都会在经验池中更新，而Target Actor网络是隔一段时间将Actor的网络参数拷贝到Target Actor网络中，实现Target Actor网络的更新。这种“滞后”更新是为了保证在训练Actor网络时训练的稳定性。Critic网络和Target Critic网络也是一样。

2.2 产生experience的过程

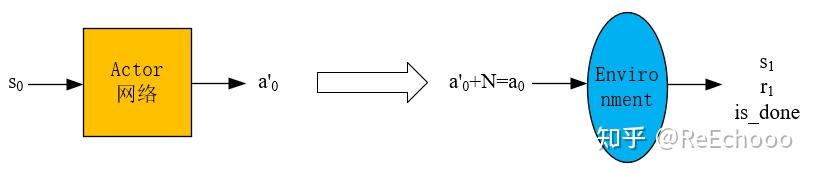
已知一个状态 𝑠0 ，通过 actor网络 得到动作 𝑎0′ ，然后再加噪声 𝑁 得到动作 𝑎0=𝑎0′+𝑁 （噪声是为了保证一定的探索，普通的高斯噪声即可），然后将 𝑎0 输入到环境中，得到 𝑠1 和 𝑟1 ，这样就得到一个experience: (𝑠0,𝑎0,𝑠1,𝑟1) ，然后将experience放入经验池中。

经验池 存在的意义是为了消除experience的相关性，因为强化学习中前后动作通常是强相关的，而将它们打散，放入经验池中，然后在训练神经网络时，随机地从经验池中选出一批experience，这样能够使神经网络训练地更好。

 

2.3 Actor网络的更新流程

从经验池中取出一批experience，这里以一个experience： (𝑠0,𝑎0,𝑠1,𝑟1) 为例讲述训练神经网络的过程。

 

 

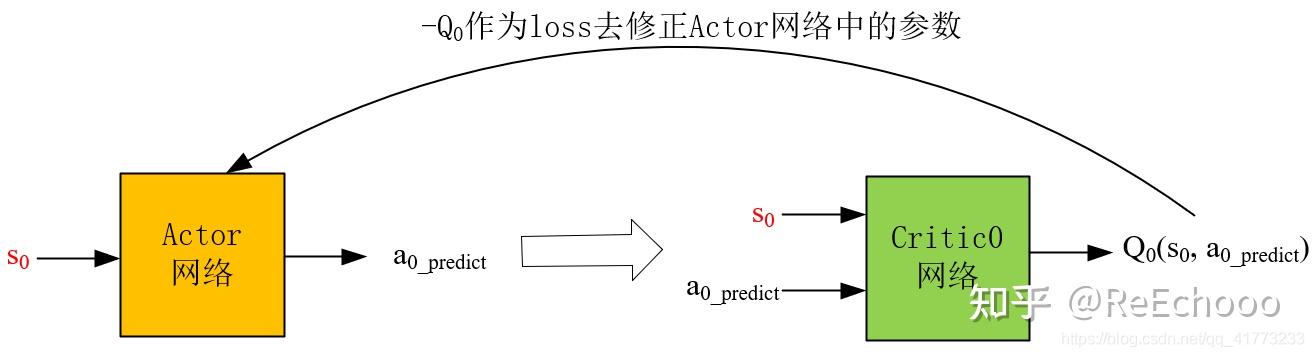
其中：红色字母代表已知项。

结合2.1中对Actor网络的描述可知，Actor网络的loss函数就是-Q，-Q越小越好。这个-Q需要由Critic0网络（用Critic1网络也是完全可行的）得到，如上图所示。

将experience中的 𝑠0 输入到Actor网络中，得到预测的动作 𝑎0_𝑝𝑟𝑒𝑑𝑖𝑐𝑡 ，这里不加噪声了，直接将 𝑠0 和 𝑎0_𝑝𝑟𝑒𝑑𝑖𝑐𝑡 输入到Critic0网络中，得到Q值，然后将-Q作为loss函数，修正Actor网络。

pytorch代码示意如下，其中actor_evaluate_net即为actor网络，critic0_evaluate_net即为critic0网络：

pred_action_tensor = self.actor_evaluate_net(state_tensor)
        pred_action_tensor = pred_action_tensor.clamp(self.action_low, self.action_high)
        pred_state_action_tensor = torch.cat([state_tensor, pred_action_tensor], 1)
        critic_pred_tensor = self.critic0_evaluate_net(pred_state_action_tensor)
        actor_loss_tensor = -critic_pred_tensor.mean()
        self.actor_optimizer.zero_grad()
        actor_loss_tensor.backward()
        self.actor_optimizer.step()

 

值得注意的是，Actor网络是最重要的，因为它直接决定了我们采取策略的好坏（从2.2小节中也可以看出，与环境互动的网络只有Actor网络），而想要训练出一个好的Actor网络，需要一个准确的Critic网络来评价它，因此 TD3的剩下5个网络 都是 为了创造 出一个 尽可能精确的Critic网络 （而DDPG是用3个网络创造出一个尽可能精确的Critic网络，TD3是DDPG的改进版）

2.4 Critic网络的更新流程

接着上述experience： (𝑠0,𝑎0,𝑠1,𝑟1) 为例讲述训练Critic网络的过程

 

 

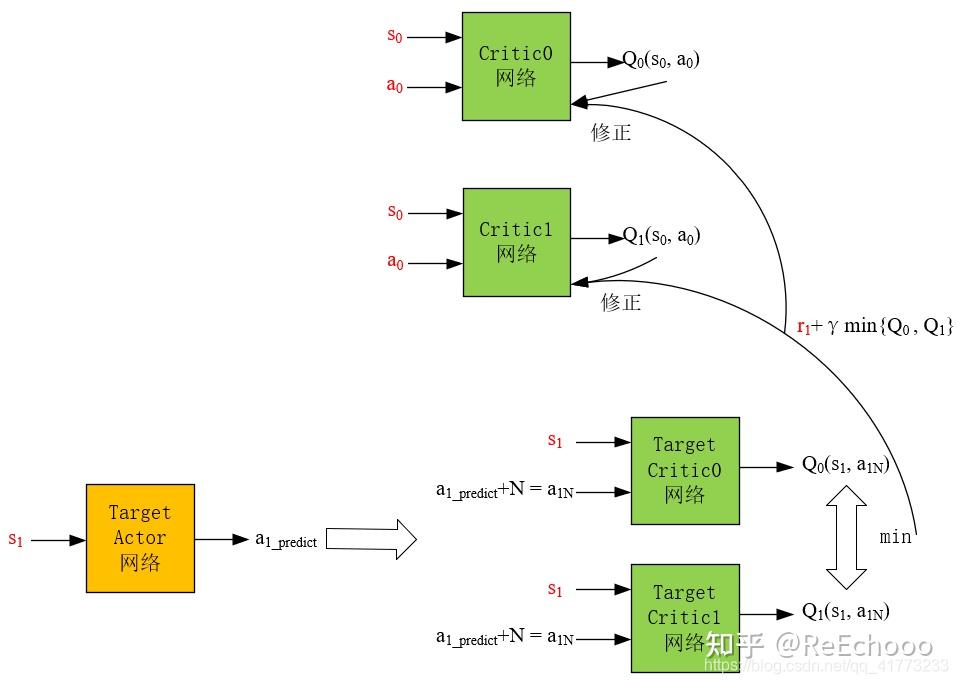
其中：红色字母代表已知项。

结合2.1中对Critic网络的描述可知，Critic网络需要使预测的Q值越精确越好，原本的 DDPG算法 只是借助Target Actor网络和Target Critic网络对Critic网络进行修正，其中 Target Actor网络的目的 是为了让Critic网络更容易稳定收敛，如果用频繁更新的Actor网络做下一步动作的预测，会导致Critic网络很难收敛， Target Critic网络的目的 与Target Actor网络的目的相同，也是想用一个更新不频繁的网络让Critic网络稳定收敛。

TD3算法用了 两个Target Critic网络 是考虑到在实际的应用中，Critic网络总是过高的估计Q值，它借鉴了DDQN的思想，采用两个网络对Q值进行估计，然后选择较小的那个，这样尽可能地 避免过高地估计Q值 。（DDQN是两个估计价值Q的网络一个网络负责找动作，一个网络负责找动作对应的Q值）

也正是因为用了两个Target Critic网络，所以频繁更新的Critic网络也需要采用两个，用 𝑟1+𝛾∗𝑚𝑖𝑛{𝑄0(𝑠1,𝑎1𝑁),𝑄1(𝑠1,𝑎1𝑁)} 来更新两个Critic网络，即用 𝑟1+𝛾∗𝑚𝑖𝑛{𝑄0(𝑠1,𝑎1𝑁),𝑄1(𝑠1,𝑎1𝑁)} 分别与 𝑄0(𝑠0,𝑎0) 和 𝑄1(𝑠0,𝑎0) 做均方差，然后作为loss对Critic网络进行梯度下降。

此外，还要注意 TD3的一个小trick ，它 给Target Actor网络的预测动作 𝑎1_𝑝𝑟𝑒𝑑𝑖𝑐𝑡 加了一个噪声 𝑁 ，变为动作 𝑎1𝑁 之后，才作为两个Target Critic网络的输入，文章认为这样做能够鼓励探索，从而让下一步的Q值更精确。（但是DDPG并没有这样做）

当然最后当时机合适时（这个通常是自己设置迭代次数），需要将Critic网络的参数更新到Target Critic网络参数中，将Actor网络的参数更新到Target Actor网络参数中，通常采用软更新的方式，即 延迟软更新 。

pytorch代码示意如下：

next_action_tensor = self.actor_target_net(next_state_tensor)
        noise_tensor = (0.2 * torch.randn_like(action_tensor, dtype=torch.float))
        noisy_next_action_tensor = (next_action_tensor + noise_tensor
                    ).clamp(self.action_low, self.action_high)
        next_state_action_tensor = torch.cat([next_state_tensor, noisy_next_action_tensor], 1)
        next_q0_tensor = self.critic0_target_net(next_state_action_tensor).squeeze(1)
        next_q1_tensor = self.critic1_target_net(next_state_action_tensor).squeeze(1)
        next_q_tensor = torch.min(next_q0_tensor, next_q1_tensor)
        critic_target_tensor = reward_tensor + (1. - done_tensor) * self.gamma * next_q_tensor
        critic_target_tensor = critic_target_tensor.detach()

        state_action_tensor = torch.cat([state_tensor, action_tensor], 1)
        critic_pred0_tensor = self.critic0_evaluate_net(state_action_tensor).squeeze(1)
        critic0_loss_tensor = self.critic0_loss(critic_pred0_tensor, critic_target_tensor)
        self.critic0_optimizer.zero_grad()
        critic0_loss_tensor.backward()
        self.critic0_optimizer.step()

        critic_pred1_tensor = self.critic1_evaluate_net(state_action_tensor).squeeze(1)
        critic1_loss_tensor = self.critic1_loss(critic_pred1_tensor, critic_target_tensor)
        self.critic1_optimizer.zero_grad()
        critic1_loss_tensor.backward()
        self.critic1_optimizer.step()

 

2.5 总结

TD3的伪代码如下所示，TD3相比于DDPG有三个改进的地方：

一是 将一个Target Critic网络变为两个Target Critic网络，取两者较小的作为下一状态的Q值，从而避免Q值过高地被估计。

二是 对Target Actor 网络的输出进行了加噪声处理，从而使得Target Critic网络的预测输出Q值尽可能精确。

三是 采用了延迟软更新的方式去更新一个Target Actor 网络、两个Target Critic网络，以及采用延迟更新的方式更新Actor网络。这样做的好处可以参考什么是TD3算法？（附代码及代码分析）