强化学习之图解SAC算法

SAC算法简介

转自：https://zhuanlan.zhihu.com/p/385658411

柔性动作-评价（Soft Actor-Critic，SAC）算法的网络结构有5个。SAC算法解决的问题是 离散动作空间和连续动作空间 的强化学习问题，是 off-policy 的强化学习算法（关于on-policy和off-policy的讨论可见：强化学习之图解PPO算法和TD3算法）。

SAC的论文有两篇，一篇是《Soft Actor-Critic Algorithms and Applications》，2018年12月挂arXiv，其中SAC算法流程如下所示，它包括1个actor网络，4个Q Critic网络：

 

 

一篇是《Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor》，2018年1月挂arXiv，其中SAC算法流程如下所示，它包括1个actor网络，2个V Critic网络（1个V Critic网络，1个Target V Critic网络），2个Q Critic网络：

 

 

本文介绍的算法思路是1个actor网络，2个V Critic网络（1个V Critic网络，1个Target V Critic网络），2个Q Critic网络。而另一种SAC算法思路可以参考openAI的spinning up教程：openAI spinning up

1. 网络结构

关于SAC算法的网络结构图解，笔者认为此链接的讲解也非常地好：Soft Actor-Critic，本文和此链接的说法一致。

 

 

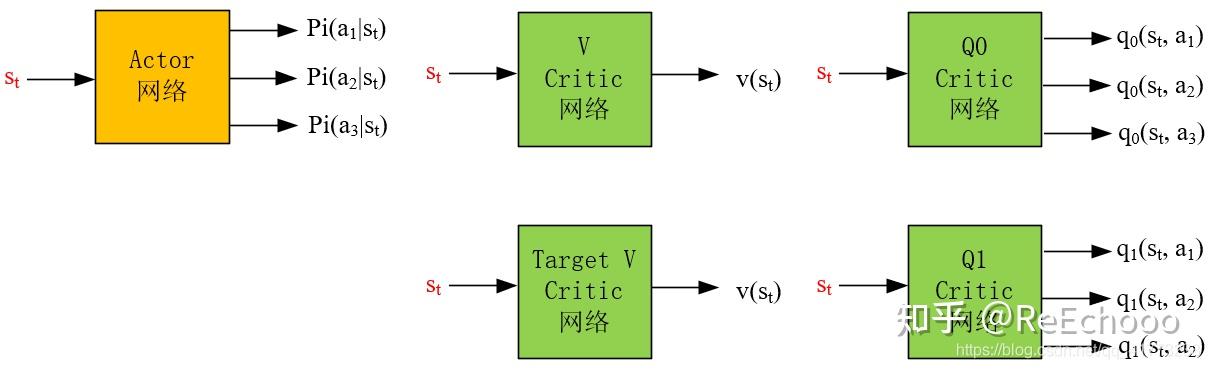
一个actor网络，四个critic网络，分别是状态价值估计 𝑣 和Target 𝑣 网络；动作-状态价值估计 𝑄0 和 𝑄1 网络。

actor网络的输入为状态，输出为动作概率 𝜋(𝑎𝑡|𝑠𝑡) （对于离散动作空间而言）或者动作概率分布参数（对于连续动作空间而言）

critic网络的输入为状态，输出为状态的价值。其中 V Critic 网络 的输出为 𝑣(𝑠) ，代表 状态价值的估计 ； Q Critic 网络 的输出为 𝑞(𝑠,𝑎) ，代表 动作-状态对价值 （以下简称为 动作价值 ） 的估计 ；

因为在SAC算法中为了鼓励探索，增加了熵的概念，所以它actor和critic网络的训练目标和常规不含熵的算法（如TD3，PPO）的训练目标不一样。

在SAC算法中，如果 actor网络 输出的动作越能够使一个综合指标（既包含动作价值 𝑞 ，又包含熵 ℎ ）变大，那么就越好。

如果 Q critic网络 输出的动作价值 𝑞 越准确（根据贝尔曼方程可知， 𝑞 是否准确依赖于 𝑣 是否准确），那么就越好。

如果 V critic网络 输出的状态价值 𝑣 越准确，那么就越好。但需要注意的是，因为SAC中加了熵的概念，所以状态价值 𝑣 并不是我们通常理解的 𝑣(𝑠) ，它其中还加了熵这一项。

接下来只说SAC的算法流程，而不对其中的公式做过多的解释，具体SAC算法的推导过程可以参考《最前沿：深度解读Soft Actor-Critic 算法》。

2. 产生experience的过程

已知一个状态 𝑠𝑡 ，通过 actor网络 得到所有动作的概率 𝜋(𝑎|𝑠𝑡) （图中以三个动作： 𝑎1,𝑎2,𝑎3 为例），然后依概率采样得到动作 𝑎𝑡=𝑎2 ，然后将 𝑎2 输入到环境中，得到 𝑠𝑡+1 和 𝑟𝑡+1 ，这样就得到一个experience: (𝑠𝑡,𝑎2,𝑠𝑡+1,𝑟𝑡+1) ，然后将experience放入经验池中。

以上是离散动作的情况，如果是连续动作，就输出概率分布的参数（比如高斯分布的均值和方差），然后按照概率分布去采样得到动作 𝑎𝑡 .

经验池 存在的意义是为了消除experience的相关性，因为强化学习中前后动作通常是强相关的，而将它们打散，放入经验池中，然后在训练神经网络时，随机地从经验池中选出一批experience，这样能够使神经网络训练地更好。

 

 

3. Q Critic网络的更新流程

 

 

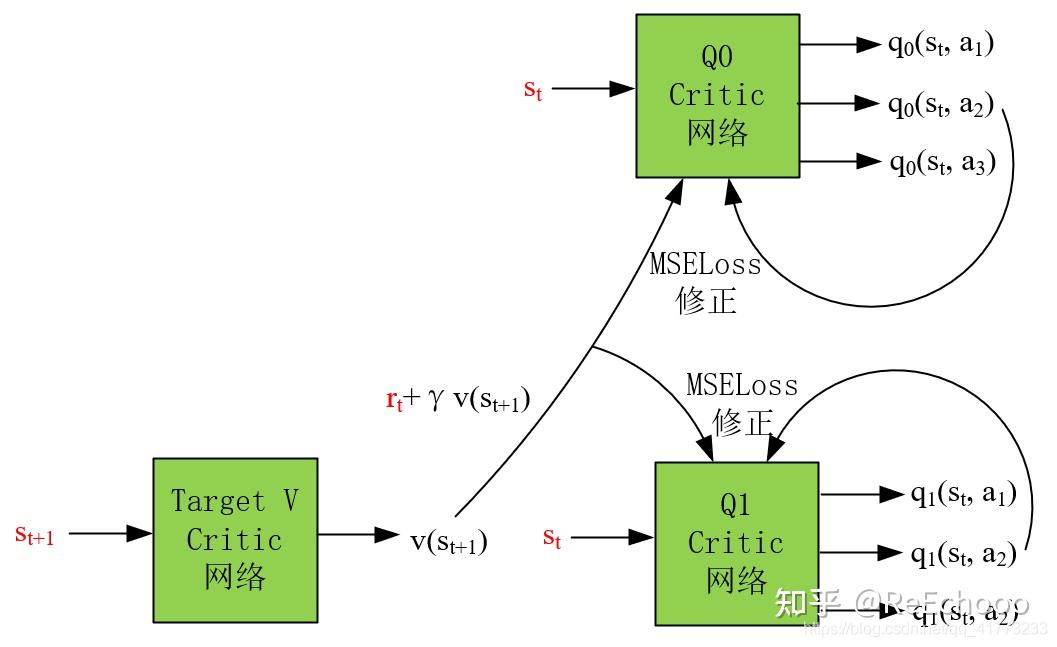
拿从经验池buffer中采出的数据 (𝑠𝑡,𝑎𝑡,𝑠𝑡+1,𝑟𝑡+1) 进行Critic网络的更新，以 (𝑠𝑡,𝑎2,𝑠𝑡+1,𝑟𝑡+1) 为例。

基于最优贝尔曼方程，用 𝑈𝑡(𝑞)=𝑟𝑡+𝛾𝑣(𝑠𝑡+1) 作为状态 𝑠𝑡 的 真实价值估计 ，而用实际采用的动作 𝑎2 的 𝑞𝑖(𝑠𝑡,𝑎2) 值 其中，(其中，𝑖=0,1) 作为状态 𝑠𝑡 的 预测价值估计 ，最后用MSEloss作为Loss函数，对神经网络 𝑄0 , 𝑄1 进行训练。

注意取MSELoss就意味着对 从经验池buffer中取一个batch的数据 进行了 求平均的操作 ，即：

𝐿𝑜𝑠𝑠=1|𝐵|∑(𝑠𝑡,𝑎𝑡,𝑟𝑡+1,𝑠𝑡+1)∈𝐵[𝑞𝑖(𝑠𝑡,𝑎𝑡;𝑤(𝑖))−𝑈𝑡(𝑞)]2

pytorch代码如下：

# train Q critic
        next_v_tensor = self.v_target_net(next_state_tensor)
        q_target_tensor = reward_tensor.unsqueeze(1) + self.gamma * (1. - done_tensor.unsqueeze(1)) * next_v_tensor
        all_q0_pred_tensor = self.q0_net(state_tensor)
        q0_pred_tensor = torch.gather(all_q0_pred_tensor, 1, action_tensor.unsqueeze(1))
        q0_loss_tensor = self.q0_loss(q0_pred_tensor, q_target_tensor.detach())
        self.q0_optimizer.zero_grad()
        q0_loss_tensor.backward()
        self.q0_optimizer.step()

        all_q1_pred_tensor = self.q1_net(state_tensor)
        q1_pred_tensor = torch.gather(all_q1_pred_tensor, 1, action_tensor.unsqueeze(1))
        q1_loss_tensor = self.q1_loss(q1_pred_tensor, q_target_tensor.detach())
        self.q1_optimizer.zero_grad()
        q1_loss_tensor.backward()
        self.q1_optimizer.step()

4. V Critic网络的更新流程

 

 

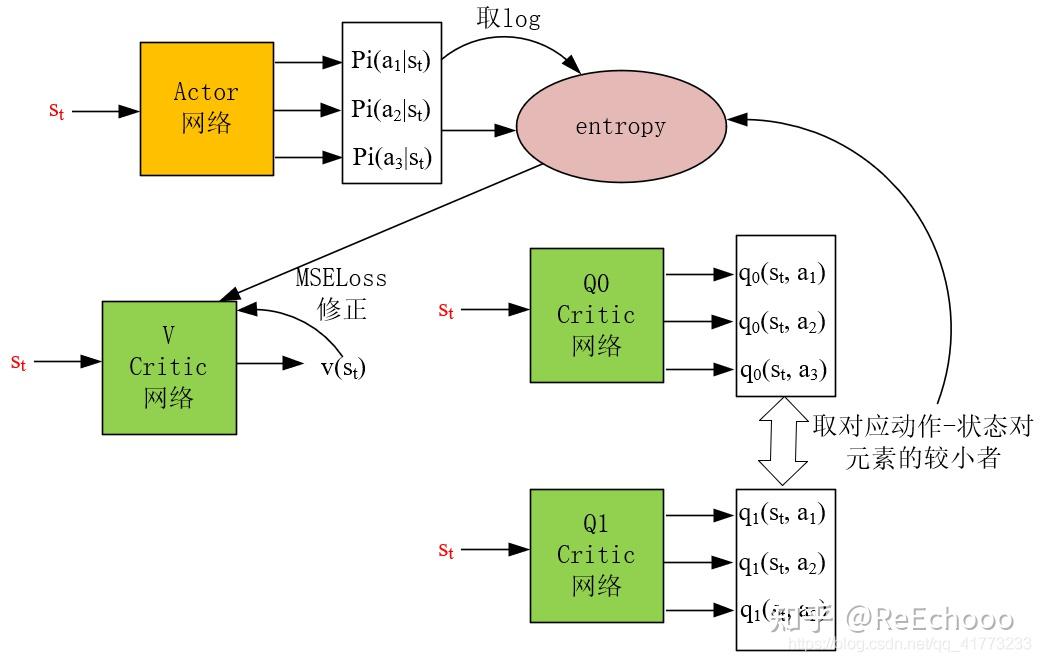
拿从经验池buffer中采出的数据 (𝑠𝑡,𝑎𝑡,𝑠𝑡+1,𝑟𝑡+1) 进行V Critic网络的更新，接着 (𝑠𝑡,𝑎2,𝑠𝑡+1,𝑟𝑡+1) 的例子。

用含熵的式子进行状态价值估计，即下式作为V critic网络输出的真实值：

𝑈𝑡(𝑣)=𝐸𝑎𝑡′∼𝜋(⋅|𝑠𝑡;𝜃)[min𝑖=0,1𝑞𝑖(𝑠𝑡,𝑎𝑡′;𝑤(𝑖))−𝛼ln⁡𝜋(𝑎𝑡′|𝑠𝑡;𝜃)]=∑𝑎𝑡′∈𝐴(𝑠𝑡)𝜋(𝑎𝑡′|𝑠𝑡;𝜃)[min𝑖=0,1𝑞𝑖(𝑠𝑡,𝑎𝑡′;𝑤(𝑖))−𝛼ln⁡𝜋(𝑎𝑡′|𝑠𝑡;𝜃)]

可以看到 𝜋(𝑎𝑡′|𝑠𝑡;𝜃) 、 min𝑖=0,1𝑞𝑖(𝑠𝑡,𝑎𝑡′;𝑤(𝑖)) 、 ln⁡𝜋(𝑎𝑡′|𝑠𝑡;𝜃) 这三项和图中的Loss三个输入箭头完全一致。

用V critic网络的输出作为预测值，最后用MSEloss作为Loss函数，对神经网络 𝑉 进行训练。

注意取MSELoss就意味着对 从经验池buffer中取一个batch的数据 进行了 求平均的操作 ，即：

𝐿𝑜𝑠𝑠=1|𝐵|∑(𝑠𝑡,𝑎𝑡,𝑟𝑡+1,𝑠𝑡+1)∈𝐵[𝑣(𝑠𝑡;𝑤(𝑣))−𝑈𝑡(𝑣)]2

pytorch代码如下：

# train V critic
        q0_tensor = self.q0_net(state_tensor)
        q1_tensor = self.q1_net(state_tensor)
        q01_tensor = torch.min(q0_tensor, q1_tensor)
        prob_tensor = self.actor_net(state_tensor)
        ln_prob_tensor = torch.log(prob_tensor.clamp(1e-6, 1.))
        entropic_q01_tensor = prob_tensor * (q01_tensor -
                self.alpha * ln_prob_tensor)
        # OR entropic_q01_tensor = prob_tensor * (q01_tensor - \
        #         self.alpha * torch.xlogy(prob_tensor, prob_tensor)
        v_target_tensor = torch.sum(entropic_q01_tensor, dim=-1, keepdim=True)
        v_pred_tensor = self.v_evaluate_net(state_tensor)
        v_loss_tensor = self.v_loss(v_pred_tensor, v_target_tensor.detach())
        self.v_optimizer.zero_grad()
        v_loss_tensor.backward()
        self.v_optimizer.step()

        self.update_net(self.v_target_net, self.v_evaluate_net)

 

5. Actor网络的更新流程

 

 

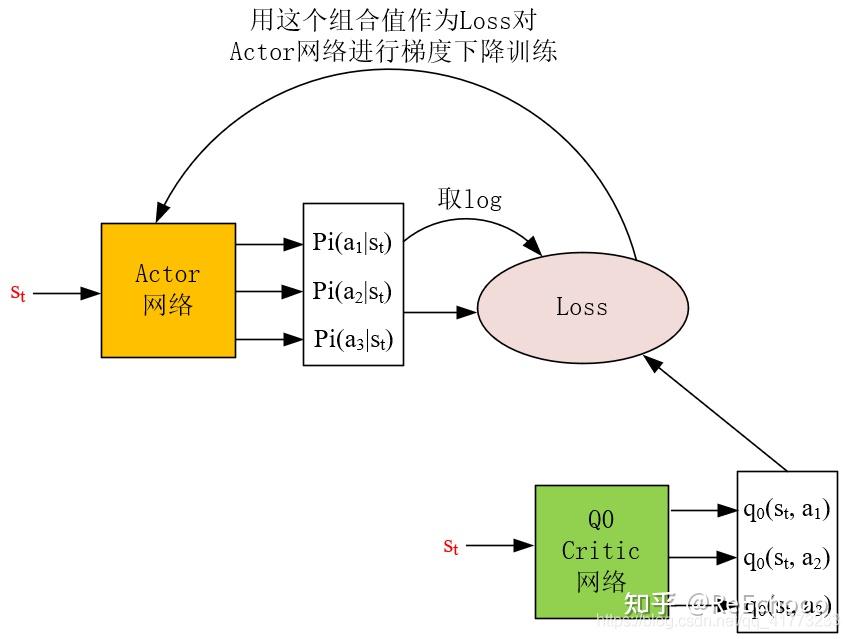
对actor网络训练的loss稍微有些复杂，其表达式为：

𝐿𝑜𝑠𝑠=−1|𝐵|∑(𝑠𝑡,𝑎𝑡,𝑟𝑡+1,𝑠𝑡+1)∈𝐵𝐸𝑎𝑡′∼𝜋(⋅|𝑠𝑡;𝜃)[𝑞0(𝑠𝑡,𝑎𝑡′)−𝛼ln⁡𝜋(𝑎𝑡′|𝑠𝑡;𝜃)]

𝐸𝑎𝑡′∼𝜋(⋅|𝑠𝑡;𝜃)[....] 代表需要对中括号里面的项取期望，注意： 𝑎𝑡′ 并不是在buffer中取出的数据 (𝑠𝑡,𝑎𝑡,𝑟𝑡+1,𝑠𝑡+1) 中的 𝑎𝑡 ，而是重新用actor网络 𝜋 预测的所有可能的动作，因此对于离散动作空间，常有以下的等价计算方法：

𝐸𝑎𝑡′∼𝜋(⋅|𝑠𝑡;𝜃)[𝑞0(𝑠𝑡,𝑎𝑡′;𝑤(0))−𝛼ln⁡𝜋(𝑎𝑡′|𝑠𝑡;𝜃)]=∑𝑎𝑡′∈𝐴(𝑠𝑡)𝜋(𝑎𝑡′|𝑠𝑡;𝜃)[𝑞0(𝑠𝑡,𝑎𝑡′;𝑤(0))−𝛼ln⁡𝜋(𝑎𝑡′|𝑠𝑡;𝜃)]

可以看到 𝜋(𝑎𝑡′|𝑠𝑡;𝜃) 、 𝑞0(𝑠𝑡,𝑎𝑡′;𝑤(0)) 、 ln⁡𝜋(𝑎𝑡′|𝑠𝑡;𝜃) 这三项和图中的Loss三个输入箭头完全一致。需要注意的是 𝑞0(𝑠𝑡,𝑎𝑡′;𝑤(0)) 可以用 𝑞1(𝑠𝑡,𝑎𝑡′;𝑤(1)) 替换，这两个Q critic网络在功能上是等价的。

𝐵 代表经验池buffer，即求Loss的时候还需要对经验池中取出的样本取平均。这样能够体现取出的样本平均意义下的好坏。

其中： 𝛼 是熵的奖励系数，它决定熵 ln⁡𝜋(𝑎𝑡+1|𝑠𝑡;𝜃) 的重要性，越大越重要。

pytorch代码如下：

# train actor
        prob_q_tensor = prob_tensor * (self.alpha * ln_prob_tensor - q0_tensor)
        actor_loss_tensor = prob_q_tensor.sum(axis=-1).mean()
        self.actor_optimizer.zero_grad()
        actor_loss_tensor.backward()
        self.actor_optimizer.step()