强化学习中的奇怪概念(一)——On-policy与off-policy

转自:https://zhuanlan.zhihu.com/p/346433931

本文主要介绍和梳理on-policy/off-policy概念，文章中内容的逻辑结构(同每小节标题)如下：

• 策略需要有探索能力(随机性)
• 策略如何做到随机探索？
• Off-policy方法——将收集数据当做一个单独的任务
• On-policy——行为策略与目标策略相同
• 总结
• 常见困惑
• 困惑1：为什么有时候off-policy需要与重要性采样配合使用？
• 困惑2：为什么Q-Learning算法(或DQN)身为off-policy可以不用重要性采样？
• 困惑3：SARSA算法(on-policy)像是在进行值函数估计，为什么能收敛到最优策略？

2. 策略需要有探索能力(随机性)

抛开RL算法的细节，几乎所有RL算法可以抽象成如下的形式：

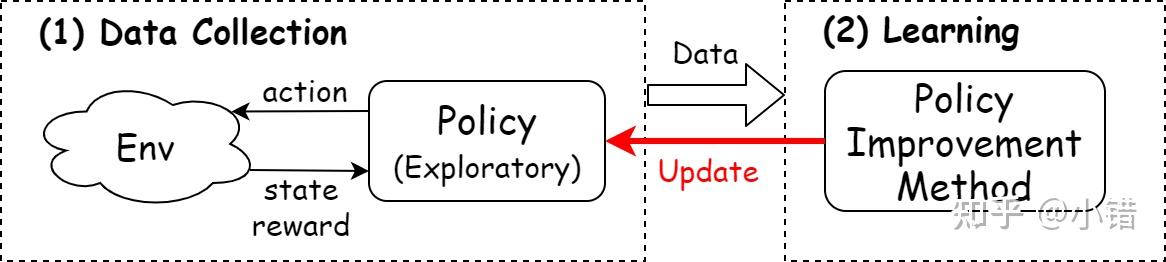
图1 RL算法的两个任务

RL算法中都需要做两件事：(1)收集数据(Data Collection)：与环境交互，收集学习样本; (2)学习(Learning)样本：学习收集到的样本中的信息，提升策略。

RL算法的最终目标是学习每种状态下最优的动作，而在训练过程中，收敛(到最优策略𝜋∗)前的当前策略𝜋并非最优，所以它提供的动作并非最优。为了找到动作空间里潜在的最优动作，算法必须尝试当前策略𝜋认为的非最优的动作，因此RL算法中的策略需要有随机探索(Exploration)的能力。

2. 策略如何做到随机探索

RL算法中的策略分为确定性(Deterministic)策略与随机性(Stochastic)策略:

• 确定性策略𝜋(𝑠)为一个将状态空间𝑆映射到动作空间𝐴的函数，即𝜋:𝑆→𝐴。它本身没有随机性质，因此通常会结合𝜖-greedy或往动作值中加入高斯噪声的方法来增加策略的随机性。
• 随机性策略𝜋(𝐴𝑡|𝑆𝑡)是条件为𝑆𝑡∈𝑆情况下，动作𝐴𝑡的条件概率分布。它本身带有随机性，获取动作时只需对概率分布进行采样即可。

为了能不让思路显得凌乱，本文仅讨论Q函数构造的确定性策略及其增加随机性的方式。用Q函数构造确定性策略是一种常见的策略形式，其具体方式是：

𝜋(𝑠)=arg⁡max𝑎𝑄(𝑠,𝑎)

即选取Q值最大的动作为最优动作。(注意：一般只有在动作空间离散的情况下采用这种策略，若动作空间连续上式中的最大化操作需要经过复杂的优化求解过程。)

可用𝜖-greedy方法将上述确定性策略改造成具有探索能力的策略：

𝜋𝜖(𝑠)={arg⁡max𝑎𝑄(𝑠,𝑎),with probability 1−𝜖random action,with probability 𝜖

即，以𝜖的概率选择随机动作(Exploration)，以1−𝜖的概率按照确定性策略𝜋(𝑠)选取动作。

3. Off-policy方法——将收集数据当做一个单独的任务

(本文尝试另一种解释的思路，先绕过on-policy方法，直接介绍off-policy方法。)

RL算法中需要带有随机性的策略对环境进行探索获取学习样本，一种视角是：off-policy的方法将收集数据作为RL算法中单独的一个任务，它准备两个策略：行为策略(behavior policy)与目标策略(target policy)。行为策略是专门负责学习数据的获取，具有一定的随机性，总是有一定的概率选出潜在的最优动作。而目标策略借助行为策略收集到的样本以及策略提升方法提升自身性能，并最终成为最优策略。Off-policy是一种灵活的方式，如果能找到一个“聪明的”行为策略，总是能为算法提供最合适的样本，那么算法的效率将会得到提升。

我最喜欢的一句解释off-policy的话是：the learning is from the data off the target policy（引自《Reinforcement Learning An Introduction》）。也就是说RL算法中，数据来源于一个单独的用于探索的策略(不是最终要求的策略)。以Q-Learning为例，它的算法流程如下：

图2 Q-Learning算法伪代码

算法流程图不够直观，笔者将算法中的值函数更新式改写成另外一种形式后将算法用图描绘。

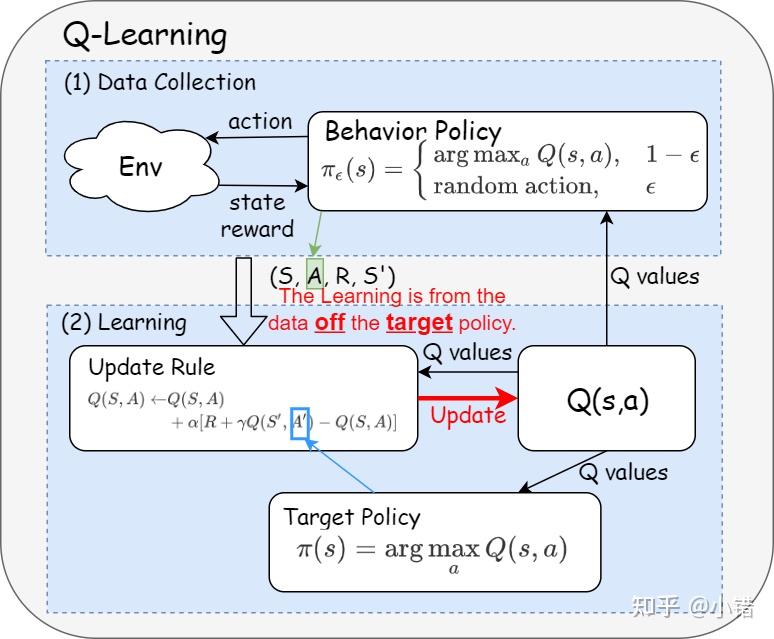
图3 Q-Learning算法流程

如图所示，Q-Learning数据收集部分用的是由Q函数构造的𝜖-greedy策略𝜋𝜖(𝑠)(行为策略)，而它的最终目标是greedy策略 𝜋(𝑠) (目标策略)。Q函数更新规则(update rule)中的训练样本(𝑆,𝐴,𝑅,𝑆′)是由行为策略𝜋𝜖(而非目标策略)提供，因此它是典型的off-policy方法。

困惑1：为什么有时候off-policy需要与重要性采样配合使用？

重要性采样是用一个概率分布的样本来估计某个随机变量关于另一个概率分布的期望。

假设已知随机策略𝜋(𝑎|𝑠)，现在需要估计策略𝜋对应的状态值𝑉𝜋，但是只能用另一个策略 𝜋′(𝑎|𝑠) 获取样本。对于这种需要用另外一个策略的数据(off-policy)来精确估计状态值的任务，需要用到重要性采样的方法，具体做法是在对应的样本估计量上乘上一个权重(𝜋与𝜋′的相对概率)，称为重要性采样率。

以off-policy Monte Carlo估计为例，它的步骤为：

(1) 由𝜋′与环境交互生成一条样本轨迹： (𝑠0,𝑎0,𝑟0,𝑠1,𝑎1,𝑟1...,𝑠𝑇,𝑎𝑇,𝑟𝑇) ，𝑇(𝑠)表示轨迹样本中状态为s时间点的集合。|𝑇(𝑠)|为该集合的元素的总数量。

(2) t时刻之后的轨迹序列关于𝜋与 𝜋′ 的似然分别为∏𝑘=𝑡𝑇𝜋(𝑎𝑘|𝑠𝑘)𝑃𝑟(𝑠𝑘+1|𝑠𝑘,𝑎𝑘)与 ∏𝑘=𝑡𝑇𝜋′(𝑎𝑘|𝑠𝑘)𝑃𝑟(𝑠𝑘+1|𝑠𝑘,𝑎𝑘)，对应的重要性采样率为：

𝜌𝑡𝑇=∏𝑘=𝑡𝑇𝜋(𝑎𝑘|𝑠𝑘)𝑃𝑟(𝑠𝑘+1|𝑠𝑘,𝑎𝑘)∏𝑘=𝑡𝑇𝜋′(𝑎𝑘|𝑠𝑘)𝑃𝑟(𝑠𝑘+1|𝑠𝑘,𝑎𝑘)=∏𝑘=𝑡𝑇𝜋(𝑎𝑘|𝑠𝑘)∏𝑘=𝑡𝑇𝜋′(𝑎𝑘|𝑠𝑘)

(3) t时刻之后的总回报为𝐺𝑡=∑𝑘=𝑡𝑇𝛾𝑘−𝑡𝑟𝑘 。

(4) 按照MC方法估计状态s对应的状态值：

𝑉(𝑠)=∑𝑡∈𝑇(𝑠)𝜌𝑡𝑇𝐺𝑡|𝑇(𝑠)|

最后再次强调，如果需要用off-policy方法估计/预测状态值或动作值时，需要用到重要性采样。

困惑2：为什么Q-Learning算法(或DQN)身为off-policy可以不用重要性采样？

𝑄∗(𝑠,𝑎) 为最优策略对应的Q函数，最优Q函数遵循如下最优贝尔曼等式： $$ 𝑄∗(𝑠,𝑎)=∑𝑠′,𝑟𝑃𝑟(𝑠′,𝑟|𝑠,𝑎)[𝑟+𝛾max𝑎′𝑄∗(𝑠′,𝑎′)]

Q-Learning的思想是从任意初始化的Q函数出发，以最优贝尔曼方程为标准调整Q函数。观察Q函数在第n轮更新时的更新式：

𝑄𝑛+1(𝑆,𝐴)←𝑄𝑛(𝑆,𝐴)+𝛼[𝑅+𝛾max𝑎′𝑄𝑛(𝑆′,𝑎′)−𝑄𝑛(𝑆,𝐴)]

可以看到它实际是以最优贝尔曼的估计量 𝑅+𝛾max𝑎′𝑄𝑛(𝑆′,𝑎′)为目标(target)，让 𝑄𝑛+1(𝑆,𝐴) 尽量该目标。需要注意到：最优贝尔曼等式右侧的期望只与状态转移分布有关而与策略无关，不论训练数据(𝑆,𝐴,𝑅,𝑆′)来自于哪个策略，按照Q-Learning的更新式更新都能使Q函数接近 𝑄∗(𝑠,𝑎) 。因此，Q-Learning可以不采用重要性采样。(DQN算法同理)

4. On-policy——行为策略与目标策略相同

前面提到off-policy的特点是：the learning is from the data off the target policy，那么on-policy的特点就是：the target and the behavior polices are the same。也就是说on-policy里面只有一种策略，它既为目标策略又为行为策略。SARSA算法即为典型的on-policy的算法，下图所示为SARSA的算法示意图，可以看出算法中只有一种策略，训练的数据来自于它。

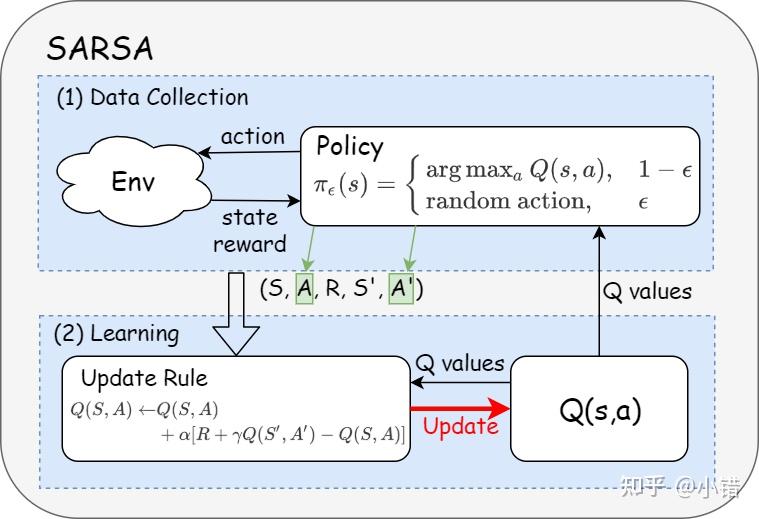
图3 SARSA算法流程

困惑3：SARSA算法(on-policy)像是在进行值函数估计，为什么能收敛到最优策略？

更新式中用到的策略也是𝜖-greedy算法。𝜖的概率是用随机动作，对策略的提升没有帮助；但另外有1−𝜖的概率，按照arg⁡max𝑎𝑄(𝑠,𝑎)选取动作，即对策略进行提升。可以发现𝜖-greedy策略是一种完全不同于用条件概率分布表示的策略，只要𝜖较小，它自带策略提升的功能。

5. 总结

• off-policy的最简单解释: the learning is from the data off the target policy。
• On/off-policy的概念帮助区分训练的数据来自于哪里。
• Off-policy方法中不一定非要采用重要性采样，要根据实际情况采用（比如，需要精确估计值函数时需要采用重要性采样；若是用于使值函数靠近最优值函数则不一定）。

一个人埋头学习强化学习几年，最近才想着多和别人交流。发现挺多初学者和我当初一样面对强化学习的一些奇怪的概念感到云里雾里，最典型的就是On-policy/off-policy与on-line/off-line概念傻傻分不清楚。RL的研究者构造这些概念的目的是为了更好地区分不同算法间的细节，强调不同算法之间的本质区别，但对初学者来说这些概念可能却成为学习强化学习路上的一个绊脚石。写这篇文章的目的是希望帮助对相关概念(如on/off-policy和on/off-line)有困惑的读者理解它们的本质。需要强调的是这些概念是用于理解RL算法的细节差异，不应该成为一种死板的概念，如果不能抓住它背后的本质，只是单纯知道如何区分算法是on-policy还是off-policy是on-line还是off-line没有太大意义。