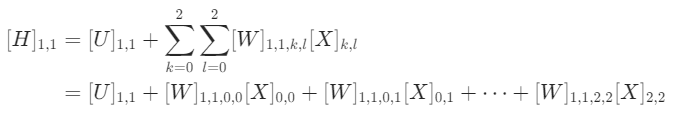卷积理解
全连接层公式的解析
整体理解
该公式描述的是全连接层如何将输入图像的像素信息转换为隐藏表示的像素信息。全连接层的目的是让每个隐藏神经元都能接收来自每个输入像素的信息,从而实现对输入图像的特征提取和表示。
公式细节
- 偏置项:公式中的\([U]_{i,j}\)是偏置参数,它为每个隐藏表示位置\((i, j)\)处的像素提供了一个基础值,不依赖于输入图像,用于调整隐藏神经元的激活程度。
- 权重张量与输入图像的乘积:\(\sum_{k}\sum_{l}[W]_{i,j,k,l}[X]_{k,l}\)这部分表示将四阶权重张量W与输入图像X进行乘积求和操作。权重张量W的维度是\((i, j, k, l)\),其中\((i, j)\)对应隐藏表示的位置,\((k, l)\)对应输入图像的位置。通过对所有输入图像像素位置\((k, l)\)进行求和,实现了每个隐藏神经元与所有输入像素的连接,\([W]_{i,j,k,l}\)表示了从输入图像位置\((k, l)\)到隐藏表示位置\((i, j)\)的连接权重。
- 等价形式:\(\sum_{a}\sum_{b}[V]_{i,j,a,b}[X]_{i+a,j+b}\)是公式的另一种等价表示形式。这里的\([V]_{i,j,a,b}\)也是一种权重参数,它表示从输入图像中以\((i, j)\)为基准偏移\((a, b)\)位置的像素到隐藏表示位置\((i, j)\)的权重。这种形式更强调了权重与输入图像像素位置的相对关系。
与多层感知机的对比
在多层感知机中,通常使用权重矩阵来实现输入到隐藏层的映射。而这里使用四阶权重张量是为了更好地处理图像数据这种具有二维空间结构的数据。权重矩阵只能处理一维的输入特征向量,无法直接考虑图像像素的二维空间关系。使用四阶权重张量可以更灵活地对图像的不同位置进行加权求和,从而更好地捕捉图像中的空间特征。
计算过程示例
假设输入图像X是一个\(3\times3\)的矩阵,隐藏表示H也是一个\(3\times3\)的矩阵。权重张量W的维度为\((3, 3, 3, 3)\),偏置参数U是一个\(3\times3\)的矩阵。对于隐藏表示H中位置\((1, 1)\)处的像素\([H]_{1,1}\),其计算过程为: