[翻译]卷积计算细节：矩阵乘法实现卷积

0. 介绍

在本文中，我将解释如何将2D卷积实现为矩阵乘法。 该说明来自于CS231n(用于视觉识别的卷积神经网络)的笔记。 大家应该已经熟悉深度神经网络中卷积运算的概念。 如果没有，这个代码仓库有十分形象的动画来演示说明什么是卷积。 可以在此处下载用于重现本文计算内容的代码。

1. 正文

1.1 来看一个小例子

介绍现在有一个4x4的图像X，其像素值如图所示：

 

 

同时我们来定义一个二维卷积的参数

kernel size: 2x2
padding: 0 
stride: 1
bias: 0
output channels: 1 
initial weights W: [[1,2],[3,4]]

这样就总共有了9个2X2的patch

想想这是为什么？下面的图解很好解释了这个问题

 

 

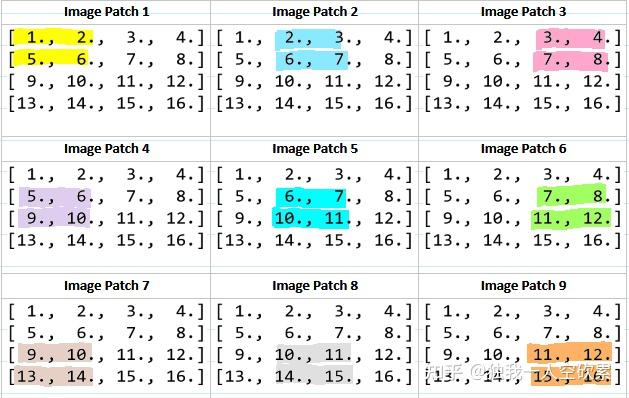
而每一个patch可以展开成4维的列向量得到矩阵P，颜色与上图都是一一对应的呢！

同理，将卷积核铺平成列向量K长得就是这个样子

 

 

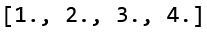
大功告成 !

做一做简单矩阵乘法得到结果

 

 

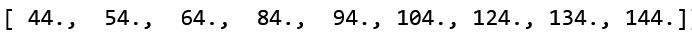
然后做一个简单的reshape得到最终结果

 

 

当然要注意到的是这里我们没有使用padding,就是使用了也无非是在image加零进行同样的操作。

1.2 再来一个大例子

1+1=2 总是简单的，如果输入，输出都是多个通道又是怎么回事呢？

想想呀！

这里我们假设输入为三通道，输出为二通道，其余不变，先来看看输入矩阵

 

 

再来看看卷积核，这里我认为你已经十分明确了解卷积核的概念。重复一次，对于3输入2输出的要求，应该有3*2=6个卷积核。

 

 

这里的铺平只是多了几步而已。

1. 输入： 将同一位置的patch按通道顺序铺平形成矩阵
2. 卷积核： 将每一组卷积核铺平成列向量
3. 做矩阵乘法
4. reshape 还原为矩阵形式

上图解！

输入和卷积核的展开

 

 

 

 

结果

 

 

2. 有啥用？

为什么我们要深入理解这个细节呢？从学术角度来讲，He et. al. (2015)利用矩阵乘法和矩阵的特性获得了更好的初始化方法，从挣钱的角度，译者本人在面试的时候被问道了这个问题，如果能答出来，想必也是让人耳目一新吧！

3. 总结

本文利用两个例子说明了矩阵乘法如何实现2D卷积，如果有什么不懂还请在下方留言告知我。

但是呢！

如果是1D卷积呢？ 想想！原文中也做了解释呢！

 

转自：https://zhuanlan.zhihu.com/p/360859627