P13099 [FJCPC 2025] VERTeX 题解

P13099 [FJCPC 2025] VERTeX 题解

题目传送门
这里提供一种大常数无脑做法。
我们注意到每一条边限定其相邻两个节点。
在 \(N-1\) 条边全都给出后，各节点间的线性关系应都能确定下来。
此时我们可以设 \(1\) 号节点的权值为 \(k\)，即可用 \(k\) 表示出所有节点的权值。
对于样例 \(2\) 即有如下图的表示

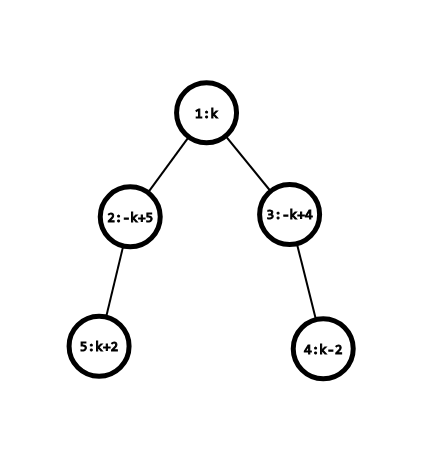
我们注意到所有节点的权值可分为 \(k+b (b \in \mathbb{R})\) 与 \(-k+b (b \in \mathbb{R})\) 两种表示，因此我们将其分为两个集合 \(S_0=\{x \mid x=-k+b\}\) 与 \(S_1=\{x \mid x=k+b\}\)
并定义

\[\begin{cases} l_0=\min \limits_{x \in S_0} (x+k)\\ l_1=\min \limits_{x \in S_1} (x-k)\\ r_0=\max \limits_{x \in S_0} (x+k)\\ r_1=\max \limits_{x \in S_1} (x-k) \end{cases} \]

（其实就是取了常数部分）
易得 \(k\) 的取值合法当且仅当满足：

\[\begin{cases} l_0-k>0\\ l_1+k>0\\ r_0-k<inf\\ r_1+k<inf \end{cases} \]

化简后即为

\[\max(-l_1,r_0-inf)<k<\min(l_0,inf-r_1) \]

最后输出时钦定一个合法的 \(k\) 值即可。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
const int inf=1e9;
int n,k[2][N],l0=0x3f3f3f3f,l1=0x3f3f3f3f,r0=-0x3f3f3f3f,r1=-0x3f3f3f3f,kl,kr,kk;
vector<pair<int,int>> s[N];
pair<bool,int> o[N];
void dfs(int x,int fa){
	for(auto p:s[x]){
		if(p.first==fa) continue;
		bool opt=o[x].first^1;
		o[p.first].first=opt;
		o[p.first].second=p.second-o[x].second;
		k[opt][++k[opt][0]]=o[p.first].second;
		dfs(p.first,x);
	}
}
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
	cin>>n;
	for(int i=1,u,v,w;i<n;i++){
		cin>>u>>v>>w;
		s[u].push_back(make_pair(v,w));
		s[v].push_back(make_pair(u,w));
	}
	o[1].first=1;
	dfs(1,0);
	for(int i=1;i<=k[0][0];i++) l0=min(l0,k[0][i]);
	for(int i=1;i<=k[1][0];i++) l1=min(l1,k[1][i]);
	for(int i=1;i<=k[0][0];i++) r0=max(r0,k[0][i]);
	for(int i=1;i<=k[1][0];i++) r1=max(r1,k[1][i]);
	kl=max(-l1,r0-inf);
	kr=min(l0,inf-r1);
	if((kl>=kr)||kr-1<=0){
		cout<<"NO";
		return 0;
	}
	cout<<"YES"<<'\n';
	kk=kr-1;
	for(int i=1;i<=n;i++) cout<<kk*(o[i].first ? 1 : -1)+o[i].second<<' ';
}