[hdu6566]The Hanged Man

A. The Hanged Man on hdu

给 \(n\) 个节点的一棵树 \((V,E)\)，每个节点有权值 \(a_i,b_i\)，定义：

\(f(x)\) 为：在树上选一些节点得到节点集合 \(S\) 满足 \(\forall (u,v) \in E:u\notin S \lor v\notin S\)，\(f(x)\) 为这些集合中满足 \(\sum _{i\in S} a_i=x\) 且 \(\sum _{i\in S}b_i\) 最大化的个数。求 \(1 \sim m\) 的 \(f(x)\)。

\(1\le n\le50, 1 \le a_i\le m \le 5000, b_i \le 10^6\)

易得暴力 dp。\(f_{i,j,0/1}\) 为节点 \(i\) 选/不选时，和为 \(j\) 的方案数，注意要维护一个辅助的数组表示最大值。

这里树上背包合并 \(\mathcal O(m^2)\) 无法承受，考虑转为熟悉的序列背包合并（单次 \(\mathcal O(m)\)，总共 \(n\) 次）。

将节点按树上 \(\tt dfs\) 序重标号后转移。考虑 \(i \to i+1\) 时的情况。

1. \(\mathrm{fa}_{i+1}=i\)，这种情况最好，只需使用 \(i\) 的信息转移即可。
2. \(\mathrm{fa}_{i+1}\neq i\)，\(i+1\) 跳到另一棵子树去了。这时就要求我们之前转移时得存下它的父亲。哪些是需要存的呢？

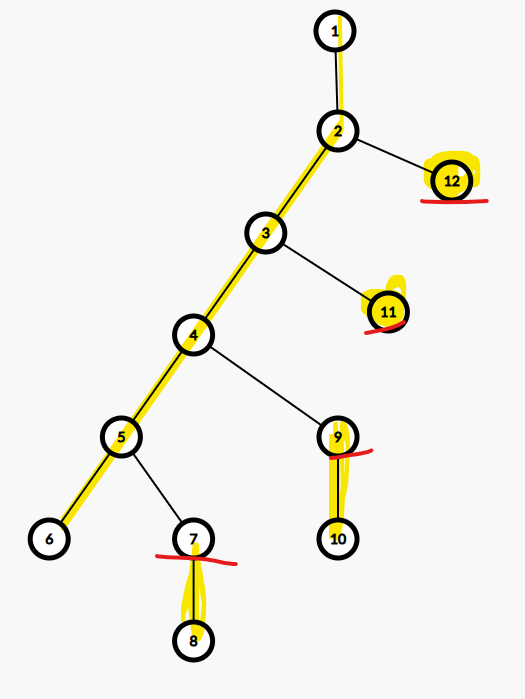
如图，用红色标记出来的是跳跃的点，他们的父亲都是需要提前存下来的。可以看出，树由若干个 \(\tt dfs\) 序连续的链条剖开了。除了包含 \(1\) 的链，其他的链链顶的父亲都需提前记录以消除后效性。对于每个节点，我们需要记录的是位于其所在链上的每个满足是一个链顶的父亲的节点（这个链顶 \(\tt dfs\) 序大于当前节点，且深度不超过当前节点），这一块用状压实现。如果是一条链上长了很多节点，复杂度就会上天，最高可达 \(\mathcal O(2^\frac{n}{2})\)。

这种树的剖分结构影响复杂度的问题，很自然能想到重链剖分，我们知道，重剖后一个节点到祖先的路径上最多只有 \(\mathcal O(\log n)\) 条轻边，尝试着把这个应用进去。

考虑一个非常规的树剖，记录 \(\tt dfs\) 序时优先往轻边走。然后就可以发现每个节点需要额外记录的仅有 \(\mathcal O(\log n)\) 个点。这样子就不会出现一个节点 \(u\) 的重儿子所在子树往轻儿子中跳，只会从某个轻子树跳到 \(u\) 的一个儿子。这样的话，尽管 \(u\) 会被某个轻儿子记录下来，但这一定是经过了一条轻边，字数大小砍半了的，因此一个节点只会额外记录除它自己的 \(\mathcal O(\log n)\) 个节点，状压复杂度为 \(\mathcal O(2^{\log n})=\mathcal O(n)\)。（真是奇了！）

于是我们改一下 dp：\(f_{i,S,j}\) 表示当前转移到 \(\tt dfs\) 序为 \(i\) 的节点 \(u\)，\(u\) 记录的节点和它自己的是否被选的状态为 \(S\)，\(j\) 表示已选物品总体积 \(\sum a_k\) 的值。

然后转移就简单了。复杂度降为 \(\mathcal O(n^2m)\) 轻松跑过。

几个实现 Hint：提前跳轻边找到所有需记录的节点，然后在转移时建立映射方便 \(S\) 的转移。使用二元结构体来方便转移 \(f,g\)，大大增强可读性。

Click to find the code

#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define pb push_back
#define eb emplace_back
const int N = 64, M = 10005, mod = 998244353, inf = 0xc0c0c0c0c0c0c0c0;
template<typename Tp>
inline void tomax(Tp& x, Tp y) { x = x < y ? y : x; }
template<typename Tp>
inline void tomin(Tp& x, Tp y) { x = x < y ? x : y; }
int n, m, a[N], b[N];
vector<int> G[N];
int sz[N], son[N], tp[N], fa[N];
void dfs1(int x, int fa) {
    sz[x] = 1, son[x] = 0;
    ::fa[x] = fa;
    for (auto y : G[x]) {
        if (y == fa) continue;
        dfs1(y, x);
        sz[x] += sz[y];
        if (!son[x] || sz[y] > sz[son[x]]) son[x] = y;
    }
}
int dfn[N], nfd[N], dfc;
void dfs2(int x, int top, int fa=0) {
    dfn[x] = ++dfc, tp[x] = top;
    nfd[dfc] = x;
    for (auto y : G[x]) {
        if (y == fa || y == son[x]) continue;
        dfs2(y, y, x);
    }
    if (son[x]) dfs2(son[x], top, x);
}
struct node {
    int v, c;
    inline friend node& operator += (node& a, const node& b) {
        if (a.v < b.v) a.v = b.v, a.c = b.c;
        else if (a.v == b.v) a.c += b.c;
        return a;
    }
} f[2][N][M];
vector<int> lin[N];
inline void solve() {
    cin >> n >> m;
    _f(i, 1, n) cin >> a[i] >> b[i], G[i].clear();
    _f(i, 2, n) {
        int u, v;
        cin >> u >> v;
        G[u].eb(v), G[v].eb(u);
    }
    dfc = 0;
    dfs1(1, 0), dfs2(1, 1);
    _f(i, 1, n) {
        lin[dfn[i]].clear();
        for (int u = i; u; u = fa[tp[u]]) lin[dfn[i]].eb(u);
    }
    memset(f[1], 0, sizeof(f[1]));
    f[1][0][0] = {0, 1}, f[1][1][a[nfd[1]]] = {b[nfd[1]], 1};
    _f(x, 2, n) {
        int s = lin[x-1].size(), t = lin[x].size(), p;
        static int mp[N];
        memset(mp, -1, sizeof(mp));
        memset(f[x&1], 0, sizeof(f[x&1]));
        for (int i = 0; i < s; ++i) {
            if (lin[x-1][i] == fa[nfd[x]]) p = i;
            for (int j = 0; j < t; ++j) if (lin[x-1][i] == lin[x][j]) mp[i] = j; 
        }
        for (int msk = 0; msk < 1<<s; ++msk) {
            int cur = 0;
            for (int i = 0; i < s; ++i) if ((msk>>i&1) && ~mp[i]) cur |= 1<<mp[i];
            _f(i, 0, m) if (f[x-1&1][msk][i].c) {
                f[x&1][cur][i] += f[x-1&1][msk][i];
                if (!(msk>>p&1) && i+a[nfd[x]] <= m)
                    f[x&1][cur|1][i+a[nfd[x]]] += {f[x-1&1][msk][i].v+b[nfd[x]], f[x-1&1][msk][i].c};
            }
        }
        
    }
    _f(i, 1, m) {
        node res={0,0};
        for (int msk = 0; msk < (1<<lin[n].size()); ++msk)
            res += f[n&1][msk][i];
        cout << res.c << (i == m ? '\n' : ' ');
    }
}
signed main() {
    FASTIO;
    int _; cin >> _;
    _f(_t, 1, _) {
        cout << "Case " << _t << ":\n";
        solve();
    }
    return 0;
}