NOIP 复习(dp 杂题)
全是 dp 呀??????????????????????
Day 1
A. 前往大都会 on loj 完整数据
跑单源最短路得到 \(d\) 解决了第一问,建出最短路图,其中的每条边 \((u,v,w)\) 都满足 \(d_v=d_u+w\)。
然后这就是个有向无环图,按 \(d\) 排序就是一个拓扑序。
问题变成在这个有向无环图上找一个路径最大化平方和。最短路图把原图中的铁路划分成了若干段,我们在分段斜优就行了。不是很常规,写的比较奇怪。
一开始一直 92 是因为斜率优化写错了(维护成直线了,应维护点集构成的凸壳算截距)。
B. Circular Barn P on luogu
过于水了……
首先起手式断环成链。我的做法是枚举第一个区间的长度然后直接 dp 就行了。暴力 dp 是 \(\mathcal O(n^2k)\) 所以用决策单调性分治优化成 \(\mathcal O(nk\log n)\)。总复杂度 \(\mathcal O(n^2k\log n)\)。
有点卡常,因为存在 \(O(n^2k)\) 的做法。
C. 小 \(\omega\) 的仙人掌 on becoder
有可能点不进去,讲讲题意。
给你一个二元组 \((a_i,b_i)\) 序列,求最小的区间 \([l,r]\) 的长度,其中 \([l,r]\) 满足这里面的每个二元组选或不选,使得 \(\sum {a_i} = w\) 且 \(\sum b_i \le k,1 \le a_i \le w \le 5 \times 10^3, 1 \le k \le 10^9, 1 \le s \le 10^4\)。如果无解,请输出 “-1”。
从小到大枚举 \(l\) 并找到维护最小满足条件的 \(r\)。\(r\) 不会往前移动,\(l\) 也只会向前,因此就是一个队列扫过去。麻烦就在怎么动态维护队列上的背包,因为背包是个不可删除之物(但可以撤销)。
于是就有了双栈模拟队列,左边一个右边一个,两个腚对腚,头就朝外,左栈需维护从栈底到栈顶的每一次背包转移后的 dp 数组,右栈只需维护栈顶的 dp 数组即可。询问时直接左栈右栈背包合并即可(因为只查一个值,所以是 \(\mathcal O(w)\))。左栈弹空了,就把右栈全删了倒左栈里(没错要有这个勇气)。
每个元素只会被进入右栈一次,弹出右栈一次,倒左栈里一次,弹出左栈里一次,复杂度为 \(\mathcal O(ws)\) (加上背包转移和合并)。
这道题真真是一个很典的技巧了, 可是仍未想到。
Click to view the code
#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define LL long long
#define PII pair<int,int>
#define pb push_back
#define eb emplace_back
const int N = 4e5+5, mod = 998244353, inf = 0x3f3f3f3f;
template<typename Tp>
inline void tomax(Tp& x, Tp y) { x = x < y ? y : x; }
template<typename Tp>
inline void tomin(Tp& x, Tp y) { x = x < y ? x : y; }
int n, m, k;
int a[N], b[N];
stack<pair<int, vector<int>>> s1;
int s2[N], tp;
vector<int> t2(1, 0);
inline void ins(vector<int>& f, int x) {
_r(i, m, a[x]) f[i] = min(f[i-a[x]]+b[x], f[i]);
}
inline void pour() {
fill(t2.begin(), t2.end(), inf);
t2[0] = 0;
vector<int> tm(t2);
_r(i, tp, 1) ins(tm, s2[i]), s1.emplace(s2[i], tm);
tp = 0;
}
inline void pop() {
if (s1.empty()) pour();
if (s1.size()) s1.pop();
}
inline int merge(const vector<int> &a, const vector<int> &b) {
int res = inf;
_f(i, 0, m) res = min(res, a[i]+b[m-i]);
return res;
}
int main() {
FASTIO;
cin >> n >> m >> k;
_f(i, 1, n) cin >> a[i] >> b[i];
t2.resize(m+1, inf);
t2[0] = 0;
int ans = n+1;
for (int l = 1, r = 0; l <= n; ++l) {
while (r < n && (s1.size()?merge(t2, s1.top().second):t2[m]) > k) ins(t2, ++r), s2[++tp] = r;
if ((s1.size()?merge(t2, s1.top().second):t2[m]) > k) break;
ans = min(ans, r-l+1);
pop();
}
cout << (ans == n + 1 ? -1 : ans);
return 0;
}
Day 2
A. The Hanged Man on hdu
😭这题出的直击痛点,骇死人了。
给 \(n\) 个节点的一棵树 \((V,E)\),每个节点有权值 \(a_i,b_i\),定义:
\(f(x)\) 为:在树上选一些节点得到节点集合 \(S\) 满足 \(\forall (u,v) \in E:u\notin S \lor v\notin S\),\(f(x)\) 为这些集合中满足 \(\sum _{i\in S} a_i=x\) 且 \(\sum _{i\in S}b_i\) 最大化的个数。求 \(1 \sim m\) 的 \(f(x)\)。
\(1\le n\le50, 1 \le a_i\le m \le 5000, b_i \le 10^6\)
易得暴力 dp。\(f_{i,j,0/1}\) 为节点 \(i\) 选/不选时,和为 \(j\) 的方案数,注意要维护一个辅助的数组表示最大值。
这里树上背包合并 \(\mathcal O(m^2)\) 无法承受,考虑转为熟悉的序列背包合并(单次 \(\mathcal O(m)\),总共 \(n\) 次)。
将节点按树上 \(\tt dfs\) 序重标号后转移。考虑 \(i \to i+1\) 时的情况。
- \(\mathrm{fa}_{i+1}=i\),这种情况最好,只需使用 \(i\) 的信息转移即可。
- \(\mathrm{fa}_{i+1}\neq i\),\(i+1\) 跳到另一棵子树去了。这时就要求我们之前转移时得存下它的父亲。哪些是需要存的呢?
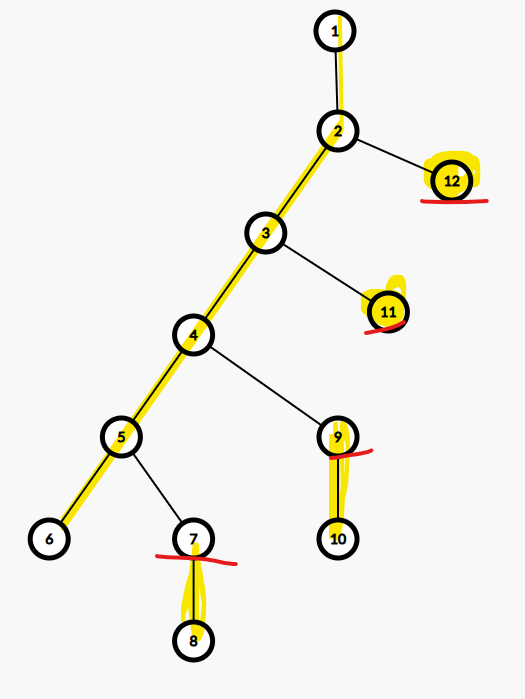
如图,用红色标记出来的是跳跃的点,他们的父亲都是需要提前存下来的。可以看出,树由若干个 \(\tt dfs\) 序连续的链条剖开了。除了包含 \(1\) 的链,其他的链链顶的父亲都需提前记录以消除后效性。对于每个节点,我们需要记录的是位于其所在链上的每个满足是一个链顶的父亲的节点(这个链顶 \(\tt dfs\) 序大于当前节点,且深度不超过当前节点),这一块用状压实现。如果是一条链上长了很多节点,复杂度就会上天,最高可达 \(\mathcal O(2^\frac{n}{2})\)。
这种树的剖分结构影响复杂度的问题,很自然能想到重链剖分,我们知道,重剖后一个节点到祖先的路径上最多只有 \(\mathcal O(\log n)\) 条轻边,尝试着把这个应用进去。
考虑一个非常规的树剖,记录 \(\tt dfs\) 序时优先往轻边走。然后就可以发现每个节点需要额外记录的仅有 \(\mathcal O(\log n)\) 个点。这样子就不会出现一个节点 \(u\) 的重儿子所在子树往轻儿子中跳,只会从某个轻子树跳到 \(u\) 的一个儿子。这样的话,尽管 \(u\) 会被某个轻儿子记录下来,但这一定是经过了一条轻边,字数大小砍半了的,因此一个节点只会额外记录除它自己的 \(\mathcal O(\log n)\) 个节点,状压复杂度为 \(\mathcal O(2^{\log n})=\mathcal O(n)\)。(真是奇了!)
于是我们改一下 dp:\(f_{i,S,j}\) 表示当前转移到 \(\tt dfs\) 序为 \(i\) 的节点 \(u\),\(u\) 记录的节点和它自己的是否被选的状态为 \(S\),\(j\) 表示已选物品总体积 \(\sum a_k\) 的值。
然后转移就简单了。复杂度降为 \(\mathcal O(n^2m)\) 轻松跑过。
几个实现 Hint:提前跳轻边找到所有需记录的节点,然后在转移时建立映射方便 \(S\) 的转移。使用二元结构体来方便转移 \(f,g\),大大增强可读性。
Click to find the code
#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define pb push_back
#define eb emplace_back
const int N = 64, M = 10005, mod = 998244353, inf = 0xc0c0c0c0c0c0c0c0;
template<typename Tp>
inline void tomax(Tp& x, Tp y) { x = x < y ? y : x; }
template<typename Tp>
inline void tomin(Tp& x, Tp y) { x = x < y ? x : y; }
int n, m, a[N], b[N];
vector<int> G[N];
int sz[N], son[N], tp[N], fa[N];
void dfs1(int x, int fa) {
sz[x] = 1, son[x] = 0;
::fa[x] = fa;
for (auto y : G[x]) {
if (y == fa) continue;
dfs1(y, x);
sz[x] += sz[y];
if (!son[x] || sz[y] > sz[son[x]]) son[x] = y;
}
}
int dfn[N], nfd[N], dfc;
void dfs2(int x, int top, int fa=0) {
dfn[x] = ++dfc, tp[x] = top;
nfd[dfc] = x;
for (auto y : G[x]) {
if (y == fa || y == son[x]) continue;
dfs2(y, y, x);
}
if (son[x]) dfs2(son[x], top, x);
}
struct node {
int v, c;
inline friend node& operator += (node& a, const node& b) {
if (a.v < b.v) a.v = b.v, a.c = b.c;
else if (a.v == b.v) a.c += b.c;
return a;
}
} f[2][N][M];
vector<int> lin[N];
inline void solve() {
cin >> n >> m;
_f(i, 1, n) cin >> a[i] >> b[i], G[i].clear();
_f(i, 2, n) {
int u, v;
cin >> u >> v;
G[u].eb(v), G[v].eb(u);
}
dfc = 0;
dfs1(1, 0), dfs2(1, 1);
_f(i, 1, n) {
lin[dfn[i]].clear();
for (int u = i; u; u = fa[tp[u]]) lin[dfn[i]].eb(u);
}
memset(f[1], 0, sizeof(f[1]));
f[1][0][0] = {0, 1}, f[1][1][a[nfd[1]]] = {b[nfd[1]], 1};
_f(x, 2, n) {
int s = lin[x-1].size(), t = lin[x].size(), p;
static int mp[N];
memset(mp, -1, sizeof(mp));
memset(f[x&1], 0, sizeof(f[x&1]));
for (int i = 0; i < s; ++i) {
if (lin[x-1][i] == fa[nfd[x]]) p = i;
for (int j = 0; j < t; ++j) if (lin[x-1][i] == lin[x][j]) mp[i] = j;
}
for (int msk = 0; msk < 1<<s; ++msk) {
int cur = 0;
for (int i = 0; i < s; ++i) if ((msk>>i&1) && ~mp[i]) cur |= 1<<mp[i];
_f(i, 0, m) if (f[x-1&1][msk][i].c) {
f[x&1][cur][i] += f[x-1&1][msk][i];
if (!(msk>>p&1) && i+a[nfd[x]] <= m)
f[x&1][cur|1][i+a[nfd[x]]] += {f[x-1&1][msk][i].v+b[nfd[x]], f[x-1&1][msk][i].c};
}
}
}
_f(i, 1, m) {
node res={0,0};
for (int msk = 0; msk < (1<<lin[n].size()); ++msk)
res += f[n&1][msk][i];
cout << res.c << (i == m ? '\n' : ' ');
}
}
signed main() {
FASTIO;
int _; cin >> _;
_f(_t, 1, _) {
cout << "Case " << _t << ":\n";
solve();
}
return 0;
}
🏆 牛 trick + 今日最麻烦的题
B. 旅行 on newcoder on becoder
发现从 \(S\to T\) 路径上的任一个点出发 dp 出 \(S\) 和 \(T\) 的背包后就很好做了,合并只需 \(\mathcal O(k)\)。
大水,把询问离线下来点分治即可。复杂度 \(\mathcal O((n+q)k \log n)\) 看着很大,但点分治常数挺小的。
Click to seek the code
#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define pb push_back
#define eb emplace_back
const int N = 200005, M = 50, mod = 998244353, inf = 0xc0c0c0c0c0c0c0c0;
template<typename Tp>
inline void tomax(Tp& x, Tp y) { x = x < y ? y : x; }
template<typename Tp>
inline void tomin(Tp& x, Tp y) { x = x < y ? x : y; }
int n, m, q, a[N];
vector<int> G[N];
vector<int> qu[N];
int sz[N], s[N], t[N];
int rt, mx, sum;
bool del[N];
void getrt(int x, int fa) {
static int root;
if (!fa) root = x;
int re = 0;
sz[x] = 1;
for (auto y : G[x]) {
if (y == fa || del[y]) continue;
getrt(y, x);
sz[x] += sz[y];
re = max(re, sz[y]);
}
re = max(re, sum-sz[x]);
if (!rt || mx > re) mx = re, rt = x;
}
struct node {
int id, x, bj;
};
int res[N];
int f[N][M];
void calc(int x) {
static node p[N<<1];
int t = 0, cnt = 0;
for (auto it : qu[x]) p[++t] = {it, x, 0};
function<void(int, int)> dfs;
dfs = [&](int x, int fa) {
for (auto it : qu[x]) p[++t] = {it, x, cnt};
for (int i = 0; i < m; ++i) f[x][(i+a[x])%m] = (f[fa][i]+f[fa][(i+a[x])%m])%mod;
for (auto y : G[x]) {
if (del[y] || y == fa) continue;
dfs(y, x);
}
};
memset(f[x], 0, sizeof(f[x]));
f[x][0]=1;
for (auto y : G[x])
if (!del[y])
++cnt, dfs(y, x);
stable_sort(p+1, p+t+1, [](const node& a, const node& b) { return a.id < b.id; });
_f(i, 2, t) {
auto [id, S, c] = p[i-1];
auto [id2, T, b] = p[i];
if (id==id2&&(c^b)) {
res[id] = 0;
for (int j = 0; j < m; ++j) (res[id] += (f[S][j]+f[S][(j-a[x]+m)%m])*f[T][(m-j)%m]) %= mod;
}
}
}
void divide(int x) {
del[x] = 1, calc(x);
for (auto y : G[x])
if (!del[y])
rt = mx = 0, sum = sz[y], getrt(y, 0), divide(rt);
}
inline void solve() {
cin >> n >> m;
_f(i, 1, n) G[i].clear(), qu[i].clear();
_f(i, 2, n) {
int u, v;
cin >> u >> v;
G[u].eb(v), G[v].eb(u);
}
_f(i, 1, n) cin >> a[i], a[i] %= m;
cin >> q;
_f(i, 1, q) {
cin >> s[i] >> t[i];
if (s[i]^t[i]) qu[s[i]].eb(i), qu[t[i]].eb(i);
else res[i] = 1+(!a[s[i]]);
}
rt = mx = 0, sum = n, getrt(1, 0), divide(rt);
_f(i, 1, q) cout << res[i] << '\n';
}
signed main() {
FASTIO;
int _ = 1;
// cin >> _;
_f(_t, 1, _) solve();
return 0;
}
C. Resurrection on luogu
比较奇了。首先最终的图一定是棵树。以 \(n\) 为根,则题目所给性质可转变为 \(\mathrm{fa}_i >i\)。考虑断一条边 \((u, \mathrm{fa}_u)\),则 \(u\) 所在连通块选的节点就是 \(u\),\(\mathrm{fa_u}\) 所在连通块选的是一个 \(u\) 的祖先。
然后这个限制太松了,不是充分条件,尝试把它变得更紧一些。观察发现假如两个节点 \(u, v\),其中 \(u\) 是 \(v\) 的祖先,满足最终树上的 \(u\) 连向的祖先深度小于 \(v\) 连向的祖先,这是不可能完成的。如图。
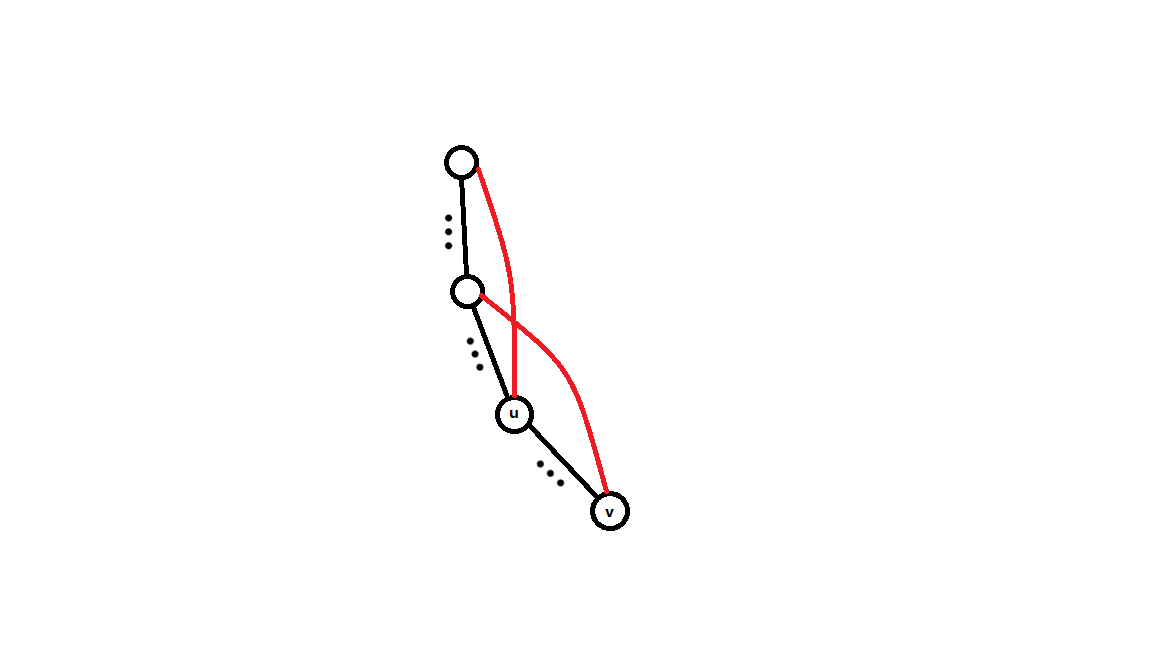
这种情况不可能做到某种顺序做到两个边都连上,但除了这种情况以外的只要是往祖先连边的均为合法最终状态。
因此可以设计 dp 为 \(f_{i,j}\) 表示 \(i\) 节点的子树中的节点只能连 \(j\) 个祖先节点,因为不能相交只能包含或相离,于是就很好转移了。根据乘法原理,每颗子树中的节点互不相扰,将方案总数相乘即可。
这里 \(k\) 枚举的是 \(u\) 选的 \(j\) 个祖先节点中深度第 \(k\) 大的,所以子节点可以连的减少到了 \(k\) 个 \(u\) 的祖先节点,加上 \(u\) 自己也可以被连,因此总共为 \(k+1\)。
D. \(カンガルー\) (kangaroo) on luogu
先修改一下题意,装了袋鼠 \((a_j,b_j)\) 后的袋鼠 \((a_i,b_i)\) 变为 \((a_i,b_j)\),然后想象袋鼠 \(j\) 就消失了。这样子好解释一点。
按 \(a_i\) 从大到小排序,那么排在后面的不可能装排在前面的因为 \(\forall i < j:a_i \ge a_j > b_i\)。先记录一下第 \(i\) 只袋鼠能被 \(cnt_i\) 只袋鼠装下,显然这 \(cnt_i\) 全出自 \(i\) 之前的袋鼠。
于是就起手定义状态吧!
- \(i\):当前枚举到第 \(i\) 只袋鼠。
- \(j\):有多少只袋鼠被钦定不会被装。
插句话:只用这两个好像不太行,忽视了题目的最终要求:未装袋鼠的袋鼠不能继续装未被装的袋鼠。
- \(k\):有多少只仍可以装被钦定不会被装的袋鼠的袋鼠。
转移考虑刷表,假设已经知道了 \(f_{i-1,j,k}\) 的值。
- \(f_{i, j, k-1} \gets f_{i-1,j,k} \times k\),因为 \(\forall i<j:a_i \ge a_j > b_j\) 因此这个袋鼠被装进去过后很能装的袋鼠也变萎弱了,没有能力再装 \(i\) 之前的所有袋鼠,包括已钦定的不被装的袋鼠。而且这个很能装的袋鼠一定是可以装 \(i\) 的,至少在目前看来。
- \(f_{i,j,k} \gets f_{i-1,j,k} \times (cnt_i-(i-1-j)-k)\),因为 \(cnt_i\) 首先肯定包含了 \(k\) 代表的所有袋鼠,然后又不能装在已经消失的袋鼠(虽然这些袋鼠除了最后一个被装的都可以装袋鼠 \(i\),但他们已然湮灭)里,所以要先将 \((i-1-j)\) 个消失的袋鼠附加最外面那个袋鼠(它也可以装袋鼠 \(i\) 但它并没有装而是选择了前面的,因此不能再装了)删去。
- \(f_{i,j,cnt_{i}-(i-1-j)} \gets f_{i-1,j,k}\) 新钦定一个不被装的袋鼠,将 \(k\) 赋值为之前所有能装他的而且还没装的袋鼠(这些袋鼠一定包含了之前那 \(k\) 个袋鼠)。
然后转移就完了。
Day 3
A. 摩天大楼 高層ビル街/Skyscraper on luogu
没多少好讲的,主要是一个插入 dp 和拆绝对值的经典 trick。
\(|a_i-a_j|\) 的绝对值让人很不爽,于是就先让 \(a\) 从小到大排序,方便转移时直接拆成 \(a_i-a_j\) 直接算贡献就可以了。
对于排列问题可以使用插入 dp。具体的,确定 \([1,i]\) 的相对顺序考虑 \(i+1\) 的转移。由于一个费用提前计算的思想,我们先钦定若干个空位允许以后的插入,非空位的就不允许插入,则在以后的插入中不用考虑空位两旁的数。令 \(f_{i,j,k}\) 表示 \([1,i]\) 的相对顺序确定,预留了 \(j\) 个中间的空位插入(同时两边的空位是一定存在的),贡献为 \(k\),答案就是 \(\sum _{i\le L}f_{n,0,i}\)。可惜复杂度并不佳,因为 \(k\) 的转移中出现了负贡献使得无法控制 \(k\) 这一维的大小,直接上涨至 \(\mathcal O(\sum a_i)=\mathcal O(nL)\),总的复杂度达到 \(\mathcal O(n^3L)\) 接近 \(10^9\) 无法承受。
于是想到了拆 \(a_i-a_j\) 的技巧,使得贡献持续为正,将 \(k\) 的大小降低到 \(\mathcal O(L)\)。
我们只需知道留了多少空位并在每次转移时把这些空位的贡献全加上 \(a_i-a_{i-1}\) 即可,删除一个空位即为不在往上加。
所以还得加上两维表示两边是否被封上了,新的定义为 \(f_{i,0/1,0/1,j,k}\)。
转移就比较简单了。
Click to see the code
#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
const int N = 105, M = 1005, mod = 1e9+7;
int n, m, a[N];
int f[2][2][2][N][M];
inline int csum(const int& x, const int& y) { return (x+y)%mod; }
inline void cadd(int& x, int y) { x = csum(x, y); }
signed main() {
FASTIO;
cin >> n >> m;
_f(i, 1, n) cin >> a[i];
stable_sort(a+1, a+n+1);
for (int u : {0,1}) for (int v : {0,1}) f[1][u][v][0][0] = 1;
_f(i, 2, n) {
memset(f[i&1], 0, sizeof(f[i&1]));
_f(j, 0, i-1) _f(k, 0, m) for (int u : {0,1}) for (int v : {0,1}) {
int nk = k+(a[i]-a[i-1])*((j<<1)+u+v), &s = f[i-1&1][u][v][j][k];
if (nk <= m) {
if (j > 0) for (int a : {-1, 1}) for (int b : {-1, 1})
cadd(f[i&1][u][v][j+(a+b>>1)][nk], s*j);
if (u) for (int uu : {0, 1}) for (int ad : {0, 1})
cadd(f[i&1][uu][v][j+ad][nk], s);
if (v) for (int vv : {0, 1}) for (int ad : {0, 1})
cadd(f[i&1][u][vv][j+ad][nk], s);
}
}
}
cout << accumulate(f[n&1][0][0][0], f[n&1][0][0][0]+m+1, 0, csum);
return 0;
}
B. Snuke Panic (2D)
cdq 转移条件复杂的 dp。很典,注意先递归左边,然后递推,再递归右边即可。
C. Optimal Binary Search Tree on luogu
容易的 dp。子树在原序列上是一个连续段,所以用 \(f_{l,r}\) 表示 \([l,r]\) 区间构成二叉搜索树的答案,证明四边形不等式是容易的。直接优化即可到 \(\mathcal O(n^2)\)。
No Code!
D. Constant Sum Subsequence on atcoder
朴素的 dp。\(f_i\) 表示一些序列和的最小值,这些序列必须满足将其贪心的放入 \(A\) 中(尽量靠前),恰好会匹配到 \(A_i\) 结束。转移是容易的 \(f_i=A_i+\displaystyle\min_{p_i\le j < i}{f_j}\),\(p_i\) 表示 \(A_i\) 上一次出现的位置。发现转移是循环的,在 \(i \ge 2n\) 时满足 \(f_{i+n}-f_{i}=f_i-f_{i-n}\),暴力处理 \(f\) 前 \(3n\) 位即可。
\(4.5\times 10^6\) 跑起来够呛。
Day 4
A. Tree Degree Subset Sum on atcoder
题意简洁明了。就是求一个带有特殊性质的背包。我们来整理一下。设节点度数为 \(d_i\),则物品体积可看作 \(1\),价值看作 \(d_i\)。
- \(\sum d_i =2n-2\)
- \(d_i\ge1\)
我们声称这道题不会用到除上面两个性质以外的树上性质。我们断言将 \(\mathbf{d}_i\) 减去 \(\mathbf{1}\) 会使分析更简单。观察到减了之后,对于价值和为 \(s\) 的所有物品选择方案,这些方案的物品个数是连续的一段,考虑证明(采用洛谷题解的证法)。
假设价值和为 \(s\),满足 \(d_i=0\) 的共 \(z\) 个。假设总价值为 \(s\),选的物品最多的为 \(R_s\),选的物品最少的为 \(L_s\)。
需要说明 \([L_s,L_s+z]\) 与 \([R_s-z,R_s]\) 的并在整数域上等价于 \([L_s,R_s]\)。
即证 \(R_s-L_s \le 2z-1\)。
设任意选择方案,总体积为 \(v\),总价值为 \(w\),则 \(w-v=\sum {(d_i-1)} \in [-z, n-2-(n-z)]\),即 \(w-v \in [-z,z-2]\)。
然后也应该能看出来了。
最后直接最大最小背包 dp 统计答案就好了。
B. Neko Rules the Catniverse (Large Version)
给定参数 \(n,k,m\),你需要求有多少个大小为 \(k\) 的序列 \(a\) 满足如下三个条件:
任意两个元素其权值不同。
对于任意 \(i\) 满足 \(1\le i\le k\) 有 \(1\le a_i\le n\)。
对于任意 \(i\) 满足 \(2\le i\le k\) 有 \(a_i\le a_{i-1}+m\)。
答案对 \(10^9+7\) 取模。
数据范围:
\(1\le n\le 10^9\),\(1\le k\le \min(n,12)\),\(1\le m\le 4\)。
*3000 但确实不知道难点在哪里?(bushi
按序列位置 dp?算了吧,第二维太大了(需要 \(\mathcal O(n)\)),而且市面上几乎找不到优化第二维的方法。因为条件要求序列元素互不相同,所以考虑按值域 dp。虽然第一维增大了,但似乎剩下的维度都与 \(n\) 无关了,剩下的 \(2\) 个 \(k,m\) 小的离谱,所以考虑就这么干。\(f_{i,j,S}\) 表示在值域 \([1,i]\) 选数(不一定每个数都存在于序列中),满足已填了 \(j\) 个位置,\(S\) 则表示 \(i-m+1 \sim i\) 这些值是否存在于序列中。
转移很简单了,最后发现第二维很小而且转移是线性的,直接上矩阵优化即可。
C. Sum Balance on codeforces
无聊的 dp。确定每个盒子里装的整数之和,只需要求总和后除以 \(k\) 即可(不可整除则为无解),然后对于每个未满足条件的盒子用外面的替换里面的(题目限制了只会存在一个替换后刚好满足条件的),然后找环,状压子集枚举转移就好了。
D. 单调队列 on luogu
题目求的是被弹出的元素之和,我们可以发现一个元素若是想要被弹出,那么就找到下一个比它大的弹出。这个很好找,所以我们只需要维护只有一个元素的队列(如果被弹出,那么下一个比它大的会把他们俩中间的全弹了),我们设当前枚举至 \(i\),前面都弹空了,元素和最大为 \(f_i\)。转移很简单了:\(f_{p_i} \gets f_i+s_{{i,p_i-1}}\),或者不做贡献:\(f_{i+1} \gets f_i\) 条件是 \(a_i > a_{i+1}\)。代码中给的另一种写法。
Click to admire the code
#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
const int N = 1e6+5, M = 1005, inf = 0xc0c0c0c0c0c0c0c0;
int n, c[N], a[N], p[N], s[N], f[N], t;
signed main() {
FASTIO;
cin >> n;
_f(i, 1, n) cin >> c[i];
_f(i, 1, n) cin >> a[i];
_f(i, 1, n) p[i] = p[i-1]+c[i];
a[0] = n+1, s[++t] = 0;
int res = inf;
_f(i, 1, n) {
f[i] = inf;
while (t > 0 && a[s[t]] < a[i]) f[i] = max(f[i], p[i-1]-p[s[t]-1]+f[s[t]]), --t;
f[i] = max(f[i], f[s[t]]+p[i-1]-p[s[t]]);
s[++t] = i;
res = max(res, f[i]);
}
cout << res;
return 0;
}
E. NOI 嘉年华 still on luogu
古早 NOI 题,还挺好玩(NO!)。dp 是容易看出来的(只要你不像👇军一样看错题)。
设 \(f_{i,j}\) 表示考虑 \([1,i]\) 的时间区段,左会场有 \(j\) 个活动时,右会场最多有 \(f_{i,j}\) 个活动。转移是容易的,第一问也解决了。
第二问强制要求第 \(i\) 个活动举行那么需要预留一个完全包含 \([l_i,r_i]\) 的区间。只要把刚刚的 \(f\) 反过来跑得到 \(g\)。枚举就好了
brute force
#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
const int N = 405, M = 1005, inf = 0xc0c0c0c0c0c0c0c0;
int n, a[N], b[N], p[N], t;
int cnt[N][N], pre[N][N], suf[N][N], f[N][N];
signed main() {
FASTIO;
cin >> n;
_f(i, 1, n) cin >> a[i] >> b[i], b[i]+=a[i], p[++t] = a[i], p[++t] = b[i];
stable_sort(p+1, p+t+1);
t = unique(p+1, p+t+1)-p-1;
_f(i, 1, n) a[i] = lower_bound(p+1, p+t+1, a[i])-p, b[i] = lower_bound(p+1, p+t+1, b[i])-p;
_f(l, 1, t) _f(r, l, t) _f(i, 1, n)
cnt[l][r] += l <= a[i] && b[i] <= r;
memset(pre, 0xc0, sizeof(pre)), memset(suf, 0xc0, sizeof(suf));
_f(i, 1, t) pre[i][0] = suf[i][0] = 0;
_f(i, 1, t) _f(j, 0, cnt[1][i]) _f(k, 1, i) {
pre[i][j] = max(pre[i][j], pre[k][j]+cnt[k][i]);
if (j >= cnt[k][i]) pre[i][j] = max(pre[i][j], pre[k][j-cnt[k][i]]);
}
_r(i, t, 1) _f(j, 0, cnt[i][t]) _f(k, i, t) {
suf[i][j] = max(suf[i][j], suf[k][j]+cnt[i][k]);
if (j >= cnt[i][k]) suf[i][j] = max(suf[i][j], suf[k][j-cnt[i][k]]);
}
int ans = 0;
_f(i, 0, cnt[1][t]) ans = max(ans, min(i, pre[t][i]));
cout << ans << '\n';
_f(l, 1, t)
_f(r, l, t) {
_f(x, 0, cnt[1][l]) {
_f(y, 0, cnt[r][t]) {
f[l][r] = max(f[l][r], min(x+y+cnt[l][r], pre[l][x]+suf[r][y]));
}
}
}
_f(i, 1, n) {
ans = 0;
_f(l, 1, a[i])
_f(r, b[i], t)
ans = max(ans, f[l][r]);
cout << ans << '\n';
}
return 0;
}
怀着认真严肃的态度,再来讲讲 \(\mathcal O(n^3)\)。发现 \(x\) 增大时,\(y\) 的最优决策位置将变小,故使用双指针维护即可。
但这种方法容易被 \(\times\) 所以不放了。
F. 演讲者 on luogu
今日次水题(你猜猜第一是谁)。
首先容易发现 \(z\) 的演讲是从 \(x \to y\) 的路径上的某个点出发再返回。然后直接对每个点维护从该点出发结束于该点的最大贡献。(当然可以不走,就只留当前点的贡献 \(c_i\))。
熟练地剖分即可。
Click to read the code
#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
const int N = 2e5+5, M = 1005, inf = 0xc0c0c0c0c0c0c0c0;
int n, q, c[N];
vector<PII> G[N];
int f[N], a[N], d[N];
int dep[N], fa[N], sz[N], son[N];
void dfs1(int x, int fa) {
sz[x] = 1, son[x] = 0;
::fa[x] = fa;
for (auto [y, z] : G[x]) {
if (y == fa) continue;
dep[y] = dep[x]+1;
d[y] = d[x]+z;
dfs1(y, x);
sz[x] += sz[y];
if (!son[x] || sz[son[x]] < sz[y]) son[x] = y;
}
}
int dfn[N], dfc, tp[N];
void dfs2(int x, int top) {
dfn[x] = ++dfc, tp[x] = top;
if (son[x]) dfs2(son[x], top);
for (auto [y, z] : G[x]) {
if (dfn[y]) continue;
dfs2(y, y);
}
}
void dfs(int x, int fa) {
f[x] = c[x];
for (auto [y, z] : G[x]) {
if (y == fa) continue;
dfs(y, x);
f[x] = max(f[x], f[y]-2*z);
}
}
void dp(int x, int fa) {
a[dfn[x]] = f[x];
int m = G[x].size(), i = 0;
vector<int> pre(m), suf(m);
for (auto [y, z] : G[x]) pre[i] = max(f[y]-2*z, (i > 0 ? pre[i-1] : inf)), i++;
i = m;
for (auto it = G[x].rbegin(); it != G[x].rend(); ++it, i--) {
auto [y, z] = *it;
suf[i-1] = max(f[y]-2*z, (i < m ? suf[i]:inf));
}
i = 0;
for (auto [y, z] : G[x]) {
if (y^fa) {
f[x] = max(c[x], max(i > 0 ? pre[i-1] : inf, i < m-1 ? suf[i+1] : inf));
f[y] = max(f[y], f[x]-2*z);
dp(y, x);
}
i++;
}
}
int st[20][N];
inline void st_prework() {
_f(i, 1, n) st[0][i] = a[i];
_f(k, 1, 19)
_f(x, 1, n)
st[k][x] = max(st[k-1][x], st[k-1][min(n, x+(1<<k-1))]);
}
inline int maxof(int l, int r) {
int k = log2(r-l+1);
return max(st[k][l], st[k][r-(1<<k)+1]);
}
inline int query(int x, int y) {
int dis = 0, res = 0;
while (tp[x] != tp[y]) {
if (dep[tp[x]] < dep[tp[y]]) swap(x, y);
res = max(res, maxof(dfn[tp[x]], dfn[x])), dis += d[x]-d[fa[tp[x]]], x = fa[tp[x]];
}
if (dfn[x] < dfn[y]) swap(x, y);
return max(res, maxof(dfn[y], dfn[x]))-(dis+abs(d[x]-d[y]));
}
signed main() {
FASTIO;
cin >> n >> q;
_f(i, 1, n) cin >> c[i];
_f(i, 2, n) {
int u, v, w;
cin >> u >> v >> w;
G[u].emplace_back(v, w), G[v].emplace_back(u, w);
}
dfs1(1, 0), dfs2(1, 1);
dfs(1, 0), dp(1, 0);
// _f(i, 1, n) dfs(i, 0), a[dfn[i]] = f[i];
st_prework();
_f(i, 1, q) {
int s, t;
cin >> s >> t;
cout << query(s,t)+c[s]+c[t] << '\n';
}
return 0;
}
Day 5
A. 沈阳大街 2 on luogu
排序,dp 即可。太板了。
Update on 2025/10/5.
我对不起你,你不板。这个分属性两两匹配还是挺不好想的。详见 ARC207A,居然想了 1h,哭晕。
Update on 2025/11/5
你咋这么六,CSP-S T4 也用你的另一个 trick。
B. Another n-dimensional chocolate bar on codeforces
趣极。首先 dp 是容易发现的。考虑前 \(i\) 位,当前 \(\prod b_j\) 为 \(p\) 的答案最大值为 \(f_{i,p}\)。这个 dp 是 \(\mathcal O(nk)\) 且难以优化的。考虑换个思路,\(p\) 表示 \(\left\lceil\dfrac{k}{\prod b_j}\right\rceil\) 即未来加入的 \(b_j\) 乘积最小值。
转移写为 \(f_{i,p} \to f_{i+1,\lceil \frac{p}{b_i} \rceil}\times\lfloor \dfrac{a_i}{b_i}\rfloor \times \dfrac{1}{a_i}\),其中 \(b_i \in [1,p]\)。然后根据一个很好的性质:\(\lceil \frac{x}{y}\rceil=\lfloor \frac{x-1}{y} \rfloor + 1\)(在均为正整数时成立),所以 \(\left\lceil \dfrac{\lceil \frac{x}{y}\rceil}{z}\right\rceil=\lfloor \dfrac{x-1}{yz}\rfloor+1\)。
可以发现 \(p\) 的取值只有 \(\sqrt k\) 种,而转移可以只保留 \(\lfloor \frac{p}{x}\rfloor\) 相同的 \(x\) 的最大值从 \(f_{i-1,x}\) 转移到 \(f_{i,p}\)。题解声称时间复杂度为 \(\mathcal O(nk^{0.75})\)。
C. Gellyfish and Eternal Violet on codeforces
好题。大胆的定义状态并观察性质。大多数题解讲的都很清楚,所以也不详细讲了。
观察发现当怪物的生命值不全相同时,不管抽到哪个肯定砍怪更好(除了最小值为 \(1\) 且处于闪耀状态时)。所以这一段直接贪就很好(也很好算,虽然最后因精度问题而被迫用 dp 解决这一段)。
剩下一段就直接使用最暴力的 dp 就好了。复杂度 \(\mathcal O(nmV)\)。
Day 6 NOIP 模拟赛
A. 可爱的数列 on becoder
不讲了,没啥意义。一道黄。
B. GAS-Fire Extinguishers / 击退 on luogu
贪心好题。不过乱搞 \(70\)。
考虑自下而上地贪心,则在当前 \(u\) 处两个点 \(x,y\) 距离(\(d(x,u)+d(u,y)\))为 \(k\) 和 \(k-1\) 的都应直接处理,而其他的不应处理。
令 \(f_{i,j}\) 表示点 \(i\) 子树内距离点 \(i\) 为 \(j\) 的灭火器还能灭的节点个数,显然往上走时经过一节点能灭就灭该节点。同时令 \(g_{i,j}\) 表示 \(i\) 子树内等待被灭的节点。显然可以通过子树的贪心结果更新 \(f_{i,j},g_{i,j}\) 并在结束后贪心灭节点即可。
Click to check the code(because it may be incorrect!)
#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define int long long
#define PII pair<int, int>
#define pb push_back
#define eb emplace_back
const int N = 4e5 + 5, mod = 998244353, inf = 0x3f3f3f3f;
template <typename Tp>
inline void tomax(Tp& x, Tp y) {
x = x < y ? y : x;
}
template <typename Tp>
inline void tomin(Tp& x, Tp y) {
x = x < y ? x : y;
}
int n, m, k;
vector<int> G[N];
int f[N][25], g[N][25], ans;
inline int ceil(int x, int m) { return x ? (x - 1) / m + 1 : 0; }
void dfs(int x, int fa) {
for (auto y : G[x]) {
if (y == fa)
continue;
dfs(y, x);
_f(i, 1, k) f[x][i] += f[y][i - 1], g[x][i] += g[y][i - 1];
}
_f(i, 1, k) f[x][i] = min(f[x][i], n);
++g[x][0];
if (g[x][k]) {
int t = ceil(g[x][k], m);
f[x][0] = min(t * m, n);
ans += t;
}
_f(i, 0, k) {
int t = min(f[x][i], g[x][k - i]);
f[x][i] -= t, g[x][k - i] -= t;
}
_f(i, 0, k - 1) {
int t = min(f[x][i], g[x][k - 1 - i]);
f[x][i] -= t, g[x][k - 1 - i] -= t;
}
}
signed main() {
FASTIO;
cin >> n >> m >> k;
_f(i, 2, n) {
int u, v;
cin >> u >> v;
G[u].eb(v), G[v].eb(u);
}
dfs(1, 0);
_f(w, 0, k) _r(i, w, 0) {
int j = w - i;
int t = min(f[1][i], g[1][j]);
f[1][i] -= t, g[1][j] -= t;
}
cout << ans + ceil(accumulate(g[1], g[1] + k + 1, 0), m);
return 0;
}
C. 扫地机器人 原题:[CEOI 2025] lawnmower on luogu
不好评价了……反正挺暴力的。
\(f_{i,j}\) 是一个显然的定义,\(j\) 表示收集箱剩余多少草。
然后用线段树整体转移即可,时间复杂度 \(\mathcal O(n \log c)\) 离散化可以做到 \(\log n\)。
Click to appreciate the code
#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define pb push_back
#define eb emplace_back
const int N = 2e5+5, mod = 1e9+7, inf = 0x3f3f3f3f3f3f3f3f;
template<typename Tp>
inline void tomax(Tp& x, Tp y) { x = x < y ? y : x; }
template<typename Tp>
inline void tomin(Tp& x, Tp y) { x = x < y ? x : y; }
int n, c, b, a[N], v[N];
struct SegmentTree {
struct node {
int ls, rs, mn, tag;
} tr[N*100];
#define ls(p) tr[p].ls
#define rs(p) tr[p].rs
#define mn(p) tr[p].mn
#define tag(p) tr[p].tag
int tot, rt;
SegmentTree() { tot = 0, tr[0] = {0, 0, inf, 0}; }
inline int newnode() {
int p = ++tot;
tr[p] = {0, 0, inf, 0};
return p;
}
inline void cover(int &p, int v) {
if (!p) p = newnode();
mn(p) += v, tag(p) += v;
}
inline void pushdown(int p) {
if (tag(p)) {
cover(ls(p), tag(p)), cover(rs(p), tag(p));
tag(p) = 0;
}
}
inline void upd(int& p, int l, int r, int x, int v) {
if (!p) p = newnode();
if (l==r) return mn(p) = v, tag(p) = 0, void();
pushdown(p);
int mid = (l+r)>>1;
x <= mid ? upd(ls(p), l, mid, x, v) : upd(rs(p), mid+1, r, x, v);
mn(p) = min(mn(ls(p)), mn(rs(p)));
}
inline void add(int &p, int l, int r, int L, int R, int v) {
if (!p) p = newnode();
if (L <= l && r <= R) return cover(p, v);
pushdown(p);
int mid = (l+r)>>1;
if (L <= mid) add(ls(p), l, mid, L, R, v);
if (mid < R) add(rs(p), mid+1, r, L, R, v);
mn(p) = min(mn(ls(p)), mn(rs(p)));
}
inline void add(int L, int R, int v) {
if (L <= R) add(rt, 0, c-1, L, R, v);
else add(rt, 0, c-1, 0, R, v), add(rt, 0, c-1, L, c-1, v);
}
inline int qry() { return mn(rt); }
} sgt;
int sum;
#undef int
long long mow(int n_, int c_, int b_, vector<int>& a_, vector<int>& v_) {
FASTIO;
n = n_, c = c_, b = b_, sum = b;
_f(i, 1, n) a[i] = a_[i-1], sum += a[i];
_f(i, 1, n) v[i] = v_[i-1], sum += (v[i]-1)/c*(a[i]+b), v[i] = (v[i]-1)%c+1;
#define int long long
int del = 0;
sgt.upd(sgt.rt, 0, c-1, del, 0);
_f(i, 1, n) {
int l = c-v[i]+1, r = c-1;
if (l <= r) sgt.add((l+del)%c, (r+del)%c, a[i]+b);
del = (del-v[i]+c)%c;
int re = sgt.mn(sgt.rt);
if (n == i) return re+sum;
sgt.upd(sgt.rt, 0, c-1, del, re+b);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号