[HDU5072]Coprime

Description

从元素个数为 \(n\) 的给定数集中选择三个元素使得这三个数两两互质或两两不互质，求选择这样三个数的方案数。\(n \le 10^5, a_i \le 10^5\).

Analysis

选择三个元素 \(a,b,c\)，不考虑顺序，只有可能出现 \(4\) 种情况：

1. \(a,b\) 互质，\(b,c\) 和 \(c,a\) 不互质。
2. \(a,b\) 不互质，\(b,c\) 和 \(c,a\) 互质。
3. \(a,b\) 和 \(b,c\) 和 \(c,a\) 互质。
4. \(a,b\) 和 \(b,c\) 和 \(c,a\) 不互质。

• 题目求的是 3,4 两种情况方案之和。
• 枚举三个数或两个数时间复杂度都会炸，只能最多枚举一个数，那就先枚举起。
• 可以先考虑互质不互质的一些相关性质。（不过似乎没有什么好的性质）
• 只有四种情况，考虑先求 1,2 方案数。
• 感觉 1,2 更复杂了。

找一下他们的统一点。考虑 1,2 情况的三元组中，满足与另两个数关系不同的数的个数一定恰为 \(2\) 个。并且 3,4 情况的这样的数的个数不存在。

使用一张 \(n\) 个节点的完全图可能更好理解。对于 \(\gcd(x,y)=1\) 在 \(x,y\) 之间连接黑色边，否则连接红色边。

我们要统计的是 二黑一红 or 二红一黑 的三元环个数，观察这样的三元环。

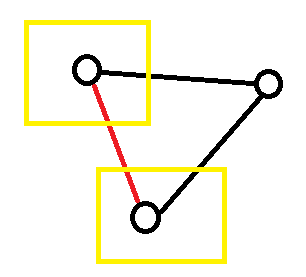
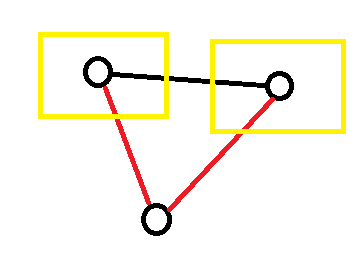
这两个框出的角叫做异色角，每个三元环中有两个这样的角。（且 3，4 情况无异色角）因此，统计异色角个数即可统计出 1，2 情况的三元环个数。令异色角个数为 \(\rm dca\)，则答案为 \(\dbinom{n}{3}-\dfrac{\mathrm{dca}}{2}\)。

Solution

用你喜欢的办法统计异色角即可。

sol1（Dog Army 的，侵删）复杂度 $\mathcal O(n \sqrt n)$，略劣于 sol2

你被骗了

sol2

复杂度：\(\mathcal O(n p 2 ^ p)\)，\(p\) 是 \(a_i\) 的因子种类数最大值（可以证明不超过 \(7\)）。

#include <bits/stdc++.h>
using namespace std;
#define _f(i, l, r) for (int i = l; i <= r; ++i)
#define _r(i, r, l) for (int i = r; i >= l; --i)
#define FASTIO ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define LL long long
#define int long long
#define PII pair<int,int>
#define pb push_back
#define eb emplace_back
const int N = 4e5+5, mod = 998244353;
template<typename Tp>
inline void tomax(Tp& x, Tp y) { x = max(x,y); }
template<typename Tp>
inline void tomin(Tp& x, Tp y) { x = min(x,y); }
int n, a[N], cnt[N];
string s;
int p[N], m;
bool v[N];
inline void primes(int n) {
    _f(i, 2, n) {
        if (v[i]) continue;
        p[++m] = i;
        for (int j = i<<1; j <= n; j += i)
            v[j] = 1;
    }
}
inline void prework(int n) {
    _f(i, 1, n)
        for (int j = i<<1; j <= n; j += i)
            cnt[i] += cnt[j];
}
inline void solve() {
    cin >> n;
    __builtin_memset(cnt,0,sizeof(cnt));
    _f(i, 1, n) cin >> a[i], ++cnt[a[i]];
    prework(100000);
    int res = 0;
    _f(i, 1, n) {
        int t = a[i];
        int h[10], ct=0;
        for(int j=1;p[j]*p[j]<=t;++j) {
            if (t % p[j] == 0) h[ct++] = p[j];
            while (t % p[j] == 0) t /= p[j];
        }
        if (t > 1) h[ct++] = t;
        int ans = 0;
        for (int msk = 0; msk < 1<<ct; ++msk) {
            int lcm = 1, op = 1;
            for (int j = 0; j < ct; ++j)
                if (msk >> j & 1)
                    lcm *= h[j], op = -op;
            ans += op*(cnt[lcm]-1);
        }
        res += (n-ans-1)*ans;
    }
    cout << n*(n-1)/2*(n-2)/3-(res>>1) << '\n';
}
signed main() {
    FASTIO;
    int _;
    cin >> _;
    primes(500);
    while (_--) solve();
    return 0;
}