多项式总结
Lagrange 插值法
板题
给定 \(n\) 个点 \((x_i,y_i)\),确定一个 \(n-1\) 次多项式 \(f(x)\).一般只要求给出 \(f(k)\) 的值即可.
朴素解法
使用高斯消元法,待定系数法代入每个 \(x_i\) 即可,时间复杂度 \(O(n^3)\).
Lagrange 插值(\(x_i\) 随机)
令 \(f(x)=\sum a_m x^m\).
尝试构造 \(p_i\),使得:
什么东西可以满足这个呢?于是又找到了:
所有 \(x_1,x_2,\dots,x_n\) 中,只有 \(l_i(x_i) \not = 0\),所以把它变成 \(p_i(x)\) 也很简单:
用 \(p_i\) 来表示 \(f(x)\):
这是显然的,因为 \(p_i(x)\) 只在 \(x=x_i\) 时值为 \(1\),其它值 \(x_j\) 代入都为 \(0\).
于是可以展开:
暴力 \(n^2\) 展开或求值就可以了.
求 \(p_i\) 的过程暴力 \(O(n^2)\),求值也是 \(O(n^2)\).
\(x_i\) 自己定
可以自己找一些性质比较好的 \(x_i\).
例题:给定 \(n,k\),求 \(\sum\limits_{i=1}^{n} i^k\).要求在与 \(n\) 无关的 \(O(k \log k)\) 的时间内解决.
猜想答案是一个关于 \(n\) 的多项式,令为 \(f_k(n)\).
- 对于 \(k=0\),\(f_0(n) = n\);
- 对于 \(k=1\),\(f_1(n) = \dfrac{n(n+1)}{2}=\dfrac{n^2}{2}+\dfrac{n}{2}\).
- \(\dots\)
根据前辈的观察发现他就是个 \(k+1\) 次多项式,证明略.
选 \(k+2\) 个 \(n\) 暴力求,复杂度为 \(O(k\log k)\).插值即可.但是暴力插是 \(O(k^2)\) 的.
选哪些 \(n\) 可以算得更快?
\(O(k^2)\) 插值的瓶颈在于 \(x_i-x_j\) 那一坨的求值,其他...
- \(x-x_j\) 在 \(x\) 值确定情况下可以 \(O(n)\) 预处理所有 \(\prod (x-x_j)\),调用时乘上 \(x-x_i\) 的逆元即可.
- 枚举 \(i\) 求值是 \(O(1)\) 的,总的来说是 \(O(n)\).
令 \(x_i=i\),\(\prod _{i\not ={j}} (x_i-x_j)\) 就好求了,分成 \(i<j\) 和 \(i>j\) 两段,于是就等于 \((-1)^{i-1}(i-1)!(n-i)!\),可以预处理.
于是 \(O(k\log k)\) 求值,\(O(n)\) 插值就完了.
与 DP 结合
例题:calc
暴力 DP:\(f(n,m)\) 为 \(a_n \le m\) 的长为 \(n\) 的单调不减数列个数.因为实际上求得是无序,答案为 \(f(n,k) \times n!\).\(f(0,i)=1\).
\[f(n,m)=f(n-1,m-1) \times m + f(n,m-1) \]
猜想 \(f(n,m)\) 在 \(n\) 固定时是关于 \(m\) 的多项式 \(g_n(m)\),证明如下.
按照套路,寻找转移式中的差分:
\(g_n(m)-g_n(m-1)=g_{n-1}(m-1) \times m\)
假设 \(g_{n-1}(x)\) 是多项式成立.显然 \(g_0(x)\) 是 \(0\) 次多项式.
那么右边的式子就是一个多项式.由于是差分,累加得到 \(g_n(m)-g_n(0)=m\sum \limits_{i=1}^{m}g_{n-1}(i-1)\)
\(g_n(0)=0\),所以因为左边只剩 \(g_n(m)\),而右边 \(g_{n-1}(i-1)\) 也是多项式,所以左边也是多项式.\(m\sum \limits_{i=1}^{m}\) 使得 \(g_{n}(m)\) 的次数为 \(g_{n-1}(i-1)\) 次数 \(+2\).
数学归纳法得到:\(g_k(x)\) 为 \(2k\) 次多项式.
直接暴力求解 \(g_n(m)\) 前 \(2n+1\) 项,\(O(n)\) 插值即可.
多项式乘法(卷积),快速幂
Tips:傅里叶变换与 OI 关系不大,所以不说.
离散傅里叶变换 DFT
一个 \(n\) 次多项式 \(f(x) = \sum \limits_{m=0}^n a_mx^m\), 我们一般采用系数表示法,也就是只保存 \(a_m\) 的值.
这种表示方法的局限性在于做多项式乘法(卷积)时,两个相乘的多项式都要枚举 \(a_m\),总的时间复杂度是 \(O(n^2)\) 的.
众所周知,多项式 \(f(x)\) 可以用 \(n+1\) 个点值表示出来.
多项式的乘法可以在特定的 \(x\) 处轻松表示出来:看多项式乘法的定义式:\(h(x)=f(x)g(x)\),就是用 \(f(x)\) 和 \(g(x)\) 的点值表达式 \((x,f(x)),(x,g(x))\) 的 \(y\) 值大小相乘得到 \((x,f(x)g(x))\),结果就是 \(h(x)\) 的点值表达式.
我们不妨找出 \(n+1\) 个特定的 \(x_i\) 值得到每个 \(f(x_i),g(x_i)\),然后相乘得到 \(h(x_i)\),在将其还原.
但求值的过程是 \(O(n)\) 的,求 \(O(n)\) 个点的对应点值的复杂度飙到了 \(O(n^2)\),还不如直接暴力卷呢.如何更快?
快速傅里叶变换 FFT
前置知识简述
复数的代数表示法:一个复数可以形容成 \(x+y\mathrm{i}\),\(\mathrm{i}\) 是虚数单位表示 \(\sqrt{-1}\).
三角表示法:复数 \(z=r(\cos \theta +\mathrm{i}\sin\theta)\).\(r\) 就是代数表示法中 \((0,0)\) 连到 \((a,b)\) 线段长度,\(\theta\) 就是其与 \(x\) 轴的夹角.复数相乘相当于 \(r\) 相乘,\(\theta\) 相加.
寻找一些有好的性质的点,尽量能够重复利用之前的计算结果,DFT 的效率将能得到质变.
在复数集 \(\mathbb{C}\) 中,有一系列周期性变化的数 \(\omega_n^k\),名叫单位复根.在复平面上,这 \(n\) 个数呈现将单位圆平均分为 \(n\) 分的样子,就像这样(一个 \(n=8\) 时的例子):
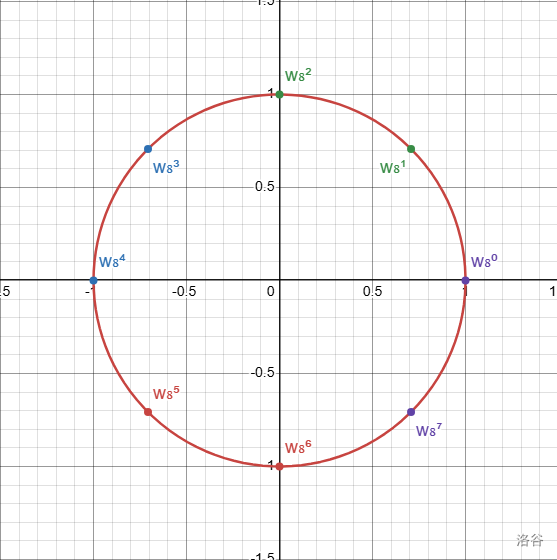
单位复根的定义:\(\omega_n^k=e^{\mathrm{i}\frac{2k\pi}{n}}=\cos \dfrac{2k\pi}{n}+\mathrm{i} \sin \dfrac{2k\pi}{n}\)
性质:
- \(\omega _{2n}^{2k}=\omega_n^k\)
- \(\omega_n^{k+\frac{n}{2}}=-\omega_{n}^k\)
- \(\omega_n^n=\omega_n^0=1\)
这几个性质将会在 FFT 中发挥重要作用.
考虑将单位复根 \(\omega_n^0,\omega_n^1,\dots,\omega_n^{n-1}\) 代入 \(n\) 项的多项式(注意次数变成了项数).
不妨设 \(n=2^k,k\in \mathbb{N}\).这样 \(n\) 可以一直分成两个子问题递归.如果 \(n\) 不是 \(2\) 的整数次幂,补位即可.
令 \(f(x)=\sum\limits_{m=0}^{n-1} a_mx^m\).
考虑将它拆分成奇次幂和偶次幂:
定义下面两个多项式:
于是:
分别代入 \(\omega_n^k,\omega_n^{k+\frac{n}{2}}\).注意到 \(A,B\) 均是偶函数.
我们现在把问题分解成了 \(A(x)\) 和 \(B(x)\) 这两个 \(\dfrac{n}{2}\) 项多项式分别代入 \(\omega_{\frac{n}{2}}^0,\omega_{\frac{n}{2}}^1,\dots,\omega_{\frac{n}{2}}^{\frac{n}{2}-1}\) 求值的子问题.问题一分为二,所以总共会分出 \(\log_2 n\) 层,每一层总共是 \(O(n)\) 次求值,时间复杂度为 \(O(n \log n)\).边界在 \(n=1\) 时,直接返回常数项.
可以写分治解决,但有一种常数更优秀的做法,待会介绍.
快速傅里叶逆变换 IFFT
我们还需要将点值转成系数,一个更常用的表示形式.
考虑如何反解 \(a_i\).现在我们存储着每一个 \(f(\omega_n^k)\) 的值:
愉快地往 \(F(x)\) 中代入 \(\omega_{n}^{0},\omega_{n}^{-1},\dots,\omega_{n}^{-n+1}\),得到:
注意到 \(\sum\limits_{m=0}^{n-1}(\omega_{n}^{l-k})^m\) 的取值在 \(l=k \pmod{n}\) 时取 \(n\),\(l\not ={k}\pmod{n}\) 时取 \(0\),因此,\(F(\omega_n^{-k})=a_k\times n\).
根据 \(\omega_n^{k}\) 的周期性,\(\omega_n^{-k}=\omega_{n}^{n-k}\).综上,我们仍然可以用与 FFT 相似的方法分治求 \(a_i\).
具体地,把 FFT 中 \(\omega_n^k\) 逐个改为 \(\omega_n^{-k}\),最后 FFT 出来的结果全部除以 \(n\) 就得到了 \(a_i\).
实现 luogu P3803
分治的方法很暴力,不多说了.我也只写过倍增.
假设 \(n=2^k\).
模拟分治的过程,可以得出一种倍增写法,辅助空间仅为 \(O(1)\):分治共有 \(k\) 层,第 \(k\) 层 \(a_i\) 的顺序是什么样的呢?
结论:对 \(i\) 二进制拆解,然后反转,就是 \(a_i\) 的位置 \(i'\).例如 \(n=2^3\) 时,在第 \(k\) 层 \(a_{(001)_2}\) 实际处于 \((100)_2\) 位置,也就是 \(a_1\) 处于 \(8\) 位置.证明略.
暴力比较好想,但没有优化好写.我们可以直接写出 \(O(n)\) 的代码.
#define rep(i, l, r) for(int i = l; i <= r; ++i)
inline void change() {
int n = f.size();
vector<int> rev(n);
rep(i, 1, n-1) rev[i] = rev[i>>1]>>1|((i&1)*(n>>1));
rep(i, 0, n-1) if (i < rev[i]) swap(f[i], f[rev[i]]);
}
这个函数将 \(f\) 的每一位转到了它在第 \(k\) 层的实际位置.\(\tt rev[i]\) 表示 \(i\) 的实际位置.按 \(0 \to n-1\) 的顺序依次寻找,显然 \(\tt rev[0]=0\).\(\left\lfloor\dfrac{i}{2}\right\rfloor\) 的二进制反转应该是 \(i\) 的二进制反转前面若干位,因此直接赋值.当 \(i\) 二进制最后一位是 \(1\) 时,还要赋给第 \(k-1\) 位为 \(1\).
然后模拟分治每一层合并操作即可.这里可以把 IFFT 也放一起,on=-1 时执行 IFFT.
inline void fft(int on) {
int n = f.size();
change();
for (int h = 2; h <= n; h<<=1) {
comp wn = comp(cos(2*PI/h), on*sin(2*PI/h)); // 单位根一次的变化量
for (int j = 0; j < n; j += h) {
comp w = comp(1, 0); // 单位根
for (int i = j; i < j+(h>>1); ++i, w = w*wn) {
int k = i+(h>>1);
comp a = f[i], b = w*f[k];
f[i] = a+b, f[k] = a-b;
}
}
}
if (on == -1) {
rep(i, 0, n-1)
f[i] /= n;
}
}
模板题完整代码
#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l; i <= r; ++i)
#define per(i, r, l) for (int i = r; i >= l; --i)
#define LL long long
#define int long long
#define comp complex<double>
using namespace std;
const int N = 1<<21, mod = 998244353;
const double PI = acos(-1);
inline int qpow(int a, int b) {
int res = 1;
for (; b; b >>= 1, a=a*a%mod) if (b&1) res = res*a%mod;
return res;
}
int n, m, k;
struct fft_poly {
vector<comp> f;
fft_poly(int n, comp v) : f(vector<comp>(n, v)) {}
inline auto begin() { return f.begin(); }
inline auto end() { return f.end(); }
inline auto size() { return f.size(); }
inline auto resize(int n, int v) { return f.resize(n, v); };
inline comp& operator[](int x) { return f[x]; }
inline void change() {
int n = f.size();
vector<int> rev(n);
rep(i, 1, n-1) rev[i] = rev[i>>1]>>1|((i&1)*(n>>1));
rep(i, 0, n-1) if (i < rev[i]) swap(f[i], f[rev[i]]);
}
inline void fft(int on) {
int n = f.size();
change();
for (int h = 2; h <= n; h<<=1) {
comp wn = comp(cos(2*PI/h), on*sin(2*PI/h));
for (int j = 0; j < n; j += h) {
comp w = comp(1, 0);
for (int i = j; i < j+(h>>1); ++i, w = w*wn) {
int k = i+(h>>1);
comp a = f[i], b = w*f[k];
f[i] = a+b, f[k] = a-b;
}
}
}
if (on == -1) {
rep(i, 0, n-1)
f[i] /= n;
}
}
inline friend fft_poly operator * (fft_poly a, fft_poly b) {
int n = a.size()+b.size();
int k = ceil(log2(n));
n = 1<<k;
fft_poly c(n, 0);
a.resize(n, 0), b.resize(n, 0);
a.fft(1), b.fft(1);
rep(i, 0, n-1) c[i] = a[i]*b[i];
c.fft(-1);
return c;
}
inline friend void qpow(fft_poly& res, fft_poly& a, int b) {
for (; b; b >>= 1) {
if (b & 1) res = res*a;
a = a*a;
}
}
};
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m;
fft_poly f(n+1, 0), g(m+1, 0);
for (auto& it : f) cin >> it;
for (auto& it : g) cin >> it;
f = f*g;
rep(i, 0, n+m) cout << (int)(f[i].real()+0.5) << ' ';
return 0;
}
快速数论变换 NTT
快速傅里叶变换本身没问题,但计算机上它的精度......
能不能在整数范围上就可以实现更快的 DFT?在数论板块上有这样一个与单位复根类似的数.
原根简述
定义:若 \(\nexists x\in \mathbb{N},x < \varphi(p):g^x\not\equiv 1\pmod p\),则称 \(g\) 为 \(p\) 的原根.\(\varphi(p)\) 为欧拉函数,表示与 \(p\) 互质且小于等于它的正整数个数.
性质(\(p\) 为素数):
- \(g^1,g^2,\dots,g^{\varphi(p)}\) 在模 \(p\) 意义下互不相等.
- \(g^n \equiv g^{n+\varphi(p)}\pmod p\).(循环性)
对于一个素数 \(p\) 来说 \(\varphi(p)=p-1\),若能满足 \(\left.n=2^k\right|p-1\),原根 \(g\) 就可以替代 \(\omega_n\) 了.这个素数模数我们一般取 \(p=998244353=2^{23}\times7\times17+1\),这时 \(g=3\).更多模数参见NTT 模数和原根表.
具体地,\(\omega_n^k\) 可以用 \(g^{\frac{(p-1)k}{n}}\) 替换即可达到相同的效果.
注意除法改为乘逆元,勤取模.
模板题完整代码
#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l; i <= r; ++i)
#define per(i, r, l) for (int i = r; i >= l; --i)
#define LL long long
#define int long long
#define comp complex<double>
using namespace std;
const int N = 1<<21, mod = 998244353;
inline int qpow(int a, int b) {
int res = 1;
for (; b; b >>= 1, a=a*a%mod) if (b&1) res = res*a%mod;
return res;
}
int n, m, k;
struct ntt_poly {
vector<int> f;
ntt_poly(int n, int v) : f(vector<int>(n, v)) {}
inline auto begin() { return f.begin(); }
inline auto end() { return f.end(); }
inline auto size() { return f.size(); }
inline auto resize(int n, int v) { return f.resize(n, v); };
inline int& operator[](int x) { return f[x]; }
inline void change() {
int n = f.size();
vector<int> rev(n);
rep(i, 1, n-1) rev[i] = rev[i>>1]>>1|((i&1)*(n>>1));
rep(i, 0, n-1) if (i < rev[i]) swap(f[i], f[rev[i]]);
}
inline void ntt(int on) {
int n = f.size();
change();
for (int h = 2; h <= n; h<<=1) {
int wn = qpow(on==1?3:qpow(3,mod-2), (mod-1)/h);
for (int j = 0; j < n; j += h) {
int w = 1;
for (int i = j; i < j+(h>>1); ++i, w = w*wn%mod) {
int k = i+(h>>1);
int a = f[i], b = w*f[k]%mod;
f[i] = (a+b)%mod, f[k] = (a-b+mod)%mod;
}
}
}
if (on == -1) {
int inv = qpow(n, mod-2);
rep(i, 0, n-1)
f[i] = f[i]*inv%mod;
}
}
inline friend ntt_poly operator * (ntt_poly a, ntt_poly b) {
int n = a.size()+b.size();
int k = ceil(log2(n))+0.5;
n = 1<<k;
ntt_poly c(n, 0);
a.resize(n, 0), b.resize(n, 0);
a.ntt(1), b.ntt(1);
rep(i, 0, n-1) c[i] = a[i]*b[i]%mod;
c.ntt(-1);
return c;
}
inline friend void qpow(ntt_poly& res, ntt_poly& a, int b) {
for (; b; b >>= 1) {
if (b & 1) res = res*a;
a = a*a;
}
}
};
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m;
ntt_poly f(n+1, 0), g(m+1, 0);
for (auto& it : f) cin >> it;
for (auto& it : g) cin >> it;
f = f*g;
rep(i, 0, n+m) cout << f[i] << ' ';
return 0;
}
经典题目
卷积形式转化-快速傅立叶之二
例题:现有 \(\{a_i\}\),\(\{b_i\}\) 两个长为 \(n\) 的序列,令 \(c_k=\sum\limits_{i=k}^na_ib_{i-k}\).下标从 \(0\) 开始.
将 \(\{a_i\}\) 反转得到 \(\{a'_i\}\),则 \(a'_{n-i-1}=a_i\).
这是一个卷积的形式,直接上 FFT 即可.
高精度乘法(加强版)
例题:给定正整数 \(a,b\),求 \(a \times b\).
令 \(x=10\),\(a,b\) 可以分别写做多项式,直接上 FFT 或 NTT 都可.
串匹配
给定主串 \(S\) 和模式串 \(T\),\(10^5\ge|S|\ge|T|\ge1\).下标从 \(0\) 开始.\(n = |S|,m=|T|\).
例题 \(1\):对于 \(0\le i \le n-m\),给出 \(T\) 是否与 \(S\) 从 \(i\) 开始的 \(m\) 个字符组成的子串相等.
例题 \(2\):对于 \(0\le i \le n-m\),给出 \(T\) 与 \(S\) 从 \(i\) 开始的 \(m\) 个字符组成的子串能匹配上多少个字符,也就是 \(\sum \limits_{j=0}^{m-1}[S_{i+j}=T_j]\).
例题 \(3\):\(S,T\) 中存在通配符,可以与任何字符匹配.同样求例题 \(1\) 的答案.
-
例题 \(1\):
-
法一:\(n\) 项式 \(f\) 的 \(i\) 次项系数 \(f_i=S_i\),\(m\) 项式 \(g\) 的 \(i\) 次项系数 \(g_i=T_{m-i-1}\).这里指 ASCII 码值.
构造 \(c_k=\sum\limits_{i=0}^{m-1}(S_{i+k}-T_i)^2=\sum\limits_{i=0}^{m-1}(f_{i+k}-g_{m-i-1})^2\),当且仅当 \(c_k=0\) 时,\(k\) 处答案为‘是’.
将 \(f\),\(g\) 分别 DFT 后,\(ret_i:=(f_i-g_i)^2\),再把 \(ret\) 逆变换回去,则 \(c_k=ret_{m+k-1}\).时间复杂度 \(O(n \log n)\).
-
法二:分别考虑每一个字符,假设当前考虑 \(ch\).令 \(f_i=[ch \neq S_i],g_i=[ch = T_i]\).
注意这个逻辑:由于当前只考虑 \(ch\),因此 \(g_i=1\) 表示 \(T_i\) 必须有对应的 \(S_{i+k}\) 来匹配它,而 \(f_i=0\) 表示 \(S_i\) 这一位可以匹配上 \(T_{i-k}\).当且仅当存在一位需要匹配的 \(T_i\) 没有匹配到 \(S_{i+k}\),两者相乘为 \(1\).
因此,令 \(h_k=\sum\limits_{i=0}^{m-1}f_{i+k}g_i\),则 \(h_k=0\) 表示仅考虑 \(ch\) 的情况下能匹配得起.只有每个字符得到的 \(h_k\) 均等于 \(0\),\(k\) 处答案为‘是’.时间复杂度 \(O(|\Sigma|n\log n)\)
-
-
例题 \(2\):
需要另一个奇妙的构造,借鉴例题 \(1\) 的法二,我们略改一改.改 \(f_i=[ch=S_i],\)令 \(h_k=\sum\limits_{i=0}^{m-1}f_{i+k}g_i\),只有当 \(S_{i+k}=T_i\) 时,相乘等于 \(1\) 会被统计进答案.对每一个字符做相同的卷积,每次得到的 \(h_k\) 加和得到答案.时间复杂度 \(O(|\Sigma|n\log n)\).
-
例题 \(3\):
-
法一:模仿例题 \(1\) 法一,令通配符的对应 \(f_i=0,g_{m-j-1}=0\).构造 \(c_k=\sum\limits_{i=0}^{m-1}(f_{i+k}-g_{m-i-1})^2f_{i+k}g_{m-i-1}\),当且仅当 \(c_k=0\) 时,\(k\) 处答案为‘是’.
正确性不证自明.
-
法二:模仿例题 \(1\) 法二,考虑每个字符 \(ch\) 时,把通配符当作 \(ch\) 来看.
-
多项式快速幂
您这么神仙,肯定会自己发明,不要欺负蒟蒻了 T_T.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号