题解：P11095 [ROI 2021] 旅行 (Day 2)

Link & Luogu.

图论好题，但我比赛时就没有往边双上想啊啊啊。。。

题意： 给定一个 \(n\) 个点 \(m\) 条边的带权无向图，可能有重边，无自环。对于每个节点 \(u \neq 1\)，求出一条迹 \(1 \rightsquigarrow u\)，最小化迹上的边权最大值与边权最小值的和。\(n, m \le 3 \times 10 ^ 5, w \le 10 ^ 9\)。

\(\mathbf{Subtask~3.~}\) 所有一端点是 \(\mathbf 1\) 的边的边权为 \(\mathbf{10 ^ 9}\)

那么所有迹上的边权最大值均为 \(10 ^ 9\)，我们仅需求出边权最小值最小的迹。迹相关问题，不妨从边连通性的角度考虑。

我们知道，\(1 \rightsquigarrow u\) 上的桥是必选的，考虑进行边双缩点，那一个边双内贡献怎么处理呢？实际上，我们有如下引理：

\(\mathbf{Lemma~1.}\) 边双中，对于任意一点 \(x\) 和任意一边 \(e\)，存在经过 \(x, e\) 的回路。

\(\mathbf{Lemma~2.}\) 边双中，对于任意两点 \(x, y\) 和任意一边 \(e\)，存在 \(x \rightsquigarrow e \rightsquigarrow y\) 的迹。

上述引理中的斜体名词的解释参考 OI-Wiki / 图论相关概念 / 路径。

\(\mathbf{Proof.}\)

由 Menger 定理，我们有如下基本事实：边双中，对于任意两点 \(x, y\)，存在经过 \(x, y\) 的回路。

对于 \(\mathbf{Lemma~1.}\)：

• 令 \(e = (u, v)\)，新建虚点 \(w\) 并将 \(e\) 视作 \((u, w)\) 和 \((w, v)\)，则删去 \((u, w)\) 或 \((w, v)\) 都等价于原图删去 \(e\)，不改变边连通性。
• 由基本事实，存在经过 \(x, w\) 的回路，这条回路必然经过 \(u, v\)，于是该回路是符合条件的回路。\(\square.\)

对于 \(\mathbf{Lemma~2.}\)：

• 由 \(\mathbf{Lemma~1.}\)，存在经过 \(x, e\) 的回路 \(C_x\)，当存在 \(C_x\) 使得 \(y \in C_x\) 时满足条件

• 同理，存在经过 \(y, e\) 的回路 \(C_y\)，当存在 \(C_y\) 使得 \(x \in C_y\) 时满足条件。

• 排除上述特殊情况，\(C_x, C_y\) 有公共边 \(e\)，\(x, y\) 均不在 \(C_x, C_y\) 的公共边（集）上，那么直接从 \(x\) 通过 \(C_x\) 走到 \(e\)，再按照走过 \(e\) 的方向（顺/逆时针）通过 \(C_y\) 走到 \(y\) 即可。\(\square.\)

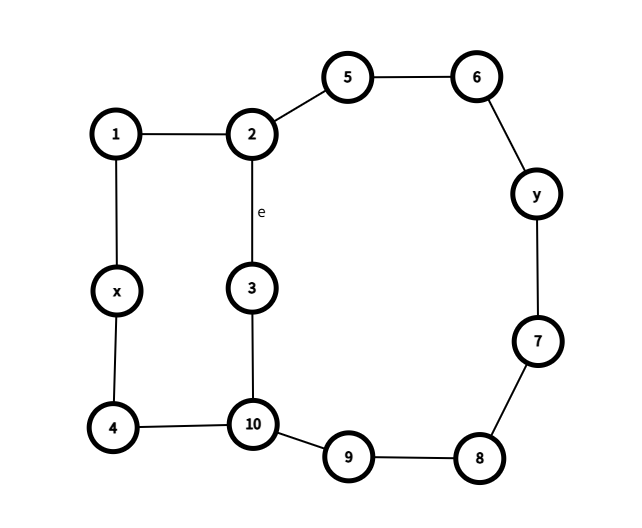
\(\mathbf{Lemma~2.}\) 说明，对于一个边双，我们总可找到一条路径经过其内部边权最小的边。于是我们建出边双缩点树，将每个边双对应点的点权设为其内部最小边权，以节点 \(1\) 的对应点为根做一遍 dfs 即可求出答案。\(\mathcal O(n + m)\)。

\(\mathbf{Subtask~7.~n, m \le 2000}\)

往 \(\mathbf{Subtask~3.}\) 去靠：将所有边按边权从小到大排序，依次加边。加到边 \((u, v, w)\) 时，钦定边权最大值为 \(w\)，套用 \(\mathbf{Subtask~3.}\) 的做法再加上 \(w\) 更新答案。\(\mathcal O(n ^ 2 + nm)\)。

\(\mathbf{Subtask~8.~n \le 5000}\)

\(m\) 没有特殊性质了，但注意到很多边是没用的：考虑新增边 \((u, v, w)\)，由于 \(\mathbf{Subtask~3.}\) 的做法仅依赖连通性和边双连通性，于是若 \(u, v\) 已双连通，因为我们是按 \(w\) 升序加边的，这条边一定是没有贡献的。

考虑维护，用两个并查集分别维护连通性和边双连通性即可。显然有用边仅有 \(2(n - 2)\) 条。

套用 \(\mathbf{Subtask~7.}\) 做法可做到 \(\mathcal O(n ^ 2 + m\log m)\)。

namespace Connectivity {
    struct DSU {
        int fa[N];
        void init(){ iota(fa + 1, fa + n + 1, 1); }
        int find(int u){ return u == fa[u] ? u : fa[u] = find(fa[u]); }
        void merge(int u, int v){ fa[u] = v; }
    } C, EDC;
 
    void init(){ C.init(), EDC.init(); }
    int merge(int u, int v){
        int uf, vf;
        if((uf = C.find(u)) != (vf = C.find(v))) return C.merge(uf, vf), 0;
        else if((uf = EDC.find(u)) != (vf = EDC.find(v))) return EDC.merge(uf, vf), 1;
        else return 2;
    }
} using namespace Connectivity;

\(\mathbf{Subtask~10.~}\) 正解

考虑对加边过程动态维护最小边权。我们将有用边分为两类：

• 影响连通性的边：
  这即为 Kruskal 求 MST 的过程，这样的边一定在 MST 上，于是我们提前建出 MST（以 \(1\) 为根），在 MST。
  对于每个连通块，它一定是最小生成树的一个连通子图，钦定深度最小的点为该连通块的根。这样，每个连通块都是 MST 的一个子树（可能残缺）。

• 影响边双连通性的边：
  考虑该边两端点 \(u, v\) 当前所属的连通块的边双缩点树，\((u, v)\) 与树上 \(u \rightsquigarrow v\) 构成一个环，缩起来即可。
  拉到 MST 上考虑，该连通块是 MST 的一个子树，在 MST 上加边和缩点。

考虑维护节点 \(i\) 到节点 \(1\) 最小边权 \(f_i\)。

对于影响连通性的边 \((u, v, w)\)，钦定 \(v\) 是 \(u\) 在 MST 上的父亲，转移式：

\[f_x \gets \min(f_x, w), x \in \operatorname{subtree}(u) \]

对于影响边双连通性的边 \((u, v, w)\)，将 MST 上 \(u \rightsquigarrow v\) 上所有点缩起来，转移式

\[f_x \gets \min(f_x, w, f_u, f_v), x \in \operatorname{subtree}(\operatorname{lca}(u, v)) \]

每个连通块都是 MST 的一个子树（可能残缺），以上两种转移均可以在 MST 上用 dfs 序 + 线段树维护即可。再开一棵线段树，在加入影响边双连通性的边时，用 \(\min(w, f_u, f_v) + w\) 去更新子树的答案。（为什么在加入影响连通性的边时不用更新答案的线段树？因为在与 \(1\) 合并前更新没有意义，与 \(1\) 合并后不会再作为儿子被更新）

还没完。拉到 MST 上维护确实让问题更简单了，但这回影响到每个连通块的独立性。具体的，原来可能没连通的一部分，也在某次子树修改中被改到，虽然这样的 \(f\) 是对的，但是这个东西算早了，导致可能还没有合并这个子树和节点 \(1\) 就已经用不合法的 \(w\) 更新了答案。

解决方式也很简单，一个连通块与节点 \(1\) 所在连通块合并时，用当前的 \(w\) 重算一遍该连通块的答案即可。

\(\mathcal O(n \log n + m \log m)\)。没了，将近 4k，应该是我的问题。

// godmoo's code
#include <bits/stdc++.h>
#define eb emplace_back
#define ep emplace
#define fi first
#define se second
#define mkp make_pair
#define lbd lower_bound
#define ubd upper_bound
#define mathmod(a) (((a) % MOD + MOD) % MOD)
#define mem(a, b) memset(a, b, sizeof(a))
#define cpy(a, b) memcpy(a, b, sizeof(b))
#define ckmx(a, b) (a = max(a, b))
#define ckmn(a, b) (a = min(a, b))
#define all(a) a.begin(), a.end()
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef tuple<int, int, ll> t3;
const int N = 3e5 + 5;
const ll INF = 0x3f3f3f3f3f3f3f3fll;
int n, m, in[N], out[N], tim, ft[N], dep[N];
vector<int> G[N];
vector<t3> E;
namespace Connectivity {
    struct DSU {
        int fa[N];
        void init(){ iota(fa + 1, fa + n + 1, 1); }
        int find(int u){ return u == fa[u] ? u : fa[u] = find(fa[u]); }
        void merge(int u, int v){ fa[u] = v; }
    } C, EDC;
 
    void init(){ C.init(), EDC.init(); }
    int merge(int u, int v){ return ((u = C.find(u)) != (v = C.find(v))) ? (C.merge(u, v), 0) : 1; }
    int check(int u, int v){
        int uf, vf;
        if((uf = C.find(u)) != (vf = C.find(v))) return 0;
        else if((uf = EDC.find(u)) != (vf = EDC.find(v))) return 1;
        else return 2;
    }
} using namespace Connectivity;
 
struct SegTree{
    ll f[N << 2];
    void pushdown(int u){ ckmn(f[u << 1], f[u]), ckmn(f[u << 1 | 1], f[u]), f[u] = INF; }
    void build(){ mem(f, 0x3f); }
    void modify(int u, int l, int r, int ql, int qr, ll x){
        if(ql <= l && r <= qr) return ckmn(f[u], x), void();
        int mid = l + r >> 1; pushdown(u);
        if(ql <= mid) modify(u << 1, l, mid, ql, qr, x);
        if(qr > mid) modify(u << 1 | 1, mid + 1, r, ql, qr, x);
    }
    void change(int u, int l, int r, int p, ll x){
        if(l == r) return f[u] = x, void();
        int mid = l + r >> 1; pushdown(u);
        p <= mid ? change(u << 1, l, mid, p, x) : change(u << 1 | 1, mid + 1, r, p, x);
    }
    ll query(int u, int l, int r, int p){
        if(l == r) return f[u];
        int mid = l + r >> 1; pushdown(u);
        return min(f[u], p <= mid ? query(u << 1, l, mid, p) : query(u << 1 | 1, mid + 1, r, p));
    }
} T1, T2;
 
int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    for(int i = 1, u, v, w; i <= m; i++) cin >> u >> v >> w, E.eb(u, v, w);
    sort(all(E), [](t3 x, t3 y){ return get<2>(x) < get<2>(y); }), init();
    for(auto [u, v, w] : E) if(!merge(u, v)) G[u].eb(v), G[v].eb(u); // MST
 
    function<void(int, int)> dfs = [&](int u, int fa){
        in[u] = ++tim, ft[u] = fa, dep[u] = dep[fa] + 1;
        for(int v : G[u]) if(v != fa) dfs(v, u);
        out[u] = tim;
    }; dfs(1, 0);
 
    T1.build(), T2.build(), init();
 
    for(auto [u, v, w] : E){
        int res = check(u, v);
        if(!res){
            if(dep[u] < dep[v]) swap(u, v);
            T1.modify(1, 1, n, in[u], out[u], w), C.merge(u, v);
            function<void(int, int, ll)> upd = [&](int u, int fa, ll w){
                if(C.find(u) != 1) return;
                T2.change(1, 1, n, in[u], T1.query(1, 1, n, in[u]) + w);
                for(int v : G[u]) if(v != fa) upd(v, u, w);
            }; upd(u, v, w);
        }
        else if(res == 1){
            u = EDC.find(u), v = EDC.find(v);
            ll wgt = min({w, T1.query(1, 1, n, in[u]), T1.query(1, 1, n, in[v])});
            while(u != v){
                if(dep[u] < dep[v]) swap(u, v);
                EDC.merge(u, ft[u]), u = EDC.find(u);
            }
            T1.modify(1, 1, n, in[u], out[u], wgt);
            T2.modify(1, 1, n, in[u], out[u], wgt + w);
        }
    }
     
    for(int i = 2; i <= n; i++) cout << T2.query(1, 1, n, in[i]) << "\n";
    cout << flush;
    return 0;
}