26牛客寒假算法训练营1题解

学习总结

学习到了状态压缩，我们直接转换为二进制，再直接把二进制转换为数字就可以了。
用的时候这样用就可以了 x>>j.
对于多种选择方案用状态压缩有时候会解决很多问题

A.A+B Problem

题目描述

有八个独立的数位显示器，每个显示器的每个二极管被点亮的概率为，管与管之间互相独立，显示器

之间也相互独立，求分别显示出两个四位合法数字，且数字之和等于输入的常数的概率。

每个显示器至少亮 1 根（不能全灭）
每个显示器显示的是合法数字 0..9 0..90..9
上排 4 个拼成四位数 A AA，下排 4 个拼成四位数 B BB，满足 A + B = C A+B=CA+B=C（允许前导 0）

解题

我们可以去先算显示当个数d的概率，七段码，每一个对应两种状态，0，1

那我们完全可以用状态压缩来得到这个所以的情况。

例如显示0

01110111

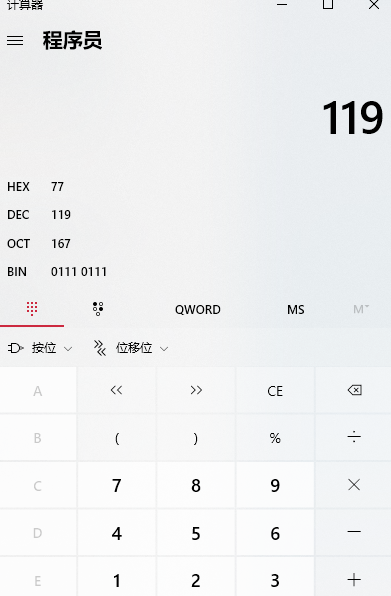
也就是119，其他的以此类推。

然后我们可以得到每一个数的概率，因为每一个都要亮的概率，所以我们先把每一个数的概率算出来，用

x>>j&1来得到这个数到底是1还是0

最后直接把一个四位数的表示方法写出来，我们直接用取最后一位一直取，如果不够就直接前导零，然后相乘概率。

得到c的话直接枚举a，然后得到b=c-a；

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7,MOD=998244353;
int a[N],b[N],c[N],pre[N];
//相当于0的话就中间那个不亮，1110111，以此类推。
int segMask[10] = {
        119, 36, 93, 109, 46, 107, 123, 37, 127, 111
};
int ksm(int p,int q,int mod){
    int result=1;
    p%=mod;
    while(q){
        if(q&1)result=result*p%mod;
        p=p*p%mod;
        q>>=1;
    }
    return result%mod;
}

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int inv100=ksm(100,MOD-2,MOD);
    int x[7];
    int C;
    cin>>C;
    //先得到这个，x[i] = p_i / 100 (mod MOD)
    for(int i=0;i<7;i++){
        int p;
        cin>>p;
        x[i]=(1ll*p%mod*inv100)%mod;
    }
    vector<int>x1(10,1);//统计出0-9这些数在一个的时候的概率。
    for(int i=0;i<10;i++){
        for(int j=0;j<7;j++){
            if(segMask[i]>>j&1){
                x1[i]*=x[j];
            }else{
                x1[i]*=(1+MOD-x[j]);
            }
            x1[i]%=MOD;
        }
    }
    //开始拼接，四位数的-》x的概率
    auto cacl=[&](int x)->int{
        if(x==0)return x1[0]%MOD*x1[0]%MOD*x1[0]%MOD*x1[0]%MOD;

        int ans=1;
        int len=0;
        while(x>0){
            ans*=x1[x%10]%MOD;//取最后一位
            ans%=MOD;
            x/=10;
            len++;
        }
        for(int i=0;i<4-len;i++){//处理前导零的情况。
            ans*=(x1[0])%MOD;
            ans%=MOD;
        }
        return ans;
    };

    int ans=0;
    for(int A=0;A<=C;A++){
        int B=C-A;
        ans+=(cacl(A)%MOD*cacl(B)%MOD);
        ans%=MOD;
    }
    cout<<ans<<endl;

	return 0;
}

B. 【Card Game】

题目描述

有 2n 张牌，数字是 1..2n 的一个排列，分给两人各 n 张。

小红的出牌顺序固定为队列 b1..b**n ；小苯的牌是集合 a1..a**n ，他可以在开局前任意重排自己的出牌顺序。

解题思路

我们可以发现我们的小苯赢的数量是大于小红最小牌的个数，
我们可以思考，我们一直开始让小红放第一个最小，我只需要把小苯比他大的都放在前面就可以了，然后就会出现分界限，后面的都的不了分，前面的都能得到分。

方案数 = 得分的排序x不得分的排序mod998244353。

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7,MOD=998244353;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    int x=0,y=0,mi=1e8;
    vector<int>a(n);
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    for(int i=0;i<n;i++){
        int m;
        cin>>m;
        mi=min(mi,m);
    }
    for(int i=0;i<n;i++){
        if(a[i]>=mi){
            x++;
        }else{
            y++;
        }
    }
    int ans=0;
    for(int i=1;i<=x;i++){
        ans=(ans*i)%MOD;
    }
    for(int i=1;i<=y;i++){
        ans=(ans*i)%MOD;
    }
    cout<<ans<<endl;
	return 0;
}

c--Array Covering

题目描述

给定长度为 n 的数组 a1,a2,…,a**n 。你可以进行任意次操作：

选择一对下标 l,r （1≤l<r≤n ），把开区间 (l,r) 内的所有元素都赋值为端点较大者：

对所有 j （l<j<r ），令 a**j:=max(a**l,a**r) 。

问：经过任意次操作后，数组元素和 ∑a**i 的最大值是多少。

题解

假设序列中某个最大值下标为 idx （有多个最大值的情况下，随便选一个即可），则：

我们永远可以通过最多两次操作，选中 [1,idx] 和 [idx,n] 把数组中，除了第一个位置，和最后一个位置以外的所有数字都变成数组的最大值。

因此答案就是：最大值 ×(n−2) ，再加上 a1 和 a**n 即可。

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    vector<int>m(n+1);
    int mx=0;
    for(int i=1;i<=n;i++){
        cin>>m[i];
        mx=max(m[i],mx);
    }
    cout<<m[0]+m[1]+(n-2)*mx;
	return 0;
}

E. 【Block Game】

题目描述

有一排 n 个方块，初始为 a1,a2,…,a**n ，另外有一个"万能方块"数值为 k 。你可以进行任意次操作（可为 0 次）：

把万能方块插到最左边；
最右边第 n 个方块被挤出，成为新的万能方块；
其余方块整体右移一位。

操作若干次后，记最终：

从左往右第一个方块的数字为 A ；
最终万能方块的数字为 B ；

求最大化 A+B 的值。

题解

我们可以把它现象成一个0，n的数组，但是是循环，首位相连的，我们会发现，我们只需要去判断相连元素的和的最大值就是答案，应为总是有一个时刻会使得他们要分开。

相当于判断元素的和的最大值

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n,k;
    cin>>n>>k;
    vector<int>v(n+1);
    v[n]=k;
    for(int i=1;i<=n;i++){
        cin>>v[i];
    }
    int ma=-2e7;
    for(int i=0;i<n;i++){
        ma=max(ma,v[i]+v[(i+1)%n]);
    }
    cout<<ma<<endl;
	return 0;
}

G【Digital Folding】

题目描述

将正整数 x 的十进制数位反转，并去掉反转后的前导 0，得到新数。

给定一个区间l，r求里面最大的反转函数

题解

我们先将数用string存储，方便后续的操作等我们可以分类去讨论，

当R为1000000这个时候，答案肯定不是与R位数相同，可能，如果l==r,那只能等于1了，如果不等于那必定是R-1，为答案，减去1后相当于数字全为9，长度少了一而已
第二个答案，肯定可以取到相同的位数，我们直接考虑从，如果l的长度比r小，那么直接让l变成属于r长度的1000001，然后我们去枚举到那个数是相同的，第k给位置，然后继续去把后面的全部变成9，有一个前提如果后面全是9，那就第k位不要去减-1，如果没有那就减去1，然后输出答案就行了

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    string s1,s2;
    cin>>s1>>s2;
    int l= stoll(s1);
    int r=stoll(s2);
    int n=s2.size();

    string t="1";
    //先让其变成10000000，
    for(int i=0;i<n-1;i++){
        t+='0';
    }
    //分类讨论
    if(t==s2){
        if(s1==t){
            cout<<1<<endl;
        }else{
            cout<<r-1<<endl;
        }
        return 0;
    }
    if(s1.size()<s2.size()){
        s1=t;
        s1+='1';
    }
    string ans;
    int k=-1;
    for(int i=0;i<n;i++){
        if(s1[i]!=s2[i]){
            k=i;
            break;
        }
    }
    if(k==-1){//不能找到相同的那就只能去反转了
        ans=s1;
        while (ans.size()>1&&ans.back()=='0'){
            ans.pop_back();
        }
        reverse(ans.begin(),ans.end());
    }else{
        bool ok=1;
        for(int i=k+1;i<n;i++){
            ans+='9';
            ok&=(s2[i]=='9');
        }
        ans+=(s2[k]-!ok);
        for(int i=k-1;i>=0;i--){
            ans+=s1[i];
        }
    }
    cout<<ans<<endl;


	return 0;
}

H. Blackboard

给定一个序列，表示运算式：问有多少种把替换成（位运算按位或）的

方式，使得不改变运算式的值。（不替换也是一种方案，且特别的：本题中认为运算优先级大于

解题代码

解题代码就是线性dp

K. 【Constructive】

题目描述

给定正整数 n ，需要构造一个长度为 n 的数组 a1,a2,…,a**n ，满足：

每个 a**i 都是正整数；
所有元素乘积等于所有元素之和：∏ai=∑ai ；
所有元素互不相同；
若存在，输出字典序最小的解；否则输出 NO。

思考，我们想到了只有当n=1，n=3的时候才有结果。

为什么这样说呢因为我们知道，要使得这个东西乘积和求i和相等，这个一般是升序，发现当n=4的时候，字典序最小的为

1，2，3，4----》加起来为10 乘为24了，那后面的无论怎么都不可能相等了，已经是大于了

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    if(n==1||n==3){
        cout<<"Yes"<<endl;
        for(int i=1;i<=n;i++){
            cout<<i<<" ";
        }
    }else{
        cout<<"No"<<endl;
    }

	return 0;
}

L.【Need Zero】

题目描述

给定正整数 n （1≤n≤105 ）。

你必须恰好执行一次操作：选择一个正整数 x （1≤x≤105 ），令 n:=n×x 。

要求操作后 n 的个位数为 0 ，输出满足条件的最小 x 。

分析：当我们要得到10的倍数，相当于也就是小于10的数这些数的答案，所以我们得到，一共4个情况1，2，5，10；

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    if(n%10==0){
        cout<<1<<endl;
    }else if(n%2==0){
        cout<<5<<endl;
    }else if(n%5==0){
        cout<<2<<endl;
    }else{
        cout<<10<<endl;
    }

	return 0;
}

posted @ 2026-02-05 13:08 Godjian 阅读(0) 评论(0) 收藏举报

刷新页面返回顶部

Godjian

欲望以提升热枕，毅力以磨平高山！

26牛客寒假算法训练营1题解

26牛客寒假算法训练营1题解

学习总结

A.A+B Problem

题目描述

解题代码

B. 【Card Game】

题目描述

解题代码

c--Array Covering

题目描述

解题代码

E. 【Block Game】

题目描述

解题代码

G【Digital Folding】

题目描述

解题代码

H. Blackboard

解题代码

K. 【Constructive】

题目描述

解题代码

L.【Need Zero】

题目描述

解题代码

公告