C++算法算法训练第十二天

C++算法算法训练第十二天

以下为牛客挑战

今日收获

知道了小根堆的写法
priority_queue<int,vector<int>,greater<int>>q;
用于小根堆，每次直接用top（）取，得到里面最小的。

问图中有多少个连续的子集
0001100
我们只需要取判断，s[i]!=s[i+1]的个数就行了。我们可以看到一共有3个。

费马小定理求逆元。
ksm(2,mod-2,mod)---》2的-1次方。

组合数学
 for(int i=2;i<=n;i++){
        f[i]=f[i-1]*i%mod;//表示阶乘
        g[i]=g[i-1]*ksm(i,mod-2,mod)%mod;//阶乘的倒数
    }

image-20260202164527769

牛客小白月赛128

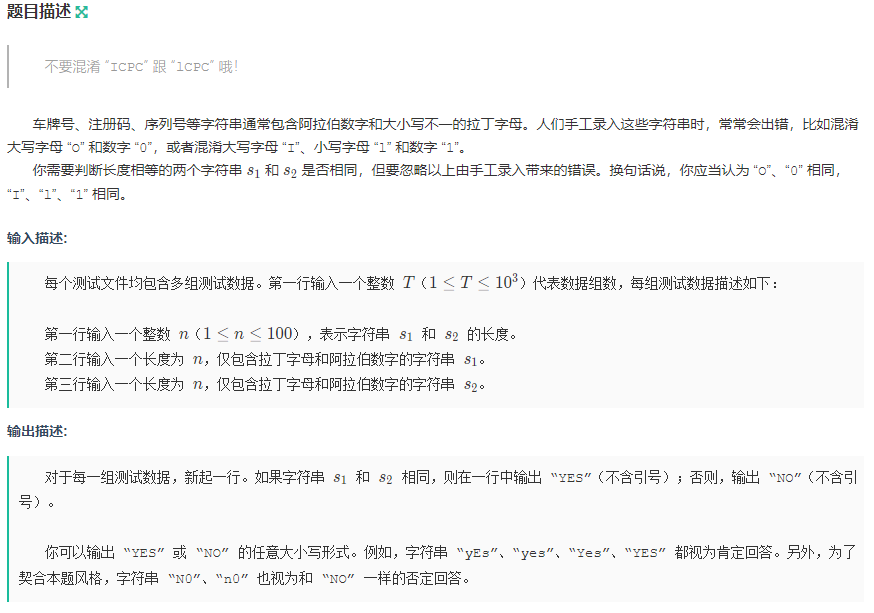
模糊匹配

image-20260131202831033

4
9
Apple0123
Apple0123
5
AKIOI
AK101
10
ilovezaoly
1loveza0Iy
6
banana
BANANA

YES
YES
NO
NO

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
void solve(){
    int n;
    cin>>n;
    string s,s1;
    cin>>s>>s1;
    for(int i=0;i<n;i++){
        if(s[i]=='O'){
            s[i]='0';
        }
        if(s1[i]=='O'){
            s1[i]='0';
        }
        if(s[i]=='I'||s[i]=='l'){
            s[i]='1';
        }
        if(s1[i]=='I'||s1[i]=='l'){
            s1[i]='1';
        }
    }
   
    if(s==s1){
        cout<<"YES"<<endl;

    }else{
        cout<<"NO"<<endl;
    };
};
signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    TESTS{
        solve();
    };

	return 0;
}

只留专一数

image-20260131211349373

2
2
8 15
1
6

YES
NO

实际上我们通过观察，当选择一个数的时候

选两个不同的位置 i, j
令 a[i] = a[i] ^ a[j]（a[i] 的 a[j] 次方）
令 a[j] = a[n']（用最后一个元素覆盖）
n' 减1（相当于数组长度-1，丢弃最后一个元素）

那么我们当到达最后一个的时候到底是什么一个情况

实际上最后会变成
a1^(a2*a3*a4*a5*a6*....ak)

指数部分是所有参与运算的其他数的乘积。

假设我们选 a[i] 作为最终的底数，其他所有数都作为指数的一部分：

  • 最终 a[1] = a[i]^{(其他所有数的乘积)}
  • 指数部分不影响不同质因数的种类，只影响次数
  • 所以只要 a[i] 本身是专一数，最终结果也是专一数！

所以只要我们的数组中存在这个数，我们就可以得到专一数

具体解法

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
void solve(){
    int n;
    cin>>n;
    vector<int>v(n+1);
    for(int i=1;i<=n;i++){
        cin>>v[i];
    }
    for(int i=1;i<=n;i++){
        int flag=0;// 统计v[i]的不同质因数个数
        for(int j=2;j*j<=v[i];j++){
            if(v[i]%j)continue;// j不是因数，跳过
            flag++;
            while (v[i]%j==0)v[i]/=j;// 除尽这个质因数
        }
        if(v[i]>1)flag++;// 还剩一个大于1的质因数
        // 如果a[i]本身是专一数（不同质因数个数<=1）
        if(flag<=1){
            cout<<"YES"<<endl;
            return ;
        }
    }
    cout<<"NO"<<endl;

};
signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    TESTS{
        solve();
    };

	return 0;
}

牛客周赛 Round 129

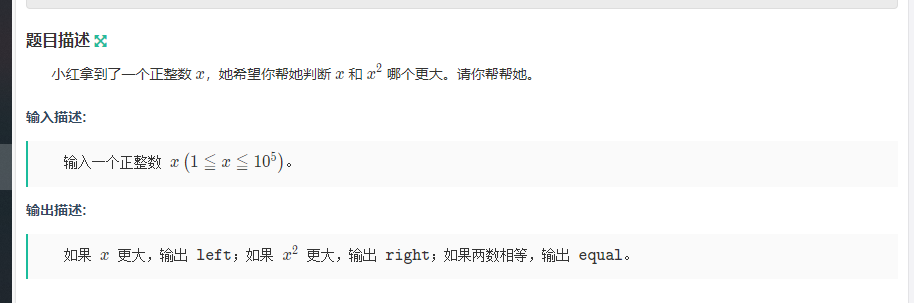
小红的大小判断

小红的大小判断

image-20260202135547702

3

right

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int x;
    cin>>x;
    if(x>x*x){
        cout<<"right";
    }else{
        cout<<"equal";
    }
	return 0;
}

小红的大小再判断

B-小红的大小再判断_牛客周赛 Round 129 (nowcoder.com)

image-20260202140119795

示例1

abc

right

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    string s,s1;
    cin>>s;
    s1=s;
    reverse(s1.begin(),s1.end());
    if(s>s1){
        cout<<"left";
    }else if(s==s1){
        cout<<"equal";
    }else{
        cout<<"right";
    }
	return 0;
}

小红的肥鹅健身房

C-小红的肥鹅健身房_牛客周赛 Round 129 (nowcoder.com)

image-20260202150447988

示例1

2 3 3
1 0 0
1 1 1

3 1

这个我们可以去考虑优先队列（小根堆），它可以帮我们每次取出的都是最小的，top（）；

取出最小的后和后一个开始比较，如果开始的后一个的相同就把这个数+1添加到小根堆中。然后一直取和pop

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n,m,k;
    cin>>n>>m>>k;
    priority_queue<int,vector<int>,greater<int>>q;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            int x;
            cin>>x;
            if(x>0)q.push(x);
        }
    }
    int ans=0,ans1=0;
    while (q.size()>1){
        int s=q.top();
        q.pop();
        if(s==q.top()){
            q.pop();
            q.push(s+1);
            ans++;
            if(s+1>=k){
                ans1++;
            }
        }
    }
    cout<<ans<<" "<<ans1;

	return 0;
}

小红的神秘密码解锁

D-小红的神秘密码解锁_牛客周赛 Round 129 (nowcoder.com)

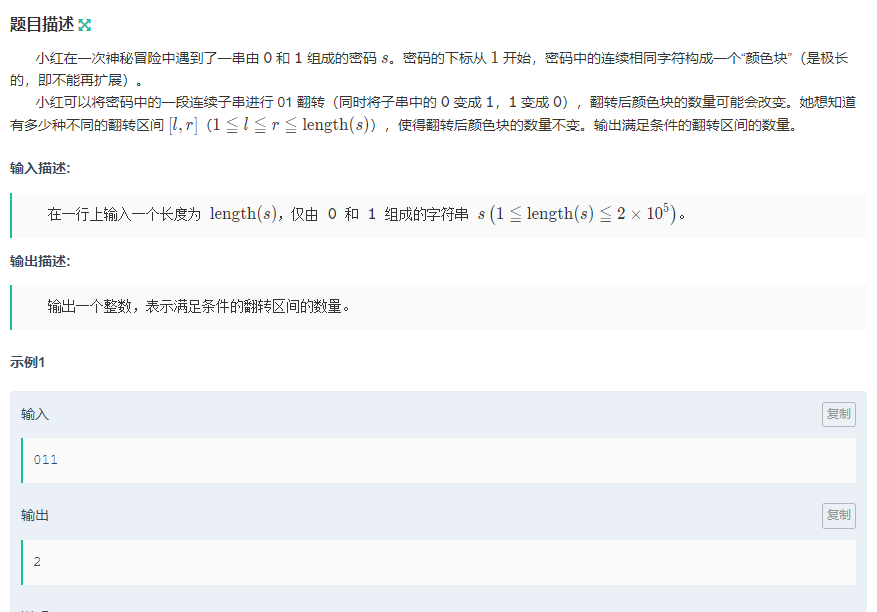
image-20260202153721408

示例1

011

2

颜色快我们可以这样去认为，连续相同数个数的类数。

0001100
我们只需要取判断，s[i]!=s[i+1]的个数就行了。我们可以看到一共有3个。

知道这个规律就行了

我们可以有这样的一种规律，我们取的区间的贡献只和开头和结尾有关

image-20260202154342975

假设开始和前面的不一样那么就会得到减一的贡献，相同得到加一的贡献奖。

所以抵消的话后面的就要为相呼应的加上一和减去一就行了，所以我们只需要枚举这个字符串就行了，单枚举到减1的时候就去看看前面有多少个加一的。然后相反就看看有多少减1的。

最后要加上一个特殊的就是全部反转的

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    string s;
    cin>>s;
    int same=0,nsame=0;
    int ans=0;
    for(int i=0;i+1<s.size();i++){
        if(s[i]!=s[i+1]){
            ans+=same;
            nsame++;
        }else{
            ans+=nsame;
            same++;
        }
    }
    cout<<ans+1;
	return 0;
}

小红的多维空间冒险

E-小红的多维空间冒险_牛客周赛 Round 129 (nowcoder.com)

image-20260202162228631

3

12 12 4

这个题说的 根号k，我们就可以把外面包裹的去掉。

（x-y）的平方且x，y属于0和1只需要求两个的异或就行了

x^y--相同为0，不同为1，
所以对于k，我们只要选定k个位置为不同的，n-k为相同的，所以用排列组合
2的k次法表示k个位置每个位置都有两种不同的方式。n-k也一样。

但是最后要再除去2，我们没有规定u，v顺序，当时题目看到把这两种视为相同的一种。

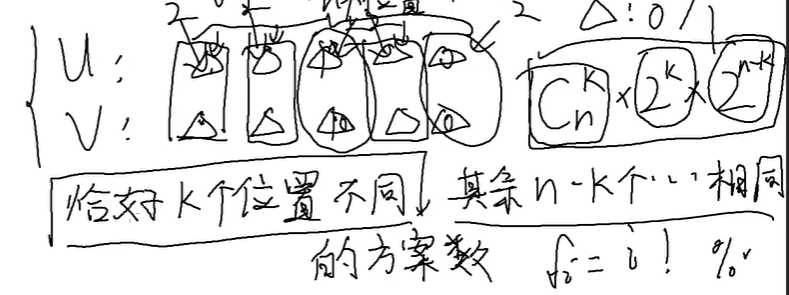
image-20260202163526351

从n中选k个。

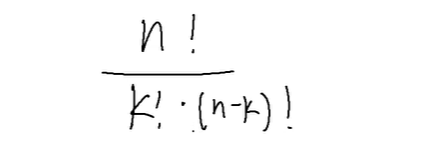
image-20260202161127580

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int ksm(int p,int q,int mod){
    int result=1;
    p=p%mod;
    while (q>0){
        if(q&1){
            result=(1ll*result*p)%mod;
        }
        q>>=1;
        p=(1ll*p*p)%mod;
    }
    return result%mod;
}
signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    vector<int>f(n+1,1),g(n+1,1);
    for(int i=2;i<=n;i++){
        f[i]=f[i-1]*i;
        g[i]=g[i-1]*ksm(i,mod-2,mod);
    }

    auto C=[&](int n,int k)->int{
        if(n<k)return 0;
        return f[n]*g[n-k]%mod*g[k]%mod;
    };
    for(int k=1;k<=n;k++){
        int cur=C(n,k)*ksm(2,k,mod)%mod;
        cur=(cur*ksm(2,n-k,mod)%mod);
        cur=(cur* ksm(2,mod-2,mod))%mod;
        cout<<cur<<" ";
    }

	return 0;
}

小红的魔法树探险

F-小红的魔法树探险_牛客周赛 Round 129 (nowcoder.com)

image-20260202184330519

3
1 2
2 3

500000006

这个题就是我们可以去想想到底是每个点有子树和节点，我们选择那条路就是节点分之一的概率，我们可以去枚举1到所有顶点的期望，

期望==前面所有概率乘积x这个节点的深度。

dfs遍历

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int ksm(int p,int q,int mod){
    int result=1;
    p=p%mod;
    while (q>0){
        if(q&1){
            result=(1ll*result*p)%mod;
        }
        q>>=1;
        p=(1ll*p*p)%mod;
    }
    return result%mod;
}
signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    vector<vector<int>>g(n+1);
    for(int i=0;i<n-1;i++){
        int u,v;
        cin>>u>>v;
        g[u].push_back(v);
        g[v].push_back(u);
    }

    int ans=0;
    auto dfs=[&](auto &&self,int u,int fa,int s,int dep)->void{
        s*=ksm(g[u].size(),mod-2,mod);
        s%=mod;
        if(u>1){
            ans+=s*dep%mod;
            ans%=mod;
        }
        for(auto &v:g[u]){
            if(v==fa)continue;
            self(self,v,u,s,dep+1);
        }
        s*=g[u].size();//回溯
        s%=mod;
    };
    dfs(dfs,1,0,1,1);

    cout<<ans<<endl;

	return 0;
}
posted @ 2026-02-02 19:02  Godjian  阅读(7)  评论(0)    收藏  举报