C++算法训练第十天

以下为牛客挑战

今日收获

当在二维数组中，n，m的行和列改变不会影响结果时候，我们直接设置把n换成小的，再进行讨论结果。

知道了最小公倍数怎么求，两个数相乘/最大公因数

int lcm(int x,int y){
    return x/__gcd(x,y)*y;
}
gcd
return b == 0 ? a : gcd(b, a % b);


c++建树
vector<vector<int>>g(n+1);//这个是关键
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        g[u].emplace_back(v);
        g[v].emplace_back(u);
    }
dfs找最大的深度
int maxDepth;                 // 全局答案
vector<vector<int>> g;        // 邻接表

// 当前点 u，父节点 fa，当前深度 d
void dfs(int u, int fa, int d)
{
    maxDepth = max(maxDepth, d);          // 更新最深
    for (int v : g[u])
        if (v != fa)                      // 防止走回父节点
            dfs(v, u, d + 1);
}

牛客周赛 Round 120

无穷无尽的力量

A-无穷无尽的力量_牛客周赛 Round 120 (nowcoder.com)

aba

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cout<<"a";
    }
    cout<<"b";
    for(int i=0;i<n;i++){
        cout<<"a";
    }

	return 0;
}

无穷无尽的字符串

B-无穷无尽的字符串_牛客周赛 Round 120 (nowcoder.com)

1 3

1 1 1

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main() {

    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int l, r;
    cin >> l >> r;
    int a = 0, b = 0, c = 0;
    while (l % 3 != (r + 1) % 3) {
        if (l % 3 == 1) ++a;
        else if (l % 3 == 2) ++b;
        else ++c;
        ++l;
    }
    a += (r - l + 1) / 3;
    b += (r - l + 1) / 3;
    c += (r - l + 1) / 3;
    cout << a << " " << b << " " << c << endl;
    return 0;
}

无穷无尽的力量2.0

C-无穷无尽的力量2.0_牛客周赛 Round 120 (nowcoder.com)

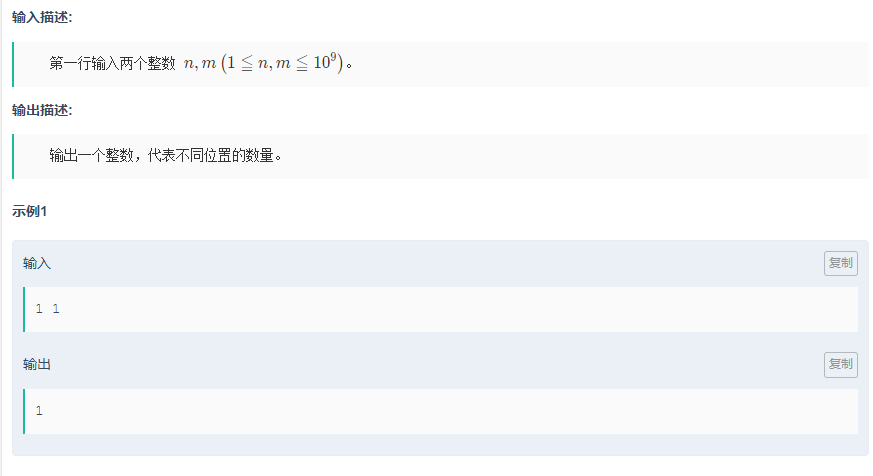
第一点：我们发现n，m行和列交换没有任何关系，不影响答案，所以我们直接先选着一种方案，我们选n<=m,如果大于直接交换位置。

swap(n,m);

我们通过画图来分类讨论

n只有一行时候

n只有两行时候

我们发现只要增加两列就能增加一个

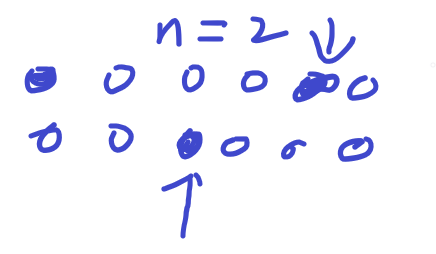
cout<<1+(m-1)/2;

当n=m=3

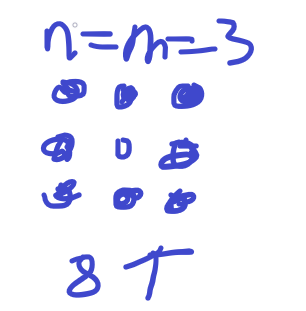
其他情况

我们发现这些都能涂满

cout<<n*m;

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n,m;
    cin>>n>>m;
    if(n>m){
        swap(n,m);
    }
    if(n<=1){
        cout<<1;
    }else if(n==2){
        cout<<1+(m-1)/2;
    }else if(n==3&&m==3){
        cout<<8;
    }else{
        cout<<n*m;
    }


	return 0;
}

无穷无尽的小数

D-无穷无尽的小数_牛客周赛 Round 120 (nowcoder.com)

1 1
2
3

1
8

这个题开始还是不好理解的，但是看了解析，发现好多了

循环小数的长度肯定是在lcm（n，m），这个是最小公倍数。

先把长度补齐哦，然后再减，但是我们需要判断一下到底一开始到底要不要借位，我们发现，当a的字典序小于b时候，就需要去一开始就借位了，所以s=-1，最后模拟计算过程就可以了

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;

int lcm(int x,int y){
    return x/__gcd(x,y)*y;
}
signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n,m;
    string a,b;
    string c,d;
    cin>>n>>m;
    cin>>c;
    cin>>d;
    int k=lcm(n,m);

    for(int i=0;i<k/n;i++){
        a+=c;
    }
    for(int i=0;i<k/m;i++){
        b+=d;
    }


    int s=0;
    if(a<b){
        s=-1;//表示借位/
    }
    string ans;
    for(int i=k-1;i>=0;i--){
        int cur=(a[i]-'0')+s-(b[i]-'0');
        if(cur<0){
            cur+=10;
            s=-1;
        }else{
            s=0;
        }

        ans+=(cur+'0');
    }
    reverse(ans.begin(),ans.end());
    cout<<ans.size()<<endl;
    cout<<ans<<endl;
	return 0;
}

无穷无尽的树

dfs+树上dp

E-无穷无尽的树_牛客周赛 Round 120 (nowcoder.com)

2 2 1 1 0 0

这个题的意思是给我一个树，先把叶子减去，然后去算每一个点的树中深度最深的节点有多少个

算的是个数，我们可以用dfs去算

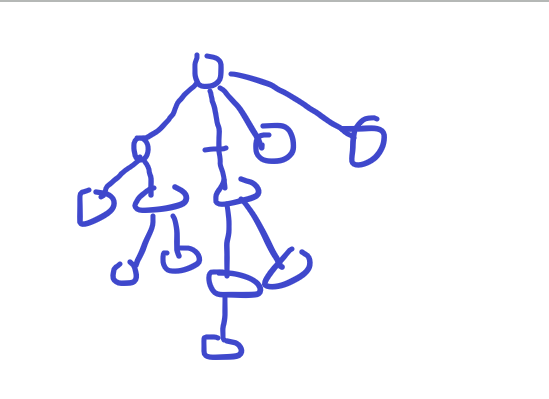
返回的是深度。

我们就可以去用树上dp去弄，dfs遍历加树上dp

无穷无尽的数

F-无穷无尽的数_牛客周赛 Round 120 (nowcoder.com)

3 1 6
123

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;


signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    vector<vector<int>>g(n+1);
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        g[u].emplace_back(v);
        g[v].emplace_back(u);
    }

    vector<int>ans(n+1);
	//返回的是深度，和个数
    auto dfs=[&](auto &&self,int u,int fa)->pair<int,int>{
        if(u>1&&g[u].size()==1){//判断是不是叶子
            return {-1,0};
        }
        int mx=-1;
        int  cnt=0;
        for(auto &v:g[u]){
            if(v==fa)continue;
           
            auto [depth,c]=self(self,v,u);#depth这个是深度，c是个数
                //找到这个最大的深度
            if(depth+1>mx){
                mx=depth+1;
                cnt=c;
            }else if(depth+1==mx){
                cnt+=c;
            }

        }
        if(mx==0){
            cnt=1;
        }
        ans[u]=cnt;
        return {mx,cnt};
    };
    dfs(dfs,1,0);

    for(int i=1;i<=n;i++){
        cout<<ans[i]<<" ";
    }

	return 0;
}

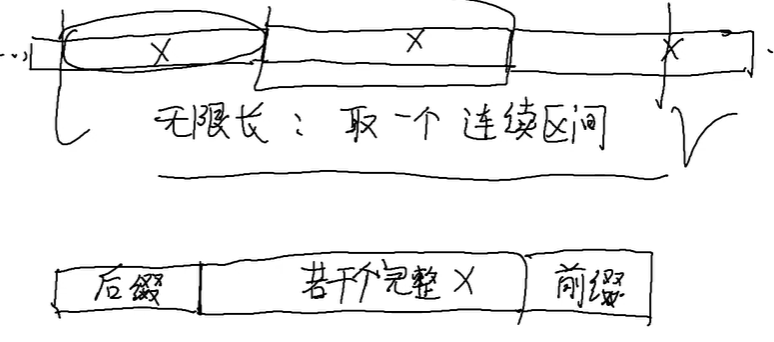
解题代码

#include <bits/stdc++.h>
using namespace std;
#define inf 1e18
#define endl '\n'
#define int long long
typedef  long long ll;
typedef pair<int, int> pii;
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
const int N = 2e5 + 9, M = 2e5 + 9, mod = 998244353;
int ksm(int b,int p){
	int res=1;
	if(p>=mod-1){
		p=p%(mod-1)+(mod-1);
	}
	while(p){
		if(p&1) res=res*b%mod;
		b=b*b%mod;
		p>>=1;
	}
	return res;
}
void solve() {
	int n,l,r;
	cin >> n >> l >> r;
	string s;
	cin >> s;
	s=" "+s;
	vector<int> pre(n+1);
	vector<int> mi(n+1);
	mi[0]=1;
	int b=10;
	for(int i=1;i<=n;i++){
		mi[i]=mi[i-1]*b%mod;
		pre[i]=(pre[i-1]*b%mod+s[i]-'0')%mod;
	}
//	auto get=[&](int l,int r)->int{
//		return (pre[r]-pre[l-1]*mi[r-l+1]%mod+mod)%mod;	
//	};
	//直接算f(x)
	//k块完整的加上一块不完整的，这样就好算多了
	int inv=ksm(mi[n]-1,mod-2);
	auto f=[&](int x)->int{
		int k=x/n;
		int r=x%n;
		int res=mi[r]*pre[n]%mod*(ksm(b,k*n)-1+mod)%mod*inv%mod;
		res=(res+pre[r])%mod;
		return res;
	};
	int ans=(f(r)-f(l-1)*ksm(10,r-l+1)%mod+mod)%mod;
	cout << ans << endl;
	
}
/*

*/
signed main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	int t = 1;
//	cin >> t;
	while (t--) {
		solve();
	}
	return 0;
}

posted @ 2026-01-23 16:31 Godjian 阅读(1) 评论(0) 收藏举报

刷新页面返回顶部

Godjian

欲望以提升热枕，毅力以磨平高山！

C++算法训练第十天

C++算法训练第十天

今日收获

牛客周赛 Round 120

无穷无尽的力量

解题代码

无穷无尽的字符串

解题代码

无穷无尽的力量2.0

解题代码

无穷无尽的小数

解题代码

无穷无尽的树

dfs+树上dp

无穷无尽的数

解题代码

解题代码

公告