C++小白训练第五天

C++小白训练第五天

以下为牛客挑战

今日收获

存放相同的东西的序号时候可以用vector
vector<vector<int>>f(N);
这样就不会像二维数组一样被动

区间递归
变化不大的
f[i]=f[i-1]+{-1,1,0}

牛客周赛 Round 123

(34条未读私信) 牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ

小红玩牌

A-小红玩牌_牛客周赛 Round 123

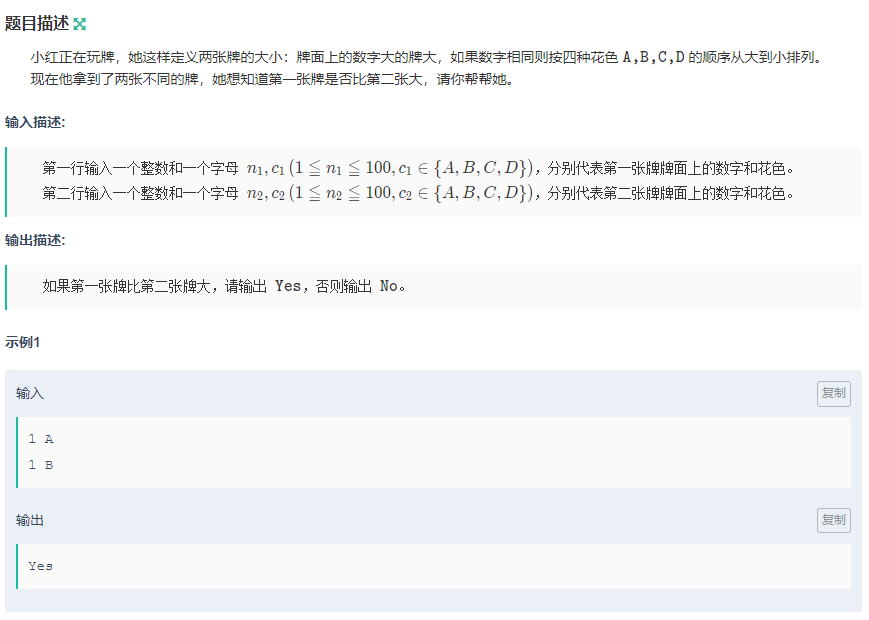
解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n1,n2;
    string s1,s2;
    cin>>n1>>s1;
    cin>>n2>>s2;
    if(n1>n2){
        cout<<"Yes"<<endl;
    }else if(n1==n2){
        if(s1<s2){
            cout<<"Yes"<<endl;
        }else{
            cout<<"No"<<endl;
        }
    }else{
        cout<<"No"<<endl;
    }

	return 0;
}

小红作弊

B-小红作弊_牛客周赛 Round 123

很简单只需要我们直接看看哪里多了的，多了的就是

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    vector<array<int,2>>ans(14);
    int x1=0,x2;
    for(int i=1;i<=13;i++){
        cin>>ans[i][0];
    }
    for(int i=1;i<=13;i++){
        cin>>ans[i][1];
    }
    for(int i=1;i<=13;i++){
        int m=ans[i][0]+ans[i][1];

        if(m>4){
           x1+=m-4;
        }
        if(m<4){
            x2+=4-m;
        }
    }
    cout<<x1<<endl;

	return 0;
}

小红出对

C-小红出对_牛客周赛 Round 123

5
1 A
1 B
3 A
2 A
3 B

输出

4
1 2
3 5

这个题目就是去掉重复的，然后记录下每一个种类的序号就行了

就是实现不好实现，但是我发现了我们可以用二维数组来存取一下

用vector存储

vector<vector<int>>f(N); 
if(!g[a][b]){
            g[a][b]=1;
            f[a].push_back(i);//相同的放在一个地方
    }

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;


signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    vector<array<int,4>>g(N);
    vector<vector<int>>f(N);
    int n;
    cin>>n;
    int ans=0;
    for(int i=1;i<=n;i++){
        int a;
        string s;
        cin>>a>>s;
        int b=s[0]-'A';
        if(!g[a][b]){
            g[a][b]=1;
            f[a].push_back(i);
        }
    }
    for(int i=1;i<N;i++){
        ans+=f[i].size()/2*2;//向下取整
    }
    cout<<ans<<endl;
    for(int i=1;i<N;i++){
        if(f[i].size()>=2){
            for(int j=0;j<f[i].size()-1;j+=2){
                cout<<f[i][j]<<" "<<f[i][j+1]<<endl;
            }
        }
    }

	return 0;
}

小红打牌

排列组合一下

D-小红打牌_牛客周赛 Round 123

10
1 1 1 2 2 2 1 1 1 1

1

这个题思路就是，我们先统计一下全都的到底有出现的次数那些是大于1次的，那些是大于3次的个数。

然后去枚举数，确定s[i]那么s[i+1]也就确定，只要两个都大于等于3，我们就可以开始下一步了。

首先，我们先把自己在之前那部分的>1和>3的那部分剪掉。

再确定自己减完之后到底还有没有多余的了，有就加上作为最后两个对子的东西，nx是差不多还剩两个的了，只能自己提供一个的，然后ny，就是可以提供两组相同的数给我组成飞机

实际就是找两对的组合，因为6张牌已经确定了。
里面的局部变量
nx：大于等于二的数量的，

ny：大于4的，就可以自己提供两个了

解题代码

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=998244353;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    int ans=0;
    vector<int>s(N,0);
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        s[x]++;
    }
    int x=0,y=0;
    for(int i=1;i<N;i++){
        x+=(s[i]>1);
        y+=(s[i]>3);
    }

    for(int i=1;i<N-1;i++){
        if(s[i]>=3&&s[i+1]>=3){
            int nx=x,ny=y;
            //先把自己的那个先减去了，然后再加上到底自己的状态是多少。
            nx-=(s[i]>1)+(s[i+1]>1);
            ny-=(s[i]>3)+(s[i+1]>3);
            nx+=(s[i]-3>1)+(s[i+1]-3>1);
            ny+=(s[i]-3>3)+(s[i+1]-3>3);
            //Ny表示我自己就能提供两个，不需要你们给我提供了，nx是需要和别人一起组合才能成功，所以就排列组合
            ans=(ans+nx*(nx-1)/2+ny)%mod;
        }
    }
    cout<<ans<<endl;

	return 0;
}

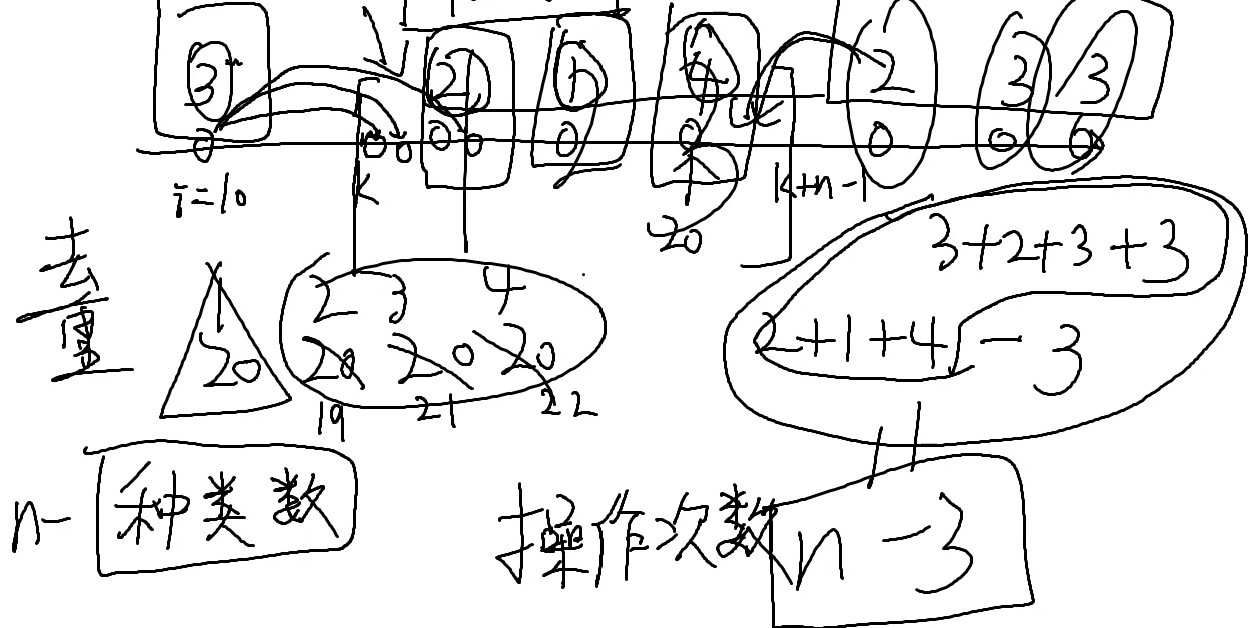
小红出牌

区间递归

E-小红出牌（easy）_牛客周赛 Round 123

5
5 3 1 2 4

1 2 3 2 1

暴力就是对新加入的直接进行排序加遍历就行了

正解要用到递归

一共有3个可能，就是前面的f[i-1]--->f[i]变化的范围很小，只有-1，1，0；
所以我们就可以通过这个来做手脚。

我们可以用两个map数组L，R，来维护一段区间在边差那个，的权值，和区间右边差哪个的权值
第一种情况:
-1 相当于右边的R[x]>0且是存在缺少的，左边L[x]也是一样存在和大于零
我们就可以少1，并且把原来的减去就可以了。

1的话是没有，也没有大于0的，那就把这个数左右两边加加一下

0的话有两种一个是左边，一个是右边，分开讨论就行了
左的话就继续向[x-1]++;
右边的话就[x+1]++;

f[i]=f[i-1]+{-1,1,0}

暴力

开始想到的暴力的解法，只能过20%

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    vector<int>s(n);
    for(int i=0;i<n;i++){
        cin>>s[i];
    }
    for(int i=0;i<n;i++){
        vector<int>m;
        int count=0;
        for(int j=0;j<i+1;j++){
            m.push_back(s[j]);
        }
        sort(m.begin(),m.end());
//        for(int j=0;j<m.size();j++){
//            cout<<m[j]<<" ";
//        }
//        cout<<endl;
        if(m.size()==1){
            cout<<1<<" ";
            continue;
        }
        for(int k=0;k<m.size()-1;k++){

            if(m[k]+1!=m[k+1]){
                count++;
            }

        }

        cout<<++count<<" ";
    }

	return 0;
}

正解

#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];

signed main(){

	std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin>>n;
    map<int,int>L,R;
    int sum=0;//维护一个答案；
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        int add=1;
        if(L.count(x)&&L[x]>0&&R.count(x)&&R[x]>0){
            L[x]--;
            R[x]--;
            add=-1;
        }else if(L.count(x)&&L[x]>0){
            L[x]--;
            L[x-1]++;
            add=0;
        }else if(R.count(x)&&R[x]>0){
            R[x]--;
            R[x+1]++;
            add=0;
        }else{
            //单前的左右两边一起维护一下
            R[x+1]++;
            L[x-1]++;
        }
        sum+=add;
        cout<<sum<<" ";
    }

	return 0;
}