落谷题单题
落谷题单题
蓝桥杯省一秘诀 - 题单 - 洛谷 | 计算机科学教育新生态
1.挖地雷
[P2196 NOIP 1996 提高组] 挖地雷 - 洛谷
题目描述
在一个地图上有 N (N≤20) 个地窖,每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使某人能挖到最多的地雷。
输入格式
有若干行。
第 1 行只有一个数字,表示地窖的个数 N。
第 2 行有 N 个数,分别表示每个地窖中的地雷个数。
第 3 行至第 N+1 行表示地窖之间的连接情况:
第 3 行有 n−1 个数(0 或 1),表示第一个地窖至第 2 个、第 3 个 … 第 n 个地窖有否路径连接。如第 3 行为 11000⋯0,则表示第 1 个地窖至第 2 个地窖有路径,至第 3 个地窖有路径,至第 4 个地窖、第 5 个 … 第 n 个地窖没有路径。
第 4 行有 n−2 个数,表示第二个地窖至第 3 个、第 4 个 … 第 n 个地窖有否路径连接。
……
第 n+1 行有 1 个数,表示第 n−1 个地窖至第 n 个地窖有否路径连接。(为 0 表示没有路径,为 1 表示有路径)。
输出格式
第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格。
第二行只有一个数,表示能挖到的最多地雷数。
输入输出样例
输入 #1复制
5
10 8 4 7 6
1 1 1 0
0 0 0
1 1
1
输出 #1复制
1 3 4 5
27
说明/提示
【题目来源】
NOIP 1996 提高组第三题
题解:
dfs题解
本题那么好的一道dfs爆搜题,为啥要用DP?(本蒟蒻不会DP)
思路很简单,由于n很小,完全可以枚举每一个点当起点, 同时记录路径;下面贴代码
神奇分割线
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
using namespace std;
bool f[21][21];//记录是否有路径相连
int a[21];//记录地雷数
int path[21],ans[21],cnt;//path记录路径,ans记录答案,cnt记录走了多少个点
bool b[21];//记录该点是否走过
int n;
int maxx;//记录挖的最大地雷数
bool chck(int x)//检查是否还能继续往下挖
{
for(int i=1;i<=n;i++)
{
if(f[x][i]&&!b[i]) return false;
}
return true;
}
void dfs(int x,int stp,int sum)//x记录现在位置,stp记录走了几个点,sum记录挖的地雷数
{
if(chck(x))
{
if(maxx<sum)//更新最大值和路径
{
maxx=sum;
cnt=stp;
for(int i=1;i<=stp;i++)
ans[i]=path[i];
}
return ;
}
for(int i=1;i<=n;i++)//寻找下一个能去的地方
{
if(f[x][i]&&!b[i])
{
b[i]=1;//标记走过
path[stp+1]=i;//记录路径
dfs(i,stp+1,sum+a[i]);
b[i]=0;//回溯
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<n;i++)
for(int j=i+1;j<=n;j++)
{
cin>>f[i][j];//这里是单向边,题目没啥清楚,导致我调了半个小时;
}
for(int i=1;i<=n;i++)
{
b[i]=1;
path[1]=i;//记录起点
dfs(i,1,a[i]);
b[i]=0;
}
for(int i=1;i<=cnt;i++)
cout<<ans[i]<<' ';
cout<<endl<<maxx;
return 0;
}
dp题解
由于正解是DP,那我们就用DP
(尽管数据很水可以搜索)
老样子,DP考虑3件事:数组、方程、初始化
一.数组
通过对线性动规的学习我们知道
这类题目的数组大多都是一个一维数组
这题作为典型题目之一,自然逃不出一维数组的手掌心
我们用*d*p*i*表示挖地雷时以点i为终点所能挖到的最大地雷数
用a**i表示第i个点的地雷数
然后用顺推的方式从2一直推到*n*
最后输出d**p数组存储的最大值即可
二.方程
我们可以借鉴一下最长XX子序列的思路:
for(int i=2;i<=n;++i){
dp[i]=0;
for(int j=i-1;j>0;--j){
if(a[i]>a[j]){
dp[i]=max1(dp[i],dp[j]);
}
}
dp[i]++;
if(dp[i]>ans) ans=dp[i];
}
对于dpi,用j从1到i-1枚举
如果从j到i有路可走且dpj>dpi
那就把dpi的值更新为dpj
枚举结束后把dpi的值加上第i个点的地雷数
一句话,找出点*j*使得*j*<*i*,*d*p*j*为最大值且*i*,*j*之间有通路
再加上第*i*个点的地雷数
状态转移方程:
dpi=a**i + max(d**p1 , d**p2 … dpi−1)
三.初始化
首先,d**p1=a1
其次,对于dpi(2<=i<=n),有两种选择:
一是都初始化为0
二是都初始化为a**i
前者需在枚举完之后加上a**i,但判断条件较为简略
后者不需再加上a**i,但判断条件略显繁琐
笔者在此选后者
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int dp[M],p[M],pos;
bool rd[M][M];
void DFS(int x){
if(p[x])DFS(p[x]);
cout<<x<<" ";
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,ans=0;
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++){
cin>>rd[i][j];
}
dp[1]=a[1];
for(int i=2;i<=n;i++){
dp[i]=a[i];
for(int j=i-1;j>0;j--){
if(rd[j][i]&&dp[i]<dp[j]+a[i]){
dp[i]=dp[j]+a[i];
p[i]=j;
}
}
if(ans<dp[i]){
ans=dp[i];
pos=i;
}
}
DFS(pos);
cout<<endl<<ans;
return 0;
}
#include<iostream>
#include<cstdio>
#define maxn 201//数组开大一点
#define fo(x) for(register int i=1;i<=x;++i)//宏定义,省事
using namespace std;
bool rd[maxn][maxn];
//rd[i][j]记录i到j是否是通路
//dp[i]表示以i为终点所能挖到的最大地雷数
//a[i]表示第i个点的地雷数
int a[maxn],dp[maxn],p[maxn],pos;//p[i]表示i的前趋
void DFS(int x){//倒着输出
if(p[x]) DFS(p[x]);//如果x有前趋,继续搜
cout<<x<<" ";
}
int main(){
int n,ans=0;
cin>>n;
fo(n) scanf("%d",&a[i]);
fo(n-1)
for(register int j=i+1;j<=n;++j){//按格式输入路径
scanf("%d",&rd[i][j]);
}
dp[1]=a[1];//初始化
for(register int i=2;i<=n;++i){//从2开始到n结束
dp[i]=a[i];//初始化
for(register int j=i-1;j>0;--j){//枚举寻找最大值
if(rd[j][i]&&dp[i]<dp[j]+a[i]){
//有路径且大于目前的最大值
dp[i]=dp[j]+a[i];//更新
p[i]=j;//记录i的前趋为j
}
}
if(ans<dp[i]){//更新答案
ans=dp[i];
pos=i;//记录取点的位置
}
}
DFS(pos);//先输出最优路径
cout<<endl<<ans;//再输出答案
return 0;//后话:此题可概括为“最长连通子序列”
}
2.P10387 [蓝桥杯 2024 省 A] 训练士兵
[P10387 蓝桥杯 2024 省 A] 训练士兵 - 洛谷
在蓝桥王国中,有 n 名士兵,这些士兵需要接受一系列特殊的训练,以提升他们的战斗技能。对于第 i 名士兵来说,进行一次训练所需的成本为 p**i 枚金币,而要想成为顶尖战士,他至少需要进行 c**i 次训练。
为了确保训练的高效性,王国推出了一种组团训练的方案。该方案包含每位士兵所需的一次训练,且总共只需支付 S 枚金币(组团训练方案可以多次购买,即士兵可以进行多次组团训练)。
作为训练指挥官,请你计算出最少需要花费多少金币,才能使得所有的士兵都成为顶尖战士?
输入格式
输入的第一行包含两个整数 n 和 S,用一个空格分隔,表示士兵的数量和进行一次组团训练所需的金币数。
接下来的 n 行,每行包含两个整数 p**i 和 c**i,用一个空格分隔,表示第 i 名士兵进行一次训练的金币成本和要成为顶尖战士所需的训练次数。
输出格式
输出一行包含一个整数,表示使所有士兵成为顶尖战士所需的最少金币数。
输入输出样例
输入 #1复制
3 6
5 2
2 4
3 2
输出 #1复制
16
说明/提示
题解:
很明显的一个贪心,考虑贪心策略:
我们先把士兵按训练的次数排序,让士兵单独训练一次。如果成本高于报团训练的成本 S,我们就让剩下的士兵报团训练,否则就让士兵单独训练。
#include <bits/stdc++.h>
using namespace std;
#define all(a) a.begin(), a.end()
#define debug(a) cout << a << "\n";
#define pb push_back
#define mp make_pair
#define mem(a, b) memset(a, b, sizeof(a))
#define endl "\n"
typedef long long ll;
constexpr int MAXN = 1e5 + 10;
struct Node
{
ll cost; // 单词训练的花费
ll sum; // 训练次数
};
bool cmp(const Node &a, const Node &b)
{
return a.sum < b.sum; // 按训练次数排序
}
int main()
{
int n;
ll S, tot = 0, used = 0, cnt = 0; // tot: 总花费, cnt: 最小花费
cin >> n >> S;
vector<Node> a(n);
for (int i = 0; i < n; i++)
{
cin >> a[i].cost >> a[i].sum;
tot += a[i].cost;
}
sort(a.begin(), a.end(), cmp);
for (int i = 0; i < n; i++)
{
if (tot >= S) // 花费比组团的大,报团
{
cnt += (a[i].sum - used) * S;
tot -= a[i].cost;
used += a[i].sum - used;
}
else // 否则就单独训练
{
cnt += (a[i].sum - used) * a[i].cost;
tot -= a[i].cost;
}
}
cout << cnt << endl;
return 0;
}
3.小苯的区间和疑
题目描述
帅气的大白熊这天向小苯提出了一个问题,他给了小苯一个长度为 n 的数组 a 。
他想知道,对于所有 1≤i≤n 的下标 i ,都从数组中选择一段连续的区间 [l,r] 使得 l≤i≤r ,即选择一个包含 i 的区间的话,这段区间和最大是几?
请聪明的你帮帮小苯解答吧。
输入格式
输入包含两行。 第一行一个正整数 n(1≤n≤2×105)。 第二行 n 个整数 a**i(−109≤a**i≤109),表示这个数组。
输出格式
输出包含一行 n 个整数。 其中第 i 个整数代表,选择一段包含 a**i 的区间,这段区间的最大和。
输入输出样例
输入 #1复制
4
1 -2 3 -4
输出 #1复制
2 2 3 -1
输入 #2复制
3
-1 -1 -1
输出 #2复制
-1 -1 -1
说明/提示
样例解释1
i=1 ,选择 [1,3],结果是: 1+(−2)+3=2。是最优解。
i=2 ,选择 [1,3]
i=3 ,选择 [3,3]
i=4 ,选择 [3,4]
题解:区间和的进阶
由题目可知我们相当于要求区间和,那么我们想到前缀和,然pre{r}-pre[l-1]那么我们应该让前面的和最大,让后面的小,所以要枚举每一个位置,的后面的最大值,和前面最小值。
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
//int a[N],b[N],c[N],pre[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
vector<int>a(n);
vector<int>s(n);
for(int i=1;i<=n;i++){
cin>>a[i];
s[i]=s[i-1]+a[i];//前缀和
}
vector<int>pre(n+1),suf(n+2,-1e18);
for(int i=1;i<=n;i++){
pre[i]=min(pre[i-1],s[i]);//该点前缀的小值,
}
for(int i=n;i>0;i--){
suf[i]=max(suf[i+1],s[i]);//该点后缀的大值
}
pre[0]=0;
for(int i=1;i<=n;i++){
cout<<suf[i]-pre[i-1]<<" ";
}
return 0;
}
4.最大子段和
题目描述
给出一个长度为 n 的序列 a,选出其中连续且非空的一段使得这段和最大。
输入格式
第一行是一个整数,表示序列的长度 n。
第二行有 n 个整数,第 i 个整数表示序列的第 i 个数字 a**i。
输出格式
输出一行一个整数表示答案。
输入输出样例
输入 #1复制
7
2 -4 3 -1 2 -4 3
输出 #1复制
4
说明/提示
样例 1 解释
选取 [3,5] 子段 {3,−1,2},其和为 4。
数据规模与约定
- 对于 40% 的数据,保证 n≤2×103。
- 对于 100% 的数据,保证 1≤n≤2×105,−104≤a**i≤104
题解1(前缀区间和):
同区间和疑惑类似
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
//int a[N],b[N],c[N],pre[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
vector<int>a(n+1);
vector<int>s(n+1);
for(int i=1;i<=n;i++){
cin>>a[i];
s[i]=s[i-1]+a[i];
}
vector<int>pre(n+1),suf(n+2,-1e18);
for(int i=1;i<=n;i++){
pre[i]=min(pre[i-1],s[i]);
}
for(int i=n;i>0;i--){
suf[i]=max(suf[i+1],s[i]);
}
pre[0]=0;
int max1=-1e18;
for(int i=1;i<=n;i++){
if((suf[i]-pre[i-1])>max1){
max1=suf[i]-pre[i-1];
}
}
cout<<max1<<endl;
return 0;
}
题解2dp
dp[i]表示到达i时候 b[i] 表示截止到 i 时,第 i 个数所在的有效序列的元素和。
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
int ans=-1e18;
vector<int>v(n+1);
vector<int>dp(n+1);
for(int i=1;i<=n;i++){
cin>>v[i];
if(i==1)dp[i]=v[i];
else{
dp[i]=max(v[i],dp[i-1]+v[i]);
}
ans=max(dp[i],ans);
}
cout<<ans<<endl;
return 0;
}
题解3贪心
第二种写法我们可以先从第一个数开始选,用一个变量存当前的和。当我们发现这个变量的值小于 0 时,那还不如不选,我们就直接重新将变量赋值为 0 即可。此外,还要有一个存答案的变量,在每一次存当前的和的变量值发生改变时,就更新最大值
#include <bits/stdc++.h>
using namespace std;
int n,x,sum,ans=-1e9;
int main(){
cin>>n;
for(int i = 1;i<=n;i++){
cin>>x;
sum+=x;
ans=max(ans,sum);
if(sum<0) sum=0;
}
cout<<ans;
return 0;
}
5.绝世好题
题目描述
给定一个长度为 n 的数列 a**i,求 a**i 的子序列 b**i 的最长长度 k,满足 b**i&b**i−1=0,其中 2≤i≤k, & 表示位运算取与。
输入格式
输入文件共 2 行。 第一行包括一个整数 n。 第二行包括 n 个整数,第 i 个整数表示 a**i。
输出格式
输出文件共一行。 包括一个整数,表示子序列 b**i 的最长长度。
输入输出样例
输入 #1复制
3
1 2 3
输出 #1复制
2
说明/提示
对于100%的数据,1≤n≤100000,a**i≤109。
题解1暴力
只能拿90;
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int f[N];
signed main() {
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
int ans=0;
for(int i=1;i<=n;i++)cin>>a[i],f[i]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<i;j++){
if(a[i]&a[j]){
f[i]=max(f[i],f[j]+1);//找到最大值
}
ans=max(ans,f[i]);
}
}
cout<<ans<<endl;
return 0;
}
题解dp
#include<bits/stdc++.h>
using namespace std;
const int maxn = 32;
int dp[maxn];
int Max,ans;
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i){
int b;
scanf("%d",&b);
for(int c=0;c<=31;++c){//枚举每一个二进制位
if((1<<c)&b)Max=max(Max,dp[c]+1);
}
for(int c=0;c<=31;++c){//更新满足条件的二进制位的最大值
if((1<<c)&b)dp[c]=max(Max,dp[c]);
}
ans=max(ans,Max);//统计最大值答案
}
cout<<ans<<"\n";
return 0;
}
6.单词接龙
[P1019 NOIP 2000 提高组] 单词接龙 - 洛谷
NOIP2000 提高组 T3
题目描述
单词接龙是一个与我们经常玩的成语接龙相类似的游戏,现在我们已知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”(每个单词都最多在“龙”中出现两次),在两个单词相连时,其重合部分合为一部分,例如 beast 和 astonish,如果接成一条龙则变为 beastonish,另外相邻的两部分不能存在包含关系,例如 at 和 atide 间不能相连。
输入格式
输入的第一行为一个单独的整数 n 表示单词数,以下 n 行每行有一个单词,输入的最后一行为一个单个字符,表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在。
输出格式
只需输出以此字母开头的最长的“龙”的长度。
输入输出样例
输入 #1复制
5
at
touch
cheat
choose
tact
a
输出 #1复制
23
说明/提示
样例解释:连成的“龙”为 atoucheatactactouchoose。
n≤20。
题解dfs解决
直接深搜这个string,然后再判断是否用了2次然后拼接;
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
//int a[N],b[N],c[N],pre[N];
string s[N];
char c;
int n;
int vis[N];//判断枚举的次数
int ans=0;
void dfs(const string&cmp){
ans=max(ans,(int)(cmp.size()));//记录最大值;
for(int i=1;i<=n;i++){
if(vis[i]>=2)continue;
for(int j=1;j<min(cmp.size(),s[i].size());j++){
if(cmp.substr(cmp.size()-j)==s[i].substr(0,j)){
vis[i]++;
dfs(cmp+s[i].substr(j));
vis[i]--;
}
}
}
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)cin>>s[i];
cin>>c;
for(int i=1;i<=n;i++){//枚举每一个为c开头的字母然后满足
if(s[i][0]==c){
vis[i]++;
dfs(s[i]);
vis[i]--;
}
}
cout<<ans<<endl;
return 0;
}
7.数字接龙(2024省b)
[P10427 蓝桥杯 2024 省 B] 数字接龙(疑似错题) - 洛谷
本题目前未找到任何做法(在不进行特判的情况下)进行有效剪枝通过 n=10,k=1 的数据。由于本题疑似错题,因此本题不提供评测以及题解区。
题目描述
小蓝最近迷上了一款名为《数字接龙》的迷宫游戏,游戏在一个大小为 n×n 的格子棋盘上展开,其中每一个格子处都有着一个 0⋯k−1 之间的整数。游戏规则如下:
- 从左上角 (0,0) 处出发,目标是到达右下角 (n−1,n−1) 处的格子,每一步可以选择沿着水平 / 垂直 / 对角线方向移动到下一个格子。
- 对于路径经过的棋盘格子,按照经过的格子顺序,上面的数字组成的序列要满足:0,1,2,⋯,k−1,0,1,2,⋯,k−1,0,1,2⋯。
- 途中需要对棋盘上的每个格子恰好都经过一次(仅一次)。
- 路径中不可以出现交叉的线路。例如之前有从 (0,0) 移动到 (1,1),那么再从 (1,0) 移动到 (0,1) 线路就会交叉。
为了方便表示,我们对可以行进的所有八个方向进行了数字编号,如下图 2 所示;因此行进路径可以用一个包含 0⋯7 之间的数字字符串表示,如下图 1 是一个迷宫示例,它所对应的答案就是:41255214。
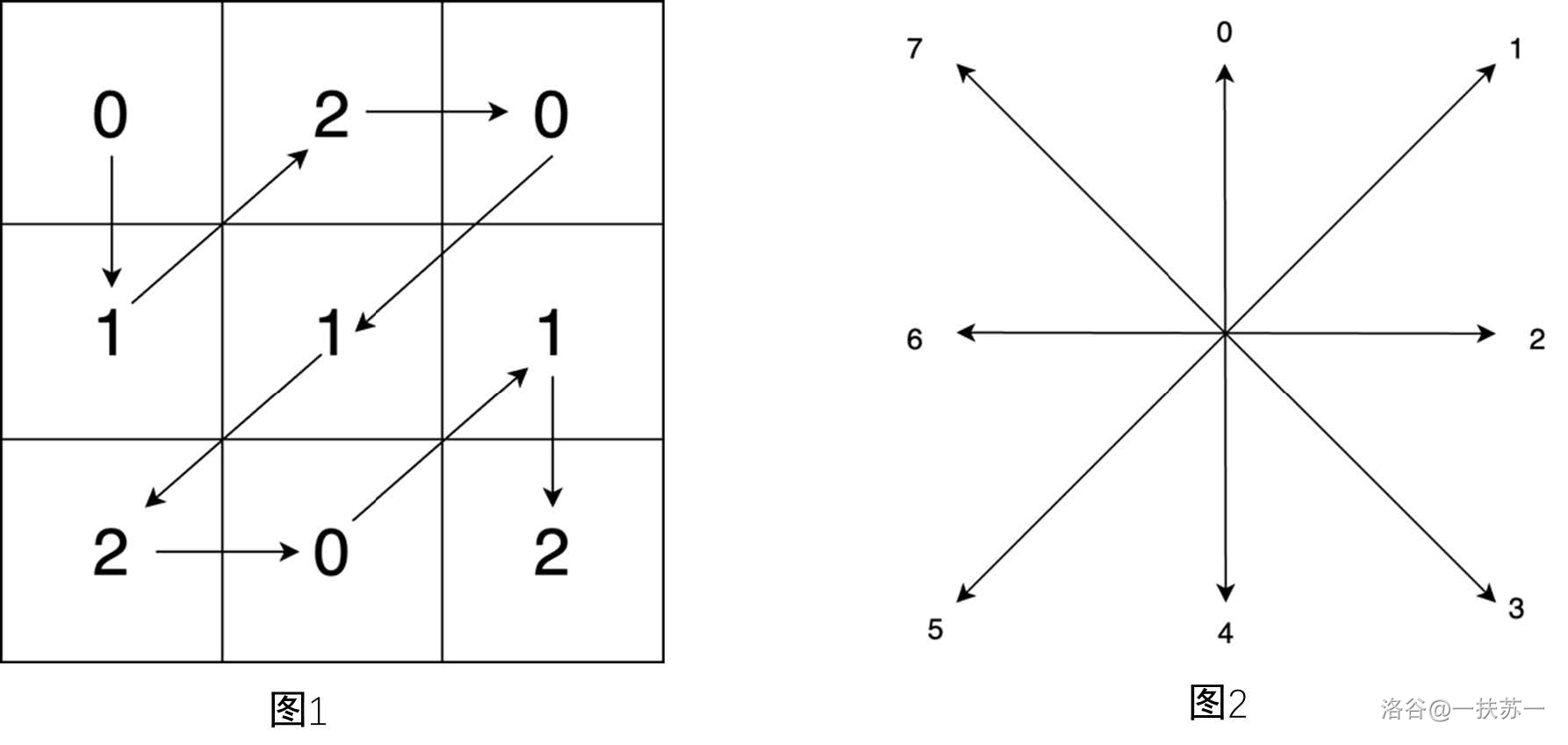
现在请你帮小蓝规划出一条行进路径并将其输出。如果有多条路径,输出字典序最小的那一个;如果不存在任何一条路径,则输出 −1。
输入格式
第一行包含两个整数 n,k。 接下来输入 n 行,每行 n 个整数表示棋盘格子上的数字。
输出格式
输出一行表示答案。如果没有对应的路径,输出 −1。
输入输出样例
输入 #1复制
3 3
0 2 0
1 1 1
2 0 2
输出 #1复制
41255214
说明/提示
数据规模与约定
- 对 80% 的数据,n≤5。
- 对全部的测试数据,1≤n,k≤10。
题解dfs8方向
方向
//八个方向;
//int dx[]={-1,0,1,0};
//int dy[]={0,-1,0,1};
int dx[]={-1,-1,0,1,1,1,0,-1};
int dy[]={0,1,1,1,0,-1,-1,-1};
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int n,k;
bool vis[M][M];
int m[M][M]={0};
string ans;
//八个方向;
//int dx[]={-1,0,1,0};
//int dy[]={0,-1,0,1};
int dx[]={-1,-1,0,1,1,1,0,-1};
int dy[]={0,1,1,1,0,-1,-1,-1};
void dfs(int x,int y,int pre,string s,int dep){
if(x==n&&y==n&&dep==n*n){
ans=s;
return;
}
for(int i=0;i<8;i++){
int bx=x+dx[i];
int by=y+dy[i];
if(bx<1||bx>n||by<1||by>n)continue;
if(vis[bx][by])continue;
//防止交叉;
if(i==1&&vis[x-1][y]&&vis[x][y+1])continue;
if(i==3&&vis[x][y+1]&&vis[x+1][y])continue;
if(i==5&&vis[x][y-1]&&vis[x+1][y])continue;
if(i==7&&vis[x][y-1]&&vis[x-1][y])continue;
//判断这个是不是满足1.,....k
if(m[bx][by]<k&&m[bx][by]==pre+1||pre+1==k&&m[bx][by]==0){
vis[bx][by]=1;
dfs(bx,by,m[bx][by],s+to_string(i),dep+1);
if(!ans.empty())return;
vis[bx][by]=0;
}
}
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
cin>>m[i][j];
}
string emp;
vis[1][1]=1;
dfs(1,1,0,emp,1);
if(ans.empty()){
cout<<"-1"<<endl;
}else{
cout<<ans<<endl;
}
return 0;
}
8.打开所有的灯
题目背景
pmshz在玩一个益(ruo)智(zhi)的小游戏,目的是打开九盏灯所有的灯,这样的游戏难倒了pmshz。。。
题目描述
这个灯很奇(fan)怪(ren),点一下就会将这个灯和其周围四盏灯的开关状态全部改变。现在你的任务就是就是告诉pmshz要全部打开这些灯。
例如
0 1 1
1 0 0
1 0 1
点一下最中间的灯【2,2】就变成了
0 0 1
0 1 1
1 1 1
再点一下左上角的灯【1,1】就变成了
1 1 1
1 1 1
1 1 1
达成目标。最少需要2步。
输出2即可。
输入格式
九个数字,3*3的格式输入,每两个数字中间只有一个空格,表示灯初始的开关状态。(0表示关,1表示开)
输出格式
1个整数,表示最少打开所有灯所需要的步数。
输入输出样例
输入 #1复制
0 1 1
1 0 0
1 0 1
输出 #1复制
2
说明/提示
这个题水不水,就看你怎么考虑了。。。。
题解:dfs;
每个点只能搞一次,不然就回来了所以可以记录一下
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
// int a[N],b[N],c[N],pre[N];
int G[5][5],ans=10;
bool vis[5][5];
int x[5]={-1,0,1,0,0};
int y[5]={0,1,0,-1,0};
bool check(){//判断一下
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++){
if(!G[i][j])
return false;
}
return true;
}
void change(int m,int n){//改变
for(int i=0;i<5;i++)G[m+x[i]][n+y[i]]^=1;
}
void dfs(int step){//记录步数
if(step>ans)return;
if(check())ans=min(ans,step);
else{
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
if(!vis[i][j]){
//回溯
vis[i][j]=1;
change(i,j);
dfs(step+1);
vis[i][j]=0;
change(i,j);
}
}
}
}
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
for(int i=1;i<=3;i++){
for(int j=1;j<=3;j++){
cin>>G[i][j];
}
}
dfs(0);
cout<<ans<<endl;
return 0;
}
10.小梦的宝石收集
题目描述
小梦有 n 颗能量宝石,其中第 i 颗的能量为 a**i,但这些能量宝石十分不稳定,随时有可能发生崩坏,导致他们全部消失!
小梦想要留住宝石们,不希望他们发生崩坏,同时他发现:如果这些宝石的能量的极差越大,则这些宝石们越不稳定,因此他希望最小化这些宝石的能量的极差(最大值减去最小值的差值)。
小梦有一招点石成金的技能,这个技能可以以如下方式改变一些宝石的能量:
∙ 要么小梦选择一块能量最小的宝石,将他变成一块当前能量最大的宝石。
∙ 要么小梦选择一块能量最大的宝石,将他变成一块当前能量最小的宝石。
形式化的即:
∙ 选择 i (1≤i≤n,a**i=min(a1,a2,...,a**n)),执行:a**i:=ma**x(a1,a2,...,a**n)。
∙ 或选择 i (1≤i≤n,a**i=ma**x(a1,a2,...,a**n)),执行:a**i:=min(a1,a2,...,a**n)。
小梦至多可以使用 k 次上述的 ”点石成金“ 技能,他想知道这些宝石的能量极差最小可以变为多少,请你帮他算一算吧。
输入格式
本题有多组测试数据。
输入的第一行包含一个正整数 T,表示数据组数。
接下来包含 T 组数据,每组数据的格式如下:
第一行两个正整数 n,k,分别表示小梦拥有的宝石数量 n ,和他最多可以释放 “点石成金” 技能的次数 k。
第二行 n 个正整数 a**i,表示每块宝石的能量。
输出格式
对于每组测试数据:
在单独的一行输出一个整数,表示宝石能量的极差最小值。
输入输出样例
输入 #1复制
2
8 3
1 2 3 4 5 6 7 8
4 3
100 1 100 2
输出 #1复制
4
0
说明/提示
【样例 1 解释】
使用 3 次操作一,选择 min 变为 ma**x,操作完后数组变成:{8,8,8,4,5,6,7,8}。
此时数组的极差为 4 最小,可以证明不存在比 4 更优的答案。
【数据范围】
令 N 表示 T 组数据中 n 的总和。
对于 30% 的数据有:T=1,1≤k≤N≤20。
对于 60% 的数据有:1≤T≤10,1≤k≤N≤2000。
对于所有的测试数据有: 1≤T≤1000,1≤N≤5×105,0≤k≤n,0≤a**i≤109。
题解:枚举+二分答案
首先我们可以先排个序,然后既然要我们求这个最小值,显然可以得到,最小值肯定是aj-ai,这样的一对
这样问题就变成了我们知道答案,要操作的次数,
第一肯定要吧比ai小的都变大,
把aj大的都变小,但是真的就是直接求吗
i-1+n-j这样的次数吗?,但是我们发现回多出一边i-1,或者n-j,这取决于你的顺序,是按什么顺序来排放的,比如先放小的,然后放大的那,所以取一个min{i-1,n-j};
所以我们可以枚举j找到答案,但是枚举太大时间了,直接二分
j=mid;
最后计算aj-ai最小值
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
void solve(){
int n,k;
cin>>n>>k;
vector<int>v(n+1);
for(int i=1;i<=n;i++)cin>>v[i];
sort(v.begin()+1,v.end());
int ans=1e18;
for(int i=1;i<=n;i++){
int l=i,r=n;
if(i-1>k)break;
while(l<r){//二分答案
int mid=(l+r)>>1;
if((i-1)+(n-mid)+min(i-1,n-mid)<=k)r=mid;
else l=mid+1;
}
ans=min(ans,v[l]-v[i]);
}
cout<<ans<<endl;
};
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
TESTS{
solve();
};
return 0;
}
11.A-B数对
题目背景
出题是一件痛苦的事情!
相同的题目看多了也会有审美疲劳,于是我舍弃了大家所熟悉的 A+B Problem,改用 A-B 了哈哈!
题目描述
给出一串正整数数列以及一个正整数 C,要求计算出所有满足 A−B=C 的数对的个数(不同位置的数字一样的数对算不同的数对)。
输入格式
输入共两行。
第一行,两个正整数 N,C。
第二行,N 个正整数,作为要求处理的那串数。
输出格式
一行,表示该串正整数中包含的满足 A−B=C 的数对的个数。
输入输出样例
输入 #1复制
4 1
1 1 2 3
输出 #1复制
3
说明/提示
对于 75% 的数据,1≤N≤2000。
对于 100% 的数据,1≤N≤2×105,0≤a**i<230,1≤C<230。
2017/4/29 新添数据两组
题解:map的应用
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
//int a[N],b[N],c[N],pre[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,c;
cin>>n>>c;
vector<int>v(n);
map<int,int>m;
int ans=0;
for(int i=0;i<n;i++)
cin>>v[i],m[v[i]]++,v[i]-=c;
for(int i=0;i<n;i++)ans+=m[v[i]];
cout<<ans<<endl;
return 0;
}
12.Subseq
[P3131 USACO16JAN] Subsequences Summing to Sevens S - 洛谷
输入的第一行包含 N(1≤N≤50,000)。接下来的 N 行每行包含一头奶牛的整数 ID(所有 ID 都在 0…1,000,000 范围内)。
输出格式
请输出 ID 之和为 7 的倍数的最大连续奶牛组中的奶牛数量。如果不存在这样的组,则输出 0。
[显示翻译](javascript:void 0)
题意翻译
输入输出样例
输入 #1复制
7
3
5
1
6
2
14
10
输出 #1复制
5
说明/提示
在这个例子中,5+1+6+2+14=28。
题解:前缀和求区间为k倍数
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
vector<int>v(n+1);
vector<int>sum(n+1);
vector<int>mp(7,-1);//表示sum值为i的最左侧位置。
mp[0]=0;
int ans=0;
for(int i=1;i<=n;i++)cin>>v[i],sum[i]=(sum[i-1]+v[i])%7;
//找两个值相同,离的最远的区间。
//统计每个数的第一次出现位置,然后后面的就找到相同。取最大值
for(int i=1;i<=n;i++){
if(mp[sum[i]]!=-1){
ans=max(ans,i-mp[sum[i]]);
}else{
mp[sum[i]]=i;
}
}
cout<<ans<<endl;
return 0;
}
题解2dp
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int n,f[50005][7],ans;
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1,x;i<=n;i++){
cin>>x;
for(int j=0;j<7;j++){
if(f[i-1][j]){
f[i][(j+x)%7]=f[i-1][j]+1;
}
f[i][x%7]=max(f[i][x%7],1ll);
}
}
for(int i=1;i<=n;i++)
ans=max(ans,f[i][0]);
printf("%d\n",ans);
return 0;
}
13.蓝桥杯 2017 省 B] k 倍区间
题目描述
给定一个长度为 N 的数列,A1,A2,⋯A**N,如果其中一段连续的子序列 A**i,A**i+1,⋯A**j(i≤j) 之和是 K 的倍数,我们就称这个区间 [i,j] 是 K 倍区间。
你能求出数列中总共有多少个 K 倍区间吗?
输入格式
第一行包含两个整数 N 和 K (1≤N,K≤105)。
以下 N 行每行包含一个整数 A**i (1≤A**i≤105)。
输出格式
输出一个整数,代表 K 倍区间的数目。
输入输出样例
输入 #1复制
5 2
1
2
3
4
5
输出 #1复制
6
说明/提示
时限 2 秒, 256M。蓝桥杯 2017 年第八届
题解:前缀和加map
我们可以把前缀和modk的都算出来,然后,因为前缀和中,区间和(sumj-sumi)modk=0,相当于sumj%mod=sumi%k;
所以统计一下就行,每一个数组,差不多选择有n*(n-1)/2;
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int n,f[50005][7],ans;
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1,x;i<=n;i++){
cin>>x;
for(int j=0;j<7;j++){
if(f[i-1][j]){
f[i][(j+x)%7]=f[i-1][j]+1;
}
f[i][x%7]=max(f[i][x%7],1ll);
}
}
for(int i=1;i<=n;i++)
ans=max(ans,f[i][0]);
printf("%d\n",ans);
return 0;
}
//用map数组
#include<bits/stdc++.h>
#define int long long
#define PII pai<int ,int>
#define endl '\n'
using namespace std;
const int N=2e5+10,M=1e3+10;
int a[N],b[N],c[N],pre[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n ,m;cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
map<int ,int>mp;
mp[0]++;
int ans=0;
for(int i=1;i<=n;i++){
pre[i]=(pre[i-1]+a[i])%m;
mp[pre[i]]++;
}
for(auto i:mp){
// if(i.first==0)
// ans+=i.second*(i.second+1)/2;//因为为0的时候最开始就有一个一,第一个的前缀和就为0
// else
ans+=i.second*(i.second-1)/2;
}
cout<<ans<<endl;
return 0;
}
14.幸运草
题目描述
Anzu 有一个正整数数列 a1,…,a**n 和一个整数 x。她可以进行至多一次操作,选择一对正整数 1≤l≤r≤n,然后对于所有 l≤i≤r 的正整数 i 让 a**i 变成 x。现在她想要知道,在这之后,数列里所有数的和最大是多少。
输入格式
第一行,两个非负整数 n,x。
第二行,n 个正整数 a1,…,a**n。
输出格式
仅一行,一个正整数,表示答案。
输入输出样例
输入 #1复制
5 2
1 4 1 1 5
输出 #1复制
14
输入 #2复制
7 3
1 1 4 5 1 4 1
输出 #2复制
21
输入 #3复制
1 197
251
输出 #3复制
251
说明/提示
【样例解释 #1】
最优的策略是选择 l=3,r=4 进行一次操作,此时数列变为 [1,4,2,2,5],总和为 14。
题解一贪心
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,x;
cin>>n>>x;
int t,ans=0,now=0,sum=0;
for(int i=1;i<=n;i++){
cin>>t;
sum+=t;
now+=x-t;//相当于贡献了x-t
ans=max(ans,now);
if(now<0)now=0;
}
cout<<ans+sum;
return 0;
}
题解2dp选贡献,
先把贡献都算出来,然后dp一下,dp[i]表示在第i给位置前面连续的贡献的最大值。
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int dp[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,k;
cin>>n>>k;
int sum=0;
for(int i=1;i<=n;i++){
cin>>a[i];
sum+=a[i];
b[i]=k-a[i];//每个贡献值可能是负数也可能是正数
}
for(int i=1;i<=n;i++){
dp[i]=max(b[i],dp[i-1]+b[i]);//要么连接前面的要么重新练连接这个
}
int ans=-1e18;
bool flag=0;
for(int i=1;i<=n;i++){
if(b[i]>0){
flag=1;
}
ans=max(ans,dp[i]);
}
if(flag){
cout<<ans+sum;
}else{
cout<<sum;
}
return 0;
}
15李白打酒加强版
[P8786 蓝桥杯 2022 省 B] 李白打酒加强版 - 洛谷
题目描述
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒 2 斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店 N 次,遇到花 M 次。已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序,有多少种不同的可能?
注意:壶里没酒(0 斗)时遇店是合法的,加倍后还是没酒;但是没酒时遇花是不合法的。
输入格式
第一行包含两个整数 N 和 M。
输出格式
输出一个整数表示答案。由于答案可能很大,输出模 1000000007(即 109+7)的结果。
输入输出样例
输入 #1复制
5 10
输出 #1复制
14
题解三维dp
dp[i][j][k]表示,代表遇店i次,遇花j次酒剩余k斗的次数
转移有两个
选择一
dp[i][j][k]+=dp[i-1][j][k/2];从前向后推
选择二
dp[i][j][k]+=dp[i][j-1][k+1];
if(k%2==0){
f[i][j][k]+=f[i-1][j][k/2];
}
if(j>=1){
f[i][j][k]+=f[i-1][j-1][k+1];
}
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int dp[105][105][105];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,m;
cin>>n>>m;
dp[0][0][2]=1;//因为一开时候就有酒
for(int i=0;i<=n;i++){//枚举店数量
for(int j=0;j<m;j++){//枚举花的数量
if(!i&&!j)continue;
for(int k=0;k<=100;k++){//因为最多出现100次操作2,故k最大为100
if(k%2==0&&i)dp[i][j][k]+=dp[i-1][j][k/2];//我只有k可以mod2时候才要,前状态转移到后状态。
if(j)dp[i][j][k]+=dp[i][j-1][k+1];
dp[i][j][k]%=mod;
}
}
}
cout<<dp[n][m-1][1]%mod;//因为最后变成赏花---》dp[m][0];
return 0;
}
16质数补全
题目描述
Alice 在纸条上写了一个质数,第二天再看时发现有些地方污损看不清了。
- 在大于 1 的自然数中,除了 1 和它本身以外不再有其他因数的自然数称为质数
请你帮助 Alice 补全这个质数,若有多解输出数值最小的,若无解输出 −1。
例如纸条上的数字为 1∗(∗ 代表看不清的地方),那么这个质数有可能为 11,13,17,19,其中最小的为 11。
输入格式
第一行 1 个整数 t,代表有 t 组数据。
接下来 t 行,每行 1 个字符串 s 代表 Alice 的数字,仅包含数字或者 ∗,并且保证首位不是 ∗ 或者 0。
输出格式
输出 t 行,每行 1 个整数代表最小可能的质数,或者 −1 代表无解。
输入输出样例
输入 #1复制
10
1*
3**
7**
83*7
2262
6**1
29*7
889*
777*
225*
输出 #1复制
11
307
701
8317
-1
6011
2917
8893
-1
2251
题解dfs
用dfs来添加数和判断
dfs(int t,string s);
/t表示当前的位置,现在的字符串
所以要记录每一个的位置。
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
string str;
int p, pos[N];//记录‘*’的位置
bool flag = 0;//标记可以找到吗
bool prime(string s1){//判段质素
int m=stoi(s1);
if(m<=1)return 0;
for(int i=2;i*i<=m;i++){
if(m%i==0){
return 0;
}
}
return 1;
}
void dfs(int t,string s){//t表示当前的位置,现在的字符串
if(flag)return;
if(t>p){//判断
if(prime(s)){
cout<<s<<endl;
flag=1;
}
return;
}
int c=pos[t];//位置
if(c==0){//如果开头是0那也不行;
for(int i=1;i<=9;i++){
s[c]=i+'0';
dfs(t+1,s);
s[c]='*';
}
}else{
for(int i=0;i<=9;i++){
s[c]=i+'0';
dfs(t+1,s);
s[c]='*';
}
}
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while (t--){
cin>>str;
p=0;
memset(pos,0,sizeof(pos));
for(int i=0;i<str.size();i++){
if(str[i]=='*'){
pos[++p]=i;
}
}
flag=0;
if(p==0){//如果没有**时候;
if(prime(str)){
cout<<str<<endl;
}else{
cout<<-1<<endl;
}
}else{
dfs(1,str);
if(!flag)cout<<-1<<endl;
}
}
return 0;
}
17.八皇后问题
[P1219 USACO1.5] 八皇后 Checker Challenge - 洛谷
题目描述
一个如下的 6×6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。
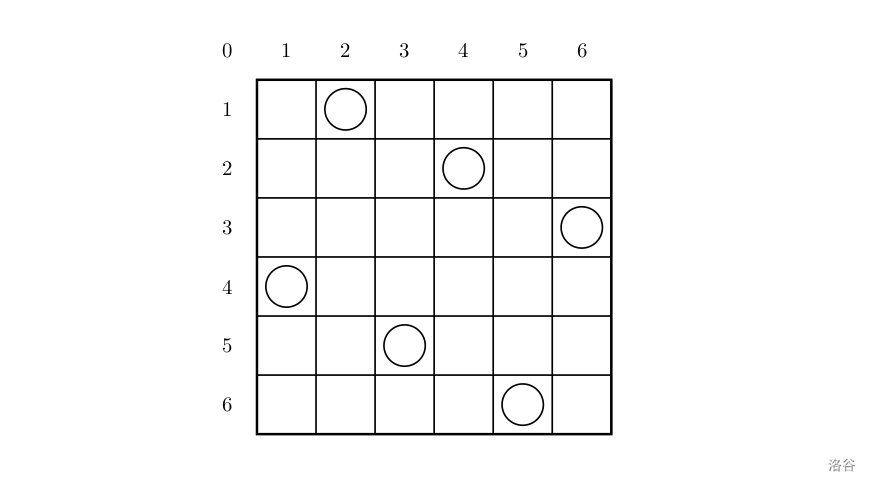
上面的布局可以用序列 2 4 6 1 3 5 来描述,第 i 个数字表示在第 i 行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。
输入格式
一行一个正整数 n,表示棋盘是 n×n 大小的。
输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
输入输出样例
输入 #1复制
6
输出 #1复制
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
题解dfs
先遍历每一个i行,确认放哪里,
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
//int a[N],b[N],c[N],pre[N];
int a[N],b[N],c[N],d[N];//分别表示行列,对角线;a[i],记录位置,
int n;
int sum=0;
void print(){
if(sum<=2){
for(int k=1;k<=n;k++){
cout<<a[k]<<" ";
}cout<<endl;
}
sum++;
}
void dfs(int i){
if(i>n){
print();
return;
}else{
for(int j=1;j<=n;j++){
if((!b[j])&&(!c[i+j])&&(!d[i-j+n])){
a[i]=j;
b[j]=1;
c[i+j]=1;
d[i-j+n]=1;
dfs(i+1);
b[j]=0;
c[i+j]=0;
d[i-j+n]=0;
}
}
}
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
dfs(1);//第一个皇后;
cout<<sum<<endl;
return 0;
}
18.n皇后问题
试题 E: 黑白皇后
时间限制: 1.0s 内存限制: 256.0MB 本题总分:35 分
****【问题描述】
给定一个 n×n 的棋盘。现在要向棋盘中放入 n 个黑皇后和 n 个白皇后,使
任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇
后都不在同一行、同一列或同一条对角线上。
问总共有多少种放法?
****【输入格式】
输入的第一行包含一个整数 n 。
****【输出格式】
输出一行包含一个整数,表示答案。
****【样例输入】
4
****【样例输出】
2
【评测用例规模与约定】
共有 10 个评测用例,评测用例各不相同。
对于所有评测用例,2 ≤ n ≤ 11 。
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[M],b[N],c[N],d[N]; // 黑皇后的列、主对角线、副对角线
int a2[N],b1[N],c1[N],d1[N]; // 白皇后的列、主对角线、副对角线
int n, sum=0, sum1=0;
void dfs2(int i2) {
if(i2 > n) {
sum++;
return;
}
int t = a[i2]; // 黑皇后在第i2行的列位置
for(int j=1; j<=n; j++) {
if(j == t) continue; // 跳过黑皇后的位置
if(!b1[j] && !c1[i2+j] && !d1[i2-j+n]) {
a2[i2] = j;
b1[j] = 1;
c1[i2+j] = 1;
d1[i2-j+n] = 1;
dfs2(i2+1);
b1[j] = 0;
c1[i2+j] = 0;
d1[i2-j+n] = 0;
}
}
}
void print() {
dfs2(1); // 开始放置白皇后
}
void dfs(int i) {
if(i > n) {
print();
return;
}
for(int j=1; j<=n; j++) {
if(!b[j] && !c[i+j] && !d[i-j+n]) {
a[i] = j;
b[j] = 1;
c[i+j] = 1;
d[i-j+n] = 1;
dfs(i+1);
b[j] = 0;
c[i+j] = 0;
d[i-j+n] = 0;
}
}
}
signed main() {
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
dfs(1); // 开始放置黑皇后
cout << sum << endl;
return 0;
}
19.[蓝桥杯 2024 省 B] 爬山
题目描述
小明这天在参加公司团建,团建项目是爬山。在 x 轴上从左到右一共有 n 座山,第 i 座山的高度为 h**i。他们需要从左到右依次爬过所有的山,需要花费的体力值为 S=∑i=1nhi。
然而小明偷偷学了魔法,可以降低一些山的高度。他掌握两种魔法,第一种魔法可以将高度为 H 的山的高度变为 ⌊H⌋,可以使用 P 次;第二种魔法可以将高度为 H 的山的高度变为 ⌊2H⌋ ,可以使用 Q 次。并且对于每座山可以按任意顺序多次释放这两种魔法。
小明想合理规划在哪些山使用魔法,使得爬山花费的体力值最少。请问最优情况下需要花费的体力值是多少。
输入格式
输入共两行。
第一行为三个整数 n,P,Q。
第二行为 n 个整数 h1,h2,...,h**n。
输出格式
输出一行一个整数表示答案。
输入输出样例
输入 #1复制
4 1 1
4 5 6 49
输出 #1复制
18
说明/提示
- 对 20% 的数据,n≤8,P=0。
- 对全部的测试数据,保证 1≤n≤105,0≤P,Q≤n,0≤h**i≤105。
题解:大根堆贪心+贪心;
priority_queue<>;
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
priority_queue<int,vector<int>,less<int>>pq;
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,p,q;
cin>>n>>p>>q;
for(int i=0;i<n;i++){
int tmp;
cin>>tmp;
pq.push(tmp);
}
while(!q&&!p) {
int m = pq.top();
pq.pop();
if ((int) sqrt(m) < (int) (m / 2)) {
p--;
m = (int) sqrt(m);
pq.push(m);
} else {
q--;
m = (int)(m /2);
pq.push(m);
}
}
while(p){
int m=pq.top();
p--;
pq.pop();
m=(int)sqrt(m);
pq.push(m);
}
while(q){
int m=pq.top();
q--;
pq.pop();
m=(int)m/2;
pq.push(m);
}
int ans=0;
while(!pq.empty()){
ans+=pq.top();
pq.pop();
}
cout<<ans<<endl;
return 0;
}
20.数列前缀和 4
这次不是数列的问题了。
题目描述
给定一个 n 行 m 列的矩阵 a,有 q 次询问,每次给定 (u,v) 和 (x,y),请你求出:
(i=u∑x**j=v∑yai,j)mod264
也就是求出以 (u,v) 为左上角、(x,y) 为右下角的矩形元素和对 264 取余数的结果。
输入格式
本题单测试点内有多组测试数据。
输入的第一行是一个整数 T,表示数据组数。接下来依次给出每组数据的输入信息:
第一行三个整数,依次表示矩阵的行数 n 和列数 m 以及询问数 q。
接下来 n 行,每行 m 个整数。第 i 行第 j 个整数表示 a**i,j。
接下来 q 行,每行四个整数,依次为 u,v,x,y,表示一组询问。
输出格式
为了避免输出过大,对于每组数据,请输出一行一个整数,表示本组数据的所有询问的答案的按位异或和。
输入输出样例
输入 #1复制
2
3 3 3
1 2 3
4 5 6
7 8 9
1 1 3 3
2 1 2 2
1 2 2 3
2 2 1
1 3
4 6
2 2 2 2
输出 #1复制
52
6
题解:二维前缀和
//但是要用unsigned long long 不然会超时
#include<bits/stdc++.h>
//#define int long long
#define int unsigned long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int sum[2050][2050];//二维前缀和;
int ans=0;
void solve(){
int n,m,q;
cin>>n>>m>>q;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int x;
cin>>x;
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+x;
}
}
ans=0;
while(q--){
int u,v,x,y;
cin>>u>>v>>x>>y;
ans^=sum[x][y]-sum[x][v-1]-sum[u-1][y]+sum[u-1][v-1];//因为是2的26次方所以我们可以用^解决,相当于转换;
}
cout<<ans<<endl;
};
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
TESTS{
solve();
};
return 0;
}
21.序列分段
题目描述
给定长度为 n 的序列 a,要求将 a 分割成恰好 k 段,每一段内的所有数字都求和,得到一个长度为 k 的序列 b。
接着,最大化以下式子的和:
i=1∑k**i×b**i。
即:b1×1+b2×2+b3×3+...+b**k×k。
更通俗的:
请最大化:“第一段的和乘 1,加上第二段的和乘 2,一直加到第 k 段的和乘 k ”。
现在,请你对每一个 k (1≤k≤n),都求出并回答上述式子的最大值吧。
输入格式
本题有多组测试数据。
输入的第一行包含一个正整数 T,表示数据组数。
接下来包含 T 组数据,每组数据的格式如下:
第一行一个正整数 n,表示序列 a 的长度。
第二行 n 个整数 a1,a2,⋯,a**n,表示序列 a。
输出格式
对于每组测试数据:
在单独的一行输出由空格分隔的 n 个整数,其中第 i 个整数表示:把数组分为 i 段时,上述式子的最大值。
输入输出样例
输入 #1复制
2
6
1 3 -4 5 -1 -2
1
100
输出 #1复制
2 4 5 3 1 -2
100
说明/提示
【样例 1 解释】
对于第一组测试数据,我们考虑 k=3 的情况,可以把序列分为:
{{1},{3,−4},{5,−1,−2}}。
此时 b={1,3+(−4),(5+(−1)+(−2))}={1,−1,2}。
而题目所求式子的值为:1×1+(−1)×2+2×3=5。
因此第一组测试数据中,第三个数字的值是 5。
(可以证明,不存在比 5 更优的答案。)
【数据范围】
令 N 表示 T 组数据中 n 的总和。
对于 30% 的数据有:T=1,1≤N≤15。
对于 60% 的数据有:1≤T≤10,1≤N≤200。
对于所有的测试数据有: 1≤T≤100,1≤N≤2×105 ,−106≤a**i≤106。
题解:思维题:
我们将选择的数做一个处理如3段的时候
00000
0 0 0 00000
0 0 0| 0 0 0| 00000
相当于排序为这样,那么可以明显知道下面就是全部的sum和也就是后缀中的sum[1],然后上面的就是某个后缀
要选择最大的,那么相当于我们可以排一个序,但是我们要把sum[1],单独拎出来,因为每一次都要sum[1],
且sum[1]不一定最大,所以对剩下的排序一下最后一一输出。
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
void solve(){
int n;
cin>>n;
vector<int>v(n+1);
vector<int>sum(n+2,0);
for(int i=1;i<=n;i++){
cin>>v[i];
}
for(int i=n;i>=1;i--){
sum[i]=sum[i+1]+v[i];
}
vector<int>ans(n+1);
ans[1]=sum[1];
vector<int>v1;
for(int i=2;i<=n;i++){
v1.push_back(sum[i]);
}
sort(v1.begin(),v1.end());
for(int i=2;i<=n;i++){
ans[i]=ans[i-1]+v1.back();
v1.pop_back();
}
for(int i=1;i<=n;i++){
cout<<ans[i]<<" ";
}
cout<<endl;
};
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
TESTS{
solve();
};
return 0;
}
题解:暴力法部分样例
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void dfs(int start, int remaining, vector<int>& current_splits, const vector<ll>& pre_sum, int n, ll& max_sum) {
if (remaining == 0) {
ll sum = 0;
int prev = 0;
for (int i = 0; i < current_splits.size(); ++i) {
int split = current_splits[i];
sum += (i + 1) * (pre_sum[split + 1] - pre_sum[prev]);
prev = split + 1;
}
sum += (current_splits.size() + 1) * (pre_sum[n] - pre_sum[prev]);
if (sum > max_sum) {
max_sum = sum;
}
return;
}
for (int i = start; i <= (n - remaining - 1); ++i) {
current_splits.push_back(i);
dfs(i + 1, remaining - 1, current_splits, pre_sum, n, max_sum);
current_splits.pop_back();
}
}
vector<ll> solve(const vector<int>& a) {
int n = a.size();
vector<ll> pre_sum(n + 1, 0);
for (int i = 1; i <= n; ++i) {
pre_sum[i] = pre_sum[i - 1] + a[i - 1];
}
vector<ll> ans(n, 0);
for (int k = 1; k <= n; ++k) {
if (k == 1) {
ans[k - 1] = pre_sum[n];
} else {
ll max_sum = LLONG_MIN;
vector<int> current_splits;
dfs(0, k - 1, current_splits, pre_sum, n, max_sum);
ans[k - 1] = max_sum;
}
}
return ans;
}
int main() {
int T;
cin >> T;
while (T--) {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
vector<ll> res = solve(a);
for (int i = 0; i < n; ++i) {
cout << res[i];
if (i != n - 1) {
cout << " ";
}
}
cout << endl;
}
return 0;
}
22. Function
题目描述
对于一个递归函数 w(a,b,c)
- 如果 a≤0 或 b≤0 或 c≤0 就返回值 1。
- 如果 a>20 或 b>20 或 c>20 就返回 w(20,20,20)
- 如果 a<b 并且 b<c 就返回 w(a,b,c−1)+w(a,b−1,c−1)−w(a,b−1,c)。
- 其它的情况就返回 w(a−1,b,c)+w(a−1,b−1,c)+w(a−1,b,c−1)−w(a−1,b−1,c−1)
这是个简单的递归函数,但实现起来可能会有些问题。当 a,b,c 均为 15 时,调用的次数将非常的多。你要想个办法才行。
注意:例如 w(30,−1,0) 又满足条件 1 又满足条件 2,请按照最上面的条件来算,答案为 1。
输入格式
会有若干行。
并以 −1,−1,−1 结束。
输出格式
输出若干行,每一行格式:
w(a, b, c) = ans
注意空格。
输入输出样例
输入 #1复制
1 1 1
2 2 2
-1 -1 -1
输出 #1复制
w(1, 1, 1) = 2
w(2, 2, 2) = 4
题解:递归加记忆化搜索
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
//int a[N],b[N],c[N],pre[N];
int a,b,c;
int f[40][40][40];//记忆化,把保存的记录下来
int fun(int x,int y,int z){
if(x<=20&&y<=20&&z<=20&&x>=0&&y>=0&&z>=0){
if(f[x][y][z])return f[x][y][z];
}
if((x<=0)||(y<=0)||(z<=0))return 1;
if((x>20)||(y>20)||(z>20))return fun(20,20,20);
if((x<y)&&(y<z))return f[x][y][z]=fun(x,y,z-1)+fun(x,y-1,z-1)-fun(x,y-1,z);
return f[x][y][z]=fun(x-1,y,z)+fun(x-1,y-1,z)+fun(x-1,y,z-1)-fun(x-1,y-1,z-1);
}
void print(){
printf("w(%lld, %lld, %lld) = %lld\n",a,b,c,fun(a,b,c));
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
while(1){
cin>>a>>b>>c;
if(a==-1&&b==-1&&c==-1){
break;
}
print();
}
return 0;
}
23.保龄球
题目描述
DL 算缘分算得很烦闷,所以常常到体育馆去打保龄球解闷。因为他保龄球已经打了几十年了,所以技术上不成问题,于是他就想玩点新花招。
DL 的视力真的很不错,竟然能够数清楚在他前方十米左右每个位置的瓶子的数量。他突然发现这是一个炫耀自己好视力的借口——他看清远方瓶子的个数后从某个位置发球,这样就能打倒一定数量的瓶子。
- ◯◯◯
- ◯◯◯ ◯
- ◯
- ◯ ◯
如上图,每个 “◯” 代表一个瓶子。如果 DL 想要打倒 3 个瓶子就在 1 位置发球,想要打倒 4 个瓶子就在 2 位置发球。
现在他想要打倒 m 个瓶子。他告诉你每个位置的瓶子数,请你给他一个发球位置。
输入格式
第一行包含一个正整数 n,表示位置数。
第二行包含 n 个正整数 a**i ,表示第 i 个位置的瓶子数,保证各个位置的瓶子数不同。
第三行包含一个正整数 Q,表示 DL 发球的次数。
第四行至文件末尾,每行包含一个正整数 m,表示 DL 需要打倒 m 个瓶子。
输出格式
共 Q 行。每行包含一个整数,第 i 行的整数表示 DL 第 i 次的发球位置。若无解,则输出 0。
输入输出样例
输入 #1复制
5
1 2 4 3 5
2
4
7
输出 #1复制
3
0
说明/提示
【数据范围】
对于 50% 的数据,1≤n,Q≤1000,1≤a**i,m≤105。
对于 100% 的数据,1≤n,Q≤100000,1≤a**i,m≤109。
题解1map记录
用map记录位置
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
map<int,int>mp;
for(int i=1;i<=n;i++){
int x;
cin>>x;
mp[x]=i;
}
int q;
cin>>q;
while (q--){
int m;
cin>>m;
cout<<mp[m]<<endl;
}
return 0;
}
题解:二分
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int n;
struct aa{
int g,w;
}gs[N];
bool cmp(aa x,aa y){
return x.g<y.g;
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>gs[i].g;
gs[i].w=i;
}
sort(gs+1,gs+n+1,cmp);
int q;
cin>>q;
while(q--){
int m;
cin>>m;
int l=0,r=n;
while(l<r){
int mid=(l+r)/2;
if(gs[mid].g<m)l=mid+1;
else r=mid;
}
if(gs[l].g!=m)cout<<"0"<<endl;
else{
cout<<gs[l].w<<endl;
}
}
return 0;
}
24学籍管理
题目描述
您要设计一个学籍管理系统,最开始学籍数据是空的,然后该系统能够支持下面的操作(不超过 105 条):
- 插入与修改,格式
1 NAME SCORE:在系统中插入姓名为 NAME(由字母和数字组成不超过 20 个字符的字符串,区分大小写) ,分数为 SCORE(0<SCORE<231) 的学生。如果已经有同名的学生则更新这名学生的成绩为 SCORE。如果成功插入或者修改则输出OK。 - 查询,格式
2 NAME:在系统中查询姓名为 NAME 的学生的成绩。如果没能找到这名学生则输出Not found,否则输出该生成绩。 - 删除,格式
3 NAME:在系统中删除姓名为 NAME 的学生信息。如果没能找到这名学生则输出Not found,否则输出Deleted successfully。 - 汇总,格式
4:输出系统中学生数量。
输入格式
无
输出格式
无
输入输出样例
输入 #1复制
5
1 lxl 10
2 lxl
3 lxl
2 lxl
4
输出 #1复制
OK
10
Deleted successfully
Not found
0
题解map的应用
mp.count(xxx)//查询这个xxx在不在mp中,
mp.erase(xxx)删除这个键
mp.size()有多少长度
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
map<string,int>mp;
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin>>n;
while(n--){
int x;
string name;
cin>>x;
if(x==1){
int score;
cin>>name>>score;
mp[name]=score;
cout<<"OK"<<endl;
}else if(x==2){
cin>>name;
if(mp.count(name)){
cout<<mp[name]<<endl;
}else{
cout<<"Not found"<<endl;
}
}else if(x==3){
cin>>name;
if(mp.count(name)){
mp.erase(name);
cout<<"Deleted successfully"<<endl;
}else{
cout<<"Not found"<<endl;
}
}else{
cout<<mp.size()<<endl;
}
}
return 0;
}
25木材仓库
题目描述
博艾市有一个木材仓库,里面可以存储各种长度的木材,但是保证没有两个木材的长度是相同的。作为仓库负责人,你有时候会进货,有时候会出货,因此需要维护这个库存。有不超过 100000 条的操作:
- 进货,格式
1 Length:在仓库中放入一根长度为 Length(不超过 109) 的木材。如果已经有相同长度的木材那么输出Already Exist。 - 出货,格式
2 Length:从仓库中取出长度为 Length 的木材。如果没有刚好长度的木材,取出仓库中存在的和要求长度最接近的木材。如果有多根木材符合要求,取出比较短的一根。输出取出的木材长度。如果仓库是空的,输出Empty。
输入格式
无
输出格式
无
输入输出样例
输入 #1复制
7
1 1
1 5
1 3
2 3
2 3
2 3
2 3
输出 #1复制
3
1
5
Empty
题解map应用
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
map<int,int>mp;
int n;
cin>>n;
for(int i=0;i<n;i++){
int x,y;
cin>>x>>y;
if(x==1){
if(mp.count(y))cout<<"Already Exist"<<endl;
else mp[y]=1;
}else{
if(mp.empty())cout<<"Empty"<<endl;
else if(mp.count(y)){
mp.erase(y);
cout<<y<<endl;
}else{
mp[y]=1;//假装存一下
auto it=mp.find(y);
auto it2=it;
it++;
if(it2==mp.begin()){//没有比它短的
cout<<it->first<<endl;
mp.erase(it);
}
else if(it==mp.end()){
cout << (--it2)->first << endl;
mp.erase(it2);
}else if(y-(--it2)->first > it->first-y){
cout << it->first << endl;
mp.erase(it);
}else{
cout << it2->first << endl;
mp.erase(it2);
}
mp.erase(y);
}
}
}
return 0;
}
26.[蓝桥杯 2023 省 B] 岛屿个数
[P9243 蓝桥杯 2023 省 B] 岛屿个数 - 洛谷
题目描述
小蓝得到了一副大小为 M×N 的格子地图,可以将其视作一个只包含字符 0(代表海水)和 1(代表陆地)的二维数组,地图之外可以视作全部是海水,每个岛屿由在上/下/左/右四个方向上相邻的 1 相连接而形成。
在岛屿 A 所占据的格子中,如果可以从中选出 k 个不同的格子,使得他们的坐标能够组成一个这样的排列:(x0,y0),(x1,y1),…,(x**k−1,y**k−1),其中 (x(i+1)modk,y(i+1)modk) 是由 (x**i,y**i) 通过上/下/左/右移动一次得来的(0≤i≤k−1),此时这 k 个格子就构成了一个「环」。如果另一个岛屿 B 所占据的格子全部位于这个「环」内部,此时我们将岛屿 B 视作是岛屿 A 的子岛屿。若 B 是 A 的子岛屿,C 又是 B 的子岛屿,那 C 也是 A 的子岛屿。
请问这个地图上共有多少个岛屿?在进行统计时不需要统计子岛屿的数目。
输入格式
第一行一个整数 T,表示有 T 组测试数据。
接下来输入 T 组数据。对于每组数据,第一行包含两个用空格分隔的整数 M,N 表示地图大小;接下来输入 M 行,每行包含 N 个字符,字符只可能是 0 或 1。
输出格式
对于每组数据,输出一行,包含一个整数表示答案。
输入输出样例
输入 #1复制
2
5 5
01111
11001
10101
10001
11111
5 6
111111
100001
010101
100001
111111
输出 #1复制
1
3
题解:bfs+bfs搜:
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int mp[100][100];
int dx[8] = {-1, -1, -1, 0, 1, 1, 1, 0};
int dy[8] = {-1, 0, 1, 1, 1, 0, -1, -1};
int ddx[]={-1,0,1,0};
int ddy[]={0,-1,0,1};
int ans=0;
int n,m;
bool st_sea[200][200],st_road[200][200];
bool check(int x,int y){
return (x>=0&&x<n&&y>=0&&y<m);
}
void bfs1(int x,int y){
queue<PII>q;
st_road[x][y]=true;
q.push({x,y});
while (!q.empty()){
auto it=q.front();
q.pop();
for(int i=0;i<4;i++){
int nx=it.first+ddx[i];
int ny=it.second+ddy[i];
if(check(nx,ny)&&mp[nx][ny]&&!st_road[nx][ny]){
st_road[nx][ny]= true;
q.push({nx,ny});
}
}
}
}
void bfs(int x,int y){
queue<PII>q;
st_sea[x][y]= true;
q.push({x,y});
while (!q.empty()){
auto it=q.front();
q.pop();
for(int i=0;i<8;i++){
int nx=it.first+dx[i];
int ny=it.second+dy[i];
if(check(nx,ny)&&!mp[nx][ny]&&!st_sea[nx][ny]){
st_sea[nx][ny]=true;
q.push({nx,ny});
}
if(check(nx,ny)&&mp[nx][ny]&&!st_road[nx][ny]){
ans++;
bfs1(nx,ny);
}
}
}
}
void solve(){
cin>>n>>m;
ans=0;
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
st_road[i][j]=st_sea[i][j]=false;
}
}
for(int i=0;i<n;i++){
string s;
cin>>s;
for(int j=0;j<m;j++){
mp[i][j]=s[j]-'0';
}
}
bool flag=0;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(!i||i==n-1||j==0||j==m-1){
if(!mp[i][j]&&!st_sea[i][j]){
flag= true;
bfs(i,j);
}
}
}
}
if(!flag){
ans=1;
}
cout<<ans<<endl;
};
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
TESTS{
solve();
};
return 0;
}
题解:bfs+dfs:
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int mp[100][100];
int dx[8] = {-1, -1, -1, 0, 1, 1, 1, 0};
int dy[8] = {-1, 0, 1, 1, 1, 0, -1, -1};
int ddx[]={-1,0,1,0};
int ddy[]={0,-1,0,1};
int ans=0;
int n,m;
bool st_sea[200][200],st_road[200][200];
bool check(int x,int y){
return (x>=0&&x<n&&y>=0&&y<m);
}
void dfs1(int x, int y) {
st_road[x][y] = true;
for (int i = 0; i < 4; ++i) {
int nx = x + ddx[i];
int ny = y + ddy[i];
if (check(nx, ny) && mp[nx][ny] && !st_road[nx][ny]) {
dfs1(nx, ny);
}
}
}
void bfs(int x,int y){
queue<PII>q;
st_sea[x][y]= true;
q.push({x,y});
while (!q.empty()){
auto it=q.front();
q.pop();
for(int i=0;i<8;i++){
int nx=it.first+dx[i];
int ny=it.second+dy[i];
if(check(nx,ny)&&!mp[nx][ny]&&!st_sea[nx][ny]){
st_sea[nx][ny]=true;
q.push({nx,ny});
}
if(check(nx,ny)&&mp[nx][ny]&&!st_road[nx][ny]){
ans++;
dfs1(nx,ny);
}
}
}
}
void solve(){
cin>>n>>m;
ans=0;
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
st_road[i][j]=st_sea[i][j]=false;
}
}
for(int i=0;i<n;i++){
string s;
cin>>s;
for(int j=0;j<m;j++){
mp[i][j]=s[j]-'0';
}
}
bool flag=0;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(!i||i==n-1||j==0||j==m-1){
if(!mp[i][j]&&!st_sea[i][j]){
flag= true;
bfs(i,j);
}
}
}
}
if(!flag){
ans=1;
}
cout<<ans<<endl;
};
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
TESTS{
solve();
};
return 0;
}
27.[蓝桥杯 2023 省 B] 飞机降落
[P9241 蓝桥杯 2023 省 B] 飞机降落 - 洛谷
N 架飞机准备降落到某个只有一条跑道的机场。其中第 i 架飞机在 T**i 时刻到达机场上空,到达时它的剩余油料还可以继续盘旋 D**i 个单位时间,即它最早可以于 T**i 时刻开始降落,最晩可以于 T**i+D**i 时刻开始降落。降落过程需要 L**i 个单位时间。
一架飞机降落完毕时,另一架飞机可以立即在同一时刻开始降落,但是不能在前一架飞机完成降落前开始降落。
请你判断 N 架飞机是否可以全部安全降落。
输入格式
输入包含多组数据。
第一行包含一个整数 T,代表测试数据的组数。
对于每组数据,第一行包含一个整数 N。
以下 N 行,每行包含三个整数 T**i,D**i,L**i。
输出格式
对于每组数据,输出 YES 或者 NO,代表是否可以全部安全降落。
输入输出样例
输入 #1复制
2
3
0 100 10
10 10 10
0 2 20
3
0 10 20
10 10 20
20 10 20
输出 #1复制
YES
NO
说明/提示
【样例说明】
对于第一组数据,可以安排第 3 架飞机于 0 时刻开始降落,20 时刻完成降落。安排第 2 架飞机于 20 时刻开始降落,30 时刻完成降落。安排第 1 架飞机于 30 时刻开始降落,40 时刻完成降落。
对于第二组数据,无论如何安排,都会有飞机不能及时降落。
【评测用例规模与约定】
对于 30% 的数据,N≤2。
对于 100% 的数据,1≤T≤10,1≤N≤10,0≤T**i,D**i,L**i≤105。
蓝桥杯 2023 省赛 B 组 D 题。
题解:dfs
枚举所有可能,每个位置都可能当开头
#include<bits/stdc++.h>
using namespace std;
struct Node{
int l;//飞机最早能降落的时间
int r;//飞机最晚能降落的时间
int t;//飞机降落需要的时间
};
int t,n,vis[15];
bool flag;
Node fj[15];
void dfs(int deep,int now){//now表示当前时间
if(deep==n){//所有飞机降落
flag=1;
return ;
}
for(int i=1;i<=n;i++){
if(!vis[i]&&fj[i].r<now) return ;//剪枝
if(!vis[i]&&fj[i].r>=now){
vis[i]=1;//标记
if(fj[i].l>now) dfs(deep+1,fj[i].l+fj[i].t);//如果开始时间比现在时间要晚
else dfs(deep+1,now+fj[i].t);
vis[i]=0;//取消标记
}
}
}
int main(){
cin>>t;
memset(vis,0,sizeof(vis));
while(t--){
cin>>n;
flag=0;
int k;
for(int i=1;i<=n;i++) cin>>fj[i].l>>k>>fj[i].t,fj[i].r=fj[i].l+k;//因为是降落的最晚时间,因此fj[i].r=fj[i].l+k
for(int i=1;i<=n;i++) vis[i]=1,dfs(1,fj[i].l+fj[i].t),vis[i]=0;
if(flag) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
题解:next_permutation();枚举
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
int n;
struct Node{
int l;//飞机最早能降落的时间
int r;//飞机最晚能降落的时间
int t;//飞机降落需要的时间
};
int flag;
Node fj[15];
bool check(){//判读可不可以;
int now=fj[a[1]].l+fj[a[1]].t;//当前时间
for(int i=2;i<=n;i++){
if(fj[a[i]].r<now)return false;
if(fj[a[i]].l>now)now=fj[a[i]].l+fj[a[i]].t;
else now+=fj[a[i]].t;
}
flag=1;
return true;
}
void solve(){
cin>>n;
int k;
flag=0;
for(int i=1;i<=n;i++) cin>>fj[i].l>>k>>fj[i].t,fj[i].r=fj[i].l+k;
for(int i=1;i<=n;i++){
a[i]=i;
}
do{
if(check()){//枚举所有可能
break;
}
} while (next_permutation(a+1,a+n+1));
if(flag)cout<<"YES"<<endl;
else cout<<"NO"<<endl;
};
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
TESTS{
solve();
};
return 0;
}
28.算式
题目描述
给出 n 个数字,不改变它们的相对位置,在中间加入 k 个乘号和 (n−k−1) 个加号,括号随便加,使最终结果尽量大。因为乘号和加号一共就是 n−1 个了,所以恰好每两个相邻数字之间都有一个符号。例如:
n=5,k=2,5 个数字分别为 1,2,3,4,5,可以加成:
1×2×(3+4+5)=241×(2+3)×(4+5)=45(1×2+3)×(4+5)=45……
输入格式
输入的第一行为两个用空格隔开的整数,分别表示表示 n 和 k。
第二行为 n 个用空格隔开的整数 a**i,代表给出的数字。
输出格式
输出文件仅一行包含一个整数,表示要求的最大的结果。
输入输出样例
输入 #1复制
5 2
1 2 3 4 5
输出 #1复制
120
说明/提示
数据规模与约定
- 对于 100% 的数据,保证 2≤n≤15,0≤k<n,0≤a**i≤9,答案小于 231。
题解:dfs+区间dp
先把所有的可能先找到,再判断加括号的问题,就用区间dp
区间dp
int n=6;
for(int l=2;l<=n;l++){
for(int i=1;i+l-1<=n;i++){
int j=i+l-1;
for(int m=i;m<j;m++){
cout<<i<<" "<<m<<" "<<j<<endl;
}
}
}
1 1 2
2 2 3
3 3 4
4 4 5
5 5 6
1 1 3
1 2 3
2 2 4
2 3 4
3 3 5
3 4 5
4 4 6
4 5 6
1 1 4
1 2 4
1 3 4
2 2 5
2 3 5
2 4 5
3 3 6
3 4 6
3 5 6
1 1 5
1 2 5
1 3 5
1 4 5
2 2 6
2 3 6
2 4 6
2 5 6
1 1 6
1 2 6
1 3 6
1 4 6
1 5 6
#include<bits/stdc++.h>
#define int long long
#define PII pair<int, int>
#define endl '\n'
using namespace std;
const int N = 16;
int a[N], s[N];
int n, k, ans = -1;
int dp[N][N];
int cal(int x, int y, int t) {
return t == 1 ? x + y : x * y;
}
void dp1() {
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= n; i++) dp[i][i] = a[i];
for (int len = 2; len <= n; len++) {
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1;
for (int m = i; m < j; m++) {
dp[i][j] = max(dp[i][j], cal(dp[i][m], dp[m+1][j], s[m]));
}
}
}
ans = max(ans, dp[1][n]);
}
void dfs(int x, int t1, int t2) {
if (x == n) {
dp1();
return;
}
// 尝试放置乘号
if (t1 < k) {
s[x] = 2;
dfs(x + 1, t1 + 1, t2);
}
// 尝试放置加号
if (t2 < (n - 1 - k)) { // 修复条件
s[x] = 1;
dfs(x + 1, t1, t2 + 1);
}
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
dfs(1, 0, 0);
cout << ans << endl;
return 0;
}
29.[蓝桥杯 2023 省 B] 整数删除
[P12085 蓝桥杯 2023 省 B] 整数删除 - 洛谷
题目描述
给定一个长度为 N 的整数数列:A1,A2,…,A**N。你要重复以下操作 K 次:
每次选择数列中最小的整数(如果最小值不止一个,选择最靠前的),将其删除。并把与它相邻的整数加上被删除的数值。
输出 K 次操作后的序列。
输入格式
第一行包含两个整数 N 和 K。
第二行包含 N 个整数,A1,A2,A3,…,A**N。
输出格式
输出 N−K 个整数,中间用一个空格隔开,代表 K 次操作后的序列。
输入输出样例
输入 #1复制
5 3
1 4 2 8 7
输出 #1复制
17 7
说明/提示
【样例说明】
数列变化如下,中括号里的数是当此操作中被选择的数:
[1] 4 2 8 7
5 [2] 8 7
[7] 10 7
17 7
【评测用例规模与约定】
对于 20% 的数据,1≤K<N≤104。
对于 100% 的数据,1≤K<N≤5×105,0≤A**i≤108。
蓝桥杯 2023 省赛 B 组 H 题。
题解:暴力(模拟)只能过一部分
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=5e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
bool st[N];
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,k;
cin>>n>>k;
for(int i=0;i<n;i++){
cin>>a[i];
}
for(int i=0;i<k;i++){
int minv=0x3f3f3f3f3f;
int pos=-1;
for(int j=0;j<n;j++){
if(minv>a[j]&&!st[j]){//找最小值
minv=a[j];
pos=j;
}
}
st[pos]=true;
for(int j=pos-1;j>=0;j--){//向前找相邻的
if(!st[j]){
a[j]+=minv;
break;
}
}
for(int j=pos+1;j<n;j++){//向后找相邻的
if(!st[j]){
a[j]+=minv;
break;
}
}
}
for(int i=0;i<n;i++){
if(!st[i]){
cout<<a[i]<<" ";
}
}
return 0;
}
题解:优先队列加链表
//整数删除:优先队列 + 模拟链表
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
typedef pair<int,int> pii;
const int N = 5e5 + 10;
int a[N], l[N], r[N];
int st[N];
void solve()
{
int n, k; cin >> n >> k;
priority_queue<pii, vector<pii>, greater<pii>>q;
for(int i = 0; i < n; i ++)
{
cin >> a[i];
q.push({a[i], i});
st[i] = a[i];
l[i] = i - 1;
r[i] = i + 1;
if(r[i] == n)
r[i] = -1;
}
int cnt = k;
while(k)
{
pii t = q.top();
q.pop();
if(t.first != st[t.second])
{
q.push({st[t.second], t.second});
continue;
}
k --;
//获取该元素在原数组中的位置
int pos = t.second;
//将该元素的相邻元素加上该数值
if(l[pos] >= 0)
st[l[pos]] += t.first;
if(r[pos] >= 0)
st[r[pos]] += t.first;
//更新相邻点的相邻元素
if(l[pos] >= 0)
r[l[pos]] = r[pos];
if(r[pos] >= 0)
l[r[pos]] = l[pos];
//该元素已经被删除,打标记
st[pos] = -1;
}
for(int i = 0; i < n; i ++)
{
if(st[i] != -1)
cout << st[i] << " ";
}
cout << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t = 1;
// cin >> t;
while(t--)
solve();
}
30.接龙数列
[P9242 蓝桥杯 2023 省 B] 接龙数列 - 洛谷
题目描述
对于一个长度为 K 的整数数列:A1,A2,…,A**K,我们称之为接龙数列当且仅当 A**i 的首位数字恰好等于 A**i−1 的末位数字(2≤i≤K)。
例如 12,23,35,56,61,11 是接龙数列;12,23,34,56 不是接龙数列,因为 56 的首位数字不等于 34 的末位数字。所有长度为 1 的整数数列都是接龙数列。
现在给定一个长度为 N 的数列 A1,A2,…,A**N,请你计算最少从中删除多少 个数,可以使剩下的序列是接龙序列?
输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,…,A**N。
输出格式
一个整数代表答案。
输入输出样例
输入 #1复制
5
11 121 22 12 2023
输出 #1复制
1
说明/提示
【样例说明】
删除 22,剩余 11,121,12,2023 是接龙数列。
【评测用例规模与约定】
对于 20% 的数据,1≤N≤20。
对于 50% 的数据,1≤N≤104。
对于 100% 的数据,1≤N≤105,1≤A**i≤109。所有 A**i 保证不包含前导 0。
蓝桥杯 2023 省赛 B 组 E 题。
题解:暴力只能拿百分之30的分
就是选和不选两种情况:选和不选就是,两种情况那么知道后面的
// 暴力代码:DFS(2^n)
#include<bits/stdc++.h>
#define endl '\n'
#define deb(x) cout << #x << " = " << x << '\n';
#define INF 0x3f3f3f3f
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n, ans;
int get_first(int x)//获取数字的最高位
{
int res = 0;
while(x)
{
res = x % 10;
x /= 10;
}
return res;
}
int get_final(int x)//获取数字的最后一位
{
return x % 10;
}
//u表示当前考虑到了第几位。
//last表示,方案中已经选了的最后一个数字是多少
//cnt表示,方案中一共有多少个数字
void dfs(int u, int cnt, int last)
{
if(u >= n)
{
ans = max(ans, cnt);
return;
}
if(n - u + cnt <= ans)
{
return;
}
//第u位数选,如果选这个数字
//就必须和前面最后一个数字构成接龙序列。
if(last == -1 || get_final(last) == get_first(a[u]))
dfs(u + 1, cnt + 1, a[u]);
//第u个数不选
dfs(u + 1, cnt, last);
}
void solve()
{
cin >> n;
for(int i = 0; i < n; i ++)
cin >> a[i];
dfs(0, 0, -1);
cout << n - ans << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t = 1;
//cin >> t;
while(t--)
solve();
}
题解:dp
dp[i];表示以i结尾的数有多少个,然后s[l-1]-'0',
dp[s[l-1]-'0']=max(dp[s[l-1]-'0'],dp[s[0]-'0']+1);
这个以dp[s[l-1]-'0']这个结尾判断是加上这个多,还是原本的本来就最大。
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=2e5+10,M=1e3+10;
int a[N],b[N];
int ans=-1;
int n;
int dp[10];//表示以i结尾的数有多少个;
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
string s;
for(int i=0;i<n;i++){
cin>>s;
int l=s.length();
dp[s[l-1]-'0']=max(dp[s[l-1]-'0'],dp[s[0]-'0']+1);
}
for(int i=0;i<10;i++){
ans=max(ans,dp[i]);
}
cout<<n-ans<<endl;
return 0;
}
31.景区导游
[P9245 蓝桥杯 2023 省 B] 景区导游 - 洛谷
题目描述
某景区一共有 N 个景点,编号 1 到 N。景点之间共有 N−1 条双向的摆渡车线路相连,形成一棵树状结构。在景点之间往返只能通过这些摆渡车进行,需要花费一定的时间。
小明是这个景区的资深导游,他每天都要按固定顺序带客人游览其中 K 个景点:A1,A2,…,A**K。今天由于时间原因,小明决定跳过其中一个景点,只带游客按顺序游览其中 K−1 个景点。具体来说,如果小明选择跳过 A**i,那么他会按顺序带游客游览 A1,A2,…,A**i−1,A**i+1,…,A**K(1≤i≤K)。
请你对任意一个 A**i,计算如果跳过这个景点,小明需要花费多少时间在景点之间的摆渡车上?
输入格式
第一行包含 2 个整数 N 和 K。
以下 N−1 行,每行包含 3 个整数 u,v,t,代表景点 u 和 v 之间有摆渡车线路,花费 t 个单位时间。
最后一行包含 K 个整数 A1,A2,…,A**K 代表原定游览线路。
输出格式
输出 K 个整数,其中第 i 个代表跳过 A**i 之后,花费在摆渡车上的时间。
输入输出样例
输入 #1复制
6 4
1 2 1
1 3 1
3 4 2
3 5 2
4 6 3
2 6 5 1
输出 #1复制
10 7 13 14
题解:数上dfs
遍历图上的路径加上和,dfs搜索树
//暴力代码:DFS
#include<bits/stdc++.h>
#define endl '\n'
#define deb(x) cout << #x << " = " << x << '\n';
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int N = 2e5 + 10;
typedef pair<int,int> pii;
map<pii, int>st;//记录从{x, y}的距离是多少
int a[N];
vector<pii>edge[N];//存图
//s表示你要求的路径的起点
//v表示你要求的路径的终点
//u表示你当前走到了哪个点
//father表示你当前这个点的父亲节点是谁。避免重复走造成死循环
//sum表示从s走到u的路径花费总和。
bool dfs(int s, int u, int father, int v, int sum)
{
if(u == v)
{
st[{s, v}] = sum;
st[{v, s}] = sum;
// cout << s << " " << v << " " << sum << endl;
return true;
}
for(int i = 0; i < edge[u].size(); i ++)
{
int son = edge[u][i].first;
if(son == father)
continue;
int w = edge[u][i].second;
if(dfs(s, son, u, v, sum + w))
return true;
}
return false;
}
void solve()
{
int n, k;
cin >> n >> k;
for(int i = 0; i < n - 1; i ++)
{
int x, y, t;
cin >> x >> y >> t;
edge[x].push_back({y, t});
edge[y].push_back({x, t});
}
for(int i = 0; i < k; i ++)
cin >> a[i];
//求出完整路线的总花费
//O(k * n)
int ans = 0;
for(int i = 0; i < k - 1; i ++)
{
dfs(a[i], a[i], -1, a[i + 1], 0);
ans += st[{a[i] ,a[i + 1]}];
}
for(int i = 0; i < k; i ++)
{
int tmp = ans;
if(i == 0)
tmp -= st[{a[i], a[i + 1]}];
else if(i == k - 1)
tmp -= st[{a[i - 1], a[i]}];
else
{
tmp -= st[{a[i - 1], a[i]}];
tmp -= st[{a[i], a[i + 1]}];
dfs(a[i - 1], a[i - 1], -1, a[i + 1], 0);
tmp += st[{a[i - 1], a[i + 1]}];
}
cout << tmp << endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t = 1;
//cin >> t;
while(t--)
solve();
}
正解:树上前缀和 + 最近公共祖先
//景区导游:树上前缀和 + 最近公共祖先
#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
int a[N], siz[N], dep[N], fa[N], son[N], top[N];
int sum[N];
int n, k;
vector<pii>edge[N];
void dfs1(int u, int father)
{
siz[u] = 1, dep[u] = dep[father] + 1;
fa[u] = father;
for(int i = 0; i < edge[u].size(); i ++)
{
int s = edge[u][i].first;
if(s == father)
continue;
dfs1(s, u);
siz[u] += siz[s];
if(siz[son[u]] < siz[s])
son[u] = s;
}
}
void dfs2(int u, int t)
{
top[u] = t;
if(son[u] == 0)
return;
dfs2(son[u], t);
for(int i = 0; i < edge[u].size(); i ++)
{
int s = edge[u][i].first;
if(s == son[u] || s == fa[u])
continue;
dfs2(s, s);
}
}
int lca(int u, int v)
{
while(top[u] != top[v])
{
if(dep[top[u]] < dep[top[v]])
swap(u, v);
u = fa[top[u]];
}
return dep[u] < dep[v] ? u : v;
}
void cal_sum(int u)
{
for(int i = 0; i < edge[u].size(); i ++)
{
int s = edge[u][i].first;
if(s == fa[u])
continue;
int w = edge[u][i].second;
sum[s] = sum[u] + w;
cal_sum(s);
}
}
void solve()
{
cin >> n >> k;
for(int i = 0; i < n - 1; i ++)
{
int x, y, t;
cin >> x >> y >> t;
edge[x].push_back({y, t});
edge[y].push_back({x, t});
}
for(int i = 1; i <= k; i ++)
cin >> a[i];
//树链剖分
dfs1(1, 0);
dfs2(1, 1);
//求树上的前缀和
cal_sum(1);
int ans = 0;
for(int i = 1; i <= k - 1; i ++)
{
int u = a[i], v = a[i + 1];
int cost = sum[u] + sum[v] - 2 * sum[lca(u, v)];
ans += cost;
}
for(int i = 1; i <= k; i ++)
{
int tmp = ans;
if(i == 1)
tmp -= sum[a[i + 1]] + sum[a[i]] - sum[lca(a[i], a[i + 1])] * 2;
else if(i == k)
tmp -= sum[a[i - 1]] + sum[a[i]] - sum[lca(a[i], a[i - 1])] * 2;
else
{
tmp -= sum[a[i + 1]] + sum[a[i]] - sum[lca(a[i], a[i + 1])] * 2;
tmp -= sum[a[i - 1]] + sum[a[i]] - sum[lca(a[i], a[i - 1])] * 2;
tmp += sum[a[i - 1]] + sum[a[i + 1]] - sum[lca(a[i + 1], a[i - 1])] * 2;
}
cout << tmp << " ";
}
cout << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int t = 1;
while(t--)
solve();
}
32.砍树
[P9246 蓝桥杯 2023 省 B] 砍树 - 洛谷
题目描述
给定一棵由 n 个结点组成的树以及 m 个不重复的无序数对 (a1,b1),(a2,b2),…,(a**m,b**m),其中 a**i 互不相同,b**i 互不相同,a**i=b**j(1≤i,j≤m)。
小明想知道是否能够选择一条树上的边砍断,使得对于每个 (a**i,b**i) 满足 a**i 和 b**i 不连通,如果可以则输出应该断掉的边的编号 (编号按输入顺序从 1 开始),否则输出 -1。
输入格式
输入共 n+m 行,第一行为两个正整数 n,m。
后面 n−1 行,每行两个正整数 x**i,y**i 表示第 i 条边的两个端点。
后面 m 行,每行两个正整数 a**i,b**i。
输出格式
一行一个整数,表示答案,如有多个答案,输出编号最大的一个。
输入输出样例
输入 #1复制
6 2
1 2
2 3
4 3
2 5
6 5
3 6
4 5
输出 #1复制
4
题解:dfs搜索
意思找到,经过最多次的边,输出
#include<bits/stdc++.h>
#define int long long
#define lll __uint128_t
#define PII pair<int ,int>
#define endl '\n'
using namespace std;
#define yn(ans) printf("%s\n", (ans)?"Yes":"No");//快速打印
#define YN(ans) printf("%s\n", (ans)?"YES":"NO");
#define REP(i, e) for (int i = 0; i < (e); ++i)
#define REP1(i, s, e) for (int i = (s); i <=(e); ++i)
#define TESTS int t; cin >> t; while (t--)
#define TEST
const int N=2e5+10,M=1e3+10,mod=1e9+7;
int a[N],b[N],c[N],pre[N];
vector<int>g[N];//建树
int n,m;
int w[N];//每一个边的边权
map<PII,int>id;//存边的边号;
//s表示你要求的路径的起点
//v表示你要求的路径的终点
//u表示你当前走到了哪个点
//father表示你当前这个点的父亲节点是谁。避免重复走造成死循环
bool dfs(int s,int u,int father,int v){
if(u==v){
return true;
}
for(int i=0;i<g[u].size();i++){
int son=g[u][i];
if(son==father)continue;
if(dfs(s,son,u,v)){
int Id=id[{u,son}];
w[Id]++;//递归回去然后标记完这个路径;
return true;
}
}
return false;
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=0;i<n-1;i++){
int x,y;
cin>>x>>y;
g[x].push_back(y);
g[y].push_back(x);
id[{x,y}]=id[{y,x}]=i;
}
for(int i=0;i<m;i++){
int x,y;
cin>>x>>y;
dfs(x,x,-1,y);
}
int ans=-1;
for(int i=n-1;i>=0;i--){
if(w[i]==m){
ans=i+1;
break;
}
}
cout<<ans<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号