梯度下降

梯度下降是一种通用的优化算法，其思想为迭代选择参数，使代价函数最小。

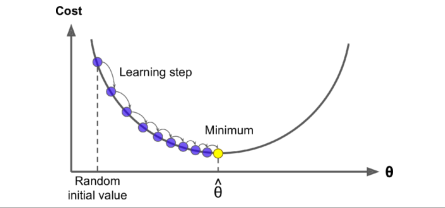
当描述梯度下降时，模型参数被随机初始化并反复调整以最小化代价函数;学习率与代价函数的斜率成正比，所以随着参数的逼近，学习率逐渐变小

学习率将决定迭代的次数与花费的时间

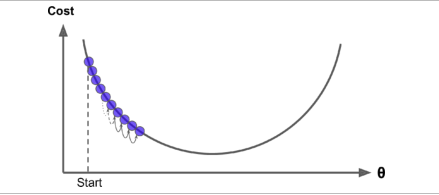
学习率太低导致迭代次数过多

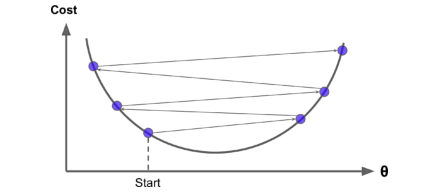
学习率太高导致算法无法收敛

不是所有的代价函数都是如上几幅图所示的碗状，现实情况的代价函数往往更复杂。

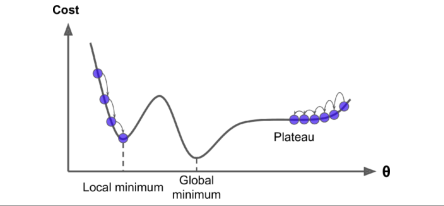
两个挑战：局部最小、耗费时间过长

若随机开始的参数从左侧开始，则算法将可能收敛到局部最小值，这不是全局最小值。如果它从右边开始，那么它将花费很长时间来跨越高原。如果你停止得太早，你将永远不会达到全局最小值。

幸运的是，对于线性回归的代价函数MSE来说，它是完美的凸函数，即函数连续，且只有一个全局最小值。只要你的学习速率不高并且等待时间足够长，那么每一次迭代都将使你接近全局最小值。

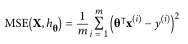
梯度下降有三种算法

批处理梯度下降（Batch Gradient Descent）

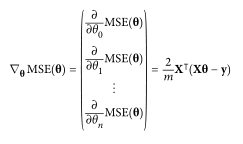
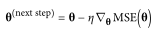
在每一步都使用批处理的训练数据计算，当训练样本数非常大时，将训练非常慢

随机梯度下降（Stochastic Gradient Descent）

批量梯度下降的主要问题是，它使用整个训练集来计算每一步的梯度，这使得它在训练集很大的时候非常慢。与之相反的是，随机梯度下降法在每一步都在训练集中随机选取一个实例，并仅基于该单一实例计算梯度。很明显，一次只处理一个实例会使算法速度快得多，因为在每个迭代中只有很少的数据需要处理。

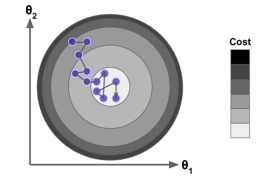
因为该算法的随机性，所以算法可以帮助跳出代价函数的局部最小值，却很难在全局最小值处安定下来。

解决该问题的方法是在每一步随机选择一个样本计算梯度时，一开始的学习率很大，帮助摆脱局部最小值。之后学习率变小，允许算法在最小值稳定下来。（类似于模拟退火）

使用随机梯度下降算法时，训练样本必须是独立同分布的，以确保达到全局最小值。确保这一点的一个简单方法是在训练期间对样本进行洗牌(shuffle)(例如，随机选择每个样本，或者在每个epoch开始时对训练集进行洗牌,然后遍历，但这样耗费时间变长)

迷你批处理梯度下降（Mini-Batch Gradient Descent）

迷你批处理在称为迷你批处理的小随机训练集上计算梯度

Plus:

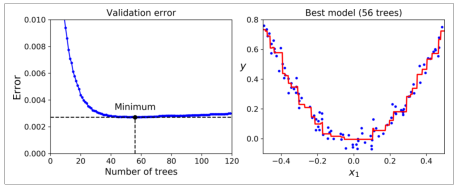
与梯度下降类似的还有梯度提升树回归（Gradient Boosting）

其大致思想是利用残差（y_new = y - tree.predict(X)）来训练基分类器。这个算法的训练速度也会受到学习率的影响，

对于GBRT来说，每一棵树等价于梯度下降的每一步，学习率的高低决定了它学习的速度以及精确度。

在学习率不高且不变的情况下，树的数量决定了耗费的时间以及拟合的程度