前言:tf-idf是很巧妙的算法,朴素贝叶斯也是很巧妙的算法,我尽量用最简短的语言进行描述,唯一不足的就是这个贝叶斯有点朴素,丢掉了很多特征的关联信息,而且tf-idf提出的这些特征是one-hot的,除了颗粒度粗点以外,对付5000标签分类量级,6000w预测数据(短标题)还是可以的;而且模型训练很快!6000千万条8G的训练数据,8线程cpu,只需跑3个小时;如果你想进一步优化的话,可以试着将分词转化为向量化,或者采用深度学习的相关方法-textcnn,或bert等最新的深度模型。
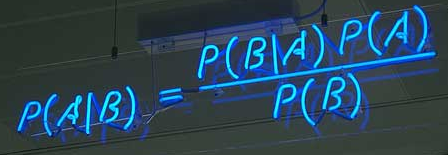
朴素贝叶斯分类器(Naïve Bayes classifier)是一种相当简单常见但是又相当有效的分类算法,在监督学习领域有着很重要的应用。朴素贝叶斯是建立在“全概率公式”的基础下的,由已知的尽可能多的事件A(语料x)、B(标签y)求得的$P(A|B)$来推断未知$P(B|A)$
优点:
- 训练:对训练数据“词语”做概率统计$P(A|B)=\frac{P(AB)} {P(A)}$,这里我们用tf-idf来训练P(A|B);
- 预测:使用朴素贝叶斯计算所有类目的概率$P(B|A)=\frac{P(A|B) P(B)}{P(A)}$;
- 适用于常规的电商短文本分类,加入部分人工干预,top3准确率可达到95%左右;
- 分类预测完全可解释,idf和P(B)受训练样本不均衡影响不大,但朴素贝叶斯的特征条件独立假设,导致丢失了很多信息;
缺点:
- 比较依赖分词效果;
- 需要大规模的训练语料,无法解决小样本问题;
- one-hot特征表示导致大规模分类任务模型文件较大(与深度模型相比)。
TF-IDF
tf-idf经常被用于提取文章的的关键词(Aoutomatic Keyphrase extraction),完全不加任何的人工干预,就可以达到很好的效果,普通人10分钟就可以理解,那我们首先来介绍下TF-IDF算法。
这里有对tf-idf的特别好的解释说明:tf-idf与余弦相似性的应用(一):自动提取关键词
这里我们根据具体的应用场景转换下,在电商的大规模短文本分类任务的场景中,通常会超过5000个品类(标签),而每个标签下的标题训练数据通常会超过1w条(而且存在严重的样本不均衡问题,tf-idf可以有效的解决样本不均衡的问题),上边tf-idf的链接是针对文章来提取的关键词,我们可以把5000个品类想象成5000篇文章,每篇文章由1w+条数的短标题组成,通过tf-idf技术,我们就很轻松的解决了类目到关键词概率计算。
总结一下:
$tf = \frac{某个词在文章1(标签y1)中出现的次数}{文档1(标签y1)的总词数} \qquad{} idf = \log {\frac{语料中文档(标签y)总数(5000个)}{包含该词的文档(标签y)数(比如123个)+1}} \qquad{} tf-idf=tf \cdot idf$
注:IDF分母加1,避免分母为0(laplace smoothing)
$P(B|A)=\frac{P(A|B) P(B)} {P(A)}$ 贝叶斯推断
贝叶斯理论,初次给我的感觉就是简单但有些绕,再到后来,我逐渐发现看似平凡的贝叶斯公式,背后却隐藏着非常深刻的原理,接下来我将用尽可能直白的话解释下贝叶斯理论。
贝叶斯推断是一种统计学方法,用来估计统计量的某种性质,与其他的统计学推断不同,它建立在主观判断的基础上。这里可能有人会问,tf-idf就能用来做分类了,为什么还要朴素贝叶斯?是的,问得好,tf-idf确实可以进行分类,但朴素贝叶斯会有效增强准确率削弱错误率(如果你之前了解过深度学习,朴素贝叶斯起到的效果有点像softmax),朴素贝叶斯是建立在“全概率公式”的基础下的,由已知的尽可能多的事件A、B求得的P(A|B)来推断未知P(B|A),是的有点玄学的意思,敲黑板!!! 这也就决定了它和tf-idf这种统计学的概率的本质区别。
贝叶斯定理:要理解贝叶斯推断,首先要知道贝叶斯定理。后者实际上是计算“条件概率”的公式。
所谓“条件概率”(Conditional probability),就是指事件B发生的情况下,事件A发生的概率,用P(A|B)来表示,嗯,没错就是上图那个公式。上学那会老师这公式都要背熟的,用的时候也都是套公式,今天我们来看一下这个公式的推理过程:
在推理之前,我们先看一个典型的例子,便于理解贝叶斯的奥妙之处。
举个例子:生病的概率
假设一种癌症,得了这个癌症的人被检测出为阳性的几率为90%,未得这种癌症的人被检测出阴性的几率为90%,而人群中得这种癌症的几率为1%,一个人被检测出阳性,问这个人得癌症的几率为多少?
猛地一看,被检出阳性,而且得癌症的话阳性的概率为90%,那想必这个人应该是难以幸免了。那我们接下来就算算看。
我们用$A$表示事件“测出为阳性”,用$B_{1}$表示“得癌症”,$B_{2}$表示“未得癌症”。根据题目,我们知道如下信息:
得癌症的概率:$P(B_{1})=0.01$ 未得癌症的概率:$P(B_{2})=0.99$ 得癌症前提下被检测出为阳性的概率:$P(A|B_{1})=0.9$ 未得癌症的前提下被检测为阳性的概率:$P(A|B_{2})=0.1$
即:$P(B_{1})=0.01, P(B_{2})=0.99, P(A|B_{1})=0.9, P(A|B_{2})=0.1$
那么我们现在想得到的是已知为阳性的情况下,得癌症的几率$P(B_{1},A)$:
$P(B_{1},A) = P(B_{1}) \cdot P(A|B_{1})=0.01\times0.9=0.009$
这里的$P(B_{1},A)$表示的是联合概率,得癌症且检测出阳性的概率是人群中得癌症的概率乘上得癌症时测出是阳性的几率,是0.009.同理可得 未得癌症且检测出为阳性的概率:
$P(B_{2},A)=P(B_{2}) \cdot P(A|B_{2})=0.99\times0.1=0.099$
这个概率是什么意思呢?其实是指如果人群中有1000个人,检测出阳性并且得癌症的人有9个,检测出阳性但未得癌症的人有99个。可以看出,检测出阳性并不可怕,不得癌症的是绝大多数的,这跟我们一开始的直觉判断是不同的!可直到现在,我们并没有得到所谓的“在检测出阳性的前提下得癌症的概率”,怎么得到呢?很简单,就是看被测出为阳性的这$108(9+99)$人里,9人和99人分别占的比例就是我们要的,也就是说我们只需要添加一个归一因子就可以了。所以检测为阳性得癌症的概率$P(B_{1}|A)=\frac{0.009}{0.009+0.099}\approx0.083$(注意$B_{1}$与$A$之间的符号“ | ”代表的是条件概率) ,阳性未得癌症的概率$P(b_{2}|A)=\frac{0.099}{0.099+0.009}\approx0.917$。这里$P(B_{1}|A), P(B_{2}|A)$中间多了一竖线“|”成为条件概率,而这个概率就是贝叶斯统计中的 后验概率!而人群中患癌症与否的概率$P(B_{1}),P(B_{2})$就是先验概率!我们知道了先验概率,根据观测值(也可以称test evidence):是否为阳性,来判断得癌症的后验概率,这就是基本的贝叶斯思想。
我们现在就能得出本题的后验概率公式为:
$P(B_{i}|A)=\frac{P(B_{i}) \cdot P(A|B_{i})}{P(B_{1}) \cdot P(A|B_{1})+P(B_{2}) \cdot P(A|B_{2})}$
多分类贝叶斯公式
我们把上面例子分母中的$B_{1},B_{2}$的下标变成$i$,由二分类变为多分类,便会得到贝叶斯公式的一般形式:
$P(B_{i}|A)=\frac{P(B_{i}) \cdot P(A|B_{i})}{\sum_{i=1}^n P(B_{i}) \cdot P(A|B_{i})}$
再根据全概率公式:$\sum_{i=1}^n P(B_{i}) \cdot P(A|B_{i})=P(A)$ 于是我们就得到了上面的那张图片:
$P(B|A)=\frac{P(B|A) \cdot P(A)}{P(B)}$
/*********************************************************************************************************************
全概率公式:如果事件$B_{1},B_{2},...$ 满足
- $B_{1},B_{2}...$ 两两互斥 即$B_{i} \cap B_{j}=\varnothing, i \ne j, i,j=1,2...,且P(B_{i})>0,i=1,2,....;$
- $B_{1} \cup B_{2}...= \Omega$,则称事件组$B_{1},B_{2}...$是样本空间$\Omega$的一个划分
设$B_{1},B_{2}...$是样本空间$\Omega$的一个划分,A为任一事件,则:$P(A)=\sum_{i=1}^\infty P(B_{i})P(A|B_{i})$
********************************************************************************************************************/
到此对贝叶斯推论的解释基本完成了,接下来我们将说明下在短文本分类中的具体应用。
短文本分类应用
短文本分类中,我们将运用朴素贝叶斯理论(Naive Bayesian),同时需要引入特征条件独立假设。
给定训练数据集(X,Y),其中每个样本(短文本)x都包含n维特征,即$x=(x_{1},x_{2},x_{3},...,x_{n})$,类标记集合含有k种类别(体育、娱乐、科技...),即$y={y_{1},y_{2},y_{3},...,y_{k}}$,如果现在来了一个新样本x,它属于哪个类别的概率最大。那么问题就转化为求解$P(y_{1}|x),P(y_{2}|x),P(y_{3}|x),...P(y_{k}|x)$ 中最大的那个,即求后验概率最大的输出:$argmax_{y_{k}}P(y_{k}|x)$;那$P(y_{k}|x)$怎么求解?答案就是贝叶斯定理:
$P(y_{k}|x)=\frac{P(x|y_{k})P(y_{k})}{P(x)}$
根据全概率公式替换分母:$P(y_{k}|x)=\frac{P(x|y_{k})P(y_{k})}{\sum_{k}P(x|y_{k})P(y_{k})}$
先不管分母(分母是个定值),分子中的$P(y_{k})$是先验概率,根据训练集就可以简单地计算出来。而条件概率$P(x|y_{k})=P(x_{1},x_{2},...,x_{n}|y_{k})$它的参数规模是指数数量级别的,假设第$i$维特征$x_{i}$可取值的个数有$S_{i}$个,类别取值个数为k个,那么参数个数为:$k \prod_{i=1}^n S_{i}$这显然不可行。针对这个问题,朴素贝叶斯算法对条件概率分布作出了独立性的假设,通俗地讲就是说假设各个维度的特征$x_{1},x_{2},x_{3}...,x_{n}$相互独立,在这个假设的前提下,条件概率可以转化为:
$P(x|y_{k})=P(x_{1},x_{2},...,x_{n}|y_{k})= \prod_{i=0}^nP(x_{i}|y_{k})$ 这样参数的规模就降到$\sum_{i=1}^nS_{i}k$
以上就是针对条件概率所作出的特征条件独立性假设,至此,先验概率$P(y_{k})$和条件概率$P(x|y_{k})$的求解问题就都解决了,那么我们是不是可以求解我们所要的后验概率$P(y_{k}|x)$答案是肯定的
关于分母是由$P(A)$和全概率公式转换来的,为定值可以不管,简化得朴素贝叶斯分类器的最终表示为:
$f(x)=argmaxP(y_{k}) \prod_{i=1}^nP(x_{i}|y_{k})$
首先感谢参考文章中无私奉献的前辈们!如果此篇文章对你有帮助请点赞支持。
由于作者水平有限,欢迎指出本文中错误之处。
参考文章:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号