麻省理工线性代数_01_方程组的几何解释

配图是:Ariana Grande,2023年世界最美女人第三名。
这是麻省理工18.06课程,线性代数(Linear Algebra),讲课的是W. Gilbert Strang。
课本用的书是《Introduction to Linear Algebra》。
course web page上有大量的exercises、matlab代码、课程的syllabus。
课程的网页是web.mit.edu/18.06。
线性代数的基础问题,求解线性方程组(solve a system of linear equations)。
方程组有n个方程,n个未知数,方程数和未知数的个数是相等的。
Row picture - 行图像
一个row picture显示一个方程。
column picture - 列图像
matrix form由row和column组成。
方程组的系数矩阵(coeffieient matrix)是什么呢?
a matrix is just a rectangular array of numbers.
一个矩阵,仅仅是一个numbers的矩形、数组(阵列),所以叫做矩阵。
上面的方程组,如果用矩阵的方式表示,就是下面的样子:
在上面的方程组中,我们把\(\left[\begin{matrix}2 & -1 \\-1 & 2 \end{matrix}\right]\)叫做the matrix of coeffieient,就是系数矩阵,我们可以记作\(A\)。
我们把\(\left[ \begin{matrix} x \\ y \end{matrix} \right]\)叫做未知数向量,x和y都是未知数,我们可以记作\(X\)。
等号右边的\(\left[ \begin{matrix} 0 \\ 3 \end{matrix} \right]\),这也是一个向量,我们可以记作\(b\)。
这样上面的线性方程组就可以写成\(AX=b\)。
row picture
看这个方程组:
行图像,就是横着看这个方程组,我们将两个方程分别画图在坐标系中,就拿到了两个直线的交点。
这个交点(1, 2),就是这个方程组的解。
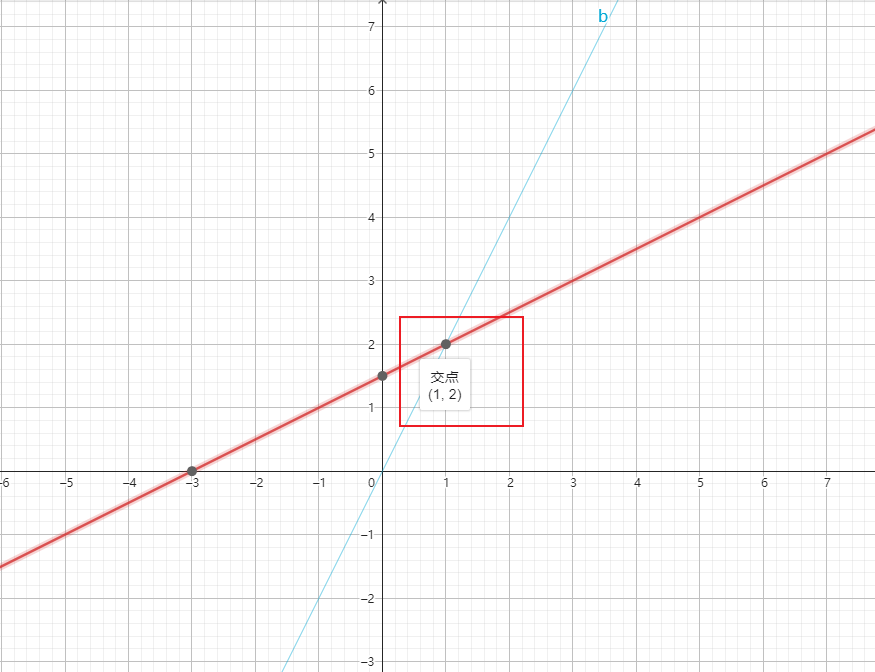
上面的图片,是使用
https://www.geogebra.org/graphing?lang=zh_CN画出来的。
column picture
我们再看这个方程组,这一次,我们竖着看。
好像一次性,看两个方程组的样子。
我们可以得到下面的式子:
上面这个方程的目的是什么?
这个方程的意思是:
怎么将\(\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right]\)这个向量和\(\left[ \begin{matrix} -1 \\ 2 \end{matrix} \right]\)这个向量正确combine组合,得到\(\left[ \begin{matrix} 0 \\ 3 \end{matrix} \right]\)这个向量(right amounts to get the vector)。
这个意思是要求我们找到正确的线性组合(linear combination)。
上面方程的左边,就是列向量的线性组合。
上面的方程组是代数形式(Algebra),那么我们怎么画图表示成几何形式呢(geometry)?
我们可以在坐标系中,将两个列向量画出来,然后再对两个列向量,作线性组合。
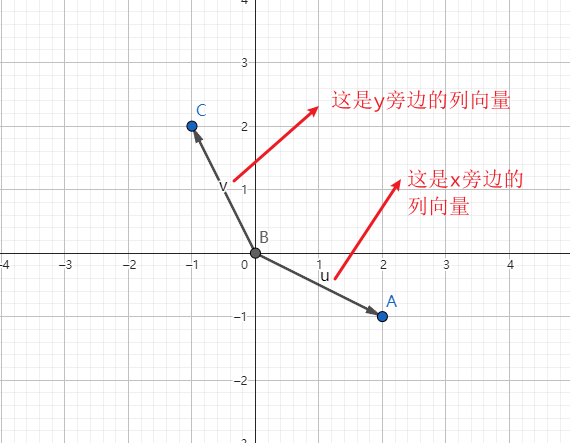
关键的一个步骤来了,我们怎么进行线性组合呢?
因为,我们已经在行图像那里求解出来了\(x=1\)和\(y=2\)这个解。
我们可以把这个解代进去,来做一下线性组合试试,代入进去就是下面的样子。
1表示1份的\(\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right]\),然后加上1份的\(\left[ \begin{matrix} -1 \\ 2 \end{matrix} \right]\),再加上1份的\(\left[ \begin{matrix} -1 \\ 2 \end{matrix} \right]\),画图就是下面的样子。
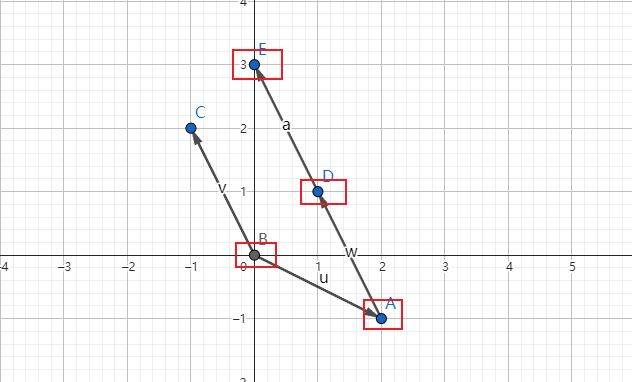
这是什么意思呢?
- 就是从原点B开始,1份的\(\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right]\)表示,向右移动2个单位(2),然后再向下移动1个单位(-1),就到了A点。
- 加上1份的\(\left[ \begin{matrix} -1 \\ 2 \end{matrix} \right]\),就是从A点开始,向左移动1个单位(-1),然后再向上移动2个单位(2),就到了D点。
- 再加上1份的\(\left[ \begin{matrix} -1 \\ 2 \end{matrix} \right]\),就是从D点开始,向左移动1个单位(-1),然后再向上移动2个单位(2),就到了E点。(如图)
这时候,我们可以看到,E点的坐标是(0, 3),写成向量的形式就是\(\left[ \begin{matrix} 0 \\ 3 \end{matrix} \right]\)。
这里有一个注意的是,一个坐标点,写成,2分量向量的形式。
这就是我们等号右边,需要线性组合出来的列向量。
思考的问题
结合上面的图、再回头看我们的公式:
看上面的式子,BC向量和BA向量,进行线性组合,\(x=1\)和\(y=2\)这种情况,我们得到了BE向量,对吧。
那么,x和y是一个代数,我们只看方程的左边,x取所有的情况,y取所有的情况,然后我们用上面的方式,进行线性组合,在等号右边,会拿到什么?
问题是:我们用所有的x,我们用所有的y,然后进行线性组合,我们会得到什么?
那么我在等号右边,能够得到任意的向量,对吗?
那么\(\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right]\)和\(\left[ \begin{matrix} -1 \\ 2 \end{matrix} \right]\)两个向量的所有线性组合,将会铺满整个坐标平面(whole plane),对吗?
两个向量怎么进行线性组合,能够得到另外的向量。
两个向量所有的线性组合,能够得到什么?
这种思想,是线性代码的基本思考方式。
三元一次方程组
下面我们要进入到three equations和three unknowns。
我们需要理解上面的方程组,然后得到这个方程组的解。
我们怎么理解这个方程组呢?
row picture是一种方式,column picture是另外一种更重要的方法。
让我们记住matrix form,因为矩阵形式是很简单的。
这是一个3×3的矩阵,有3个等式,有3个未知数。这是表示方程组左边的矩阵\(A\)。
方程组右边的向量,我们是使用\(b\)来表示的,显然应该是:
上面通过矩阵\(A\)和向量\(b\)就拿到了这个方程组的简洁形式。
然后下面我们还是开始作图:
第一步还是画row picture。
这个我们是需要在三维坐标系当中画图的。
对于上面的方程,我们先对第二个方程来思考:\(-x + 2y - z = -1\),这个方程,我们需要找到所有满足这个方程的点,然后将这些点画在一个三维坐标系当中。
你们知道这些点组成了什么吗?
一个平面,a plane。
但是我不是伦勃朗,Rembrandt,1609-1669,荷兰著名画家,所以画出来这个平面是很困难的。
第2个方程式确定了一个平面,第1个方程式当然也是可以确定一个平面的。
这两个平面相交的话,就是确定了一个线。
第3个方程式也是确定了一个平面。
这三个方程式最终是确定了一个点。
我不知道这个点在哪里,但是linear algebra可以找到它。
这里的核心点是,这三个平面是不平行的,也不特殊的。它们是相交的,它们相交在一个点上,这个点就是这个方程组的解。
row picture在两元一次方程组的时候,比较容易看到的,两条直线相交到了一个点上。
row picture在三元一次方程组的时候,比较不容易看到的,三个平面相交到了一个点上。
如果变成了四维空间,那TMD就更不直观了,更难看到了。
所以,同志们,我们不用row picture了,放弃了,不用了。
其实,我是更加倾向于column picture的。
如果我们把方程组变成这个形式,我们在左边得到了什么呢?
一个线性组合,a linear combination。
这是三个向量vectors的线性组合(linear combination)。
每个vector都是有3个dimensional。
我们需要知道怎么组合三个向量可以得到右边的玩意。
下面,我就要开始画列图像了。
第一个向量是(2, -1, 0),第二个向量是(-1, 2, 3),第三个向量是(0, -1, 4)。
跟向量有关的概念,分量component,维度dimensional。
这个方程组要求我做的是,需要将这三个向量进行线性组合,拿到右边的向量。
这个例题是很特殊的,因为这个例题是我设计的,是我挑选的。
你需要拿到的右边的向量是(0, -1, 4)。
这正好就是第三个向量,所以x=0、y=0、z=1。
我设计了这个题目,是为了能够方便找到这个方程组的解(0, 0, 1)。
下一讲当中,我们要讲解到elimination,就是消元法。
elimination是求解的系统方法,the systematic way。
所有人、或者、复杂的软件,都是通过这种方法来求解方程组的。
我们回过头来看这个图,我们保持等号左边的矩阵不变,然后考虑不同的右侧向量:
假设我们变化了右边的向量,变成了下面的样子:
右边的向量当然也是一个非常特殊的向量,是x对应向量和y对应向量的求和。这个时候,方程的解就是(1, 1, 0)。
我们把等号右边的向量叫做b,现在我们考虑一下所有b向量可能的情况。
是不是,不管b向量是什么,我们都是可以求解这个方程组的呢?
我们这么思考,就转换成为了一个代数问题:对于任意的b,我是不是都可以求解Ax = b?
如果有解的话,那么消元法就可以求解出来的。
下面,我再一次用线性组合的语言,来问一下这个问题:是否上述三个列向量所有线性组合可以铺满整个三维空间呢?
任意的b,就是三维空间当中的所有b。
上面的两个问法,其实表达的是一个意思。
\(Ax=b\)这个是什么呢?这个是我用一个矩阵乘以一个向量。
对于上面我举例的这个matrix,这个矩阵,答案是:是的。
因为这个matrix是一个non-singular matrix,是一个invertible matrix。
这是一个非奇异矩阵,这是一个可逆矩阵。
这种矩阵是我们最喜欢的矩阵。
但是对于另外的一些矩阵,答案就可能是:不是。
这个也是很容易想象和理解的,什么时候三个列向量不能够通过线性组合得到向量\(b\)呢?
如果这三个列向量处于同一个平面上,那么他们的线性组合肯定也是在这个平面上的喔,这种情况下答案就是否定的啦。
这种情况下如果\(b\)也是在这个平面中,当然,你就是可以有一个解的。
如果不在这个平面,你就求解不出来了。
这种情况下的矩阵就是奇异的singular matrix,这个矩阵就是不可逆的not invertible。
下面我们可以尝试考虑一下九个维度的情况。
nine dimensions。
假设我们有vectors具有9个components,这很难有具体的概念,我承认。
假设我们有9个方程,有9个未知数。
那么我们的方程组的每一列都是九维空间的向量。
然后,我们就可以在9维空间当中,对9个向量进行线性组合了。
然后我们通过线性组合,得到了正确的等号右边的向量\(b\)。
然后,我们还是会问这个问题,是否所有的9维向量b都是有解的呢?
当然了,这个问题,还是取决于这9个列向量的。
有的时候答案是yes,有的时候答案是no。
如果在matlab当中使用随机命令,任意选取一个9×9的随机矩阵,答案就是yes的。
这个随机矩阵就是非奇异的、可逆的,是具备一切美好矩阵的品质。
如果选取一些、相互不独立的列向量,比如九个列向量实际上只相当于8个列向量的时候,有1个列向量是没有什么实际贡献的,那么这种情况下,就会有一些向量b是没有办法求解到的。
比如第9个列向量等于第8个列向量,那么这些向量的所有线性组合最后的结果,就是某个8维的空间。
方程组的矩阵形式:
这其中\(A\)是一个矩阵,\(x\)是一个向量,\(b\)是一个向量。
这是一种乘法运算multiplication。
下面讲解,如何使用一个矩阵,乘以,一个向量。
首先,我们构造一个矩阵:
然后,我们构造一个向量:
我们如何将一个矩阵和一个向量相乘呢,其实是有两种方法的。
我们先讲解第一种方法,column方法。
下面我们讲解另外的一种解法,就是row方法,这种方法其实就是点乘。
但是,我还是倾向于colume方法。
我习惯于将一个矩阵和一个向量的乘法,看成是列的线性组合。
A times x is a combination of the columns of A.
我也希望各位用这种方法来考虑矩阵A和向量x的乘法计算。
现在我们的向量数量很少,我们可以使用column方法或者row方法,但是以后数据量变大的时候,我们最好是使用column方法。
下一节,我们将会讲解消元法,这是一种求解方程组的通用方法。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号