浅谈点分治

非常有趣的一个知识点。

所谓点分治，也就是在树上进行分治的操作。

分治可以处理许多问题，各种区间类问题很多都可以利用分治思想，例如线段树就是利用分治处理许多区间性问题。

而目前处理树上区间问题学过的只有树剖，但树剖的缺陷性其实很大，当你需要对子树进行合并操作时，树剖会有很大的局限性，因为只有当整棵树有根时，树剖的节点才会有一定的有序性，而在树无根的情况下，就不好进行操作。

所以我们引入了一个新算法，点分治（淀粉质）。

点分治的基础思想基于分治，找到一个节点，使这个节点分开的子树的节点最大的尽量小。

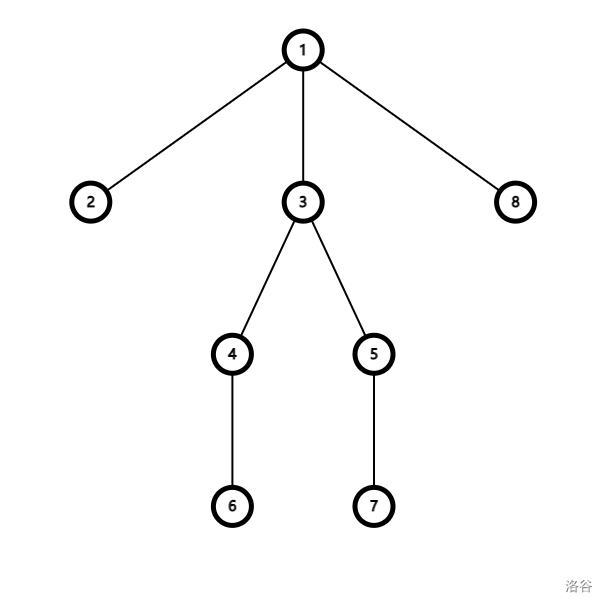
如图中，\(1\) 节点会把子树分成 \(\left\{2\right\},\left\{8\right\},\left\{3,4,5,6,7\right\}\)，子树大小为 \(1,1,5\)，那么分开最大的子树为 \(5\)。

而 \(3\) 节点会把树分成 \(\left\{1,2,4\right\},\left\{4,6\right\},\left\{5,7\right\}\)，子树大小为 \(3,2,2\)，最大的为 \(3\)，比节点 \(1\) 更小，可以证明，途中节点 \(3\) 得到的是最小的。

像节点 \(3\) 这种，把树分成若干的子树的点并使最大的子树最小的点称作树的重心，也就是我们在求解中需要寻求的点。

而由于分治不是只进行一次，所以我们对剩下来的子树继续分裂，下一次三个子树得到的重心为 \(1,4,5\)。（\(4\) 与 \(6\) 效果相同，随机取一个皆可，\(5\) 和 \(7\) 同理）

分治分为两种操作，那就是分裂与合并，所以根据题目的实际情况进行分割即可。

首先我们先看下代码。

void divide(int x,int num)//x 为目前的重心，num 有关找重心操作。
{
	vis[x]=1;
	for(int i=h[x];i!=0;i=b[i].next)
	{
		int v=b[i].to;
		if(vis[v])continue;
		root=0;//即寻找的重心。
        
     		//以下操作有关找重心。
		if(siz[v]>siz[x])tot=num-siz[x];
		else tot=siz[v];
		findzx(v,x);
     		//end
            
		divide(root,tot);
	}
}

那现在我们要做的就是找重心的操作了。

我们设 \(mp_i\) 为分裂 \(i\) 所得到最大的子树大小，\(siz_i\) 为以 \(i\) 为子树的大小。

设 \(i\) 的儿子节点为 \(j\)，树中总结点为 \(tot\)，那么：

\(mp_i=\max(mp_j,tot-siz_i)\)

寻找最小的 \(mp_i\) 即可。

void findzx(int x,int fa)
{
	siz[x]=1;
	mp[x]=0;
	for(int i=h[x];i!=0;i=b[i].next)
	{
		int v=b[i].to;
		if(vis[v]||v==fa)continue;
		findzx(v,x);
		siz[x]+=siz[v];
		mp[x]=max(mp[x],siz[v]);
	}
	mp[x]=max(mp[x],tot-siz[x]);
	if(mp[x]<mp[root])root=x;
}

以上就是点分治的所有理论知识了。

点分治难点不在理论，而是应用，接下来我们会讲解一些例题。

P3806 【模板】点分治1

这题是名牌点分治，所以我们从点分治考虑此问题。

由于它要求是否存在一条路径长度为 \(k\)，那我们可以想到，在一个点分裂以后，合并上来时将自己所有的子树做一个 \(01\) 背包。

详解一下。

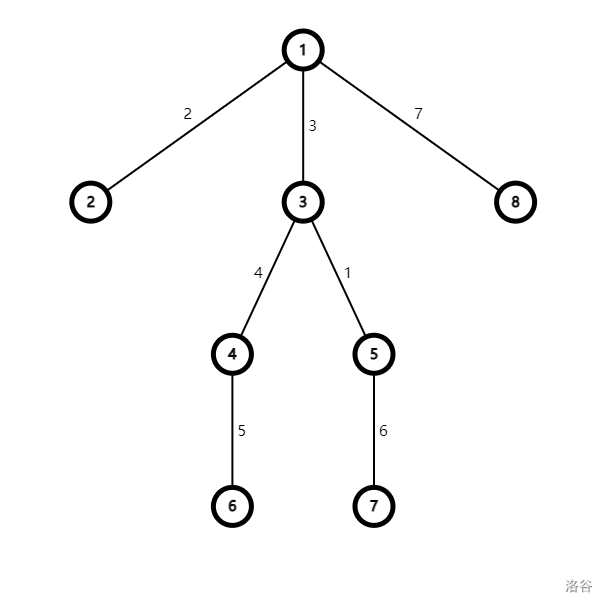
假设现在我们需要将 \(3\) 节点的所有子树进行合并。

那么看到 \(\left\{1,2,8\right\}\) 这棵子树，可以看到它包括的路径有 \(\left\{1,2\right\},\left\{1,3\right\},\left\{1,8\right\},\left\{2,1,8\right\},\left\{2,1,3\right\},\left\{3,1,8\right\}\)。

但是能路径 \(\left\{1,2\right\},\left\{1,8\right\},\left\{2,1,8\right\}\) 是无法与节点 \(3\) 合并的，肉眼可证，或说它们都与节点 \(3\) 无关，所以我们需要找到与节点 \(3\) 有关的点即可，这个好弄，只需要从节点 \(3\) 开始搜这棵子树，记录深度即可。

那么我们记录出来三棵子树合法的边长有 \(\left\{3,5,10\right\},\left\{4,9\right\},\left\{1,7\right\}\)。

要知道它们可以拼凑出来的长度，就是一个典型的 \(01\) 背包问题。

这是个好方法，但如果用传统 \(01\) 背包会 T。

我们需要对这个方法进行优化。

其实方法也很简单，因为数组间空隙很大，利用一个数组记录有哪些边长存在，而不是记录每个边长的是否存在即可。

程序中 \(judge_i\) 代表在分裂这个点时路径长 \(i\) 是否存在，\(tmp\) 记录的是搜索下去的路径长度，\(q\) 用来方便清数组。

复杂度：\(O(n\times\log(n))\)。

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
const int N=1e4+5;
const int M=105;
const int T=1e7+5;
struct node
{
	int to,data;
};
vector<node>a[N];
int n,m,t[M],root,num=1e9,vis[N],siz[N],mp[N],tot,dis[N],judge[T],tmp[N],cnt,q[N],ans[N];
void dfs(int x,int fa)
{
	int len=a[x].size();
	siz[x]=1;
	mp[x]=0;
	for(int i=0;i<len;i++)
	{
		if(vis[a[x][i].to]||a[x][i].to==fa)continue;
		dfs(a[x][i].to,x);
		siz[x]+=siz[a[x][i].to];
		mp[x]=max(mp[x],siz[a[x][i].to]);
	}
	mp[x]=max(mp[x],tot-siz[x]);
	if(mp[x]<mp[root])root=x;
}
void get_dis(int x,int fa,int num)
{
	if(num>1e7)return;
	tmp[++cnt]=num;
	int len=a[x].size();
	for(int i=0;i<len;i++)
	{
		if(a[x][i].to==fa||vis[a[x][i].to])continue;
		get_dis(a[x][i].to,x,num+a[x][i].data);
	}
}
void clac(int x)
{
	int len=a[x].size();
	int cnp=0;
	for(int i=0;i<len;i++)
	{
		if(vis[a[x][i].to])continue;
		cnt=0;
		dis[a[x][i].to]=a[x][i].data;
		get_dis(a[x][i].to,x,a[x][i].data);
		for(int j=1;j<=cnt;j++)for(int k=1;k<=m;k++)if(t[k]>=tmp[j])ans[k]|=judge[t[k]-tmp[j]];
		for(int j=1;j<=cnt;j++)q[++cnp]=tmp[j],judge[tmp[j]]=1;
	}
	for(int i=1;i<=cnp;i++)judge[q[i]]=0;
}
void solve(int x)
{
	vis[x]=1;
	clac(x);
	int len=a[x].size();
	for(int i=0;i<len;i++)
	{
		if(vis[a[x][i].to])continue;
		tot=siz[a[x][i].to];
		root=0;
		dfs(a[x][i].to,0);
		solve(root);
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<n;i++)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		a[u].push_back({v,w});
		a[v].push_back({u,w});
	}
	for(int i=1;i<=m;i++)scanf("%d",&t[i]);
	tot=n;
	root=0;
	mp[0]=1e9;
	judge[0]=1;
	dfs(1,0);
	solve(root);
	for(int i=1;i<=m;i++)
	{
		if(ans[i])puts("AYE");
		else puts("NAY");
	}
	return 0;
}

但是点分治也存在缺陷性，它很难去维护带修改的操作，每次修改的复杂度高达 \(O(n\times\log(n))\)，所以我们又引入了一个知识——点分树。

点分树是点分治中分裂的点对分裂的子树的重心建起边的一棵树。

还是此图：

那么建的点分树即为：

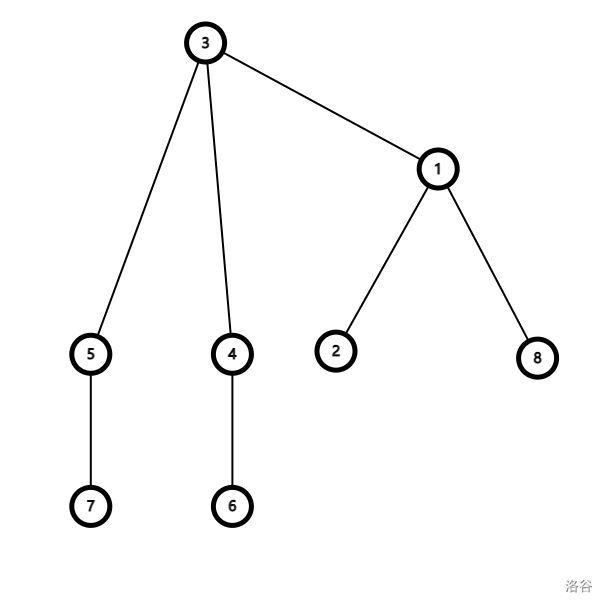
这棵树的性质极多，如在原图中 \(t\) 为 \((u,v)\) 的 \(\text{LCA}\) ，在新图中 \(t\) 在 \((u,v)\) 上。

但最重要的是，新的树深度接近于 \(\log(n)\)，所以许多乱搞的方法就可以实施了。

例题：P6329 【模板】点分树 | 震波

这题提示我们使用点分树，那就用吧。

首先先建一棵点分树。

然后看一下我们需要的操作，再在点分树上进行操作。

第一个，我们需要查询 \(k\) 以内的所有的点的权值和，这个我们可以想到利用数据结构维护。

对于点分树上的每一个点，建一棵线段树，统计其他的点与他的距离。

这个复杂度我们肯定是承受不下的，所以得想办法利用点分树的性质去优化。

我们考虑维护在点分树内任意点 \(x\) 所构成的子树中的所有点与 \(x\) 的距离为下标集合建立一棵线段树。

这个复杂度感觉上还是承受不下，但实际上是没有问题的，因为点分树最大的深度为 \(\log(n)\)，所有操作数量级别为 \(n\times\log(n)\)，而一个操作是 \(O(\log(n))\) 的，所以复杂度为 \(O(n\times\log_2^2(n))\)。

那么每次查询，从这个点 \(x\) 开始，向上搜索，对于每一个祖先节点 \(cur\)，需要查询的是 \(k-dis(x,cur)\) 距离以内的和，用线段树统计。

还有个问题，就是对于每一次统计，都会重复统计一些点，所以要进行排重。

一般的想法就是对那条路上的第一个子节点减去 \(k-dis(x,cur)-1\) 的值，但是这个想法是错的，因为点分树上的两点距离与实际的两点距离不一样。而如果你减去 \(k-dis(x,cur)-dis(cur,son)\) 也是不行的，那是在原图因为距离与 \(son\) 为 \(k-dis(x,cur)-dis(cur,son)\)，不代表与 \(cur\) 的距离为 \(k-dis(x,cur)-1\)。

那怎么办呢，实际上也很好弄，再维护一个线段树，下标代表以自己为线段树的节点与父亲的距离。

那么去重时只需去掉第二棵线段树以 \(son\) 为根的从 \(1\) 到 \(k-dis(x,cur)\) 即可。

两棵线段树的下标权值皆为节点的 \(value\) 值。

复杂度：\(O(n\times\log_2^2(n))\)。

这题得使用树剖求 \(\text{LCA}\)，否则会 T（也可能我是大常数选手……）。

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
const int N=2e5+5;
int f[N],n,m,dep[N],tot,root,siz[N],mp[N],vis[N],a[N],t[N],k,nl,nr,h[N],son[N],topp[N];
struct node2
{
	int from,to,next;
}b[N];
struct segmentree
{
	int rt[N],cnt;
	struct node
	{
		int ls,rs,data,cnt;
	}f[N*50];
	void update(int &x,int l,int r)
	{
		if(!x)x=++cnt;
		if(l==r)
		{
			f[x].data+=k;
			return;
		}
		int mid=(l+r)>>1;
		if(mid>=nl)update(f[x].ls,l,mid);
		else update(f[x].rs,mid+1,r);
		f[x].data=f[f[x].ls].data+f[f[x].rs].data;
	}
	int search(int x,int l,int r)
	{
		if(!x)return 0;
		if(l>=nl&&r<=nr)return f[x].data;
		int mid=(l+r)>>1,num=0;
		if(mid>=nl)num+=search(f[x].ls,l,mid);
		if(mid<nr)num+=search(f[x].rs,mid+1,r);
		return num;
	}
}t1,t2;
int dfs(int x,int fa)
{
	dep[x]=dep[fa]+1;
	f[x]=fa;
	int sum=1,maxn=-1;
	for(int i=h[x];i!=0;i=b[i].next)
	{
		int v=b[i].to;
		if(fa==v)continue;
		int num=dfs(v,x);
		if(num>maxn)maxn=num,son[x]=v;
		sum+=num;
	}
	return sum;
}
void dfs2(int x,int tp)
{
	topp[x]=tp;
	if(son[x])dfs2(son[x],tp);
	for(int i=h[x];i!=0;i=b[i].next)
	{
		int v=b[i].to;
		if(v==f[x]||v==son[x])continue;
		dfs2(v,v);
	}
}
int lca(int x,int y)
{
	while(topp[x]!=topp[y])
	{
		if(dep[topp[x]]<dep[topp[y]])swap(x,y);
		x=f[topp[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	return x;
}
void findzx(int x,int fa)
{
	siz[x]=1;
	mp[x]=0;
	for(int i=h[x];i!=0;i=b[i].next)
	{
		int v=b[i].to;
		if(vis[v]||v==fa)continue;
		findzx(v,x);
		siz[x]+=siz[v];
		mp[x]=max(mp[x],siz[v]);
	}
	mp[x]=max(mp[x],tot-siz[x]);
	if(mp[x]<mp[root])root=x;
}
void divide(int x,int num)
{
	vis[x]=1;
	for(int i=h[x];i!=0;i=b[i].next)
	{
		int v=b[i].to;
		if(vis[v])continue;
		root=0;
		if(siz[v]>siz[x])tot=num-siz[x];
		else tot=siz[v];
		findzx(v,x);
		a[root]=x;
		divide(root,tot);
	}
}
void ins(int x)
{
	int cur=x;
	while(cur)
	{
		if(a[cur])
		{
			nl=dep[a[cur]]+dep[x]-dep[lca(x,a[cur])]*2;
			t2.update(t2.rt[cur],0,n-1);
		}
		nl=dep[x]+dep[cur]-dep[lca(x,cur)]*2;
		t1.update(t1.rt[cur],0,n-1);
		cur=a[cur];
	}
}
int solve(int x,int kt)
{
	int cur=x,bef=0,res=0;
	while(cur)
	{
		int LCA=lca(x,cur);
		if(kt-(dep[cur]+dep[x]-2*dep[LCA])<0)
		{
			bef=cur,cur=a[cur];
			continue;
		}
		nl=0,nr=kt-(dep[cur]+dep[x]-2*dep[LCA]);
		res+=t1.search(t1.rt[cur],0,n-1);
		if(bef)nl=0,nr=kt-(dep[cur]+dep[x]-2*dep[LCA]),res-=t2.search(t2.rt[bef],0,n-1);
		bef=cur;
		cur=a[cur];
	}
	return res;
}
int read()
{
	char ch=getchar();
	int sum=0,f=1;
	while(ch<'0'||ch>'9')
	{
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		sum=(sum<<1)+(sum<<3)+(ch^48);
		ch=getchar();
	}
	return sum*f;
}
void write(int x)
{
	if(x<0)
	{
		putchar('-');
		x=-x;
	}
	if(x/10)write(x/10);
	putchar((x%10)^48);
}
int main()
{
	//freopen("P6329_1.in","r",stdin);
	//freopen("a.out","w",stdout);
	n=read(),m=read();
	for(int i=1;i<=n;i++)t[i]=read();
	int cmt=0;
	for(int i=1;i<n;i++)
	{
		int u,v;
		u=read();
		v=read();
		b[++cmt].from=u;
		b[cmt].to=v;
		b[cmt].next=h[u];
		h[u]=cmt;
		b[++cmt].from=v;
		b[cmt].to=u;
		b[cmt].next=h[v];
		h[v]=cmt;
	}
	dfs(1,0);
	dfs2(1,1);
	root=0;
	mp[0]=1e9;
	tot=n;
	findzx(1,0);
	divide(root,n);
	for(int i=1;i<=n;i++)k=t[i],ins(i);
	int bef=0;
	for(int i=1;i<=m;i++)
	{
		int opt,x,y;
		opt=read(),x=read(),y=read();
		x^=bef,y^=bef;
		if(opt==0)
		{
			y=min(y,n-1);
			int ans=solve(x,y);
			write(ans);
			putchar('\n');
			bef=ans;
		}
		if(opt==1)k=y-t[x],ins(x),t[x]=y;
	}
	return 0;
}

练习题（别指望我能做多少）：

P2634 [国家集训队]聪聪可可（比点分治板子还简单……）

P2664 树上游戏（练习题）

P3714 [BJOI2017]树的难题（上面的升级版）

P4149 [IOI2011]Race（变式板子）

P3241 [HNOI2015]开店（点分树）

P4075 [SDOI2016]模式字符串（非人做的点分治）

P4183 [USACO18JAN]Cow at Large P（好像不是很难）

P4292 [WC2010]重建计划（非人做的点分树）

P5306 [COCI2018-2019#5] Transport（不怎么难的点分治，练习题）

P2056 [ZJOI2007] 捉迷藏（目测一般的点分树）

P3345 [ZJOI2015]幻想乡战略游戏（目测一般点分树？）