树链剖分（萌新用，复习用）

树链剖分是将一棵树剖分成一条一条链，从而将树上问题转换为序列问题的操作，最常见的是轻重链剖分，这里也注重讲轻重链剖分。

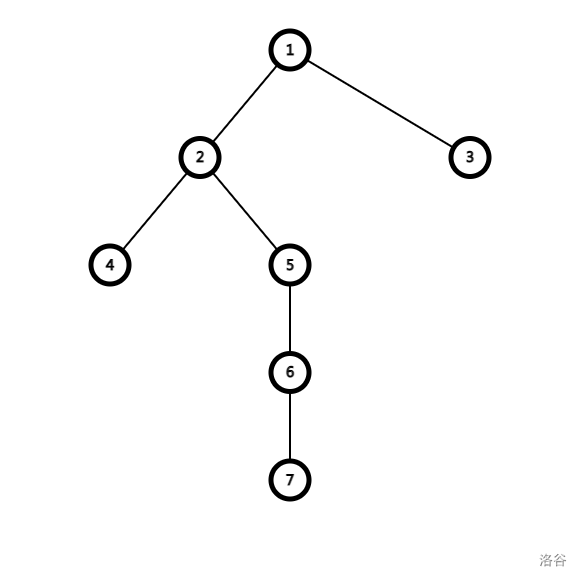
第一步：找重儿子。

对于这棵树，我们想让这棵树被剖分成一棵序列，那么就要先找到每个节点的重儿子。重儿子的定义是以儿子为根的子树大小是所有儿子中最大的。

如本图，\(4\) 为 \(2\) 的儿子，子树大小为 \(1\)，\(5\) 为 \(2\) 的儿子，子树大小为 \(3\)。所以 \(5\) 为 \(2\) 的重儿子。

用搜索遍历树，再回溯上来，进行比较即可。

int dfs1(int x,int fath)
{
	siz[x]=1;
	int len=a[x].size(),maxn=0;
	for(int i=0;i<len;i++)
	{
		if(a[x][i]==fath)continue;
		int num=dfs1(a[x][i],x);
		if(num>maxn)maxn=num,son[x]=a[x][i];
		siz[x]+=num;
	}
	return siz[x];
}

这样子的话，父亲节点与重儿子所连接的边为重边，图中 \((1,2),(2,5),(5,6),(6,7)\) 皆为重边。

重边收尾连接即为重链，图中 \((1,7)\) 即为重链。当然树上重链可以不止一条。而图中 \((2,4),(1,3)\) 为轻链。

注：首位相连的轻边不是轻链，单独的轻边才叫轻链。

第二步：找到自己所处的重链的顶端。

如图中 \(6\) 处于重链 \((1,7)\) 上，所以 \(6\) 所处链的顶端为 \(1\)。

又如 \(2\) 在重链 \((1,7)\) 与轻链 \((2,4)\) 上，那么这种情况把 \(2\) 优先看做在重链上，所以顶端为 \(1\)。

若一个节点在轻链上，那么它的顶端是它自己，如 \(4\) 的顶端是 \(4\)。

代码实现：搜索遍历，先搜重儿子，然后重儿子的顶端为父亲节点所处的顶端，将参数往下带，再搜轻儿子，改变顶端为它自己，搜下去即可。

void dfs2(int x,int tp)
{
	topp[x]=tp;
	if(son[x])dfs2(son[x],tp);
	int len=a[x].size();
	for(int i=0;i<len;i++)
	{
		if(a[x][i]==fa[x]||a[x][i]==son[x])continue;
		dfs2(a[x][i],a[x][i]);
	}
}

到此轻重链剖分的所有已经结束了，现在将轻重链剖分的应用。

1、LCA

可以证明一个点到根节点的重链个数小于等于 \(\log(n)\)。

证明：因为每分开一个重链，那么就必须有另一棵子树的大小大于等于这棵树，模拟下发现是棵完全树，所以最小为 \(\log(n)\)。

所以每一次对于两个节点，将自己对应顶部的节点所处深度大的往上跳，跳到自己顶部的父亲节点。直到两个节点所处一个重链，即顶部相同，那么此时深度小的那个点即是两点的 LCA。

int LCA(int x,int y)
{
	while(topp[x]!=topp[y])
	{
		if(dep[topp[x]]<dep[topp[y]])swap(x,y);
		x=fa[topp[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	return x;
}

2、数据结构。

常见为线段树。

在找重链时加上时间戳，代表在线段树中的节点编号。

void dfs2(int x,int tp)
{
	topp[x]=tp;
	id[x]=++cnt;
	if(son[x])dfs2(son[x],tp);
	int len=a[x].size();
	for(int i=0;i<len;i++)
	{
		if(a[x][i]==fa[x]||a[x][i]==son[x])continue;
		dfs2(a[x][i],a[x][i]);
	}
}

操作1：对 \(x\) 的子树操作，即为对编号 \(x\) 到编号 \(x+siz_x-1\) 进行区间操作。\(siz_x\) 代表以 \(x\) 为根的子树大小。

操作2：对 \(x\) 到 \(y\) 的路径操作，找到 \(x\) 与 \(y\) 的 LCA，在搜 LCA 时对每一条重链进行 \(top_x\) 到 \(x\) 的区间操作，最后再对 \(x\) 到 \(y\) 的区间操作。

注：以上操作都是树上节点对应的线段树编号进行操作。

void update_tree(int x)//对整棵子树加上一个值
{
	nl=id[x],nr=id[x]+siz[x]-1;
	update(1,1,n);
}
int search_road(int x,int y)//查询一条路径上的值
{
	int sum=0;
	while(topp[x]!=topp[y])
	{
		if(dep[topp[x]]<dep[topp[y]])swap(x,y);
		nl=id[topp[x]],nr=id[x];
		sum+=search(1,1,n);
		x=fa[topp[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	nl=id[x],nr=id[y];
	sum+=search(1,1,n);
	return sum;
}

基本上所有树剖的基础操作就到这了，总体来说思路挺简单的，就是代码有亿点复杂。

练习题：

P3384 【模板】轻重链剖分/树链剖分（模板题）

P3313 [SDOI2014]旅行（较简单的变式题）

P2590 [ZJOI2008]树的统计（练习题）

P1505 [国家集训队]旅游（练习题）

P2486 [SDOI2011]染色（较简单的变式题）

P3258 松鼠的新家（练习题）

P4069 [SDOI2016]游戏（合李超线段树）

P4211 [LNOI2014]LCA（树剖求区间 LCA，较难想到）

P4592 [TJOI2018]异或（树剖+可持久化01trie）

P5305 [GXOI/GZOI2019]旧词（会了 P4211 不算特别难）