【矩阵乘法&快速乘模板】【题解】【刷题比赛】
【矩阵乘法&快速乘模板】【题解】【刷题比赛】
P1707 刷题比赛
Solution:
很明显是一道矩阵乘法加速递推,只是推转移矩阵比较复杂。
做这种题的思路是:
- 如果递推为线性递推,且暴力递推次数很多,可以考虑矩阵优化
- 先根据要计算的信息,列出一个行数为1的状态矩阵,设为\(F_n\)。
- 再仿照\(F_n\)写出\(F_{n+1}\)。
- 再对\(F_{n+1}\)的每一项分别考虑,看这一项由\(Fn\)的哪些项乘上相应的系数转移而来,构造出转移矩阵\(A\)
- 写出\(F_1\),则\(F_n=F_1*A^{n-1}\),用矩阵快速幂的模板计算即可
另外,本题在做乘法时有可能爆long long,需要用快速乘或龟速乘来避免
龟速乘
与快速幂的思路十分类似。若要计算\(x*y\),设\(y=a_0*2^0+a_1*2^1+\cdots +a_n*2^n\)
那么由乘法分配律得,
\(
\begin{aligned}
x*y&=x*2^0*a_0+x*2^1*a_1+\cdots +x*2^n*a_n\\
&=x*2^0[a_0=1]+x*2^1[a_1=1]+\cdots +x*2^n[a_n=1] \end{aligned}
\)
那么看代码就很容易了
#define int long long
int fmul(int x,int y,int mod)
{
int res=0;
while(y)
{
if(y&1) res+=x,res%=mod;
y>>=1;
x<<=1;
x%=mod;
}
return res;
}
快速乘
龟速乘的复杂度是带个log的,因而出现了O(1)的快速乘。
其原理跟long double的精度有关,在此不做讨论,只给出代码。
#define int long long
int fmul(int x,int y,int mod)
{
unsigned int res=
(unsigned int)x*y-
(unsigned int)((long double)x/mod*y+0.5L)*mod;
return (res+mod)%mod;
}
最后给出本题代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
register int x=0,w=1;
register char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
if(ch=='-') {ch=getchar();w=-1;}
while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*w;
}
inline void write(int x)
{
if(x<0) {putchar('-');x=~(x-1);}
if(x>9) write(x/10);
putchar('0'+x%10);
}
const int N=11;
int n,mod;
int fmul(int x,int y,int mod)
{
unsigned int res=
(unsigned int)x*y-
(unsigned int)((long double)x/mod*y+0.5L)*mod;
return (res+mod)%mod;
}
//int fmul(int x,int y,int mod)
//{
// int res=0;
// while(y)
// {
// if(y&1) res+=x,res%=mod;
// y>>=1;
// x<<=1;
// x%=mod;
// }
// return res;
//}
struct Mat{
int a[N][N];
Mat(){
memset(a,0,sizeof a);
}
Mat operator*(const Mat &x)const{
Mat res;
for(int i=0;i<N;++i)
for(int j=0;j<N;++j)
for(int k=0;k<N;++k)
res.a[i][j]+=fmul(a[i][k],x.a[k][j],mod),res.a[i][j]%=mod;
return res;
}
}f,A;
Mat fpow(Mat x,int y)
{
Mat res=x;y--;
while(y)
{
if(y&1) res=res*x;
y>>=1;
x=x*x;
}
return res;
}
signed main()
{
int p,q,r,t,u,v,w,x,y,z;
n=read();mod=read();
cin>>p>>q>>r>>t>>u>>v>>w>>x>>y>>z;
f.a[0][0]=f.a[0][1]=f.a[0][2]=f.a[0][8]=f.a[0][9]=f.a[0][10]=1;
f.a[0][3]=f.a[0][4]=f.a[0][5]=3;
f.a[0][6]=w;f.a[0][7]=z;
A.a[0][3]=q;
A.a[1][4]=v;
A.a[2][5]=y;
A.a[3][0]=1;A.a[3][3]=p;A.a[3][4]=A.a[3][5]=1;
A.a[4][1]=A.a[4][3]=A.a[4][5]=1;A.a[4][4]=u;
A.a[5][2]=A.a[5][3]=A.a[5][4]=1;A.a[5][5]=x;
A.a[6][4]=1;A.a[6][6]=w;
A.a[7][5]=1;A.a[7][7]=z;
A.a[8][3]=r;A.a[8][8]=1;
A.a[9][3]=t;A.a[9][5]=A.a[9][9]=1;A.a[9][8]=2;
A.a[10][3]=A.a[10][8]=A.a[10][9]=A.a[10][10]=1;A.a[10][5]=2;
f=f*fpow(A,n-1);
printf("nodgd %lld\nCiocio %lld\nNicole %lld", f.a[0][0], f.a[0][1], f.a[0][2]);
return 0;
}
矩阵乘法的另外一种实现形式:在结构体中记录矩阵的n,m,可以减少全部当成方阵计算的常数。
Code
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
register int x=0,w=1;
register char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
if(ch=='-'){ch=getchar();w=-1;}
while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*w;
}
inline void write(int x)
{
if(x<0){putchar('-');x=~(x-1);}
if(x>9) write(x/10);
putchar(x%10+'0');
}
const int N=105,mod=2017;
int n,m;
vector<int>v[N];
struct node{
int n,m,a[N][N];
node(){memset(a,0,sizeof a);n=0,m=0;}
node operator*(const node &x)const
{
node res;
res.n=n,res.m=x.m;
for(int i=0;i<res.n;++i)
for(int j=0;j<res.m;++j)
for(int k=0;k<m;++k)
res.a[i][j]+=a[i][k]*x.a[k][j]%mod,res.a[i][j]%=mod;
return res;
}
}F,A;
int t;
node fpow(node x,int y)
{
node res=x;
y--;
while(y)
{
if(y&1) res=res*x;
y>>=1;
x=x*x;
}
return res;
}
int main()
{
n=read();m=read();
for(int i=1;i<=m;++i)
{
int x=read(),y=read();
v[x].push_back(y);v[y].push_back(x);
}
t=read();
F.n=1,F.m=n+1;
F.a[0][0]=1;
A.n=A.m=n+1;
for(int j=0;j<n;++j)
{
for(int i=0;i<v[j+1].size();++i)
{
int y=v[j+1][i];
A.a[y-1][j]=1;
}
A.a[j][j]=1;
}
for(int i=0;i<=n;++i) A.a[i][n]=1;
int ans=0;
node res=F*fpow(A,t);
for(int i=0;i<=n;++i) ans+=res.a[0][i],ans%=mod;
write(ans);
return 0;
}
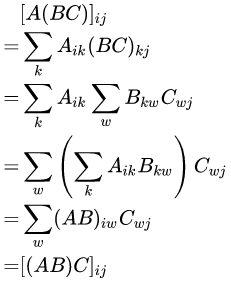
注意到矩阵乘法具有结合律的本质是:数乘对数加是具有分配律的,且加法满足交换律。
因此可以推出更广义的矩阵乘法:若\(\otimes\)对\(\oplus\)具有分配律,且\(\oplus\)满足交换律,\(A\times B(i,j)=(A(i,1)\otimes B(1,j))\oplus \cdots \oplus (A(i,k)\otimes B(k,j))\),则该矩阵乘法具有结合律,可用快速幂加速。
更简洁的表述:
若\(a\otimes (b\oplus c)=(a\otimes b)\oplus (a\otimes c),a\oplus b=b\oplus a\),则由\((\oplus,\otimes)\)定义的广义矩阵乘法满足结合律。其中\(\oplus\)为外层运算,\(\otimes\)为外层运算。
CF643F Bears and Juice
一道并不明显的矩乘优化dp
一般来说,矩乘优化递推的题目,对于题目中的\(q\),一般是开到\(1e9\)级别的,但这题只是\(2e6\)。还有矩乘一般是要求一个点处的值,但是这里需要对\([1,q]\)每个点的值都求出来。
如果每次暴力乘矩阵的话,复杂度跟暴力是相同的\(O(qp^2)\)。注意到复杂度中的q是无法避免的,考虑如何避免过多的矩阵乘法。
我们对\(q\)分块,设块的大小为\(B\),假设要求出点\(i\)的值,那么\(f_i=f_{i\%B}\times A^{i/B}\).
也就是先暴力求出前\(B\)个点的点值,后面的每个点都拆成一个矩阵乘一个向量的形式,但是矩阵乘上一个向量的复杂度仍然是\(p^2\),总复杂度还是\(qp^2\),但是我们实际用到的只是\(f\)向量\(p\)处的一个点值,因此只需\(O(p)\)就能求出。
复杂度为\(O(p^2B+q/B*p^3+pq)\),取\(B=\sqrt{pq}\)最优。
总结一下就是当递推式可以用矩阵优化,但是需要求多个点点值时,可以分块求出。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号