基础排序（二）

1.归并排序的简单实现思路：

       通过递归把待排序的数组不断进行二分，再通过三个索引追踪数组的方式 进行归并，逐步构建左右两边的有序环境。

       下面简单记录下代码：

package day1;

public class MergeSort {
    public static void main(String []arg){
    int []arr=ArrarHelp.randomArray(9, 123);
    int []e=new int[arr.length+1];
    MergeSort.sort(arr,0,arr.length-1,e); }
    public static void sort(int []arr,int s,int l,int []e){
        if(s<l){
            int mid=(s+l)/2;
            sort(arr,s,mid,e);
            sort(arr,mid+1,l,e);
            Msort(arr, s, l, e);
                }
        else{
            return;  }
        }
    
    public static void Msort(int []arr,int s,int l,int []e){
        if(s>l){
            return ; 
        }
        else{
          int mid=(s+l)/2;
          int i=s; int j=mid+1;
          for (int a=i;a<=l;a++){
              e[a]=arr[a] ;
          }
         for(int k=s;k<=l;k++)
              {   
              if(i>mid){
                  arr[k]=e[j]; j++;
              }
              else if(j>l){
                  arr[k]=e[i]; i++;              
              }
              else if(e[i]<e[j]){
                  arr[k]=e[i]; i++;
              }
              else{
                  arr[k]=e[j]; j++;
              }
      }
          for (int o : arr) {
            System.out.print(o+" ");
        }
            System.out.println();
    }
          }}

从运行结果可以很直观的看出交换顺序：

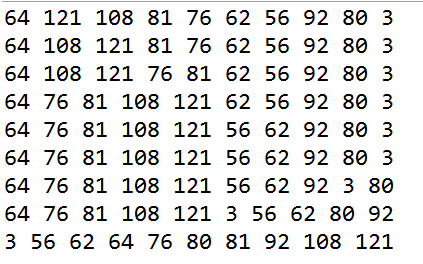（自己看得懂，没毛病。）

 

2.快速排序的简单思路

   取首位为基准数n，从左右两边开始遍历。

   不断交换左遍历大于n，右遍历小于n 数的位置，直至两索引相遇。

   交换索引与基准数的位置，最终形成 (左值<n&&右值>n)的局面。

   通过递归，重复上述流程，以此达到整体有序的目的。

   代码：

  

public static void sort(int[] arr,int l,int r){
        if(l>=r){
            return;
        }
        int i=quickSort(arr, l, r);
        sort(arr, l, i-1);
            sort(arr, i+1, r);
        
    }
    public static int quickSort(int[] arr,int l,int r){
         int i=l+1; int j=r;
         while(true)
         {
         while(i<=r&&arr[i]<arr[l]) i++;
         while(j>=l+1&&arr[j]>arr[l]) j--;
         if(i>j) break;
             swap(arr,i,j);
             i++;j--;
         }
         swap(arr,l,j);
         return j; 
        
}
       static void swap(int[] nums, int x, int y) {
           int temp = nums[x];
           nums[x]  = nums[y];
           nums[y]  = temp;
        
    }

两者都是采用分治思想，通过递归将排序分割为同等结构的子排序，以此解决问题。