离散数学 C1

概述

离散数学(Discrete mathematics) 研究离散量的结构和相互间的关系为主要目标， 充分描述了计算机科学离散性的特点。 

内容包含：数理逻辑、集合论/关系、代数结构、图论、组合数学、数论、自动机 等。

离散数学是计算机学科的数学基础

(计算机二进制的原理限制其计算精度,64位计算机最大能表示64位二进制,远不及数学中实数的"稠密",因而称之为"离散")

 

chapter 1 逻辑 The Foundations: Logic and Proofs

1.1命题逻辑 Propositional Logic

1.命题逻辑 :因和果的学说

有因有果,因推果,果反推因

涉及面极广,数学上:定理成立的证明  计算机上:程序正确性的判断

2.命题 propositional

1.命题:带有真假意义的陈述句(只能真/假,而不能又真又假),具有两种稳定状态 True(1) False(0)(命题的真值)

　　eg.1. The sun is bigger than earth.（太阳比地球大）

　　　　---- Proposition (TRUE)

　　　　2. The integer 9 is prime.（整数9是素数）

　　　　---- Proposition (FALSE)

　　　　3. This statement is false.（这个陈述是错误的）

　　　　---- Not a proposition(又真又假)

　　　　4. Please open the book.（请打开课本）

　　　　---- Not a proposition(非陈述句)

　　　　5. What time is it？ （现在几点了？）

　　　　---- Not a proposition(非陈述句)

　　　　6. x + 1 = 2.

　　　　---- Not a proposition(情况无法确定,x未知)

 2.原子命题:这些不能再分的命题称为原子命题或简单命题\

3.逻辑运算符(逻辑连接符)Logical operators ( Connectives)

------命题可以通过逻辑联结词(逻辑运算)构成新的命题----复合命题. 复合命题的真值依赖于其中简单命题的真值

因此引入p,q,s,r等字母来表示命题

1.Negation 否定词 (NOT) "¬":一个命题的否定 

　　eg. p = "今天是周二" 则 ¬p = "今天不是周二"

2.Conjunction 合取词 (AND) "^":"p和q",全真为真,有假为假

　　eg."我和她都是男生","她"不是男生(有假),该命题为假

 

 

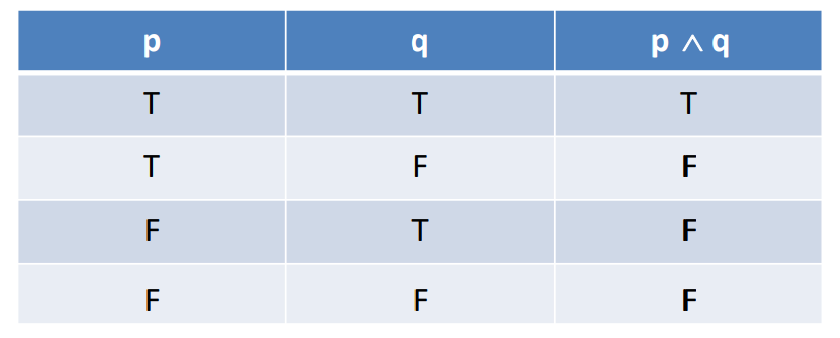
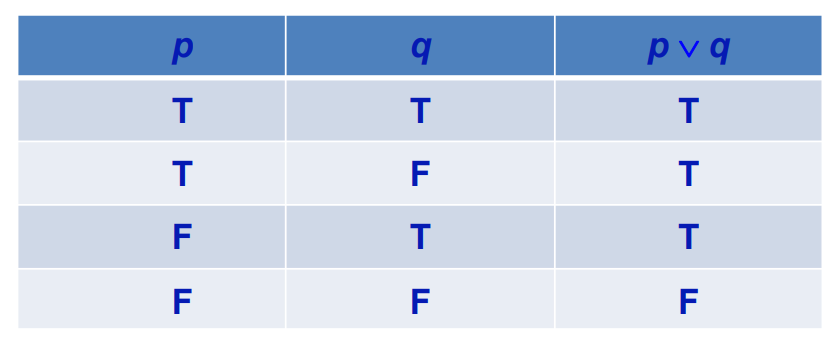
3.Disjunction 析取词 (OR)"v":"p或q",有真为真,全假为假

　　eg."今天周二或者今天下雨",如果今天既不是周二也不下雨,才为假

　　

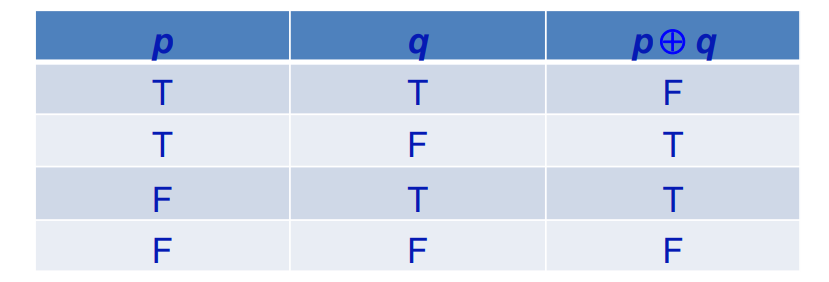
4.Exclusive or 异或词 (XOR) "⊕":"要么p,要么q",有且只有一个为真时才为真,全真全假均为假

　　容易与析取混淆,自然语言中都是或!!!

　　eg."他的生日是20号或21号",因为不可能同时是20和21号,因此都真也为假,自然都假也是假,一真一假才为真

　　

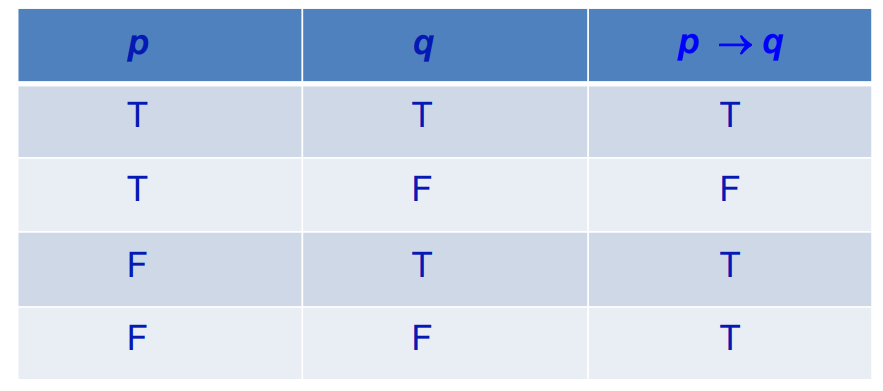
5.Implication 蕴涵词 (if – then)"→":"如果p则q",前提条件p不满足(为假),都为真;结果q实现(为真)都为真

　　eg."如果我挂科我就要再考一次高数"  1.挂科为真,再考为真,整体为真;2.挂科为假,但是刷分,再考为真,整体也为真,毕竟再考一次是事实;(前两个反映了结果实现都为真)

　　3.挂科为假,再考为假,正常情况,自然为真;4.挂科为假,再考为真,也为真(反应了条件不满足都为真)

　　

 

 

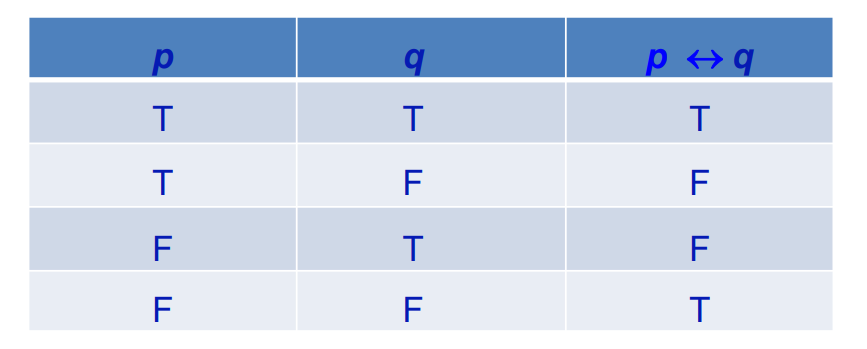
6.Biconditional 等价词 (if and only if)"↔":"p与q等价",二者相同为真,不同为假

　　eg.充要条件,前推后同时也能后推前才是真,自然二者真值要相同