20172301 《程序设计与数据结构》第七周学习总结

20172301 《程序设计与数据结构》第七周学习总结

教材学习内容总结

  • 二叉查找树是一种含有附加属性的二叉树，其左孩子小于父结点，父结点小于或者等于右孩子。

用链表实现二叉查找树

  • addElement操作：根据给定元素的值，在树中的恰当位置添加该元素。
    • 判断元素是不是Comparable，不是则抛出异常。
    • 树为空：新元素成为根结点。
    • 树非空：新元素与根元素进行比较
      • 小于：如果根的左孩子为空，成为根的左孩子；左孩子不空，遍历添加。
      • 大于：如果根的右孩子为空，成为根的右孩子；右孩子不空，遍历添加。
  • removeElement操作：从二叉查找树中删除给定的Comparable元素；找不到则抛出异常。
    • 选择替换结点的三种情况：
      （1）被删除结点没有孩子，replacement返回null；
      （2）被删除结点有一个孩子，replacement返回这个孩子 ；
      （3）被删除结点有两个孩子，replacement返回中序后继者；（处于根结点右子树上）
  • removeAllOccurrences操作：从二叉查找树中删除指定元素的所有存在。
    • 方法使用了LinkedBinaryTree类的contains方法。
  • removeMin操作：
    • 最小元素在二叉查找树的可能情况：
      （1）树根没有左孩子，树根即为最小元素，树根右孩子变成新的根结点；
      （2）树的最左侧结点为一片叶子，该叶子即为最小元素，设置其父结点的左孩子应用为null；
      （3）树的最左侧结点为内部结点，设置其父结点的左孩子引用指向最小元素的右孩子。

用有序链表实现二叉查找树

  • 树的主要使用之一就是为其他集合提供高效的实现。
操作 说明 LinkedList BinarySearchTreeList
removeFirst 删除列表的第一个元素 O(1) O(logn)
removeLast 删除列表的最后一个元素 O(n) (logn)
remove 删除列表中的查找到的第一个元素 O(n) O(logn)
first 返回列表第一个元素 O(1) O(logn)
last 返回列表最后一个元素 O(n) O(logn)
contains 判断列表是否含有一个特定元素 O(n) O(logn)
is Empty 判定列表是否为空 O(1) O(1)
size 列表中的元素数目 O(1) O(1)
add（有序列表特有） 向列表添加一个元素 O(n) O(logn)
  • add操作和remove操作都会导致树不平衡。

平衡二叉查找树

为什么树需要平衡？

如果二叉树是一棵蜕化树，他的效率可能比线性结构还要低。也就不能满足树的高效实现。

  • 右旋：指左孩子绕着其父结点向右旋转。
    • 应用情况：根结点左孩子的左子树较长路径导致不平衡
    • 方法步骤：
      • 树根左孩子元素成为新的根元素
      • 原树根元素称为新树根的右孩子元素
      • 使原树根左孩子的右孩子，成为原树根的新的左孩子
  • 左旋：指右孩子绕着其父结点向左旋转。
    • 应用情况：根结点右孩子的右子树较长路径导致不平衡
    • 方法步骤：
      • 树根右孩子元素成为新的根元素
      • 原树根元素称为新树根的左孩子元素
      • 使原树根右孩子的左孩子，成为原树根的新的右孩子
  • 左右旋：先让树根左孩子的右孩子，绕着树根的左孩子进行一次左旋，然后再让所得树根左孩子绕着树根进行一次右旋
    • 应用情况：根结点左孩子的右子树较长路径导致不平衡
  • 右左旋：先让树根右孩子的左孩子，绕着树根的右孩子进行一次右旋，然后再让所得树根右孩子绕着树根进行一次左旋。
    • 应用情况：根结点右孩子的左子树较长路径导致不平衡

AVL树

  • 平衡因子：右子树的高度减去左子树的高度。

红黑树

  • 红黑树的性质：
    • 树中的每一个结点都储存着红色或黑色，通常使用一个布尔值来实现，值false等价于红色。
    • 根结点和叶子结点（null）为黑色。为空(null)的叶子结点才为黑色。
    • 红色结点的所有孩子必定是黑色。
    • 从树根到树叶的每条路径都包含有同样数目的黑色结点。
  • 红黑树的平衡性质并没有AVL树那么严格，但是，他们的序仍然是logn。

教材学习中的问题和解决过程

  • 问题1：关于书P228页的中序后继者的理解。
  • 问题1解决方案：
    • 所谓的中序后继者意思是：中序遍历二叉树结点的后继结点
    • 如何查找中序后继者？
      • 若右子树不为空，则找到右子树最左的叶子节点；
      • 若右子树为空，且拥有右父亲节点，则找到右父亲节点；
      • 若右子树为空，且拥有左父亲节点，则找到最近的右祖先节点；
    • 而对于删除结点有两个孩子的情况时，不一定replacement返回中序后继者。也可以返回中继前驱者。 具体的需要看代码实现，而不需要局限于书本。
    • 如何查找中序前驱者？
      • 若左子树不为空，则找到左子树的最右的叶子节点；
      • 若左子树为空，且拥有左父亲节点，则找到左父亲节点；
      • 若左子树为空，且拥有右父亲节点，则找到最近的左父祖先节点；
  • 问题2：书P228的变量modCount为什么是减减。
  • 问题2解决方案：
    • 变量modcount应该是计算迭代次数的。
    • API里写的也是这样的，但是为什么删除操作要递减一。
    • 之前实现列表的删除操作也是modcount--，这个未解决。

代码调试中的问题和解决过程

  • 问题1：是否需要定义新的指针类AVLTreeNode，换句话说，AVL树和二叉查找树以及链表实现的二叉树之间的关系。

  • 问题1解决方案：

    • 首先，根据书上P240所述

    由于需要上溯树，因此AVL树通常最好实现为每个结点都包含一个指向其父结点的引用。

    • 这里的上溯树是因为，树因为插入结点或者删除结点而变得不平衡，所以每次在进行这两个操作的时候，需要更新平衡因子，从插入或者删除的那个结点开始，检查到根结点。所以，我们的指针类很可能除了指向左右孩子的指针，还需要一个指向父结点的。
    • 其次，根据书上P239所述

    对于树中的每个结点，我们都会跟踪其左、右子树的高度。

    • 由此，指针类会需要一个int型变量height，来得出结点的高度。
    • 在我实现了指针类AVLTreeNode和LinkedAVLTree的平衡方法后，我需要实现添加和删除方法。但是，AVL树和二叉查找树唯一不同的是添加和删除中如果不平衡要进行旋转。 所以，AVL树是可以继承二叉查找树的。
    • 这时，其实我陷入了一个思维误区。我写的指针类AVLTreeNode因此肯定也要继承二叉树指针类BinaryTreeNode。但是，其实根本不用这么麻烦呀！
      直接在BinaryTreeNode构建新的构造方法不就可以了！
    public BinaryTreeNode(T obj, LinkedBinaryTree<T> left, LinkedBinaryTree<T> right,int height)`
    • 存在的问题：
      虽然准确理解了AVL树中旋转平衡的操作，但是并没有整体理解代码与代码之间的关系。花费大量的时间做了无用功，同时让自己陷入了错误的循环。
      如果，我直接发现AVL树是二叉查找树的子类，那我也不会构建新的指针类。
      所以，解决代码问题，首先需要宏观的观察，确定好整体的架构，这便是UML类图的重要性。不然，尽管你细节处理的再完美，方向错了，便是越走越远。

    先设计，考虑所有的情况，再去实现。

  • 问题2：链表旋转方法的顺序问题。

  • 问题2解决方案：这里以右旋为例。

    • 根据书P238 给出右旋的操作
    • 使树根的左孩子元素成为新的根元素。
    • 使原根元素成为这个新树根的右孩子元素。
    • 使原树根的左孩子的右孩子，成为原树根的新的左孩子。
    • 所以我们实现右旋方法就可以使用一下操作，其中node是原树根，node1是新树根。
    node1 = node.left;
node1.right = node;
node.left = node1.right;
    • 然后，添加上更新高度的操作。就可以返回新的根元素。
    node.height = Math.max(height(node.left),height(node.right));
node1.height = Math.max(height(node1.left),height(node1.right));
return node1;
    • 运行，首先给我抛出的是StackOverflowError错误。

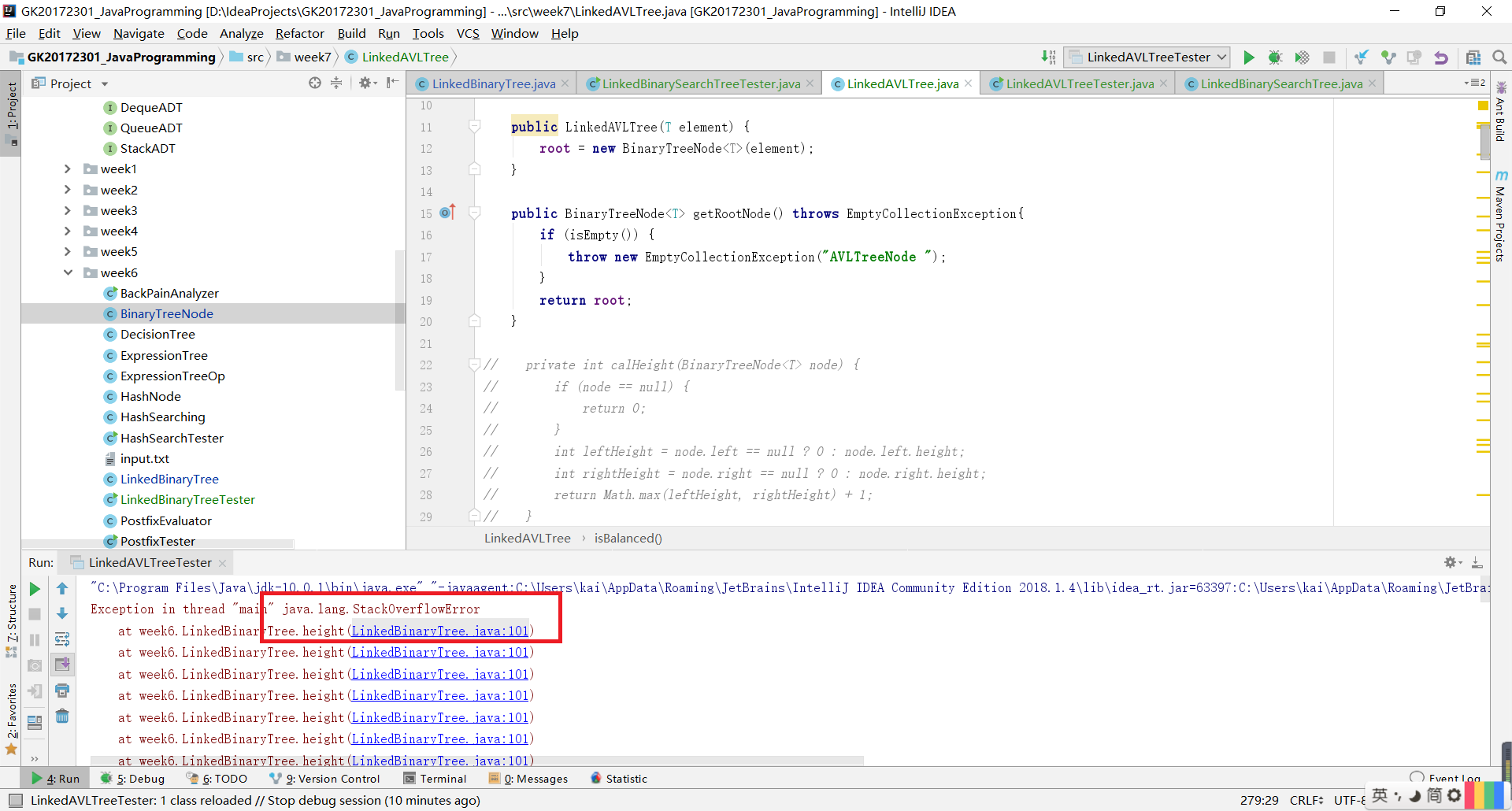
    • 当应用程序递归太深而发生堆栈溢出时，抛出该错误。也就是说，方法里出现了死递归。这个问题，我在上周侯泽洋同学的博客中也看见过。
    • 调试发现，node的左子树是无限的，这说明右旋存在问题。
      我们根据书上的操作写出来的代码，改变了node1的右子树，所以node的左子树插入的全是node，也就是无限循环的。
    • 所以，我们需要改变一下操作顺序。
    node1 = node.left;
node.left = node1.right;
node1.right = node;

    这样的操作就会更加合理，同样也不会出现死递归的错误。实现代码之前，要考虑树的子树连接顺序问题，和链表类似，不要出现丢失或者赘余的情况。

  • 问题3：AVL树添加/删除方法旋转情况的不全面。

  • 问题3解决方案：

    • AVL树旋转的原因应该是树不平衡。
    • 我初次实现代码时，旋转的判断条件是当根的平衡因子绝对值大于1的时候，所以存在一种情况，即为对于根来说是平衡的，而对于根的某一结点来说是不平衡的。
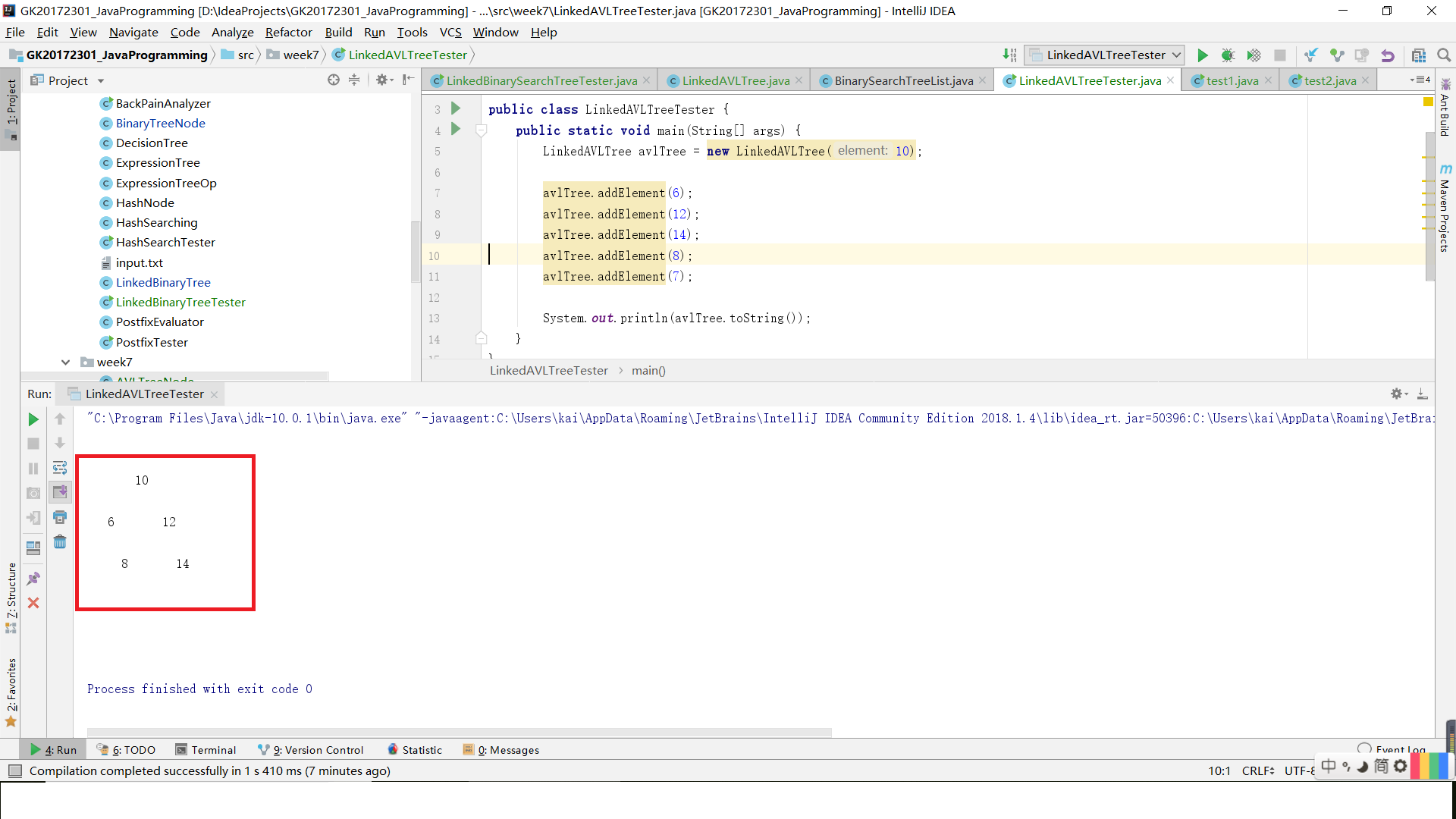
    • 这里我新建一个AVL数，在插入10,6,12,8,14之后，树是平衡的，并不需要平衡操作。
      如图

    然后，我插入数字7。
    如图

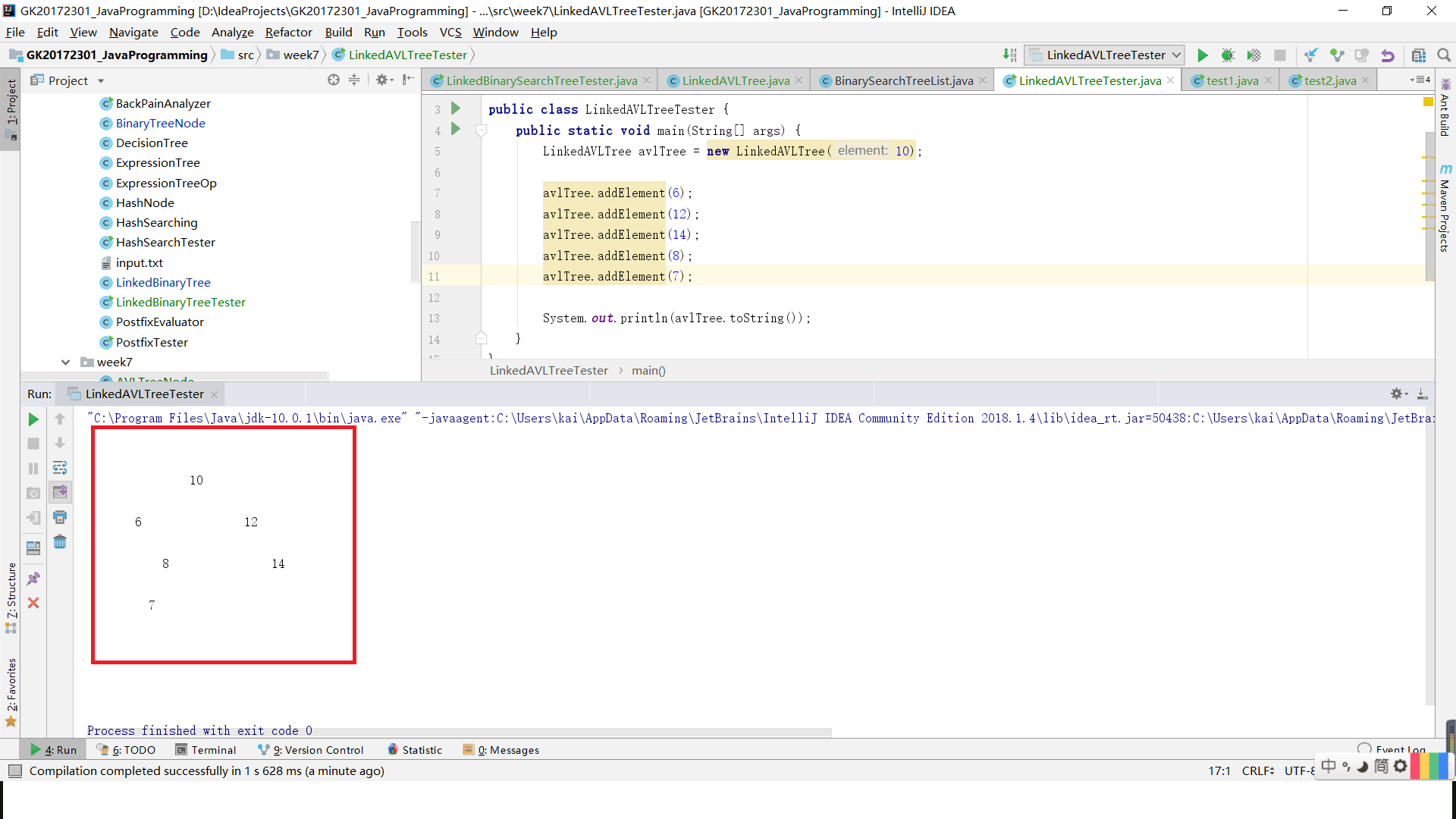
    这时，AVL树对于根来说是平衡的，但是对于根的左子树来说是不平衡的，因为根的左孩子没有左孩子。对于较为严格的AVL树来说，这是不符合规则的。

    所以，书上给出的避免操作是建立一个指向父结点的引用，通过上溯树来判断每个结点是否是平衡的。

    • 但是，我如果通过添加操作的递归在插入的时候来判断结点是否是平衡的，是否可以呢。有待实现

代码托管

上周考试错题总结

上周无错题，优秀！

结对及互评

点评过的同学博客和代码

  • 上周博客互评情况
    • 20172304
    • 段志轩同学的博客教材内容总结的越来越详细，要注意markdown的表格格式。教材问题应该能更深入一些。
    • 20172328
    • 博客同样内容很丰富，感想也是很深刻。

其他

红黑树虽然难理解，但是应用的实例很多，也需要掌握。同时，AVL树相对严格，实现代码的时候要更加严谨，考虑全部的可能和情况。从而尽可能减少错误的出现。

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 0/0 1/1 10/10
第二周 610/610 1/2 20/30
第三周 593/1230 1/3 18/48
第四周 2011/3241 2/5 30/78
第五周 956/4197 1/6 22/100
第六周 2294/6491 2/8 20/120
第七周 914/7405 1/9 20/140

参考资料

posted @ 2018-11-02 23:07  奈何明月ઇଓ  阅读(376)  评论(3)  编辑  收藏  举报
页尾