20172304 《程序设计与数据结构》第七周学习总结
20172304 《程序设计与数据结构》第七周学习总结
教材学习内容总结
本周主要学习的是二叉查找树的相关知识。二叉查找树是一种带有附加属性的二叉树,即对树中的每个结点。其左孩子都要小于父结点,而父结点又小于或等于右孩子。
二叉树结点类的操作
| 操作 | 说明 |
|---|---|
| addElement | 往树中添加一个元素 |
| removeElement | 从树中删除一个元素 |
| removeAllOccurrences | 从树中删除所指定元素的任何存在 |
| removeMin | 删除树中的最小元素 |
| removeMax | 删除树中的最大元素 |
| findMin | 返回一个指向树中最小元素的引用 |
| findMax | 返回一个指向树中最大元素的引用 |
用链表实现二叉查找
树。
1、向链表中添加元素
首先判断树的根是否为空,如果为空则插入根节点中。不为空则将添加的元素同根的左孩子进行比较。如果左孩子为空,则将元素插入左孩子,如果元素比左孩子大,则继续将元素同左孩子的左孩子进行比较,直至元素插入为止。同样,如果元素大于根,则将元素同根的右孩子进行比较,如果右孩子为空则将元素插入右孩子,如果元素大于根的右孩子则将元素继续同根的右孩子进行比较。直至元素插入为止。

2、从链表中删除元素
第一种情况:结点没有孩子
我们直接删除结点即可。
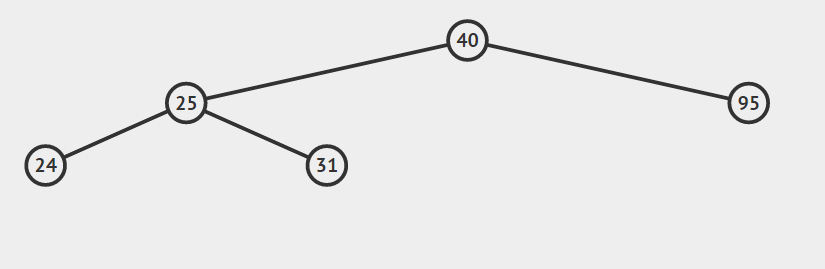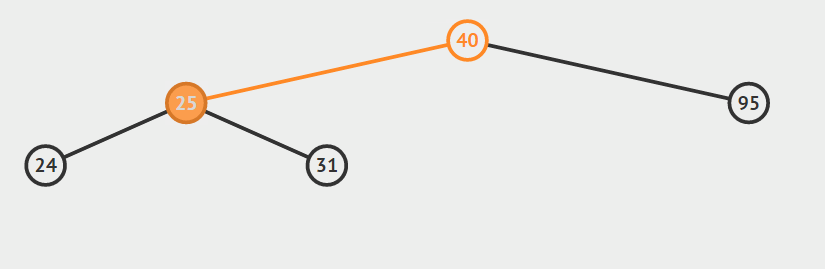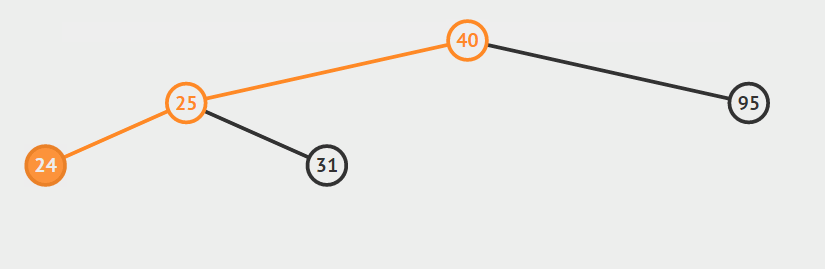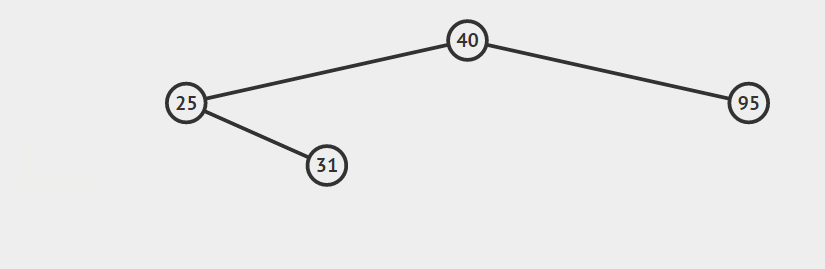
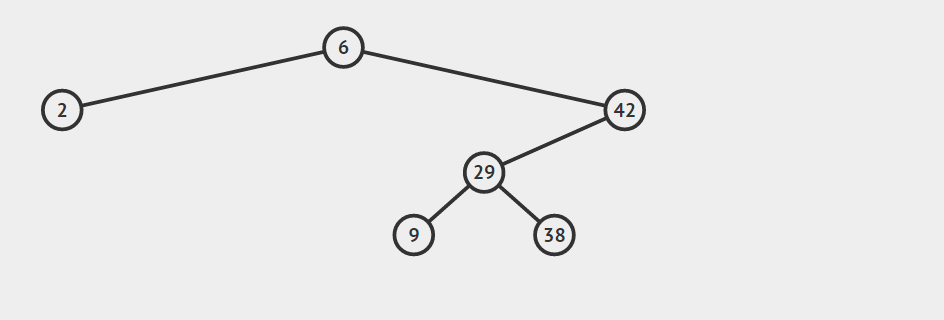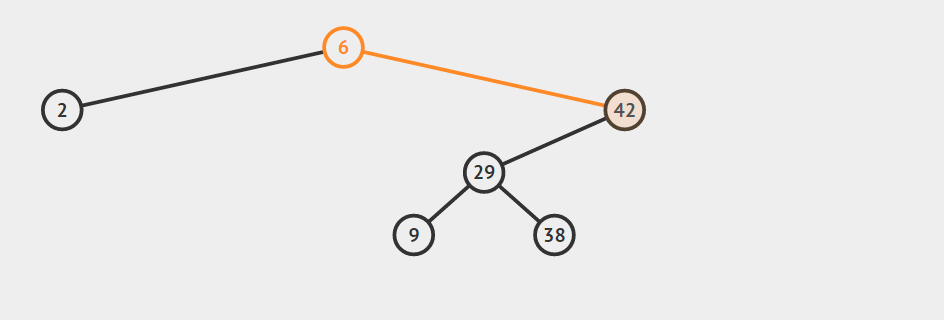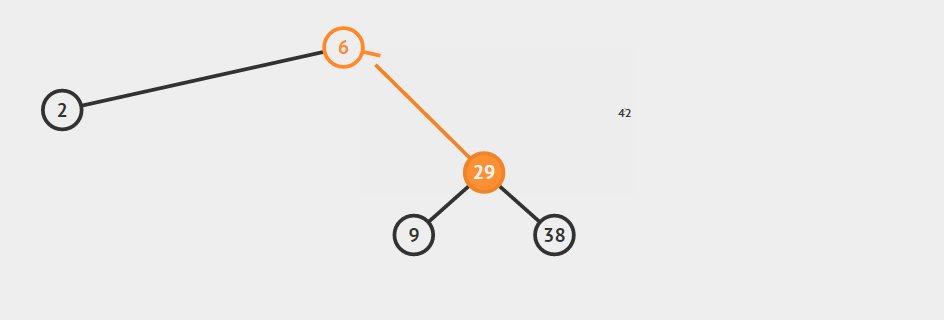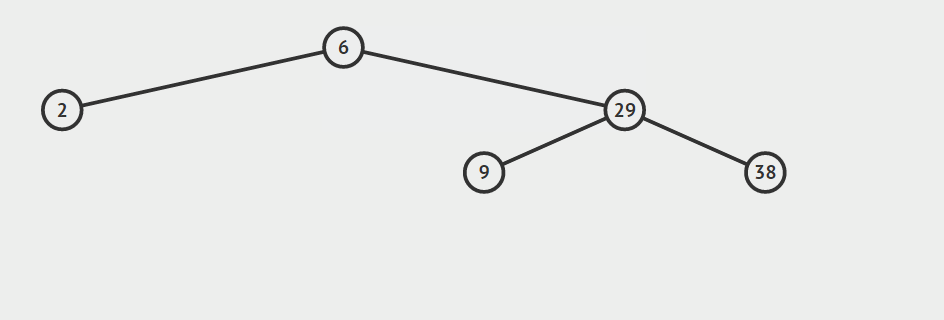
第二种情况:结点只有左孩子或者右孩子
用结点的孩子代替节点。
只有左孩子
只有右孩子
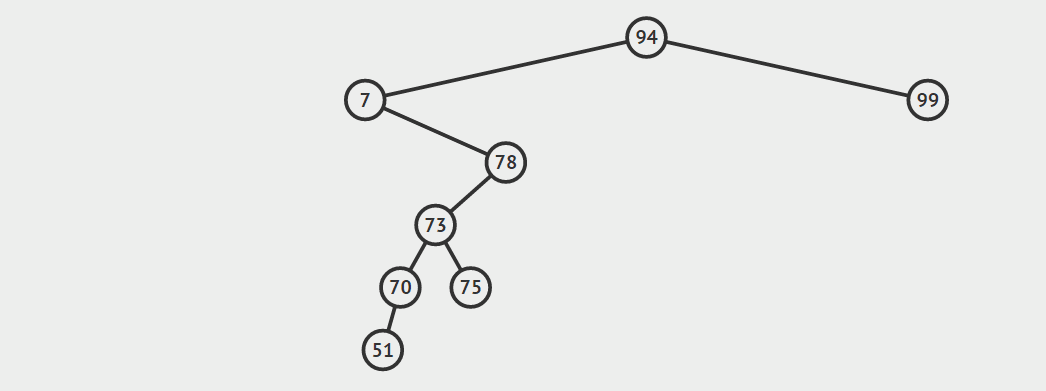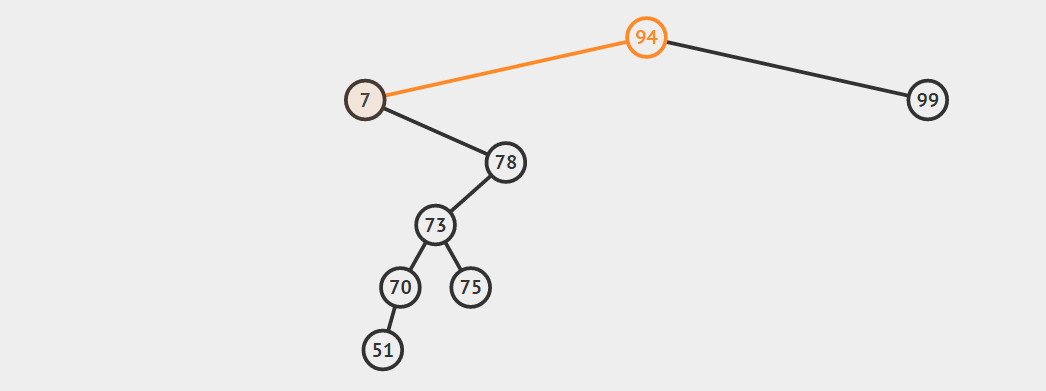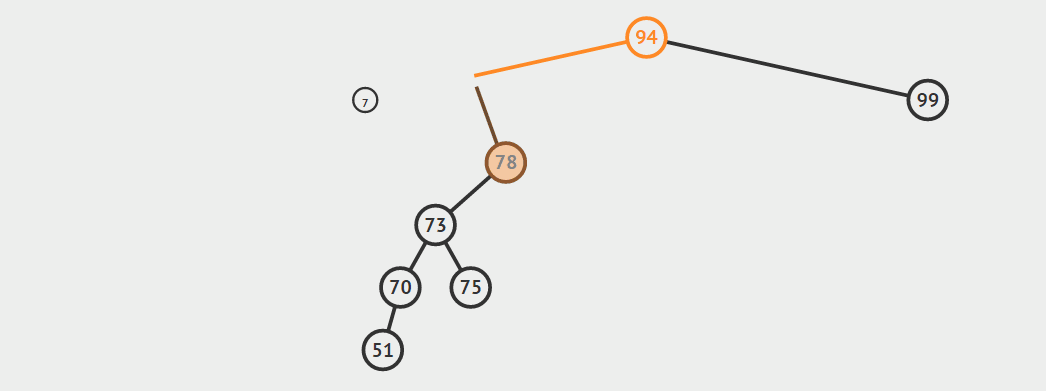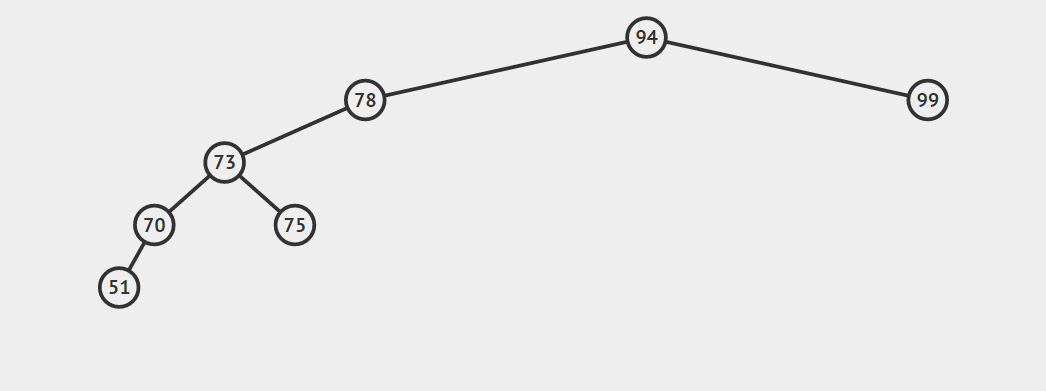
第三种情况:结点有两个孩子
找自己右孩子里面的最小值(最左)然后替换自己和它,然后删除自己
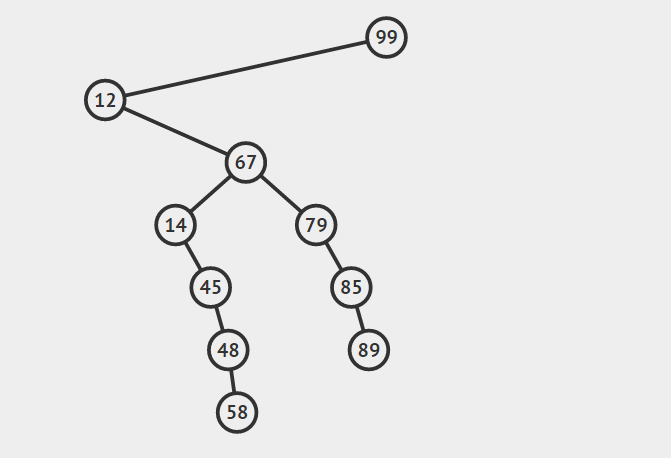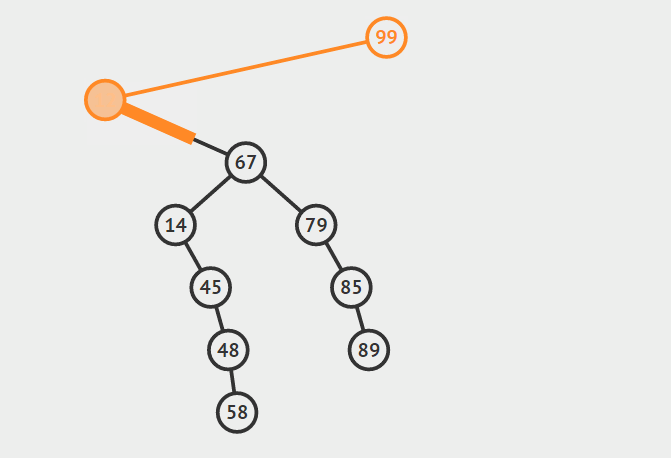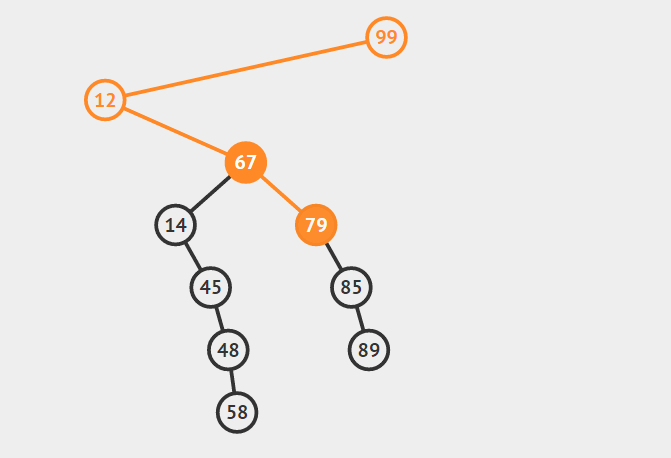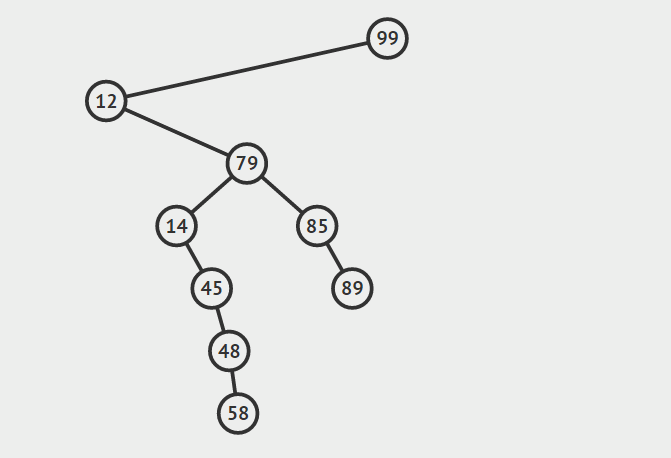
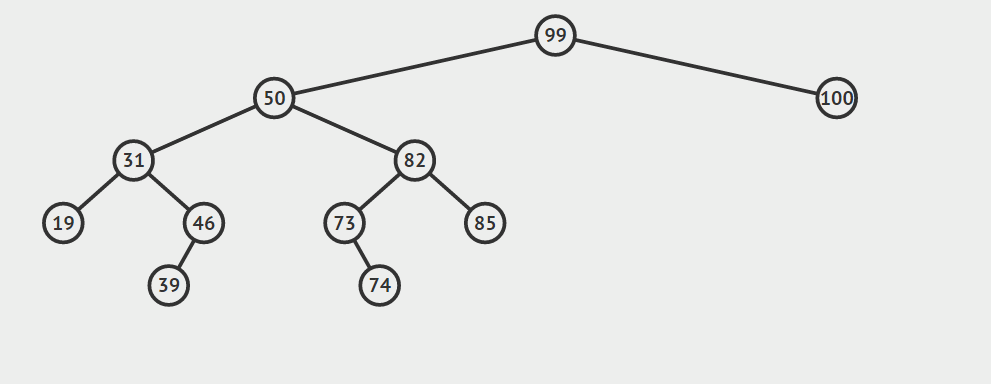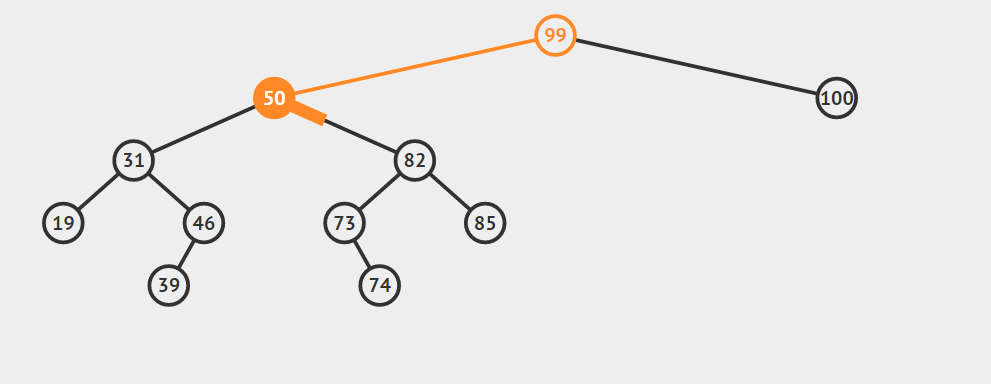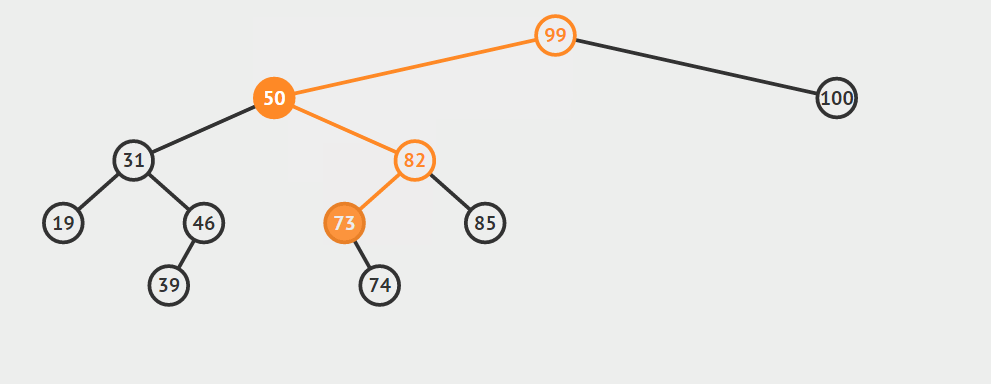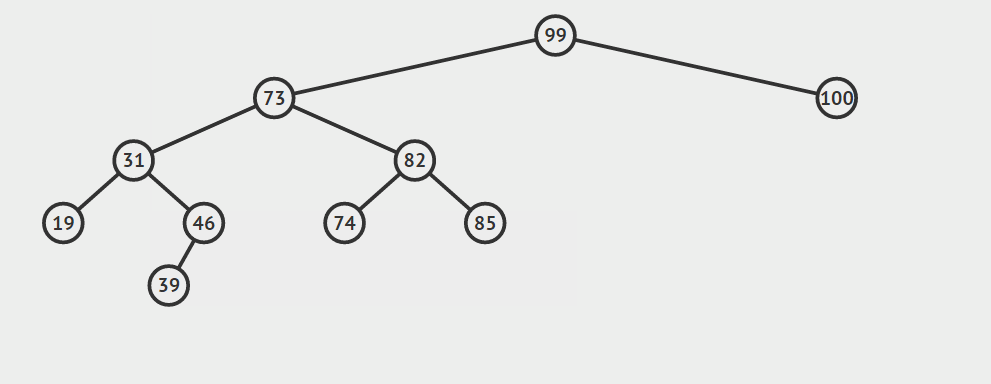
其他的操作原理较为简单就不在赘言
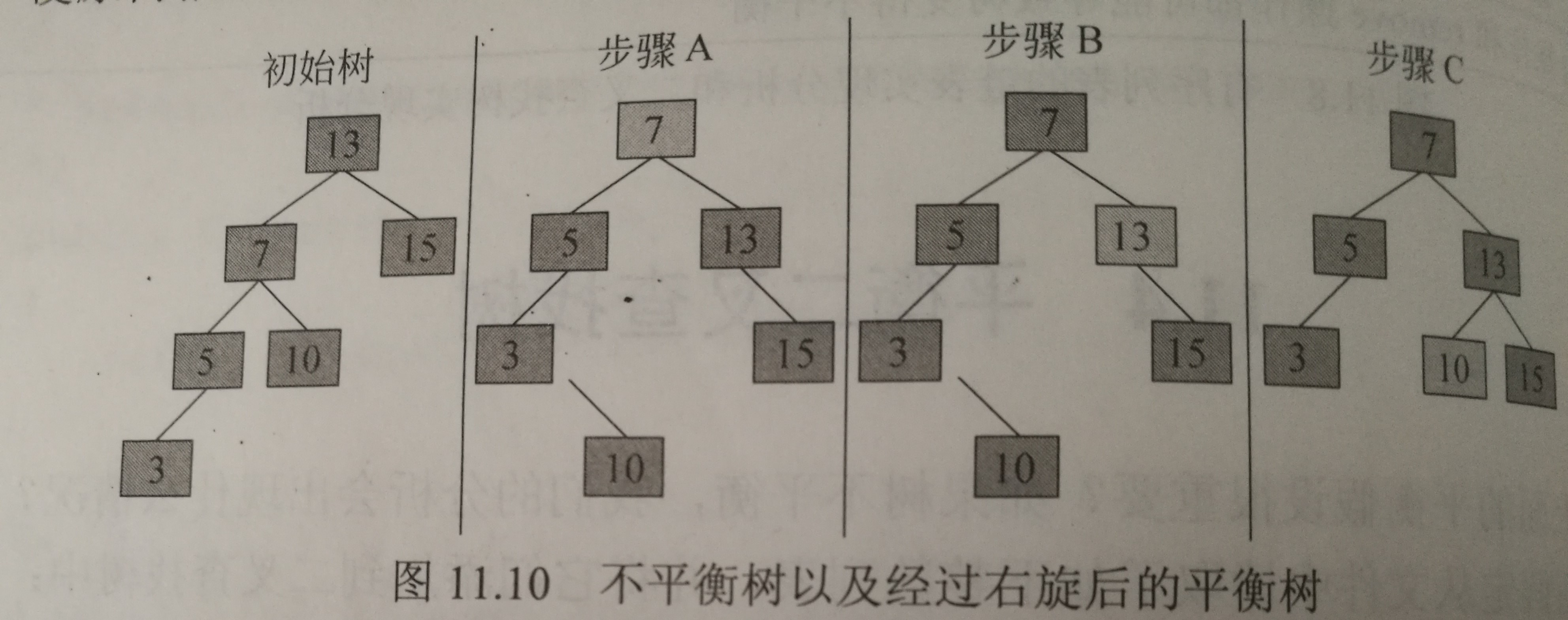
11.4平衡二叉查找树
右旋
通常是指左孩子绕着其父结点向右旋转。
如果是因为树根左孩子的左子树中较长的路径而导致的不平衡,优选可以解决它
左旋
通常是指右孩子绕着其父结点向左旋转。
对于有树根右孩子的右子树中较长路径而导致的不平衡,左旋可以解决它。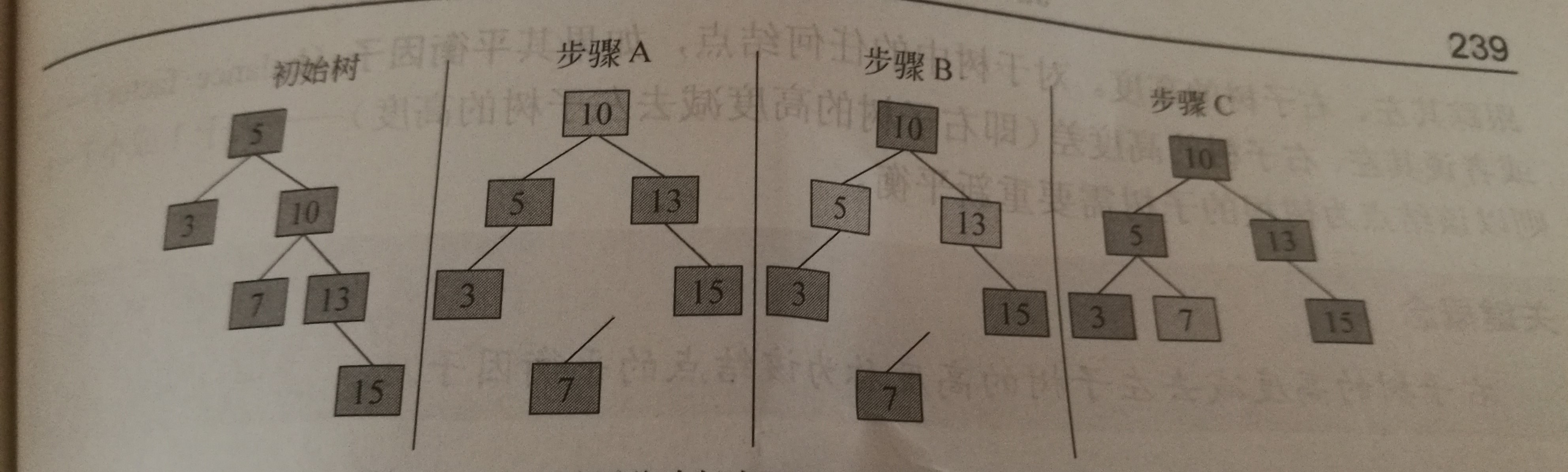
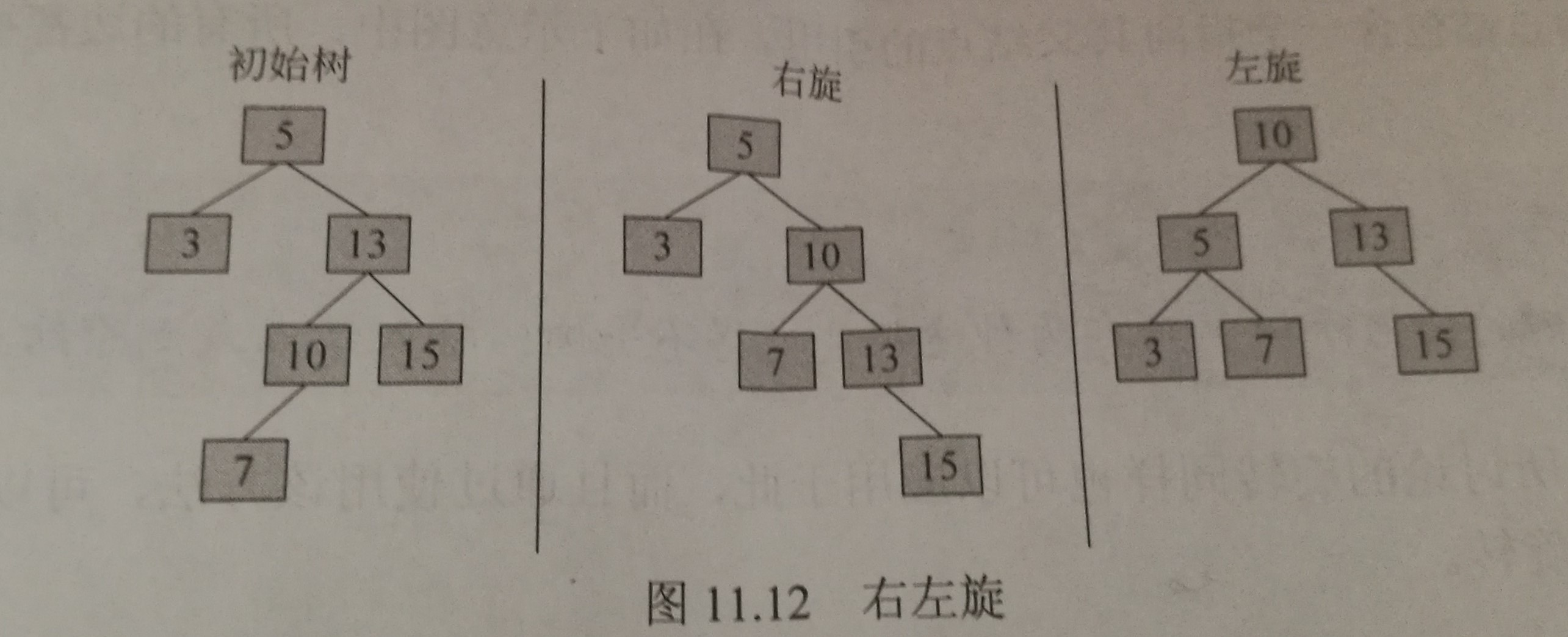
右左旋
对于由树根右孩子的左子树中较长路径而导致的不平衡。先让树根右孩子的左孩子,绕着树根的右孩子进行一次右旋,然后在让所得的树根右孩子绕着树根进行一次左旋。
左右旋
对于由树根左孩子的右子树中较长路径而导致的不平衡,我们必须先让树根左孩子的右孩子绕着树根的左孩子进行一次左旋,然后再让所得的树根左孩子绕着树根进行一次右旋。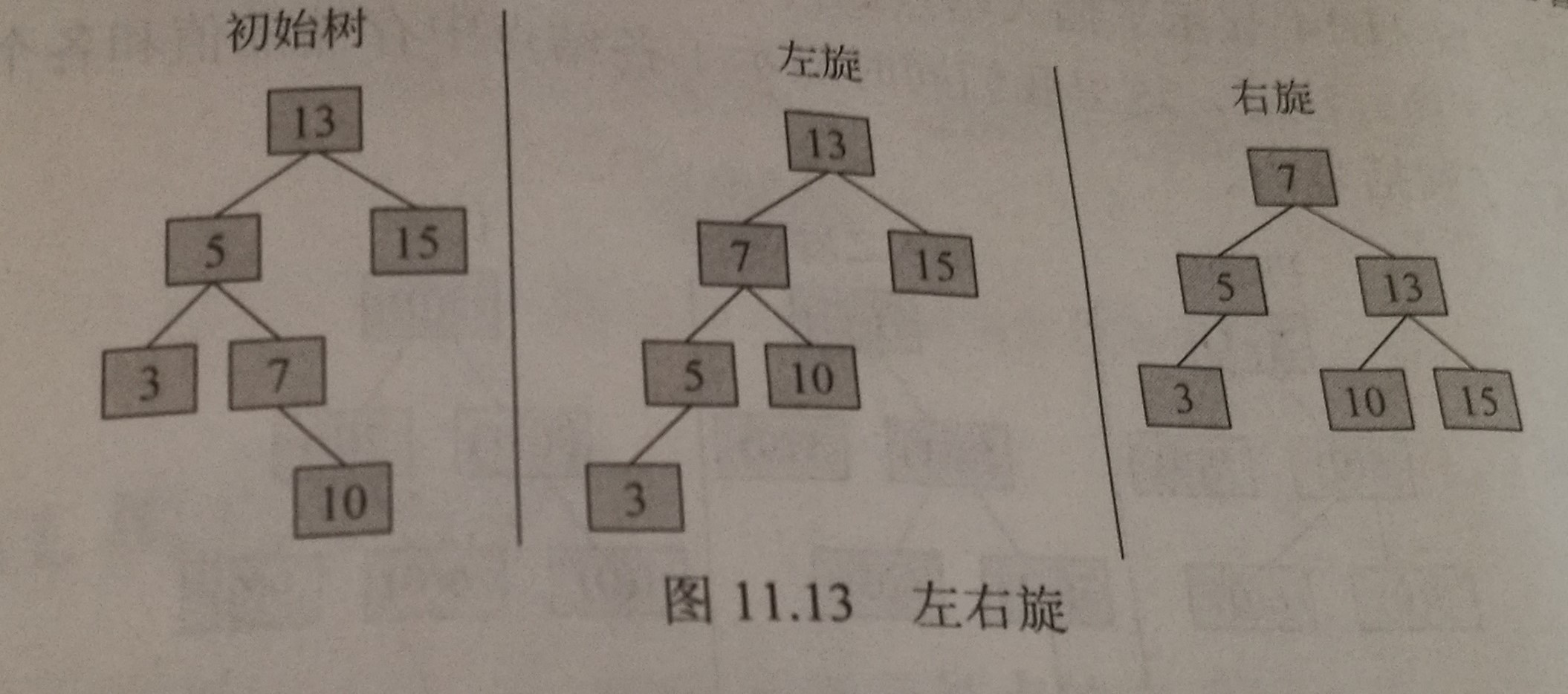
有序列表实现分析和二叉查找树实现分析
|操作|LinkedList|BinarySearchTreeList|
|removeFirst|O(1)|O(log n)|
|remove|O(n)|O(log n)|
|remove|O(n)|O(log n)|
|first|O(1)|O(log n)|
|last|O(n)|O(log n)*|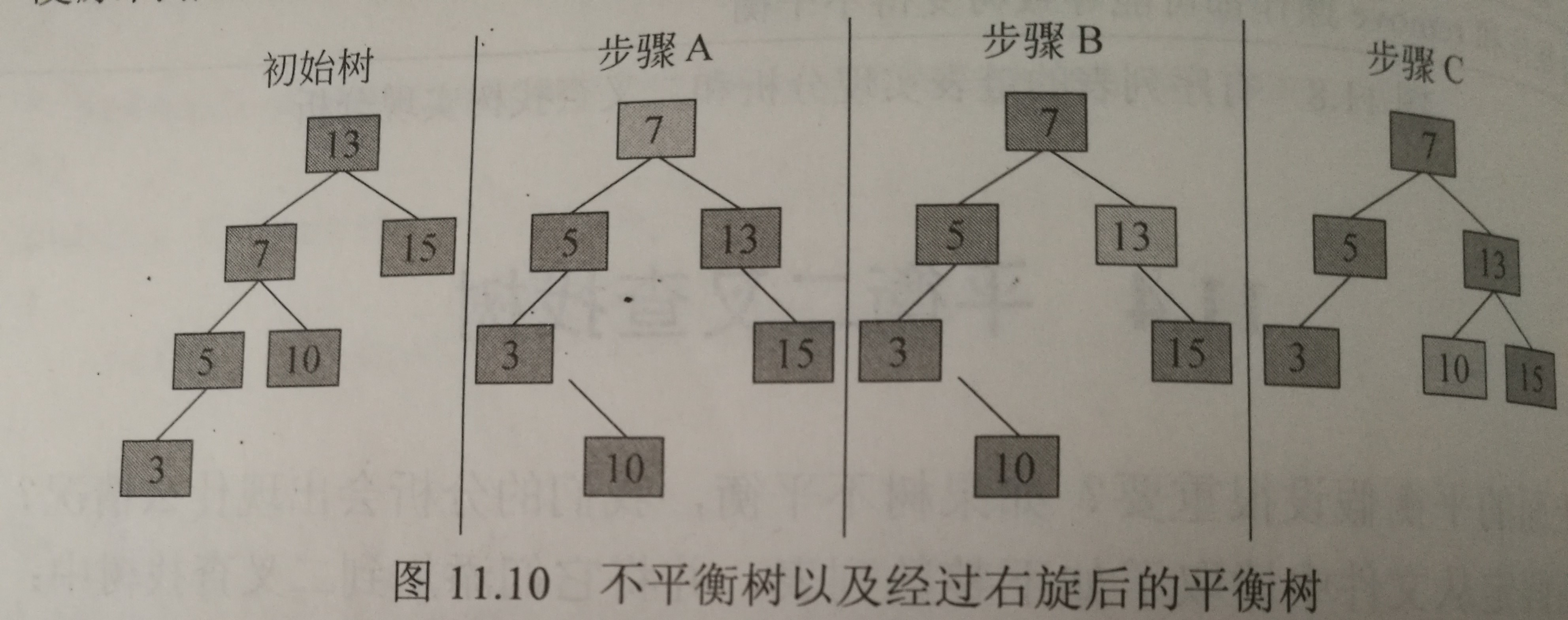
|contains|O(n)|O(log n)|
|isEmpty|O(1)|O(1)|
|size|O(1)|O(1)|
|add|O(n)|O(log n)*|
11.5 实现二叉查找树:AVL树
AVL树即二叉平衡查找树,即树的左子树和右子树的深度的绝对值之差不能超过1。
结点的平衡因子 = 左子树的高度 - 右子树的高度
插入和删除操作都会导致AVL树的自我调整(自我平衡),使得所有结点的平衡因子保持为+1、-1或0。
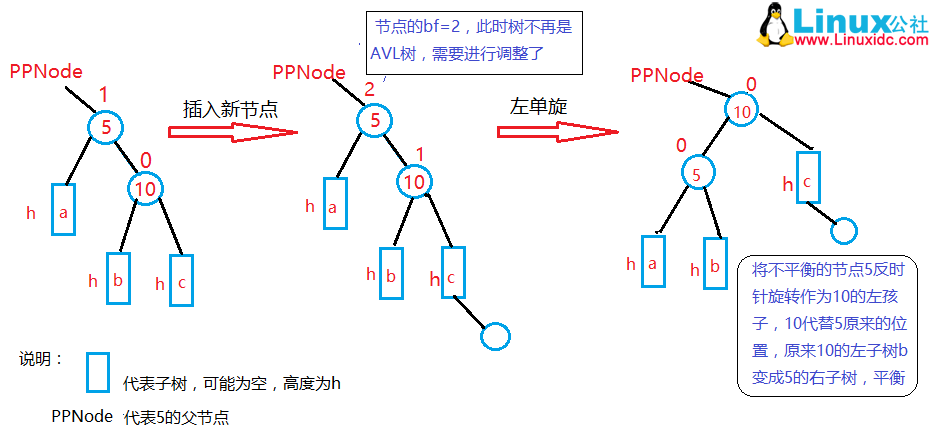
AVL树的右旋
如果某结点的平衡银子为-2,则意味着该结点的左子树中有一条过长的路径。于是我们将检查这个初始结点的左孩子的平衡因子。如果其左孩子的平衡因子是-1,则意味着较长的路径处在这个左孩子的左子树中,于是让这个左孩子绕着初始结点进行一次右旋即可平衡该树。

AVL树的左旋
如果某结点的平衡因子是+2,则意味着该结点的右子树中有一条过长的路径。如果其右孩子的平衡因子是+1,则意味着其较长的路径处在这个右孩子的右子树中,于是让这个右孩子绕着初始结点进行一次左旋即可平衡该树。
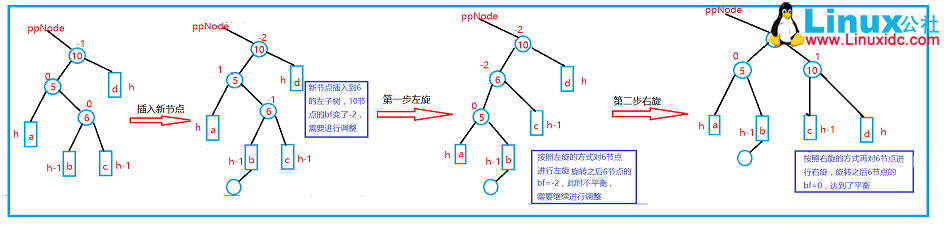
AVL树的右左旋
某结点的右子树中有一条过长的路径。如果其右孩子的平衡因子是-1,则意味着较长路径处在这个右孩子的左子树中,于是进行一次右左双旋即可重新平衡该树。

AVL树的左右旋
某结点的平衡因子为-2,则意味着该结点的左子树中有一条过长的路径。如果左孩子的平衡因子是+1,则意味着较长路径处在这个左孩子的右子树中,于是进行一次左右双旋即可重新平衡该树。
实现二叉查找树:红黑树
红黑树在AVL树的基础上有添加了两个属性:红色和黑色。
红黑树对平衡的要求没有AVL树严格
红黑树红黑颜色的要求
1.每个节点要么是红色,要么是黑色。
2.根节点必须是黑色
3.红色节点不能连续(也即是,红色节点的孩子和父亲都不能是红色)。
4.对于每个节点,从该点至null(树尾端)的任何路径,都含有相同个数的黑色节点。
红黑树能够以O(log2 n)的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。
教材学习中的问题和解决过程
问题1:书上解释蜕化树的效率比链表还要低下为什么?
回答1:因为二叉搜索树中每个结点不仅定义了其本身的元素还定义了其左孩子和右孩子的引用,而在进行查找时往往需要对其左孩子和右孩子的存在进行比较,所以效率比较低。
问题2:用Comparable接口实例化一个对象的作用。
回答2:Comparable接口是对对象进行比较的接口,使用泛型类型对对象进行实例化以后,就不必再去对他的方法进行重写了可以直接利用他实例化的对象进行compareTo比较,而且因为实例化的对象是泛型,所以利用Comparable接口进行实例化的对象可以和任何类型的对象进行比较。接口的实例化对象可以直接使用已经实现接口的类的方法。那么Comparable接口实例化一个泛型队形就可以使用它对所有对象进行比较的方法。
代码调试中的问题和解决方案
问题:在测试二叉搜索树时发现了这个问题
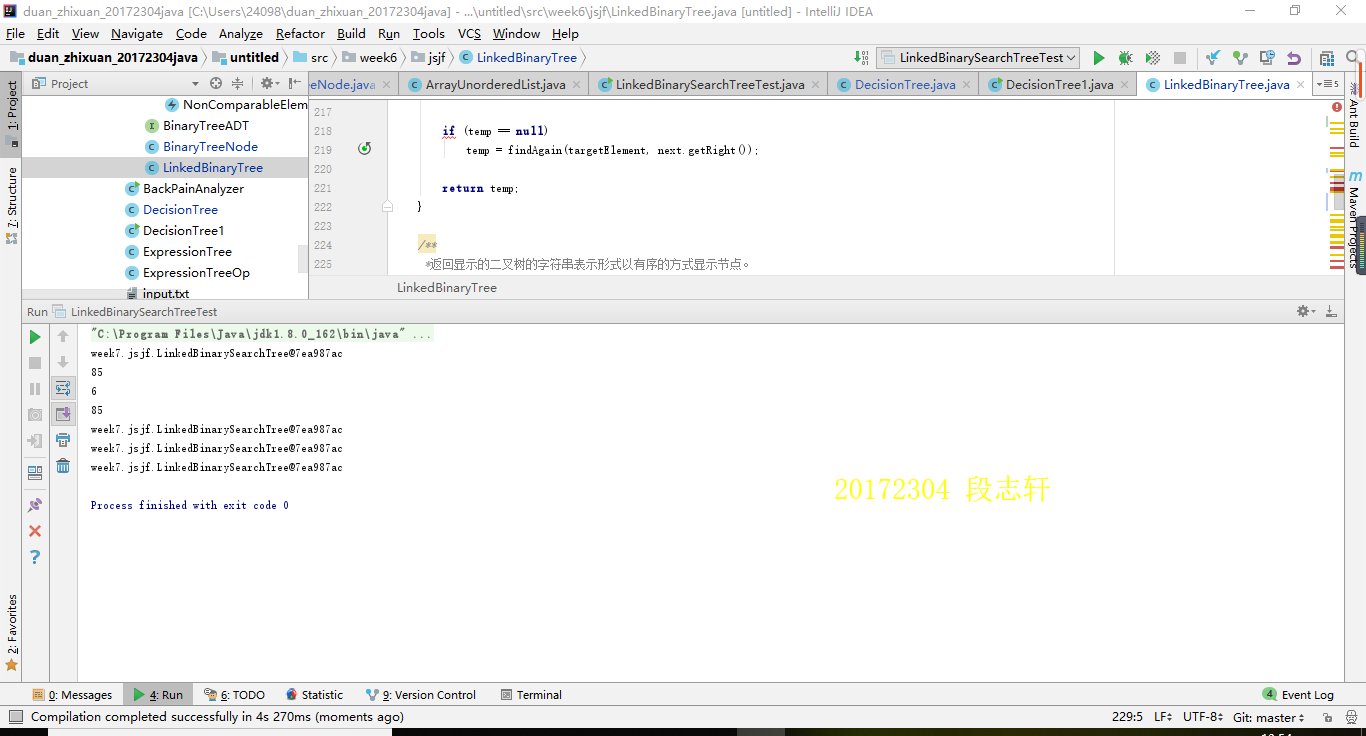
解答:后来发现是没有写toString方法,后来补上了。
@Override
public String toString()
{
UnorderedListADT<BinaryTreeNode> nodes = new ArrayUnorderedList<BinaryTreeNode>();
UnorderedListADT<Integer> levelList = new ArrayUnorderedList<Integer>();
BinaryTreeNode current;
String result = "";
int printDepth = this.getHeight();
int possibleNodes = (int)Math.pow(2, printDepth + 1);
int countNodes = 0;
nodes.addToRear(root);
Integer currentLevel = 0;
Integer previousLevel = -1;
levelList.addToRear(currentLevel);
while (countNodes < possibleNodes)
{
countNodes = countNodes + 1;
current = nodes.removeFirst();
currentLevel = levelList.removeFirst();
if (currentLevel > previousLevel)
{
result = result + "\n\n";
previousLevel = currentLevel;
for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)
result = result + " ";
}
else
{
for (int i = 0; i < ((Math.pow(2, (printDepth - currentLevel + 1)) - 1)) ; i++)
{
result = result + " ";
}
}
if (current != null)
{
result = result + (current.getElement()).toString();
nodes.addToRear(current.getLeft());
levelList.addToRear(currentLevel + 1);
nodes.addToRear(current.getRight());
levelList.addToRear(currentLevel + 1);
}
else {
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
result = result + " ";
}
}
return result;
}
运行结果
80
10 85
9 16
6 44
7
85
6
85
80
16 85
9 44
6
7
80
16
9 44
6
7
80
16
9 44
7
代码托管

(statistics.sh脚本的运行结果截图)
上周考试错题总结
-错题一
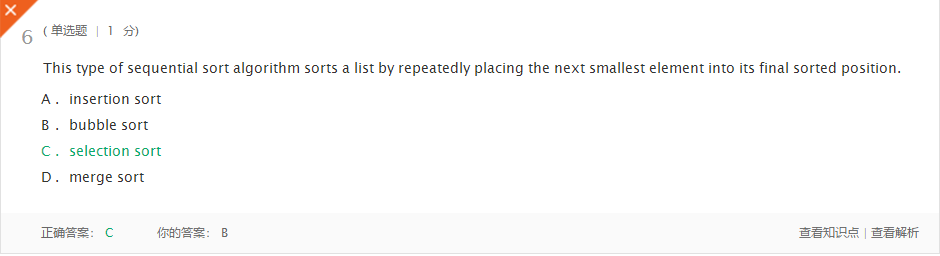
-问题解答:重复将最小的元素放到最后排序的排序应该是选择排序。
- 错误二
![]()
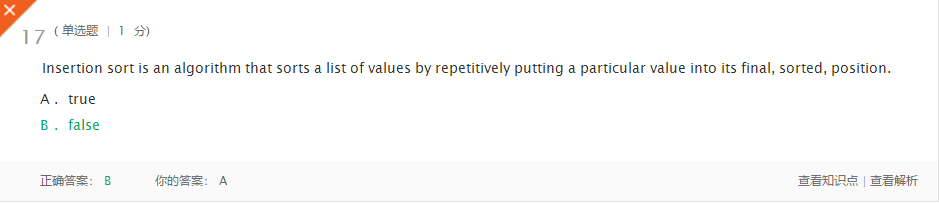
-问题解答:选择排序是通过反复的将某一特定值放到它在列表中最终已排序的位置,从而完成对某一列值的排序。而题中给定的是插入排序。插入排序是通过反复的将某一特定值插入到该列表某个已排序的子集中来完成对列表值的排序。 - 错误三
![]()
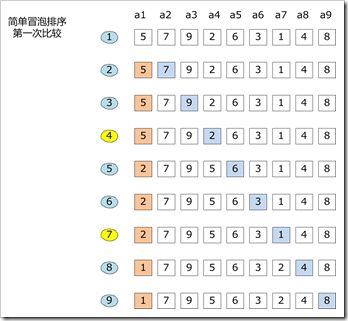
-问题解答:这道题错误的原因是我忘记了冒泡排序的流程。正常的冒泡排序应该是从第一个位置起,比较两个相邻的元素。按照排序规则进行比较,若二者的顺序不符合排序规则,则交换其位置,若符合排序规则,则进行下一组比较。
冒泡排序流程图:
![]()
博客互评
20172304郭恺郭恺同学的博客依然是一如既往的优秀,既将教材中的内容总结的详略得当,还能具体而全面的对自己的错误进行总结和提升。
20172328李馨雨李馨雨同学的博客还是很认真的。
点评过的同学博客和代码
- 上周博客互评情况
20172304郭恺同学本次的博客十分优秀,对教材的总结详略得当,而又针对自己在教材中发现的问题进行了深入的鞭辟入里的思考与解答。整个过程看起来赏心悦目给人一种美的享受。
20172328李馨雨同学的博客十分的完整与丰富,体现了她认真的学习态度。
其他(感悟、思考等,可选)
本周学习了二叉搜索树的相关知识,二叉搜索树是二叉树的扩展,但是新添了许多不懂的知识,而且利用了二叉树中所学的知识,这让我深刻体会到复习的重要性,只有充分掌握已有的知识,进行吸收转化,才能更好的利用旧知识来学习新知识。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 30/30 | 1/1 | 10/10 | |
| 第二周 | 766/796 | 1/2 | 40/50 | |
| 第三周 | 817/1613 | 1/3 | 20/70 | |
| 第四周 | 1370/3983 | 2/5 | 30/100 | |
| 第五周 | 1235/5214 | 1/6 | 10/110 | |
| 第六周 | 1328/6542 | 1/7 | 20/130 | |
| 第七周 | 1218/7860 | 1/8 | 20/150 |
参考资料
1.蓝墨云班课
2.java软件结构与数据结构
3.多动态图详细讲解二叉搜索树




 浙公网安备 33010602011771号
浙公网安备 33010602011771号