洛谷P1758 [NOI2009]管道取珠

题目：https://www.luogu.org/problemnew/show/P1758

题目描述

管道取珠是小X很喜欢的一款游戏。在本题中，我们将考虑该游戏的一个简单改版。游戏画面如图1所示：

（图1）

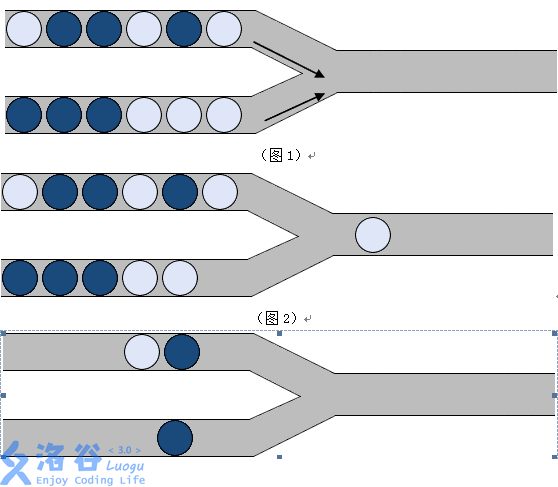
游戏初始时，左侧上下两个管道分别有一定数量的小球（有深色球和浅色球两种类型），而右侧输出管道为空。每一次操作，可以从左侧选择一个管道，并将该管道中最右侧的球推入右边输出管道。

例如：我们首先从下管道中移一个球到输出管道中，将得到图2所示的情况。

（图2）

假设上管道中有n个球, 下管道中有m个球，则整个游戏过程需要进行n+m次操作，即将所有左侧管道中的球移入输出管道。最终n+m个球在输出管道中从右到左形成输出序列。

爱好数学的小X知道，他共有C(n+m，n)种不同的操作方式，而不同的操作方式可能导致相同的输出序列。举个例子，对于图3所示的游戏情形：

（图3）

我们用A表示浅色球，B表示深色球。并设移动上管道右侧球的操作为U，移动下管道右侧球的操作为D，则共有C(2+1，1)=3种不同的操作方式，分别为UUD，UDU，DUU；最终在输出管道中形成的输出序列（从右到左）分别为BAB，BBA，BBA。可以发现后两种操作方式将得到同样的输出序列。

假设最终可能产生的不同种类的输出序列共有K种，其中：第i种输出序列的产生方式（即不同的操作方式数目）有ai个。聪明的小X早已知道，

Σai=C(n+m,n)

因此，小X希望计算得到：

Σ(ai)^2

你能帮助他计算这个值么？由于这个值可能很大，因此只需要输出该值对1024523的取模即可（即除以1024523的余数）。

说明：文中C(n+m，n)表示组合数。组合数C(a，b)等价于在a个不同的物品中选取b个的选取方案数。

输入输出格式

输入格式：

 

输入文件中的第一行为两个整数n，m，分别表示上下两个管道中球的数目。

第二行中为一个AB字符串，长度为n，表示上管道中从左到右球的类型。其中：A表示浅色球，B表示深色球。

第三行中为一个AB字符串，长度为m，表示下管道中的情形。

 

输出格式：

 

输出文件中仅一行为一个整数，即为 除以1024523的余数。

 

输入输出样例

输入样例#1： 复制

2 1
AB
B

输出样例#1： 复制

5

说明

【样例说明】

样例即为文中（图3）。共有两种不同的输出序列形式，序列BAB有1种产生方式，而序列BBA有2种产生方式，因此答案为5。

【数据规模和约定】

对于30%的数据，满足：m，n<=12；

对于100%的数据，满足：m，n<=500。

 

解析

果然noi的题就是比较恶心

我们。。。首先可以按照题目说的做法来一波暴力。

好了在noi上得了30分开不开心啊~。

暴力我就不演示了，我们是来研究dp的。。。。。。

 

首先，∑(ai^2)该怎么处理。

这个地方就非常巧妙了。

假设一种输出方案为A，能输出的方案为ai，

那么让两个人玩这个游戏，取到相同的A，方案数不就是ai^2吗。。。。。。

 

这步思路非常巧妙。

然后我们可以列出dp方程，

f[a1][a2][b1][b2]代表取的情况，a代表第一个人，1、2代表上下。

然后由于a1+a2==b1+b2，我们可以省去一维。

然后dp转移如下了，转移的条件是颜色相同：

for (a1=0;a1<=n;++a1){
        for (a2=0;a2<=m;++a2){
            for (b1=0;b1<=n;++b1){
                b2=a1+a2-b1;
                if (b2>m||b2<0) continue;
                if (a[a1+1]==a[b1+1])
                    f[a1+1][a2][b1+1]=((f[a1+1][a2][b1+1]+f[a1][a2][b1])%mod+mod)%mod;
                if (a[a1+1]==b[b2+1])  
                    f[a1+1][a2][b1]=((f[a1+1][a2][b1]+f[a1][a2][b1])%mod+mod)%mod;
                if (b[a2+1]==a[b1+1])
                    f[a1][a2+1][b1+1]=((f[a1][a2+1][b1+1]+f[a1][a2][b1])%mod+mod)%mod;
                if (b[a2+1]==b[b2+1])
                    f[a1][a2+1][b1]=((f[a1][a2+1][b1]+f[a1][a2][b1])%mod+mod)%mod;
            }
        }
    }

 

然后我们欣喜地去交了，得了70分。。。。。。

尽管我们压掉了一维，但是空间还是炸了，这样子只能再来一波玄学滚动了。。。

好的我们再交一次，结果得了10分。。。。。。

 

好了数组别忘了清0。

好了终于a了。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn=502;
const int mod=1024523;
int n,m;
char a[maxn],b[maxn],c[maxn];
int f[2][maxn][maxn];
int a1,a2,b1,b2;
int cur=0;
void trans(){
    for (int i=1;i<=n;++i){
        c[i]=a[n-i+1];
    }
    for (int i=1;i<=n;++i){
        a[i]=c[i];
    }
    for (int i=1;i<=m;++i){
        c[i]=b[m-i+1];
    }
    for (int i=1;i<=m;++i){
        b[i]=c[i];
    }
}
int main(){
    cin>>n>>m;
    cin>>a+1;
    cin>>b+1;
    trans();
    f[0][0][0]=1;
    for (a1=0;a1<=n;++a1,cur^=1){
        for (a2=0;a2<=m;++a2){
            for (b1=0;b1<=n;++b1){
                f[cur^1][a2][b1]=0;
            }
            for (b1=0;b1<=n;++b1){
                b2=a1+a2-b1;
                if (b2>m||b2<0) continue;
                if (a[a1+1]==a[b1+1])
                    f[cur^1][a2][b1+1]=((f[cur^1][a2][b1+1]+f[cur][a2][b1])%mod+mod)%mod;
                if (a[a1+1]==b[b2+1])  
                    f[cur^1][a2][b1]=((f[cur^1][a2][b1]+f[cur][a2][b1])%mod+mod)%mod;
                if (b[a2+1]==a[b1+1])
                    f[cur][a2+1][b1+1]=((f[cur][a2+1][b1+1]+f[cur][a2][b1])%mod+mod)%mod;
                if (b[a2+1]==b[b2+1])
                    f[cur][a2+1][b1]=((f[cur][a2+1][b1]+f[cur][a2][b1])%mod+mod)%mod;
            }
        }
    }
    printf("%d",f[cur^1][m][n]);
    return 0;
}