洛谷 P5392 [Cnoi2019]雪松树之约
注:此篇文章仅用来测试博客园的markdown,其他文章仍在新博客,
题目相关
题目链接:洛谷 P5392 [Cnoi2019]雪松树之约
题目描述:
我们定义一种图: 圆柱网络 \(G(L,x)\) 。
\(G(L,x)\) 表示一个有 \(L\*x\) 个节点的图。
其中每个节点用一个二元组 \((a,b)\) 表示 \(( a \in [1,L], b \in [1,x] )\) 。
对于 \(\forall i \in (1,L], \ j \in (0,x]\) ,点 \((i, j)\) 与 \((i - 1, j)\) 相连。
对于 \(\forall i \in [1,L], \ j \in (0,x)\) ,点 \((i, j)\) 与 \((i, j +1)\) 相连。
对于 \(\forall i \in [1,L]\) 点 \((i, x)\) 与点 \((i, 1)\) 相连。
现在Cirno想知道 \(G( L, x )\) 的独立集的个数。
由于你不会高精度,所以你需要将答案对 \(998244353\) 取模。
博主注:三个条件看不懂的看下面的示意图就行了。。。
输入输出格式:
输入格式
一行,两个整数, L, x。
输出格式
一行, 表示答案。
输入输出样例:
|编号|输入|输出|
|:|:|:|
|#1|3 4|181|
|#2|1000 8|124141757|
说明:
对于 前 10% 的数据 \(L, x \le 8\)
对于 前 30% 的数据 \(x \le 8\)
对于 前 50% 的数据 \(x \le 11\)
对于 100% 的数据 \(L \le 10^{18}, x \le 17\)
提示
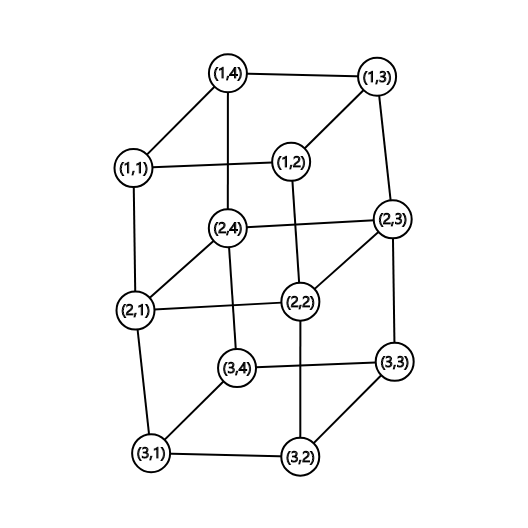
下图为 \(G(3,4)\) 的示意图。
博主乱搞
蒟蒻解析1(50%):
10%的数据:打表状压dp。
30%的数据:非常朴素的状压dp+矩阵加速。
50%的数据:虽然方案数 \(2^{11}\) 比较多,但是真正可行的方案只有199种。我们只需针对可行的方案进行处理,便可以在时间空间上得以满足。
这种减少状态的思维在 100% 的数据也得以体现。
(如果发现因为tle得了30分大概需要卡一卡常数反正我卡了)
蒟蒻代码1(50%):
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<ctime>
using namespace std;
#define ll long long
#define il inline
#define rg register
const ll mod=998244353;
struct matrix{
ll a[210][210];
void clr(){
memset(a,0,sizeof(a));
}
}u,v,ed;
ll n,x,ans;
int a_id[132000],tot;
int num[20]; int p;
il matrix unit(){
matrix tmp; tmp.clr();
for (rg int i=1;i<=200;++i)
tmp.a[i][i]=1;
return tmp;
}
il matrix operator * (matrix aa,matrix bb){
matrix tmp; tmp.clr();
for (rg int k=1;k<=tot;++k){
for (rg int i=1;i<=tot;++i){
for (rg int j=1;j<=tot;++j){
tmp.a[i][j]=((tmp.a[i][j]+aa.a[i][k]*bb.a[k][j]))%mod;
}
}
}
return tmp;
}
il matrix ksm(matrix u,ll t){
matrix tmp=unit();
while (t){
if (t&1) tmp=tmp*u;
u=u*u; t>>=1;
}
return tmp;
}
il void check(int tmp){
int xx=tmp;
p=0; memset(num,false,sizeof(num));
while (tmp){
++p;
if (tmp&1) num[p]=true;
tmp>>=1;
}
for (rg int i=2;i<=x;++i)
if (num[i]&&num[i-1]) return;
if (num[x]&&num[1]) return;
a_id[++tot]=xx; //s[xx]=1;
}
il void link(){
for (int i=1;i<=tot;++i){
for (int j=1;j<=tot;++j){
if ((a_id[i]&a_id[j])==0){
v.a[i][j]=1;
}
}
}
}
int main(){
cin>>n>>x;
for (rg int i=0;i<=(1<<x)-1;++i) check(i);
link();
if (n==1){
cout<<tot;
return 0;
}
ed=ksm(v,n-1);
for (rg int i=1;i<=tot;++i)
for (rg int j=1;j<=tot;++j){
ans=(ans+ed.a[i][j]+mod)%mod;
}
cout<<ans;
return 0;
}
蒟蒻解析2(100%)
当x为17的时候我们发现可行的方案数也达到 3571 让人无法接受。所以我们要减少方案。
方法就是将类似的方案合并,也就是将能循环互相得到的方案归到一组,成为一个总的状态,用它进行转移。
为什么可以这么做?
对于两组状态A,B,我们现在要求由A状态转移到B状态,对于任意的两个状态 \(s1,s2\in{A}\) ,它转移到B状态的方案数是相同的。
证明?显然因为这是个可以循环的结构。我们完全可以把s2旋转到s1的位置重合(属于一个方案组),同样s2时的B中状态也同时旋转到与s1时的B中状态相同。所以是等价的。
(这个道理不好说明可以意会一下。)
通过分组思维我们就可以将方案数减少到 211 种,然后就可以解决此题。
同时记录一下几个坑:
1.注意全0方案的处理。全0方案自成一组,它到任何方案组的方案数为其方案组里的状态总数,任何方案组到全0方案组的的方案数为 1 。
2.方案组可以转移到方案组自身。且注意此时方案数不一定为方案组里状态总数-1。
3.方案组里的状态总数并不一定等于 x 。
最后再来个方案组等价举例:
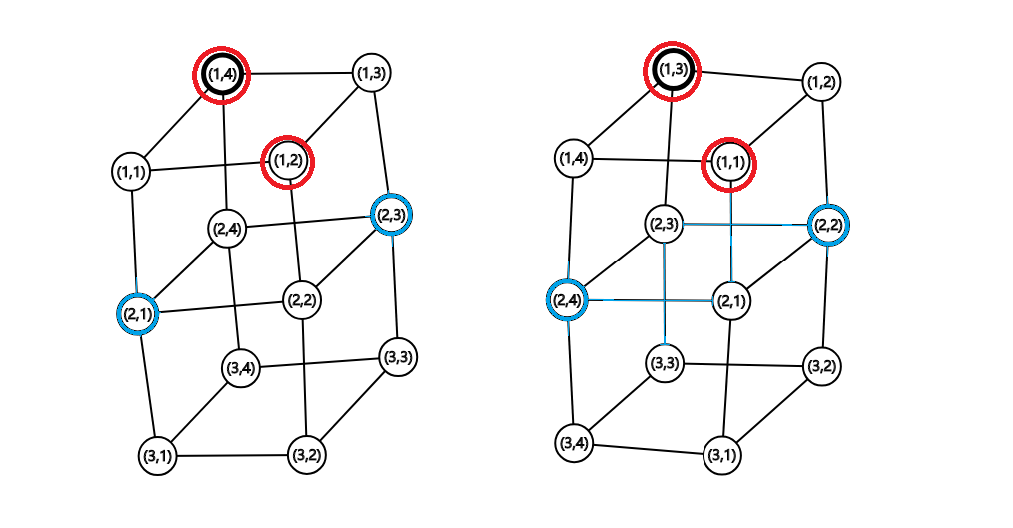
如图,第一层(红色)左右两个状态等价。它们转移到第二层(蓝色)的可选点也就是蓝色标出的点,旋转后即可相同。
蒟蒻代码(100%)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<ctime>
#include<vector>
using namespace std;
#define ll long long
#define il inline
#define rg register
const ll mod=998244353;
struct matrix{
ll a[233][233];
void clr(){
memset(a,0,sizeof(a));
}
}u,v,ed;
ll n,x,ans;
int a_id[132000],tot;
int num[20]; int p;
int s[132000],vis[132000];
vector<int> G[132000];
il matrix unit(){
matrix tmp; tmp.clr();
for (rg int i=1;i<=230;++i)
tmp.a[i][i]=1;
return tmp;
}
il matrix operator * (matrix aa,matrix bb){
matrix tmp; tmp.clr();
for (rg int k=1;k<=tot;++k){
for (rg int i=1;i<=tot;++i){
for (rg int j=1;j<=tot;++j){
tmp.a[i][j]=((tmp.a[i][j]+aa.a[i][k]*bb.a[k][j]))%mod;
}
}
}
return tmp;
}
il int work(int tmp){
if (tmp&(1<<x)) return tmp-(1<<x)+1;
else return tmp;
}
il void checkcircle(int tmp){
G[tmp].push_back(tmp);
a_id[++tot]=tmp;
s[tmp]++; vis[tmp]=1;
int nxt=work(tmp<<1);
while (!vis[nxt]){
G[tmp].push_back(nxt);
vis[nxt]=true; s[tmp]++;
nxt=work(nxt<<1);
}
}
il void check(int tmp){
if (vis[tmp]) return;
int xx=tmp;
p=0; memset(num,0,sizeof(num));
while (tmp){
++p;
if (tmp&1) num[p]=true;
tmp>>=1;
}
for (rg int i=2;i<=x;++i)
if (num[i]&&num[i-1]) return;
if (num[x]&&num[1]) return;
checkcircle(xx);
u.a[tot][tot]=s[a_id[tot]];
}
il void link(){
for (rg int i=1;i<=tot;++i){
for (rg int j=1;j<=tot;++j){
int uu=a_id[i],vv=a_id[j],sum=0,to;
if (vv==0){
v.a[i][j]=1;
continue;
}
if (uu==0){
v.a[i][j]=s[vv];
continue;
}
for (rg int k=0;k<G[vv].size();++k){
to=G[vv][k];
if ((uu&to)==0) ++sum;
}
v.a[i][j]=sum;
}
}
}
int main(){
cin>>n>>x;
for (rg int i=0;i<=(1<<x)-1;++i) check(i);
link();
matrix tmp=unit(); n--;
while (n){
if (n&1) tmp=tmp*v;
v=v*v; n>>=1;
}
ed=u*tmp;
for (rg int i=1;i<=tot;++i)
for (rg int j=1;j<=tot;++j){
ans=(ans+ed.a[i][j]+mod)%mod;
}
cout<<ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号