多维数组的索引方案与内存设计

多维数组的内存结构

类似ndarray之类的多维数组，实际上是一个连续的内存地址+一种索引方案。我们可以将一个多维数组对象分为两部分，一部分是实际存储数组数据的连续内存段，另一部分是存储数组的形状、索引方案、单元素步长、size等信息的header段。

如shape属性指定各维度的元素的数量，dtype属性指定元素类型及其解释方式，strides属性指定各维度的跨度，itemsize属性指定单个元素占用字节数。

dtype	itemsize	shape	strides	datasize	...

索引的解析

对于N维的数组，我们将将各维度的跨度存放在strides列表中，比如strides[0]表示的是数组第1维的步长。第k维的步长为

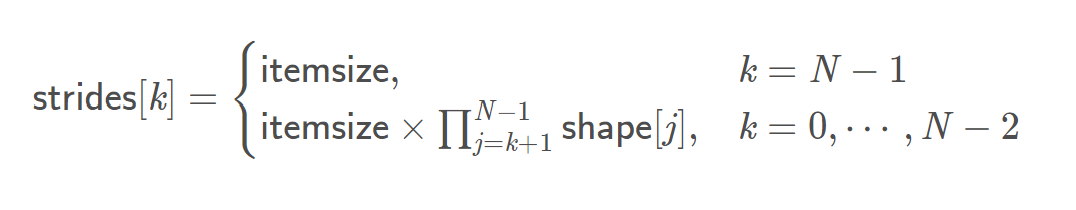
其中我们假设单元素步长为1。假设数组的首地址为&data，那么其坐标为(i0,i1,i2,...,in-1)的元素地址为

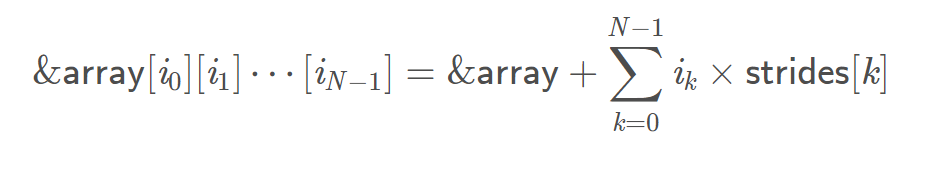
实例1
一个2x3的二维数组，它的第一维的步长是3，第二维也就是最后一维的步长是1，所以它的strides列表为[3,1]

实例2
一个2x3x4的三维数组，它的第一维的步长是3x4=12，第二维步长是4，第三维也就是最后一维的步长是1，所以它的strides列表为[12,4,1]

实例3

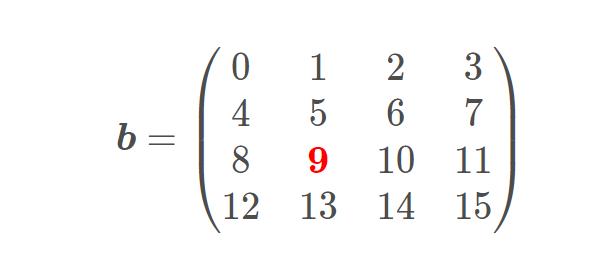
对于上面这个4x4的数组，其形状shape=(4,4)，跨度列表strides = [4,1]。
如果我们以b[2][1]的形式去访问数组元素9，那么索引的解析方案为：

&b[2][1] = &b + 2 * strides[0] + 1 * strides[1]; // &b + 9

所以我们假设数组b的数据实际存储在连续的一维内存段data[]中，那么最终b[2][1]访问的应该是data[9]