KMP算法

https://segmentfault.com/a/1190000008575379
i = 0，对于模式串的首字符，我们统一为next[0] = -1；
i = 1，前面的字符串为A，其最长相同真前后缀长度为 0，即next[1] = 0；
i = 2，前面的字符串为AB，其最长相同真前后缀长度为 0，即next[2] = 0；
i = 3，前面的字符串为ABC，其最长相同真前后缀长度为 0，即next[3] = 0；
i = 4，前面的字符串为ABCD，其最长相同真前后缀长度为 0，即next[4] = 0；
i = 5，前面的字符串为ABCDA，其最长相同真前后缀为A，即next[5] = 1；
i = 6，前面的字符串为ABCDAB，其最长相同真前后缀为AB，即next[6] = 2；
i = 7，前面的字符串为ABCDABD，其最长相同真前后缀长度为 0，即next[7] = 0。
那么，为什么根据最长相同真前后缀的长度就可以实现在不匹配情况下的跳转呢？举个代表性的例子：假如i = 6时不匹配，此时我们是知道其位置前的字符串为ABCDAB，仔细观察这个字符串，首尾都有一个AB，既然在i = 6处的 D 不匹配，我们为何不直接把i = 2处的 C 拿过来继续比较呢，因为都有一个AB啊，而这个AB就是ABCDAB的最长相同真前后缀，其长度 2 正好是跳转的下标位置。

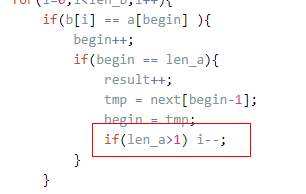
int main()
{

    char t[1000000];
    char p[10000];
    
    scanf("%s", &t);   //AVERDXIVYERDIAN
    scanf("%s", &p);   //RDXI
    
    int len_t = strlen(t);
    int len_p = strlen(p);
    //printf("%d %d\n", len_t, len_p);
    int begin;
    int end;
    int *next = (int *)malloc(sizeof(int) * len_p);
    next[0] = -1;
    next[1] = 0;
    int i;
    int tmp;
    for (i = 2; i < len_p; i++) {
        begin = 0;
        end = i-1;
        tmp = 0;
        while (begin >= end && p[begin] == p[end]) {
            begin++;
            end--;
            tmp++;
        }
        next[i] = tmp;
    }
    
    begin = 0;
    for (i = 0; i < len_t; i++) {
        if (t[i] == p[begin]) {
            begin++;
            if (begin == len_p) {
                printf("%d",i-(len_p-1)+1);
                return 0;
            }
        } else {
            tmp = next[begin];
            if (tmp == -1) {
                begin = 0;
            } else {
                begin = tmp;
                i--;
            }
        }   
    }   
    printf("No");
    return 0;
}