一些问题

总结学习 \(k\cdot p\) 遇到的小问题.

---

• 高对称点的波矢群和 \(\Gamma\) 的一致吗？
  不一致。

空间群的点群 \(G_0\) 的群元 \(R\)，分别作用在波矢 \(k\) 上，得到 \(g_0\) 个波矢量 \(Rk\)，由于 \(k\) 和 \(k+G_h\) 是等价的，可把它们看做是相同的波矢。所以，\(g_0\) 个波矢 \(Rk\) 就不一定都是不相同的。可以将点群 \(G_0\) 的群元分成两类，其中一类满足:

\[R k = k + G_h \]

另一类满足: \(R k \neq k + G_h\)。
当 \(k=\Gamma\) 点, 对于点群 \(G_0\) 任意的群元都有 \(Rk=k\)，表示 \(\Gamma\) 点的波矢群与该空间群的点群一致。当为其他高对称点时，也可能存在 \(Rk=k+G_h\)，需要具体分析。如果不是高对称点时，即除了 \(Ek=k\)外，其他群元都是 \(R k \neq k + G_h\)，表示此时的波矢群仅由恒等元构成。

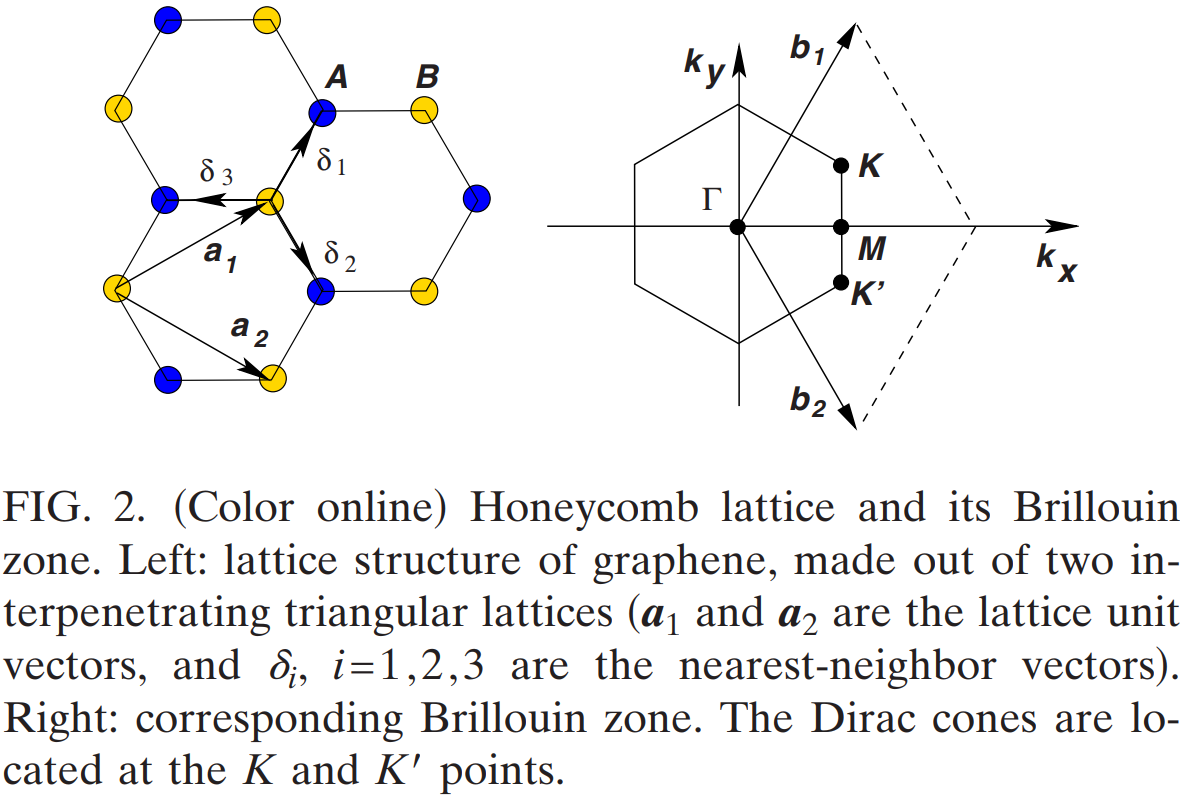
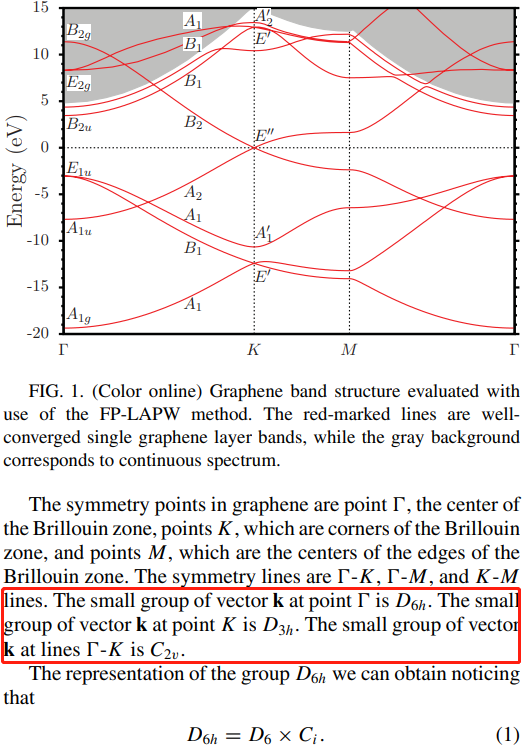
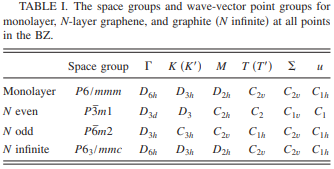
下面我们以石墨烯体系为例，它的点群是 \(D_{6h}\)，但是 \(K\) 点的波矢群却是 \(D_{3h}\)。

参考
https://blog.sciencenet.cn/home.php?mod=space&uid=1502061&do=blog&id=1201748
http://dx.doi.org/10.1103/PhysRevB.85.115418
http://dx.doi.org/10.1103/RevModPhys.81.109
http://dx.doi.org/10.1103/PhysRevB.79.125426

---

• \(H(k)^{*}\) 是矩阵的共轭还是共轭转置？
  共轭

---

• 石墨烯 AB 子格的相因子?

为什么石墨烯分A，B两类碳原子？ - waferBiscuit264的回答 - 知乎
https://www.zhihu.com/question/22700344/answer/27516017

---

• 时间反演对称性

---

• 如何确定能带的表示
  vasp2trace 计算第 n 条带的高对称点 trace。

• 用群论语言表述

\[\Gamma^{+}_{1} \not\in\Gamma^{+}_{25}\otimes\Gamma^{-}_{15}\otimes\Gamma^{+}_{25} \]

偶函数乘以奇函数乘以偶函数 = 0。