4-1-二叉树及其遍历 树的同构

4-1-二叉树及其遍历 树的同构 (25分)

 

给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

 

 

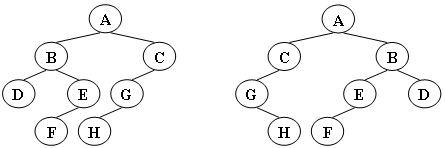
 图1

 

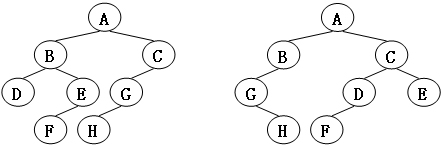
图2

现给定两棵树，请你判断它们是否是同构的。

 

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

 

输出样例1:

Yes

 

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

 

 

这道题目的解答思路其实不难，主要分为三步

-------------------------------------------------------------------------------

I.表示二叉树的方法：结构体数组，静态链表
-----------------------------------------------------------------------------

II.题目并没有说第一个输入的就是根节点，所以要找到根节点，

每个儿子都有一个连向父亲节点的边，

那么就说明只要他是儿子节点他就有连向父亲的边，

根节点没有父亲，也不会出现在别人的左右子树里面

所以根节点是唯一不会出现在别人左右子树的节点，

我们在输入数据的时候，用一个check数组判断该节点是否出现

如果没有出现那么就是根节点
--------------------------------------------------------------------------------------

III.判断两棵树是否同构，因为树的定义本身就是递归定义的，

如果两棵树同构，显然，他们的左右孩子其中必然也有，

两两同构，这就是一个递归的问题了，

#include<cstdio>
#include <iostream>
using namespace std;
#define Tree int
#define  Null -1
struct TreeNode {
    char element;
    Tree left,right;
};
TreeNode t1[10],t2[10];
//建树，找根
Tree BuildTree (TreeNode* T) {
    int n,Root;
    scanf("%d",&n);
    bool check[n];
    if(!n)return Null;
    char ele,l,r;
    for(int i=0; i<n; i++)check[i]=false;
    for(int i=0; i<n; i++) {
        scanf("%c",&ele);
        scanf("%c %c %c",&ele,&l,&r);
        T[i].element=ele;
        if(l!='-') {
            T[i].left=l-'0';
            check[T[i].left]=true;
        } else {
            T[i].left=Null;
        }
        if(r!='-') {
            T[i].right=r-'0';
            check[T[i].right]=true;
        } else {
            T[i].right=Null;
        }

    }
    for(int i=0; i<n; i++) {
        if(!check[i]) {
            Root=i;
            break;
        }
    }
    return Root;
}
//递归判断同构
bool Isomorphic(Tree r1,Tree r2) {
    if(r1==Null&&r2==Null) {
        return true;
    }
    if((r1==Null&&r2!=Null)||(r1!=Null&&r2==Null)) {
        return false;
    }
    if(t1[r1].element!=t2[r2].element)return false;
    if(t1[r1].left==Null&&t2[r2].left==Null) {
        return Isomorphic(t1[r1].right,t2[r2].right);
    }
    if((t1[r1].left!=Null&&t2[r2].left!=Null)&&t1[t1[r1].left].element==t2[t2[r2].left].element) {
        return Isomorphic(t1[r1].left,t2[r2].left)&&Isomorphic(t1[r1].right,t2[r2].right);
    } else {
        return Isomorphic(t1[r1].left,t2[r2].right)&&Isomorphic(t1[r1].right,t2[r2].left);
    }
}
int main() {
    int r1,r2;
    r1=BuildTree(t1);
    r2=BuildTree(t2);
    if(Isomorphic(r1,r2))printf("Yes");
    else printf("No");
    return 0;
}