目录
- 一元线性回归模型与多元线性回归模型
- 训练集与测试集
- 哑变量
- 自定义哑变量
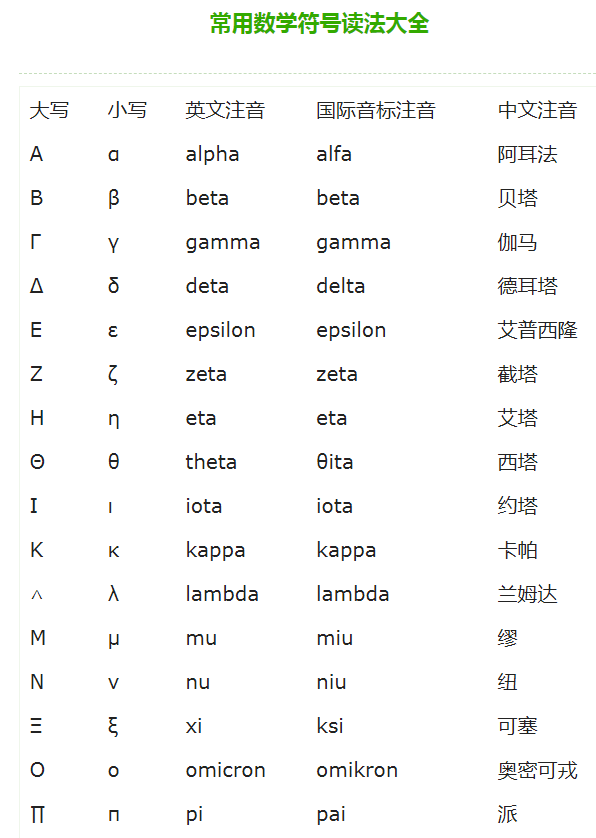
常用数学符号
网站:http://fhdq.net/sx/14.html
![]()
因变量
函数关系式中,某些特定的数会随另一个(或另几个)会变动的数的变动而变动,就称为因变量
![]()
自变量
![]()
线性回归模型
线性回归模型是一种确定变量之间的相关关系的一种数学回归模型
分类:
1.一元线性回归模型
2.多元线性回归模型
如何判断两个变量之间是否存在线性关系与非线性关系
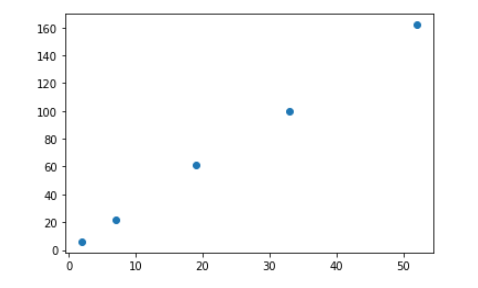
1.散点图
import numpy
import pandas
import matplotlib.pyplot as plt
X = [52,19,7,33,2]
Y = [162,61,22,100,6]
plt.scatter(X,Y)
plt.show()
![]()
2.公式计算
大于等于0.8表示高度相关
绝对值大于等于0.5小于等于0.8表示中度相关
绝对值大于等于0.3小于0.5表示弱相关
绝对值小于0.3表示几乎没有线性关系
公式代码:
#均值
XMean = numpy.mean(X)
YMean = numpy.mean(Y)
#标准差
XSD = numpy.std(X)
YSD = numpy.std(Y)
#z分数
ZX = (X-XMean)/XSD
ZY = (Y-YMean)/YSD
# 相关系数
r = numpy.sum(ZX*ZY)/(len(X))
r
![]()
3.numpy中的corrcoef方法
代码:
![]()
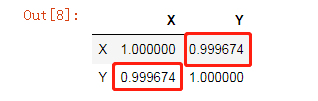
4.pandas中的corr方法:
data = pandas.DataFrame({'X':X,'Y':Y})
t2=data.corr()
t2
![]()
一元线性回归模型的应用
导入模块
import statsmodels.api as sm
sm.ols(formula, data, subset=None, drop_cols=None)
重要参数
formula:以字符串的形式指定线性回归模型的公式,如'y~x'就表示简单线性回归模型
data:指定建模的数据集
subset:通过bool类型的数组对象,获取data的子集用于建模
drop_cols:指定需要从data中删除的变量
一元线性回归模型
# 主要用来解决影响某个事物变化的元素只有一种条件的情况
y = a + bx + 误差项
"""
y是因变量 a是截距项 b是斜率项 x是自变量 误差项用于描述无法解释的部分
"""
描点划线:尽可能多的让点落在直线上 其他点到直线的距离的平方和一定要最小
![]()
案例准备
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
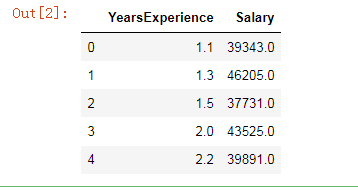
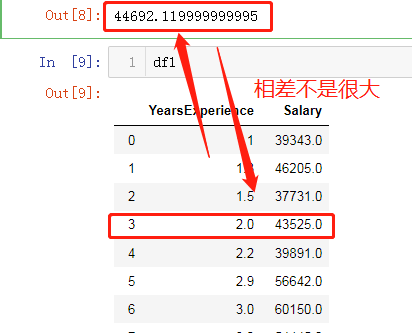
df1 = pd.read_csv(r'Salary_Data.csv')
df1.head()
![]()
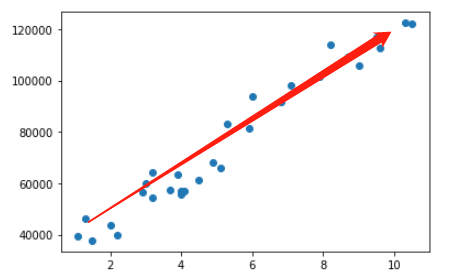
1.先通过散点图查看线性关系
plt.scatter(x=df1['YearsExperience'],y=df1['Salary'])
plt.show()
![]()
2.再通过numpy查看得知是正向线性关系
np.corrcoef(df1['YearsExperience'],df1['Salary'])
![]()
3.创建模型代码
import statsmodels.api as sm
# 利用收入数据集,构建回归模型
fit = sm.formula.ols('Salary~YearsExperience',data=df1).fit()
# 返回模型的参数值
fit.params
![]()
4.测试模型的准确性
# 假设工作了2年,猜测薪资多少?
target_salary = 25792.20 + 9449.96 * 2
target_salary
![]()
多元线性回归
# 主要用来解决影响某个事物变化的因素有多种条件的情况
y = a + b1x2 + b2x2 + b3x3 + ... + 误差项
![]()
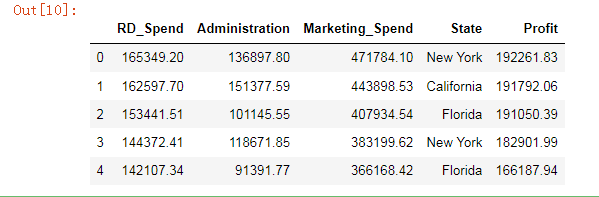
案例准备
profit = pd.read_excel(r'Predict to Profit.xlsx')
profit.head()
![]()
导入模块
from sklearn import model_selection
1.将数据划分为训练集和测试集
train,test = model_selection.train_test_split(profit,test_size=0.2,random_state=1234)
训练集与测试集
# 训练集
用于模型的训练创建
# 测试集
用于模型的测试检验
"""一般情况下训练集占总数据的80%、测试集占总数的20%"""
![]()
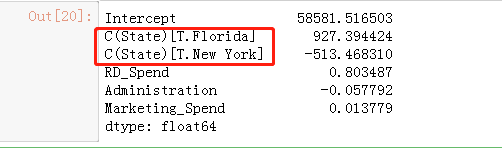
2.创建训练集模型代码:
model = sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+C(State)',data=train).fit()
model.params
![]()
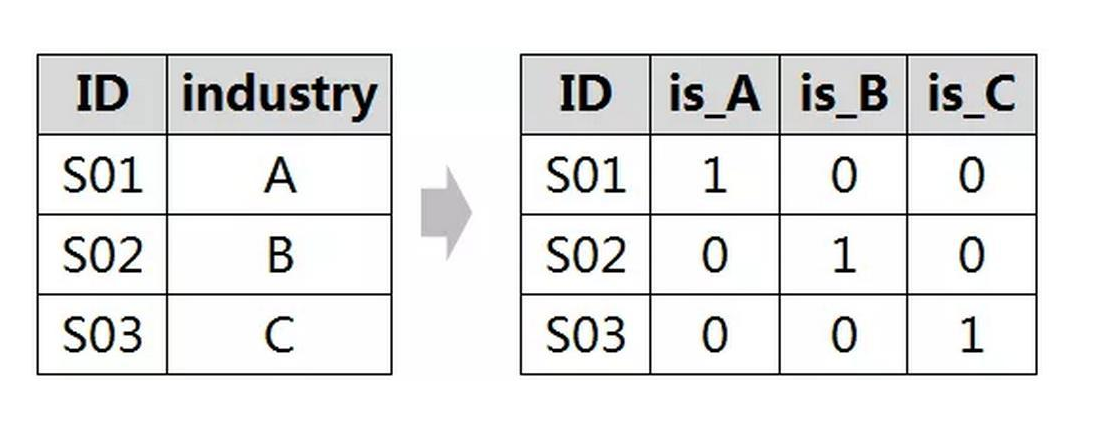
哑变量
数学模型的构建只能是数字类型的数据参与
非数字类型的数据如果要参与构建需要先转换成数字类型(该过程称之为构造哑变量)
哑变量构造完成后还需要确保多个哑变量之间不存在多种共线性
# 构造哑变量 >>> C(State)
![]()
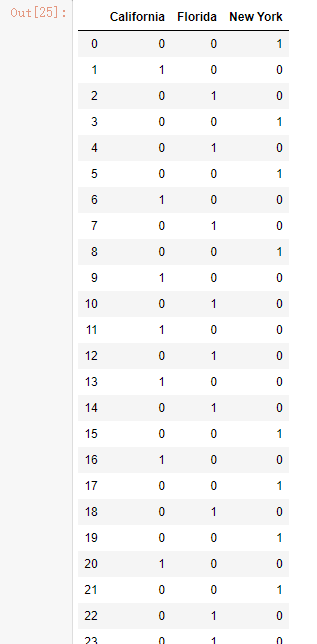
查看由State变量衍生的哑变量
dummies = pd.get_dummies(profit.State)
dummies
![]()
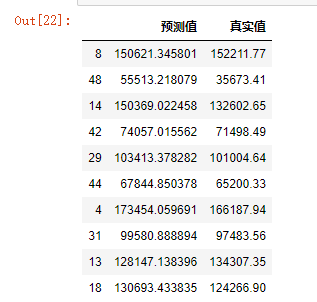
3.删除test数据集中的Profit变量,⽤剩下的⾃变量进⾏预测
test_x = test.drop(columns=['Profit'])
pred = model.predict(exog=test_x)
4.对⽐预测值和实际值的差异
pd.DataFrame({"预测值":pred,'真实值':test.Profit})
![]()
自定义哑变量
# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit,dummies], axis = 1)
# 删除State变量和California变量(因为State变量已被分解为哑变量,New York变量需要作为参照组)
Profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)
# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+Florida+California', data = train).fit()
print('模型的偏回归系数分别为:\n', model2.params)


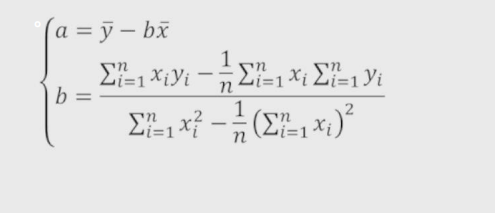


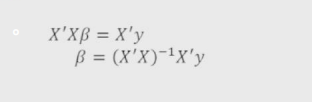





 浙公网安备 33010602011771号
浙公网安备 33010602011771号