多项式学习笔记

多项式

预备知识

多项式的表示方法

系数表示法

将$n$次多项式$A(x)$的系数$a_0,a_1,⋯,a_n$看作$n+1$维向量$\vec{a} =(a_0,a_1,⋯,a_n)$其系数表示就是向量 $\vec{a}$点值表示法

点值表示法

选取$n+1$个不同的数$x_0,x_1,⋯,x_n$对多项式进行求值，得到 $A(x_0),A(x_1),⋯,A(x_n)$那么就称${(xi,A(xi)):0≤i≤n,i∈Z}$为多项式$A(x)$的点值表示

单位根

$n$次单位根

$n$次单位根指的是满足方程$z^n=1$的复数，这些复数一共有$n$个，它们都分布在复平面的单位圆上，把单位圆等分成$n$个部分。根据复数乘法相当于模长相乘，幅角相加就可以知道，$n$次单位根的模长一定是$1$，幅角的$n$倍是$0$，这样$n$次单位根也就是

\[\begin{aligned} e^{\frac{2 \pi k i}{n}}, k=0,1,2, \cdots, n-1 \end{aligned} \]

如果记$\omega{_n}=e^{\frac{2\pi ki}{n}}$,那么$n$次单位根就是$\omega{_n^0},\omega{_n^1},\cdots,\omega{_n^{n-1}}$

单位根的性质

\[\begin{aligned} \omega_{n}^{2}=\left(e^{\frac{2 \pi i}{n}}\right)^{2}=e^{\frac{2 \pi i}{n / 2}}=\omega_ \frac{n}{2}^1\\ \omega_{n}^{\frac{n}{2}+k}=\omega_{n}^{\frac{n}{2}} \cdot \omega_{n}^{k}=-\omega_{n}^{k} \end{aligned} \]

阶

若$(a,p)=1$，且$p>1$

使$a^n\equiv 1 \ (mod\ p)$的最小的$n$称为$a$模$p$的阶，记做$\delta_p(a)$

例如：

$\delta_7(2)=3$

$2^1 \equiv 2 \ (mod \ 7)$

$2^2 \equiv 4 \ (mod \ 7)$

$2^3 \equiv 1 \ (mod \ 7)$

原根

定义

设$p$是正整数，$a$是整数，若$\delta_m(a)$等于$\phi(m)$，则称$a$为模$m$的一个原根

$\delta_7(3)=6=\phi(7)$，因此$3$是模$7$的一个原根

性质

注意原根的个数是不唯一的，正整数$m$存在原根的充要条件为$m=2,4,p^k,2p^k$,其中$p$为奇质数
每一个素数$p$都有$\phi(p−1)$个原根，事实上，每一个正整数$m$都有$\phi(\phi(m))$个原根
若$g$是素数$p$的一个原根，则$g^0,g^1,\cdots,g^{p-2}(mod \ p)$两两不同
因为$(g,p)=1$，根据费马小定理有$g^{p-1} \equiv 1 (mod \ p)$

求法

根据性质4有$g^{p-1} \equiv 1 (mod \ p)$成立当且仅当指数为$p-1$时，所以要求的原根，先对质因数分解$p-1=p_1^{a_1}p_2^{a_2}\cdots p_n^{a_n}$，枚举$i$并判断对于每个$i$是否都有$i^{\frac{p-1}{p_j}} \bmod p \neq 1$(可以通过快速幂)，最小的符合条件的$i$即为$p$的原根，对于合数，只要将前面的$p-1$换成$\phi(p)$即可

一些数的原根

多项式乘法

给定两个多项式$A(x),B(x)$

\[\begin{aligned} A(x) &=\sum_{i=0}^{n} a_{i} x^{i}=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0} \\ B(x) &=\sum_{i=0}^{n} b_{i} x^{i}=b_{n} x^{n}+b_{n-1} x^{n-1}+\cdots+b_{1} x+b_{0} \end{aligned} \]

将这两个多项式相乘得到$C(x)=\sum_{i=0}^{2 n} c_{i} x^{i}$，其中$c_{i}=\sum_{j+k=i, 0 \leq j, k \leq n} a_{j} b_{k} x^{i}$,如果一个个去算 $c_i$ 的话，要花费 $O(n^2)$的时间才可以完成，但是，这是在系数表示下计算的，如果转换成点值表示，知道了$A(x)$,$B(x)$的点值表示后，由于只有$n+1$个点，就可以直接将其相乘，在 $O(n)$的时间内得到$C(x)$的点值表示

如果能够找到一种有效的方法帮助我们在多项式的点值表示和系数表示之间转换，我们就可以快速地计算多项式的乘法了，快速傅里叶变换就可以做到这一点

快速傅里叶变换FFT

快速傅里叶变换分为两个部分，DFT 和 IDFT，分别可以在$O(nlogn)$的时间内将多项式的系数表示转化成点值表示，并且转回来，就像下面这张图所示

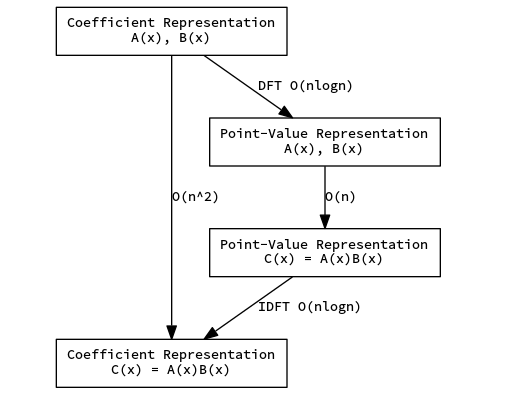
傅里叶变换DFT

DFT的作用是将一个系数表示的多项式转化成点值表示的多项式

假设现在有一个$n-1$次多项式$A(x)=\sum_{i=0}^{n-1} a_{i} x^{i}$(为了方便，假设$n=2^m$，如果不足n为则在高位补$0$)

将$n$个$n$次单位根$$\omega_{n}^{0}, \omega_{n}^{1}, \cdots, \omega_{n}^{n-1}$$，带入$A(x)$将其转化为点值表达

\[A\left(\omega_{n}^{k}\right)=\sum_{i=0}^{n-1} a_{i} \omega^{k i}, k=0,1, \cdots, n-1 \]

但是直接计算每个$\omega$的值仍需要$O(n^2)$的时间，接下来考虑按照指数的奇偶分类

\[\begin{aligned} A\left(\omega_{n}^{k}\right) &=\sum_{i=0}^{n-1} a_{i} \omega_{n}^{k i} \\ &=\sum_{i=0}^{\frac{n}{2}-1} a_{2 i} \omega_{n}^{2 k i}+\omega_{n}^{k} \sum_{i=0}^{\frac{n}{2}-1} a_{2 i+1} \omega_{n}^{2 k i} \end{aligned} \]

但是，如果直接这样递归下去，你需要带入的值还是有$n$ 个，也就是说，现在只是将系数减半，而没有将需要带入的值减半，上面的$k$还是 $0,1,⋯,n−1$，这样的话复杂度还是$O(n^2)$

但是你会注意到，根据预备知识中$\omega_{n}^{2}=\left(e^{\frac{2 \pi i}{n}}\right)^{2}=e^{\frac{2 \pi i}{n / 2}}=\omega \frac{n}{2}$和$\omega_{n}^{\frac{n}{2}+k}=\omega_{n}^{\frac{n}{2}} \cdot \omega_{n}^{k}=-\omega_{n}^{k}$，并且$\frac{n}{2}$次单位根只有$\frac{n}{2}$也就是说我们要带入的值平方以后变少了一半

也就是说，对于$K<\frac{n}{2}$时有

\[A\left(\omega_{n}^{k}\right)=\sum_{i=0}^{\frac{n}{2}-1} a_{2 i} \omega_{\frac{n}{2}}^{k i}+\omega_{n}^{k} \sum_{i=0}^{\frac{n}{2}-1} a_{2 i+1} \omega_{\frac{n}{2}}^{k i} \]

对于$K\geq\frac{n}{2}$时有令$k=K-\frac{n}{2}$

\[\begin{aligned} A(\omega{_n^{k+\frac{n}{2}}})&=\sum_{i = 0}^{\frac{n}{2} - 1}a_{2i}\omega_{\frac{n}{2}}^{ki}+\omega{_n^{k+\frac{n}{2}}}\sum_{i=0}^{\frac{n}{2}-1} a_{2 i+1} \omega_{\frac{n}{2}}^{k i}\\ &=\sum_{i = 0}^{\frac{n}{2} - 1}a_{2i}\omega_{\frac{n}{2}}^{ki}-\omega{_n^k}\sum_{i=0}^{\frac{n}{2}-1} a_{2 i+1} \omega_{\frac{n}{2}}^{k i}\\ \end{aligned} \]

设

\[\begin{aligned} A_1(x) &= \sum_{i = 0}^{\frac{n}{2}-1}a_{2i}x^{2i}\\ A_2(x) &= \sum_{i = 0}^{\frac{n}{2}-1}a_{2i+1}x^{2i+1} \end{aligned} \]

那么化简一下之前的式子可得

\[\begin{aligned} A(x)&=A_{1}\left(x^{2}\right)+x A_{2}\left(x^{2}\right)\\A\left(\omega_{n}^{k}\right) &=A_{1}\left(\omega_{n}^{2 k}\right)+\omega_{n}^{k} A_{2}\left(\omega_{n}^{2 k}\right)\\ &=A_{1}\left(\omega_{\frac{n}{2}}^{k}\right)+\omega_{n}^{k} A_{2}\left(\omega_{\frac{n}{2}}^{k}\right) \\ A\left(\omega_{n}^{k+\frac{n}{2}}\right) &=A_{1}\left(\omega_{n}^{2 k+n}\right)+\omega_{n}^{k+\frac{n}{2}}A_{2}\left(\omega_{n}^{2 k+n}\right) \\ &=A_{1}\left(\omega_{\frac{n}{2}}^{k}\right)-\omega_{n}^{k} A_{2}\left(\omega_{\frac{n}{2}}^{k}\right) \end{aligned} \]

于是我们需要带入计算的值就变成了$\omega{_{\frac{n}{2}}^0}, \omega{_{\frac{n}{2}}}, \omega{_{\frac{n}{2}}^{2}}, \cdots, \omega{_{\frac{n}{2}}^{\frac{n}{2}-1}}$，只需将奇偶指数的项分开递归计算即可，问题规模缩小了一半，所以复杂度为

\[T(n)=2 T\left(\frac{n}{2}\right)+\mathcal{O}(n)=\mathcal{O}(n \log n) \]

逆傅里叶变换IDFT

IDFT的作用是将一个点值表示的多项式转化成系数表示的多项式，它是DFT的逆

这个问题实际上相当于是一个解线性方程组的问题，也就是给出了$n$个线性方程

\[\left\{\begin{array}{ccccc}{a_{0}\left(\omega_{n}^{0}\right)^{0}} & {+} & {\cdots} & {+} & {a_{n-2}\left(\omega_{n}^{0}\right)^{n-2}} & {+} & {+a_{n-1}\left(\omega_{n}^{0}\right)^{n-1}} & {=} & {A\left(\omega_{n}^{0}\right)} \\ {a_{0}\left(\omega_{n}^{1}\right)^{0}} & {+} & {\cdots} & {+} & {a_{n-2}\left(\omega_{n}^{1}\right)^{n-2}} & {+} & {+a_{n-1}\left(\omega_{n}^{1}\right)^{n-1}} & {=} & {A\left(\omega_{n}^{1}\right)} \\ {\vdots} & {} & {\vdots} & {\vdots} & {} & {\vdots} & {} & {\vdots} \\ {a_{0}\left(\omega_{n}^{n-1}\right)^{0}} & {+} & {\cdots} & {+} & {a_{n-2}\left(\omega_{n}^{n-1}\right)^{n-2}} & {+} & {+a_{n-1}\left(\omega_{n}^{n-1}\right)^{n-1}} & {=} & {A\left(\omega_{n}^{n-1}\right)}\end{array}\right. \]

写成矩阵方程的形式就是

\[\left[\begin{array}{cccc}{\left(\omega_{n}^{0}\right)^{0}} & {\left(\omega_{n}^{0}\right)^{1}} & {\cdots} & {\left(\omega_{n}^{0}\right)^{n-1}} \\ {\left(\omega_{n}^{1}\right)^{0}} & {\left(\omega_{n}^{1}\right)^{1}} & {\cdots} & {\left(\omega_{n}^{1}\right)^{n-1}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\left(\omega_{n}^{n-1}\right)^{0}} & {\left(\omega_{n}^{n-1}\right)^{1}} & {\cdots} & {\left(\omega_{n}^{n-1}\right)^{n-1}}\end{array}\right]\left[\begin{array}{c}{a_{0}} \\ {a_{1}} \\ {\vdots} \\ {a_{n-1}}\end{array}\right]=\left[\begin{array}{c}{A\left(\omega_{n}^{0}\right)} \\ {A\left(\omega_{n}^{1}\right)} \\ {\vdots} \\ {A\left(\omega_{n}^{n-1}\right)}\end{array}\right] \]

记上面的系数矩阵为$\mathbf{V}$现在考虑下面这个矩阵$d_{i j}=\omega_{n}^{-i j}$

\[\mathbf{D}=\left[\begin{array}{cccc}{\left(\omega_{n}^{-0}\right)^{0}} & {\left(\omega_{n}^{-0}\right)^{1}} & {\cdots} & {\left(\omega_{n}^{-0}\right)^{n-1}} \\ {\left(\omega_{n}^{-1}\right)^{0}} & {\left(\omega_{n}^{-1}\right)^{1}} & {\cdots} & {\left(\omega_{n}^{-1}\right)^{n-1}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\left(\omega_{n}^{-(n-1)}\right)^{0}} & {\left(\omega_{n}^{-(n-1)}\right)^{1}} & {\cdots} & {\left(\omega_{n}^{-(n-1)}\right)^{n-1}}\end{array}\right] \]

设它们相乘后的结果是$\mathbf{E}=\mathbf{D} \cdot \mathbf{V}$，则

\[\begin{aligned} e_{ij} &=\sum_{k = 0}^{n - 1}d_{i,k}v_{k,j}\\ &=\sum_{k=0}^{n-1} \omega_{n}^{-i k} \omega_{n}^{k j}\\ &=\sum_{k=0}^{n-1} \omega_{n}^{k(j-i)} \end{aligned} \]

当$i=j$时，$e_{ij}=n$

当$i \neq j$时

\[\begin{aligned} e_ij&=\sum_{k=0}^{n-1} (\omega_{n}^{j-i})^k\\ &=\frac{1-(\omega_{n}^{j-i})^n}{1-\omega_{n}^{j-i}} \end{aligned} \]

因为$(\omega_{n}^{j-i})^n=1$，所以$e_{ij}=0$

因此可知$\mathbf{I_n}=\frac{1}{n}\mathbf{E}$，其中$\mathbf{I_n}$为基准矩阵，所以$\frac{1}{n} \mathbf{D}=\mathbf{V}^{-1}$

带回到矩阵方程中可得

\[\left[\begin{array}{c}{a_{0}} \\ {a_{1}} \\ {\vdots} \\ {a_{n-1}}\end{array}\right]=\frac{1}{n}\left[\begin{array}{cccc}{\left(\omega_{n}^{-0}\right)^{0}} & {\left(\omega_{n}^{-0}\right)^{1}} & {\cdots} & {\left(\omega_{n}^{-0}\right)^{n-1}} \\ {\left(\omega_{n}^{-1}\right)^{0}} & {\left(\omega_{n}^{-1}\right)^{1}} & {\cdots} & {\left(\omega_{n}^{-1}\right)^{n-1}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\left(\omega_{n}^{-(n-1)}\right)^{0}} & {\left(\omega_{n}^{-(n-1)}\right)^{1}} & {\cdots} & {\left(\omega_{n}^{-(n-1)}\right)^{n-1}}\end{array}\right]\left[\begin{array}{c}{A\left(\omega_{n}^{0}\right)} \\ {A\left(\omega_{n}^{1}\right)} \\ {\vdots} \\ {A\left(\omega_{n}^{n-1}\right)}\end{array}\right] \]

这样，IDFT就相当于把DFT过程中的$\omega_{n}^{i}$换成$\omega_{n}^{-i}$，然后做一次DFT，之后结果除以$n$就可以了。

这样便能实现多项式乘法了，但是上面这种递归实现的效率太低，可以通过迭代缩小常数优化复杂度

迭代实现FFT

假设现在有8个数要进行DFT，看看递归的过程

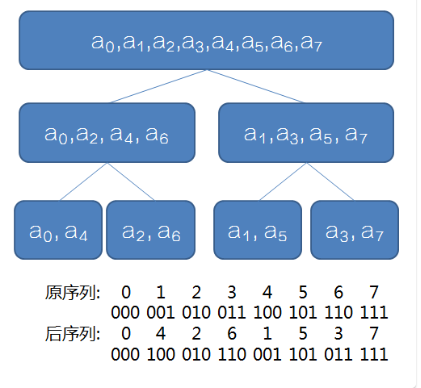
通过观察原序列和反转后的序列，不难发现原序列下标的二进制反转就是后序列，因此我们对序列按照下标的奇偶性分类的过程其实是没有必要的

这样我们可以$O(n)$的利用某种操作得到我们要求的序列，然后不断向上合并就好了

那么考虑如何$O(n)$求每个二进制的反转，可以考虑类似数位$dp$的东西

 r[i] = ( r[i >> 1] >> 1 ) | ( (i & 1) << (l - 1) )

在原序列中$i$与$i/2$的关系是：$i$可以看做是$i/2$的二进制上的每一位左移一位得来，那么在反转后的数组中就需要右移一位，同时特殊处理一下奇数要$+1$的情况即可

至此，FFT就结束了，下面附上代码

代码

/*
Problem : luogu P3803
Algorithm : FFT
Status : AC
*/
#include <bits/stdc++.h>
#include <cstring>
#include <vector>
#include <algorithm>
#include <cstdio>
#include <iostream>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;

const int INF = 0x3f3f3f3f;
const int MAXN = 5e6 + 5;
const double PI = acos(-1.0);

int n,m,len;
int r[MAXN << 1];

struct Complex{
	double x,y;
	Complex() {}
	Complex(double _x,double _y) : x(_x),y(_y) {}
	
	friend Complex operator + (const Complex &x,const Complex &y){
		return Complex(x.x + y.x,x.y + y.y);
	}

	friend Complex operator - (const Complex &x,const Complex &y){
		return Complex(x.x - y.x,x.y - y.y);
	}

	friend Complex operator * (const Complex &x,const Complex &y){
		return Complex(x.x * y.x - x.y * y.y,x.x * y.y + x.y * y.x);
	}
} a[MAXN << 1],b[MAXN << 1],c[MAXN << 1];

void FFT(Complex *a,int len,int flag){
	for(int i = 0;i < len;i++){
		if(i < r[i])
			swap(a[i],a[r[i]]);
	}
	for(int i = 2;i <= len;i <<= 1){
		Complex wn(double(cos(flag * 2 * PI / i)),double(sin(flag * 2 * PI / i)));
		for(int j = 0;j < len;j += i){
			Complex w(1,0);
			for(int k = j;k < j + i / 2;k++){
				Complex u = a[k];
				Complex t = a[k + i / 2] * w;
				a[k] = u + t;
				a[k + i / 2] = u - t;
				w = w * wn;
			}
		}
	}
	if(flag == -1){
		for(int i = 0;i < len;i++)
			a[i].x /= len;
	}
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i = 0;i <= n;i++)
		scanf("%lf",&a[i].x);
	for(int i = 0;i <= m;i++)
		scanf("%lf",&b[i].x);
	len = 1;
	int cnt = 0;
	while(len <= n + m){
		cnt++;
		len <<= 1;
	}
	for(int i = 0;i < len;i++)
		r[i] = (r[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
	FFT(a,len,1);
	FFT(b,len,1);
	for(int i = 0;i < len;i++)
		c[i] = a[i] * b[i];
	FFT(c,len,-1);
	for(int i = 0;i <= n + m;i++)
		printf("%d ",(int)(c[i].x + 0.5));
	return 0;
}

快速数论变换NTT

由于FFT涉及浮点数的运算，难免有精度的问题，在计算一些只要求整数的卷积或高精度乘法的时候就有可能由于精度出现错误，这便让我们考虑是否有在模意义下的方法，这就是快速数论变换

NTT的核心和基础就是原根$g$和FFT中$\omega$的关系

对于素数$p$，设它的原根为$G$满足$G^0,G^1,\cdots G^{p-2}$两两不同

对于一个$n$次多项式，设$g_{n}^{k}=\left(G^{\frac{p-1}{n}}\right)^{k}，k=0,1,2,\dots,n-1$。其中需要保证$\frac{p-1}{n}$ 是一个整数，由于FFT和NTT都需要把多项式的项数改为$2$的次幂，所以$n$可能是一个很大的$2$的次幂，要使得$\frac{p-1}{n}$是整数，那么$p-1$就需要包含很多个因子，但是这样的$p$并不多，这就造成了NTT的实际应用非常受限，比如$998244353=2^{23}\cdot 119 +1$就是一个非常好的NTT模数，其减$1$是$2^{23}\approx 8e6$的倍数，所以$n$的范围一般都小于$4e6$。

根据$g_n^k$的定义，我们是否能用$g_n^k$来替换$\omega_{_n}^k$？这需要我们验证它在模意义下是否具有$\omega$在FFT中所有的性质

在FFT中利用到了单位根$\omega$的如下性质：

$n$个单位复根两两不同
$\omega_{n}^{k}=\omega_{2 n}^{2 k}$
$(\omega_n^k)^n=1$
$\omega_{n}^{k}=-\omega_{n}^{k+\frac{n}{2}}$
$\omega_{n}^{a} \cdot \omega_{n}^{b}=\omega_{n}^{a+b}$

再看一下原根的性质：

根据原根的定义，$g_n^k$两两不同
$g_{2 n}^{2 k}=\left(G^{\frac{p-1}{2 n}}\right)^{2 k}=\left(G^{\frac{p-1}{n}}\right)^{k}=g_{n}^{k}$
$(g_n^k)^n=(G^{\frac{p-1}{n}})^{nk}=(G^{p-1})^k=1$
$g_{n}^{k+\frac{n}{2}}=\left(G^{\frac{p-1}{n}}\right)^{k+\frac{n}{2}}=\left(G^{\frac{p-1}{n}}\right)^{k} G^{\frac{p-1}{2}}=g_{n}^{k} G^{\frac{p-1}{2}}$ 因为$(G^{\frac{p-1}{2}})^2=G^{p-1}=1$，又根据原根的定义$G^{\frac{p-1}{2}}\neq G^{p-1}$ 所以$G^{\frac{p-1}{2}}=-1$所以$g_{n}^{k}=-g_{n}^{k+\frac{n}{2}}$
$g_n^a \cdot g_n^b=(G^{p-1})^a \cdot (G^{p-1})^b = (G^{p-1})^{a+b}=g_n^{a+b}$

所以$g_n^k$具有$\omega_n^k$的所有性质，直接将FFT中$\omega$在模意义下替换成$g$即可，其中$g_n=G^{\frac{p-1}{n}}$

至此，NTT也讲完了，下面还是附上代码

代码

/*
Problem : luogu P3803
Algorithm : NTT
Status : AC
*/
#include <bits/stdc++.h>
#include <cstring>
#include <vector>
#include <algorithm>
#include <cstdio>
#include <iostream>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;

const int INF = 0x3f3f3f3f;
const int MAXN = 5e6 + 5;
const int G = 3;
const int MOD = 998244353;
const int Gi = 332748118;

int n,m;
int a[MAXN],b[MAXN],c[MAXN],r[MAXN];

int power(int x,int y){
	int res = 1;
	while(y){
		if(y & 1)
			res = 1ll * res * x % MOD;
		x = 1ll * x * x % MOD;
		y >>= 1;
	}
	return res;
}

void NTT(int *a,int len,int flag){
	for(int i = 0;i < len;i++){
		if(i > r[i])
			swap(a[i],a[r[i]]);
	}
	for(int i = 2;i <= len;i <<= 1){
		int gn = power(flag == 1 ? G : Gi,(MOD - 1) / i);
		for(int j = 0;j < len;j += i){
			int g = 1;
			for(int k = j;k < j + (i >> 1);k++){
				int x = a[k];
				int y = 1ll * g * a[k + (i >> 1)] % MOD;
				a[k] = (x + y) % MOD;
				a[k + (i >> 1)] = (x - y + MOD) % MOD;
				g = 1ll * g * gn % MOD;
			}
		}
	}
	if(flag == -1){
		int invlen = power(len,MOD - 2);
		for(int i = 0;i < len;i++)
			a[i] = 1ll * a[i] * invlen % MOD;
	}
}

int main(){
    //freopen(".in","r",stdin);
    //freopen(".out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i = 0;i <= n;i++)
		scanf("%d",&a[i]);
	for(int i = 0;i <= m;i++)
		scanf("%d",&b[i]);
	int len = 1,cnt = 0;
	while(len <= n + m){
		cnt++;
		len <<= 1;
	}
	for(int i = 0;i < len;i++)
		r[i] = (r[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
	NTT(a,len,1);
	NTT(b,len,1);
	for(int i = 0;i < len;i++)
		c[i] = 1ll * a[i] * b[i] % MOD;
	NTT(c,len,-1);
	for(int i = 0;i <= n + m;i++)
		printf("%d ",c[i]);
	return 0;
}

任意模数NTT

模数$p$不保证能分解成$p=a \times 2^k+1$的形式时求解两个多项式$F(x)$与$G(x)$的乘积

有以下两种解决思路：

选取$3$个$10^9$级别的NTT模数，进行$3$次NTT，最后把得到的$3$个结果用CRT合并，需要用到$9$次NTT，常数巨大，这里不做赘述
对系数进行分拆后转化成FFT求解(MTT)

我们设$M_0 = \lfloor \sqrt M \rfloor$，根据带余除法可以可以将每一项的系数表示为$aM_0 + b$的形式，于是可以设

\[\begin{aligned} F(x)&=M_0A(x)+B(x)\\ G(x)&=M_0C(x)+D(x)\\ \end{aligned} \]
那么

\[F(x)G(x)=M_0^2A(x)C(x)+M_0(A(x)D(x)+B(x)C(x))+B(x)D(x) \]
这样便可以使得卷积结果中的每个数的大小在$10^{14}$级别，使用long double便可以计算了

但此时仍需要进行$8$次DFT，仍然很慢，于是myy在2016集训队论文《再探快速傅里叶变换》介绍了一种方法：令

\[P(x)=A(x)+iB(x)\\ Q(x)=C(x)+iD(x) \]
于是便有

\[P\left(w_{n}^{j}\right)[x]=\left(A[x]+i B[x]\right) (w_{n}^{j})^x=A[x]\left(\cos \left(\frac{2 \pi x j}{n}\right)+i \sin \left(\frac{2 \pi x j}{n}\right)\right)+B[x]\left(i \cos \left(\frac{2 \pi x j}{n}\right)-\sin \left(\frac{2 \pi x j}{n}\right)\right) \]
同理有

\[P\left(w_{n}^{-j}\right)[x]=A[x]\left(\cos \left(\frac{2 \pi x j}{n}\right)-i \sin \left(\frac{2 \pi x j}{n}\right)\right)+B[x]\left(i \cos \left(\frac{2 \pi x j}{n}\right)+\sin \left(\frac{2 \pi x j}{n}\right)\right) \]
记复数$m$的实部为$re(m)$，虚部为$lm(m)$因此便有

\[\begin{array}{l} A[x]=\frac{re\left(P\left(w_{n}^{j}\right)[x]\right)+re\left(P\left(w_{n}^{-j}\right)[x]\right)}{2}+i \frac{lm\left(P\left(w_{n}^{j}\right)[x]\right)-lm\left(P\left(w_{n}^{-j}\right)[x] \right)}{2} \\ B[x]=\frac{lm\left(P\left(w_{n}^{j}\right)[x] \right)+lm\left(P\left(w_{n}^{-j}\right)[x] \right)}{2}+i \frac{re\left(P\left(w_{n}^{-j}\right)[x]\right) -re\left(P\left(w_{n}^{j}\right)[x] \right)}{2} \end{array} \]
所以记

\[R(x)=A(x)Q(x)=A(x)C(x)+iA(x)D(x)\\ S(x)=B(x)Q(x)=B(x)C(x)+iB(x)D(x) \]
易知$R(x)$的实部为$A(x)C(x)$，虚部为$A(x)D(x)$，$S(x)$同理

所以最终只用$4$次DFT便可以求出$A(x)C(x)$，$A(x)D(x)$，$B(x)C(x)$，$B(x)D(x)$，最后再合并回去就能得到答案了，常数比较优秀。

代码

三模NTT

/*
Problem : luogu P4245
Algorithm : 三模NTT
Status : AC
*/
#include<bits/stdc++.h>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;

const int INF = 0x3f3f3f3f;
const int MAXN = 5e5 + 5;

int n,m,p;
int rev[MAXN];

int power(int x,int y,int MOD){
	int res = 1;
	while(y){
		if(y & 1)
			res = 1ll * res * x % MOD;
		x = 1ll * x * x % MOD;
		y >>= 1;
	}
	return res;
}

int GetInv(int x,int MOD){
	return power(x,MOD - 2,MOD);
}

const int MOD1 = 998244353,MOD2 = 1004535809,MOD3 = 469762049;
const int G = 3;
const int Gi1 = GetInv(G,MOD1),Gi2 = GetInv(G,MOD2),Gi3 = GetInv(G,MOD3);
const ll MOD12 = 1ll * MOD1 * MOD2;
const int inv1 = GetInv(MOD1,MOD2),inv2 = GetInv(MOD12 % MOD3,MOD3);

namespace ModOperation{
	int add(int x,int y,int MOD){
		x += y;
		if(x >= MOD)
			x -= MOD;
		return x;
	}
	
	int sub(int x,int y,int MOD){
		x -= y;
		if(x < 0)
			x += MOD;
		return x;
	}
}

using namespace ModOperation;

struct Int{
	int A,B,C;
	Int() {}
	Int(int x) : A(x),B(x),C(x) {}
	Int(int _A,int _B,int _C) : A(_A),B(_B),C(_C) {}
	
	friend Int operator + (const Int &x,const Int &y){
		return Int(add(x.A,y.A,MOD1),add(x.B,y.B,MOD2),add(x.C,y.C,MOD3));
	}
	
	friend Int operator - (const Int &x,const Int &y){
		return Int(sub(x.A,y.A,MOD1),sub(x.B,y.B,MOD2),sub(x.C,y.C,MOD3));
	}
	
	friend Int operator * (const Int &x,const Int &y){
		return Int(1ll * x.A * y.A % MOD1,1ll * x.B * y.B % MOD2,1ll * x.C * y.C % MOD3);
	}
	
 	int CRT(){
		ll x = 1ll * (B - A + MOD2) % MOD2 * inv1 % MOD2 * MOD1 + A;
		return (1ll * (C - x % MOD3 + MOD3) % MOD3 * inv2 % MOD3 * (MOD12 % p) % p + x) % p;
	}
} wn[MAXN][2],A[MAXN],B[MAXN],Ans[MAXN];

int Init(int n){
	int cnt = 0,len = 1;
	while(len < n){
		cnt++;
		len <<= 1;
	}
	for(int i = 0;i < len;i++)
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
	for(int i = 2;i <= len;i <<= 1){
		wn[i][1] = Int(power(G,(MOD1 - 1) / i,MOD1),power(G,(MOD2 - 1) / i,MOD2),power(G,(MOD3 - 1) / i,MOD3));
		wn[i][0] = Int(power(Gi1,(MOD1 - 1) / i,MOD1),power(Gi2,(MOD2 - 1) / i,MOD2),power(Gi3,(MOD3 - 1) / i,MOD3));
	}
	return len;
}

void NTT(Int *a,int len,int flag){
	for(int i = 0;i < len;i++){
		if(i < rev[i])
			swap(a[i],a[rev[i]]);
	}
	for(int i = 2;i <= len;i <<= 1){
		Int gn = (flag == 1 ? wn[i][1] : wn[i][0]);
		for(int j = 0;j < len;j += i){
			Int g(1);
			for(int k = j;k < j + (i >> 1);k++){
				Int x = a[k];
				Int y = g * a[k + (i >> 1)];
				a[k] = x + y;
				a[k + (i >> 1)] = x - y;
				g = g * gn;
			}
		}
	}
	if(flag == -1){
		Int invlen = Int(GetInv(len,MOD1),GetInv(len,MOD2),GetInv(len,MOD3));
		for(int i = 0;i < len;i++)
			a[i] = a[i] * invlen;
	}
}

int main(){
	//freopen(".in","r",stdin);
	//freopen(".out","w",stdout);
	scanf("%d%d%d",&n,&m,&p);
	for(int i = 0;i <= n;i++){
		int x;
		scanf("%d",&x);
		A[i] = Int(x % p);
	}
	for(int i = 0;i <= m;i++){
		int x;
		scanf("%d",&x);
		B[i] = Int(x % p);
	}
	int len = Init(n + m + 2);
	NTT(A,len,1);
	NTT(B,len,1);
	for(int i = 0;i < len;i++)
		Ans[i] = A[i] * B[i];
	NTT(Ans,len,-1);
	for(int i = 0;i <= n + m;i++)
		printf("%d ",Ans[i].CRT());
	return 0;
}

MTT

/*
Problem : luogu P4245
Algorithm : MTT
Status : AC
*/
#include<bits/stdc++.h>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#define double long double
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;

const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 5;
const double PI = acos(-1.0);

int n,m,p;
int F[MAXN],G[MAXN],Ans[MAXN],rev[MAXN];

struct Complex{
	double x,y;
	Complex() {}
	Complex(double _x,double _y) : x(_x),y(_y) {}
	
	friend Complex operator + (const Complex &x,const Complex &y){
		return Complex(x.x + y.x,x.y + y.y);
	}

	friend Complex operator - (const Complex &x,const Complex &y){
		return Complex(x.x - y.x,x.y - y.y);
	}

	friend Complex operator * (const Complex &x,const Complex &y){
		return Complex(x.x * y.x - x.y * y.y,x.x * y.y + x.y * y.x);
	}
	
	friend Complex operator / (const Complex &x,const int &y){
		return Complex(x.x / y,x.y / y);
	}
};

void FFT(Complex *a,int len,int flag){
	for(int i = 0;i < len;i++){
		if(i < rev[i])
			swap(a[i],a[rev[i]]);
	}
	for(int i = 2;i <= len;i <<= 1){
		Complex wn((double)(cos(flag * 2 * PI / i)),(double)(sin(flag * 2 * PI / i)));
		for(int j = 0;j < len;j += i){
			Complex w(1,0);
			for(int k = j;k < j + (i >> 1);k++){
				Complex u = a[k];
				Complex t = a[k + (i >> 1)] * w;
				a[k] = u + t;
				a[k + (i >> 1)] = u - t;
				w = w * wn;
			}
		}
	}
	if(flag == -1){
		for(int i = 0;i < len;i++)
			a[i] =a[i] / len;
	}
}

void MTT(int *f,int *g,int *res,int n,int m){
	static Complex a[MAXN],b[MAXN],c[MAXN],d[MAXN];
	static const int M0 = (1 << 15) - 1;
	memset(a,0,sizeof(a));
	memset(b,0,sizeof(b));
	memset(c,0,sizeof(c));
	memset(d,0,sizeof(d));
	int len = 1,cnt = 0;
	while(len < n + m){
		len <<= 1;
		cnt++;
	}
	for(int i = 0;i < len;i++)
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
	for(int i = 0;i < len;i++){
		a[i] = (Complex){f[i] & M0,f[i] >> 15};
		b[i] = (Complex){g[i] & M0,g[i] >> 15};
	}
	FFT(a,len,1);
	FFT(b,len,1);
	for(int i = 0;i < len;i++){
		int j = (len - i) & (len - 1);
		c[i] = (Complex){0.5 * (a[i].x + a[j].x),0.5 * (a[i].y - a[j].y)} * b[i];
		d[i] = (Complex){0.5 * (a[i].y + a[j].y),0.5 * (a[j].x - a[i].x)} * b[i];
	}
	FFT(c,len,-1);
	FFT(d,len,-1);
	for(int i = 0;i < len;i++){
		ll c1 = c[i].x + 0.5,c2 = c[i].y + 0.5;
		ll d1 = d[i].x + 0.5,d2 = d[i].y + 0.5;
		res[i] = (c1 % p + ((c2 + d1) % p << 15) + (d2 % p << 30)) % p;
		res[i] = (res[i] + p) % p; 
	}
}

int main(){
//	freopen("P4245_2.in","r",stdin);
//	freopen("P4245_2.ans","w",stdout);
	scanf("%d%d%d",&n,&m,&p);
	for(int i = 0;i <= n;i++){
		scanf("%d",&F[i]);
		F[i] %= p;
	}
	for(int i = 0;i <= m;i++){
		scanf("%d",&G[i]);
		G[i] %= p;
	}
	MTT(F,G,Ans,n + 1,m + 1);
	for(int i = 0;i <= n + m;i++)
		printf("%d ",Ans[i]);
	return 0;
}

分治FFT

问题引入

已知函数$g(x)$在$x\in [1,n-1]$的函数值，定义$f_{i}=\sum_{j=1}^{i} f_{i-j} g_{j}$，求$f(x)$在$x \in [1,n-1]$的值，其中$f_0=1$，答案对$998244353$取模

问题求解

这个其实很容易看出是一个卷积式子，但是对于每一个$f(x)$，我们不可能都做一次FFT，因为那样的话复杂度会退化成$\mathcal O(n^2logn)$，还不如暴力了，所以我们要考虑优化

考虑分治求解，如果我们已经知道了$f(1)\sim f(\frac{n}{2})$的值，那么可以计算出这些已知于未知部分$f(\frac{n}{2}+1)\sim f(n) $的贡献，观察原式，发现对于已知的$f(x)$，对于后面的$f(i)$都会有$f(i-j)g(j)[i-j=x]$的贡献。

所以对于一个当前的区间$l\sim r,mid=\left\lfloor\frac{l+r}{2}\right\rfloor$我们已知$f(l)\sim f(mid)$，那么它对于$f(mid+1)\sim f(r)$的贡献，可以用如下方法快速计算

我们令$A(i)=f(i+l)\{i\in[0,mid-l]\}$，$B(i)=g(i)\{i\in[1,r-l]\}$，再令$C=A\times B$,那么对于$f(mid+1)\sim f(r)$中的$f(x)$贡献就为$C(x-l-1)$，卷积的过程用NTT实现即可

那么对于整个区间$[1,n]$，我们分治下去，先计算$[1,\frac{n}{2}]$，然后计算前面对后面的贡献，然后去算$[\frac{n}{2}+1,n]$的值，类似于CDQ分治的过程

总的复杂度为$\mathcal O(nlog^2n)$

代码

/*
Problem : luogu P4721
Algorithm : ·ÖÖÎFFT
Status : AC
*/
#include<bits/stdc++.h>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;

const int INF = 0x3f3f3f3f;
const int MAXN = 2e5 + 5;
const int G = 3;
const int MOD = 998244353;
const int Gi = 332748118;

int n;
int A[MAXN],B[MAXN],rev[MAXN];

int power(int x,int y){
	int res = 1;
	while(y){
		if(y & 1)
			res = 1ll * res * x % MOD;
		x = 1ll * x * x % MOD;
		y >>= 1;
	}
	return res;
}

int GetInv(int x){
	return power(x,MOD - 2);
}

void NTT(int *a,int len,int flag){
	for(int i = 0;i < len;i++){
		if(i < rev[i])
			swap(a[i],a[rev[i]]);
	}
	for(int i = 2;i <= len;i <<= 1){
		int gn = power(flag == 1 ? G : Gi,(MOD - 1) / i);
		for(int j = 0;j < len;j += i){
			int g = 1;
			for(int k = j;k < j + (i >> 1);k++){
				int x = a[k];
				int y = 1ll * g * a[k + (i >> 1)] % MOD;
				a[k] = (x + y) % MOD;
				a[k + (i >> 1)] = (x - y + MOD) % MOD;
				g = 1ll * g * gn % MOD;
			}
		}
	}
	if(flag == -1){
		int invlen = GetInv(len);
		for(int i = 0;i < len;i++)
			a[i] = 1ll * a[i] * invlen % MOD;
	}
}

void Mul(int *a,int *b,int *res,int len){
	NTT(a,len,1);
	NTT(b,len,1);
	for(int i = 0;i < len;i++)
		res[i] = 1ll * a[i] * b[i] % MOD;
	NTT(res,len,-1);
}

void Solve(int *f,int *g,int l,int r){
	static int A[MAXN],B[MAXN],C[MAXN];
	if(l == r)
		return;
	int mid = (l + r) >> 1;
	Solve(f,g,l,mid);
	int size = r - l + 1;
	int len = 1,cnt = 0;
	while(len < size){
		len <<= 1;
		cnt++;
	}
	for(int i = 0;i < len;i++)
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
	for(int i = 0;i <= len;i++)
		A[i] = B[i] = 0;	
	for(int i = l;i <= mid;i++)
		A[i - l] = f[i];
	for(int i = 1;i <= r - l;i++)
		B[i - 1] = g[i];
	Mul(A,B,C,len);
	for(int i = mid + 1;i <= r;i++)
		f[i] = (f[i] + C[i - l - 1]) % MOD;
	Solve(f,g,mid + 1,r);
}

int main(){
	//freopen(".in","r",stdin);
	//freopen(".out","w",stdout);
	scanf("%d",&n);
	A[0] = 1;
	for(int i = 1;i < n;i++)
		scanf("%d",&B[i]);
	Solve(A,B,0,n - 1);
	for(int i = 0;i < n;i++)
		printf("%d ",A[i]);
	return 0;
}

多项式运算

多项式求逆

定义

对于一个多项式$A(x)$,如果存在$B(x)$满足$A(x)B(x) \equiv 1 (mod \ x ^n)$，则称$B(x)$为$A(x)$在模$x_n$下的逆元，记作$A^{-1}(x)$

求解过程

先考虑如何求$A^{-1}(x)$,当$n=1$时，$A(x) \equiv a_0 (mod \ p)$，$a_0$是一个常数，于是$A^{-1}=a_0^{-1}$

对于$n>1$的情况，设$B_n(x) = A_n^{-1}(x)$，由定义可知

\[B_n(x)A_n(x) \equiv 1(mod \ x^n) \]

设在$mod \ x^{\lceil \frac{n}{2}\rceil}$意义下$A_n(x)$的逆元是$B_{\frac{n}{2}}(x)$，并且我们已经求出，那么

\[A_n(x)B_{\frac{n}{2}}(x) \equiv 1 (mod \ x^{\lceil \frac{n}{2}\rceil}) \]

由$B_n(x)A_n(x) \equiv 1(mod \ x^n)$得$B_n(x)A_n(x) \equiv 1(mod \ x^{\lceil \frac{n}{2}\rceil})$，与上式相减得

\[B_n(x)-B_{\frac{n}{2}}(x) \equiv 0 (mod \ x^{\lceil \frac{n}{2}\rceil}) \]

上式两边平方得

\[B_n^{2}(x)-2 B_{\frac{n}{2}}(x) B_n(x)+B_{\frac{n}{2}}^2(x) \equiv 0 (mod \ x^{n}) \]

这里解释下为什么平方后模数$x^{\lceil \frac{n}{2}\rceil}$也会平方，因为左边的多项式在$mod \ x^{\lfloor \frac{n}{2}\rfloor}$意义下为$0$，那就说明其$0$到$\frac{n}{2}-1$ 次项的系数都为$0$，平方之后对于第$0 \leq i \leq n-1$项，其系数$a_i=\sum_{x+y=i}a_xa_y$，显然$x$和$y$之间必有一个值小于$\lfloor \frac{n}{2}\rfloor$，因此$a_i$必然是$0$，也就是说平方后在$mod \ x^n$意义下为$0$

然后对于上式乘以$A_n(x)$，整理得

\[B_n(x) \equiv 2 B_{\frac{n}{2}}(x)-A_n(x) B_{\frac{n}{2}}^2(x) (mod \ x^{n}) \]

这样就可以得到$mod \ x ^n$下的逆元了，利用FFT或NTT可在$O(nlogn)$内解决当前的问题，最后总的复杂度为

\[T(n)=T\left(\frac{n}{2}\right)+\mathcal{O}(n \log n)=\mathcal{O}(n \log n) \]

顺便一提，由上面的过程可以看出，一个多项式是否有逆元取决于其常数项$a_0$是否有逆元

代码

void GetInv(int *a,int *res,int len){
    static int tmp[MAXN];
    if(len == 1){
        res[0] = Inv(a[0]);
        return;
    }
    GetInv(a,res,(len + 1) >> 1);
    int p = 1,cnt = 0;
    while(p < (len << 1)){
        p <<= 1;
        cnt++;
    }
    for(int i = 0;i < p;i++)
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
    for(int i = 0;i < p;i++)
        tmp[i] = a[i];
    for(int i = len;i < p;i++)
        tmp[i] = 0;
    NTT(tmp,p,1);
    NTT(res,p,1);
    for(int i = 0;i < p;i++)
        res[i] = 1ll * (2ll - 1ll * res[i] * tmp[i] % MOD + MOD) % MOD * res[i] % MOD;
    NTT(res,p,-1);
    for(int i = len;i < p;i++)
        res[i] = 0;
}

多项式除法

定义

给一个$n$次多项式$A(x)$和一个$m(m\leq n)$次多项式$B(x)$,求一个$n-m$次的多项式$D(x)$$($高次项不存在则补$0$$)$和一个$m-1$次的多项式$R(x)$满足

\[A(x)=D(x) B(x)+R(x) \]

求解过程

首先会想到$R(x)$很碍事，想办法消除$R(x)$的影响之后直接求逆即可

现在给出了一个$n$次多项式$A(x)$，下面进行一个神奇的操作，记$A^R(x)=x^nA(\frac{1}{x})$，不难发现

\[\begin{aligned} A^R(x)&=x^nA(\frac{1}{x})\\ &=x^n\sum_{i=0}^na_i(\frac{1}{x})^i\\ &=\sum_{i=0}^na_i(\frac{1}{x})^ix^n\\ &=\sum_{i=0}^na_ix^{n-i}\\ &=\sum_{i=0}^na_{n-i}x^i \end{aligned} \]

相当于将$A(x)$的系数反转，将$$A(x)=D(x) B(x)+R(x)$$中的$x$用$\frac{1}{x}$替代，再在等式两边同时乘上$x^n$可得

\[\begin{aligned} x^{n} A\left(\frac{1}{x}\right) &=x^{n-m} D\left(\frac{1}{x}\right) x^{m} B\left(\frac{1}{x}\right)+x^{n-m+1} x^{m-1} R\left(\frac{1}{x}\right) \\ A^{R}(x) &=D^{R}(x) B^{R}(x)+x^{n-m+1} R^{R}(x) \end{aligned} \]

到这里会发现一个有趣的事情，$D(x)$的次数反转后不会高于$n-m$，而$x^{n-m+1}R^R(x)$的最低次项次数高于 $n-m$，于是把上面的式子放到$mod \ x^{n-m+1}$的意义下看，$R(x)$的影响被消除了，并且不会影响到$D(x)$，所以式子变成

\[A^{R}(x)=D^{R}(x) B^{R}(x) \quad\left(\bmod x^{n-m+1}\right) \]

这样只需求一个逆元即可得到$D_R(x)$，然后反转即可得到$D(x)$，最后在回带得到$R(x)$

代码

void Mul(int *a,int *b,int *res,int n,int m){
    static int f[MAXN],g[MAXN];
    memset(f,0,sizeof(f));
    memset(g,0,sizeof(g));
    int len = 1,cnt = 0;
    while(len <= (n + m)){
        len <<= 1;
        cnt++;
    }
    for(int i = 0;i <= n;i++)
        f[i] = a[i];
    for(int i = 0;i <= m;i++)
        g[i] = b[i];
    for(int i = 0;i < len;i++)
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
    NTT(f,len,1);
    NTT(g,len,1);
    for(int i = 0;i < len;i++)
        res[i] = 1ll * f[i] * g[i] % MOD;
    NTT(res,len,-1);
}

void Divide(int *a,int *b,int *D,int *R,int n,int m){
	static int InvB[MAXN],tmp[MAXN];
	reverse(a,a + n + 1);
	reverse(b,b + m + 1);
	GetInv(b,InvB,n - m + 1);
	Mul(a,InvB,D,n - m,n - m);
	reverse(D,D + n - m + 1);
	reverse(a,a + n + 1);
	reverse(b,b + m + 1);
	Mul(b,D,tmp,m,n - m);
	for(int i = 0;i < m;i++)
		R[i] = (a[i] - tmp[i] + MOD) % MOD;	
}

多项式ln

定义

给出一个$n-1$次多项式$A(x)$，求一个多项式$B(x)$满足$B(x) \equiv \ln A(x)$

求解过程

设$B(x)=\ln A(x)$，对两边求导得

\[B'(x)=\frac{1}{A(x)}A'(x)=\frac{A'(x)}{A(x)} \]

只需对$A(x)$求个逆元得到$B'(x)$后再积分回去即可

求导公式：$(x^a)'=ax^{a-1}$

积分公式：$\int x^adx=\frac{1}{a+1}x^{a+1}$

代码

void Integral(int *a,int *b,int len){
	for(int i = 1;i < len;i++)
		b[i] = 1ll * a[i - 1] * Inv(i) % MOD;
	b[0] = 0;
}

void Derivation(int *a,int *b,int len){
	for(int i = 1;i < len;i++)
		b[i - 1] = 1ll * a[i] * i % MOD;
	b[len - 1] = 0;
}

void Getln(int *a,int *res,int len){
    static int da[MAXN],inva[MAXN],tmp[MAXN];
    memset(da,0,sizeof(da));
    memset(inva,0,sizeof(inva));
    memset(tmp,0,sizeof(tmp));
    Derivation(a,da,len);
    GetInv(a,inva,len);
    Mul(da,inva,tmp,len,len);
    Integral(tmp,res,len);
}

多项式牛顿迭代

定义

给出一个多项式$G(x)$，求一个多项式$F(x) mod \ x^n$满足$G(F(x))\equiv 0 (mod \ z^n)$

求解过程

首先当$n=1$时，$G(F(x))\equiv 0 (mod\ x)$，假设现在已经求出了

\[G\left(F_{0}(x)\right) \equiv 0(mod \ x^{\lceil\frac{n}{2}\rceil}) \]

然后考虑如何扩展到$mod \ x^n$下，可以把$G(F(x))$在$F_0(x)$处泰勒展开

\[\begin{aligned} G(F(x)) &=G\left(F_{0}(x)\right) \\ &+\frac{G^{\prime}\left(F_{0}(x)\right)}{1 !}\left(F(x)-F_{0}(x)\right) \\ &+\frac{G^{\prime \prime}\left(F_{0}(x)\right)}{2 !}\left(F(x)-F_{0}(x)\right)^{2} \\ &+\cdots \end{aligned} \]

因为$F(x)$和$F_0(x)$的前${\lceil\frac{n}{2}\rceil}$项即$a_0,a_1,\cdots,a_{{\lceil\frac{n}{2}\rceil}}$相同，所以对于$(F(x)-F_0(x))^k,k=2,3,4,\cdots$的最低系数非$0$项的次数大于$2{\lceil\frac{n}{2}\rceil}$,所以对于$(F(x)-F_0(x))^k,k=2,3,4,\cdots$的值在模$x^n$下为$0$可以得到

\[G(F(x)) \equiv G\left(F_{0}(x)\right)+G^{\prime}\left(F_{0}(x)\right)\left(F(x)-F_{0}(x)\right)\left(mod \ x^{n}\right) \]

然后因为$G(F(x))\equiv 0(mod \ x^n)$，所以可得

\[G\left(F_{0}(x)\right)+G^{\prime}\left(F_{0}(x)\right)\left(F(x)-F_{0}(x)\right)\left(mod \ x^{n}\right)\equiv 0(mod \ x^n) \]

整理得

\[F(x) \equiv F_{0}(x)-\frac{G\left(F_{0}(x)\right)}{G^{\prime}\left(F_{0}(x)\right)}\left(mod \ x^{n}\right) \]

注意，这里的$G'$要理解为关于$F_0(x)$的偏导数，因为$G$本质上可以写作$G(x,y)$，且是满足$G(x,F)=0$的二元形式幂级数。而上式应该写成

\[F(x)=F_0(x)-\frac{G(x,F_0(x))}{\frac{\partial G}{\partial y}(x,F_0)}(mod\ x^n) \]

应用

用牛顿迭代法推一下多项式求逆：

求$A(x)$ 的逆. 因为要套到牛顿迭代的式子里，这次我们设$F(x)$满足$A(x)F(x)\equiv 1\pmod{x^n}$

根据牛顿迭代，我们要找一个$ G(x)$ 满足 $G(F(x))\equiv 0\pmod{x^n}$，我们可以令$G(F(x))=F(x)^{-1}-A(x)$ ，因为$A(x)$ 和$F(x)$是互为逆的，所以这个式子中的$F(x)$就是我们要的答案.

根据牛顿迭代，有：

\[\begin{aligned} G(F(x))&=F_{0}(x)-\frac{G\left(F_{0}(x)\right)}{G^{\prime}\left(F_{0}(x)\right)}\\ &=F_{0}(x)-\frac{F_{0}(x)^{-1}-A(x)}{-F_{0}(x)^{-2}}\\ &=2 F_{0}(x)-F_{0}(x)^{2} A(x)\\ \end{aligned} \]

多项式开方

定义

给定一个$n-1$次多项式$A(x)$，求一个在$mod\ x^n$意义下的多项式$B(x)$，满足$B^2(x) \equiv A(x) \ (mod\ x^n)$

求解过程

法一

因为$B^2(x) \equiv A(x) \ (mod\ x^n)$，所以$B^2(x)-A(x) \equiv 0 \ (mod\ x^n)$

设$G(B(x))=B^2(x)-A(x) \ (mod\ x^n)$，由于$A(x)$为常数，所以$G'(B(x))=2B(x)$

进行牛顿迭代得

\[\begin{aligned} B(x) &\equiv B_{0}(x)-\frac{G\left(B_{0}(x)\right)}{G^{\prime}\left(B_{0}(x))\right.} \quad\left(\bmod x^{n}\right)\\ &\equiv\frac{A(x)+B_{0}^{2}(x)}{2 B_{0}(x)} \quad\left(\bmod x^{n}\right)\\ &\equiv \frac{A(x)}{2B_0(x)}+\frac{B_0(x)}{2}\quad\left(\bmod x^{n}\right)\\ \end{aligned} \]

法二

考虑倍增，若求得$B^{\prime 2}(x) \equiv A(x)(mod x^{\lceil\frac{n}{2}\rceil})$，并已知$\left.B^{2}(x) \equiv A(x)(mod \ x \lceil\frac{n}{2}\rceil\right)$，所以

\[\begin{aligned} B^{2}(x)-B^{\prime 2}(x) &\equiv 0 (mod \ x \lceil\frac{n}{2}\rceil)\\ B^{4}(x)+B^{4}(x)-2 B^{2}(x) B^{\prime 2}(x) &\equiv 0 \quad\left(\bmod x^{n}\right)\\ B^{4}(x)+B^{\prime 4}(x)+2 B^{2}(x) B^{\prime 2}(x) &\equiv 4 B^{2}(x) B^{\prime 2}(x) \quad\left(\bmod x^{n}\right)\\ B^{2}(x)+B^{\prime 2}(x) & \equiv 2 B(x) B^{\prime}(x) \quad\left(\bmod x^{n}\right) \\ A(x)+B^{\prime 2}(x) & \equiv 2 B(x) B^{\prime}(x) \quad\left(\bmod x^{n}\right) \\ B(x) & \equiv \frac{A(x)+B^{\prime 2}(x)}{2 B^{\prime}(x)} \quad\left(\bmod x^{n}\right) \end{aligned} \]

代码

void GetSqrt(int *a,int *res,int len){
	static int B[MAXN];
	if(len == 1){
		res[0] = 1;
		return;
	}
	GetSqrt(a,res,(len + 1) >> 1);
	for(int i = 0;i < (len << 1);i++)
		B[i] = 0;
	GetInv(res,B,len);
	Mul(a,B,B,len,len);
	for(int i = 0;i < len;i++)
		res[i] = 1ll * (B[i] + res[i]) * inv2 % MOD;
}

多项式EXP

定义

给出一个$n-1$次多项式$A(x)$，求一个$mod \ x^n$下的多项式满足$B(x) \equiv e^{A(x)}$

求解过程

设$F(x)=e^{A(x)}$，两边同时取$ln$得

\[\ln F(x) - A(x) = 0 \]

构造函数$G(F(x))=\ln F(x)-A(x)$，因为$A(x)$可以看作常数，所以$G'(F(x))=\frac{1}{F(x)}$，根据牛顿迭代有

\[\begin{aligned} F(x) &\equiv F_{0}(x)-\frac{G\left(F_{0}(x)\right)}{G^{\prime}\left(F_{0}(x)\right)}\\ &\equiv F_0(x) - \frac{\ln F_0(x)-A(x)}{\frac{1}{F_0(x)}}\\ &\equiv F_0(x)(1-\ln F_0(x)+A(x))\ (mod \ x^n) \end{aligned} \]

最后$F(x)$的常数项是$1$，复杂度为$$\mathcal{O}(n \log n)$$

代码

void GetExp(int *a,int *res,int len){
    static int f[MAXN],g[MAXN];
    if(len == 1){
        res[0] = 1;
        return;
    }
    GetExp(a,res,(len + 1) >> 1);
    int p = 1,cnt = 0;
    while(p < (len << 1)){
        p <<= 1;
        cnt++;
    }
    for(int i = 0;i < p;i++)
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
    for(int i = 0;i < (len << 1);i++)
        f[i] = g[i] = 0;
    for(int i = 0;i < len;i++)
        g[i] = a[i];
    Getln(res,f,len);
    NTT(res,p,1);
    NTT(f,p,1);
    NTT(g,p,1);
    for(int i = 0;i < p;i++)
        res[i] = 1ll * (1ll - f[i] + g[i] + MOD) % MOD * res[i] % MOD;
    NTT(res,p,-1);
    for(int i = len;i < p;i++)
        res[i] = 0;
}

多项式快速幂

定义

给出一个$n-1$次多项式$A(x)$，求一个在模$x^n$下的多项式$B(x)$满足$B(x)=A(x)^k \ (mod \ x ^ n)$

求解过程

如果直接像普通快速幂那样倍增的乘的画，复杂度是$O(n\log n\log k)$的

由于$a^k=e^{k\ln a}$，所以有

\[A(x)^k = e^{k \ln A(x)} \]

直接求$\ln$后再$Exp$回去即可

代码

void GetPow(int *a,int *res,int k,int len){
	static int tmp[MAXN];
	memset(tmp,0,sizeof(tmp));
	Getln(a,tmp,len);
	for(int i = 0;i < len;i++)
		tmp[i] = 1ll * k * tmp[i] % MOD;
	GetExp(tmp,res,len);
}

完整模板

完整模板（旧）

const int MOD = 998244353;
const int G = 3;
const int Gi = 332748118;

int power(int x,int y){
	int res = 1;
	while(y){
		if(y & 1)
			res = 1ll * res * x % MOD;
		x = 1ll * x * x % MOD;
		y >>= 1;
	}
	return res;
}

void NTT(int *a,int len,int flag){
	for(int i = 0;i < len;i++){
		if(i > r[i])
			swap(a[i],a[r[i]]);
	}
	for(int i = 2;i <= len;i <<= 1){
		int gn = power(flag == 1 ? G : Gi,(MOD - 1) / i);
		for(int j = 0;j < len;j += i){
			int g = 1;
			for(int k = j;k < j + (i >> 1);k++){
				int x = a[k];
				int y = 1ll * a[k + (i >> 1)] * g % MOD;
				a[k] = (x + y) % MOD;
				a[k + (i >> 1)] = (x - y + MOD) % MOD;
				g = 1ll * gn * g % MOD;
			}
		}
	}
	if(flag == -1){
		int inv = power(len,MOD - 2);
		for(int i = 0;i < len;i++)
			a[i] = 1ll * a[i] * inv % MOD;
	}
}

void GetInv(int *a,int *res,int len){
	static int tmp[MAXN];
	if(len == 1){
		res[0] = power(a[0],MOD - 2);
		return;
	}
	GetInv(a,res,(len + 1) >> 1);
	int cnt = 0,p = 1;
	while(p < (len << 1)){
		p <<= 1;
		cnt++;
	}
	for(int i = 0;i < p;i++)
		r[i] = (r[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
	for(int i = 0;i < p;i++)
		tmp[i] = a[i];
	for(int i = len;i < p;i++)
		tmp[i] = 0;
	NTT(tmp,p,1);
	NTT(res,p,1);
	for(int i = 0;i < p;i++)
		res[i] = 1ll * (2ll - 1ll * tmp[i] * res[i] % MOD + MOD) % MOD * res[i] % MOD;
	NTT(res,p,-1);
	for(int i = len;i < p;i++)
		res[i] = 0;
}

void Derivation(int *a,int *res,int len){
	for(int i = 1;i < len;i++)
		res[i - 1] = 1ll * i * a[i] % MOD;
	res[len - 1] = 0;
}

void Integral(int *a,int *res,int len){
	for(int i = 1;i < len;i++)
		res[i] = 1ll * power(i,MOD - 2) * a[i - 1] % MOD;
	res[0] = 0;
}

void Mul(int *a,int *b,int *res,int n,int m){
	static int f[MAXN],g[MAXN];
	int cnt = 0,len = 1;
	while(len < (n + m)){
		len <<= 1;
		cnt++;
	}
	for(int i = 0;i < len;i++)
		r[i] = (r[i >> 1] >> 1) | ((i & 1) << (cnt - 1));
	for(int i = 0;i < n;i++)
		f[i] = a[i];
	for(int i = n;i < len;i++)
		f[i] = 0;
	for(int i = 0;i < m;i++)
		g[i] = b[i];
	for(int i = m;i < len;i++)
		g[i] = 0;
	NTT(f,len,1);
	NTT(g,len,1);
	for(int i = 0;i < len;i++)
		res[i] = 1ll * f[i] * g[i] % MOD;
	NTT(res,len,-1);
}

void Getln(int *a,int *res,int len){
	static int da[MAXN],inva[MAXN],tmp[MAXN];
	memset(da,0,sizeof(da));
	memset(inva,0,sizeof(inva));
	memset(tmp,0,sizeof(tmp));
	Derivation(a,da,len);
	GetInv(a,inva,len);
	Mul(inva,da,tmp,len,len);
	Integral(tmp,res,len);
}

void GetSqrt(int *a,int *res,int len){
	static int B[MAXN];
	if(len == 1){
		res[0] = 1;
		return;
	}
	GetSqrt(a,res,(len + 1) >> 1);
	for(int i = 0;i < (len << 1);i++)
		B[i] = 0;
	GetInv(res,B,len);
	Mul(a,B,B,len,len);
	for(int i = 0;i < len;i++)
		res[i] = 1ll * (B[i] + res[i]) * inv2 % MOD;
}

void Divide(int *a,int *b,int *D,int *R,int n,int m){
	static int InvB[MAXN],tmp[MAXN];
	reverse(a,a + n + 1);
	reverse(b,b + m + 1);
	GetInv(b,InvB,n - m + 1);
	Mul(a,InvB,D,n - m,n - m);
	reverse(D,D + n - m + 1);
	reverse(a,a + n + 1);
	reverse(b,b + m + 1);
	Mul(b,D,tmp,m,n - m);
	for(int i = 0;i < m;i++)
		R[i] = (a[i] - tmp[i] + MOD) % MOD;	
}

void GetExp(int *a,int *res,int len){
	static int f[MAXN],g[MAXN];
	if(len == 1){
		res[0] = 1;
		return;
	}
	GetExp(a,res,(len + 1) >> 1);
	int cnt = 0,p = 1;
	while(p < (len << 1)){
		p <<= 1;
		cnt++;
	}
	for(int i = 0;i < p;i++)
		f[i] = g[i] = 0;
	for(int i = 0;i < len;i++)
		g[i] = a[i];
	Getln(res,f,len);
	NTT(res,p,1);
	NTT(f,p,1);
	NTT(g,p,1);
	for(int i = 0;i < p;i++)
		res[i] = 1ll * (1ll - f[i] + g[i] + MOD) % MOD * res[i] % MOD;
	NTT(res,p,-1);
	for(int i = len;i < p;i++)
		res[i] = 0;
}

void GetPow(int *a,int *res,int k,int len){
	static int tmp[MAXN];
	memset(tmp,0,sizeof(tmp));
	Getln(a,tmp,len);
	for(int i = 0;i < len;i++)
		tmp[i] = 1ll * k * tmp[i] % MOD;
	GetExp(tmp,res,len);
}

完整模板（新）

const int MOD = 998244353;
const int N = 20;
const int G = 3;
const int MAXN = 3e5 + 5;

typedef vector<int> poly;
void print(const poly &a) {for(int i = 0;i < (int)a.size();i++) cout << a[i] << " "; cout << endl;}

namespace Poly{
    const int mod = 998244353;
    int rev[MAXN],w[MAXN],wn[N];

    void addmod(int &x,int y) {x += y; if(x >= mod) x -= mod;}
    void submod(int &x,int y) {x -= y; if(x < 0) x += mod;}
    int add(int x,int y) {addmod(x,y); return x;}
    int sub(int x,int y) {submod(x,y); return x;}
    int power(int x,int y) {int res = 1; while(y) {if(y & 1) res = (ll) res * x % mod; x = (ll) x * x % mod; y >>= 1;} return res;}
    int Inv(int x) {return power(x,mod - 2);}

    void InitNTT(int n){
        wn[n] = power(G,(mod - 1) / (1 << n));
        for(int i = n - 1;i >= 0;i--) wn[i] = (ll) wn[i + 1] * wn[i + 1] % mod;
    }

    int Init(int n){
        int len = 1; while(len < n) len <<= 1;
        for(int i = 0;i < len;i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) * (len >> 1));
        for(int i = 1, t = 1;i < len;i <<= 1, t += 1){
            w[i] = 1;
            for(int j = 1;j < i;j++) w[i + j] = (ll) w[i + j - 1] * wn[t] % mod;
        }
        return len;
    }

    void NTT(poly &a,int flag){
        int n = a.size();
        for(int i = 0;i < n;i++) if(i < rev[i]) swap(a[i],a[rev[i]]);
        for(int i = 2;i <= n;i <<= 1){
            int mid = (i >> 1);
            for(int j = 0;j < n;j += i){
                for(int k = j;k < j + mid;k++){
                    int x = a[k], y = (ll) a[k + mid] * w[k - j + mid] % mod;
                    a[k] = add(x,y); a[k + mid] = sub(x,y);
                }
            }
        }
        if(flag == -1){
            reverse(a.begin() + 1,a.begin() + n); int invn = Inv(n);
            for(int i = 0;i < n;i++) a[i] = (ll) a[i] * invn % mod;
        }
    }

    poly PolyAdd(const poly &A,const poly &B){
        poly res = A;
        for(int i = 0;i < (int)A.size();i++) addmod(res[i],B[i]);
        return res;
    }

    poly PolyMul(const poly &A,const poly &B,int need = 0){
        int n = A.size(), m = B.size();
        if(n < 5 || m < 5){
            poly a; a.resize(n + m - 1);
            for(int i = 0;i < n;i++)
                for(int j = 0;j < m;j++) addmod(a[i + j],(ll) A[i] * B[j] % mod);
            if(need) a.resize(need);
            return a;
        }
        int len = Init(n + m);
        poly a = A, b = B; a.resize(len), b.resize(len);
        NTT(a,1); NTT(b,1);
        for(int i = 0;i < len;i++) a[i] = (ll)a[i] * b[i] % mod;
        NTT(a,-1); a.resize(need ? need : n + m - 1); return a;
    }

    poly PolyInv(const poly &A){
        int n = A.size(); if(n == 1) {return {Inv(A[0])};}
        poly a = A, b = PolyInv(poly(A.begin(),A.begin() + ((n + 1) >> 1)));
        int len = Init(n << 1); a.resize(len), b.resize(len); NTT(a,1); NTT(b,1);
        for(int i = 0;i < len;i++) 
            b[i] = (ll) sub(2,(ll)a[i] * b[i] % mod) * b[i] % mod;
        NTT(b,-1); b.resize(n); return b;
    }

    poly PolyDeriv(const poly &A){
        int n = A.size(); poly a = A;
        for(int i = 1;i < n;i++) a[i - 1] = (ll)i * A[i] % mod;
        a[n - 1] = 0; return a;
    }

    poly PolyInter(const poly &A){
        int n = A.size(); poly a = A;
        for(int i = 1;i < n;i++) a[i] = (ll)A[i - 1] * power(i,mod - 2) % mod;
        a[0] = 0; return a;
    }

    pair<poly,poly> PolyMod(const poly &A,const poly &B){
        int n = A.size(), m = B.size();
        if(n < m) return make_pair(poly(1),A);
        poly a = A, b = B;
        reverse(a.begin(),a.end()); reverse(b.begin(),b.end());
        b.resize(n - m + 1); b = PolyInv(b); a.resize(n - m + 1);
        a = PolyMul(a,b,n - m + 1); reverse(a.begin(),a.end());
        b = PolyMul(a,B,m - 1);
        for(int i = 0;i < m - 1;i++) b[i] = sub(A[i],b[i]);
        return make_pair(a,b);
    }

    poly PolyLn(const poly &A){
        int n = A.size(); poly a = A;
		for(int i = 1;i < n;i++) a[i - 1] = (ll)i * A[i] % mod;
		a[n - 1] = 0; a = PolyMul(a,PolyInv(A),n);
		for(int i = n - 1;i >= 1;i--) a[i] = (ll)a[i - 1] * power(i,mod - 2) % mod;
		a[0] = 0; return a;
    }

    poly PolyExp(const poly &A){
        int n = A.size(); if(n == 1) return {1};
        poly b = PolyExp(poly(A.begin(),A.begin() + ((n + 1) >> 1))); b.resize(n);
        poly c = PolyLn(b); for(int i = 0;i < n;i++) c[i] = sub(A[i],c[i]);
        addmod(c[0],1); poly d = PolyMul(b,c,n); return d;
    }

	poly PolyPow(const poly &A,int k){
		int n = A.size(); poly a; a.resize(n);
        if(!k) {a[0] = 1; return a;}
        int p = 0; while(p < n && !A[p]) p += 1;
        if((ll)p * k >= n) return a; int m = n - p * k; a.resize(m);
        int coef = power(A[p],k), icoef = power(A[p],mod - 2);
        for(int i = 0;i < m;i++) a[i] = (ll)A[i + p] * icoef % mod;
        a = PolyLn(a);
		for(int i = 0;i < m;i++) a[i] = (ll)a[i] * k % mod;
		a = PolyExp(a); poly b; b.resize(n);
        for(int i = 0;i < m;i++) b[i + p * k] = (ll)a[i] * coef % mod;
        return b;
	}

    poly tmp[MAXN];
    #define lson k << 1
    #define rson k << 1 | 1

    void pre_eval(const poly &A,int k,int l,int r){
        if(l == r){
            tmp[k].resize(2); tmp[k][0] = sub(0,A[l]);
            tmp[k][1] = 1; return;
        }
        int mid = (l + r) >> 1;
        pre_eval(A,lson,l,mid); pre_eval(A,rson,mid + 1,r);
        tmp[k] = PolyMul(tmp[lson],tmp[rson]);
    }

    void solve_eval(const poly &A,const poly &B,poly &C,int k,int l,int r){
        if(r - l <= 30){
            for(int i = l;i <= r;i++)
                for(int j = A.size() - 1;j >= 0;j--)
                    C[i] = (A[j] + (ll)C[i] * B[i] % mod) % mod;
            return;
        }
        int mid = (l + r) >> 1;
        solve_eval(PolyMod(A,tmp[lson]).second,B,C,lson,l,mid);
        solve_eval(PolyMod(A,tmp[rson]).second,B,C,rson,mid + 1,r);
    }

    poly PolyEval(const poly &A,const poly &B){
        int m = B.size();
        pre_eval(B,1,0,m - 1); poly c; c.resize(m);
        solve_eval(PolyMod(A,tmp[1]).second,B,c,1,0,m - 1); return c;
    }

    poly solve_itpl(const poly &A,int k,int l,int r){
        if(l == r) return {A[l]};
        int mid = (l + r) >> 1;
        return PolyAdd(PolyMul(solve_itpl(A,lson,l,mid),tmp[rson]),PolyMul(solve_itpl(A,rson,mid + 1,r),tmp[lson]));
    }

    poly PolyItpl(const poly &A,const poly &B){
        int n = A.size(); pre_eval(A,1,0,n - 1);
        poly a; a.resize(n);
        solve_eval(PolyDeriv(tmp[1]),A,a,1,0,n - 1);
        for(int i = 0;i < n;i++) a[i] = (ll)B[i] * Inv(a[i]) % MOD;
        return solve_itpl(a,1,0,n - 1);
    }

    #undef lson
    #undef rson

    struct Initializer {Initializer() {InitNTT(N - 1);}} initializer;
}

posted @ 2021-01-23 21:21 关怀他人阅读(217) 评论(0) 收藏举报

刷新页面返回顶部

关怀他人

多项式学习笔记

多项式

预备知识

多项式的表示方法

系数表示法

点值表示法

单位根

\(n\)次单位根

单位根的性质

阶

原根

定义

性质

求法

多项式乘法

快速傅里叶变换FFT

傅里叶变换DFT

逆傅里叶变换IDFT

迭代实现FFT

代码

快速数论变换NTT

代码

任意模数NTT

代码

分治FFT

问题引入

问题求解

代码

多项式运算

多项式求逆

定义

求解过程

代码

多项式除法

定义

求解过程

代码

多项式ln

定义

求解过程

代码

多项式牛顿迭代

定义

求解过程

应用

多项式开方

定义

求解过程

法一

法二

代码

多项式EXP

定义

求解过程

代码

多项式快速幂

定义

求解过程

代码

完整模板

完整模板（旧）

完整模板（新）

公告