2020集训队作业选做part1
AGC 023E
Solution
首先考虑如何计算排列\(p\)的个数,设\(cnt[i]\)表示\(a_j\geq i\)的个数,那么满足条件的排列\(p\)的总数\(tot\)就是\(tot=\prod cnt[i]−(n−i)\),这是因为考虑从\(n\)开始填数,对于每个数字\(i\),它一共有\(cnt[i]\)个位置可以填,但是后面的数字需要占用\(n−i\)个位置,所以还剩下\(cnt[i]−(n−i)\)个位置可以填。
考虑一对\(i,j\),满足\(i<j\),根据\(a_i\)和\(a_j\)的关系可以分成一下几种情况:
- \(a_i=a_j\),显然对于任意一种满足条件的方案,要么\(pi>pj\)要么\(pi<pj\),并且两两对称,所以满足\(p_i>p_j\)的排列数恰好为\(\frac{tot}{2}\)。
- \(a_i<a_j\),当\(p_j \in [a_i+1,a_j]\)的时候,显然不会产生逆序对,而当\(p_j \in [1,a_i]\)的时候,方案数和\(a_i=a_j\)的情况是一样的,所以可以令\(a_j=a_i\),然后计算此时的排列个数,除以\(2\)就是这种情况的答案,不过修改\(a_j\)的值会使得\([a_i+1,a_j]\)中的\(cnt\)减少\(1\),那么令\(d_i=\frac{cnt_i-1-(n-i)}{cnt_i-(n-i)}\),于是方案数就变成了\(tot \times \prod_{k=a_i+1}^{a_j}d_k\),可以写成前缀积的形式,用树状数组维护前面所有合法的前缀积之和即可,但是\(D\)可能为\(0\),所以对于每个\(i\)只统计它前面不为\(0\)的那一段的答案即可。
- \(a_i>a_j\),考虑问题的反面,即用总方案数减去\(p_i<p_j\)的方案数,就转化成了上一种情况。
Code
int n,tot = 1,ans;
int a[MAXN],d[MAXN],invd[MAXN],cnt[MAXN],pos[MAXN],numzero[MAXN];
void addmod(int &x,int y) {x += y; if(x >= MOD) x -= MOD;}
void submod(int &x,int y) {x -= y; if(x < 0) x += MOD;}
int add(int x,int y) {addmod(x,y); return x;}
int sub(int x,int y) {submod(x,y); return x;}
struct BIT{
int SIZE;
int c1[MAXN],c2[MAXN];
void resize(int _size){
SIZE = _size;
}
void init(){
memset(c1,0,sizeof(c1));
memset(c2,0,sizeof(c2));
}
BIT(){
init();
}
int lowbit(int x){
return x & -x;
}
void modify(int x,int val){
while(x <= SIZE){
addmod(c1[x],val);
c2[x] += 1;
x += lowbit(x);
}
}
int querysum(int x){
int res = 0;
while(x >= 1){
addmod(res,c1[x]);
x -= lowbit(x);
}
return res;
}
int querynum(int x){
int num = 0;
while(x >= 1){
num += c2[x];
x -= lowbit(x);
}
return num;
}
} bit;
int power(int x,int y){
int res = 1;
while(y){
if(y & 1)
res = 1ll * res * x % MOD;
x = 1ll * x * x % MOD;
y >>= 1;
}
return res;
}
int main(){
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
scanf("%d",&n);
for(int i = 1;i <= n;i++)
scanf("%d",&a[i]);
for(int i = 1;i <= n;i++){
scanf("%d",&a[i]);
cnt[a[i]] += 1;
}
for(int i = n;i >= 1;i--)
cnt[i] += cnt[i + 1];
for(int i = 1;i <= n;i++)
cnt[i] -= n - i;
for(int i = 1;i <= n;i++)
tot = 1ll * tot * cnt[i] % MOD;
pos[0] = d[0] = 1;
for(int i = 1;i <= n;i++){
int x = 1ll * (cnt[i] - 1) * power(cnt[i],MOD - 2) % MOD;
numzero[i] = numzero[i - 1];
d[i] = d[i - 1];
if(!x)
pos[++numzero[i]] = i;
else
d[i] = 1ll * d[i] * x % MOD;
invd[i] = power(d[i],MOD - 2);
}
bit.resize(n);
for(int i = 1;i <= n;i++){
addmod(ans,1ll * sub(bit.querysum(a[i]),bit.querysum(pos[numzero[a[i]]] - 1)) * d[a[i]] % MOD * tot % MOD * inv2 % MOD);
bit.modify(a[i],invd[a[i]]);
}
bit.init();
for(int i = n;i >= 1;i--){
submod(ans,1ll * sub(bit.querysum(a[i] - 1),bit.querysum(pos[numzero[a[i]]] - 1)) * d[a[i]] % MOD * tot % MOD * inv2 % MOD);
addmod(ans,1ll * bit.querynum(a[i] - 1) * tot % MOD);
bit.modify(a[i],invd[a[i]]);
}
printf("%d\n",ans);
return 0;
}
AGC 032F
Lemma
在\([0,1)\)上随机取\(n-1\)个点,把线段分成了\(n\)段中所有段长度的最小值的期望是\(\frac{1}{n^2}\)
证明:设最短的一段长度为\(x\),那么剩下的\(n-1\)段的长度都要大于等于\(x\),考虑先将每条线段的长度减去\(x\),于是就变成了在剩下的长度为\(1-nx\)的线段上随机取\(n-1\)个点,那么就有
于是
如果考虑次长段的期望,那么就是剩下的\(1-nx\)中最短的一段的期望,即
于是可以归纳得出第\(k\)短的长度的期望为
Solution
首先可以转化一下题意,令其中某一条边为起点,顺时针每\(\frac{2}{3}\pi\)划分为一个区域,将三个区域中的线段分别染成红绿蓝三种颜色,然后把所有线段的夹角\(\mod \frac{2}{3}\pi\)之后都放到一个区间内,于是问题就变成了
在\([0,\frac{2}{3}\pi)\)中随机取\(n-1\)个点,然后将每个点随机染成红绿蓝三种颜色中的一种,求两端颜色不同的线段长度的最小值的期望
考虑枚举答案是第\(k\)小的线段,那么要求前\(k-1\)小的线段必须同色,根据容斥可以得出这样的概率为\(\frac{1}{3^{k-1}}-\frac{1}{3^k}\),然后根据上面的Lemma不难得出答案为
Code
int n,ans;
int fac[MAXN],ifac[MAXN];
int main(){
scanf("%d",&n);
fac[0] = ifac[0] = 1;
for(int i = 1;i <= n;i++)
fac[i] = 1ll * fac[i - 1] * i % MOD;
ifac[n] = Inv(fac[n]);
for(int i = n - 1;i >= 1;i--)
ifac[i] = 1ll * ifac[i + 1] * (i + 1) % MOD;
int inv3 = Inv(3);
for(int i = 1,tmp = inv3;i <= n;i++,tmp = 1ll * tmp * inv3 % MOD)
addmod(ans,1ll * tmp * ifac[n - i + 1] % MOD * fac[n - i] % MOD);
ans = 1ll * ans * ifac[n] % MOD * fac[n - 1] % MOD;
printf("%d\n",ans);
return 0;
}
CF 516D
Solution
不难发现距离某个点最远的点必定是直径的两个端点之一,记\(d_u\)为到\(u\)最远的点的距离,考虑以直径的中点作为根(即\(D_u\)最小的\(u\)),那么这棵树一定满足\(d_u\leq d_{fa_u}\),将所有点按照\(d\)排序,枚举连通块中最深的点(也是连通块中\(d\)最大的点),然后用双指针扫一遍,用并查集维护连通块大小即可。
Code
int n,Q,len,rt,ans;
ll L;
int head[MAXN],size[MAXN],f[MAXN],vis[MAXN],ord[MAXN];
ll dis[MAXN],d[MAXN];
struct Edge{
int to,next,w;
} e[MAXN << 1];
void add_edge(int u,int v,int w){
e[++len] = (Edge){v,head[u],w};
head[u] = len;
}
void dfs(int u,int fa){
d[u] = max(d[u],dis[u]);
if(dis[u] > dis[rt]) rt = u;
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(v == fa) continue;
dis[v] = dis[u] + e[i].w;
dfs(v,u);
}
}
bool cmp(const int &x,const int &y){
return d[x] < d[y];
}
int Find(int x){
if(x == f[x]) return x;
return f[x] = Find(f[x]);
}
void Merge(int x,int y){
x = Find(x); y = Find(y);
if(x == y) return;
if(size[x] > size[y]) swap(x,y);
f[x] = y;
size[y] += size[x];
ans = max(ans,size[y]);
}
void Solve(){
memset(vis,0,sizeof(vis));
scanf("%lld",&L);
ans = 0;
for(int i = 1;i <= n;i++)
f[i] = i, size[i] = 1;
for(int i = n,j = n;i >= 1;i--){
while(d[ord[j]] > d[ord[i]] + L){
size[Find(ord[j])] -= 1;
j -= 1;
}
vis[ord[i]] = 1;
for(int k = head[ord[i]];k != -1;k = e[k].next){
int v = e[k].to;
if(vis[v]) Merge(ord[i],v);
}
}
printf("%d\n",ans);
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d",&n);
for(int i = 1,u,v,w;i < n;i++){
scanf("%d%d%d",&u,&v,&w);
add_edge(u,v,w);
add_edge(v,u,w);
}
dfs(1,0);
int t = rt; rt = 0; dis[t] = 0;
dfs(t,0);
dis[rt] = 0;
dfs(rt,0);
for(int i = 1;i <= n;i++)
ord[i] = i;
sort(ord + 1,ord + 1 + n,cmp);
scanf("%d",&Q);
while(Q--)
Solve();
return 0;
}
ARC 098F
Solution
根据观察不难发现以下三个结论:
- 每个节点最多捐赠一次,因为捐赠更多一定不优
- 捐赠了某个点之后不会再访问这个点,因为如果会再次访问,先捐赠了一定不优
- 每次到达一个点\(i\)之后,无论是否捐赠,剩余钱数应该不小于\(max(a_i-b_i,0)\)
那么不难得出一种贪心策略:首先选择一个点\(u\),假设删掉\(u\)后形成了\(k\)个连通块,则先捐赠掉\(k-1\)个,然后捐赠\(u\),最后捐赠剩下的一个连通块。
接下来考虑如何确定点\(u\),考虑两个点\(x,y\),先捐赠\(x\)再捐赠\(y\)的限制是\(a_x+b_y\),先捐赠\(y\)再捐赠\(x\)的限制是\(a_y+b_x\),因为要求限制最小,那么先选\(x\)的条件是\(a_x+b_y\leq a_y+b_x\),即\(a_i-b_i\leq a_j-b_j\),也就是\(c_i\leq c_j\),于是我们选择\(c_i\)最大的点作为\(u\)即可。
可以发现每次选择的\(u\)构成了一个树形结构,且满足\(c_i\leq c_{fa_i}\),这棵树可以通过将所有点按\(c_i\)从小到达排序后用并查集维护每个点所属的连通块求出。
于是便可以树形dp了,记\(dp_i\)为捐赠点\(i\)和它的所有子树至少需要多少钱,\(sum_i\)表示\(i\)子树中的所有点的\(b_i\)之和,那么可以枚举最后捐赠的子树进行转移
当\(u\)为叶子的时候有\(dp_u=max(a_i,b_i)\)
Code
int n,m,len;
int head[MAXN],f[MAXN],a[MAXN],b[MAXN],ord[MAXN],vis[MAXN];
ll sum[MAXN],dp[MAXN],c[MAXN];
vector<int> G[MAXN];
struct Edge{
int to,next;
} e[MAXN << 1];
void add_edge(int u,int v){
e[++len] = (Edge){v,head[u]};
head[u] = len;
}
int Find(int x){
if(x == f[x]) return x;
return f[x] = Find(f[x]);
}
void dfs(int u){
sum[u] = b[u];
if(G[u].empty()){
dp[u] = max(a[u],b[u]);
return;
}
for(int v : G[u]){
dfs(v);
sum[u] += sum[v];
}
dp[u] = llINF;
for(int v : G[u])
dp[u] = min(dp[u],sum[u] - sum[v] + max(dp[v],c[u]));
}
bool cmp(const int &x,const int &y){
return c[x] < c[y];
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++){
scanf("%d%d",&a[i],&b[i]);
ord[i] = f[i] = i;
c[i] = max(0,a[i] - b[i]);
}
sort(ord + 1,ord + 1 + n,cmp);
for(int i = 1,u,v;i <= m;i++){
scanf("%d%d",&u,&v);
add_edge(u,v); add_edge(v,u);
}
for(int i = 1;i <= n;i++){
int u = ord[i];
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(vis[v] && Find(v) != u){
G[u].push_back(Find(v));
f[Find(v)] = u;
}
}
vis[u] = 1;
}
dfs(ord[n]);
printf("%lld\n",dp[ord[n]]);
return 0;
}
CF 505E
Solution
考虑二分\(m\)天后最高的竹子的高度\(H\),那么问题就转化成了是否存在一种方案使得\(m\)天后竹子高度都\(\leq H\),如果按照题意一天一天的模拟,就需要考虑把竹子高度减\(p\)后\(<0\)的情况,会比较麻烦,所以可以考虑反向思考,即假设所有竹子都已长到了\(H\),每次生长操作相当于每个竹子高度会减少\(a_i\),而每次砍竹子的操作相当于增加\(p\)的高度。
开始时,对每一个竹子计算出其需要多少次会降低到负高度,用堆维护,每次取出最快的可能下落到负高度的\(k\)个竹子,进行增加高度的操作。最后判断每一天是否有竹子的高度变成负数即可。
其实二分的本质是为了确定“尽可能的靠后砍竹子”的标准。反向思考是为了便于贪心处理策略。
Code
int n,m,k,p;
int h[MAXN],a[MAXN];
ll curH[MAXN];
priority_queue<pli,vector<pli>,greater<pli> > q;
bool Check(ll H){
while(!q.empty()) q.pop();
for(int i = 1;i <= n;i++){
curH[i] = H;
if(H - 1ll * m * a[i] < h[i])
q.push(make_pair(H / a[i],i));
}
for(int i = 1;i <= m;i++){
for(int j = 1;j <= k;j++){
if(q.empty()) return 1;
pli cur = q.top(); q.pop();
if(cur.first < i) return 0;
int id = cur.second;
curH[id] += p;
cur.first = curH[id] / a[id];
if(curH[id] - 1ll * m * a[id] < h[id])
q.push(cur);
}
}
return q.empty();
}
int main(){
scanf("%d%d%d%d",&n,&m,&k,&p);
for(int i = 1;i <= n;i++)
scanf("%d%d",&h[i],&a[i]);
ll l = 0,r = llINF,res = 0;
while(l <= r){
ll mid = (l + r) >> 1;
if(Check(mid)){
res = mid;
r = mid - 1;
}else
l = mid + 1;
}
printf("%lld\n",res);
return 0;
}
AGC 023D
Solution
如果\(X_1<S<X_N\),考虑第\(1\)栋楼和第\(N\)栋楼。
若\(P_1\geq P_N\),那么车一定会先去第\(1\)栋楼,因为就算先向右到达了第\(N-1\)栋楼,接下来也一定是先去第\(1\)栋楼,所以住在第\(N\)栋楼里的人为了尽早回家,肯定会和\(1\)投一样的票。
那么可以考虑将\(P_1+=P_N\),然后删掉第\(N\)栋楼,计算这种情况下到达第\(1\)栋楼的时间,加上\(X_N-X_1\)就是答案。
如果\(P_1<P_N\)同理。
那么这样便可以一直递归下去,直到不满足\(X_1<S<X_N\)为止,顺便统计答案即可。
Code
int n,S;
int X[MAXN];
ll P[MAXN];
ll Solve(int l,int r,int tar){
if(S <= X[l])
return X[r] - S;
if(S >= X[r])
return S - X[l];
if(P[l] >= P[r]){
P[l] += P[r];
return (tar == l) * (X[r] - X[l]) + Solve(l,r - 1,r - 1);
}else{
P[r] += P[l];
return (tar == r) * (X[r] - X[l]) + Solve(l + 1,r,l + 1);
}
}
int main(){
scanf("%d%d",&n,&S);
for(int i = 1;i <= n;i++)
scanf("%d%lld",&X[i],&P[i]);
printf("%lld\n",Solve(1,n,(P[1] >= P[n]) ? 1 : n));
return 0;
}
AGC 032E
Solution
经过观察和打表可知,最后的答案一定是这样:
存在一个分界点,满足分界点左边每一对和都\(<m\),分界点右边每一对和都\(\geq m\),且满足分界点左边和右边都是最大和最小的匹配,次大和次小的匹配,以此类推
证明:分类讨论即可。
于是可以直接二分出最靠右的分界点,计算答案即可。
Code
int n,m,ans;
int a[MAXN];
bool Check(int p){
for(int i = 1;i <= ((n - p) >> 1);i++){
if(a[i + p] + a[n - i + 1] < m)
return 0;
}
return 1;
}
int main(){
scanf("%d%d",&n,&m);
n <<= 1;
for(int i = 1;i <= n;i++)
scanf("%d",&a[i]);
sort(a + 1,a + 1 + n);
int l = 0,r = n >> 1,pos = 0;
while(l <= r){
int mid = (l + r) >> 1;
if(Check(mid << 1)){
pos = mid << 1;
r = mid - 1;
}else
l = mid + 1;
}
for(int i = 1;i <= (pos >> 1);i++)
ans = max(ans,a[i] + a[pos - i + 1]);
for(int i = 1;i <= ((n - pos) >> 1);i++)
ans = max(ans,a[i + pos] + a[n - i + 1] - m);
printf("%d\n",ans);
return 0;
}
CF 555E
Solution
首先将原图进行边双缩点,不难发现可以将\(s\)和\(t\)都在同一个边双里的询问忽略,因为可以通过给边双内的边定向使得其中任意两点都能互相到达。
于是在缩点后原图就变成了一颗树,那么限制\((s,t)\)相当于将树上\(s\to t\)的路径上的边全部定向,具体可以通过树上差分计算每条边\((u,v)\)被定向成\(u\to v\)的次数\(a\)和\(v\to u\)的次数\(b\),最后只需dfs一遍判断每条边的\(a\)和\(b\)是否有一个为\(0\)即可。
Code
int n,m,Q,len = 1,tim,colNum,tot;
int head[MAXN],vis[MAXN << 1],low[MAXN],dfn[MAXN],col[MAXN];
int dep[MAXN],f[MAXN][LOG],up[MAXN],down[MAXN],belong[MAXN];
vector<int> g[MAXN];
struct Edge{
int to,next;
} e[MAXN << 1];
struct Query{
int u,v;
} q[MAXN];
void add_edge(int u,int v){
e[++len] = (Edge){v,head[u]};
head[u] = len;
}
void tarjan(int u,int fa){
dfn[u] = low[u] = ++tim;
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(v == fa) continue;
if(!dfn[v]){
tarjan(v,u);
low[u] = min(low[u],low[v]);
if(low[v] > dfn[u])
vis[i] = vis[i ^ 1] = 1;
}else
low[u] = min(low[u],dfn[v]);
}
}
void dfs1(int u){
col[u] = colNum;
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(col[v] || vis[i]) continue;
dfs1(v);
}
}
void dfs2(int u,int fa){
belong[u] = tot;
dep[u] = dep[fa] + 1;
f[u][0] = fa;
for(int i = 1;i < LOG;i++)
f[u][i] = f[f[u][i - 1]][i - 1];
for(auto v : g[u]){
if(v == fa) continue;
dfs2(v,u);
}
}
int LCA(int u,int v){
if(dep[u] < dep[v]) swap(u,v);
for(int i = LOG - 1;i >= 0;i--){
if(dep[f[u][i]] >= dep[v])
u = f[u][i];
}
if(u == v) return u;
for(int i = LOG - 1;i >= 0;i--){
if(f[u][i] != f[v][i]){
u = f[u][i];
v = f[v][i];
}
}
return f[u][0];
}
bool Check(int u,int fa){
for(auto v : g[u]){
if(v == fa) continue;
if(!Check(v,u) || (up[v] && down[v]))
return false;
up[u] += up[v];
down[u] += down[v];
}
return true;
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d%d",&n,&m,&Q);
for(int i = 1,u,v;i <= m;i++){
scanf("%d%d",&u,&v);
add_edge(u,v); add_edge(v,u);
}
for(int i = 1;i <= n;i++)
if(!dfn[i]) tarjan(i,0);
for(int i = 1;i <= n;i++)
if(!col[i]) colNum++, dfs1(i);
for(int i = 1;i <= n;i++){
for(int j = head[i];j != -1;j = e[j].next){
int v = e[j].to;
if(col[i] < col[v]){
g[col[i]].push_back(col[v]);
g[col[v]].push_back(col[i]);
}
}
}
for(int i = 1;i <= colNum;i++)
if(!belong[i]) tot++, dfs2(i,0);
for(int i = 1,u,v;i <= Q;i++){
scanf("%d%d",&u,&v);
q[i] = (Query){col[u],col[v]};
}
for(int i = 1;i <= Q;i++){
int u = q[i].u,v = q[i].v;
if(u == v) continue;
if(belong[u] != belong[v]){
printf("No\n");
return 0;
}
int lca = LCA(u,v);
up[u] += 1, up[lca] -= 1;
down[v] += 1, down[lca] -= 1;
}
for(int i = 1;i <= colNum;i++){
if(!f[i][0] && !Check(i,0)){
printf("No\n");
return 0;
}
}
printf("Yes\n");
return 0;
}
AGC 022E
Solution
首先考虑如何判断一个数列是否合法。
考虑维护一个栈,满足从栈顶到栈底是由一段连续的\(0\)和一段连续的\(1\)组成。从左到右将每一个数加入栈中,考虑加入的数是什么
- 若加入的数为\(0\):
- 若栈顶为\(0\),如果栈内有\(2\)个\(0\),那么可以替换成一个\(0\),否则入栈。
- 若栈顶为\(1\),直接入栈即可。
- 若加入的数为\(1\):
- 若栈顶为\(0\),则新加入的\(1\)可以和栈顶的\(0\)抵消,因为再加入一个数,这三个数的中位数之和新加入的数有关。
- 若栈顶为\(1\),如果栈内只有一个\(1\)则入栈,否则忽略它。
最后只需要判断栈内\(1\)的个数是否大于等于\(0\)的个数即可。
不难发现栈中\(0\)和\(1\)的个数只有可能是\(0\sim 2\),于是便可以dp了,设\(f_{i,a,b}\)表示看到了第\(i\)位,栈内有\(a\)个\(1\)和\(b\)个\(0\)的方案数。接下来考虑转移:
- \(s[i+1]=0\),则有转移:
- \(s[i+1]=1\),则有转移:
- 若这一位为?,则将上面两种转都做一遍即可。
时间复杂度为\(\mathcal O(n)\)
Code
int n;
int f[MAXN][3][3];
char s[MAXN];
int main(){
scanf("%s",s + 1);
n = strlen(s + 1);
f[0][0][0] = 1;
for(int i = 0;i < n;i++){
if(s[i + 1] != '1'){
for(int a = 0;a <= 2;a++){
addmod(f[i + 1][a][1],f[i][a][2]);
addmod(f[i + 1][a][2],f[i][a][1]);
addmod(f[i + 1][a][1],f[i][a][0]);
}
}
if(s[i + 1] != '0'){
for(int a = 0;a <= 2;a++){
addmod(f[i + 1][a][0],f[i][a][1]);
addmod(f[i + 1][a][1],f[i][a][2]);
}
addmod(f[i + 1][1][0],f[i][0][0]);
addmod(f[i + 1][2][0],f[i][1][0]);
addmod(f[i + 1][2][0],f[i][2][0]);
}
}
int ans = 0;
for(int a = 0;a <= 2;a++){
for(int b = 0;b <= a;b++)
addmod(ans,f[n][a][b]);
}
printf("%d\n",ans);
return 0;
}
CF 679E
Solution
操作\(1\)和操作\(2\)是线段树的基本操作,而操作\(3\)比较棘手。由于\(42\)的幂次在\(10^{18}\)以内只有\(11\)个,考虑在线段树中维护每个数到其距离最近的好数的距离\(dis\),然后对于操作\(3\),每次暴力区间加直到整棵树的最小\(dis\)为\(0\)。如果只有区间加,总复杂度就是\(\mathcal O(11n\log n)\),对于操作\(2\),如果一段区间值域相同,同时更新就好了,根据势能分析那套理论,复杂度还是复杂度还是\(\mathcal O(11n\log n)\)。
Code
const ll pow42[] = {1ll,42ll,1764ll,74088ll,3111696ll,130691232ll,5489031744ll,230539333248ll,9682651996416ll,406671383849472ll,17080198121677824ll,717368321110468608ll};
int n,Q;
ll a[MAXN];
namespace SegmentTree{
struct Tree{
int l,r;
int log;
ll dis,tag,cov;
} tree[MAXN << 2];
#define lson k << 1
#define rson k << 1 | 1
int log42(const ll &x){
return int(lower_bound(pow42,pow42 + 12,x) - pow42);
}
void update(int k){
tree[k].dis = min(tree[lson].dis,tree[rson].dis);
}
void applyadd(int k,ll v){
if(tree[k].cov)
tree[k].cov += v;
else
tree[k].tag += v;
tree[k].dis -= v;
}
void applycov(int k,ll v){
tree[k].log = log42(v);
tree[k].dis = pow42[tree[k].log] - v;
tree[k].cov = v;
tree[k].tag = 0;
}
void down(int k){
if(tree[k].cov){
applycov(lson,tree[k].cov);
applycov(rson,tree[k].cov);
tree[k].cov = 0;
}
if(tree[k].tag){
applyadd(lson,tree[k].tag);
applyadd(rson,tree[k].tag);
tree[k].tag = 0;
}
}
void Build(int k,int l,int r){
tree[k].l = l;
tree[k].r = r;
if(l == r){
tree[k].log = log42(a[l]);
tree[k].dis = pow42[tree[k].log] - a[l];
return;
}
int mid = (l + r) >> 1;
Build(lson,l,mid);
Build(rson,mid + 1,r);
update(k);
}
void Modify1(int k,int l,int r,int v){
if(tree[k].l >= l && tree[k].r <= r){
applycov(k,v);
return;
}
down(k);
int mid = (tree[k].l + tree[k].r) >> 1;
if(l <= mid)
Modify1(lson,l,r,v);
if(r > mid)
Modify1(rson,l,r,v);
update(k);
}
void Modify2(int k,int l,int r,int v){
if(tree[k].l >= l && tree[k].r <= r){
applyadd(k,v);
return;
}
down(k);
int mid = (tree[k].l + tree[k].r) >> 1;
if(l <= mid)
Modify2(lson,l,r,v);
if(r > mid)
Modify2(rson,l,r,v);
update(k);
}
ll Query1(int k,int x){
if(tree[k].l == tree[k].r)
return pow42[tree[k].log] - tree[k].dis;
down(k);
int mid = (tree[k].l + tree[k].r) >> 1;
if(x <= mid)
return Query1(lson,x);
else
return Query1(rson,x);
}
ll Query2(int k){
if(tree[k].dis >= 0)
return tree[k].dis;
if(tree[k].l == tree[k].r){
ll x = pow42[tree[k].log] - tree[k].dis;
tree[k].log = log42(x);
tree[k].dis = pow42[tree[k].log] - x;
return tree[k].dis;
}
down(k);
int mid = (tree[k].l + tree[k].r) >> 1;
Query2(lson);
Query2(rson);
update(k);
return tree[k].dis;
}
}
int main(){
scanf("%d%d",&n,&Q);
for(int i = 1;i <= n;i++)
scanf("%lld",&a[i]);
SegmentTree::Build(1,1,n);
while(Q--){
int op,l,r,x;
scanf("%d",&op);
if(op == 1){
scanf("%d",&x);
printf("%lld\n",SegmentTree::Query1(1,x));
}else if(op == 2){
scanf("%d%d%d",&l,&r,&x);
SegmentTree::Modify1(1,l,r,x);
}else{
scanf("%d%d%d",&l,&r,&x);
SegmentTree::Modify2(1,l,r,x);
while(!SegmentTree::Query2(1))
SegmentTree::Modify2(1,l,r,x);
}
}
return 0;
}
AGC 029F
Solution
神仙构造题。
考虑如何才能构成一颗树,显然有一个必要条件是对于每个点\(u\),整张图除去\(u\)之外的所有点和点集存在完美匹配,具体来说就是考虑以\(u\)为根,去掉\(u\)之后剩余每个点和他的父亲对应的那条边可以刚好构成完美匹配(即考虑一张二分图左边是除了\(u\)之外的点,右边是\(E_i\),\(u\)和\(E_i\)连边当且仅当\(u\in E_i\),该图存在完美匹配)。用\(Hall\)定理来表达就是,设\(S\)为\(\{E_1,E_2\cdots E_n\}\)的任意一个子集,\(N(S)\)表示这些\(E_i\)中的点的并集,则\(|N(S)|\geq |S|+1\)。
实际上这个条件也是充分的,证明考虑如下的构造算法:首先将\(1\)去除后求出完美匹配,然后从\(1\)开始BFS,每次选择一条左边点\(u\)到右边点\(v\)的边,然后找到\(v\)的匹配点\(p_v\),若这两个点都没有被访问过,则添加一条树边\((u,p_v)\)。于是上面的命题等价于这样搜索能够遍历所有的点。因为如果某一个时刻不能走到未走过的点,那么走过的左边点个数比右边点个数多\(1\),所以左边点总个数比右边点总个数多\(1\),故现在未遍历的右边的点的集合\(T\)满足\(N(T)\leq T\),与上面\(Hall\)定理矛盾。而如果上面的命题不成立,显然无法搜出合法的方案,而这样搜索能遍历所有的点等价于原问题有解,故原命题等价于原问题有解。
时间复杂度\(\mathcal O(\sum|E_i|\sqrt n)\)
Code
int n,tot,S,T;
int p[MAXN];
pii ans[MAXN];
vector<int> G[MAXN];
namespace NetWorkFlow{
int len,maxFlow;
int head[MAXN],cur[MAXN],dep[MAXN],vis[MAXN];
queue<int> q;
struct Edge{
int to,next,flow;
} e[MAXM];
void Init(){
memset(head,-1,sizeof(head));
len = 1;
}
void add_edge(int u,int v,int flow){
e[++len] = (Edge){v,head[u],flow};
head[u] = len;
e[++len] = (Edge){u,head[v],0};
head[v] = len;
}
int bfs(){
for(int i = 0;i <= tot;i++){
cur[i] = head[i];
dep[i] = -1;
}
dep[S] = 0;
q.push(S);
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(dep[v] == -1 && e[i].flow){
dep[v] = dep[u] + 1;
q.push(v);
}
}
}
return dep[T] != -1;
}
int dfs(int u,int flow){
if(u == T){
maxFlow += flow;
return flow;
}
int used = 0,low;
for(int i = cur[u];i != -1;i = e[i].next){
cur[u] = i;
int v = e[i].to;
if(dep[v] == dep[u] + 1 && e[i].flow){
if(low = dfs(v,min(flow - used,e[i].flow))){
e[i].flow -= low;
e[i ^ 1].flow += low;
used += low;
if(used == flow)
break;
}
}
}
return used;
}
int Dinic(){
while(bfs()) dfs(S,INF);
return maxFlow;
}
bool GetAns(){
for(int u = 2;u <= n;u++){
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(v != S && !e[i].flow) p[v - n] = u;
}
}
q.push(1);
int cnt = 0;
while(!q.empty()){
int u = q.front();
q.pop();
for(int v : G[u]){
if(!vis[v]){
ans[v] = make_pair(u,p[v]);
cnt += 1;
q.push(p[v]);
vis[v] = 1;
}
}
}
return cnt == n - 1;
}
}
int main(){
NetWorkFlow::Init();
scanf("%d",&n);
S = 1;
for(int i = 2;i <= n;i++)
NetWorkFlow::add_edge(S,i,1);
for(int i = 1,x,y;i < n;i++){
scanf("%d",&x);
while(x--){
scanf("%d",&y);
if(y != 1) NetWorkFlow::add_edge(y,i + n,1);
G[y].push_back(i);
}
}
tot = T = n + n;
for(int i = 1;i < n;i++)
NetWorkFlow::add_edge(i + n,T,1);
if(NetWorkFlow::Dinic() < n - 1){
puts("-1");
return 0;
}
if(!NetWorkFlow::GetAns()){
puts("-1");
return 0;
}
for(int i = 1;i < n;i++)
printf("%d %d\n",ans[i].first,ans[i].second);
return 0;
}
CF 576D
Lemma
一个有向图中从\(u\)走到\(v\)经过恰好\(k\)步的方案数是邻接矩阵\(G\)的\(k\)次方中\(G^k[u][v]\)的值,因为矩阵乘法本质上等于转移的过程。
Solution
首先定义两个矩阵,矩阵\(A\)中\(A[i][j]\)表示当前走\(d\)步能否从\(i\)到达\(j\),矩阵\(B\)中\(B[i][j]\)表示当前\(i\to j\)的这条边已经被解锁。
先将所有边按照\(d_i\)从小到达排序,然后考虑每次加入一条边时,让\(A\)乘上\(B^{d_i-d_{i-1}}\),相当于得出了在第\(i\)条边解锁之前两点之间经过\(d\)步的状态。然后对整个图进行一次\(bfs/floyd\)即可求出当前\(1\)到\(n\)的最短路来更新答案。
这样做的时间复杂度是\(\mathcal O(n^4\log d)\),无法通过本题。
注意到矩阵中每个点的值只可能为\(0\)或者\(1\),所以用\(bitset\)优化矩阵乘法即可,时间复杂度\(\mathcal O(\frac{n^4\log d}{\omega})\)
Code
int n,m,ans = INF;
int dis[MAXN][MAXN];
struct Edge{
int u,v,d;
bool operator < (const Edge &rhs) const{
return d < rhs.d;
}
} e[MAXN];
struct Matrix{
bitset<MAXN> a[MAXN];
Matrix(){
for(int i = 1;i <= n;i++)
a[i].reset();
}
friend Matrix operator * (const Matrix &x,const Matrix &y){
Matrix res;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
if(x.a[i][j])
res.a[i] |= y.a[j];
}
}
return res;
}
} A;
int main(){
scanf("%d%d",&n,&m);
for(int i = 1;i <= m;i++)
scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].d);
sort(e + 1,e + 1 + m);
for(int i = 1;i <= n;i++)
A.a[i][i] = 1;
for(int x = 1;x <= m;x++){
Matrix B;
for(int i = 1;i < x;i++)
B.a[e[i].u][e[i].v] = 1;
int y = e[x].d - e[x - 1].d;
while(y){
if(y & 1) A = A * B;
B = B * B;
y >>= 1;
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++)
dis[i][j] = INF;
dis[i][i] = 0;
}
for(int i = 1;i <= x;i++)
dis[e[i].u][e[i].v] = 1;
for(int k = 1;k <= n;k++){
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++)
dis[i][j] = min(dis[i][j],dis[i][k] + dis[k][j]);
}
}
for(int i = 1;i <= n;i++){
if(A.a[1][i])
ans = min(ans,e[x].d + dis[i][n]);
}
}
if(ans < INF) printf("%d\n",ans);
else printf("Impossible\n");
return 0;
}
CF 639F
Solution
发现合法的条件就是所有点在同一个边双里,那么先把原图按边双缩成一棵树,询问的时候把虚树建出来,tarjan一遍整棵虚树来缩点就行了。
Code
int n,Q,len = 1,tot,m,dcc,cnt,R;
int head[MAXN],dfn[MAXN],low[MAXN],isbridge[MAXN],f[MAXN][LOG];
int belong[MAXN],tim[MAXN],dep[MAXN],root[MAXN],bel[MAXN];
vector<int> bridges;
vector<int> G[MAXN];
struct Edge{
int to,next;
} e[MAXN << 1];
void add(int u,int v){
e[++len].to = v;
e[len].next = head[u];
head[u] = len;
}
void addedge(int u,int v){
add(u,v);
add(v,u);
}
void tarjan(int u,int fa){
dfn[u] = low[u] = ++tot;
for(int i = head[u];i != -1;i = e[i].next){
if(i == (fa ^ 1))
continue;
int v = e[i].to;
if(!dfn[v]){
tarjan(v,i);
low[u] = min(low[u],low[v]);
if(low[v] > dfn[u]){
isbridge[i] = isbridge[i ^ 1] = 1;
bridges.push_back(i);
}
}else
low[u] = min(low[u],dfn[v]);
}
}
void dfs1(int u){
belong[u] = dcc;
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(belong[v] || isbridge[i])
continue;
dfs1(v);
}
}
void dfs2(int u,int fa){
tim[u] = ++cnt;
f[u][0] = fa;
dep[u] = dep[fa] + 1;
for(int i = 1;i < LOG;i++)
f[u][i] = f[f[u][i - 1]][i - 1];
for(int i = 0;i < (int)G[u].size();i++){
int v = G[u][i];
if(v == fa)
continue;
root[v] = root[u];
dfs2(v,u);
}
}
void Init(){
for(int i = 1;i <= n;i++){
if(!dfn[i])
tarjan(i,0);
}
for(int i = 1;i <= n;i++){
if(!belong[i]){
dcc += 1;
dfs1(i);
}
}
for(int i = 2;i <= len;i++){
if(isbridge[i])
G[belong[e[i].to]].push_back(belong[e[i ^ 1].to]);
}
for(int i = 1;i <= dcc;i++){
if(!root[i]){
root[i] = i;
dfs2(i,0);
}
}
for(int i = 1;i <= n;i++)
bel[i] = belong[i];
len = 1;
tot = dcc = 0;
memset(head,-1,sizeof(head));
memset(belong,0,sizeof(belong));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(isbridge,0,sizeof(isbridge));
}
int LCA(int u,int v){
if(dep[u] < dep[v])
swap(u,v);
for(int i = LOG - 1;i >= 0;i--){
if(dep[f[u][i]] >= dep[v])
u = f[u][i];
}
if(u == v)
return u;
for(int i = LOG - 1;i >= 0;i--){
if(f[u][i] != f[v][i]){
u = f[u][i];
v = f[v][i];
}
}
return f[u][0];
}
bool cmp(const int &x,const int &y){
return tim[x] < tim[y];
}
void BuildTree(vector<int> &vec){
sort(vec.begin(),vec.end(),cmp);
static int st[MAXN];
static int top,curRoot;
static vector<int> res;
top = curRoot = 0;
res = vec;
for(int i = 0;i < (int)vec.size();i++){
int u = vec[i];
if(top && root[u] != curRoot){
top -= 1;
while(top){
addedge(st[top + 1],st[top]);
top -= 1;
}
}
int lca = LCA(u,st[top]);
if(lca != st[top]){
while(top && tim[st[top - 1]] >= tim[lca]){
addedge(st[top - 1],st[top]);
top -= 1;
}
if(st[top] != lca){
addedge(st[top],lca);
st[top] = lca;
res.push_back(lca);
}
}
st[++top] = u;
curRoot = root[u];
}
while(top > 1){
addedge(st[top],st[top - 1]);
top -= 1;
}
vec = res;
}
void Rotate(int &x){
x += R;
if(x > n)
x -= n;
}
void Getedcc(const vector<int> &vec){
for(int i = 0;i < (int)vec.size();i++){
int u = vec[i];
if(!dfn[u])
tarjan(u,0);
}
for(int i = 0;i < (int)vec.size();i++){
int u = vec[i];
if(!belong[u]){
dcc += 1;
dfs1(u);
}
}
}
void Clear(const vector<int> &vec){
len = 1;
tot = dcc = 0;
for(int i = 0;i < (int)vec.size();i++){
int u = vec[i];
head[u] = -1;
dfn[u] = low[u] = belong[u] = 0;
}
for(int i = 0;i < (int)bridges.size();i++)
isbridge[bridges[i]] = isbridge[bridges[i] ^ 1] = 0;
bridges.clear();
}
int main(){
memset(head,-1,sizeof(head));
n = read(); m = read(); Q = read();
for(int i = 1;i <= m;i++){
int u = read(),v = read();
addedge(u,v);
}
Init();
for(int q = 1;q <= Q;q++){
int ni = read(),mi = read();
vector<pii> edges;
vector<int> vec,nodes;
edges.clear();
vec.clear();
nodes.clear();
for(int i = 1;i <= ni;i++){
int x = read();
Rotate(x);
x = bel[x];
vec.push_back(x);
nodes.push_back(x);
}
for(int i = 1;i <= mi;i++){
int x = read(),y = read();
Rotate(x);
Rotate(y);
x = bel[x];
y = bel[y];
if(x == y)
continue;
edges.push_back(make_pair(x,y));
nodes.push_back(x);
nodes.push_back(y);
}
sort(nodes.begin(),nodes.end());
nodes.erase(unique(nodes.begin(),nodes.end()),nodes.end());
BuildTree(nodes);
for(int i = 0;i < (int)edges.size();i++)
addedge(edges[i].first,edges[i].second);
Getedcc(nodes);
int id = belong[vec[0]];
int flag = 1;
for(int i = 1;i < (int)vec.size();i++){
if(belong[vec[i]] != id){
flag = 0;
break;
}
}
if(flag)
puts("YES");
else
puts("NO");
if(flag)
R = (R + q) % n;
Clear(nodes);
}
return 0;
}
CF 506E
Solution
为了方便,首先考虑\(n+|s|\)为偶数的情况。
考虑dp,设\(f[i][l][r]\)表示只考虑最终回文串的前\(i\)和后\(i\)个字符,它们与\(s\)尽可能匹配后\(s\)还剩下\([l,r]\)这段区间时的方案数。再设\(g_i\) 表示只考虑最终回文串的\(i\)和后\(i\)个字符,它们与\(s\)完全匹配时的方案数。
那么有转移(记\(len=r-l+1\))
- \(s_l=s_r\)且\(len\leq 2\)
- \(s_l=s_r\)且\(len>2\)
- \(s_l\neq s_r\)
此时我们可以得到一个状态数\(\mathcal O(|s|^2)\)递推\(\mathcal O(n + |s|)\)次的dp,这个dp可以矩阵乘法优化,复杂度为\(\mathcal O(|s|^6 \log(n+∣s∣))\),显然无法通过。
我们发现转移的过程其实是在一个有限状态自动机上匹配的过程,对于\(s=abaac\),转移的过程如下图
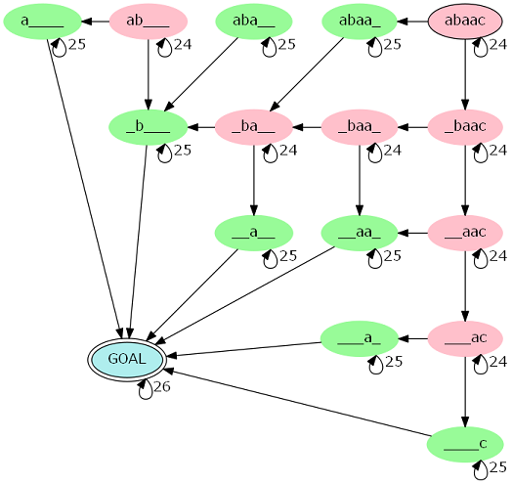
其中红点表示两端字符不相同,绿点表示两端字符相同,边表示转移。
这个自动机的节点数依旧是\(\mathcal O(|s|^2)\)的。考虑压缩这个自动机,可以发现,对于每一条从起点到终点的链,如果其上面有\(k\)个红点,那么就意味着它有\(\lceil \frac{|s|-k}2 \rceil\)个绿点,同时最终连接终点的点一定是绿点。因为除了最后连向终点的绿点,一个绿点会使得串的长度减少\(2\),一个红点会使得串的长度减少\(1\)。
而对于两条红点数量相同的链,它们对答案的贡献与红点的具体位置无关,因此本质上是一样的,这意味着本质不同的链只有\(\mathcal O(|s|)\)条。
于是我们便要求出有\(k\)个红点的链的数量。设\(h[l][r][i]\)表示从起点走到\((l,r)\)对应的节点的路径中,有多少条经过了\(i\)个红点。那么我们可以采用记忆化搜索的方法 \(\mathcal O(|s|^3)\)求出答案。
现在我们有\(\mathcal O(|s|)\)条本质不同的链,同时还知道了每条链的数量。至此我们可以对每条链做一次矩阵快速幂,时间复杂度降为\(\mathcal O(|s|^4 \log (n + |s|))\)。
但还不够,我们要想办法建出一个节点数只有\(\mathcal O(|s|)\)的自动机。具体做法如下:构建\(|s|\)个红点串成一串,从起点指出来,\(\lceil \frac{|s|}{2}\rceil\)个绿点串成一串,指向终点。对于一条由\(i\)个红点,\(\lceil \frac{|s|-i}{2}\rceil\)个绿点构成的串,我们从第i个红点向第\(\lceil \frac{|s|-i}{2}\rceil\)个绿点连一条边即可。这样一来点数就是\(\frac{3}{2}|s|\),可以用矩乘优化,复杂度为\(\mathcal O(|s|^3\log (n+|s|))\)
但这样做的常数有点大,不难发现我们只能从编号小的点转移到编号大的点,所以矩阵乘法时\(j\)只需要从\(i\)枚举到\(n\),\(k\)只需要从\(i\)枚举到\(j\)即可,这样常数可以除以\(6\)。
而对于\(|s|+n\)为奇数的情况,唯一的区别就是在最后一步时形如\((i,i+1)\)的绿点是不能直接转移到终点的。于是我们要将这些转移的贡献减去,方法是将\((i,i+1)\)这样的绿点设为终点(无自环),重新建图跑一边矩乘即可。
Code
int n,m,N,ans;
int h[MAXN][MAXN][MAXN],sum[MAXN];
char s[MAXN];
struct Matrix{
int a[MAXN][MAXN];
Matrix(bool flag = 0){
memset(a,0,sizeof(a));
if(!flag) return;
for(int i = 0;i <= N;i++)
a[i][i] = 1;
}
int* operator [] (const int &x){
return a[x];
}
const int* operator [] (const int &x) const{
return a[x];
}
Matrix operator * (const Matrix &rhs) const{
Matrix res;
for(int i = 0;i <= N;i++){
for(int k = i;k <= N;k++){
for(int j = k;j <= N;j++)
addmod(res[i][j],1ll * a[i][k] * rhs[k][j] % MOD);
}
}
return res;
}
Matrix operator ^ (int y) const{
Matrix res(1);
Matrix x = *this;
while(y){
if(y & 1) res = res * x;
x = x * x;
y >>= 1;
}
return res;
}
void print(){
for(int i = 0;i <= N;i++){
for(int j = 0;j <= N;j++)
cout << a[i][j] << " ";
cout << endl;
}
cout << endl;
}
} A;
int GetH(int l,int r,int i){
if(i < 0) return 0;
if(h[l][r][i] != -1) return h[l][r][i];
h[l][r][i] = 0;
if(l == 1 && r == n) return h[l][r][i] = (i == 0);
if(l != 1 && r != n && s[l - 1] == s[r + 1])
addmod(h[l][r][i],GetH(l - 1,r + 1,i));
if(l != 1 && s[l - 1] != s[r])
addmod(h[l][r][i],GetH(l - 1,r,i - 1));
if(r != n && s[r + 1] != s[l])
addmod(h[l][r][i],GetH(l,r + 1,i - 1));
return h[l][r][i];
}
int main(){
memset(h,-1,sizeof(h));
scanf("%s",s + 1);
scanf("%d",&m);
n = strlen(s + 1);
for(int i = 0;i < n;i++){
sum[i] = GetH(1,1,i);
for(int j = 2;j <= n;j++){
if(s[j - 1] == s[j])
addmod(sum[i],GetH(j - 1,j,i));
addmod(sum[i],GetH(j,j,i));
}
}
N = n + (n + 1) / 2 + 1;
for(int i = 1;i <= n;i++){
A[i][i] = 24;
A[i][N - (n - i + 1) / 2] = sum[i];
if(i != n) A[i][i + 1] = 1;
}
for(int i = n + 1;i < N;i++)
A[i][i + 1] = 1, A[i][i] = 25;
A[N][N] = 26;
if((n + m) & 1){
A = A ^ ((n + m + 1) >> 1);
ans = add(A[1][N],1ll * sum[0] * A[n + 1][N] % MOD);
A = Matrix();
memset(sum,0,sizeof(sum));
for(int i = 0;i < n;i++){
if(s[i] != s[i + 1]) continue;
for(int j = 0;j <= n;j++)
addmod(sum[j],GetH(i,i + 1,j));
}
for(int i = 1;i <= n;i++){
A[i][i] = 24;
A[i][N - (n - i + 1) / 2] = sum[i];
if(i != n) A[i][i + 1] = 1;
}
for(int i = n + 1;i < N;i++)
A[i][i + 1] = 1, A[i][i] = 25;
A = A ^ ((n + m + 1) >> 1);
submod(ans,add(A[1][N],1ll * sum[0] * A[n + 1][N] % MOD));
}else{
A = A ^ ((n + m) >> 1);
ans = add(A[1][N],1ll * sum[0] * A[n + 1][N] % MOD);
}
printf("%d\n",ans);
return 0;
}
AGC 022F
Solution
考虑建图,如果某一次是\(B\)向\(A\)跳的,就从\(B\)向\(A\)连边,最后显然构成了一颗树,这样的话某个点的系数就是\(2^{dep}\)乘上一个系数\(±1\),由于基数很大,我们可以认为只要两个方案中某个点的系数不同则这两个方案不同。
对于某个点,如果它多了一个儿子,那么其它儿子中的所有点的系数都会取反。所以如果一个点有\(k\)个儿子,那么其中有\(\lfloor \frac{k}{2}\rfloor\)个儿子会被取反,而且如果\(k\)为奇数,这个点自己也会被取反。所以如果我们已经知道了这棵树,那么每个点上的正负状态就是父亲的正负状态异或上父亲的儿子个数的奇偶性异或上自己的儿子个数的奇偶性
发现如果正负状态和父亲的正负有关很麻烦,我们考虑差分。建立一棵新树,其中某个点为\(1\)当且仅当它在原树中和父亲的正负相同(否则为\(−1\)),这样新的一层中点的状态只和上一层中奇数儿子的点的个数有关,然后考虑从上到下按层dp。
设\(f[i][j]\)表示考虑了\(i\)个点,其中最后一层有\(j\)个节点有奇数个儿子的方案数,然后转移的时候,我们枚举新的一层中有\(x\)个点为\(1\)(即在原树中和父亲相同),\(y\)个点为\(−1\)(即在原树中和父亲不同)。如果先不考虑自己作为奇数点的影响,那么这一层实际为\(1\)的点数是\(j+\frac{x+y−j}{2}\),相当于每个奇数点先自带一个,然后剩下的成对出现
但是由于系数为\(1\)的点有\(x\)个,所以还需要取反\(|j+\frac{x+y−j}{2}−x|\)个点,而这几个点会被取反就说明它们是这一层中的奇数点,转移过去即可。
总复杂度为\(\mathcal O(n^2)\)
Code
int n;
int f[MAXN][MAXN],C[MAXN][MAXN];
int main(){
scanf("%d",&n);
f[1][0] = f[1][1] = 1;
C[0][0] = 1;
for(int i = 1;i <= n;i++){
C[i][0] = 1;
for(int j = 1;j <= i;j++)
C[i][j] = add(C[i - 1][j - 1],C[i - 1][j]);
}
for(int i = 1;i < n;i++){
for(int j = 0;j <= i;j++){
if(!f[i][j]) continue;
for(int x = 0;x + i <= n;x++){
for(int y = 0;x + y + i <= n;y++){
if((x + y) && (x + y >= j) && (!((x + y - j) & 1)))
addmod(f[i + x + y][abs((x + y - j) / 2 + j - x)],1ll * f[i][j] * C[i + x + y][x + y] % MOD * C[x + y][x] % MOD);
}
}
}
}
printf("%d\n",f[n][0]);
return 0;
}
AGC 028E
Solution
首先肯定要按位贪心,那么我们假设现在已经确定了某个前缀,判断对于后面的所有元素是否存在某种方案使其合法。
设当前\(X\)和\(Y\)中 high 元素的个数分别为\(C_X,C_Y\),最大值分别为\(H_X,H_Y\),我们想要判断是否能将剩下的元素分配给\(X\)或者\(Y\)使得 high 元素个数相等。
假设在分配之后,\(X\)中新增的 high 元素为\(a_1,a_2,\cdots,a_{|a|}\),\(Y\)中新增的 high 元素为\(b_1,b_2,\cdots,b_{|b|}\),那么他们必须满足
- \(H_X<a_1<a_2<\cdots<a_{|a|},H_Y<b_1<b_2<\cdots<b_{|b|}\)
- \(C_X+|a|=C_Y+|b|\)
- 剩下的\(P\)中所有的 high 元素要么在\(a\)中,要么在\(b\)中,因为\(P\)中的 high 元素在新序列中仍然会是 high 元素。
然后有一个结论,那就是\(a\)和\(b\)中必有一个满足其中所有元素都是\(P\)中的 high 元素。
对于必要性,因为\(P\)中的 high 元素在分完之后一定仍然是 high 元素。
对于充分性,如果\(a,b\)中都存在high元素满足它们不是\(P\)中的 high 元素,那么我们交换它们,对于这种值来说,导致它不是\(P\)中 high 元素的位置一定恰好在另一个集合中,这样我们使两个集合的 high 元素个数同时减一,且仍然满足条件。
我们先假设\(a\)满足这个条件(\(b\)满足的情况同理)
设\(Q\)为\(P\)中剩下的 high 元素构成的个数,\(b\)中的 high 元素有\(k\)个是\(P\)中的 high 元素,\(m=|b|-k\),如果我们确定了\(b\),那么\(a\)也就随之确定了,因为\(a\)必须由\(P\)中不在\(b\)中的所有 high 元素组成。那么\(b\)要满足一下条件
- \(H_Y<b_1<b_2<\cdots<b_{|b|}\)
- \(C_X+Q-k=C_Y+|b|\),化简一下可得\(2k+m=C_X-C_Y+Q\)
考虑设所有 high 元素权值为\(2\),非 high 元素权值为\(1\),那么就相当于找一个上升子序列使得权值和为\(C_X-C_Y+Q\)。
我们发现如果我们可以得到权值\(x\),那么也一定可以得到\(x−2\),所以我们分别维护\(x\)为奇数和偶数时的最大值即可。
最后用\(f[i][0/1]\)表示以\(i\)开头的,权值和为奇数/偶数的最大权值,类似与LIS那样用线段树优化转移即可。
Code
int n;
int a[MAXN],cnt[MAXN],val[MAXN],ans[MAXN];
struct SegmentTree{
struct Tree{
int l,r;
int max;
} tree[MAXN << 2];
#define lson k << 1
#define rson k << 1 | 1
void update(int k){
tree[k].max = max(tree[lson].max,tree[rson].max);
}
void build(int k,int l,int r,int v = 0){
tree[k].l = l;
tree[k].r = r;
if(l == r){
tree[k].max = v;
return;
}
int mid = (l + r) >> 1;
build(lson,l,mid,v);
build(rson,mid + 1,r,v);
update(k);
}
void modify(int k,int x,int v){
if(tree[k].l == tree[k].r){
tree[k].max = v;
return;
}
int mid = (tree[k].l + tree[k].r) >> 1;
if(x <= mid)
modify(lson,x,v);
else
modify(rson,x,v);
update(k);
}
int query(int k,int l,int r){
if(tree[k].l >= l && tree[k].r <= r)
return tree[k].max;
int mid = (tree[k].l + tree[k].r) >> 1;
int res = -INF;
if(l <= mid)
res = max(res,query(lson,l,r));
if(r > mid)
res = max(res,query(rson,l,r));
return res;
}
#undef lson
#undef rson
} odd,even;
bool Check(int H,int Q){
if(Q < 0) return false;
if(Q & 1) return odd.query(1,H,n) >= Q;
else return even.query(1,H,n) >= Q;
}
int main(){
scanf("%d",&n);
for(int i = 1,maxx = 0;i <= n;i++){
scanf("%d",&a[i]);
if(a[i] > maxx) val[i] = 2, maxx = a[i];
else val[i] = 1;
}
odd.build(1,1,n,-INF);
even.build(1,1,n);
for(int i = n;i >= 1;i--){
int maxo = odd.query(1,a[i],n), maxe = even.query(1,a[i],n);
if(val[i] & 1){
odd.modify(1,a[i],maxe + val[i]);
even.modify(1,a[i],maxo + val[i]);
}else{
odd.modify(1,a[i],maxo + val[i]);
even.modify(1,a[i],maxe + val[i]);
}
}
for(int i = n;i >= 1;i--)
cnt[i] = cnt[i + 1] + val[i] - 1;
int CX = 0,CY = 0,HX = 0,HY = 0;
for(int i = 1;i <= n;i++){
odd.modify(1,a[i],-INF); even.modify(1,a[i],0);
if(Check(HY,CX - CY + cnt[i + 1] + (a[i] > HX)) || Check(HX,CY - CX + cnt[i + 1] - (a[i] > HX))){
ans[i] = 0;
CX += (a[i] > HX);
HX = max(HX,a[i]);
}else{
ans[i] = 1;
CY += (a[i] > HY);
HY = max(HY,a[i]);
}
}
if(CX != CY) puts("-1");
else for(int i = 1;i <= n;i++) putchar(ans[i] + '0');
return 0;
}
CF 512D
Solution
先考虑哪些点可以被遍历到。不难发现,环上的点不可能被遍历到。于是考虑先把环去掉,就得到了一个森林。但是这样之后,仍有点无法被遍历到。比如被夹在两个环之间的点。
用边双缩点判断显得太过繁琐,我们可以用类似拓扑排序的方法一层一层求出可以被遍历到的点。
之后,考虑森林中的每棵树:
-
如果这棵树有节点与环相连,那么它一定是这棵树里最后被遍历到的点。那么可以以这个点为树根,做一遍树上背包。
设\(f[i][j]\)表示在\(i\)的子树内有序地选了\(j\)个点的方案数。转移时枚举每个子树,然后把它们的\(f\)卷起来即可,即\(f[u][i+j]=f[u][i]\times f[v][j] \times \binom{i+j}{i}\)。
最后算\(i\)本身的贡献时,因为\(i\)是最后加进去的点(\(i\)的祖先一定在\(i\)后面被遍历到),直接令\(f[i][siz[i]]=f[i][siz[i]-1]\)即可。 -
如果没有节点与环相连,我们可以分别钦定树中的每个节点为根,然后做法和上述一样。将所有情况的答案加起来,对于每个\(j\),还需要除以一个\(size−j\),因为当有\(siz-j\)个点未被遍历时,被遍历到的\(j\)个点的方案会在所有以这\(siz-j\)个点为根做dp时被计算过。
最后把每棵树的贡献做一遍卷积就能得到最终的答案了。
时间复杂度\(\mathcal O(n^3)\)
Code
int n,m,len,root;
int head[MAXN],vis[MAXN],deg[MAXN],size[MAXN],C[MAXN][MAXN],inv[MAXN],res[MAXN],onCircle[MAXN],f[MAXN][MAXN],tmp[MAXN];
vector<int> vec;
queue<int> q;
struct Edge{
int to,next;
} e[MAXM];
void add_edge(int u,int v){
e[++len] = (Edge){v,head[u]};
head[u] = len;
}
void GetRoot(int u,int fa){
vis[u] = 1;
vec.push_back(u);
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(v == fa) continue;
if(onCircle[v]) root = u;
else GetRoot(v,u);
}
}
void Merge(int u,int v){
memset(res,0,sizeof(res));
for(int j = 0;j <= n;j++){
for(int k = 0;j + k <= n;k++)
addmod(res[j + k],1ll * f[u][j] * f[v][k] % MOD * C[j + k][j] % MOD);
}
for(int j = 0;j <= n;j++)
f[u][j] = res[j];
}
void dfs(int u,int fa){
memset(f[u],0,sizeof(f[u]));
f[u][0] = size[u] = 1;
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(v == fa || onCircle[v]) continue;
dfs(v,u);
size[u] += size[v];
Merge(u,v);
}
f[u][size[u]] = f[u][size[u] - 1];
}
void Init(int n){
C[0][0] = 1;
for(int i = 1;i <= n;i++){
C[i][0] = C[i][i] = 1;
for(int j = 1;j < i;j++)
C[i][j] = add(C[i - 1][j],C[i - 1][j - 1]);
}
inv[0] = inv[1] = 1;
for(int i = 2;i <= n;i++)
inv[i] = 1ll * (MOD - MOD / i) * inv[MOD % i] % MOD;
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
Init(n);
for(int i = 1,u,v;i <= m;i++){
scanf("%d%d",&u,&v);
deg[u] += 1; deg[v] += 1;
add_edge(u,v); add_edge(v,u);
}
for(int i = 1;i <= n;i++){
onCircle[i] = 1;
if(deg[i] <= 1){
q.push(i);
onCircle[i] = 0;
}
}
while(!q.empty()){
int u = q.front();
q.pop();
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(!onCircle[v]) continue;
deg[v] -= 1;
if(deg[v] <= 1){
onCircle[v] = 0;
q.push(v);
}
}
}
f[0][0] = 1;
for(int i = 1;i <= n;i++){
if(vis[i] || onCircle[i]) continue;
root = -1;
vec.clear();
GetRoot(i,0);
if(root != -1){
dfs(root,0);
Merge(0,root);
continue;
}
int tot = vec.size();
assert(tot <= n);
memset(tmp,0,sizeof(tmp));
for(int u : vec){
dfs(u,0);
for(int j = 0;j <= tot;j++)
addmod(tmp[j],f[u][j]);
}
for(int j = 0;j <= tot;j++)
tmp[j] = 1ll * tmp[j] * inv[tot - j] % MOD;
memset(f[n + 1],0,sizeof(f[n + 1]));
for(int j = 0;j <= tot;j++)
f[n + 1][j] = tmp[j];
Merge(0,n + 1);
}
for(int i = 0;i <= n;i++)
printf("%d\n",f[0][i]);
return 0;
}
AGC 020F
Solution
首先默认长度最长的那一条弧放在\([0,x]\)的位置上,然后考虑其它弧的左端点的位置。
有一个套路,考虑把左端点位置的整数部分和小数部分分开考虑,那么整数部分只有\(n\)种可能,而小数部分虽然可能性有无数种,但是它们之间的相对顺序只有\(n!\)种(默认互不相同,因为连续型随机变量取值相同的概率可以视为\(0\)),而且只有这个相对顺序会对答案有影响。
于是我们可以\(n!\)枚举小数部分的相对顺序,把圆上给拆成\(N\times C\)个点,其中第\(i \times N + j\)个点表示整数部分为\(i\),小数部分的相对顺序为\(j\),然后设\(f[i][j][S]\)表示现在考虑到点\(i\),当前最远能覆盖到点\(j\),已经选了的点的集合为\(S\)的方案数,转移有两种,一种是直接转移到\(f[i+1][j][S]\),还有一种是转移到\(f[i+1][max(j,pos)][S\cup \{x\}]\),其中\(pos\)为以\(i\)左端点放置第\(x\)条弧后能覆盖到的最远位置。
Code
int n,C;
int a[MAXN],len[MAXN];
ll facn,p,ans;
ll f[2][MAXL][MAXM];
int main(){
scanf("%d%d",&n,&C);
for(int i = 1;i <= n;i++){
scanf("%d",&len[i]);
a[i] = i;
}
sort(len + 1,len + 1 + n);
do{
memset(f,0,sizeof(f));
int cur = 0,maxState = (1 << (n - 1)) - 1;
f[cur][len[n] * n][0] = 1;
for(int i = 1;i < C * n;i++){
if(i % n == 0) continue;
memset(f[cur ^ 1],0,sizeof(f[cur ^ 1]));
int x = i % n - 1;
for(int j = i;j <= C * n;j++){
for(int S = 0;S <= maxState;S++){
f[cur ^ 1][j][S] += f[cur][j][S];
if(!(S >> x & 1))
f[cur ^ 1][min(C * n,max(j,i + len[a[x + 1]] * n))][S | (1 << x)] += f[cur][j][S];
}
}
cur ^= 1;
}
ans += f[cur][C * n][maxState];
}while(next_permutation(a + 1,a + n));
facn = p = 1;
for(int i = 1;i < n;i++)
facn *= i, p *= C;
printf("%.12Lf\n",(long double)ans / facn / p);
return 0;
}
AGC 037E
Solution
首先为了字典序最小,我们肯定是让最小的字母接在最前面,记开头的连续最小字母个数为\(len\)
如果\(s[n]\)是最小字母,且以\(s[n]\)为结尾的连续的最小字母长度为\(L\),那么\(len\)要和\(L\times 2^k\)取较大值
如果\(s[i](i\neq n)\)是最小字母,且包含\(s[i]\)的连续的最小字母长度为\(L\),那么\(len\)要和\(L\times 2^{k−1}\)取较大值
然后取这其中字典序最小的即可,复杂度\(\mathcal O(n^2)\)
Code
int n,K;
char minn = 'z';
char s[MAXN],t[MAXN],ans[MAXN];
bool cmp(char *a,char *b){
for(int i = 1;i <= n;i++){
if(a[i] != b[i])
return a[i] < b[i];
}
return false;
}
void Solve(char *s,int k){
int pos = n,len = 0;
while(pos && s[pos] == minn){
pos -= 1;
len += 1;
}
while(k && len < n){
len <<= 1;
k -= 1;
}
if(len >= n){
for(int i = 1;i <= n;i++)
putchar(minn);
exit(0);
}
for(int i = 1;i <= len;i++)
t[i] = minn;
for(int i = len + 1;i <= n;i++)
t[i] = s[pos--];
if(cmp(t,ans)){
for(int i = 1;i <= n;i++)
ans[i] = t[i];
}
}
int main(){
scanf("%d%d%s",&n,&K,s + 1);
for(int i = 1;i <= n;i++){
minn = min(minn,s[i]);
ans[i] = 'z';
s[(n << 1) - i + 1] = s[i];
}
if(s[n] == minn)
Solve(s,K);
for(int i = n;i <= (n << 1);i++){
if(s[i] == minn)
Solve(s + i - n,K - 1);
}
for(int i = 1;i <= n;i++)
putchar(ans[i]);
return 0;
}
CF 639E
Solution
首先如果我们确定了一个\(c\),提出所有常数项之后发现就是要使得\(\sum p_ix_i\)最小,也就是说一个\(t_i\)会产生\(t_i\times \sum_{k=i+1}^np_i\)的贡献,考虑\(i\)和\(i+1\),如果\(i\)在前则贡献为
如果\(i+1\)在前则贡献为
上面两式做差可得\(i\)在\(i+1\)前面的条件是\(t_i\times p_{i+1}<t_{i+1}\times p_i\),直接按照\(\frac{t_i}{p_i}\)排递增序即可。
然后要对于任意最优序列都合法,那么某段连续的\(\frac{t_i}{p_i}\)相同的可以随便排列,对于每一段算出它最大和最小的\(x_i\)就行了。对于某个\(p_i>p_j\)合法的条件是\(p_i(1−c\times \frac{xi}{T})\leq p_j(1−c\times \frac{xj}{T})\)
最后考虑二分答案,判断当前二分的\(c\)是否合法即可,具体可以按照\(p\)排序,对于一段相同的\(p\),判断是否满足条件即可。
Code
const int INF = 0x3f3f3f3f;
const ll llINF = 1e18;
const int MAXN = 2e5 + 5;
int n;
ll T;
struct Node{
int p,t;
ll x,max,min;
} a[MAXN];
bool cmp1(const Node &x,const Node &y){
return 1ll * x.t * y.p < 1ll * y.t * x.p;
}
bool cmp2(const Node &x,const Node &y){
return x.p < y.p;
}
bool Check(long double c){
long double curMax = -INF,preMax = -INF;
for(int i = 1;i <= n;i++){
if(a[i].p != a[i - 1].p)
preMax = curMax;
if((1.0 - c * a[i].max / T) * a[i].p < preMax)
return false;
checkMax(curMax,(1.0 - c * a[i].min / T) * a[i].p);
}
return true;
}
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;i++)
scanf("%d",&a[i].p);
for(int i = 1;i <= n;i++){
scanf("%d",&a[i].t);
T += a[i].t;
}
sort(a + 1,a + 1 + n,cmp1);
for(int i = 1;i <= n;i++)
a[i].x = a[i - 1].x + a[i].t;
for(int i = 1,j;i <= n;i = j){
j = i;
while(j <= n && 1ll * a[i].p * a[j].t == 1ll * a[j].p * a[i].t) j += 1;
for(int k = i;k < j;k++){
a[k].min = a[i - 1].x + a[k].t;
a[k].max = a[j - 1].x;
}
}
sort(a + 1,a + 1 + n,cmp2);
long double l = 0,r = 1,res = 0;
for(int i = 1;i <= 40;i++){
long double mid = (l + r) / 2.0;
if(Check(mid)){
res = mid;
l = mid;
}else
r = mid;
}
printf("%.7Lf\n",res);
return 0;
}
CF 559E
Solution
首先对坐标离散化,然后对所有灯按照放置的位置排序,考虑依次加入线段计算贡献,设\(f[i][j]\)表示考虑到第\(i\)个点,已经覆盖到最右端点为\(j\)的覆盖长度最大值(并不要求\([i,j]\)都被覆盖)。
初始时\(f[i][j]=f[i - 1][j]\),设\(p,l,r\)分别为灯离散化后的坐标,往左照时的端点和往右照时的端点。考虑每次添加一个灯,有两种转移
- 向右照,直接转移即可,\(f[i][j]=f[i-1][p]+dis(p,j)\),其中\(dis\)表示原坐标的差
- 向左照,此时便有可能重复计算贡献,考虑如何处理这种情况,可以强行钦定一个\(k\)让\([k,i-1]\)的所有灯全部向右照,所有这样便可以确定这些灯的最右端点\(R=max_{j=k}^{i-1}r_j\),于是便有转移\(f[i][R] = f[k-1][l] + dis(l,R)\)
考虑这样做的正确性,因为如果在\([k,i-1]\)中有线段向左,那么它的贡献早已在当前的\(i\)向右时就计算过了。
直接dp的复杂度是\(\mathcal O(n^3)\)的,考虑优化,不难发现如果倒序枚举\(k\),则\(R\)一定是单调不降的,设\(g[R]\)为对于当前的\(i\),\(f[k-1][l]+dis(l,R)\)的最大值,对其做一遍后缀最大值更新答案即可。
时间复杂度\(\mathcal O(n^2)\)
Code
int n,tot;
int b[MAXM],f[MAXN][MAXM],g[MAXM];
struct Seg{
int p,l,r;
} a[MAXN];
bool cmp(const Seg &x,const Seg &y){
return x.p < y.p;
}
int main(){
scanf("%d",&n);
for(int i = 1,len;i <= n;i++){
scanf("%d%d",&a[i].p,&len);
a[i].l = a[i].p - len; a[i].r = a[i].p + len;
b[++tot] = a[i].p; b[++tot] = a[i].l; b[++tot] = a[i].r;
}
sort(a + 1,a + 1 + n,cmp);
sort(b + 1,b + 1 + tot);
tot = unique(b + 1,b + 1 + tot) - b - 1;
for(int i = 1;i <= n;i++){
a[i].l = lower_bound(b + 1,b + 1 + tot,a[i].l) - b;
a[i].p = lower_bound(b + 1,b + 1 + tot,a[i].p) - b;
a[i].r = lower_bound(b + 1,b + 1 + tot,a[i].r) - b;
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= tot;j++) g[j] = 0;
for(int j = 1;j <= tot;j++) f[i][j] = f[i - 1][j];
int p = a[i].p,l = a[i].l,r = a[i].r;
int R = p;
g[R] = f[i - 1][l] + b[R] - b[l];
for(int j = i - 1;j >= 1;j--){
checkMax(R,a[j].r);
checkMax(g[R],f[j - 1][l] + b[R] - b[l]);
}
for(int j = tot;j >= l;j--){
checkMax(f[i][j],g[j]);
checkMax(g[j - 1],g[j] - (b[j] - b[j - 1]));
}
for(int j = p;j <= r;j++)
checkMax(f[i][j],f[i - 1][p] + b[j] - b[p]);
for(int j = 1;j <= tot;j++)
checkMax(f[i][j],f[i][j - 1]);
}
printf("%d\n",f[n][tot]);
return 0;
}
AGC 039F
Solution
首先,对于一个矩阵\(A\),它的权值等价于重新填一个矩阵\(B\),满足\(B_{i,j}\)要小于等于\(A_{i,j}\)对应位置上的那\(n+m−1\)个值中的最小值的方案数,等价于\(B\)中每行的最大值小于等于\(A\)中对应行的最小值,\(B\)中每列的最大值小于等于\(A\)中对应列的最小值的方案数。
那么最终答案可以转化为所有合法的矩阵对\((A,B)\)的个数。
设\(f[k][i][j]\)表示已经确定\(B\)中\(i\)行的最大值,以及\(A\)中\(j\)列的最小值,并且它们都小于等于\(k\)的方案数。转移分为两步
-
枚举\(B\)中有多少行的最大值为\(k+1\),然后对于已经确定最小值的列,在\(A\)中填上大于等于\(k+1\)的数,对于没有确定最小值的列,在\(B\)中填上小于等于\(k+1\)的数,并满足在这些行中,每行至少有\(1\)个\(k+1\)。
-
枚举\(A\)中有多少列的最小值为\(k+1\),然后对于已经确定最大值的行,在\(A\)中填上大于等于\(k+1\)的数,并保证这些列中每列至少有一个数为\(k+1\),对于没有确定最大值的行,在\(B\)中填上小于等于\(k+1\)的数。
额外记一个\(0/1\)表示转移的两步,注意需要预处理转移的系数,不然会TLE。
时间复杂度\(\mathcal O(nmk(n+m))\)
Code
int n,m,K,MOD;
int C[MAXN][MAXN],coef[MAXN][MAXN][MAXN][2],f[MAXN][MAXN][MAXN][2];
int power(int x,int y){
int res = 1;
while(y){
if(y & 1) res = 1ll * res * x % MOD;
x = 1ll * x * x % MOD;
y >>= 1;
}
return res;
}
void Init(int N){
C[0][0] = 1;
for(int i = 1;i <= N;i++){
C[i][0] = C[i][i] = 1;
for(int j = 1;j < i;j++)
C[i][j] = add(C[i - 1][j],C[i - 1][j - 1]);
}
}
int main(){
scanf("%d%d%d%d",&n,&m,&K,&MOD);
Init(max(n,m));
for(int k = 1;k <= K;k++){
for(int i = 0;i <= m;i++){
int t = 1ll * power(K - k + 1,i) * sub(power(k,m - i),power(k - 1,m - i)) % MOD;
coef[k][i][0][0] = 1;
for(int j = 1;j <= n;j++)
coef[k][i][j][0] = 1ll * coef[k][i][j - 1][0] * t % MOD;
}
}
for(int k = 1;k <= K;k++){
for(int i = 0;i <= n;i++){
int t = 1ll * power(k,n - i) * (sub(power(K - k + 1,i),power(K - k,i))) % MOD;
coef[k][i][0][1] = 1;
for(int j = 1;j <= m;j++)
coef[k][i][j][1] = 1ll * coef[k][i][j - 1][1] * t % MOD;
}
}
f[1][0][0][0] = 1;
for(int k = 1;k <= K;k++){
for(int i = 0;i <= n;i++){
for(int j = 0;j <= m;j++){
for(int l = 0;l <= n - i;l++)
addmod(f[k][i + l][j][1],1ll * f[k][i][j][0] * C[n - i][l] % MOD * coef[k][j][l][0] % MOD);
for(int l = 0;l <= m - j;l++)
addmod(f[k + 1][i][j + l][0],1ll * f[k][i][j][1] * C[m - j][l] % MOD * coef[k][i][l][1] % MOD);
}
}
}
printf("%d\n",f[K + 1][n][m][0]);
return 0;
}
CF 575A
Solution
不难发现题目中\(f\)为二阶其次线性递推,可以通过矩阵快速幂优化转移。由题意得\(f\)满足
所以有
对于题目中给定的\(m\)个\(s\),不难发现它们把整个\(1\)到\(k\)的区间分成了\(m\)段,对于每段分别快速幂即可,具体开一颗长度为\(n\)的线段树维护每个循环节,对于每个给定的\(s\),在线段树上修改对应位置上矩阵的值即可。
时间复杂度\(\mathcal O(n+m(\log n +\log k)\)
Code
int n,m,MOD;
int s[MAXN];
ll K;
struct Query{
ll x;
int k,v;
} q[MAXN << 1];
bool cmp(const Query &x,const Query &y){
return x.x < y.x;
}
struct Matrix{
#define N 2
int a[N + 1][N + 1];
Matrix(bool flag = 0){
memset(a,0,sizeof(a));
if(!flag) return;
for(int i = 1;i <= N;i++) a[i][i] = 1;
}
Matrix(int A,int B,int C,int D){
a[1][1] = A; a[1][2] = B; a[2][1] = C; a[2][2] = D;
}
int* operator [] (const int &x){
return a[x];
}
Matrix operator * (const Matrix &rhs) const{
Matrix res;
for(int i = 1;i <= N;i++){
for(int k = 1;k <= N;k++){
for(int j = 1;j <= N;j++)
addmod(res.a[i][j],1ll * a[i][k] * rhs.a[k][j] % MOD);
}
}
return res;
}
Matrix operator ^ (ll y) const{
Matrix res(1);
Matrix x = *this;
while(y){
if(y & 1) res = res * x;
x = x * x;
y >>= 1;
}
return res;
}
void print(){
for(int i = 1;i <= N;i++){
for(int j = 1;j <= N;j++)
cout << a[i][j] << " ";
cout << endl;
}
cout << endl;
}
} a[MAXN],b[MAXN];
namespace SegmentTree{
struct Tree{
int l,r;
Matrix val;
} tree[MAXN << 2];
#define lson k << 1
#define rson k << 1 | 1
void update(int k){
tree[k].val = tree[lson].val * tree[rson].val;
}
void Build(int k,int l,int r){
tree[k].l = l;
tree[k].r = r;
if(l == r){
tree[k].val = a[l];
return;
}
int mid = (l + r) >> 1;
Build(lson,l,mid);
Build(rson,mid + 1,r);
update(k);
}
void Modfiy(int k,int x){
if(tree[k].l == tree[k].r){
tree[k].val = b[x];
return;
}
int mid = (tree[k].l + tree[k].r) >> 1;
if(x <= mid)
Modfiy(lson,x);
else
Modfiy(rson,x);
update(k);
}
Matrix Query(){
return tree[1].val;
}
#undef lson
#undef rson
}
int main(){
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
scanf("%lld%d%d",&K,&MOD,&n);
for(int i = 0;i < n;i++){
scanf("%d",&s[i]);
s[i] %= MOD;
}
for(int i = 1;i <= n;i++)
a[i] = b[i] = Matrix(0,s[i - 1],1,s[i % n]);
SegmentTree::Build(1,1,n);
scanf("%d",&m);
for(int i = 1,y;i <= m;i++){
scanf("%lld%d",&q[i].x,&y);
q[i + m].x = q[i].x + 1;
q[i].k = 2; q[i + m].k = 1;
q[i].v = q[i + m].v = y % MOD;
}
m <<= 1;
sort(q + 1,q + 1 + m,cmp);
while(m && q[m].x > K) m -= 1;
Matrix ans(1);
ll p = 0;
for(int i = 1,j = 1;i <= m;i = j){
ll t = (q[i].x - 1) / n;
while(j <= m && (q[j].x - 1) / n == t) j += 1;
ans = ans * (SegmentTree::Query() ^ (t - p));
p = t;
for(int k = i,x;k < j;k++){
x = (q[k].x - 1) % n + 1;
b[x][q[k].k][2] = q[k].v;
SegmentTree::Modfiy(1,x);
}
if(t == K / n) break;
ans = ans * SegmentTree::Query();
p += 1;
for(int k = i,x;k < j;k++){
x = (q[k].x - 1) % n + 1;
b[x] = a[x];
SegmentTree::Modfiy(1,x);
}
}
ll t = K / n;
ans = ans * (SegmentTree::Query() ^ (t - p));
for(int i = 1;i <= K % n;i++)
ans = ans * b[i];
printf("%d\n",ans[2][1]);
return 0;
}
AGC 031F
Solution
首先转化一下问题,倒着来做,一开始有一个数\(0\), 每次走过一条边该数变为乘以\(2\)再加上这条边的边权。用\((u,x)\)代表一个状态,表示当前在点\(u\),权值在模\(MOD\)下为\(x\)。
有一条边\((u,v,c)\),那么可以走到的状态是
由于\(MOD\)是奇数,所以存在\(k>1\)使得\(2^k\equiv 1 (\mod p)\),所以状态是循环的,由\((u,x)\)出发最终还会走回\((u,x)\),所以可以认为递推关系是双向的,即\((u,x)\Leftrightarrow (v,2x+c)\)
接下来考虑如果连接点\(u\)的两条边边权分别为\(a,b\),则
于是我们可以选择这样一条路
事实上,因为存在\(4\)的逆元,那么\(4x\)可以表示任何数,那么就相当于
接着考虑不同的点,\((u,x)\Leftrightarrow(v,2x+w)\), 设\(u\)循环节长度为\(t_u\),那么\(v\)的循环节长度为\(2t_u\),和其本身的取\(gcd\)得\(gcd(t_u,2t_v)=gcd(t_u,t_v)\)(\(2\)可以去掉是因为\(2\)与\(3g_u\)互质因而与\(t_u\)互质)。由于整个图是联通的,这可以扩展到所有点,也就是对于所有\((u,x)\)有\((u,x)\Leftrightarrow(u,x+T)\),令\(t=gcd_{u=1}^nt_u=gcd(3gcd_{i=1}^m(w_i-w_1),MOD)\),\(g=gcd_{i=1}^m(w_1-w_1)\)。显然有\(t=g\)或\(t=3g\)。
整理一下,同一点所有模\(t\)同余的状态是一样的,而所有边权是模\(g\)同余的,且\(t=g\)或\(t=3g\)。
这样,我们可以把题目中的\(MOD\)直接改成\(t\), 不会对答案有任何影响,那么现在所有边权在模\(g\)意义下都相等,设为\(z\),于是可以吧所有状态的\(x\)加\(z\),所有边权减\(z\),则之前所有性质仍成立,因为
这样的话边权都是\(g\)的倍数了,而因为\((u,x)\Leftrightarrow(u,4x+3c)\),而\(c\)又是\(g\)的倍数,那么可以认为\((u,x)\Leftrightarrow(u,4x)\),于是有
也就是说,对于每个点,我们只有\(6\)种状态有用。可以用并查集把所有在同一个连通块里的点缩起来,对于询问,只需要判断\((t,z)\)和\((s,z+r)\)是否连通,可以得到
对于每个\(p\)预处理一下\(z2^p\)的奇偶性即可。
时间复杂度\(O(6(n+m+q)\alpha (n)+p)\)
Code
int n,m,Q,MOD,g,z;
int u[MAXN],v[MAXN],f[MAXN],c[MAXN];
bool flag[2][MAXM];
int GetId(int u,int p,int q){
return (u - 1) * 6 + p * 3 + q + 1;
}
int gcd(int a,int b){
if(b == 0) return a;
return gcd(b,a % b);
}
int Find(int x){
if(x == f[x]) return x;
return f[x] = Find(f[x]);
}
void Merge(int u,int v){
u = Find(u); v = Find(v);
if(u != v) f[u] = v;
}
int main(){
scanf("%d%d%d%d",&n,&m,&Q,&MOD);
g = MOD;
for(int i = 1;i <= m;i++){
scanf("%d%d%d",&u[i],&v[i],&c[i]);
g = gcd(g,abs(c[i] - c[1]));
}
MOD = gcd(3 * g,MOD);
z = c[1] % g;
for(int i = 1;i <= n * 6;i++) f[i] = i;
for(int i = 1;i <= m;i++){
int w = (c[i] / g) % 3;
for(int p = 0;p < 2;p++){
for(int q = 0;q < 3;q++){
Merge(GetId(u[i],p,q),GetId(v[i],p ^ 1,(q * 2 + w) % 3));
Merge(GetId(v[i],p,q),GetId(u[i],p ^ 1,(q * 2 + w) % 3));
}
}
}
for(int i = 0,t = z;i < MOD;i++){
flag[i & 1][t] = 1;
t = t * 2 % MOD;
}
while(Q--){
int s,t,r;
scanf("%d%d%d",&s,&t,&r);
for(int p = 0;p < 2;p++){
for(int q = 0;q < 3;q++){
if(Find(GetId(t,0,0)) == Find(GetId(s,p,q)) && flag[p][(r + z + (3 - q)* g) % MOD]){
puts("YES");
goto NEXT;
}
}
}
puts("NO");
NEXT: continue;
}
return 0;
}
AGC 033D
Solution
不难发现如果每次从中间分,\(\log m+\log m\)次就变成\(1\times 1\)的格子,代价是\(0\),所以答案最多是\(\log +\log m\)。
因此可以将值放进状态中,设\(dp[i][j1][j2][k]\)表示左上角是\((i,j1)\),右上角是\((i,j2)\) ,用\(k\)的代价,往下最长能延伸到哪行。
转移的时候考虑横着切还是竖着切。
- 横着切:\(f[i][j1][j2][k]=dp [dp[i][j1][j2][k−1]+1][j1][j2][k−1]\)
- 竖着切:设\([j1,j3]\)和\([j3+1,j2]\)为分出的两部分,那么\(dp[i][j1][j3][k−1]\)和\(dp[i][j3+1][j2][k−1]\)的最小值是这样分的答案,那么\(f[i][j1][j2][k]\)即为最小值中的最大值。至此我们得出了\(\mathcal O(m)\)的暴力转移。
而因为dp值明显随矩阵增大而增大,所以可二分\(j3\)。即考虑二分找出最大的\(min(dp[i][j1][j3][k−1],dp[i][j3+1][j2][k−1])\),左比右大往左,反过来则往右。
初始化出所有\(k=0\)的情况即可。
时间复杂度\(\mathcal O(n^3\log^2 n)\),但因常数较小,能过。
Code
int n,m;
int pre[MAXN][MAXN],f[MAXN][MAXN][MAXN][LOG];
char s[MAXN][MAXN];
int GetSum(int a,int b,int c,int d){
return pre[c][d] - pre[a - 1][d] - pre[c][b - 1] + pre[a - 1][b - 1];
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++)
scanf("%s",s[i] + 1);
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++)
pre[i][j] = pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1] + (s[i][j] == '.');
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
for(int k = j;k <= m;k++){
int l = i,r = n,res = i - 1;
while(l <= r){
int mid = (l + r) >> 1;
int t = GetSum(i,j,mid,k);
if(t == 0 || t == (mid - i + 1) * (k - j + 1)){
res = mid;
l = mid + 1;
}else
r = mid - 1;
}
f[i][j][k][0] = res;
}
}
}
int k;
for(k = 1;f[1][1][m][k - 1] < n;k++){
for(int len = 1;len <= m;len++){
for(int i = 1;i <= n;i++){
for(int j1 = 1,j2 = len;j2<= m;j1++,j2++){
f[i][j1][j2][k] = f[i][j1][j2][k - 1];
checkMax(f[i][j1][j2][k],f[f[i][j1][j2][k - 1] + 1][j1][j2][k - 1]);
if(f[i][j1][j2][k] == n) continue;
int l = j1,r = j2 - 1,res = 0;
while(l <= r){
int mid = (l + r) >> 1;
int x = f[i][j1][mid][k - 1],y = f[i][mid + 1][j2][k - 1];
checkMax(res,min(x,y));
if(x < y)
r = mid - 1;
else
l = mid + 1;
}
checkMax(f[i][j1][j2][k],res);
}
}
}
}
printf("%d\n",k - 1);
return 0;
}
CF 547D
Solution
考虑转化一下问题: 将点看成连接其横坐标和纵坐标的边, 相当于要为每一条边定向, 使得每一个点的入度与出度的差的绝对值不超过\(1\)。
这很容易可以转化成一个欧拉回路的问题: 显然度数为偶数的点入度等于出度, 而度数为奇数的点入出度恰好差\(1\)。我们将度数为奇数的点连一条虚拟边到一个虚拟点, 由于的度数为奇数的点必然是偶数个, 那么虚拟点的度数也为偶数, 我们对新图跑欧拉回路对边定向即可。
时间复杂度\(\mathcal O(n)\)
Code
int n,len = 1;
int head[MAXN],deg[MAXN],vis[MAXM],ans[MAXN];
struct Edge{
int to,next;
} e[MAXM];
void add_edge(int u,int v){
e[++len] = (Edge){v,head[u]};
head[u] = len;
}
void dfs(int u){
for(int &i = head[u];i;i = e[i].next){
int v = e[i].to;
int e = i >> 1;
if(vis[e]) continue;
vis[e] = 1;
if(e <= n) ans[e] = i & 1;
else ans[e] = 0;
dfs(v);
}
}
int main(){
scanf("%d",&n);
for(int i = 1,u,v;i <= n;i++){
scanf("%d%d",&u,&v);
v += N;
add_edge(u,v); add_edge(v,u);
deg[u] += 1; deg[v] += 1;
}
for(int i = 1;i <= (N << 1);i++){
if(deg[i] & 1){
add_edge(0,i);
add_edge(i,0);
}
}
for(int i = 1;i <= (N << 1);i++)
dfs(i);
for(int i = 1;i <= n;i++)
putchar(ans[i] ? 'r' : 'b');
return 0;
}
ARC 097F
Solution
首先把所有黑色的叶子去掉,因为它们是没用的。然后考虑一种最简单的遍历,从某个节点出发按\(dfs\)序遍历每个节点,这样每条边会被经过恰好\(2\)次,每个点会被经过\(deg_i\)次,然后对于每个点再单独考虑这样操作之后是否变成了黑色,如果不是的话还需要一次额外的操作,记这种情况下的总次数为\(sum\)。
然后考虑如何确定起点\(S\)和终点\(T\),不难发现从\(S\)到\(T\)的最少游走次数就是在上面\(dfs\)的基础上,\(S\)到\(T\)路径上的每条边都少走一次,路径上的每个点(不包括\(S\)和\(T\))也都少走一次。那么我们可以去掉\(S\)和\(T\),考虑中间那条链最长能减少多少贡献。中间那条路径删掉之后的贡献就是点数\(+1−\)黑点个数\(+\)白点个数(这里的颜色为\(dfs\)之后的颜色),那么可以看做黑点贡献\(0\),白点贡献\(2\),求一条两端点不在叶子上的最长链的长度\(d\),其实就是求带权直径的长度,dp即可,最后的答案就是\(sum−d−1+1=sum-d\)。
Code
int n,len,sum,root,dia,cnt;
int head[MAXN],vis[MAXN],f[MAXN],w[MAXN],deg[MAXN];
char s[MAXN];
struct Edge{
int to,next;
} e[MAXN << 1];
void add_edge(int u,int v){
e[++len] = (Edge){v,head[u]};
head[u] = len;
}
void dfs(int u,int fa){
vis[u] = (s[u] == 'W');
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(v == fa) continue;
dfs(v,u);
vis[u] |= vis[v];
if(vis[v]) deg[u] += 1;
}
if(u != root) deg[u] += 1;
if(!vis[u]) return;
sum += 2;
if((deg[u] & 1) && s[u] == 'B') sum += 1, w[u] = 2;
if(!(deg[u] & 1) && s[u] == 'W') sum += 1, w[u] = 2;
f[u] = w[u];
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(v == fa) continue;
checkMax(dia,f[u] + f[v]);
checkMax(f[u],f[v] + w[u]);
}
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d",&n);
for(int i = 1,u,v;i < n;i++){
scanf("%d%d",&u,&v);
add_edge(u,v); add_edge(v,u);
}
scanf("%s",s + 1);
for(int i = 1;i <= n;i++){
cnt += (s[i] == 'W');
if(s[i] == 'W') root = i;
}
if(cnt <= 1) return printf("%d\n",cnt),0;
dfs(root,0);
printf("%d\n",sum - dia - 2);
return 0;
}
CF 671D
Solution
设\(f_i\)表示覆盖\(i\)子树内的所有边以及\(i\)与其父亲的边的最小权值,那么答案为\(\sum_{x \in \operatorname{son}(1)}f_x\)。
然而并不是所有\(f\)是最优的,对于一种覆盖\(i\)子树内的所有边和\(i\)与其父亲的边的方案,可能它并不是最小权值,但是它向上延伸得 更长。
因此要存下所有可能最优的方案,同时要计算其中的最小值,不难想到用小根堆维护。具体来说,对于节点\(u\)开一个小根堆,维护覆盖\(i\)的子树内的边和\(i\)与其父亲的边的所有可能最优的方案。初始时,对于一条路径\((x,y)\),将其加入\(x\)对应的小根堆里。
接下来考虑如何转移,即当\(x \in \operatorname{son}(y)\)时,如何将\(x\)上的方案转移到\(y\)上。对于一个权值为\(k\)的方案:
- 如果向上延伸超过了\(y\),则这种方案在\(y\)的小根堆里的权值应该为\(k + \sum_{z \in \operatorname{son}(y)} f_z\)。
- 如果正好向上延伸到\(y\),则这种方案不应该出现在\(y\)上,需要被删掉。
这时候可以发现,一个点有来自多个儿子的小根堆,显然需要将它们合并起来,于是将小根堆改为左偏树即可。
同时还需要支持整棵左偏树加上一个定值,可以通过打懒标记实现。
对于需要扔掉的方案,由于不需要实时删除,因此考虑暂时先保留它们,当它们成为小根堆的根时再弹出即可。
时间复杂度为\(\mathcal O(n \log n)\)。
Code
int n,m,len;
int head[MAXN],dep[MAXN],rt[MAXN];
ll f[MAXN];
vector<pii> vec[MAXN];
struct Edge{
int to,next;
} e[MAXN << 1];
void add_edge(int u,int v){
e[++len] = (Edge){v,head[u]};
head[u] = len;
}
namespace Heap{
int tot;
struct Tree{
int l,r,fa,dis;
int x;
ll tag,val;
} tree[MAXN];
#define lson(x) tree[(x)].l
#define rson(x) tree[(x)].r
#define fa(x) tree[(x)].fa
int NewNode(int x,int val){
tree[++tot].x = x;
tree[tot].val = val;
tree[tot].dis = 1;
return tot;
}
void apply(int k,ll v){
tree[k].tag += v;
tree[k].val += v;
}
void down(int k){
if(tree[k].tag){
apply(lson(k),tree[k].tag);
apply(rson(k),tree[k].tag);
tree[k].tag = 0;
}
}
ll Top(int k){
return tree[k].val;
}
int Merge(int x,int y){
if(!x || !y) return x | y;
if(tree[x].val > tree[y].val) swap(x,y);
down(x);
rson(x) = Merge(rson(x),y);
fa(rson(x)) = x;
if(tree[rson(x)].dis > tree[lson(x)].dis) swap(lson(x),rson(x));
tree[x].dis = tree[rson(x)].dis + 1;
return x;
}
int Erase(int k,int d){
while(k && dep[tree[k].x] >= d){
down(k);
k = Merge(lson(k),rson(k));
}
return k;
}
#undef lson
#undef rson
#undef fa
}
void dfs(int u,int fa){
dep[u] = dep[fa] + 1;
for(pii p : vec[u])
rt[u] = Heap::Merge(rt[u],Heap::NewNode(p.first,p.second));
ll sum = 0;
for(int i = head[u];i != -1;i = e[i].next){
int v = e[i].to;
if(v == fa) continue;
dfs(v,u);
sum += f[v];
Heap::apply(rt[v],-f[v]);
rt[u] = Heap::Merge(rt[u],rt[v]);
}
Heap::apply(rt[u],sum);
rt[u] = Heap::Erase(rt[u],dep[u]);
if(!rt[u]) puts("-1"), exit(0);
f[u] = Heap::Top(rt[u]);
}
int main(){
memset(head,-1,sizeof(head));
scanf("%d%d",&n,&m);
for(int i = 1,u,v;i < n;i++){
scanf("%d%d",&u,&v);
add_edge(u,v); add_edge(v,u);
}
for(int i = 1,x,y,z;i <= m;i++){
scanf("%d%d%d",&x,&y,&z);
vec[x].push_back(make_pair(y,z));
}
dep[1] = 1;
ll ans = 0;
for(int i = head[1];i != -1;i = e[i].next){
int v = e[i].to;
dfs(v,1);
ans += f[v];
}
printf("%lld\n",ans);
return 0;
}
CF 547E
Solution
先对\(s\)建出广义 SAM ,对每个点开一颗线段树维护每个串出现的次数,不难发现询问即为 parent tree 上一个点的子树内一段区间的和,直接在 parent tree 线段树合并即可。
时间复杂度\(\mathcal O(n\log n)\)
Code
int n,Q;
char s[MAXN];
int rt[MAXN],pos[MAXN];
namespace SegmentTree{
int tot;
struct Tree{
int l,r;
int sum;
} tree[MAXN * 35];
#define lson(x) tree[(x)].l
#define rson(x) tree[(x)].r
void update(int k){
tree[k].sum = tree[lson(k)].sum + tree[rson(k)].sum;
}
void Modify(int &k,int l,int r,int x){
if(!k) k = ++tot;
tree[k].sum += 1;
if(l == r) return;
int mid = (l + r) >> 1;
if(x <= mid)
Modify(lson(k),l,mid,x);
else
Modify(rson(k),mid + 1,r,x);
}
int Query(int k,int l,int r,int ql,int qr){
if(!k) return 0;
if(l >= ql && r <= qr) return tree[k].sum;
int mid = (l + r) >> 1;
int res = 0;
if(ql <= mid)
res += Query(lson(k),l,mid,ql,qr);
if(qr > mid)
res += Query(rson(k),mid + 1,r,ql,qr);
return res;
}
int Merge(int x,int y,int l,int r){
if(!x || !y) return x | y;
int k = ++tot;
if(l == r) return tree[k].sum = tree[x].sum + tree[y].sum, k;
int mid = (l + r) >> 1;
lson(k) = Merge(lson(x),lson(y),l,mid);
rson(k) = Merge(rson(x),rson(y),mid + 1,r);
return update(k), k;
}
}
struct SAM{
int last,tot;
int son[MAXN][26],len[MAXN],fa[MAXN],rk[MAXN],bac[MAXN];
SAM() {last = tot = 1;}
void extend(int c){
static int p,q,np,nq;
p = last;
if(son[p][c]){
q = son[p][c];
if(len[q] == len[p] + 1) return last = q, void();
nq = ++tot; len[nq] = len[p] + 1;
memcpy(son[nq],son[q],sizeof(son[q]));
fa[nq] = fa[q]; fa[q] = nq;
for(;p && son[p][c] == q;p = fa[p]) son[p][c] = nq;
return last = nq, void();
}
last = ++tot;
np = tot; len[np] = len[p] + 1;
for(;p && !son[p][c];p = fa[p]) son[p][c] = np;
if(!p) return fa[np] = 1, void();
q = son[p][c];
if(len[q] == len[p] + 1) return fa[np] = q, void();
nq = ++tot;
memcpy(son[nq],son[q],sizeof(son[nq]));
len[nq] = len[p] + 1;
fa[nq] = fa[q];
fa[q] = fa[np] = nq;
for(;son[p][c] == q;p = fa[p]) son[p][c] = nq;
}
void init(){
for(int i = 1;i <= tot;i++) bac[len[i]] += 1;
for(int i = 1;i <= tot;i++) bac[i] += bac[i - 1];
for(int i = tot;i >= 1;i--) rk[bac[len[i]]--] = i;
for(int i = tot;i > 1;i--)
rt[fa[rk[i]]] = SegmentTree::Merge(rt[fa[rk[i]]],rt[rk[i]],1,n);
}
} sam;
int main(){
scanf("%d%d",&n,&Q);
for(int i = 1;i <= n;i++){
scanf("%s",s + 1);
int len = strlen(s + 1);
sam.last = 1;
for(int j = 1;j <= len;j++){
sam.extend(s[j] - 'a');
SegmentTree::Modify(rt[sam.last],1,n,i);
}
pos[i] = sam.last;
}
sam.init();
while(Q--){
int l,r,k;
scanf("%d%d%d",&l,&r,&k);
printf("%d\n",SegmentTree::Query(rt[pos[k]],1,n,l,r));
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号