利用desmos动态展示最大似然概率

最近碰到最大似然概率的问题，题目一变就出错，痛心！深感没有搞清楚这个求解的意义，有必要搞清楚最大似然值和概率是什么。
传统概率视角：给定参数θ，数据X出现的可能性 \(P(X∣θ)\)
统计推断视角：我已经看到了数据X，哪个θ最可能产生这些数据？

最大似然估计的核心思想：

“我现在手上有一组观测数据。在众多可能的参数值中，我选择那个让这组数据出现概率最大的参数值作为估计。”

最大似然概率的核心就是一个断言：假设就是参数为\(\hat θ_{MLE}\)时，样本的联合概率密度最大

\[\hat θ_{MLE}​=arg​max_θ​L(θ) \]

概率密度最大时一般就是极值点中的一个。如果没有极值点的话，就证明函数单调，那概率最大的情况只能在边界点取得。
但是这个参数是变化的，为了更好的理解，区别于静态的函数曲线，想到用desmos去画
我采用了经典的投骰子来探究，其满足伯努利分布
样本情况为，统计10次，发生7次，也就是B(10,θ)。对于动态曲线，就相当于观察x=7时的概率变化情况
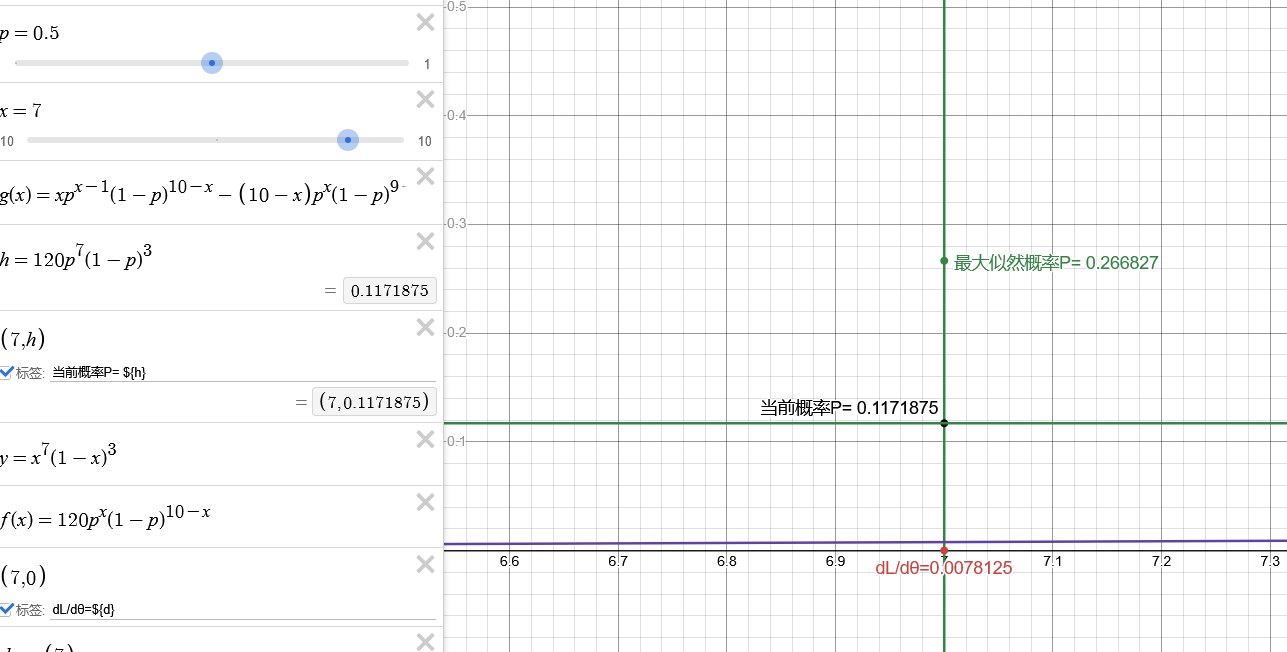
可以看到，在导数项0逼近时，样本概率也逼近最大值。而在参数θ趋近于0或1时，概率P也趋近于0，这很符合我们直觉

而在参数p也就是θ恰好为0.7时，导数为0，样本概率也达到最大值

而且我调参数发现，\(θ=0.5\)恰好就是一条直线，也就是骰子质量均匀的情况

但还是不能忘记强调，最大似然只是武断和假设，不是真实情况