题解：[AGC035D] Add and Remove

题面

[AGC035D] Add and Remove

题面翻译

题目描述

有一个由 \(N\) 张牌组成的牌堆，每一张牌上都写有一个非负整数。自顶部开始，第 \(i\) 张牌上的数字为 \(A_i\)。

Snuke 将重复以下操作，直至牌堆里只剩两张卡为止：

• 从牌堆里选择三张连续的卡。
• 把三张卡中位于中间位置的卡吃掉。
• 把剩余的两张卡上的数字加上被吃掉的卡的数字后按照原来的顺序放回牌堆。

请找出最后剩下的两张牌上所写的数字之和最小是多少。

样例 \(1\) 解释

通过执行以下操作，可以使剩余两张牌的数字之和最小：

• 最初，牌堆的数字自顶向下为 \(3,1,4,2\)。
• 选择自顶向下的前三张牌，吃掉写有数字 \(1\) 的卡牌，在剩余的两张牌中每张牌的数字加 \(1\)，放回至原来位置。现在牌堆的数字自顶向下为 \(4,5,2\)。
• 选择自顶向下的前三张牌，吃掉写有数字\(5\)的卡牌，在剩余的两张牌中每张牌的数字加 \(5\)，放回至原来位置。现在牌堆的数字自顶向下为 \(9,7\)。
• 剩下的两张牌的数字之和为 \(16\)。

题目描述

非負整数のひとつ書かれたカードが $ N $ 枚積まれた山があります。上から $ i $ 番目のカードに書かれた整数は $ A_i $ です。

すぬけ君は、以下の操作をカードが $ 2 $ 枚になるまで繰り返します。

• 連続して積まれている $ 3 $ 枚のカードを選ぶ。
• $ 3 $ 枚のうち真ん中のカードを食べる。
• あとの $ 2 $ 枚のカードに書かれている整数を、その整数に食べたカードに書かれていた整数を足してできる整数に書き換える。
• 食べなかった $ 2 $ 枚のカードを、順序を保ったまま山のもとの位置に戻す。

最終的に残る $ 2 $ 枚のカードに書かれた整数の和の最小値を求めてください。

输入格式

入力は以下の形式で標準入力から与えられる。

$ N $ $ A_1 $ $ A_2 $ $ ... $ $ A_N $

输出格式

最終的に残る $ 2 $ 枚のカードに書かれた整数の和の最小値を出力せよ。

样例 #1

样例输入 #1

4
3 1 4 2

样例输出 #1

16

样例 #2

样例输入 #2

6
5 2 4 1 6 9

样例输出 #2

51

样例 #3

样例输入 #3

10
3 1 4 1 5 9 2 6 5 3

样例输出 #3

115

提示

制約

• $ 2\ \leq\ N\ \leq\ 18 $
• $ 0\ \leq\ A_i\ \leq\ 10^9\ (1\leq\ i\leq\ N) $
• 入力はすべて整数である

Sample Explanation 1

以下の操作を行うことで、最終的に残る $ 2 $ 枚のカードに書かれた整数の和を最小にできます。 - 最初、カードに書かれた整数は順に $ 3,1,4,2 $ である。 - $ 1,2,3 $ 番目のカードを選ぶ。$ 1 $ の書かれた $ 2 $ 枚目のカードを食べ、残ったカードに書かれた整数に $ 1 $ を足し、山のもとの位置に戻す。カードに書かれた整数は順に $ 4,5,2 $ となる。 - $ 1,2,3 $ 番目のカードを選ぶ。$ 5 $ の書かれた $ 2 $ 枚目のカードを食べ、残ったカードに書かれた整数に $ 5 $ を足し、山のもとの位置に戻す。カードに書かれた整数は順に $ 9,7 $ となる。 - 最後に残った $ 2 $ 枚のカードに書かれた整数の和は $ 16 $ になる。

题解

思路

这道题的正解对于蒟蒻还是太难了（毕竟是一道紫题）。

仔细阅读体面就可以发现 \(n \le 18\)，所以真正有变化的只有 \(16\) 位，因此一共有 \(16! = 20922789888000\) 也不是很大，但是这对于 $O\left ( n \right ) $ 还是太大了，所以这里采用 爬山算法。

我们将每一种排列方式记为 \(x\) 轴上的某一个点，最终的结果就是 \(y\) 轴的对应值。

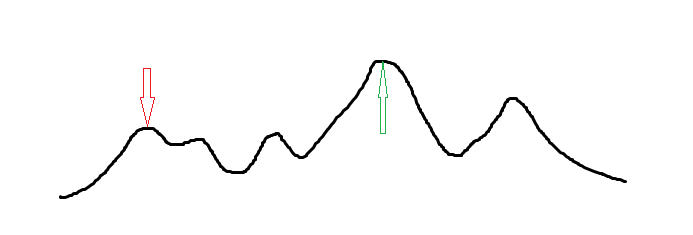
上图来自于 OI WiKi

对于无论是哪一种排列方式，都应当将这个排列的最终结果计算出来。这里使用链表来进行计算，当然也可以选择其它的算法。

int check() {
	for (int i = 1; i <= n; i++) {
		l[i] = i - 1;
		r[i] = i + 1;
		v[i] = a[i];
	}
	for (int i = 2; i < n; i++) {
		v[l[b[i]]] += v[b[i]];
		v[r[b[i]]] += v[b[i]];
		l[r[b[i]]] = l[b[i]];
		r[l[b[i]]] = r[b[i]];
	}
	return v[1] + v[n];
}

check() 函数写好后，就应当开始写爬山算法的核心代码了。

void work() {
	random_shuffle(b + 2, b + n); //随机打乱
	int now = check(), nxt;
	for (int i = 1; i <= 1145; i++) {
		int p = rand() % (n - 2) + 2, q = rand() % (n - 2) + 2;//随机取数
		swap(b[p], b[q]);
		nxt = check();
		if (nxt < now) 	now = nxt;
		else	swap(b[p], b[q]); //交换回来
	}
	ans = min(ans, now);
}

代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, a[20], ans = 1145141919810, l[20], r[20], v[20], b[20];

int check() {
	for (int i = 1; i <= n; i++) {
		l[i] = i - 1;
		r[i] = i + 1;
		v[i] = a[i];
	}
	for (int i = 2; i < n; i++) {
		v[l[b[i]]] += v[b[i]];
		v[r[b[i]]] += v[b[i]];
		l[r[b[i]]] = l[b[i]];
		r[l[b[i]]] = r[b[i]];
	}
	return v[1] + v[n];
}

void work() {
	random_shuffle(b + 2, b + n);
	int now = check(), nxt;
	for (int i = 1; i <= 1145; i++) {
		int p = rand() % (n - 2) + 2, q = rand() % (n - 2) + 2;
		swap(b[p], b[q]);
		nxt = check();
		if (nxt < now) 	now = nxt;
		else	swap(b[p], b[q]);
	}
	ans = min(ans, now);
}


signed main() {
	double begin = clock();
	cin.tie(0), cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i++)	cin >> a[i];
	for (int i = 1; i <= n; i++)	b[i] = i;
	if (n == 2) {
		cout << a[1] + a[n] << "\n";
		return 0;
	}
	while (clock() - begin <= 1.8 * CLOCKS_PER_SEC) {
		work();
	}
	cout << ans;
	return 0;
}