排序算法

堆排序（heapSort）

 算法思想：

  堆是一种叫做完全二叉树的数据结构，可以分为大根堆、小根堆，而堆排序就是基于这种结构产生的算法。大根堆指的是每个节点的值都大于或者等于其左右子节点的值，小根堆指的是每个节点的值都小于或者等于其左右子节点的值。
  1、首先将待排序的数组构造成一个大根堆，此时整个数组的最大值就是堆结构的顶端。
  2、将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1。
  3、将剩余的n-1个数再构造大根堆，再将顶端数与n-1位置的数交换，如此反复执行，可以得到有序数组。
  Ps：升序大根堆，降序为小根堆。
  构造大根堆：
  对于一个完全二叉树，在填满的情况下，每一层的元素个数是上一层的两倍，根节点数量是1，所以最后一层的节点数量应该是之前所有层节点总数+1，所以最后一层的第一个节点（第一个叶子节点）的索引应该是节点总数/2，而最后一个非叶子节点的索引=节点总数/2-1。对于填不满的二叉树，第一个叶子节点一定是节点总数/2，所以最后一个非叶子节点的索引=节点总数/2-1。
  找到了最后一个非叶子节点，和它的左右节点中最大的值进行比较，如果大就交换位置。

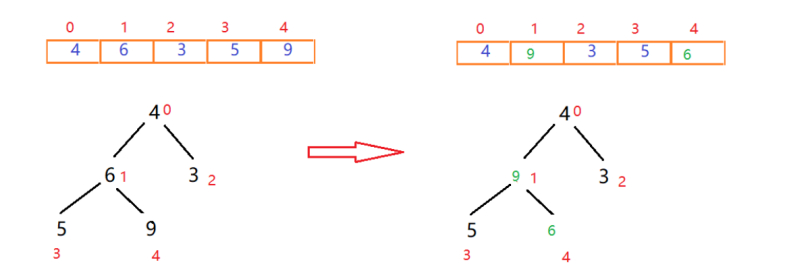
  再往前寻找下一个非叶子节点，用它和它的左右节点中最大值进行比较。在此图中应该是交换4和9的位置。

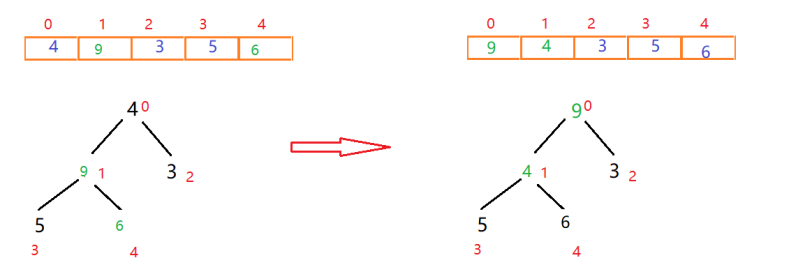
  交换完后发现仍小于其子节点，则再进行调整（递归），调整完后就构造出来了一个大根堆。

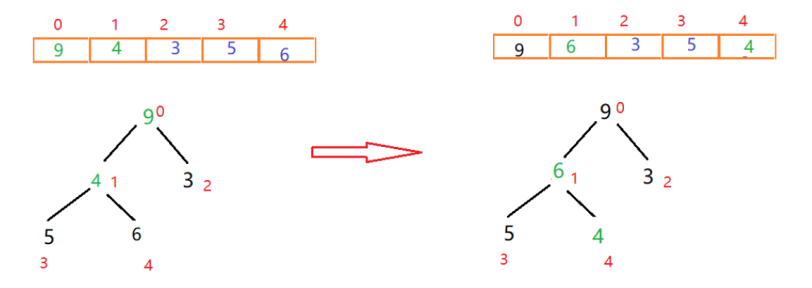
 算法复杂度分析

  堆排序包括两个阶段，初始化建堆和重建堆，下面分别分析这两部分的算法时间复杂度。
  1、初始化建堆只需要对二叉树的非叶子节点调用构造大根堆函数maxHeapify，从下至上，从右至左选取非叶子节点调用maxHeapify函数，这里假设高度为k，则从倒数第二层右边的节点开始，每个节点都需要和子节点进行比较然后交换，再往上层的节点如果发生交换了，还需要和交换后的子树再次进行交换，逐渐递归。
  所以每一层总节点时间计算为s=2^i-1（k-i），其中i表示第几层，2^i-1表示该层上有多少个元素，而（k-i）表示节点要向下比较的次数。
  所以S=2^(k-2)1+2^(k-3)2+……+2⁽¹⁾（k-2）+2⁽⁰⁾（k-1）从k-1层到1层
  S=2^k-k-1，又因为k为完全二叉树的深度，而log₂（n）=k
  得到S=n-log₂（n）-1，所以初始化建堆的时间复杂度为O（n）
  2、排序重建堆，在取出堆顶点放到对应位置并把原堆的最后一个节点填充到堆顶点之后，需要对堆进行重建，需要对堆的顶点调用maxHeapify函数。每次重建意味着一个节点出堆，所以需要将堆的容量减一，随着堆的容量减少，层数会下降，函数的时间复杂度会变化。重建堆共需要n-1次循环，每次循环的比较次数为log₂（i），则相加为log₂（2）+log₂（3）+……+log₂（n-1）+log₂（n）≈log₂（n！）
  可以证明log（n！）和nlog（n）是同阶函数
  ∵(n/2)^(n/2)≤n！≤nⁿ
  ∴n/4log（n）=n/2log（n^0.5）≤n/2log（n/2）≤log（n!）≤nlog（n）
  所以时间复杂度为O（nlogn），总的时间复杂度为O（n+nlogn）=O（nlogn）。
  由于整个计算步骤数量并不受数组原始排序结果的影响，所以最坏情况下的时间复杂度也为O（nlogn），最坏情况和平均情况相同。

 算法代码：

//交换两个元素的值
void swap(int *a,int *b){
    int temp=*a;
    *a=*b;
    *b=temp;
}
// 构造大根堆
void maxHeapify(int arr[],int n,int i){
    int largest = i;//初始化最大值为根节点，这里的largest是索引值
    int l = 2*i+1;//左子节点索引
    int r = 2*i+2;//右子节点索引
    //如果左子节点大于根节点，更新最大值索引
    if(l<n&&arr[l]>arr[largest]){
        largest = l;
    }
    //如果右子节点大于根节点，更新最大值索引
    if(r<n&&arr[r]>arr[largest]){
        largest = r;
    }
    //如果最大值索引不是根节点，交换元素并递归调整堆
    if(largest!=i){
        swap(&arr[i],&arr[largest]);//交换根节点和最大值
        //递归调整堆
        maxHeapify(arr,n,largest);
    }
}
//堆排序函数
void heapSort(int arr[],int n){
    // 构造大根堆
    for(int i=n/2-1;i>=0;i--){
        maxHeapify(arr,n,i);
    }
    // 从堆顶一个个取出元素
    for(int i=n-1;i>0;i--){
        // 交换堆顶元素和最后一个元素
        swap(&arr[0],&arr[i]);
        // 调整堆,排除已排序完的元素
        maxHeapify(arr,i,0);    
    }
}

归并排序（mergeSort）

 算法思想：

  归并排序是一种基于分治的算法，用于将一个数组列表分为两个子数组，递归地对子数组进行排序，然后将两个已排序的数组合并为一个有序的数组。
  1、分割（Divide）：将待排序的数组或列表分为两个大致相等的子数组。
  2、排序：递归的对子数组进行排序，直到子数组的大小为1。
  3、合并（Merge），将两个已排序的子数组合并为一个有序的数组，将两个子数组按顺序比较元素，并按顺序合并它们。

 算法复杂度分析：

  归并排序总时间=分解时间+子序列排序时间+合并时间（这里因为无论每个序列中有多少数都是 折中分解，所以分解时间为常数，忽略不计）
  由于在合并时，两个子序列已经排序好，所以用T（n）表示归并排序所用的时间
  假定合并过程所用时间为cn，其中c为一个整数，则有

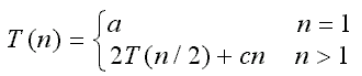
  则T（n）=2（2T（n/4）+cn/2）+cn
      =4T（n/4）+2cn
      =2^kT（1）+kcn
  因为n=2^k，所以上式=an+cnlogn，对于一般的整数n，可以假定2^k＜n≤2^k+1
  T（n）≤T（2^k+1）
  所以T（n）=O（nlogn），因为归并排序的时间并不依赖于数组的起始状态，所以归并排序的最好、最坏、平均情形的时间复杂度都是O（nlogn），并且它是稳定的。

 算法代码：

//合并两个子数组
void merge(int arr[],int l,int m,int r){
    int i,j,k;
    int n1 = m-l+1;//左子数组长度
    int n2 = r-m;//右子数组长度
    //创建临时数组来存储子数组
    int L[n1],R[n2];
    //将数据复制到临时数组
    for(int i=0;i<n1;i++){
        L[i]=arr[l+i];
    }
    for(int j=0;j<n2;j++){
        R[j]=arr[m+1+j];
    }
    // 合并临时数组L[]和R[]到arr[l..r]中
    i=0,j=0,k=l;//初始化索引值
    while(i<n1&&j<n2){
        if(L[i]<=R[j]){
            arr[k]=L[i];
            i++;
        }
        else{
            arr[k]=R[j];
            j++;
        }
        k++;
    }
    //复制L[]的剩余元素
    while(i<n1){
        arr[k]=L[i];
        i++,k++;
    }
    //复制R[]的剩余元素
    while(j<n2){
        arr[k]=R[j];
        j++,k++;
    }   
}
// 归并排序算法
void mergeSort(int arr[],int l,int r){
    if(l<r){
        //计算数组中间位置
        int m = (l+r)/2;
        //递归排序左子数组
        mergeSort(arr,l,m);
        //递归排序右子数组
        mergeSort(arr,m+1,r);
        //合并左右子数组
        merge(arr,l,m,r);
    }
}

 快速排序（quickSort）

 算法思想：

  快速排序是一种基于分治的排序算法，也是对冒泡排序的一种改进。其基本思想是通过一趟排序将待排数据分成两个独立的部分，对这两个部分进行排序使得其中一部分所有的数据比另一部分小，然后继续递归排序这两部分，最后实现所有数据有序。
  1、先从数组中挑出一个元素，称为“基准”（pivot）。可以选择第一个元素、最后一个元素、中间元素或者是随机元素作为基准。
  2、分区（Partition）：将数组中的其他元素按照与基准元素的大小关系分为两个子数组，一个子数组中的元素小于基准元素，另一个子数组的元素大于基准元素。同时，基准元素所在的位置也确定了。切分的过程先从数组的右端开始向左遍历，找到一个小于基准值的元素，再从数组左端开始向右遍历，找到一个大于等于基准值的元素，而后交换他们的位置，反复此过程，当两个遍历的指针相遇时，将相遇地点的值与数组l段的值交换并返回索引值。
  3、递归（Recursive）排序：递归地对两个子数组进行排序，将排序问题拆分为两个子问题。当递归到了最底部时，数组的大小是零或一，也就是已经排序好了。

 算法复杂度分析：

  平均情况：

    当基准值选取在随机的第k个位置，（1≤k≤n）

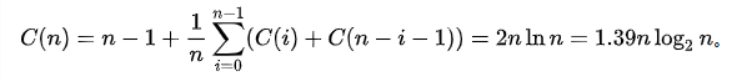
    n-1是分割所使用的比较次数。因为基准值是相当均匀地落在排列好的数列次序之任何地方，总和就是所有可能分割的平均。

  最优情况：

    每次基准值的选取都恰好把数组对半分开，，递归树的深度最浅为log₂（n）
    T(n) ≤ 2T(n/2) + n，T(1) = 0
    T(n) ≤ 2(2T(n/4)+n/2) + n = 4T(n/4) + 2n
    T(n) ≤ 4(2T(n/8)+n/4) + 2n = 8T(n/8) + 3n
    ......
    T(n) ≤ nT(1) + (log₂n)×n = O(nlogn)

  最坏情况：

    当原序列有序时，每次基准值都选择最大或者最小值，此时退化为冒泡排序，比较次数就变成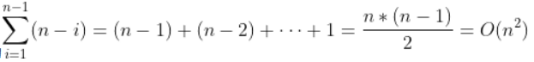，时间复杂度为O（n²）。

  算法代码：

// 划分函数
int partition(int arr[],int l,int r){
    int pivot = arr[l];// 基准值pivot
    int i=l,j=r;
    while(i!=j){
        //从右往左寻找比基准值小的元素
        while(arr[j]>=pivot&&i<j){
            j--;
        }
        //从左往右寻找比基准值大的元素
        while(arr[i]<=pivot&&i<j){
            i++;
        }
        //交换两个元素
        if(i<j){
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    //将基准值与i和j相等的元素交换
    arr[l] = arr[i];
    arr[i] = pivot;
    return i;//返回索引值
}
// 快速排序算法
void quickSort(int arr[],int l,int r){
    int index;
    if(l>r)
        return ;
    if(l<r){
        index = partition(arr,l,r);//划分
        quickSort(arr,l,index-1);//对左半部分进行快速排序
        quickSort(arr,index+1,r);//对右半部分进行快速排序
    }
}