LeetCode 栈与队列篇(12、155、84、239)
20. 有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 1:
输入: "()"
输出: true
示例 2:
输入: "()[]{}"
输出: true
示例 3:
输入: "(]"
输出: false
示例 4:
输入: "([)]"
输出: false
示例 5:
输入: "{[]}"
输出: true
solution1 往stack放右括号
class Solution {
public boolean isValid(String s) {
//整一个栈
Stack<Character> stack = new Stack<Character>();
for (char c : s.toCharArray()) {
if (c == '{') stack.push('}');
else if (c == '[') stack.push(']');
else if (c == '(') stack.push(')');
else if (stack.isEmpty() || stack.pop() != c) return false;
}
return stack.isEmpty();
}
}
solution2 往stack放左括号
class Solution {
public boolean isValid(String s) {
if (s.length() == 0) return true;
if ((s.length() & 1) == 1) return false;
Stack<Character> stack = new Stack<>();
Map<Character,Character> map = new HashMap<>();
map.put(')','(');
map.put(']','[');
map.put('}','{');
for (int i = 0 ;i < s.length();i++) {
char c = s.charAt(i);
if (c == '(' || c == '[' || c == '{'){
stack.push(c);
}else{
if (stack.size() == 0 || map.get(c) != stack.pop()) {
return false;
}
}
}
return stack.isEmpty();
}
}
solution3 暴力解法,遍历数组,有对称消掉并继续,没对称结束
class Solution {
// private static final Map<Character,Character> = new HashMap<>()
public boolean isValid(String s) {
if (s.length() == 0) return true; //空
if ((s.length() & 1) == 1) return false; // 奇数、位运算
int length;
do{
length = s.length();
s = s.replace("()","").replace("[]","").replace("{}","");
}while(length!=s.length());
return s.length() == 0;
}
}
solution4 字符串加递归
class Solution {
public boolean isValid(String s) {
if (s.contains("()") || s.contains("[]") || s.contains("{}")) {
return isValid(s.replace("()","").replace("[]","").replace("{}",""));
}else {
return "".equals(s);
}
}
}
155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
示例:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
提示:
pop、top 和 getMin 操作总是在 非空栈 上调用。
solution1
//整两个栈
class MinStack {
Stack<Integer> stack;
Stack<Integer> minStack;
public MinStack() {
stack = new Stack<>();
minStack = new Stack<>();
}
public void push(int x) {
stack.push(x);
if (minStack.isEmpty() || x <= minStack.peek()) minStack.push(x);
}
public void pop() {
if (stack.pop().equals(minStack.peek())) minStack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return minStack.peek();
}
}
solution2
//一个栈
class MinStack {
Stack<Integer> stack;
Integer i;
public MinStack() {
stack = new Stack<>();
}
public void push(int x) {
if (i != null && x <= i) {
stack.push(i);
i = x;
}
if (i == null) i = x;
stack.push(x);
}
public void pop() {
if (stack.pop().equals(i) && !stack.isEmpty()) {
i = stack.pop();
}
if (stack.isEmpty()) i = null;
}
public int top() {
return stack.peek();
}
public int getMin() {
return i;
}
}
class MinStack {
int min = Integer.MAX_VALUE;
Stack<Integer> stack = new Stack<Integer>();
public void push(int x) {
//当前值更小
if(x <= min){
//将之前的最小值保存
stack.push(min);
//更新最小值
min=x;
}
stack.push(x);
}
public void pop() {
//如果弹出的值是最小值,那么将下一个元素更新为最小值
if(stack.pop() == min) {
min=stack.pop();
}
}
public int top() {
return stack.peek();
}
public int getMin() {
return min;
}
}
solution3
//存差值
class MinStack {
Stack<Long> stack;
long i;
/** initialize your data structure here. */
public MinStack() {
stack = new Stack<>();
}
public void push(int x) {
if (stack.isEmpty()){
i = x;
stack.push(x-i);
}else {
if (x < i) {
stack.push(x-i);
i = x;
}else{
stack.push(x-i);
}
}
}
public void pop() {
Long pop = stack.pop();
//弹出后恢复上一个最小值
if ( pop < 0 ) {
i = i - pop;
}
}
public int top() {
long top = stack.peek();
if (top < 0) {
return (int)i;
}else{
return (int)(top + i);
}
}
public int getMin() {
return (int)i;
}
}
84. 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
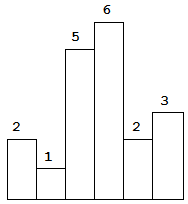
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
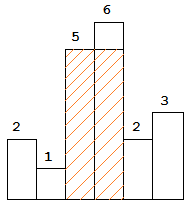
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
solution1
//暴力解法1
//时间复杂度为(n^3)Java 超时
class Solution {
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0) return 0;
int max = heights[0];
for (int i = 0; i < heights.length; i ++) {
for (int j = i; j < heights.length; j ++) {
//每两个之间的最小值为高
int min = heights[j];
for (int k = i;k <= j; k++){
min = Math.min(min,heights[k]);
max = Math.max(max,min*(k-i+1));
}
}
}
return max;
}
}
solution2
//暴力2,以每个柱子为最低点,找到对应的矩形
//时间复杂度为(n^2)
class Solution {
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0) return 0;
int max = 0;
for (int i = 0; i < heights.length; i ++) {
//遍历左边,找是否有比本身大的
int left = i;
while (left > 0 && heights[left-1] >= heights[i]){
left --;
}
//遍历右边,找是否有比本身小的
int right = i;
while (right < heights.length - 1 && heights[right+1] >= heights[i]) {
right ++;
}
max = Math.max((right - left + 1)*heights[i],max);
}
return max;
}
}
solution3
// 时间、空间复杂度均为O(n)
// 每个的左右边界为比它小的值,栈从小到大放,可以保证左边界,遇到比它小的为右边界,即可计算矩形面积
class Solution {
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0) return 0;
Stack<Integer> stack = new Stack<>();
stack.push(-1);
int max = 0;
//按从小到大插入栈,确保每个插入的值知道它的左边界,遇到比它小的即确定右边界
for (int i = 0; i < heights.length; i ++) {
while (stack.peek() != -1 && heights[stack.peek()] >= heights[i]) {
max = Math.max(max,heights[stack.pop()] * (i - stack.peek() - 1));
// 确定了左右边界,右边界为比它小的,左边界为栈里比它小的后一位
}
stack.push(i);
}
//清空栈
while (stack.peek() != -1)
max = Math.max(max, heights[stack.pop()] * (heights.length - stack.peek() - 1));
return max;
}
}
solution4
//用两个数组
class Solution {
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0) {
return 0;
}
//整两个数组记录每个数的左右边界,即从左算和右算的最小值
int[] lessFromLeft = new int[heights.length];
int[] lessFromRight = new int[heights.length];
lessFromRight[heights.length - 1] = heights.length;
lessFromLeft [0] = -1;
// 确定左边界
for (int i = 1;i < heights.length; i++){
int p = i-1;
while (p >= 0 && heights[p] >= heights[i]) {
p = lessFromLeft[p];
}
lessFromLeft[i] = p;
}
//确定右边界
for (int i = heights.length - 2;i >= 0;i --){
int p = i + 1;
while(p < heights.length && heights[p] >= heights[i]){
p = lessFromRight[p];
}
lessFromRight[i] = p;
}
int max = 0;
for (int i = 0; i < heights.length; i ++){
max = Math.max(max,(lessFromRight[i]-lessFromLeft[i]-1)*heights[i]);
}
return max;
}
}
239. 滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length
solution1 暴力法
//时间复杂度为O(nk),Java代码无法通过
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int[] result = new int[nums.length-k+1];
for (int i = 0;i < nums.length-k+1;i ++) {
int max = Integer.MIN_VALUE;
for (int j = i;j < i+k;j++) {
max = Math.max(max,nums[j]);
}
result[i] = max;
}
return result;
}
}
solution2 双端队列
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums.length == 0 || k == 0) return nums; //判空
int[] result = new int[nums.length-k+1]; //返回的结果
Deque<Integer> dq = new ArrayDeque<>(); // 双端队列,从小到大
for (int i = 0; i < nums.length ;i ++){
if (!dq.isEmpty() && dq.peek() < i - k + 1) {
dq.poll();
}
//移除队列内比要插入的小的元素,保证最后一位为最大值
while (!dq.isEmpty() && nums[dq.peekLast()] <= nums[i]) {
dq.pollLast();
}
dq.offer(i);
if (i-k+1 >= 0){ //遍历到第3个开始存值
result[i-k+1] = nums[dq.peek()];
}
}
return result;
}
}
solution3 分块法
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums == null || nums.length == 0) {
return null;
}
int[] maxfromleft = new int[nums.length];
int[] maxfromright = new int[nums.length];
maxfromleft[0] = nums[0];
maxfromright[nums.length - 1] = nums[nums.length - 1];
//分块 整两个数组记录
for (int i = 1;i < nums.length;i++) {
//从左到右遍历 保证块内从左到右增大
if (i%k == 0) maxfromleft[i] = nums[i];
else maxfromleft[i] = Math.max(maxfromleft[i-1],nums[i]);
//从右到左遍历 保证块内从右到左递增
int j = nums.length - 1 - i;
if (j%k == 0) maxfromright[j] = nums[j];
else maxfromright[j] = Math.max(maxfromright[j+1],nums[j]);
}
int[] output = new int[nums.length - k + 1];
for (int i = 0;i < nums.length - k +1;i ++) {
output[i] = Math.max(maxfromleft[i+k-1],maxfromright[i]);
//取窗口涉及到的左块内最右的值,右块内最左的值进行比较
}
return output;
}
}
//用lamda
public static int[] slidingWindowMax(final int[] in, final int w) {
final int[] max_left = new int[in.length];
final int[] max_right = new int[in.length];
max_left[0] = in[0];
max_right[in.length - 1] = in[in.length - 1];
for (int i = 1; i < in.length; i++) {
max_left[i] = (i % w == 0) ? in[i] : Math.max(max_left[i - 1], in[i]);
final int j = in.length - i - 1;
max_right[j] = (j % w == 0) ? in[j] : Math.max(max_right[j + 1], in[j]);
}
final int[] sliding_max = new int[in.length - w + 1];
for (int i = 0, j = 0; i + w <= in.length; i++) {
sliding_max[j++] = Math.max(max_right[i], max_left[i + w - 1]);
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号