CF Educational Codeforces Round 180 (Rated for Div. 2)

地址：https://codeforces.com/contest/2112

A

直接在 \([1,100]\) 范围内枚举即可。

B

注意到如果把一段区间 \([l,r]\) 操作后，我们可以得到 \([\min\limits_{i=l}^{r} a_i,\max\limits_{i=l}^{r} a_i]\) 中的任意一个数。然后问题转化为求最小的 \(r-l-1\)，使得对于 \(l,r\) 存在一个 \(mid\)，满足 \([l,mid]\) 和 \([mid+1,r]\) 能够操作出来的数的区间相交（偏移量可以不超过 \(1\)），然后发现若数值区间相交则某区间的端点肯定被另一区间偏移不超过 \(1\) 后包含，所以可以留下一个数不操作，这样是等效的，然后对于每个数，去看它左右两边最早什么时候能够操作出包含（偏移 \(\leq 1\)）它的区间就行了。可以直接 \(O(n^2)\) 跑，能过，好像还可以二分，但没必要。

C

求满足条件的三元组 \((a_i,a_j,a_k)\)，其中 \(i<j<k\)。直接枚举 \(j,k\)，可以推不等式得出 \(i\) 的范围，然后发现 \(k\) 固定时，随着 \(j\) 递减，\(i\) 的最小值递增，所以直接双指针，是 \(O(n^2)\) 的。

D

容易发现，每条出边至少增加一条路径，所以 good pairs 数量至少为 \(n-1\)。构造 good pairs 数量为 \(n-1\) 的定向方案是容易的，如下图：

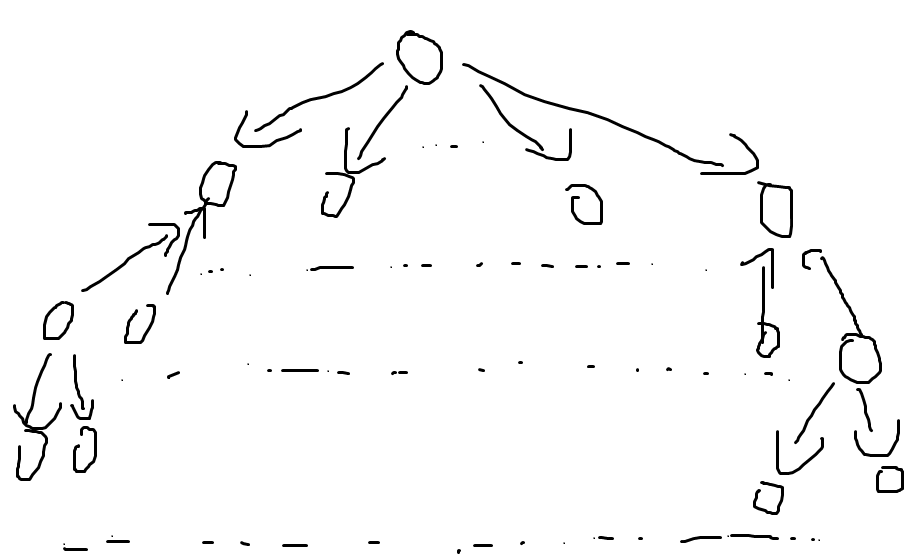
每种定向方案都可以从上述方案更改过来，所以我们考虑把树从 \(n-1\) 个点对调整为 \(n\) 个。

上述方案每条路径的长度都为 \(1\)，因此我们需要将一些路径的方案改为长度至少为 \(2\)。但是我们发现当路径长度大于 \(2\) 时，至少会增加 \(2\)，这样点对数量已经大于 \(n\)。因此，我们只能将路径长度修改为 \(2\)。但是同时我们只希望点对数量增加 \(1\)，所以我们只能修改一条路径。

假设我们修改之后得到了一条长度为 \(2\) 的路径 \(u \to r \to v\)。如果 存在另一条树边 \((r,t)\)，其中 \(t \neq u,t \neq v\)，如下图 (1)：

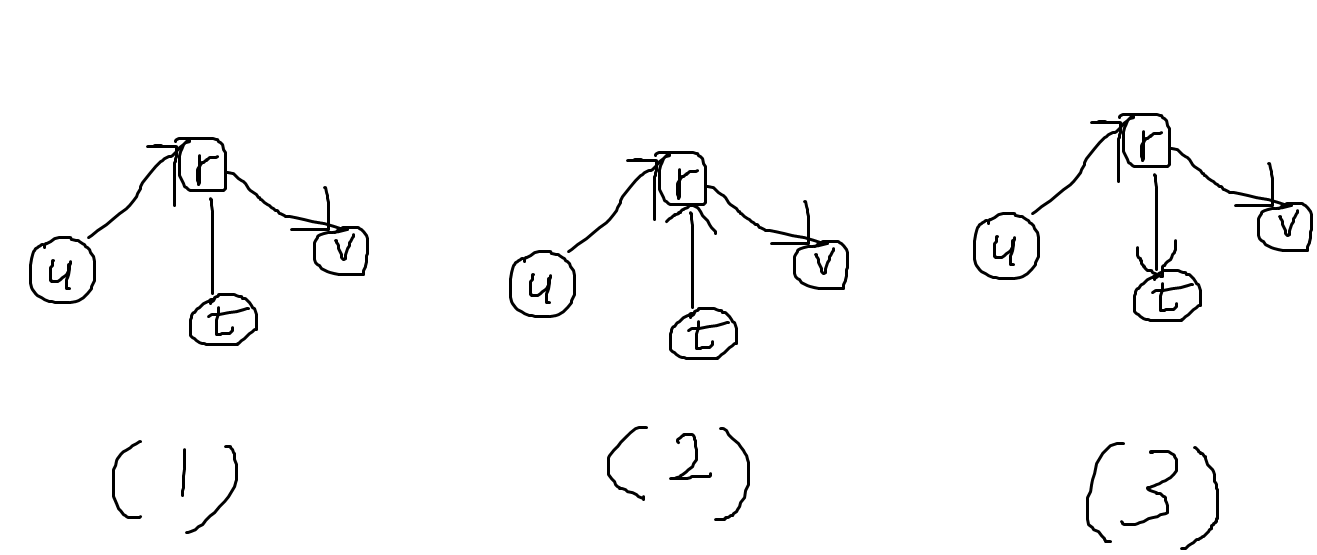
那么如果我们按照 (2) 中的方式定向，则又会多出一条 \(t \to r \to v\)；若按照 (3) 中方式定向，会多出 \(u \to r \to t\)。所以如果 \(\deg(r) > 2\)，那么点对增量也至少是 \(2\)。所以修改路径的中心 \(r\) 的 \(\deg\) 必须是 \(2\)。

所以我们得到了无解条件：树中不存在 \(\deg\) 为 \(2\) 的点。若树中存在一个 \(\deg\) 为 \(2\) 的点 \(r\)，那么方案是好构造的：

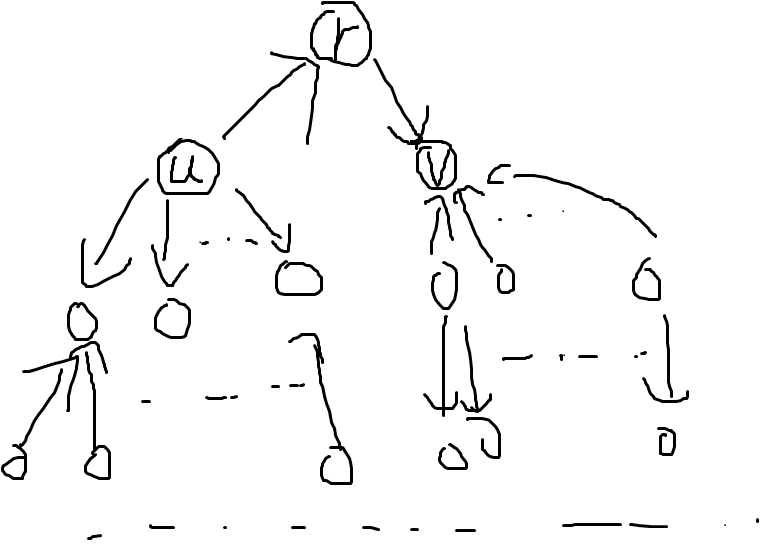
这样就做完了。

E

我们先考虑一个弱化问题：给定一棵树，计算有多少种 beautiful 的染色方案。

我们发现一个性质：若一个点是蓝色的，那么它的子树内的点都必须是蓝色的；若一个点是黄色的，那么它的子树内的点都必须是黄色的，原因如下：

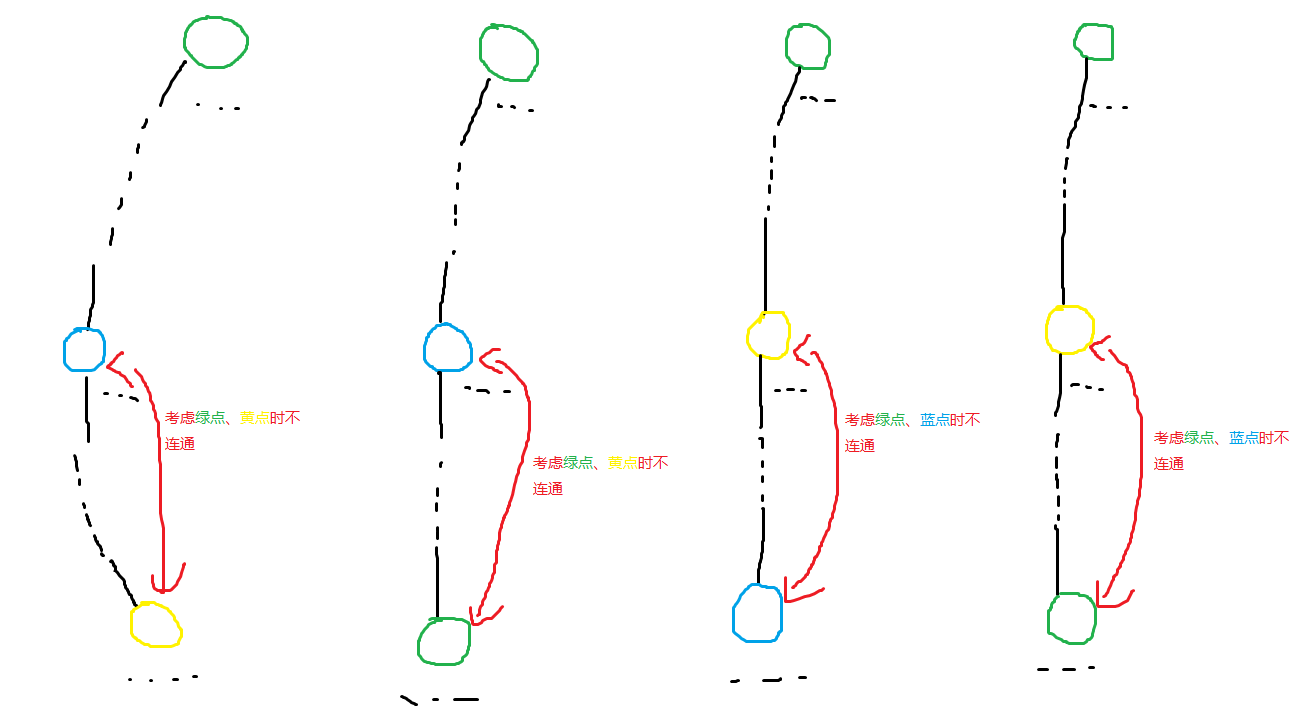
而若一个点是绿色的，那么由于绿色点可以和任何的点连通，所以它对它的子树没有约束。

因此我们可以设计动态规划求解。设 \(f_u\) 表示当 \(u\) 点为绿色时，其整颗子树染成 beautiful 方案的方案数。那么对于一个儿子 \(v\)，当它染绿色时，方案数为 \(f_v\)；当它为蓝色或黄色时，整棵子树就只有一种染色方案，所以 \(v\) 对 \(u\) 贡献为 \(f_v + 2\)，\(f_u = \prod\limits_{v \in son(u)} (f_v + 2)\)。

那么对于原问题，我们也可以使用动态规划求解。设 \(dp_i\) 表示当根为绿色，且树中 beautiful 的染色方案数恰为 \(i\) 的最小节点数。边界情况显然为 \(dp_1 = 1\)。对于 \(dp_i\)，我们枚举它的最后一棵子树的根节点为绿色时染色方案数加上 \(2\) 之后是 \(j\)，那么 \(f_i = \min (f_{\frac{i}{j}}+f_{j-2})\)。我们预处理每个数的因数，然后枚举时枚举因数即可，时间复杂度为 \(O(n \log n)\)。