多项式全家桶

前言

傻逼。

多项式求逆

对于 \(n-1\) 次多项式 \(A(x)\)，求 \(B(x) = \frac{1}{A(x)}\)。由于 \(B(x)\) 可能有无穷项，所以我们只取前 \(n\) 项，即：

\[B(x) A(x) \equiv 1 \pmod{x^n} \]

\(O(n^2)\) 暴力是容易的，我们考虑倍增求解。

首先判断边界，\(B(x)\) 的零次项 \(B_0 \equiv \frac{1}{A_0} \pmod{p}\)，所以若 \(A_0\) 无逆元则无解。

假设我们现在已知 \(B_m(x) A(x) \equiv 1 \pmod{x^m}\)，求 \(B_{2m}(x)\)。

由于 \(B_m(x)\) 和 \(B_{2m}(x)\) 的前 \(m\) 项是一样的，所以：

\[B_{2m}(x) - B_{m}(x) \equiv 0 \pmod{x^m} \]

两边同时平方可得：

\[\begin{aligned} (B_{2m}(x) - B_{m}(x))^2 \equiv 0 &\pmod{x^{2m}} \\ B_{2m}(x)^2 - 2 B_{2m}(x) B_{m}(x) + B_{m}(x)^2 \equiv 0 &\pmod{x^{2m}} \end{aligned} \]

由于：

\[B_{2m}(x) A(x) \equiv 1 \pmod{x^{2m}} \]

所以我们可以在同余式两边同乘 \(A(x)\) 得到：

\[\begin{aligned} A(x) B_{2m}(x)^2 - 2 A(x) B_{2m}(x) B_{m}(x) + A(x) B_{m}(x)^2 \equiv 0 &\pmod{x^{2m}} \\ B_{2m}(x) - 2 B_m(x) + A(x) B_{m}(x)^2 \equiv 0 &\pmod{x^{2m}} \\ B_{2m}(x) \equiv 2 B_m(x) - A(x) B_{m}(x)^2 &\pmod{x^{2m}} \end{aligned} \]

这样我们只需找到第一个 \(m\) 使得 \(m\) 是 \(2\) 的整次幂 \(k\) 且 \(m \geq n\)，时间复杂度是 \(\sum\limits_{i=0}^{k} k 2^k = O(n \log n)\)。注意，在每一层倍增时，\(A\) 只能取前 \(2m\) 项，因为只有前 \(2m\) 项有贡献，且若不取前 \(2m\) 项时间复杂度为 \(O(n \log^2 n)\)。

多项式除法（多项式取模）

给定 \(A(x),B(x)\)，最高次分别为 \(n,m\)，求多项式 \(Q(x)\) 和 \(R(x)\)，使得：

\[A(x) = B(x) Q(x) + R(x) \]

其中 \(R(x)\) 的最高次不超过 \(m-1\)，所以不足 \(m-1\) 次的可以补 \(0\)，不影响求解。

我们设 \(A'(x)\) 表示 \(A(x)\) 系数反转（reverse）之后的值，可以发现：

\[A'(x) = x^n A(\frac{1}{x}) \]

然后可以推式子：

\[\begin{aligned} A(x) &= B(x) Q(x) + R(x) \\ A(\frac{1}{x}) &= B(\frac{1}{x}) Q(\frac{1}{x}) + R(\frac{1}{x}) \\ x^n A(\frac{1}{x}) &= x^m B(\frac{1}{x}) \cdot x^{n-m} Q(\frac{1}{x}) + x^{n-m+1} \cdot x^{m-1} R(\frac{1}{x}) \\ A'(x) &= B'(x) Q'(x) + x^{n-m+1} R'(x) \\ A'(x) &\equiv B'(x) Q'(x) + x^{n-m+1} R'(x) \pmod{x^{n-m+1}} \\ A'(x) &\equiv B'(x) Q'(x) \pmod{x^{n-m+1}} \\ Q'(x) &\equiv \frac{A'(x)}{B'(x)} \pmod{x^{n-m+1}} \end{aligned} \]

我们发现这样我们算出来的 \(Q'(x)\) 的最高次为 \(x^{n-m}\)，而 \(Q(x)\) 的最高次也为 \(x^{n-m}\)，所以只需要把 \(Q'(x)\) 反过来就能得到 \(Q(x)\)，最后通过 \(R(x) = A(x) - B(x) Q(x)\) 得到 \(R(x)\)。时间复杂度 \(O(n \log n)\)。

多项式开根

给定 \(n-1\) 次多项式 \(A(x)\)，求 \(B(x)\) 满足：

\[B(x)^2 \equiv A(x) \pmod{x^n} \]

还是考虑倍增。

对于边界，\(B_0^2 \equiv A_0 \pmod{p}\)。

假设我们现在已知 \(B_m(x)^2 \equiv A(x) \pmod{x^m}\)，求 \(B_{2m}(x)\)。

由于 \(B_m(x)\) 和 \(B_{2m}(x)\) 的前 \(m\) 项是一样的，所以：

\[B_{2m}(x) - B_{m}(x) \equiv 0 \pmod{x^m} \]

两边同时平方可得：

\[\begin{aligned} (B_{2m}(x) - B_{m}(x))^2 \equiv 0 &\pmod{x^{2m}} \\ B_{2m}(x)^2 - 2 B_{2m}(x) B_{m}(x) + B_{m}(x)^2 \equiv 0 &\pmod{x^{2m}} \end{aligned} \]

由于：

\[B_{2m}(x)^2 \equiv A(x) \pmod{x^{2m}} \]

所以：

\[\begin{aligned} A(x) - 2 B_{2m}(x) B_{m}(x) + B_{m}(x)^2 \equiv 0 &\pmod{x^{2m}} \\ B_{2m}(x) \equiv \frac{A(x) + B_{m}(x)^2}{2 B_{m}(x)} &\pmod{x^{2m}} \\ B_{2m}(x) \equiv \frac{A(x)}{2 B_{m}(x)} + \frac{B_{m}(x)}{2} &\pmod{x^{2m}} \end{aligned} \]

时间复杂度为 \(O(n \log n)\)。

多项式多点求值

给定 \(n\) 次多项式 \(A(x)\) 和 \(m\) 个点 \(x_1,x_2,\cdots,x_m\)，求\(A(x_1),A(x_2),\cdots,A(x_m)\)。

暴力显然是 \(O(nm)\)的。我们考虑在 \(m\) 比较小的情况下怎么求解。

\(m\) 较小时，\(O(m^2)\) 是个可接受的时间复杂度，所以我们考虑降次，即求一个不超过 \(m\) 次的多项式 \(C(x)\) 满足 \(C(x_i) = A(x_i)\)。

我们构造一个 \(B(x) = \prod\limits_{i=1}^{m} (x - x_i)\)，易发现 \(B(x_i) = 0\)。

我们考虑应用多项式取模，直接让 \(C(x)\) 为 \(A(x)\) 模 \(B(x)\)，即：

\[A(x) = B(x) Q(x) + C(x) \]

由于对于所有给定点， \(B(x_i) = 0\)，所以此时 \(A(x_i) = C(x_i)\)。这样就完成了降次。可以发现 \(B(x)\) 可以用类似归并的分治求解，时间复杂度为 \(O(m \log^2 m)\)。

但是带值的部分时间复杂度还是 \(O(m^2)\)，还要继续优化。我们发现带值的部分也可以优化。

我们设 \(B_{l,r}(x) = \prod\limits_{i=l}^{r} (x - x_i)\)。我们考虑分治解决带值问题。具体的，对于区间 \([l,r]\)，我们先让当前的 \(A\) 去模 \(B_{l,r}\)，用得到的 \(C\) 可以算出 \(A(x_l),A(x_{l+1}),\cdots,A(x_r)\)，然后我们再把 \(C\) 传到左右两半区间 \([l,mid]\) 和 \([mid+1,r]\) 里，如下图：

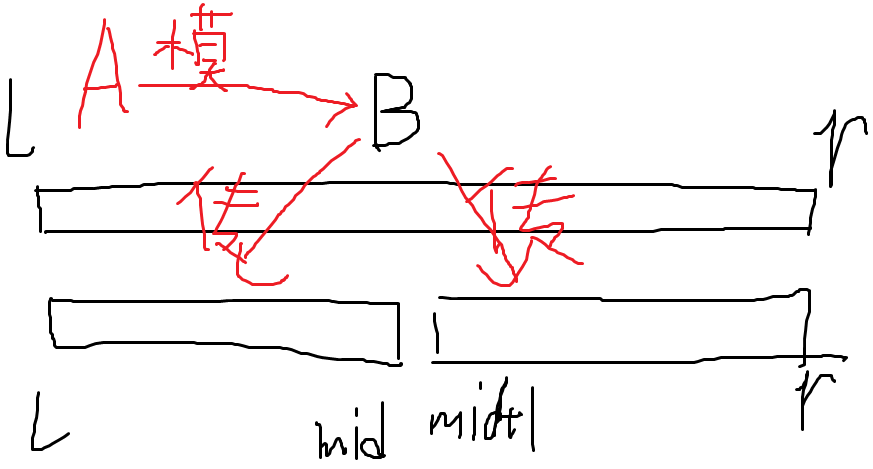
我们发现，当我们传到最底层的时候，由于区间长度只有 \(1\)，所以 \(B\) 的最高次也只有 \(1\)，所以 \(C\) 的次数为 \(0\)，只有常数项，直接就是我们要求的 \(A(x_i)\)。这样我们就在 \(O(n \log^2 n)\) 的时间复杂度内得到了答案。

线性递推

给定 \(a_1,a_2,\cdots,a_{m}\) 和 \(f_0,f_1,\cdots,f_{m-1}\)，对于 \(f_n (n \geq m)\)：

\[f_n = \sum\limits_{i=1}^{m} a_i f_{n-i} \]

再给定 \(n\)，求 \(f_{n}\)。

我们知道递推式的特征方程是：

\[x^m = \sum\limits_{i=1}^{m} a_i x^{m-i} \]

我们发现只用 \(f\) 的前 \(m\) 项就可以表示出所有 \(f_n\)，所以我们只需要求出 \(x_n\) 的特征方程就行了。还是考虑倍增求解。

假设我们已经求出 \(x^k\)，现在考虑求出 \(x^{2k}\)。

首先我们直接对 \(x^k\) 平方就可以得到 \(x^{2k}\)，但是这样表达式中最大次数就是 \(x^{m-1} \cdot x^{m-1} = x^{2m-2}\)，而我们想要的是 \(x^{m-1}\)。

我们发现：

\[x^m - \sum\limits_{i=1}^{m} a_i x^{m-i} = 0 \]

所以我们可以采用多点求值时所用的“模 \(0\)”的方法，即给 \((x^k)^2\) 模上 \(x^m - \sum\limits_{i=1}^{m} a_i x^{m-i}\)，这样，由于 \(x^m - \sum\limits_{i=1}^{m} a_i x^{m-i} = 0\)，所以余式的结果与原式相等。然后可以采用类似快速幂的方式去实现即可。时间复杂度 \(O(m \log m \log n)\)。

多项式导数 / 积分

对于多项式：

\[f(x) = \sum\limits_{i=0}^{n} a_i x^i \]

其导数：

\[f'(x) = \sum\limits_{i=0}^{n-1} (i+1) a_{i+1} x^i \]

其积分：

\[\int f(x) d x = \sum\limits_{i=1}^{n+1} \frac{a_{i-1}}{i} x^i \]

多项式 \(\ln\) / \(\exp\)

多项式 \(\ln\)

首先，若 \(\ln f(x)\) 存在，则

\[[x^0] f(x) = 1 \]

否则当 \(a_0 \neq 1\) 时，在模 \(p\) 意义下，找不到 \(e^k (k \in Z)\) 使得 \(e^k \equiv a_0 \pmod{p}\)。

求解 \(\ln f(x)\) 时，我们考虑先求导再积分。

\[\ln f(x) = \int \frac{d \ln f(x)}{d x} dx \]

其中 \(\frac{d \ln f(x)}{d x}\) 是 \(\ln f(x)\) 这一复合函数的导数，所以

\[\frac{d \ln f(x)}{d x} = \ln' f(x) \cdot f'(x) = \frac{1}{f(x)} \cdot f'(x) = \frac{f'(x)}{f(x)} \]

\[\ln f(x) = \int \frac{f'(x)}{f(x)} dx \]

我们在模 \(x^n\) 意义下求出 \(f'(x),\frac{1}{f(x)}\)，相乘后再求积分即可。时间复杂度 \(O(n \log n)\)。

多项式 \(\exp\)

首先，若 \(\exp f(x)\) 存在，则

\[[x^0]f(x) = 0 \]

否则当 \(a_0 \neq 0\) 时，在模 \(p\) 意义下，找不到 \(c\)，使得 \(e^{a_0} \equiv c \pmod{p}\)。

为了更快的求解，我们使用牛顿迭代法。

我们设 \(g(x) = \exp f(x)\)，则

\[f(x) = \ln g(x) \]

\[\ln g(x) - f(x) = 0 \]

我们设

\[F(g(x)) = \ln g(x) - f(x) \]

\[g_n(x) \equiv \exp f(x) \pmod{x^n} \]

那么

\[\begin{aligned} g_{2n}(x) &\equiv g_n(x) - \frac{F(g_n(x))}{F'(g_n(x))} \pmod{x^{2n}} \\ &\equiv g_n(x) - \frac{\ln g_n(x) - f(x)}{\frac{1}{g_n(x)}} \pmod{x^{2n}} \\ &\equiv g_n(x) - g_n(x)(\ln g_n(x) - f(x)) \pmod{x^{2n}} \end{aligned} \]

这样时间复杂度为 \(O(n \log n)\)。

多项式快速幂

给定 \(n-1\) 次多项式 \(A(x)\) 和常数 \(k\)，求：

\[B(x) \equiv A(x)^k \pmod{x^n} \]

直接跑快速幂是 \(O(n \log n \log k)\) 的。在 \(k \leq 10^{10^5}\) 时显然无法通过。我们考虑对同余式左右两边先取对数，再取指数，同余式仍然成立。

\[\begin{aligned} \ln B(x) \equiv \ln A(x)^k &\pmod{x^n} \\ \ln B(x) \equiv k \ln A(x) &\pmod{x^n} \\ B(x) \equiv \exp (k \ln A(x)) &\pmod{x^n} \end{aligned} \]

这样就可以先求 \(\ln A(x)\)，乘上 \(k\) 后再 \(\exp\) 回去即可，时间复杂度 \(O(n \log n)\)。

但是当 \(a_0 \neq 1\) 时，根据定义，我们无法求出 \(\ln A(x)\)。此时我们找到最小的 \(\Delta\) 满足 \(a_{\Delta} \neq 0\)，然后我们可以令 \(A(x) = a_{\Delta} x^{\Delta} A^{\ast}(x)\)，相当于把 \(A(x)\) 右移 \(\Delta\) 位，然后把最低位变为 \(1\)。这样我们得到

\[B(x) \equiv a_{\Delta}^{k} x^{k \Delta} A^{\ast}(x)^k \pmod{x^n} \]

对于 \(A^{\ast}(x)^k\)，我们再使用上述方法求解即可。时间复杂度仍为 \(O(n \log n)\)。注意，在 \(\exp (k \ln A^{\ast}(x))\) 中，\(k\) 要对 \(p\) 取模；在 \(a_{\Delta}^{k}\) 中，\(k\) 要对 \(p-1\) 取模；在 \(x^{k \Delta}\) 中，由于 \(k \Delta\) 是位移量，所以不能取模。