二叉树

226. 翻转二叉树

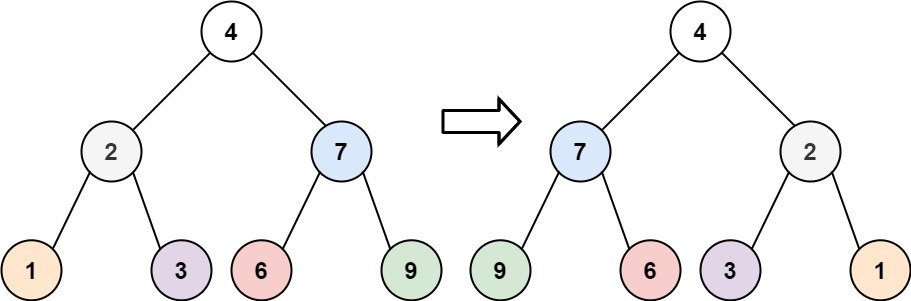
给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

解题思路：

对于每一个节点来说，先将其左右子节点交换，然后分别递归处理左右节点

func invertTree(root *TreeNode) *TreeNode {
    if root == nil {
        return nil
    }
    root.Left, root.Right = root.Right, root.Left // 交换左右节点
    invertTree(root.Left)
    invertTree(root.Right)
    return root
}

101. 对称二叉树

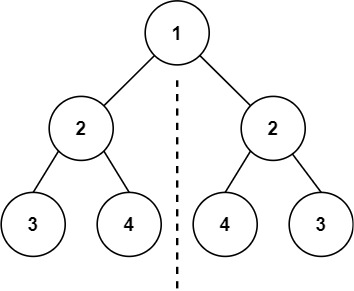
给你一个二叉树的根节点 root ，检查它是否轴对称。

解题思路：

使用一个另外的递归函数，传递的参数是两个节点，这样可以用来比较，返回值是 bool 类型，表示这两个节点对应的子树是否满足对称要求。

func isSymmetric(root *TreeNode) bool {
    if root == nil {
        return true
    }
    equal := isSymmetric_check(root.Left, root.Right)
    return equal
}

func isSymmetric_check(node1, node2 *TreeNode) bool {
    if node1 == nil && node2 == nil { // 都是 nil
        return true
    }
    if node1 == nil || node2 == nil { // 只有一个为 nil
        return false
    }
    if node1.Val != node2.Val {
        return false
    }
    var equal bool
    if equal = isSymmetric_check(node1.Left, node2.Right); !equal {
        return false
    }
    if equal = isSymmetric_check(node1.Right, node2.Left); !equal {
        return false
    }
    return true
}

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

解题思路

使用层序遍历的方式，depth 开始为0，每遍历一层 depth + 1，直到队列中没有元素了，那就说明层序遍历结束。

func maxDepth(root *TreeNode) int {
    queue := list.New()
    if root == nil {
        return 0
    }
    queue.PushBack(root)
    depth := 0

    for queue.Len() != 0 {
        size := queue.Len()
        for i := 0; i < size; i++ {
            node := queue.Remove(queue.Front()).(*TreeNode)
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        depth++
    }

    return depth
}

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明： 叶子节点是指没有子节点的节点。

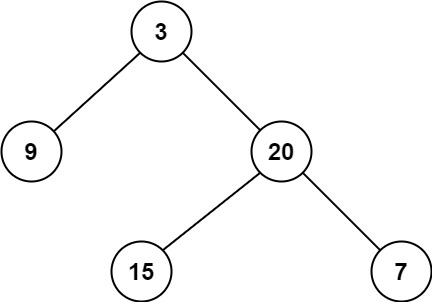
输入： root = [3,9,20,null,null,15,7]
输出： 2

解题思路

首先使用层序遍历，如果遍历的过程中发现一个节点的左右子节点都是 nil，说明这个节点就是最浅的节点了（最浅的节点在同一层可能有多个）

遍历到最浅的节点直接返回就可以了。

如果在最后返回，那么说明这棵树所有的叶子节点深度都一样，都在同一层。

func minDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }

    queue := list.New()
    queue.PushBack(root)
    depth := 0
    for queue.Len() != 0 {
        size := queue.Len()
        for i := 0; i < size; i++ {
            node := queue.Remove(queue.Front()).(*TreeNode)
            if node.Left == nil && node.Right == nil {
                depth++      // 找到最浅的叶子节点了，depth++
                return depth // 返回
            }
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
        depth++ // 遍历了一层，需要增加深度
    }
    return depth // 如果在这里返回，那么说明所有的叶子节点深度都一样
}

222. 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

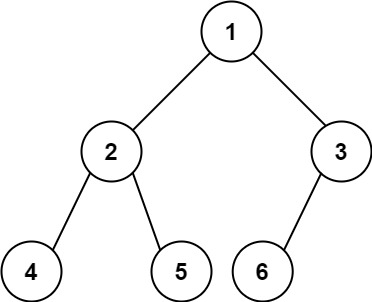
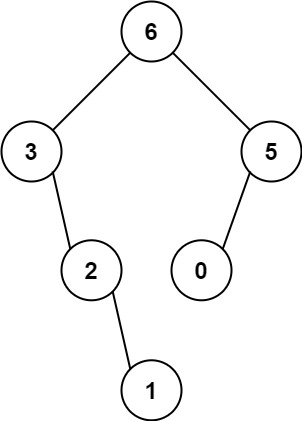
输入： root = [1,2,3,4,5,6]
输出： 6

解题思路：

这道题使用前序遍历即可解决

func countNodes(root *TreeNode) int {
    if root == nil {
        return 0
    }

    leftCount, rightCount := 0, 0
    if root.Left != nil {
        leftCount = countNodes(root.Left)
    }
    if root.Right != nil {
        rightCount = countNodes(root.Right)
    }

    return leftCount + rightCount + 1
}

110. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

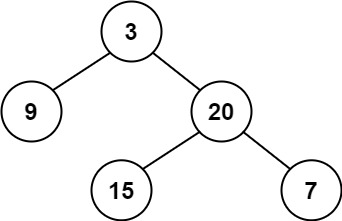
输入： root = [3,9,20,null,null,15,7]
输出： true

解题思路：

首先考虑如何建立递归函数，因为递归函数需要传递两个关键的信息，一个是子树的高度，一个是这个子树是否是平衡二叉树，所以我们就建立一个有两个返回值的递归函数。

当子树不是平衡二叉树的时候，子树的树高就已经不重要了，所以我们这时候可以直接忽略掉树高，使用-1来代替。

当子树是平衡二叉树的时候，子树的树高还有作用，这时候我们才需要使用返回子树的树高。

func isBalanced(root *TreeNode) bool {
    if root == nil {
        return true
    }

    _, ok := isBalanced_height(root)
    return ok
}

func isBalanced_height(node *TreeNode) (int, bool) {
    if node == nil {
        return 0, true
    }

    leftHeight, rightHeight := 0, 0
    var ok bool
    if node.Left != nil {
        if leftHeight, ok = isBalanced_height(node.Left); !ok {
            return -1, false // 这时候树的高度已经不重要了，直接返回否即可
        }
    }
    if node.Right != nil {
        if rightHeight, ok = isBalanced_height(node.Right); !ok {
            return -1, ok // 返回否
        }
    }

    if leftHeight - rightHeight > 1 || rightHeight - leftHeight > 1 {
        return -1, false // 返回否
    }

    if leftHeight > rightHeight {
        return leftHeight + 1, true
    } else {
        return rightHeight + 1, true
    }
}

257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

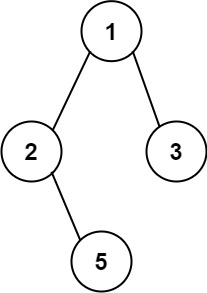
输入： root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

解题思路：

使用递归 + 回溯算法来进行处理，递归函数传递的参数：当前节点的指针，结果集，当前路径

总体结构与递归 + 回溯模板相同

func binaryTreePaths(root *TreeNode) []string {
    if root == nil {
        return nil
    }

    res := make([]string, 0)
    subRes := make([]int, 0)

    treepaths_backTracking(root, &res, &subRes)
    return res
}

func treepaths_backTracking(node *TreeNode, res *[]string, subRes *[]int) {
    if node == nil {
        return // 不应该被执行到这里
    }
    if node.Left == nil && node.Right == nil { // 到了叶子节点
        *subRes = append(*subRes, node.Val)  // 加入当前节点
        tmp := treepaths_encode(*subRes)     // 编码
        *res = append(*res, tmp)             // 加入到结果集
        *subRes = (*subRes)[:len(*subRes)-1] // 回溯
        return
    }

    /** ---------------- bug 记录 ------------------
    这里将 node.Val 加入了两遍！
    if node.Left != nil {
        subRes = append(subRes, node.Val)
        treepaths_backTracking(node.Left, res, subRes)
    }
    if node.Right != nil {
        subRes = append(subRes, node.Val)
        treepaths_backTracking(node.Right, res, subRes)
    }
    */
    *subRes = append(*subRes, node.Val) // 递归前
    if node.Left != nil {
        treepaths_backTracking(node.Left, res, subRes) // 递归
    }
    if node.Right != nil {
        treepaths_backTracking(node.Right, res, subRes) // 递归
    }
    *subRes = (*subRes)[:len(*subRes)-1] // 回溯
}

func treepaths_encode(subRes []int) string {
    res := ""
    for idx, val := range subRes {
        if idx == len(subRes)-1 {
            res += strconv.Itoa(val)
            break
        }
        res += strconv.Itoa(val) + "->"
    }
    return res
}

404. 左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

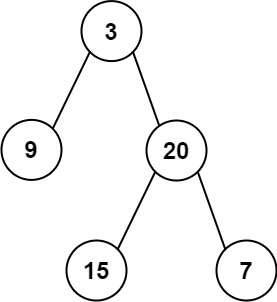
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

解题思路：

这道题是递归算法的使用，确定递归函数传递的参数：当前节点指针，左叶子之和的指针（只有传递指针更改和的时候才有用）。

然后就使用递归模板就可以了，注意判断左叶子，然后判断左子树，右子树不用判断。

func sumOfLeftLeaves(root *TreeNode) int {
    sum := 0
    sum_backTracking(root, &sum)
    return sum
}

func sum_backTracking(node *TreeNode, sum *int) {
    if node == nil { // 空节点
        return
    }

    if node.Left == nil && node.Right == nil { // 叶子节点
        return
    }

    if node.Left != nil && node.Left.Left == nil && node.Left.Right == nil { // 左叶子
        *sum += node.Left.Val
    }

    if node.Left != nil && !(node.Left.Left == nil && node.Left.Right == nil) { // 左子树，不是左叶子
        sum_backTracking(node.Left, sum)
    }
    if node.Right != nil { // 右子树
        sum_backTracking(node.Right, sum)
    }
}

513. 找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

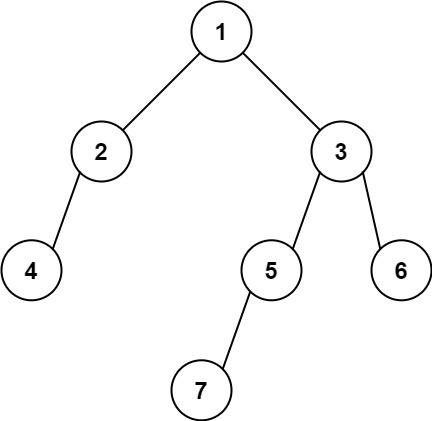
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

解题思路：

采用层序遍历的方法，每一层都找到最左面的，然后最后一层就是最后更新的，直接返回即可。

func findBottomLeftValue(root *TreeNode) int {
    if root == nil {
        return 0
    }

    queue := list.New()
    queue.PushBack(root)
    res := 0
    for queue.Len() != 0 {
        size := queue.Len()
        for i := 0; i < size; i++ {
            node := queue.Remove(queue.Front()).(*TreeNode)
            if i == 0 { // 最左面的节点
                res = node.Val
            }
            if node.Left != nil {
                queue.PushBack(node.Left)
            }
            if node.Right != nil {
                queue.PushBack(node.Right)
            }
        }
    }
    return res
}

437. 路径总和 III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

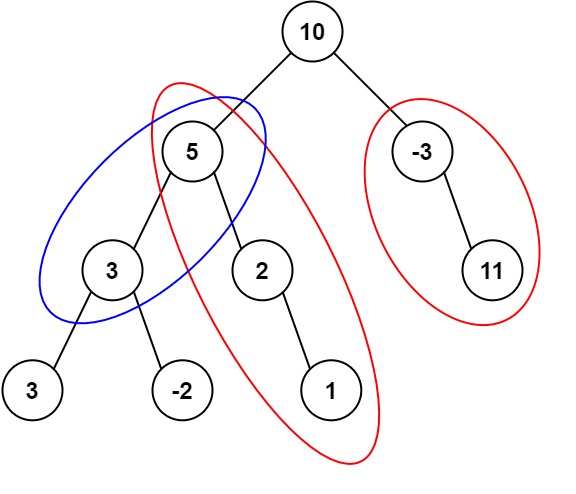
输入： root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出： 3
解释： 和等于 8 的路径有 3 条，如图所示。

解题思路：

这道题乍一看好像每两个节点直接的距离都需要进行计算才能得出结论，但是仔细一瞅：如果从上往下看，每个节点往下的满足条件的路径有很多种，没办法统计。但是要是从下往上看，每个节点满足条件的路径就是：从当前节点为开始节点，以到根节点路径上的节点为终点。

所以我们就需要记录从根节点到当前节点的路径上的节点值，然后通过计算这些节点值的和，就可以知道以当前节点为终点有没有满足条件的路径

递归函数传递的值就是我们上述用到的。

func pathSum(root *TreeNode, targetSum int) int {
    paths := make([]int, 0)
    sum := 0
    pathSum_backTracking(root, &paths, targetSum, &sum)
    return sum
}

// 递归函数，paths 代表当前节点到根节点路径上的节点值（未把当前节点加入）
func pathSum_backTracking(node *TreeNode, paths *[]int, target int, sum *int) {
    if node == nil {
        return
    }

    *paths = append(*paths, node.Val) // 将当前节点的值加入到路径中
    pathSum_judge(paths, target, sum) // 判断从当前节点出发，到根节点或者中间节点这么一段路径中，有几段满足要求
    if node.Left != nil {
        pathSum_backTracking(node.Left, paths, target, sum) // 递归
    }
    if node.Right != nil {
        pathSum_backTracking(node.Right, paths, target, sum) // 递归
    }
    *paths = (*paths)[:len(*paths)-1] // 回溯
}

// 判断从当前节点出发，到根节点或者中间节点这么一段路径中，有几段满足要求
func pathSum_judge(paths *[]int, target int, sum *int) {
    count := 0
    for i := len(*paths) - 1; i >= 0; i-- { // 这条路径应该从最靠近当前节点的地方开始，向根节点的方向去找
        count += (*paths)[i] // 更新和
        if count == target {
            *sum += 1
        }
    }
}

654. 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

解题思路：

首先这道题一看就是需要使用递归函数来递归求解的，先设计递归函数：传入值为数组，左界限和右界限；然后

func constructMaximumBinaryTree(nums []int) *TreeNode {
    root := Maxi_build(nums, 0, len(nums)-1)
    return root
}

// 找到数组左右下标 [left,right] (左闭右闭) 的最大值
func Maxi_find(nums []int, left, right int) int {
    if left > right {
        return 0
    }

    max := nums[left]
    maxIndex := left
    for left <= right {
        if nums[left] > max {
            max = nums[left]
            maxIndex = left
        }
        left++
    }

    return maxIndex
}

// 递归函数，递归建立二叉树
func Maxi_build(nums []int, left, right int) *TreeNode {
    if left > right {
        return nil
    }
    maxIdx := Maxi_find(nums, left, right)
    root := TreeNode{
        Val:   nums[maxIdx],
        Left:  Maxi_build(nums, left, maxIdx-1),  // 左子树
        Right: Maxi_build(nums, maxIdx+1, right), // 右子树
    }
    return &root
}

617. 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

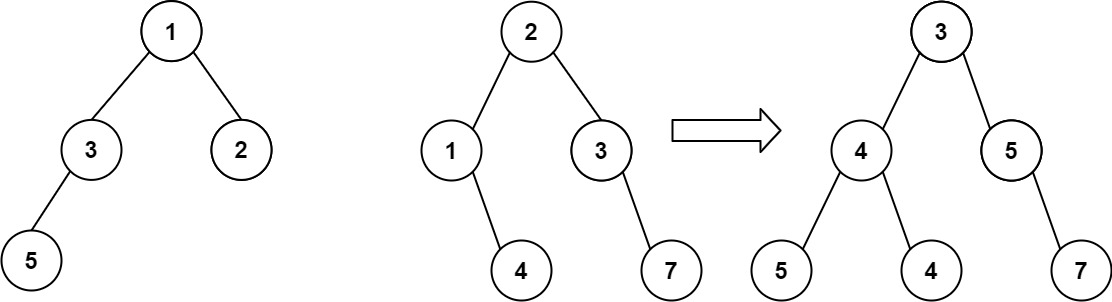
输入： root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

解题思路：

直接递归就可以，注意不同条件的处理方式不同。

func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
    if root1 == nil && root2 == nil {
        return nil
    }
    if root1 == nil { // root1 == nil && root2 != nil
        return root2
    }
    if root2 == nil { // root2 == nil && root1 != nil
        return root1
    }
    res := &TreeNode{
        Val: root1.Val + root2.Val,
        Left: mergeTrees(root1.Left, root2.Left),
        Right: mergeTrees(root1.Right, root2.Right),
    }
    return res
}

posted @ 2022-12-23 22:05 kohn 阅读(19) 评论(0) 收藏举报

刷新页面返回顶部