python: Algorithm II
# encoding: utf-8
# 版权所有 2023 ©涂聚文有限公司
# 许可信息查看:
# 描述: Dijkstras Algorithm in Python 迪杰斯特拉算法 最短路径算法
# Author : geovindu,Geovin Du 涂聚文.
# IDE : PyCharm 2023.1 python 311
# Datetime : 2023/9/26 16:38
# User : geovindu
# Product : PyCharm
# Project : EssentialAlgorithms
# File : DijkstrasAlgorithm.py
# explain : 学习
import sys
class DijkstrasAlgorithm(object):
"""
Dijkstra's Algorithm
"""
# Find which vertex is to be visited next
def to_be_visited(vertices:list,edges:list):
"""
:param vertices
:param edges:
:return:
"""
global visited_and_distance
global num_of_vertices
v = -10
for index in range(num_of_vertices):
if visited_and_distance[index][0] == 0 \
and (v < 0 or visited_and_distance[index][1] <=
visited_and_distance[v][1]):
v = index
return v
def Dijkstras(vertices:list,edges:list):
"""
Dijkstra's Algorithm
:param vertices
:param edges:
:return:
"""
global visited_and_distance
global num_of_vertices
num_of_vertices = len(vertices[0])
visited_and_distance = [[0, 0]]
for i in range(num_of_vertices - 1):
visited_and_distance.append([0, sys.maxsize])
for vertex in range(num_of_vertices):
# Find next vertex to be visited
to_visit = DijkstrasAlgorithm.to_be_visited(vertices,edges)
for neighbor_index in range(num_of_vertices):
# Updating new distances
if vertices[to_visit][neighbor_index] == 1 and \
visited_and_distance[neighbor_index][0] == 0:
new_distance = visited_and_distance[to_visit][1] \
+ edges[to_visit][neighbor_index]
if visited_and_distance[neighbor_index][1] > new_distance:
visited_and_distance[neighbor_index][1] = new_distance
visited_and_distance[to_visit][0] = 1
i = 0
# Printing the distance
for distance in visited_and_distance:
print("Dijkstra's Algorithm Distance of ", chr(ord('a') + i),
" from source vertex: ", distance[1])
i = i + 1
# encoding: utf-8
# 版权所有 2023 ©涂聚文有限公司
# 许可信息查看: Ford-Fulkerson Algorithm
# 描述:Ford-Fulkerson算法(FFA)是一种 贪婪算法 ,用于计算流网络中的最大流量
# Author : geovindu,Geovin Du 涂聚文.
# IDE : PyCharm 2023.1 python 311
# Datetime : 2023/9/26 15:27
# User : geovindu
# Product : PyCharm
# Project : EssentialAlgorithms
# File : FordFulkersonAlgorithm.py
# explain : 学习
from collections import defaultdict
# Ford-Fulkerson algorith in Python
from collections import defaultdict
class Graph:
"""
Ford-Fulkerson Algorithm
"""
def __init__(self, graph):
"""
:param graph:
"""
self.graph = graph
self. ROW = len(graph)
# Using BFS as a searching algorithm
def searching_algo_BFS(self, s, t, parent):
"""
:param s:
:param t:
:param parent:
:return:
"""
visited = [False] * (self.ROW)
queue = []
queue.append(s)
visited[s] = True
while queue:
u = queue.pop(0)
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
queue.append(ind)
visited[ind] = True
parent[ind] = u
return True if visited[t] else False
# Applying fordfulkerson algorithm
def ford_fulkerson(self, source, sink):
"""
:param source:
:param sink:
:return:
"""
parent = [-1] * (self.ROW)
max_flow = 0
while self.searching_algo_BFS(source, sink, parent):
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min(path_flow, self.graph[parent[s]][s])
s = parent[s]
# Adding the path flows
max_flow += path_flow
# Updating the residual values of edges
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
# encoding: utf-8
# 版权所有 2023 ©涂聚文有限公司
# 许可信息查看:Kruskal’s Minimum Spanning Tree (MST) Algorithm Kruskal Algorithm kruskal算法(克鲁斯卡尔算法)
# 描述: https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/
# https://www.programiz.com/dsa/kruskal-algorithm
# Author : geovindu,Geovin Du 涂聚文.
# IDE : PyCharm 2023.1 python 311
# Datetime : 2023/9/26 14:13
# User : geovindu
# Product : PyCharm
# Project : EssentialAlgorithms
# File : KruskalAlgorithm.py
# explain : 学习
import sys
import os
class Graph(object):
"""
Kruskal Algorithm kruskal算法(克鲁斯卡尔算法)
"""
def __init__(self, vertices):
"""
:param vertices:
"""
self.V = vertices
self.graph = []
def addEdge(self, u, v, w):
"""
:param u:
:param v:
:param w:
:return:
"""
self.graph.append([u, v, w])
# Search function
def find(self, parent, i):
"""
:param parent:
:param i:
:return:
"""
if parent[i] == i:
return i
return self.find(parent, parent[i])
def applyUnion(self, parent, rank, x, y):
"""
:param parent:
:param rank:
:param x:
:param y:
:return:
"""
xroot = self.find(parent, x)
yroot = self.find(parent, y)
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
else:
parent[yroot] = xroot
rank[xroot] += 1
# Applying Kruskal algorithm
def kruskalAlgo(self):
"""
:return:
"""
result = []
i, e = 0, 0
self.graph = sorted(self.graph, key=lambda item: item[2])
parent = []
rank = []
for node in range(self.V):
parent.append(node)
rank.append(0)
while e < self.V - 1:
u, v, w = self.graph[i]
i = i + 1
x = self.find(parent, u)
y = self.find(parent, v)
if x != y:
e = e + 1
result.append([u, v, w])
self.applyUnion(parent, rank, x, y)
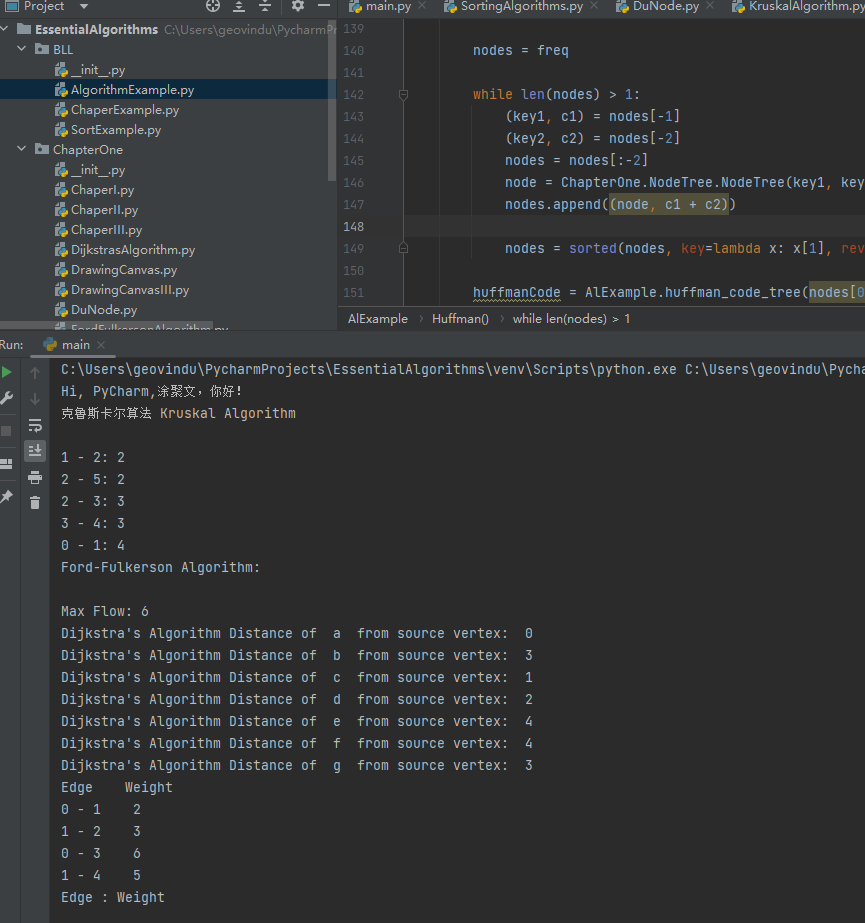
print("克鲁斯卡尔算法 Kruskal Algorithm\n")
for u, v, weight in result:
print("%d - %d: %d" % (u, v, weight))
# encoding: utf-8
# 版权所有 2023 ©涂聚文有限公司
# 许可信息查看:
# 描述:
# Author : geovindu,Geovin Du 涂聚文.
# IDE : PyCharm 2023.1 python 311
# Datetime : 2023/9/28 8:32
# User : geovindu
# Product : PyCharm
# Project : EssentialAlgorithms
# File : HuffmanAlgorithm.py
# explain : 学习
import ChapterOne.NodeTree
class HuffmanAlgorithm(object):
"""
Huffman code 霍夫曼编码
"""
@staticmethod
def HuffmanCodeTree(node:ChapterOne.NodeTree.NodeTree, left=True, binString=''):
"""
:param left:
:param binString:
:return:
"""
if type(node) is str:
return {node: binString}
(l, r) = node.children()
d = dict()
d.update(HuffmanAlgorithm.HuffmanCodeTree(l, True, binString + '0'))
d.update(HuffmanAlgorithm.HuffmanCodeTree(r, False, binString + '1'))
return d
# encoding: utf-8
# 版权所有 2023 ©涂聚文有限公司
# 许可信息查看:Prim's Algorithm
# 描述:
# Author : geovindu,Geovin Du 涂聚文.
# IDE : PyCharm 2023.1 python 311
# Datetime : 2023/9/26 17:18
# User : geovindu
# Product : PyCharm
# Project : EssentialAlgorithms
# File : PrimsAlgorithm.py
# explain : 学习
import sys
class Graph(object):
"""
Prim's Algorithm
"""
def __init__(self, vertices):
"""
:param vertices:
"""
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
# A utility function to print
# the constructed MST stored in parent[]
def printMST(self, parent):
"""
:param parent:
:return:
"""
print("Edge \tWeight")
for i in range(1, self.V):
print(parent[i], "-", i, "\t", self.graph[i][parent[i]])
# A utility function to find the vertex with
# minimum distance value, from the set of vertices
# not yet included in shortest path tree
def minKey(self, key, mstSet):
"""
:param key:
:param mstSet:
:return:
"""
# Initialize min value
min = sys.maxsize
for v in range(self.V):
if key[v] < min and mstSet[v] == False:
min = key[v]
min_index = v
return min_index
# Function to construct and print MST for a graph
# represented using adjacency matrix representation
def primMST(self):
"""
:return:
"""
# Key values used to pick minimum weight edge in cut
key = [sys.maxsize] * self.V
parent = [None] * self.V # Array to store constructed MST
# Make key 0 so that this vertex is picked as first vertex
key[0] = 0
mstSet = [False] * self.V
parent[0] = -1 # First node is always the root of
for cout in range(self.V):
# Pick the minimum distance vertex from
# the set of vertices not yet processed.
# u is always equal to src in first iteration
u = self.minKey(key, mstSet)
# Put the minimum distance vertex in
# the shortest path tree
mstSet[u] = True
# Update dist value of the adjacent vertices
# of the picked vertex only if the current
# distance is greater than new distance and
# the vertex in not in the shortest path tree
for v in range(self.V):
# graph[u][v] is non zero only for adjacent vertices of m
# mstSet[v] is false for vertices not yet included in MST
# Update the key only if graph[u][v] is smaller than key[v]
if self.graph[u][v] > 0 and mstSet[v] == False \
and key[v] > self.graph[u][v]:
key[v] = self.graph[u][v]
parent[v] = u
self.printMST(parent)
@staticmethod
def PrimsTwo():
"""
:return:
"""
INF = 9999999
# number of vertices in graph
V = 5
# create a 2d array of size 5x5
# for adjacency matrix to represent graph
G = [[0, 9, 75, 0, 0],
[9, 0, 95, 19, 42],
[75, 95, 0, 51, 66],
[0, 19, 51, 0, 31],
[0, 42, 66, 31, 0]]
# create a array to track selected vertex
# selected will become true otherwise false
selected = [0, 0, 0, 0, 0]
# set number of edge to 0
no_edge = 0
# the number of egde in minimum spanning tree will be
# always less than(V - 1), where V is number of vertices in
# graph
# choose 0th vertex and make it true
selected[0] = True
# print for edge and weight
print("Edge : Weight\n")
while (no_edge < V - 1):
# For every vertex in the set S, find the all adjacent vertices
# , calculate the distance from the vertex selected at step 1.
# if the vertex is already in the set S, discard it otherwise
# choose another vertex nearest to selected vertex at step 1.
minimum = INF
x = 0
y = 0
for i in range(V):
if selected[i]:
for j in range(V):
if ((not selected[j]) and G[i][j]):
# not in selected and there is an edge
if minimum > G[i][j]:
minimum = G[i][j]
x = i
y = j
print(str(x) + "-" + str(y) + ":" + str(G[x][y]))
selected[y] = True
no_edge += 1
# encoding: utf-8
# 版权所有 2023 ©涂聚文有限公司
# 许可信息查看:
# 描述: Kruskal Algorithm kruskal算法(克鲁斯卡尔算法)
# Author : geovindu,Geovin Du 涂聚文.
# IDE : PyCharm 2023.1 python 311
# Datetime : 2023/9/26 14:16
# User : geovindu
# Product : PyCharm
# Project : EssentialAlgorithms
# File : AlgorithmExample.py
# explain : 学习
import ChapterOne.KruskalAlgorithm
import ChapterOne.FordFulkersonAlgorithm
import ChapterOne.DijkstrasAlgorithm
import ChapterOne.PrimsAlgorithm
import ChapterOne.HuffmanAlgorithm
import ChapterOne.NodeTree
class AlExample(object):
"""
"""
def Krusal(self):
"""
Kruskal Algorithm kruskal算法(克鲁斯卡尔算法)
:return:
"""
g = ChapterOne.KruskalAlgorithm.Graph(6)
g.addEdge(0, 1, 4)
g.addEdge(0, 2, 4)
g.addEdge(1, 2, 2)
g.addEdge(1, 0, 4)
g.addEdge(2, 0, 4)
g.addEdge(2, 1, 2)
g.addEdge(2, 3, 3)
g.addEdge(2, 5, 2)
g.addEdge(2, 4, 4)
g.addEdge(3, 2, 3)
g.addEdge(3, 4, 3)
g.addEdge(4, 2, 4)
g.addEdge(4, 3, 3)
g.addEdge(5, 2, 2)
g.addEdge(5, 4, 3)
g.kruskalAlgo()
def FoordFulkerson(self):
"""
Ford-Fulkerson Algorithm
:return:
"""
graph = [[0, 8, 0, 0, 3, 0],
[0, 0, 9, 0, 0, 0],
[0, 0, 0, 0, 7, 2],
[0, 0, 0, 0, 0, 5],
[0, 0, 7, 4, 0, 0],
[0, 0, 0, 0, 0, 0]]
g = ChapterOne.FordFulkersonAlgorithm.Graph(graph)
source = 0
sink = 5
print("Ford-Fulkerson Algorithm:\n")
print("Max Flow: %d " % g.ford_fulkerson(source, sink))
def Dijkstras(self):
"""
Dijkstra's Algorithm 迪杰斯特拉算法 最短路径算法
:return:
"""
vertices = [[0, 0, 1, 1, 0, 0, 0],
[0, 0, 1, 0, 0, 1, 0],
[1, 1, 0, 1, 1, 0, 0],
[1, 0, 1, 0, 0, 0, 1],
[0, 0, 1, 0, 0, 1, 0],
[0, 1, 0, 0, 1, 0, 1],
[0, 0, 0, 1, 0, 1, 0]]
edges = [[0, 0, 1, 2, 0, 0, 0],
[0, 0, 2, 0, 0, 3, 0],
[1, 2, 0, 1, 3, 0, 0],
[2, 0, 1, 0, 0, 0, 1],
[0, 0, 3, 0, 0, 2, 0],
[0, 3, 0, 0, 2, 0, 1],
[0, 0, 0, 1, 0, 1, 0]]
ChapterOne.DijkstrasAlgorithm.DijkstrasAlgorithm.Dijkstras(vertices,edges)
def Prim(self):
"""
Prim's Algorithm
:return:
"""
g = ChapterOne.PrimsAlgorithm.Graph(5)
g.graph = [[0, 2, 0, 6, 0],
[2, 0, 3, 8, 5],
[0, 3, 0, 0, 7],
[6, 8, 0, 0, 9],
[0, 5, 7, 9, 0]]
g.primMST()
def PrimTwo(self):
"""
:return:
"""
ChapterOne.PrimsAlgorithm.Graph.PrimsTwo()
def Huffman(self):
"""
Huffman Coding 霍夫曼编码
:return:
"""
string = 'BCAADDDCCACACAC'
# Calculating frequency
freq = {}
for c in string:
if c in freq:
freq[c] += 1
else:
freq[c] = 1
freq = sorted(freq.items(), key=lambda x: x[1], reverse=True)
nodes = freq
while len(nodes) > 1:
(key1, c1) = nodes[-1]
(key2, c2) = nodes[-2]
nodes = nodes[:-2]
node = ChapterOne.NodeTree.NodeTree(key1, key2)
nodes.append((node, c1 + c2))
nodes = sorted(nodes, key=lambda x: x[1], reverse=True)
huffmanCode = ChapterOne.HuffmanAlgorithm.HuffmanAlgorithm.HuffmanCodeTree(nodes[0][0])
print(' Char | Huffman code 霍夫曼编码\n')
print('----------------------')
for (char, frequency) in freq:
print(' %-4r |%12s' % (char, huffmanCode[char]))
调用:
al=BLL.AlgorithmExample.AlExample()
al.Krusal()
al.FoordFulkerson()
al.Dijkstras()
al.Prim()
al.PrimTwo()
al.Huffman()

哲学管理(学)人生, 文学艺术生活, 自动(计算机学)物理(学)工作, 生物(学)化学逆境, 历史(学)测绘(学)时间, 经济(学)数学金钱(理财), 心理(学)医学情绪, 诗词美容情感, 美学建筑(学)家园, 解构建构(分析)整合学习, 智商情商(IQ、EQ)运筹(学)生存.---Geovin Du(涂聚文)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号