OO第三单元总结
一、写在前面
何为契约式编程?何为规格?为什么要使用JML语言?我认为如果不把这些问题梳理清楚的话其实很难体会为何课程组设置了此单元。
1、契约式编程
1.1 历史
来源于Wikipedia:
The term was coined by Bertrand Meyer in connection with his design of the Eiffel programming language and first described in various articles starting in 1986 and the two successive editions (1988, 1997) of his book Object-Oriented Software Construction.
Eiffel Software applied for trademark registration for "Design by Contract" in December 2003, and it was granted in December 2004.抓重点:
契约式编程这一术语是由Bertrand Meyer提出的。他面向对象编程最早、最有声望的支持者之一,代表作有《面向对象的软件构造》,而DbC也正好就是在该书的1988年版中被提及。
1.2 概念
The central idea of DbC is a metaphor on how elements of a software system collaborate with each other on the basis of mutual obligations and benefits.
The metaphor comes from business life, where a "client" and a "supplier" agree on a "contract" that defines.抓重点:
契约式编程其实是一个形象的比喻。就像在商业生活中客户和商家之间通过某种“契约”来规范行为。
-
商家必须要提供某种商品(也就是所谓的“obligation”),同时也期待从客户那里获得他支付的费用(所谓的“benefit”)
-
客户必须要为商品付钱(所谓的“obligation”),并希望在付款后得到商品(所谓的“benefit”)
-
两方都需要满足一定的义务,而这些义务就被写在我们所说的“契约”当中。
如果放在我们的编程过程中,某一方法的调用者就是client,而这个方法就是supplier,方法的调用者的义务是必须要满足一定的条件(也就是前置条件preCondition)这对方法的benefit就是不用考虑除此之外的情况。而方法的义务是要返回正确的结果(也就是后置条件postCondition),这对调用者的好处是我拿到了正确的结果。
1.3 特点
(以JML为例)
-
准确定义和表示方法行为的正确性
-
更加可靠地开展测试
-
将设计与实现相分离,以此控制架构的复杂程度
个人理解:
一开始接触规格的时候觉得规格是反直觉的,因为我认为它把简单的东西说得复杂了,自己写代码的时候一行注释就可以解释的事情为什么要使用这么多的符号来表示?但是经过了两次作业的锻炼之后,我意识到规格化语言确实可以使定义和行为更加准确,可以避免自然语言注释所带来的二义性。比如说如下这个例子:
//假设有一个场景,有很多学校的很多老师在进行学术交流活动
//这时,我需要将“几个学校的老师放到一个Group里面进行交流”
//二义性:是几所学校各一名老师,还是一个学校的几个老师?
使用JML:
第一种理解:
ensures (\forall int i; 0 <= i && i < allSchools.length; group.add(allSchools[i].getOneTeacher))
第二种理解:
ensures (\forall int i; 0 <= i && i < teacherNum; group.add(MySchool.getTeacher(i))显然,使用规格化的语言可以避免自然语言讲述的过程中所带来的潜在歧义,保证了程序设计人员和代码编写人员能够“手脑一致”,减少bug发生的概率。
但是这其实还不是最重要的,最重要的是契约式编程可以不用聚焦于具体的代码实现细节,而可以从宏观功能的层面来设计好一个类/方法/数据的行为。提前规定好前置条件和后置条件,并规划好类和类、方法和方法之间的联系有利于后续迭代开发,避免功能的重复或缺失对性能/正确性产生影响。
2、JML剖析
2.1 JML是什么
The Java Modelling Language (JML) is a specification language for Java.
JML follows the Design-by-Contract Programming Paradigm: this means that it describes pre/post conditions of code that must be respected in order to get the correct and expected behavior.翻译:JML是JAVA的规格化语言,是基于契约式编程(DbC)思想提出的。也就是说,由前置条件和后置条件可以规定程序的正确行为。
2.2 JML的优点
-
易于学习。JML本身的语法和句法都与JAVA语言非常接近。方便快捷易上手,不用花很多时间多学习一门语言
-
JML规格模型和具体的代码实现并没有非常大的不同。大多数时候可以直接照着JML来写代码,而不用再费力气将规格翻译成具体的代码
-
有很多支持JML的工具比如说
OpenJML,JMLUnit,JMLEclipse等
二、架构设计
1、整体架构
其实整体架构没有什么发挥空间,毕竟大家都是根据JML来完成代码的。个人认为难点在于梳理清楚整个社交网络是如何运行的。因为指导书其实并没有对整个网络进行一个概括式地介绍,所以在刚开始确实需要研究各个类和各个属性的意义。本人绘画水平有限,简单绘制了如下所示的示意图:
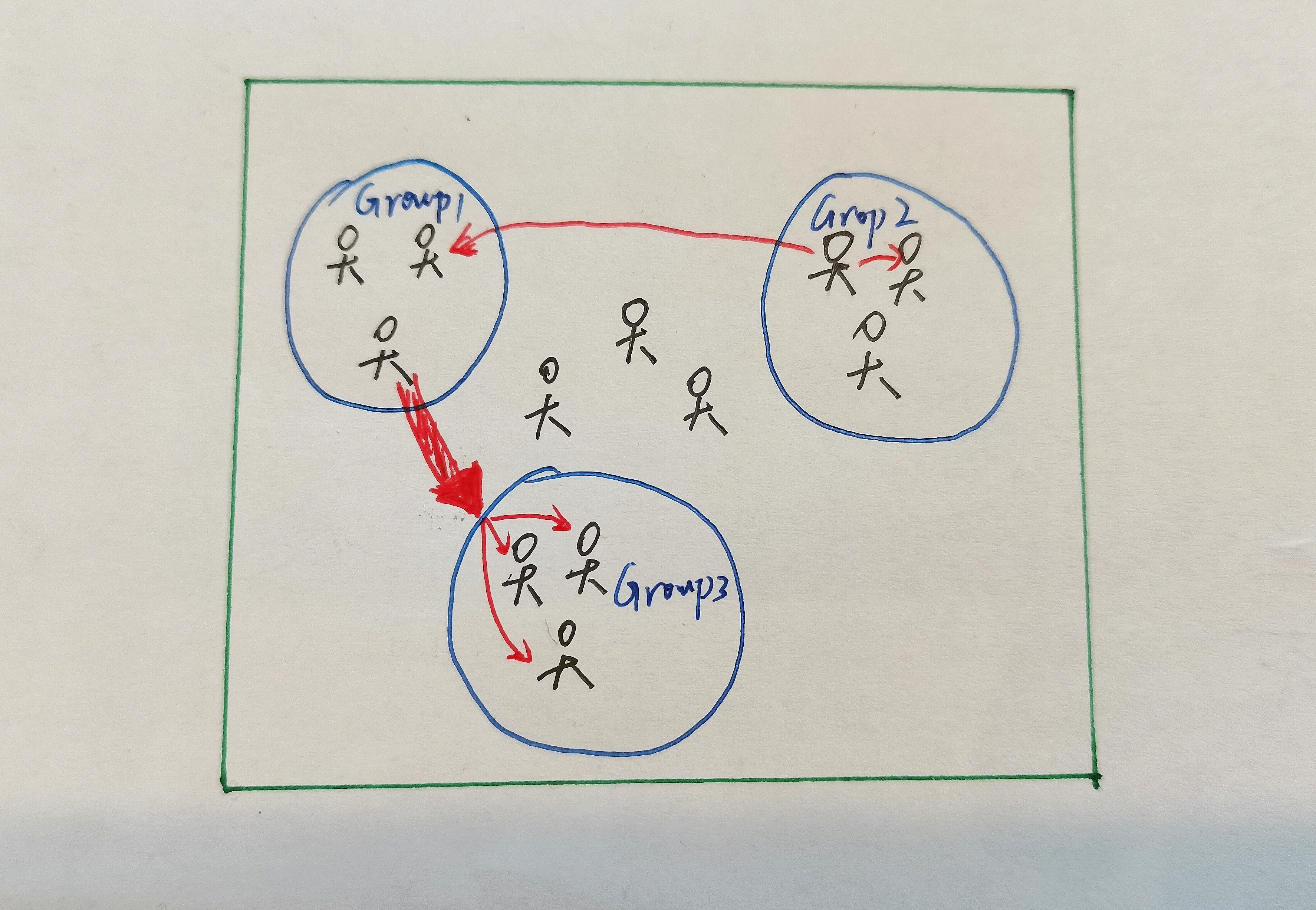
在一个社交网络中(图中绿框)可以有很多的Person和很多的Group,对于Group,我们姑且把它理解成为一群志同道合的人,他们聚集成为了一个团体。我们可以向整个Network中添加Person或Group,也可以将某一个Person加入某一个Group。相互之间通信的方式就是发送Message。我们定义了两种Message,一种是一对一的Message,从一个Person直接送达另一个Person;另一种是一对多的Message,从一个Person直接发送给一个Group,这个Group中的每个人都会收到这个Message。这仅仅是一个概括得不能再概括的解释,其中忽视了海量的细节,但是我认为理解这个Network的运行模式有利于代码的书写。
2、图模型构建
本单元三次作业一共用到了三种不同的图算法,包括并查集、Kruskal算法和Dijkstra算法。
2.1、并查集
在第一次作业中,isCircle和queryBlocksum需要对两个图节点之间是否连通以及所有连通集的个数进行统计。使用for循环来进行判断固然正确,但是效率极低,会达到O(n^2)的复杂度,强测是否会超时暂且不清楚,但是互测一定会被打烂。因此,为了以最低的时间复杂度实现代码,我们就需要使用到并查集。传统的并查集算法在每次查询时都会进行递归调用,从最底层开始向上直到找到根节点。但是若整个树退化为一条链,这样的方式会导致代码运行效率较低。如下图所示

因此我在作业中使用了路径压缩算法。
private static int find(int p) {
if (!parents.get(p).equals(p)) {
parents.replace(p,find(parents.get(p)));
}
return parents.get(p);
}也就是说,我们尽可能将每一个连通集中的节点都直接连到根节点上,这样在查询时时间复杂度较小。

2.2、Kruskal算法
Kruskal算法是一个经典的用来计算最小生成树的算法。之所以选择Kruskal算法而不使用Prim算法,是因为在第九次作业中已经实现了并查集算法,而Kruskal算法判断加入一条边后是否成环就是使用并查集算法。基于迭代开发的思想,尽可能少地增加代码,我在第十次作业中选择了使用Kruskal算法。使用Kruskal需要对所有的边进行排序,这可以使用java自带的排序功能来实现。
Collections.sort(edges, new Comparator<Edge>() {
@Override
public int compare(Edge o1, Edge o2) {
return Integer.compare(o1.getValue() - o2.getValue(), 0);
}
});
2.3、Dijkstra算法
Dijkstra算法是一个经典的最短路径算法,除了它之外,常见的还有Floyd算法(多源最短路)和Bellman-Ford算法(可处理负边)。考虑到Floyd算法在图会不断变动的情况下时间复杂度较高,不利于控制CPU时间,同时在图中又不存在负边,因此我选择了使用Dijkstra算法来计算最短路径。
在算法实现的过程中,每次循环都需要找到距离起点距离最小且没被访问过的节点,这时可以使用java的优先队列PriorityQueue来实现。PriorityQueue内部维护了一个小顶堆,堆排序的时间复杂度应该为O(n\log n) ,相对于传统二重循环O(n^2)的复杂度来说有一定的提升。其实应该还可以使用斐波那契堆进一步优化,不过本人不才,没有进一步地研究下去。
核心代码如下所示:
public int dijkstra(int start,int end) {
PriorityQueue<Nodeing> pq = new PriorityQueue<>((n1, n2) -> n1.getVal() - n2.getVal());
HashSet<Integer> visited = new HashSet<>();
HashMap<Integer,Integer> dis = new HashMap<>(); //the first element is id; the second element is distance;
for (int i : nodes) {
dis.put(i,INF);
}
dis.replace(start,0);
pq.add(new Nodeing(start,0));
while (!pq.isEmpty()) {
Nodeing node = pq.poll();
int point = node.getId();
if (visited.contains(point)) {
continue;
}
visited.add(point);
for (int connected : graph.get(point).keySet()) {
if (!visited.contains(connected)
&& graph.get(point).get(connected) + node.getVal() < dis.get(connected)) {
dis.replace(connected,graph.get(point).get(connected) + node.getVal());
pq.add(new Nodeing(connected,dis.get(connected)));
}
}
}
return dis.get(end);
}
class Nodeing {
private final int id;
private final int val;
public Nodeing(int id,int val) {
this.id = id;
this.val = val;
}
public int getId() {
return id;
}
public int getVal() {
return val;
}
}
三、问题分析
1、自身问题
在本单元三次作业中,第二次作业出现了一些尴尬的失误,由于课程组测试点较为仁慈,没有出现全军覆没的情况而仅仅只是寄了三个强测点。问题出现在query group value sum指令的处理上。第一次作业中,我使用的是和JML完全一致的双重循环遍历的方式,每次查询时都会使用O(n^2)的复杂度去计算。为了提升性能,在第二次作业中我将value值的维护放在了每一次Group中添加或删除一个人的时候。但是在优化的过程中却“失去了本心”,忘记了value值是要重复计算的(比如A和B是相互联系的,即使值是一样的,在qgvs指令中仍要计算 A->B 和 B->A)。我还寻思着value值不应该重复计算啊。这种主观臆断导致了我qgvs指令完美地为正确值的二分之一。那我难道没有对拍吗?尴尬的事情来了——和我对拍的同学拥有同款错误,所以在对拍过程中我们没发现任何问题。感谢仁慈的测试点,不然我俩将以泪洗面了(x)。玩笑归玩笑,这个bug还是警醒我一定要根据JML来完成代码,如果代码有优化变动也需要在改动完后重新阅读JML规格,保证自己的优化是符合规格定义的。
2、他人问题
主要是性能问题。
-
第一次作业的性能问题出现在没有使用并查集,而是每次调用
isCircle函数的时候都使用DFS进行一遍搜索。中测和强测貌似没有问题,但是在互测中可以被定点数据给轰炸超时(先添加一定量的person和relation进去,随后疯狂query block sum和isCircle)。 -
第二次作业最大的问题在于
query group value sum指令。若是采取复杂度为O(n^2)的双重循环,每次查询时都进行一遍计算,将会使CPU运行时间超时。因此需要动态维护,在添加和删除组内成员时就维护好,这样可以使用O(1)复杂度来查询。数据构造方式也很简单,只保留一个Group,添加一定量的person和relation,并将这些person全部加入Group中,然后疯狂qgvs指令就行了。 -
第三次作业没有发现明显的性能问题。
四、关于测试
本单元测试我主要采用了 “随机” + “构造” 的方式,并通过与他人对拍来验证结果的正确性。
-
“随机”测试主要通过程序自动生成大量代码。由于代码量大,可以给程序运行给予一定的压力,配合上CPU时间的统计,可以判断程序是否会在特定情况下超时。这种方式十分简单粗暴,但是胜在量大,能以量取胜。
-
“构造”测试主要是通过阅读JML代码,考虑特殊的边界情况有针对性地手动构造数据。一个非常经典的例子就是在Group中计算年龄的平均值时,如果在代码中忘记对人数进行特判,就会导致错误
/*@ ensures \result == (people.length == 0? 0 : ((\sum int i; 0 <= i && i < people.length; @ (people[i].getAge() - getAgeMean()) * (people[i].getAge() - getAgeMean())) / @ people.length)); @*/ public /*@ pure @*/ int getAgeVar();错误实现:当Group中人数为0时,会出现\frac{0}{0}的错误情况:
public int getAgeVar() { int sum = 0; for (Person p:people) { int tmp = p.getAge() - getAgeMean(); sum += tmp * tmp; } sum /= people.size(); return sum; }正确实现:注意到JML规格特别有在
people.length==0的时候进行特判,所以在实现时也应该将特判加入代码中public int getAgeVar() { if (people.isEmpty()) { return 0; } else { int sum = 0; for (Person p:people) { int tmp = p.getAge() - getAgeMean(); sum += tmp * tmp; } sum /= people.size(); return sum; } }俗话说得好,“The devil is in the details”,这种情况在随机测试的数据轰炸中不一定会被测试到(因为生成的数据很难全部覆盖,与生成方式有关),因此就需要人工阅读JML规格代码,观察代码中的细节,并针对性地构造数据。另一个很经典的例子就是在
addToGroup指令中有对Group中人数的限制,互测时就有部分同学忘记考虑这个点了。/* @ public normal_behavior @ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id2) && @ (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1) && @ getGroup(id2).hasPerson(getPerson(id1)) == false && @ getGroup(id2).people.length < 1111; //细节 .......................................................... @ public normal_behavior @ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id2) && @ (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1) && @ getGroup(id2).hasPerson(getPerson(id1)) == false && @ getGroup(id2).people.length >= 1111; //细节 */
五、额外架构扩展
1、题目:
假设出现了几种不同的Person
-
Advertiser:持续向外发送产品广告
-
Producer:产品生产商,通过Advertiser来销售产品
-
Customer:消费者,会关注广告并选择和自己偏好匹配的产品来购买 -- 所谓购买,就是直接通过Advertiser给相应Producer发一个购买消息
-
Person:吃瓜群众,不发广告,不买东西,不卖东西
如此Network可以支持市场营销,并能查询某种商品的销售额和销售路径等 请讨论如何对Network扩展,给出相关接口方法,并选择3个核心业务功能的接口方法撰写JML规格(借鉴所总结的JML规格模式)
2、整体设计:
可以观察到,Advertiser、Producer、Customer都是某一类特殊的人,因此可以考虑让三者继承Person类,在其中给予特殊的方法。同时需要新建一个Product类,其中记录有产品的id和value。考虑到与原有社交网络的兼容性,可以考虑增加三种Message子类型:PurchaseMessage,ProduceMessage,AdvertiseMessage。
-
Advertiser:可以拥有一个Product属性,在收到Producer的ProduceMessage后即可增加,表明可以推销哪些商品。同时会记录商品的生产厂商,方便连接Customer和Producer。也可以拥有一个subscribers[]属性,表明有哪些客户订阅了自己的广告。 -
Producer:可以拥有Product属性,表明自己生产的商品是什么。 -
Customer:感觉加上一个Preference属性表明自己所偏爱的产品就行了。
3、JML规格实现:
3.1 市场营销做广告
/*@public normal_behavior
@requires contains(id1) && getPerson(id1) instanceof Advertiser && containsMessage(id2) && getMessage(id2) instanceof AdvertiseMessage;
@assignable messages;
@assinable getPerson(id1).subscribers[].preference;
@ensures \old(getPerson(id1).subscribers) == getPerson(id1).subscribers;
@ensures !containsMessage(id2) && messages.length == \old(messages.length) - 1 &&
@ (\forall int i; 0 <= i && i < \old(messages.length) && \old(messages[i].getId()) != id;
@ (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i]))));
@ensures (\forall int i; 0 <= i && i < \old(getPerson(id1).subscriber.length);
@getPerson(id1).subscriber[i].getPreference.length == \old(getPerson(id1).subscriber[i].getPreference.length) + 1);
@also
@public exceptional_behavior
@signals (MessageIdNotFoundException e) !containsMessage(id);
@signals (PersonIdNotFoundException e) !contains(id1);
*/
public void advertise(int id1, int id2) throws MessageIdNotFoundException, PersonIdNotFoundException3.2 生产商品
/*@ public normal_behavior
@ requires contains(id1) && getPerson(id1) instanceof Producer && containsMessage(id2)
@&& getMessage(id2) instanceof ProduceMessage && getPerson(id1) == getMessage(id2).getPerson1();
@assignable messages;
@assignable getMessage(id2).getPerson2().getProduct();
@ensures !containsMessage(id2) && messages.length == \old(messages.length) - 1 &&
@ (\forall int i; 0 <= i && i < \old(messages.length) && \old(messages[i].getId()) != id;
@ (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i]))));
@ ensures (\forall int i; 0 <= i && i < \old(getMessage(id2).getPerson2().getProducts().size());
@ \old(getMessage(id2)).getPerson2().getProducts().get(i+1) == \old(getMessage(id2).getPerson2().getProducts().get(i)));
@ ensures \old(getMessage(id2)).getPerson2().getProducts().get(0) == \old(getMessage(id2));
@ ensures \old(getMessage(id2)).getPerson2().getProducts().size() == \old(getMessage(id2).getPerson2().getProducts().size()) + 1;
@also
@public exceptional_behavior
@ signals (MessageIdNotFoundException e) !containsMessage(id2);
@signals (PersonIdNotFoundException e) !contains(id1);
@*/
public void advertise(int id1, int id2) throws MessageIdNotFoundException, PersonIdNotFoundException3.3 查询某个Producer的总销售额
/*@public normal_behavior
@requires contains(id) && getPerson(id) instanceof Producer;
@ensures \result == getPerson(id).getTotalSales();
@also
@public exceptional_behavior
@signals (PersonIdNotFoundException e) !contains(id);
*/
public int querySales(int id);
本单元给我最大的感觉就是“严谨”。这可能也是契约式编程的一个特点,只要你严格地按照JML规格来实现代码,你的程序功能就不会出错。同时在学习的过程中,我也体会到要写出一个完备的JML规格并非易事,其中需要覆盖各种情况,不重不漏,设计人员需要对代码的功能有非常全面的了解才能完成此任务。但是,由于性能的要求,我们又不能完全按照JML中的实现方式来写代码,需要进行一定的优化,而在优化的过程中我有几次“失去了本心”

