2025.6~2025.12半年做题记录合集

闲话

这里记录了我半年的做题记录，中间有很多咕咕咕内容，等到下一年再补吧。

2025.6

小奇的博弈 紫难度

题意

\(1\times n\) 的棋盘上有 \(k\) 个白黑交替的棋子，两玩家博弈，每次玩家 \(1/2\) 可以将 \(1\sim d\) 个 白/黑 棋子移动若干格，不能跨过其他棋子或出界，不能操作者输，对必胜局面计数。

题解

设相邻白-黑的间距大小为 \(g_1,g_2,\dots g_{\frac{k}{2}}\)，则问题可以转化为有 \(\frac{k}{2}\) 堆石子，每次取走 \(1\sim d\) 堆石子的任意个石子，不能操作者输。

这是 NIM 游戏的拓展，必败条件是石子个数二进制不进位加法和的每一位模 \((d+1)\) 为 0。

如果确定了 \(\sum_i g_i\)，则可以通过组合数算出方案数，因此考虑对 \(\sum_i g_i\) 进行 DP。

\(dp_{i,sumd}\) 表示考虑二进制前 \(i\) 为，\(\sum_i g_i\) 和为 \(sumd\) 的方案数。

则有转移方程 \(dp_{i,sumd}\leftarrow \sum\limits_{0\leq j\times (d+1)\leq \frac{k}{2}\land sumd-2^{i}\times j\times (d+1)\geq 0} dp_{i-1,sumd-2^{i}\times j\times (d+1)}\times \binom{\frac{k}{2}}{j\times (d+1)}\)。

最后枚举 \(\sum_i g_i\) 计算必败情况数 \(res\)，则答案为 \(\binom{n}{k}-res\)。

提交记录

CF1062F Upgrading Cities *2900

题意

给定一张有向无环图，若节点 \(x\) 满足至多存在一个节点 \(y\)，使得 \(x\) 和 \(y\) 互相不可达，则 \(x\) 节点是关键点，求关键点的个数。

题解

看到 DAG 可达性问题，考虑拓扑排序。

显然，拓扑排序的任意时刻，在队列中的点两两不可达。

记 \(u\) 能到达的点个数和能到达 \(u\) 的点个数之和为 \(cnt_u\)（不含 \(u\)），当 \(cnt_u\geq n-2\) 时 \(u\) 合法。

分析节点 \(u\) 出队列后时的队列大小 \(|Q|\)。记 \(u\) 是第 \(i\) 个出队的节点。

• \(|Q|=0\)
  • 后面没有入队的点都可以从 \(u\) 到达，\(cnt_u\leftarrow cnt_u+n-i\)。
• \(|Q|=1\)
  • 记 \(v\) 为队列中的元素。
  • 如果存在边 \((v,w)\) 且此时 \(w\) 入度为 \(1\)，则 \(v,w\) 都与 \(u\) 不可达，\(u\) 不合法，\(cnt_u\leftarrow -\infin\)。
  • 否则 \(u\) 可以到达的点数为后面没有入队的点减 \(1\)，\(cnt_u\leftarrow cnt_u+n-i-1\)。
• \(|Q|\geq 2\)
  • 显然 \(u\) 不合法，\(cnt_u\leftarrow -\infin\)。

正着做一遍，之后把边反转在做一遍，统计 \(cnt_u\geq n-2\) 的个数即可。

提交记录

P4630 [APIO2018] 铁人两项 紫

题意

给定一张简单无向图，问有多少三元组 \((s,c,f)\)，满足 \(s,c,f\) 互不相同，且存在一条 \(s\rightarrow c\rightarrow f\) 的简单路径。

题解

学习圆方树做的第一题。

点双的性质之一是任意两点的简单路径并等于整个点双。

建出圆方树后，确定起点和终点，则中转点的方案数就是路径上所有方点所属点双的并集大小减 \(2\)（减去起点和终点）。

将方点点权设为所属点双大小，圆点点权设为 \(-1\)，则两点在圆方树上的点权和恰好是所有方点所属点双的并集大小减 \(2\)。

于是问题转化为统计圆方树上所有有序点对路径中点权之和，可以用简单的树上 DP 实现。

提交记录

P9829 [ICPC 2020 Shanghai R] Traveling Merchant 紫

题意

给定一张简单无向图，点权为 \(0\) 或 \(1\)，从 \(1\) 号点开始行走，每次只能走两端点权不同的边，每次离开一个点的时候该点的点权自动取反，判断是否存在一种经过无穷个点的行走方案。

题解

分析性质，存在无穷路径，当且仅当：存在一个奇环，恰有一条同色边，且同色边的一个端点可以作为起点。

即同色边的一个端点可以从 \(1\) 不经过环上节点达到。

只加入异色边，则存在无穷盈利的路径可以等价为存在一条同色边 \((u,v)\)，满足：

• 存在一条从 \(1\) 开始，顺次经过 \(1\rightarrow u\rightarrow v\) 或 \(1\rightarrow v\rightarrow u\) 的简单路径。
  • 解释一下：
  • 其中 \(u\rightarrow v\)（或 \(v\rightarrow u\)）是奇环上路径，\(1\rightarrow u\) （或 \(1\rightarrow v\)）表示不经过环上路径的前提下从 \(1\) 到 \(u\)（或 \(v\)）。
  • 由于要求简单路径，所以上述性质得到保证。

三点连通性问题，考虑圆方树。

利用圆方树的性质，存在 \(1\rightarrow u\rightarrow v\) 的简单路径，等价于：

• 圆方树以 \(1\) 为根，存在两个方点 \(p,q\)，满足圆点 \(u\) 属于方点 \(p\)，圆点 \(v\) 属于方点 \(q\)，且 \(p\) 为 \(q\) 的祖先。

问题在于一个圆点可能属于多个方点。贪心的，我们取 \(u\) 在圆方树上的父亲节点 \(fa_u\) 作为 \(u\) 所属的方点。

容易证明，此时 \(v\) 属于哪个方点是无关紧要的，为了方便可以取 \(fa_v\) 作为 \(v\) 所属的方点。

所以枚举同色边 \((u,v)\)，判断 \(fa_u\) 和 \(fa_v\) 是否构成祖孙关系即可（注意特判 \(1\) 号点）。只要有一条同色边符合条件答案就是 yes，否则答案为 no。

提交记录

agc071_c Orientable as Desired *2740

题意

给定一个简单连通无向图 \(G\)，判断是否存在满足以下所有条件的长度为 \(N\) 的非负整数序列 \(X = (X_1, X_2, \dots, X_N)\)：

• 对于每个 \(v = 1, 2, \dots, N\)，\(X_v\) 不超过图 \(G\) 中顶点 \(v\) 的度数
• 不存在一种对 \(G\) 的 \(M\) 条边进行定向的方法，使得得到的有向图中每个顶点 \(v\) 的入度或出度等于 \(X_v\)

题解

先摆结论。如果且仅如果同时满足以下两个条件，就不存在可行的 \(X\)：

1. \(G\) 是二分图；
2. 对图中每个顶点 \(v\)，把与 \(v\) 相邻的边按照它们所在的点双进行分类。设这些类别的大小分别为 \(c_1,c_2,\dots,c_k\)，那么必须能用这些 \(c_i\) 的某个子集之和，表示从 \(0\) 到 \(\deg(v)=c_1+c_2+\cdots+c_k\) 之间的每一个整数。

思考过程与证明如下：

令 \(X = (0, 0, \dots, 0)\)。发现一个点要么入度为 \(0\)，要么出度为 \(0\)，且相邻点的情况不能相同。因此如果 \(G\) 不是二分图，答案为 Yes。

下面只考虑 \(G\) 是二分图的情况。

令 \(X = (0, 0, \dots, X_u, \dots, 0)\)。如果 \(u\) 和 \(u\) 的两个相邻点 \(a,b\) 在同一点双内，即 \(a\) 不经过 \(u\) 能到达 \(b\)，由于 \(G\) 是二分图， \(a\) 和 \(b\) 与 \(u\) 的边方向一致。

因此将 \(u\) 的相邻边根据所在点双分类，设这些大小为 \(c_1,c_2,\dots,c_k\)。

那么相当于要选出 \(c_i\) 的某个子集作为 \(u\) 的入度或出度，选不出来即无解。

因此必要性得证，接下来证明充分性。

如果原图是一棵树，那么可以自上而下进行构造，显然能通过调整子节点构造出合法方案。

对于原图不是树的情况，建出圆方树，先按 \(X\) 全零构造，之后调整。自上而下调整，此时一个点的子节点表示一个点双。节点 \(u\) 向上指的边方向肯定是相同的，因此可以通过调整 \(u\) 子节点所对点双来组成任意的 \(X_u\)。

因此充分性得证。

提交记录

CF475E Strongly Connected City 2 *2700

题意

给一个无向图，你需要给所有边定向，使定向之后存在最多的点对 \((a,b)\) 使得从 \(a\) 能到 \(b\)。

题解

对于边双内部的点和边，肯定存在一种定向方式使得这些点互相可达。具体定向方式是选出一个环，环上边顺时针定向，环外点至少有两条边不重复到环上的路径（因为这是边双），令这两条路径方向相反即可。

将边双缩为一个点，原图变为一棵树，点有点权。问题转化为带权的树上问题。

猜测最优解树的形态如下：

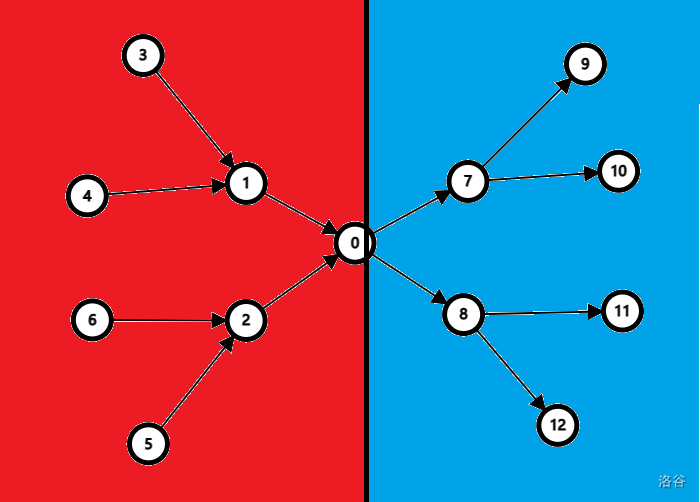
证明：

即证明上述树形态可以经过若干次不优调整变为任意形态。

只考虑蓝色区域调整，红色区域同理。考虑一条边 \((u,v)\) 的翻转，翻转前答案为 \(ans_u+ans_v+sz_u\times sz_v\)，翻转后答案为 \(ans_u+ans_v+sz_u\)，此处 \(sz_u\) 表示这条边 \(u\) 方向连通快的信息，而非子树信息。其余变量名同理。显然调整不优。

(todo) : 证明多次调整仍然不优。

简单分析即可得出两边大小尽可能平均，因此：非重心直接选重儿子放一边，轻儿子放一边；重心对子树大小背包即可。

朴素背包可以通过，无需 bitset 优化。

提交记录

CF1338E JYPnation *3500

题意

给定一张 \(n\) 个点的竞赛图，特别地，满足图中不存在如下这样的四个点 \(a, b, c, d\)：

• 其中 \(a, b, c\) 三个点形成三元环，即 \(a \to b \to c \to a\)，且它们都向 \(d\) 连边，即 \((a, b, c) \to d\)。

计算 $ \sum_{1 \le i < j \le n} \text{dis}(i, j) $

如果 \(x\) 无法到达 \(y\) 则规定 \(\text{dis}(x, y) = 614 \times n\)。

\(n\leq 8000\)。

题解

首先如果两个点不在同一 SCC 中，则贡献为 \(614n+1\)，下面只考虑两点在同一 SCC 的情况。

首先 \(dis(u,v)\leq 3\)，因为如果 \(dis(u,v)=4\) 则存在不合法的导出子图（如图）。

考虑对 \(dis(u,v)=1\) 和 \(dis(u,v)=2\) 的点对计数，前者就是 SCC 内的边数，重点考虑后者。

\(dis(u,v)=2\)，当且仅当：

• 不存在 \(u\rightarrow v\) 的边。
• 存在 \(u\rightarrow a\) 和 \(a\rightarrow v\) 的边。

直接做是 \(O(n^3)\) 的，瓶颈在于需要枚举 \(u\) 的相邻点 \(a\)。

继续分析性质，如果存在边 \(v\rightarrow u\)，\(u\rightarrow a\)，\(a\rightarrow v\)，\(u\rightarrow b\)，\(a\rightarrow b\)，则必定存在边 \(b\rightarrow v\)。

这告诉我们如果 \(u\) 的邻点中存在 \(a,b\) 和边 \(a\rightarrow b\)，则没必要枚举 \(a\)，此时称 \(b\) 支配了 \(a\)。进一步，由于这是竞赛图，因此 \(u\) 的邻点中存在一个导出子图，满足这个子图是 SCC，且不被任何其他邻点支配。找到其中一个点判断是否能到 \(v\) 即可。

时间复杂度 \(O(n^2)\)，由于本题存在不缩点、常数更优秀的算法，因此这个算法需要卡常。

卡常技巧：注意数组访问顺序，循环时将数组缓存到局部指针。

提交记录

CF1864H Asterism Stream *3200

题意

给定变量 \(x\)，初始为 \(1\)，每次等概率随机进行以下两种操作之一：

1. \(x\leftarrow x+1\)

2. \(x\leftarrow x\times 2\)

求期望多少次操作之后 \(x\geq n\)，对 \(998244353\) 取模。

题解

\(E(x\geq n)=\sum\limits_{i=1}^{n-1} P(x=i)\)。

问题转化为求解若干次操作后，\(x<n\) 的概率之和。

以下令 \(n:=n-1\)。

考虑枚举操作二的次数，然后在操作二之间穿插操作一。

设操作二的个数为 \(L\)，在倒数第 \(i\) 个操作二后进行的操作一会被放大 \(2^{i-1}\) 倍，因此本质上是对满足如下条件的序列 \((c_0,c_1,\dots,c_{L+1})\) 计数，其中序列 \((c_0,c_1,\dots,c_{L+1})\) 的权重为 \(2^{-\sum\limits_{i=1}^{L+1} c_i}\)。（注意 \(c_0\) 仅仅是把小于变为等于，并没有实际含义，也不计入权重中概率运算）

• \(c_0+c_1+c_2\times 2^1+c_3\times 2^{2}+\cdots+c_{L+1}\times 2^{L}+2^L=n\)。

加上 \(2^L\) 是因为 \(x\) 初始为 \(1\)。

考虑将 \(c\) 拆为二进制，记 \(a[b]\) 表示 \(a\) 在二进制下第 \(b\) 为的值（\(0\) 或 \(2^b\)）。

原条件为：

\[(\sum_i c_0[i])+(\sum_i c_1[i])+(\sum_i c_2[i])\times 2^1+(\sum_i c_3[i])\times 2^{2}+\cdots+(\sum_i c_{L+1}[i])\times 2^{L}=n-2^L \]

考虑答案也拆为二进制，进行数位 DP。

其中答案的 \(2^i\) 系数为：

\[c_0[i]+c_1[i]+c_2[i-1]+c_3[i-2]+\cdots +c_{\min\{i+1,L+1\}}[i-\min\{i+1,L+1\}+1] \]

令 \(f_{i,j}\) 表示 \(2^{-(c_0[i]+c_1[i]+c_2[i-1]+c_3[i-2]+\cdots +c_{\min\{i+1,L+1\}}[i-\min\{i+1,L+1\}+1])}\) 之和，可以简单背包算。

之后就是基本的数位 DP，\(dp_{i,j}\) 表示正在决策自低向高的第 \(i\) 位，上一位进位为 \(j\) 的权重和，转移为：

\[dp_{i+1,\lfloor \frac{(j+k)}{2}\rfloor } \leftarrow dp_{i,j}\times f_{i,k} \ \ \ ((j+k)\equiv \lfloor \frac{n}{2^i}\rfloor\pmod 2) \]

提交记录

CFgym102411D Double Palindrome *????

题意

定义一个字符串是好的，当且仅当它要么本身是一个回文串，要么能被划分成两个回文串。

给定 \(n,k\)，求长度不超过 \(n\)，字符集大小为 \(k\) 的好的字符串个数，对 \(10^{9}+7\) 取模。

题解

定义一个串是本原的当且仅当其有唯一方式拆分成两个回文串。

如果我们能证明一个符合条件的串一定能够被一个本原串循环拼出来，且方案唯一，则我们可以通过如下方式计数：

• 令 \(f_i\) 表示长度为 \(i\) 的符合条件字符串之和，但是其中一个字符串会被算重【划分方案】次。

• \[f_{i}=\sum\limits_{i=0}^{n-1} k^{\lceil \frac{i}{2} \rceil+\lceil \frac{n-i}{2} \rceil}=\left\{\begin{matrix} n\times k^{\frac{n}{2}+1} (n\equiv 1\pmod 2) \\ \frac{n}{2}\times k^{\frac{n}{2}}+\frac{n}{2}\times k^{\frac{n}{2}+1} (n\equiv 0\pmod 2) \end{matrix}\right.\]

• 令 \(g_i\) 表示长度为 \(i\) 的本原串个数，但是其中一个字符串会被算重【划分方案】次。显然本原串划分方案为 \(1\)，因此 \(g_i\) 实际不会算重。
• \(g_i=f_i-\sum\limits_{d|n\land d\neq n} g_d\times \frac{n}{d}\)，乘上 \(\frac{n}{d}\) 表示乘上不是本原串中算重的部分。

接下来证明结论。

• 若一个串 s 有至少两种拆分方式，则存在一个本原串循环节。

  • （todo）

• 所有本原串复制若干遍得到的串不同。

  • （todo）

提交记录

P9563 Be Careful 2 黑

题意

\(n\times m\) 的平面上有 \(k\) 个点，求平面上不包含这些点的正方形面积之和。

题解

考虑容斥，枚举被包含的点集 \(S\)，设完全包含 \(S\) 的正方形面积和为 \(f_S\)，则答案为 \(\sum\limits_{S} f_S\times (-1)^{|S|}\)。

完全包含 \(S\)，即完全包含 \((Xmin(S),Ymin(S)),(Xmax(S),Ymax(S))\) 这个矩形。

注意到如果这个矩形内部有点，那么这个点选或不选，对答案造成的贡献为相反数，可以抵消。

因此真正有用的矩形满足只有边界上有禁止点。

为了避免算重，可以离散化时维护一个严格偏序关系，这样离散化后任意两点 \(x,y\) 都不同，并且一个 \(y\) 对应唯一的 \(x\)。

具体的，离散化二分查找时这样写：

for(int i=1;i<=k;i++){
	a[i].x=lower_bound(bx+1,bx+1+k,a[i].x)-bx;
	bx[a[i].x]--;//变化在这里
	a[i].y=lower_bound(by+1,by+1+k,a[i].y)-by;
	by[a[i].y]--;//变化在这里
}

之后枚举矩形的 \(Ymin\) 和 \(Ymax\)（分别记为 \(y1,y2\)），根据上下 \(y\) 值找到唯一对应的两个点 \((x1,y1),(x2,y2)\)，则矩形左右边界一定是 \(x1,x2\) 或者 \(x1,x2\) 在 \(y\in (y1,y2)\) 的点中的某个前驱或后继。需要保证矩形内部没有点。

为了避免求前驱后继的 \(log\) 因子，枚举矩形可以这么写（\(rk_i\) 表示离散化后 \(y=i\) 的点的 \(x\) 值）：

for(int yl=1;yl<=k;yl++){
	sub(ans,calc(rk[yl],rk[yl],yl,yl));
	int mn=0,mx=k+1;
	for(int yr=yl+1;yr<=k;yr++){
		int xl=rk[yl],xr=rk[yr];
		if(xr<mn||xr>mx) continue;
		if(xr>xl){
			add(ans,calc(xl,xr,yl,yr));
			sub(ans,calc(xl,mx,yl,yr));
			sub(ans,calc(mn,xr,yl,yr));
			add(ans,calc(mn,mx,yl,yr));
			mx=xr;
		}else{
			add(ans,calc(xr,xl,yl,yr));
			sub(ans,calc(xr,mx,yl,yr));
			sub(ans,calc(mn,xl,yl,yr));
			add(ans,calc(mn,mx,yl,yr));
			mn=xr;
		}
	}
}

最后会产生 \(O(k^2)\) 个矩形，需要我们 \(O(1)\) 计算包含矩形的正方形面积之和。

正方形有三个属性——边长 \(d\)，左下角 \(x\)，左下角 \(y\)。

若一个正方形 \((d,x,y)\) 包含矩形 \((xl\sim xr,yl\sim yr)\) 且不出界，则需要满足：

• \(\max\{xr-xl,yr-yl\}\leq d\leq \min\{n,m\}\)

• \(0\leq x\leq xl,xr\leq x+d\leq n-d\)

• \(0\leq y\leq yl,yr\leq y+d\leq m-d\)

满足条件的正方形 \((d,x,y)\) 贡献为 \(n^2\)。

因此答案为：

\[\sum\limits_{d=\min\{n,m\}}^{\max\{xr-xl,yr-yl\}} d^2\times ((\min\{xl,n-d\}-\max\{0,xr-d\}+1)\times (\min\{yl,m-d\}-\max\{0,yr-d\}+1) \]

这是一个不超过 \(5\) 段的四次分段函数，每一段形如 \(\sum\limits_{i=l}^r ai^4+bi^3+ci^2+di^1+e\)。

我们有公式：

\[\sum_{k=1}^{n} k = \frac{n(n+1)}{2}\\\sum_{k=1}^{n} k^{2} = \frac{n(n+1)(2n+1)}{6}\\\sum_{k=1}^{n} k^{3} = \left( \frac{n(n+1)}{2} \right)^{2}\\\sum_{k=1}^{n} k^{4} = \frac{n(n+1)(2n+1)\bigl(3n^{2}+3n-1\bigr)}{30} \]

因此直接计算即可。

提交记录

[ARC138F] KD Tree 黑

题意

给定一个长为 \(n\) 的点列 \((i,p_i)\)，其中 \(\{p_i\}\) 是一个 \(1\) 到 \(n\) 的排列。

每次操作可以选择 \(x/y\) 和一个坐标，将点列分成左右/上下两边（保持两边的相对顺序不变），分别递归下去，直到只剩下一个点，把它加入答案序列末尾。

求最终能生成多少种不同的答案序列，对 \(10^9+7\) 取模。

\(n\leq 30\)。

题解

让我们假定每次划分操作都会与至少一个点重合，这些重合点会被分到左/上部分。

显然一个结果序列会对应多个操作序列，考虑选取代表元。

贪心地从结果序列反向构建操作序列，按照 \(x,y\) 操作交替的顺序从小到大构造。

如果有 \(k+1\) 个点，那么将点离散化后可能进行的操作为 \(x=2,y=2,x=3,y=3,\dots x=k,y=k\)。依次尝试直到遇到符合条件的操作进行操作即可。

同时我们定义一步操作的字典序为在 \(x=2,y=2,x=3,y=3,\dots x=k,y=k\) 这个序列里的排名。

使用 \(dp(l,r,u,d)\) 表示第 \(l\) 至第 \(r\) 个点，\(u\leq p_i\leq d\) 的子集答案。

实际上划分出的子集种类是 \(O(n^4)\) 的，因此实现的时候可以直接用二进制状态，状压点是否在集合内来表示。

转移时，沿着 \(i\) 竖着切会分为 \([l,i]\) 和 \((i,r]\) 两部分，则贡献为 \(dp(l,i,u,d)\times dp(i+1,r,u,d)\)。

但是要让这一步是 \([l,i]\) 中字典序最小的。

考虑容斥，假设这一步不是字典序最小的，设 \(\alpha\) 为实际最小字典序操作，则如果结果重复，则【\(\alpha\) 划分出来的先进行递归的点】一定属于【这一步划分出来先递归的点】。

因此记忆化搜索跑 DP，使用状压记状态，每次枚举操作 \(\alpha\)，计算划分出来的集合，判子集并减掉。

转移时需要额外维护 \(f_i\) 表示由字典序第 \(i\) 小的操作划分出的集合 \(S\) 内的点中，所有操作的字典序都大于本次操作的方案数。

具体转移如下：

int res=0;
int f[65]={};
for(int i=0;i<tmp.size();i++){
	int tres=dp(tmp[i]);
	for(int j=0;j<i;j++){
		if((tmp[j]&tmp[i])==tmp[j]){
			tres=(tres-f[j]*dp(tmp[i]^tmp[j])%mod+mod)%mod;
		}
	}
	f[i]=tres;
	tres=tres*dp(st^tmp[i])%mod;
	res=(res+tres)%mod;
}

提交记录

P10013 [集训队互测 2023] Tree Topological Order Counting 紫

题意

给定一颗 \(n\) 个点的有根树和权值序列 \(b\)。

对每个点 \(u\)，定义 \(f(u)\) 为，在所有这颗树的合法拓扑序 \(\{a\}\) 中，\(b_{a_u}\) 之和。

现在对 \(1 \le u \le n\)，求 \(f(u) \bmod 10^9+7\)。

\(n\leq 5000\)。

题解

题解写在洛谷了

上面那个链接如果不行，就点这个

提交记录

The_3rd_Universal_Cup_Stage 9_Xi'an_Problem_M Random Variables *????

题意

对于一个长度为 \(n\) 取值为 \([1,m]\) 的正整数数组 \(\{a\}\)，求其中出现次数最多的数字的出现次数的期望。

题解

对出现次数最多的数字的出现次数为 \(k\) 的序列计数，这个很不好做，因此考虑容斥，令 \(f_k\) 表示出现次数最多的数字的出现次数 \(\leq k\) 的序列个数，则答案为 \(\sum\limits_{k=1}^{n} (f_k-f_{k-1})\times k\)。

考虑如何计算 \(f_k\)，本质上是 \(n\) 个不同的球放入 \(m\) 个不同的盒子，每个盒子不超过 \(k\) 个球的方案数。

这个可以 DP，枚举 \(k\)，令 \(dp_{i,j}\) 表示 \(i\) 个球放入 \(j\) 个不同的盒子，每个盒子不超过 \(k\) 个球的方案数。

初始值 \(dp_{0,j}=1\)。

则有转移方程式：

\[dp_{i,j}\leftarrow \underbrace{dp_{i-1,j}\times j}_{\text{新加入一个球，有 $j$ 个盒子可以放入}}-\underbrace{dp_{i-(k+1),j-1}\times \underbrace{\binom{i-1}{k}\times j}_{\text{选出一个盒子，再在 $i-1$ 个球中选 $k$ 个沾满这个盒子}}}_{\text{减去不合法的情况，不合法说明 $i$ 放入了一个满盒子，放入 $i$ 后盒子里有 $k+1$ 个球}} \]

最后令 \(f_k=dp_{n,m}\)。

考虑 \(dp_{n,m}\) 从 \(j\leq m\) 的哪里转移而来。

\(dp_{n,m}\leftarrow dp_{n-x\times (k+1),j-x}\times C\)。

因此当第二维度小于 \(m-\frac{n}{k+1}\) 时，这个地方的 \(dp\) 值是无效的，不会对 \(dp_{n,m}\) 产生任何贡献。

因此直接把有效状态拿出来 DP 即可，时间复杂度 \(O(\sum\limits_{k=1}^{n} \sum\limits_{i=1}^{n} \sum\limits_{j=m-\frac{n}{k+1}}^{m} 1)=O(\sum\limits_{i=1}^{n}\sum\limits_{k=1}^{n} \frac{n}{k+1})=O(n^2\ln n)\)。

提交记录

P9482 [NOI2023] 字符串 紫

题意

给定一个长度为 \(n\) 的字符串 \(s[1: n]\)。有 \(q\) 次询问，每次询问给定两个参数 \(i, r\)。你需要求出有多少 \(l\)，满足如下条件:

• \(1 \leq l \leq r\)。
• \(s[i: i+l-1]\) 字典序小于 \(\operatorname{Reverse}(s[i+l: i+2l-1])\)。

题解

\(F(i,j)\) 表示 \(s[i:i+2j-1]\) 是否符合条件。

则有：

\(F(i,j)=\begin{cases}0 & s_i > s_{i+2j-1} \,\cup\, j = 0 \\1 & s_i < s_{i+2j-1} \\F(i+1, j-1) & s_i = s_{i+2j-1}\end{cases}\)

扫描线算 \(F\)，对于当前 \(i\)，将 \(F(i,x)\) 看做关于 \(x\) 的函数，使用 bitset 维护这个函数。

每次往前扫的时候先将 \(F\) 左移一位，之后将 \(s_i>s_{i+2j-1}\) 的位置设为 \(0\)，将将 \(s_i<s_{i+2j-1}\) 的位置设为 \(1\)。

额外维护两只 bitset \(a_{c},b_{c}\) 分别表示当前 \(s_i>s_{i+2j-1}\) 和 \(s_i<s_{i+2j-1}\) 的位置。

需要分奇偶维护。

询问就是查 \(F(i)\) 大小为 \(r\) 的前缀中 \(1\) 的个数。

卡常，要手写 bitset。

提交记录

只有一题，因为这题太恶心了做了一下午加一晚上 QAQ。

P10016 [集训队互测 2023] 虹 黑

评价：追忆 plus，炫酷卡常题。

\(19901991^2\equiv 1 \pmod {20242024}\)，所以只需要考虑指数的奇偶性即可，那么考虑 bitset。

将 \(w\) 和 \(z\) 对 \(2\) 取余，维护 bitset \(W\) 和 \(Z\)，查询 \((l,r,u)\) 时，假设 \(W=(w_1,w_2,\dots w_n)\)，\(Z=(z_{\gcd(u,1)},z_{\gcd(u,2)},\dots z_{\gcd(u,n)})\)，设 \(C\) 为 \(W\operatorname{AND} Z\) 中 \([l,r]\) 间 \(1\) 的个数，则答案为 \(19901991\times C+1\times (r-l+1-C)\)。

如何算 \(W\)

维护 \(W_i\) 表示在第 \(i\) 次操作后 \(w\) 的 bitset，由于我们只关心奇偶性，因此一开始令 \(W_i\) 为这次操作修改的位置集合，最后做一遍前缀异或和即可。

考虑分块求每次修改的位置集合。

首先 \([l,r]\) 的最小虹就是每个点到根的路径并集除去 \([l,r]\) 中所有点 \(\operatorname{lca}\) 的父亲到根的路径，先不管所有点 \(\operatorname{lca}\) 的父亲到根的路径，考虑如何求 \([l,r]\) 到根的路径并。

由于数据随机，所以当 \(l,r\) 在同一块内时直接 \(O(n)\) 暴力即可。

否则拆成整块和散块，离线处理。

预处理 \(blk_i\) 表示第 \(i\) 块的最小虹集合，枚举每个点并往上跳，跳到已经访问过的节点就停止，代码大概长这样：

for(int i=1;i<=n;i++){
	int u=i;
	while(u){
		if(blk[id[i]].test(u)) break;
		blk[id[i]].set(u);
		u=f[u][0];
	}
}

离线后散块同样暴力处理，第一次遇到分块上这种离线查询，贴个代码：

vector<int> qryblk[305][305],qrypre[80005],qrysuf[80005],qryup[80005];
void dfsW(int u,int fa){//这里下面讲
	for(int x:qryup[u]) W[x]^=w;
	for(int v:V[u]){
		if(v==fa) continue;
		w.set(v,1);
		dfsW(v,u);
		w.set(v,0);
	}
}
void initW(){
	for(int i=1;i<=tot;i++){
		w.reset();
		for(int j=i;j<=tot;j++){
			w|=blk[j];
			for(int x:qryblk[i][j]) W[x]|=w;
		}
	}
	for(int i=1;i<=tot;i++){
		w.reset();
		for(int j=L[i];j<=R[i];j++){
			int u=j;
			while(u){
				if(w.test(u)) break;
				w.set(u);
				u=f[u][0];
			}
			for(int x:qrypre[j]) W[x]|=w;
		}
	}
	for(int i=1;i<=tot;i++){
		w.reset();
		for(int j=R[i];j>=L[i];j--){
			int u=j;
			while(u){
				if(w.test(u)) break;
				w.set(u);
				u=f[u][0];
			}
			for(int x:qrysuf[j]) W[x]|=w;
		}
	}
	w.reset();
	w.set(1,1);
	dfsW(1,0);//这里下面讲
	w.set(1,0);
}

然后考虑 \([l,r]\) 中所有点 \(\operatorname{lca}\) 的父亲到根的路径怎么去掉，设所有点 \(\operatorname{lca}\) 的父亲到根的路径的点集合 \(X\)，则让对应的 \(W\) 异或上 \(X\) 即可。

首先要求出 \([l,r]\) 中所有点的 \(\operatorname{lca}\)，这个可以计算相邻 \(\operatorname{lca}\) 后用 ST 表取深度最小的点来做。

然后把这个操作也离线下来，最后做一遍 dfs 即可（代码在上面）。

如何算 \(Z\)

给出一个十分暴力的代码：

int g[80005];
void brute(int now,int lst,int pw){
	for(auto x:qry[now]){
		int c=calc(x.l,x.r,x.t);//calc 表示处理当前询问。
		ans[x.t]=(1ll*c*19901991+x.r-x.l+1-c+20242024)%20242024;
	}
	for(int i=lst;i<=cnt;i++){
		if(1ll*now*pri[i]>n) break;
		int t=now*pri[i];
		int npw=pri[i];
		if(i==lst) npw*=pw;
		for(int j=npw;j<=n;j+=npw){
			g[j]*=pri[i];
			Z.set(j,z[g[j]]&1);
		}
		brute(t,i,npw);
		for(int j=npw;j<=n;j+=npw){
			g[j]/=pri[i];
			Z.set(j,z[g[j]]&1);
		}
	}
}

发现在 \(n=80000\) 时计算量大概在 \(4\times 10^7\) 左右。

大概就是暴搜一个数的质因子组成，实时维护 \(Z\)，每次增加一个质因子。假如将质因子 \(p^c\) 增加为 \(p^{c+1}\)，则所有是 \(p_{c+1}\) 倍数的数与当前数的 \(\gcd\) 都会乘上 \(p\)。

如何处理询问

求 \(Z\) 时处理询问，直接把两个 bitset 与起来求 \([l,r]\) 之间的 popcount 即可。这里使用了手写 bitset。

int calc(int l,int r,int t){//这里的小写 w 指上文中的 Z。
	int B=64;
	int idxl=l/B,idxr=r/B;
	int reml=l&(B-1),remr=r&(B-1);
	int res=0;
	if(idxl==idxr){
		res=__builtin_popcountll(W[t].bits[idxl]&w.bits[idxr]&(~0ull<<reml)&(~0ull>>(63-remr)));
		return res;
	}
	res+=__builtin_popcountll(W[t].bits[idxl]&w.bits[idxl]&(~0ull<<reml));
	for(int i=idxl+1;i<=idxr-1;i++){
		res+=__builtin_popcountll(W[t].bits[i]&w.bits[i]);
	}
	res+=__builtin_popcountll(W[t].bits[idxr]&w.bits[idxr]&(~0ull>>(63-remr)));
	return res;
}

闲话

洛谷评测机跑的很快，不做任何卡常即可通过，但本题在 qoj 和 vjudge 上极度卡常，需要用快速读入+手写 bitset。

在洛谷的提交记录

在 qoj 加上快读卡常的提交记录

P8861 线段 黑

题意

有一个初始为空的线段集，你需要处理 \(q\) 组询问，每组询问的格式为如下三种之一：

1. 加入一条新线段 \([l_i,r_i]\)。
2. 将线段集里所有与 \([l_i,r_i]\) 相交的线段修改为其与 \([l_i,r_i]\) 的交。
3. 求出线段集里所有与 \([l_i,r_i]\) 相交的线段与 \([l_i,r_i]\) 的交的长度和。

强制在线。

题解

首先假设没有操作 \(2\)。

那么可以使用树状数组处理。

具体地，维护四颗权值树状数组，分别表示 \(\sum [l=i],\sum i\times [l=i],\sum [r=i],\sum i\times [r=i]\)。

那么假设查询区间是 \([l,r]\)，我们需要求：

\[\sum_{[L,R]}\bigl|[L,R]\cap[l,r]\bigr|=\sum_{\text{交}}\bigl(\min(R,r)-\max(L,l)\bigr) \]

那么考虑求出 \(\sum min(R,r)\) 和 \(\sum -max(L,l)\)，再把不相交区间多算的部分减掉。

这部分代码：

void addl(int l,int v){
	bitl.add(l,v);
	bitlx.add(l,v*l);
}
void addr(int r,int v){
	bitr.add(r,v);
	bitrx.add(r,v*r);
}
int query(int l,int r){
	//min(R,r)-max(L,l)
	int res=0;
	//\sum min(R,r)
	res+=bitrx.sum(r)+r*(bitr.sum(n)-bitr.sum(r));
	//\sum -max(L,l)
	res-=bitlx.sum(n)-bitlx.sum(l)+l*bitl.sum(l);
	//左侧负贡献\sum_{R<l} R-l 
	res-=bitrx.sum(l-1)-l*bitr.sum(l-1);
	//右侧\sum_{L>r} r-L 
	res-=r*(bitl.sum(n)-bitl.sum(r))-(bitlx.sum(n)-bitlx.sum(r));
	return res;
}

然后发现 \(l\) 和 \(r\) 对答案贡献其实是独立的。

接下来考虑维护操作二。

subtask 5 启示我们使用猫树分治，把区间 \([l,r]\) 拍到满足 \(L\leq l\leq mid<r\leq R\) 的线段树节点上。

每个节点开一个小根堆和一个大根堆，分别维护左端点和右端点。

同时用数组记录每对左端点和右端点的匹配关系，这个修改要用。使用两个并查集分别缩掉左端点和右端点相同的节点，这样可以做到修改均摊。

加入是简单的。

修改 \([l,r]\) 时，按如下操作遍历：

• \([l,r]\) 与 \([L,R]\) 无交集，或 \([L,R]\in [l,r]\)，直接返回。

• \(L\leq l\leq mid<r\leq R\)。

  • 左右端点分别对 \(l,r\) 取 \(\max,\min\)，直接用堆暴力做，然后并查集缩点保证复杂度。

• \(r\leq mid\)。

  • 不断 pop 堆中元素直到 \(l'>r\)，找出 \(l'\leq r\) 的所有区间，暴力下放到左子树即可。

• \(l>mid\)，与 \(r\leq mid\) 同理。

堆中还要维护所对应并查集的根节点，即堆维护的是一个 pair。

放一个修改代码：

void ins(int p,int l,int r,int u,int x){
	if(bvld[u]){
		int v=mch[u];
		bvld[u]=bvld[v]=0;
		int L=min(x,val[fd(v)]),R=max(x,val[fd(v)]);
		sz[fd(u)]--,sz[fd(v)]--;
		int newl=max(L,l),newr=min(R,r);
		addl(L,-1);
		addr(R,-1);
		if(newl!=newr){
			addl(newl,1);
			addr(newr,1);
			insert(p,newl,newr);//insert是操作一插入区间的函数。
		}
	}
	for(int v:V[u]) ins(p,l,r,v,x);
}
void modify(int p,int l,int r){
	if(l<=t[p].l&&t[p].r<=r) return;
	int mid=(t[p].l+t[p].r)/2;
	if(r<=mid){
		while(!t[p].ql.empty()){
			auto x=t[p].ql.top();
			if(x.first>r) break;
			t[p].ql.pop();
			ins(p*2,l,r,x.second,x.first);
		}
		modify(p*2,l,r);
	}else if(l>mid){
		while(!t[p].qr.empty()){
			auto x=t[p].qr.top();
			if(x.first<l) break;
			t[p].qr.pop();
			ins(p*2+1,l,r,x.second,x.first);
		}
		modify(p*2+1,l,r);
	}else{
		int newrt=0;
		while(!t[p].ql.empty()){
			auto x=t[p].ql.top();
			if(x.first>=l) break;
			t[p].ql.pop();
			addl(x.first,-sz[x.second]);
			newrt=merge(newrt,x.second);
		}
		if(newrt){
			val[newrt]=l;
			addl(l,sz[newrt]);
			t[p].ql.push({l,newrt});
		}
		newrt=0;
		while(!t[p].qr.empty()){
			auto x=t[p].qr.top();
			if(x.first<=r) break;
			t[p].qr.pop();
			addr(x.first,-sz[x.second]);
			newrt=merge(newrt,x.second); 
		}
		if(newrt){
			val[newrt]=r;
			addr(r,sz[newrt]);
			t[p].qr.push({r,newrt});
		}
		modify(p*2,l,r);
		modify(p*2+1,l,r);
	}
}

查询调 query 就行了。

提交记录

P11236 [KTSC 2024 R1] 水果游戏 黑

题意

给定一个长度 \(n(n\leq 10^5)\) 的序列 A，每个数字代表水果等级。
一次合并操作可以把相邻且数值相同的两个水果合成更大的一个（数值 +1）。
在 \(q(q\leq 10^5)\) 次在线操作中，需要支持：

1. 区间查询 play_game(l,r)
   ─ 返回区间 A[l…r] 经过任意次合并后能得到的最大水果等级。
2. 单点修改 update_game(p,v)
   ─ 把位置 p 处的水果替换为等级 v (1…10)。

题解

考虑没有修改怎么做。

先缩连续段，表示成 \(\{(val_1,cnt_1),(val_2,cnt_2),\dots\}\)。

其中 \((val,cnt)\) 表示 \(val\) 连续出现 \(cnt\) 次。

考虑一个谷结构，即 \(val_1>val_2<val_3\)。

那么需要让 \(val_2\) 提升到 \(\min\{val_1,val_3\}\)，设 \(d=\min\{val_1,val_3\}-val_2\)，如果 \(cnt_2\) 不是 \(2^d\) 的倍数，说明中间一定有数字够不到 \(\min\{val_1,val_3\}\)，因此这个段会断开，分成两个子问题。

因为是相邻合并，考虑维护一个栈结构，末尾不断消除谷结构，直到不存在谷后将当前节点入栈。

为了保证节点数 \(O(V)\)，每次遇到段会断开的情况，就将 \((+\infin,1)\) 入栈，前面递减的部分就因为谷结构一次性被消除，最后序列里只剩下开头的递增部分和结尾的递减部分。

可以使用递归实现栈结构的维护。

void push_back(int val,int cnt){
	if(!cnt) return;
	while(tot>=2&&a[tot-1].val>a[tot].val&&a[tot].val<val){
		int v=a[tot].val,c=a[tot].cnt;
		tot--;
		if(a[tot].val==inf&&val==inf) continue;
		int d=min(val,a[tot].val)-v;
		push_back(v+d,c>>d);
		if(c&((1<<d)-1)){
			push_back(inf,1);
			push_back(v+d,c>>d);
		}
	}
	if(!tot) a[++tot]={val,cnt};
	else if(a[tot].val==val) a[tot].cnt+=cnt;
	else a[++tot]={val,cnt};
	if(a[tot].val<inf){
		res=max(res,a[tot].val+__lg(a[tot].cnt));
	}
}

然后发现加入元素的过程中，栈里面最多有一个单峰的东西，点个数 \(O(V)\)，因此直接丢到线段树上，查询时暴力合并即可。

//暴力合并
node operator+ (const node &b) const{
	node c;
	c.res=max(res,b.res);
	for(int i=1;i<=tot;i++){
		c.push_back(a[i].val,a[i].cnt);
	}
	for(int i=1;i<=b.tot;i++){
		c.push_back(b.a[i].val,b.a[i].cnt); 
	}
	return c;
}

查询时需要在两边加上 \((+\infin,1)\)，这样就可以消除完所有节点，保证答案更新彻底。

int play_game(int l,int r){
	tmp=newnode(inf)+query(1,l,r)+newnode(inf);
	return tmp.res;
}

提交记录

P6261 [ICPC 2019 WF] Traffic Blights 黑

题意

街道上有 \(n\) 个红绿灯，第 \(i\) 个灯距离街道最西端 \(x_i\) 米，以【持续 \(r_i\) 秒的红灯，再持续 \(g_i\) 秒的绿灯】作为一周期，不断重复。在时刻 \(0\)，所有的红绿灯都恰好刚变为红灯。

有一辆汽车在随机时刻出现在了街道最西端，向东以 \(1~ \rm m/s\) 龟速行驶，直到遇到第一个红灯时停下，求：

• 它有多大的概率通过所有红绿灯？
• 如果它停下来了，它在每个红绿灯处停下的概率有多大？

\(1\leq n\leq 500,1\leq r+g\leq 100,q\leq x\leq 10^5\)

题解

设 \(p_i\) 表示通过前 \(i\) 个灯的概率，则在第 \(i\) 个灯停下的概率为 \(p_{i-1}-p_{i}\)。

街道周期为 \(M=\operatorname{lcm}_{i=1}^{n} (r_i+g_i)\)，题目等价于求 \([0,M-1]\) 内随机一个整数，通过前 \(i\) 个灯的概率。

假设开始时间为 \(X\)，则能通过前 \(i\) 个灯，当且仅当：\(\forall_{1\leq j\leq i}(X+x_j)\bmod (r_j+g_j)\geq r_j\)。

特殊情况

考虑特殊情况，假设 \((r_i+g_i)\) 全部互质。

根据中国剩余定理，任何模数互质的同余方程组在周期内有唯一解，即：

给定任何剩余序列

\[a_1,\dots ,a_n,\qquad 0\le a_i<T_i, \]

总存在 唯一 的

\[X\in[0,M) \]

使得

\[(X+x_i)\equiv a_i\pmod{T_i}\qquad(\forall i). \]

也就是说 \((X+x_i)\bmod (r_i+g_i)\) 构成的序列与开始时间 \(X\) 一一对应，所以每项算概率可以独立算，通过前 \(i\) 个灯的概率为 \(\prod\limits_{j=1}^{i} \frac{g_j}{r_j+g_j}\)。

一般情况

取 \(V=2520\)，把开始时间 \(X\) 表示成 \(kV+b\)，那么枚举 \(b\)，设 \(k\) 是变量，根据经典结论，\(b\) 每次增加 \(V\)，模 \(r_i+g_i\) 的周期为 \(\frac{r_i+g_i}{\gcd(r_i+g_i,V)}\)。

发现 \(0\sim 100\) 中的每个数 \(v\)，都满足 \(\frac{v}{\gcd(v,V)}\) 是一个质数的若干次幂，则可以把周期底数相同的灯看做一个等价类，每个等价类中的灯周期向该类中最长周期对齐（其实就是直接按最长周期算）。

算的时候，不同周期之间是独立的，可以分别计算。

维护 \(stop_{i,j}\) 表示在 \(j\bmod i\) 时刻开始会不会被周期为 \(i\) 的灯拦下，然后枚举模周期的余数，用古典概型计算概率即可。

代码中的 now 可以类比特殊情况的 \(\prod\limits_{j=1}^{i} \frac{g_j}{r_j+g_j}\)（只是类比好理解，其实公式完全不同）。

void calc(int b){
	memset(stop,0,sizeof(stop));
	p[0]++;
	double now=1;
	for(int i=1;i<=n;i++){
		int d=m[i]/__gcd(V,m[i]);
		int M=mx(d);
		int cnt=0,tot=0;
		for(int j=0;j<M;j++){
			if(stop[M][j]) continue;
			if(pass[i][(j*V+b)%m[i]]){
				cnt++;
			}else{
				stop[M][j]=1;
			}
			tot++;
		}
		if(!tot) break;
		now=now*cnt/tot;
		p[i]+=now;
	}
}

提交记录

P12734 理解 蓝

题意

有 \(n\) 个历史事件，每个事件可能依赖一个编号更小的前置事件（\(p_i<i\)，若 \(p_i=0\) 则无前置）。现在有 \(m\) 个题目，每个题目要求你记起特定的事件。

你可以通过：

• 回想（直接记起事件 \(u\)，耗时 \(r_u\)）；
• 联想（从已记起的事件 \(p_v\) 联想到其后继 \(v\)，耗时 \(t_v\)）来记起事件。
• 忘记（忘掉一个事件）。

记忆容量限制为最多同时记起 \(k\) 个事件。事件一旦忘记，就不能再重新记起。

求记起 \(m\) 个事件的最小时间（不要求同时记起来，只要求 \(m\) 个事件都被记起过即可）。

\(n\leq 10^5,k\leq 10\)。

题解

回想节点 \(i\) 并向下联想，联想出来的点是一个连通快，删去连通块后原问题划分为若干个子问题，因此考虑树形 DP。

状态

令 \(f_{i,j}\) 表示 \(i\) 为根的子树，可以向下联想最多 \(j-1\) 个事件，不考虑 \(i\) 的贡献，解决子树内所有题目的最小时间。

特别的，\(f_{i,0}\) 表示不回想 \(i\)，\(f_{i,1}\) 表示回想了 \(i\)，但不往下联想。

答案

将 \(0\) 号点连向所有的根，令 \(r_0=+\infin\)，最终答案为 \(f_{0,0}\)。

初值

初始时对于叶子节点 \(u\)，\(f_{u,x}=0\ (x\geq 1)\)。若 \(u\) 是一道题目要求的事件，则 \(f_{u,0}=+\infin\)，否则 \(f_{u,0}=0\)。

转移

先考虑特殊的 \(f_{u,0}\)，若 \(u\) 是一道题目要求的事件，则 \(f_{u,0}=+\infin\)，否则 \(f_{u,0}=\sum\limits_{v\in u} \min\{f_{v,0},f_{v,k}+r_v\}\)，表示对下面的点是否被回想进行决策。

考虑特殊的 \(f_{u,1}\)，和 \(f_{u,0}\) 一样都不能对下面节点造成影响，唯一区别是不用考虑若 \(u\) 是否是题目要求的事件，\(f_{u,1}=\sum\limits_{v\in u} \min\{f_{v,0},f_{v,k}+r_v\}\)。

考虑 \(f_{u,x}\ (x\geq 2)\)，转移大概是选一个儿子 \(v0\)，先解决其他儿子后再联想 \(v0\)，并忘掉父亲。

令

\[a_{v,x}\;=\;\min\!\Bigl(\,\min\!\bigl(f_{v,0},\;f_{v,k}+r_v\bigr),\;f_{v,x-1}+t_v\Bigr), \qquad b_{v,x}\;=\;f_{v,x}+t_v. \]

\(a_{v,x}\) 表示不忘父亲继续往下联想，\(b_{v,x}\) 表示忘掉父亲。

则有：

\[\boxed{ f_{u,x}\;=\; \sum_{v\in V_u} a_{v,x}\;+\; \min\!\Bigl(0,\;\min_{v\in V_u} (b_{v,x}-a_{v,x})\Bigr) }. \]

提交记录

P12607 三叉求和 紫

题意

有一棵深度无穷大的以 \(0\) 为根的三叉树，节点 \(i\) 的儿子分别是节点 \(3i+1,3i+2,3i+3\)。

设节点 \(i\) 的点权为 \(a_i\)。对于 \(0\le j\le 2\)，有 \(a_{3i+j+1}=3\times a_i+j\)，特别的，\(a_0=0\)。

你的任务是求从根出发，找长度 \(=d\) 的简单路径，并使得该路径经过的所有点的点权和为 \(k\)。你需要求出所有合法路径的条数。

然而 \(k\) 并不唯一，\(k\) 的三进制表示中仅有某些位是已知的，而其它的位将以字符 \(\tt ?\) 表示。你需要对所有可能的 \(k\) 在上述问题中的答案求和，最后再对 \(10^9+7\) 取模。

题解

设序列 \(\{b\}\)，\(b_i\in \{0,1,2\}\)，表示第 \(i\) 次向那个方向走。

重新定义题目中的序列 \(\{a\}\)，\(a_i\) 表示走完第 \(i\) 步到达的节点点权。

则 \(a_i=\sum\limits_{j=1}^{i} b_j\times 3^{i-j}\)。

题目要求 \(\sum\limits_{i=1}^{d} a_i=k\)，即 \(\sum\limits_{i=1}^{d} \sum\limits_{j=1}^{i} b_j\times 3^{i-j}=k\)。

\(b_i\) 的系数是 \(3\) 的若干次方，这个式子看着就很数位 DP，把 \(b_i\) 的贡献按照系数分类。

\[\sum\limits_{i=1}^{d} \sum\limits_{j=1}^{i} b_j\times 3^{i-j} \\ =\sum_{x=0}^{d} \sum_{i=1}^{d} \sum_{j=1}^i\ [i-j=x]\times 3^x\times b_j \\ 发现此时 i 没有用处，只用限制 1\leq i=j+x\leq d 即可。 \\ 原式=\sum_{x=0}^{d} \sum_{j=1}^{d-x} 3^x\times b_{j} \\ =\sum_{x=0}^{d} 3^x\times \sum_{j=1}^{d-x} b_{j} \\ 记 s_i=\sum_{j=1}^{d-i} b_j \\ 原式=\sum_{x=0}^{d} 3^x\times s_x \]

那么对 \(s\) 进行三进制数位 DP，由于 \(s_d=0\)，故从高位开始，\(f_{pos,lst,up}\) 表示高 \(pos-1\) 位已确定，\(s_{pos-1}=j\)，这一位需要向上进位 \(up\)，剩余未确定位置的方案数。

答案和初值是显然的。

转移为 \(f_{pos,lst,up}=\sum\limits_{x=0}^2 f_{pos+1,lst+x,3\times up+now-(lst+x)}\)。

其中，\(now\) 表示 \(k\) 这一位的数字，当 \(k\) 这一位为 ? 时，枚举 \(now=0,1,2\) 即可。

我们得到了 \(O(n^3)\) 做法，但是题目要求 \(O(n^2)\)。

我们充分发扬人类智慧，使用递推实现转移，然后猜测 \(f_{pos,lst,*}\) 只有 \(O(1)\) 个接近的非 \(0\) 位置，维护 \(l_{pos,lst},r_{pos,lst}\) 表示非 \(0\) 区间的左右端点，只转移非 \(0\) 位置即可。

本地测试极限数据（全为 ?）大概 0.6 秒，复杂度 \(O(能过)\)

提交记录

P3195 [HNOI2008] 玩具装箱 紫

发现以前学斜率优化没写这题，刚好复习一下。

题意

标准序列划分问题，区间 \([i,j]\) 的贡献为 \(\big(j-i+(\sum\limits_{k=i}^{j} C_k)-L\big)^2\)。

题解

令 \(S_i=i+\sum\limits_{j=1}^i C_j\)，\(f_i\) 表示前 \(i\) 项以 \(i\) 结尾的答案，\(L'=L+1\)。

易得：

\[f_i=\min\limits_{j=0}^{i-1} \{f_j-2 S_i S_j+S_j^2+2S_jL'\}+S_i^2-2 S_i L'+L'^2。 \]

令 \(X(i)=S_i,Y(i)=S_i^2+2 S_i L'+f_i,K(i)=2\times S_i,B(i)=f_i,C(i)=S_i^2-2 S_i L'+L'^2\)，则有：

\[f_i=\min\limits_{j=0}^{i-1} \{Y(j)-K(i)\times X(j)\}+C(i) \]

斜率优化即可。

P2305 [NOI2014] 购票 黑

题意

给你一棵树，每个点有三个系数 \(l,p,q\) 表示你能选择一个点 \(v\)，满足 \(v\) 是当前点的 \(d(d\leq l)\) 级祖先，花费 \(d\times p+q\) 元到达 \(v\)。

求每个点到 \(1\) 的最短路，\(n\leq 10^5\)。

题解

令 \(fa^k_i\) 表示 \(i\) 的 \(k\) 级祖先，\(g_i\) 表示 \(i\) 到根的最短路，则有：

\[g_i=\min_{d=1}^{l_i} \{g_{fa^k_i}+d\times p_i+q_i\} \]

然后考虑链的部分分，把 \(d\) 拆成到根距离相减的形式，然后斜率优化即可。

最后考虑树，使用点分治优化，处理子树 \(u\) 时，为了保证转移顺序正确：

1. 找到重心 \(rt\) 后，先递归处理包含 \(u\) 的子树
2. 然后处理 \(rt\) 到 \(u\) 的链这一段对不包含 \(u\) 的子树的转移
3. 最后递归处理不包含 \(u\) 的子树。

特别的，把 \(rt\) 视为包含 \(u\) 的子树中的一个节点。

先推斜率优化式子，\(dis_i\) 表示 \(i\) 到根的距离。

\[g_i=\min_{j} \{g_j+d\times p_i+q_i\} \\ g_i=\min_{j} \{g_j-dis_j\times p_i\}+dis_i\times p_i+q_i \]

然后就可以维护一个斜率优化队列了。

处理第二步的时候往下把这个子树所有点搜出来，按能到达的最小深度 \(dis_i-l_i\) 降序排序，之后类似扫描线，扫到 \(i\) 时，让 \(rt\) 不断往父亲跳，记挑到的点是 \(now\)，满足 \(dis_i-l_i\leq dis_{now}\)，然后把 \(now\) 丢到队列里即可。

点分治内有排序，时间复杂度 \(O(n\log^2 n)\)。

提交记录

P3381 【模板】最小费用最大流 模版

学习费用流。

提交记录

P2756 飞行员配对方案问题 绿

板刷网络流与线性规划 24 题。

二分图匹配模版。

提交记录

P4016 负载平衡问题 蓝

板刷网络流与线性规划 24 题。

增加原点 \(s\)，汇点 \(t\)，把原运输图每条边连上流量为 \(+\infin\)、价格为 \(1\) 的边，原点向大于平均值的点连流量为【与平均值的差】、价格 \(0\) 的边，汇点向小于平均值的点连流量为【与平均值的差】、价格 \(0\) 的边。

然后跑最小费用最大流即可。

提交记录

P4014 分配问题 蓝

建出二分图匹配模型，跑最（小/大）费用最大流即可。

提交记录

P4015 运输问题 蓝

与上题相同

提交记录

网络流题单前面的题都比较简单，直接贴题号了

P3254 提交记录

P3355 提交记录

P2763 提交记录

P2765 魔术球问题 蓝

对于相加是平方数的数对，小数向大数连边，构成一个 DAG。

每次加入一个球，求 DAG 的最小路径覆盖是否 \(\leq n\) 即可。

将原图每个顶点拆分为出点 \(pi'\) 和入点 \(pi''\)，原图的边 \(pi\to pj\) 转化为二分图中 \(pi'\) 与 \(pj''\) 的边‌。

则有：最小路径覆盖数 = 原图顶点数 - 二分图最大匹配数‌。

提交记录

P1251 餐巾计划问题 紫

标准网络流建模。

建模方法：

//源汇点，商店
shop=2*N+1,S=2*N+2,T=2*N+3;
mcmf.add(S,shop,inf,0);
//回收点 1~N
for(int i=1;i<=N;i++) mcmf.add(S,i,r[i],0);
//提供点&传送链 N+1~2N
mcmf.add(shop,N+1,inf,p); 
for(int i=2;i<=N;i++) mcmf.add(N+i-1,N+i,inf,0);
for(int i=1;i<=N;i++){
	if(i+m<=N) mcmf.add(i,N+i+m,inf,f);
	if(i+n<=N) mcmf.add(i,N+i+n,inf,s);
}
for(int i=1;i<=N;i++) mcmf.add(N+i,T,r[i],0);

提交记录

CF2046D For the Emperor! *3100

题意

给定一个 有向图，包含 \(n\) 个点和 \(m\) 条边。第 \(i\) 个点上有 \(a_i\) 个人。

你可以选择一些结点发放一份计划，接下来每个人可以沿着边自由移动，如果一个人从一个收到过计划的点移动到一个没有收到计划的点，那么可以令其收到计划。

你需要让所有的点都收到计划，求最少需要在多少个结点发放计划，或者报告无解。

\(a_i\leq n\leq 200,m\leq 800\)。

题解

先缩点变成 DAG，问题与原问题等价。

构造费用流模型：令 \(B\to +\infin\)，经过所有点很难用最大流刻画，因此我们的思路是：保证最大流总是能取到的情况下，经过一个点的费用是 \(-B\)，发放一个计划的代价是 \(1\)。这样求出最小费用后再模 \(B\) 就是我们想要的费用。

套路的将 DAG 拆点，先把图中的边连 \(u\to v\) 上，出点 \(P_u\) 连入点 \(Q_v\)，点 \(u\) 被经过可以刻画为经过边 \(P_u\to Q_u\)。

然后我们设保证能取到的最大流为 \(\sum a_i\)，我们建立约束点 \(F_u\)，建边 \(s\to_{(a_u,0)} F_u\)，建边 \(Q_u\to_{(+\infin,0)} T\)。

为了保证只有一个点第一次经过才被计费，这样建边：\(P_u\to Q_u\) 连两条边，一条 \((1,1)\)，一条 \((+\infin,0)\)。

然后让 \(F_u\) 提供一个人给 \(P_u\) 来复制计划，剩余全给 \(Q_u\)。即 \(F_u\to_{(1,1)} P_u\)，\(f_u\to_{+\infin,0} Q_u\)。

跑最小费用最大流，完结散花 QwQ。

提交记录

AT_abc397_g [ABC397G] Maximize Distance 紫

题意

给定一个包含 \(N\) 个顶点和 \(M\) 条边的有向图。顶点编号为 \(1,2,\dots,N\)，其中第 \(j\) 条边（\(j=1,2,\dots,M\)）从顶点 \(u_j\) 指向顶点 \(v_j\)。保证从顶点 \(1\) 到顶点 \(N\) 是可达的。

初始时，所有边的权重均为 \(0\)。当从 \(M\) 条边中恰好选择 \(K\) 条边并将其权重改为 \(1\) 时，求修改后的图中顶点 \(1\) 到顶点 \(N\) 的最短距离的最大可能值。

\(N\leq 30\)，\(K\leq M\leq 100\)。

题解

二分答案，求令最短路 \(=d\) 时最少改几条边。

当 \(d=1\) 时是最小割问题。

当 \(d\neq 1\) 时，令 \(dis_i\) 表示 \(1\) 到 \(i\) 的距离，相当与给每个 \(dis_i\) 赋值，满足三角不等式，且如果存在边 \(u\to v\)，满足 \(dis_v=dis_u+1\)，需要支付 \(1\) 费用。

拆点，每个 \(dis_u\) 拆成 \(b_{u,1}\sim b_{u,d}\)，\(b_{u,x}=[dis_{u} \leq x]\)。

则有限制：

• 如果 \(b_{i,j}=0\)，则 \(b_{i,j+1}\neq 1\)。
• 对于边 \(u\to v\)，如果这条边有贡献，当且仅当 \(b_{u,j}=0,b_{u,j-1}=1,b_{v,j}=1\)。
• \(b_{1,0}=1,b_{n,d-1}=0\)。

因此按照如下方式连边跑最小割：

• \(b_{i,j}\to_{+\infin} b_{i,j+1}\)。
• \(b_{u,j}\to_{1} b_{v,j}\)，\(b_{u,j}\to_{+\infin} b_{u,j+1}\)。
• \(S\to_{0} b_{1,0},T\to_{0} b_{n,d-1}\)。

实现时直接令 \(S=b_{1,0},T=b_{n,d-1}\) 即可。

提交记录

Express Eviction *????

题意

在 \(N\times M\) 的网格中，有若干障碍，每个障碍在四个格点组成的方格中，一个障碍可以 ban 掉周围四个

格点，你要在格点上行走，从 \((0,0)\) 走到 \((N,M)\)，最少移除多少障碍？

题解

考虑最小点割，如果两个障碍的 \(x,y\) 坐标都相差不超过 \(2\)，那么两个障碍会把之间的格点 ban 掉，所以新建左下和右上各 \(N+M\) 个虚点，把相差不超过 \(2\) 的障碍连边，相当于最少移除几个障碍使得左下到不了右上，因此跑最小点割即可。

最小点割的做法为将一个点拆为入点 \(in(i)\) 和出点 \(out(i)\)，连接 \(in(i)\to out(i)\) 流量为删掉这个点的代价（对于本题，虚点为 \(+\infin\)，图上障碍为 \(1\)）。对于图上边 \((u,v)\)，连接 \(out(u)\to in(v)\)，流量为 \(+\infin\)。

提交记录

[ARC142E] Pairing Wizards 黑

题意

有 \(n\) 个巫师，第 \(i\) 个巫师有 \(a_i\) 的法力并计划打败 \(b_i\) 法力的怪兽。

构造 \(\{A_n\}\)，使得对于给定的 \(m\) 组 \((x, y)\)，均有 \(A_x \geq b_x, A_y \geq b_y\) 或 \(A_y \geq b_x, A_x \geq b_y\)。

请最小化 \(\sum\limits_{i=1}^n |A_i - a_i|\)。

题解

先对于所有 \((x,y)\)，把 \(a_x,a_y\) 向 \(\min\{b_x,b_y\}\) chkmin，然后限制转化为 \(a_x\geq \max\{b_x,b_y\} \lor a_y\geq \max\{b_x,b_y\}\)，下文中的 \(a_i\) 指 chkmin 完的 \(a_i\)。

考虑最小割。

把第 \(i\) 点拆为 \(V-a_i+1\) 个点：\(c_{i,0},c_{i,1},\dots,c_{i,V-a_i}\)。其中 \(c_{i,j}\) 向 \(c_{i,j-1}\) 连流量为 \(+\infin\) 的边，\(c_{i,j}(j>0)\) 向 \(T\) 连接流量为 \(1\) 的边。

让 \(a_i\) 增加 \(k\)，可以刻画为强制让 \(c_{i,k}\) 无法到达 \(T\)，这样需要割掉 \(c_{i,1\sim k}\) 向 \(T\) 的连边。

考虑限制 \(a_x\geq z\lor a_y\geq z\)，可以让 \(S\) 向 \(c_{y,z-a_y}\) 连接 \(z-a_x\) 的边，则要么割掉 \(z-a_x\) 边，表示将 \(a_x\) 上调至 \(z\)，要么割 \(c_{y,1\sim z-a_y}\) 的所有边，表示将 \(a_y\) 上调至 \(z\)。

但是这样会有问题，对于限制 \((x,y_1)\)，\((x,y_2)\)，\(S\) 会向外连接两条调整 \(a_x\) 的边，它们如果都被割掉，就算重了。

那么考虑固定一条边的边权。

具体地，假设 \(b_x\leq b_y\)，连接 \(S\to c_{y,0}\)，边权为 \(b_y-a_y\)，连接 \(c_{y,0}\to c_{x,b_y-a_x}\)，边权为 \(+\infin\)。

这种效果和上面建模的效果相同，但是注意到 \(S\to c_{y,0}\) 的边权只有 \(1\) 种，所以可以通过只保留若干 \(S\to c_{y,0}\) 边中的一条边，来实现去重。

建完图跑最小可就行了。

提交记录

CF1427G One Billion Shades of Grey *3300

题意

给定一个 \(n \times n\) 的棋盘，其边界上所有位置均填好了数字，你需要在剩余 \((n-2) \times (n-2)\) 个位置上填数，部分位置已经“破损”，在输入时用 \(-1\) 描述，此处无法填数。

对于一种填数方案，定义一对相邻（四连通）的均不为“破损”的格子的贡献为其填入的数字的差值的绝对值，定义此填数方案的权值为各个相邻的格子的贡献之和。

你需要最小化权值，输出可以得到的最小权值。

\(3\leq n\leq 200\)。

题解

如果边上的点都是 \(1,2\)，可以连边跑最小割。

一般情况下，\(v_r-v_l=(v_r-v_{r-1})+(v_{r-1}-v_{r-2})+\cdots +(v_{l+1}-v_l)\)。

然后枚举 \(v_i\)，把 \(\leq v_i\) 的连向 \(S\)，把 \(>v_i\) 的连向 \(T\)，求得最大流 \(f\)，对答案产生的贡献为 \(f\times (v_{i+1}-v_i)\)。

相当于每次删一条边，在加一条边，求最大流。使用退流技巧即可。

提交记录

Knights of Night *????

题意

给定一张二分完全图去掉 \(m\) 条边，剩下的边满足 \(u, v\) 之间的边权为 \((a_u + a_v) \bmod 998244353\)。

对于 \(1 \leq i \leq k\) 的所有 \(i\)，求匹配 \(i\) 条边的最大权重。

题解

核心思想：保留 \(O(\operatorname{poly}(k))\) 条边进行匹配。

首先对于每个左部点，只有边权前 \(k\) 大的右部点是有用的，因此可以筛选出 \(nk\) 条边。

对于每个右部点，只有边权前 𝑘 大的左部点是有用的，因此在上一步筛选的 \(nk\) 条边中再筛一遍。

之后考虑每次匹配一条边，会占用两个点，每个点可能有 \(k\) 条出边。因此匹配一条边会废掉两点的其他至多 \(2k\) 条出边，\(k\) 次匹配最多废掉 \(2k^2\) 条出边。因此在之前筛选的基础上保留前 \(2k^2\) 条边进行匹配即可。

匹配方法就是跑最大费用最大流，每次流 \(1\)，重复 \(k\) 次。

提交记录

[AGC031E] Snuke the Phantom Thief *3514

题意

在二维平面上，有 \(n\) 颗珠宝，第 \(i\) 颗珠宝在 \((x_i,y_i)\) 的位置，价值为 \(v_i\)。

现在有一个盗贼想要偷这些珠宝。

现在给出 \(m\) 个限制约束偷的珠宝，约束有以下四种：

• 横坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
• 横坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
• 纵坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
• 纵坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。

现在问你在满足这些约束的条件下，盗贼偷的珠宝的最大价值和是多少。

题解

通过数据范围看出这是一道网络流题目。把一个点拆成表示横纵坐标的两点，发现原问题类似于带限制的二分图最大权匹配，因此考虑费用流建模。

使用偷的珠宝的总个数 \(k\) 作为最大流，枚举 \(k\)。

把一个点拆成表示横纵坐标的两点，先按横坐标排序，限制【横坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗】可以转化为偷的第 \(b_i+1\) 至 \(k\) 颗横坐标都大于 \(a_i\)，限制【横坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗】可以转化为偷的第 \(1\) 至 \(k-b_i\) 颗横坐标都小于 \(a_i\)。

再按纵坐标排序，限制【纵坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗】可以转化为偷的第 \(b_i+1\) 至 \(k\) 颗纵坐标都大于 \(a_i\)，限制【纵坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗】可以转化为偷的第 \(1\) 至 \(k-b_i\) 颗纵坐标都小于 \(a_i\)（其实这一段和上一段同理）。

这样我们知道了横/纵坐标排名为 \(i\) 的珠宝的横/纵坐标范围，进而知道了横/纵坐标排名为 \(i\) 的珠宝可以是哪些。

因此我们建立两个二分图：

1. 左部点为横坐标排名，右部点为珠宝拆点后表示横坐标的点。
2. 左部点为纵坐标排名，右部点为珠宝拆点后表示纵坐标的点。

对于每个二分图内部，左右部点之间的边按上面的规则连流量 \(1\) 费用 \(0\) 的边。

由于两个二分图右部点是同一个珠宝拆点形成，因此两个二分图右部点之间表示相同珠宝的点还需要连接流量 \(1\) 费用 \(v\) 的边（\(v\)​ 是这个珠宝的价值）。

然后第一个二分图左部点全连向 \(S\)，第二个二分图左部点全连向 \(T\)，跑最大费用最大流即可。

为了确保流的方向正确，需要将第二个二分图内部的边反向（即右部点连向左部点）。

提交记录

Gym-102201J Jealous Teachers *????

题意

给定一张二分图，左边有 \((n - 1)\) 个点 \(P_i\)，右边有 \(n\) 个点 \(Q_i\)，按照以下规则连边。其中第三类边会在题目中给出，问最大流能否达到 \(n(n - 1)\)。同时需要给出中间流量的方案。满足 \(n \leq 10^5\), \(m \leq 2 \times 10^5\)。

边的连接规则如下：

• 从源点 \(S\) 到左边的每个点 \(P_i\) 有一条容量为 \(n\) 的边：\((S, P_i, n)\)。
• 从右边的每个点 \(Q_i\) 到汇点 \(T\) 有一条容量为 \(n - 1\) 的边：\((Q_i, T, n - 1)\)。
• 在某些给定的左边点 \(P_i\) 和右边点 \(Q_j\) 之间有一条容量为无穷大的边：\((P_i, Q_j, \infty)\)。

题解

引理1：若有解，则二分图存在大小为 \((n-1)\) 的匹配。

证明：首先 \(S\to P_i\) 的边要全部流满才能有解，若不存在大小为 \((n-1)\) 的匹配，则根据 Hall 定理，左侧存在一个点集 \(A\) ，记其能到达的点集为 \(B\)，满足 \(|A|>|B|\)，则有 \(|A|n>|B|(n-1)\)，\(A\) 流不满，因此无解。

因此我们先找到一个匹配，然后流 \((n-1)(n-1)\) 的流量，最后使用右侧未匹配的一个点进行增广，如果能找到若干条增广路经过左侧所有点，就有解了。

做法证明：有解相当于任意删右边一个点，都有完美匹配。考虑由“删掉i”变换为“删掉j”的过程，相当于找到一条 \(i\to j\) 的增广路，所以任意找一组匹配，如果能从失配点找到增广树，到达所有点，则一定有解。

提交记录

额感觉没有完全理解增广路，Mark 一下回头重写一遍。

（另一个人的做题记录，感觉证明更严谨 qaq）

以下认为老师构成左部点，学生构成右部点，即左部点有 \(n\) 个而右部点只有 \(n-1\) 个。

求完美匹配所以考虑先拆下点用 Hall 定理判定合法性。

即有对于任意左部点集合 \(S\)，有 \((n-1)\lvert S\rvert\leq n\lvert N(S)\rvert\)，变下形即 \(\frac{n-1}{n}\leq\frac{\lvert{N(S)}\rvert}{\lvert S\rvert}\)。

显然当 \(|S|<n\) 时这个东西等价于 \(\lvert S\rvert\leq\lvert N(S)\rvert\)，这说明我们任意删除一个左部点均满足剩下的 \(2(n-1)\) 个点存在完美匹配，显然我把每个左部点删一次跑一个二分图匹配，然后把这 \(n\) 组二分图匹配拼起来就是答案。

直接做的复杂度是 \(O(nm\sqrt n)\) 的，但是考虑这其中任意两组二分图匹配的差异都不算很大，具体来说，先把 \(n\) 点删了跑一次二分图匹配，然后将当前状态改为将 \(i\) 点删了的二分图匹配只需要寻找一条在残量网络上 \(n\to i\) 的路径翻转流量即可。所以只需要在残量网络上找一个以 \(n\) 为根的生成树就行了，时间复杂度瓶颈在于第一遍 dinic，为 \(O(m\sqrt n)\) ，可过。

P2764 最小路径覆盖问题 紫

题意

求 DAG 最小路径覆盖。

题解

拆入点和出点，做二分图最大匹配。先将原图视为 \(n\) 个点，每个匹配相当于合并边的左右端点，使用并查集构造答案。

提交记录

CF1721F Matching Reduction *2800

题意

给定一个二分图，其中左边有 \(n_1\) 个点，右边有 \(n_2\) 个点，共 \(m\) 条边，编号为 \(1 \sim m\)。你需要在线地进行如下 \(q\) 个操作：

• 操作 1：删去最少数量的点，使得二分图的最大匹配减少恰好 1，并在删除之后，输出当前最大匹配中所有边的编号之和。
• 操作 2：输出当前在最大匹配中的所有边的编号。

第二种询问只有 \(O(1)\) 次。

题解

引理 1：每次删去仅一个点就可以让最大匹配减少 \(1\)。

引理 1 证明：显然删掉一个点会使最大匹配最多减少 \(1\)，设二分图最大独立集为 \(I\)，最大匹配边集为 \(M\)，所有点构成的集合为 \(V\)，则根据结论 \(|M|=|V|-|I|\)，每次删去一个不在独立集里的点，\(|V|\) 减少 \(1\)，\(|I|\) 不变，因此\(|M|\) 减少 \(1\)。因此可以每次删去一个不在独立集里的点，让最大匹配减少 \(1\)。

因此我们先求出最大匹配，通过最大匹配构造最大独立集，此时不在最大独立集里的点一定被匹配，每次删掉一个不在最大独立集里的点，并删除其匹配边即可。

二分图最大独立集构造方法：先求最大匹配，然后从左侧未匹配点按增广路 bfs 整张图，最大独立集就是左侧未匹配点 + 右侧未被访问的点。（todo）证明这个构造方法的正确性。

提交记录

QOJ # 7185 Poor Students

题意

共有 \(k\) 门课程和 \(n\) 名学生，每名学生需要选择恰好一门课程并通过该课程的考试。如果学生 \(i\) 选择了考试 \(j\)，则该学生的挫败感为 \(c_{i,j}\)。对于每门考试 \(j\)，选择该考试的学生人数不得超过 \(a_j\)。求学生们可能达到的最小总挫败感。

题解

标准费用流模型，但是数据范围太大了流不动。

考虑费用流选择增广路的流程，\(S\to stu_0\to cls_1\to stu_1\to cls_2\to stu_2\to \cdots \to stu_{u-1}\to cls_u\to T\)。

找到增广路后，将原来的匹配方案改成 \(stu_0\to cls_1,stu_1\to cls_2, \dots ,stu_{u-1}\to cls_u\)。

对于每对课程 \((j,k)\)，如果有一个学生 \(i\) 在进行增广时由 \(j\) 换课为 \(k\)，则产生 \(c_{i,k}-c_{i,j}\) 的贡献。

因此我们每新加入一个学生 \(i\) 时，建立一个课程间的图，课程 \(j\) 和课程 \(k\) 之间用堆维护一个边集，表示目前选 \(j\) 的所有学生（记为 \(t\)）的 \(c_{t,k}-c_{t,j}\) 值，实时维护课程被多少学生选择了，类似匈牙利二分图匹配进行增广，每次增广选择最短路。

每次增广使用 SPFA，复杂度 \(O(nVE+nk^2\log n)=O(nk^3+nk^2\log n)\)。

提交记录

P1361 小M的作物 紫

题意

有两片土地，分别是 A 和 B，有 \(n\) 种作物，每种作物有一个种子。将第 \(i\) 种作物种在 A 上，可以获得 \(x_i\) 的收益。将第 \(i\) 种作物种在 B 上，可以获得 \(y_i\) 的收益。
存在一些作物组合（共 \(Q\) 组），对于第 \(i\) 组组合：

• 如果该组合中的所有作物都种在 A 上，可以获得额外 \(p_i\) 的收益。
• 如果该组合中的所有作物都种在 B 上，可以获得额外 \(q_i\) 的收益。

制定一种种植作物的方法，使得总收益最大。

题解

直接最小割建模，每个点向 \(S,T\) 分别连接 \(x_i,y_i\) 的边，还有 \(Q\) 个特殊点点，向 \(S,T\) 分别连接 \(p_i,q_i\) 的边。

对于每个特殊点和 \(S\) 或 \(T\) 的连边，要求如果一个边集里任意一条边被割掉，那么这条边也要割掉。

这里有一个建模技巧叫做“并联”建模：

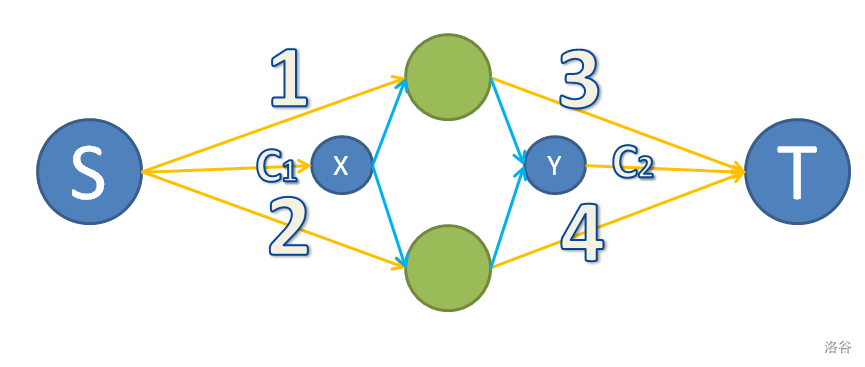
其中蓝色的边权为 \(+\infin\)，不能割。

那么我们发现，如果要使任意一个绿点分离 \(S\)，必须要割掉 \(c_1\) 这条边。

那么直接这样建模就行了。

提交记录

CF2081 B. Balancing *2500

题意

Ecrade 有一个整数数组 \(a_1, a_2, \ldots, a_n\)。保证对于每个 \(1 \le i < n\)，\(a_i \neq a_{i+1}\)。

Ecrade 可以通过若干次操作将数组变为严格递增的数组。

每次操作中，他可以选择两个整数 \(l\) 和 \(r\)（\(1 \le l \le r \le n\)），并将 \(a_l, a_{l+1}, \ldots, a_r\) 替换为任意 \(r-l+1\) 个整数 \(a'_l, a'_{l+1}, \ldots, a'_r\)。替换后的数组需要满足以下约束：

• 对于每个 \(l \le i < r\)，\(a'_i\) 和 \(a'_{i+1}\) 之间的比较关系必须与原数组中 \(a_i\) 和 \(a_{i+1}\) 的比较关系相同。即，若原数组中 \(a_i < a_{i+1}\)，则替换后必须有 \(a'_i < a'_{i+1}\)；若原数组中 \(a_i > a_{i+1}\)，则替换后必须有 \(a'_i > a'_{i+1}\)；若原数组中 \(a_i = a_{i+1}\)，则替换后必须有 \(a'_i = a'_{i+1}\)。

题解

找到所有 \(a_i>a_{i+1}\) 的位置，发现每次至多消去两个位置，然后看看第一个位置前面和最后一个位置后面的两个数能不能装下中间的数，分类讨论下即可。

提交记录

CF2081 D. MST in Modulo Graph *2700

题意

给定 \(n\) 个点点权 \(a_1,a_2,\dots ,a_n\)，两个点之间的边权为 \(\max\{a_i,a_j\}\bmod \min\{a_i,a_j\}\)，求这张完全图的 MST。

题解

先去重，然后对于每个二元组 \((a_i,j)\)，\(a\in [j\times a_i,(j+1)\times a_i)\) 的点中只有 \(a\) 最小的点和 \(i\) 连边是有用的，然后边的个数就变成了 \(O(n\ln n)\) 条，跑 kruskal 即可。

提交记录

CF2081C Quaternary Matrix *2600

题意

若矩阵中所有元素均为 \(0\)、\(1\)、\(2\) 或 \(3\)，则称该矩阵为四元矩阵。

当四元矩阵 \(A\) 满足以下两个性质时，Ecrade 称其为好矩阵：

1. 矩阵 \(A\) 的每一行中所有数字的按位异或（bitwise XOR）结果等于 \(0\)。
2. 矩阵 \(A\) 的每一列中所有数字的按位异或（bitwise XOR）结果等于 \(0\)。

Ecrade 有一个 \(n \times m\) 的四元矩阵。他想知道将该矩阵变为好矩阵所需修改的最少元素数量，并希望得到其中一个可能的修改后矩阵。

题解

算出每行和每列的异或和，每次操作相当于选一个行和一个列同时异或上一个数字。

先把行和列相同的数字消，此时 行/列 异或和必定只有两种元素，列/行 异或和必定只有一种元素。

然后匹配 行a，行b，列c 之类的情况，发现可以两步消除。

然后匹配 行a，行a，列b，列b 之类的情况，发现可以三步消除。

然后因为行异或和异或上列异或和等于 0，所以我们就做完了。

提交记录

P2766 最长不下降子序列问题 紫

题意

给定正整数序列 \(x_1 \ldots, x_n\)。

1. 计算其最长不下降子序列的长度 \(s\)。
2. 如果每个元素只允许使用一次，计算从给定的序列中最多可取出多少个长度为 \(s\) 的不下降子序列。
3. 如果允许在取出的序列中多次使用 \(x_1\) 和 \(x_n\)（其他元素仍然只允许使用一次），则从给定序列中最多可取出多少个不同的长度为 \(s\) 的不下降子序列。

\(1 \le n\le 500\)

题解

第一问直接 DP 即可。

第二、三问使用网络流，首先考虑拆点模拟 DP 状态，将一个点拆为 \(O(V)\) 个点，点 \((i,j)\) 表示以 \(i\) 结尾 LIS 为 \(j\) 的状态。然后直接连接所有 \((i,j)\to (i',j+1) (i'>i)\) 的边，跑网络流就是对的。

但是这样一共 \(O(n^2)=(常数)\times 2.5\times 10^5\) 条边，复杂度不能接受。

重新考虑 LIS 的 DP 数组 \(f\)，对于满足 \(j<f_i\) 点 \((i,j)\) 是没用的，因为之后怎么也取不到 LIS，对于满足 \(j>f_i\) 点 \((i,j)\) 也是没用的，因为根本不可能流到这里。

然后只保留点 \((i,f_i)\) 建图即可，点数变成 \(O(n)\)，边数还是 \(O(n^2)\)，dinic 在单位流量稠密图上的复杂度为 \(O(n^{\frac{8}{3}})\)，可以通过。

额数据过水不拆点也能过，但实际是需要拆点保证每个点经过一次的，发了个 工单。

提交记录

P3308 [SDOI2014] LIS 紫

题意

给定序列 \(A\)，序列中的每一项 \(A_i\) 有删除代价 \(B_i\) 和附加属性 \(C_i\)。请删除若干项，使得 \(A\) 的最长上升子序列长度减少至少 \(1\)，且付出的代价之和最小，并输出方案。

如果有多种方案，请输出将删去项的附加属性排序之后，字典序最小的一种。

题解

建图方式和上一题一模一样，只是把不同点之间的连边从 \(1\) 改成了 \(+\infin\)，入点和出点的连边改成了 \(b_i\)，求最小割。

问题就是怎么让最小割的字典序最小。

按 \(c\) 从小到大枚举边，假设枚举到了 \(i\)，把第 \(i\) 条边删掉然后看此时最小割是否恰好减少 \(b_i\)，如果是，就把 \(i\) 加入最小割集合。然后就做完了。

卡常。

判断是不是最小割时不用重跑 dinic，直接看在残量网络上 \(u\) 能不能向 \(v\) 增广即可（即令 \(S=u,T=v\) 然后调用 dinic 的 bfs）。删边时可以使用退流技巧卡常，这样写：

G.maxflow(T,i+n,T,b[i]);
G.maxflow(i,S,T,b[i]);
G.del(i,i+n);

提交记录

（todo）有只跑一遍 dinic 的做法？

P3227 [HNOI2013] 切糕 紫

题意

给你一个长 \(P\)、宽 \(Q\)、高 \(R\) 的长方体点阵。每个点有一个非负的不和谐值 \(v(x,y,z)\)。一个合法的切面满足以下两个条件：

• 对于每个 \(P\times Q\) 个纵轴，需指定恰一个切割点 \(f(x,y)\)，满足 \(1\le f(x,y)\le R\)。
• 对于所有的 \(1\le x,x'\le P\) 和 \(1\le y,y'\le Q\)，若 \(|x-x'|+|y-y'|=1\)，则 \(|f(x,y)-f(x',y')| \le D\)，其中 \(D\) 是给定的一个非负整数。

求总的切割点上不和谐值之和的最小值。

题解

看到奇怪的数据范围，考虑最小割模型，边转点，没有第二个限制可以直接做，然后考虑如何刻画第二个限制，发现对于相邻的 \((x,y),(x',y')\)，只需要增加无穷边 \((k-1,x,y)\to (k-1-d,x',y')\) 和 \((k+d,x,y)\to (k,x',y')\) 即可。因为这样可以使 \((k-1,x,y)\to (k,x,y)\) 的边被割掉后必须再割掉一个 \(((k-d)\sim (k+d-1),x',y')\to ((k-d+1)\sim (k+d),x',y')\) 的边才能让 \((k-1,x,y)\) 和 \((k,x,y)\) 真正不连通。

然后跑 dinic 就做完了。

提交记录

额，翻看题解后发现 \((k-1,x,y)\to (k-1-d,x',y')\) 和 \((k+d,x,y)\to (k,x',y')\) 只需添加一种边也是正确的。

P8987 [北大集训 2021] 简单数据结构 黑

题意

实现一个数据结构，维护一个长度为 \(n\) 的序列 \(a\)，支持以下操作 \(q\) 次。

1. 给定 \(v\)，将所有 \(a_i\) 变为 \(\min(a_i, v)\)。
2. 将所有 \(a_i\) 变为 \(a_i + i\)。
3. 给定 \(l, r\)，询问 \(\sum_{i=l}^r a_i\)。

\(1\leq n,q\leq 2\times 10^5\)。

题解

首先如果 \(a\) 初始时都是 \(0\)，那么可以发现 \(a\) 一直是单调的，线段树上二分即可。

这启示我们若 \(a_i=a_j\)，则之后的每一时刻必定满足 \(a_i\leq a_j\)。因此对于一般情况，操作一可以让大于 \(v\) 的数字在之后的操作都变得单调，进一步发现，对于某一次操作时被操作一影响过的位置集合 \(S\)， \(S\) 中的数字也是单调的。证明的话就讨论任意两个元素的大小关系即可。

然后就考虑一个数字在第几次操作二被影响，设第 \(j\) 次操作一前面有 \(cnt_j\) 个操作二，对第 \(i\) 个元素进行二分答案，第 \(i\) 个数在 \([1,mid]\) 被影响，当且仅当 \(\exist j\in [1,mid],a_i+cnt_j\times i\geq v_j\)，变形得 \(\min\limits_{j=1}^{mid} \{v_j-i\times cnt_j\}\leq a_i\)，不等式左侧是一个经典的斜率优化形式，可以通过维护凸包解决，因此对于所有位置，可以整体二分，动态维护凸包求得每个位置加入集合 \(S\) 的时间。也可以分块，每个块维护一个凸包，然后一个块一个块往后跳，找到第一个满足条件的块暴力即可。这里我实现的时候使用了 \(O(\sqrt {n})\) 的分块做法。

然后后面就好做了，对于 \(S\)，维护一颗线段树，支持线段树上二分，区间推平。对于 \([1,n]/S\)，维护一颗树状数组即可。

提交记录

CF1787G Colorful Tree Again *3000

题意

给定一棵有 \(n\) 个节点的树，边有边权和颜色。每个点有被摧毁和不被摧毁两种状态，初始所有点都没被摧毁。定义一条简单路径是好的，当且仅当路径仅有某一种颜色 \(c\) 构成，且所有颜色为 \(c\) 的边都在这条简单路径里，且路径上所有节点都没被摧毁。

你需要处理两种操作：

1. 摧毁一个节点；
2. 修复一个节点。

每个操作之后，你都需要输出最长的好的路径长度。若没有输出 \(0\)。

题解

首先如果颜色 \(c\) 不构成一条链，那么不可能有颜色 \(c\) 的好路径，如果颜色 \(c\) 构成一条链，那么当这条链所有点没有被摧毁时，这条链就是好路径。

那么其实问题相当于给定 \(O(n)\) 条路径，每次摧毁或修复一个点，问最长的完好的路径长度。

发现这题的难点在于改一个点会影响到最多 \(O(n)\) 条路径的状态，进一步发现，修改点 \(i\) 所影响的路径中，至多有一条路径的 \(\operatorname{lca}\neq i\)（即经过这个点和这个点父亲的路径，记为路径 \(L\)），于是考虑将每个路径的 \(\operatorname{lca}\) 处记贡献，每个点存储 \(\operatorname{lca}\) 为这个点的所有路径，这个点的贡献就是这个点存储的所有路径的长度最大值，答案就是所有点贡献的最大值，每次 ban 点的时候直接把这个点贡献去掉，然后在路径 \(L\) 的 \(\operatorname{lca}\) 处删掉 \(L\) 的贡献即可。修复点也是同理的

考虑使用数据结构维护上面的东西。

全局维护一个数据结构，表示每个点的贡献组成的集合，支持：删除、插入、求最大值。

每个点维护一个数据结构，表示以这个点为 \(\operatorname{lca}\) 的路径集合，支持：删除、插入、求最大值。

这些操作可以使用可删堆维护，然后就做完了。

提交记录

CF1464F My Beautiful Madness *3500

题意

给定一颗大小为 \(n (n \leq 2 * 10^5)\) 的树，\(m (m \leq 2 * 10^5)\) 次操作，维护一个初始为空的路径集合 \(P\)。

定义树上一条路径的 \(d\) 邻居（一个点集）\(S\) 为：\(x \in S\) 当前仅当存在一个路径上的点 \(y\) 满足 \(dis(x, y) \leq d\)。

操作分为三种：

1. 输入 \(u, v\)，在 \(P\) 中加入 \(u\) 到 \(v\) 的路径。
2. 输入 \(u, v\)，删除 \(P\) 中一个 \(u\) 到 \(v\) 的路径。
   （注意 \(u\) 到 \(v\) 的路径与 \(v\) 到 \(u\) 的路径是相同的，若有多个 \(u\) 到 \(v\) 的路径只删除一个）
3. 输入 \(d\)，询问 \(P\) 中所有路径的 \(d\) 邻居交集是否为空，若不为空输出 Yes，否则输出 No。

题解

核心思路：对于每个操作 \(3\)，选一个特殊点 \(X\)，满足如果存在交集，则 \(X\) 一定在交集内，然后将问题转化为判定问题。

考虑集合 \(P\) 中 lca 深度最大的路径，取其 lca，记为 \(l\)，记 \(l\) 的 \(d\) 级祖先 \(X\)，可以证明，若存在交集则 \(X\) 一定在交集内，换句话说，如果 \(X\) 不在交集内，则不存在交集。

考虑如何判定 \(X\) 是否在交集内，仿照刚才的思路，取 \(X\) 的 \(d\) 级祖先 \(Y\)，要求所有路径与子树 \(Y\) 有交。

把路径分为类：

1. lca 在 \(Y\) 子树外
2. lca 在 \(Y\) 子树内

对于第一类路径，要求其端点必须与子树 \(Y\) 有交。

对于第二类路径，要求其到 \(X\) 的最短距离小于等于 \(d\)。

第一类路径已经能通过 dfn 序+二维数点做了，考虑第二类路径。

考虑一条路径到 \(X\) 的距离在哪个点取最小值：

1. 与 \(X\to Y\) 的链无交时，这个路径的 lca 处到 \(X\) 的距离取最小值。
2. 与 \(X\to Y\) 的链有交时，其 lca 处不一定取到最小值，但一定满足 \(\leq d\) 的条件。

因此只计算 \(X\) 到第二类路径 lca 的最大值，然后判断其是否小于 \(d\) 即可。

然后就变成了这样的问题：

1. 启用一个点
2. 关闭一个点
3. 查询一个点到一个子树内所有启用的点的距离最大值。

这个东西直接线段树维护直径就能解决，然后就做完了。

提交记录

The 2nd Universal Cup Finals F. World of Rains *????

题意

有一个 \(N \times M\) 网格，初始所有格子都没有水，每秒发生以下事件：

1. 降雨：对于每个当前没有水滴的单元格，魔法猫咪独立且随机地决定是否在该单元格中创建一个新的水滴。
2. 移动（除了在第 \(S+1\) 秒）：所有现有的水滴由于重力和风同时移动。一个位于单元格 \((x, y)\) 的水滴移动到单元格 \((x+1, y+d_i)\)。
3. 消失：任何移出 \(N \times M\) 网格边界的水滴将永久消失。

任务是计算不同可能的降雨场景的数量。两个场景被认为是不同的，当且仅当在某个单元格 \((i, j)\) 和某个时间 \(t\)（\(1 \leq t \leq S+1\)）中，在一个场景中创建了水滴，而在另一个场景中没有。结果需要对 \(998,244,353\) 取模。

题解

水珠不固定，移动很困难，因此考虑相对的移动整个矩形网格。

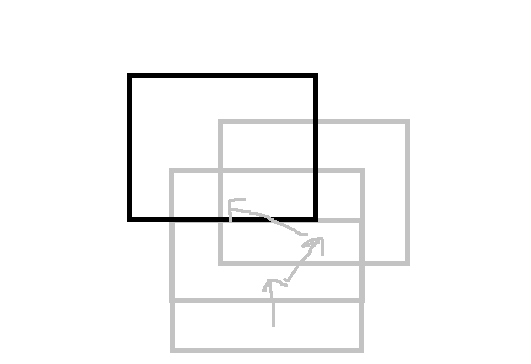
如果一个格点被 \(K\) 个矩形包含，则有 \(K+1\) 种情况：

• 一直不放水珠。
• 在第 \(i\ (1\leq i\leq K)\) 时刻放置水珠，之后保持有水的状态。

因此，如果将一个格子被覆盖的时间段拿出来单独算，那么计算方法为：将被覆盖的时间分为若干连续段，则这个格子对答案的贡献为 \(\prod (连续段长度+1)\)，之后将所有点贡献乘起来即可。

现在我们会了多项式复杂度做法，考虑优化。

考虑每一列的贡献，如果这一列被连续覆盖了 \(K\) 秒（相同的列被不连续时段覆盖则视为两列），则被覆盖的每个格子的覆盖次数自上而下形如：

\(1,2,\dots ,\min\{N,K\},\min\{N,K\},\min\{N,K\},\dots ,2,1\)

其中 \(N\) 与题目定义相同，表示矩形的行数。

如果知道 \(K\)，直接预处理阶乘，使用快速幂运算上面所有数的乘积即可。

现在要维护这些列，考虑双端队列维护连续段，每次向左/右平移相当于多出来一个连续段，在从另一端删除若干个离开矩形的连续段，然后再 fix 一个段的区间。维护时可以类比 fhq_treap 维护区间集合。

每个列的连续段在离开时算贡献，每次离开时至多增加一个连续段，复杂度 \(O(\sum S \log {N})\)。

提交记录

补 2025.6.15 模拟赛，于 2025.6.18 下午进行 vp。

T1

题意

给你一个长度为 \(n\) 的序列，每次操作可以交换相邻两项，问至少几次操作使序列满足：

• 存在 \(k\)，使序列在 \([1,k]\) 单调不降，在 \([k,n]\) 单调不增。

题解

part 1. 胡扯

先听我瞎扯一段。枚举 \(k\)，然后把 \([1,k]\) 内部变成单调不降，把 \([k,n]\) 内部变成单调不增。记 \(f(z)=\sum\limits_{1\leq x< y\leq z} a_x>a_y,g(z)=\sum\limits_{z\leq x< y\leq n} a_x<a_y\)，则答案为 \(\min\limits_{k=0}^n f(k)+g(k+1)\)。

当然，这是错的。

Hack：

6
10 9 1 6 6 6

正确答案为 2，上述算法得到 3。

part 2. 正解

拆交换贡献，若两个数 \(a,b\) 进行交换，且 \(a<b\)，则在点 \(a\) 处记贡献。

观察序列最终形态，题目要求可等价为：

• 对于任意 \(i\)，要么 \(i\) 左边都比 \(i\) 小，要么 \(i\) 右边都比 \(i\) 小。

结合我们拆贡献的方法，得出：

• 如果 \(i\) 左边都比 \(i\) 小，那么这个点在需要与在原序列上左边比他大的数字进行交换。
• 如果 \(i\) 右边都比 \(i\) 小，那么这个点在需要与在原序列上右边比他大的数字进行交换。
• 对于上述两条，任意两点之间计算独立。

因此每个点的贡献为 \(\min \{左边比它小的数的个数，右边比它小的数的个数\}\)。

最终答案如下：

\[\sum\limits_{i=1}^{n} \min \{\sum\limits_{j=1}^{i-1} [a_j < a_i],\sum\limits_{j=i+1}^{n} [a_j < a_i]\} \]

可以轻松做到 \(O(n\log n)\)。

这道题启示我们在思路错误的时候及时更换整体思路（相信大多数人的第一想法都是 part 1 中的想法）。

提交记录

T2

题意

有一个数轴，你初始时在点 \(x\)，可以在任意时刻执行以下操作：

• 假设你现在在点 \(a\)，选择任意的 \(b\)，移动到点 \(b\) 并花费 \(|b-a|\) 元。

同时，有 \(n\) 个区间 \([l,r]\)，你需要按输入顺序执行以下操作：

• 假设你现在在点 \(a\)，选择一个 \(b\) 满足 \(l\leq b\leq r\)，不进行移动并花费 \(|b-a|\) 元。

求最小花费。

题解

slopetrick 的板子。

先设计一个 \(O(nV)\) 的 DP，\(dp_{i,j}\) 表示时刻 \(i\) 在位置 \(j\) 的最小花费，转移显然。

打表发现 DP 数组可以分为至多三段，一段斜率 \(-1\)，一段斜率 \(0\)，一段斜率 \(1\)。

考虑如何证明这件事情，初始时，DP 数组分为两段，即 \([-\infin,x]\) 斜率为 \(-1\)，\([x,+\infin]\) 斜率为 \(1\)。

加入区间 \([l,r]\) 会让 \([-\infin,l]\) 的斜率加 \(1\)，\([r,\infin]\) 的斜率减 \(1\)。

然后分类讨论，维护斜率为 \(0\) 的段就行了，代码非常短。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int inf=1e18;
int n,x;
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>x;
	int L=x,R=x,V=0; 
	for(int i=1;i<=n;i++){
		int l,r;
		cin>>l>>r;
		if(l<=L&&R<=r) continue;
		else if(L<=l&&r<=R){
			L=l,R=r;
		}else if(R<=l){
			V+=l-R;
			L=R;
			R=l;
		}else if(l<=R&&R<=r){
			L=l;
		}else if(r<=L){
			V+=L-r;
			R=L;
			L=r;
		}else if(l<=L&&L<=r){
			R=r;
		}
	}
	cout<<V<<"\n";
	return 0;
}

提交记录

T4

刚看 T3 感觉不太能做，于是来看 T4 了。

题意

【CSP-S 2024 T3 染色】的加强版。

给定一个长度为 \(n\) 的正整数数组 \(A\)，其中所有数从左至右排成一排。

你需要将 \(A\) 中的每个数染成红色或蓝色之一，然后按如下方式计算最终得分：

设 \(C\) 为长度为 \(n\) 的整数数组，对于 \(A\) 中的每个数 \(A_i\)（\(1 \leq i \leq n\)）：

• 如果 \(A_i\) 左侧没有与其同色的数，则令 \(C_i = A_i\)。
• 否则，记其左侧与其最靠近的同色数为 \(A_j\)，则令 \(C_i = |A_i-A_j|\)。

你的最终得分为 \(C\) 中所有整数的和，即 \(\sum \limits_{i=1}^n C_i\)。你需要最小化最终得分，请求出最终得分的最小值。

题解

看标题，这道题首次出现时间应该是在 2023-9-27，所以这道题的出题人压中了 CSP-S 2024 的第三题？（大雾）

仿照【CSP-S 2024 T3 染色】，记 \(S_i=\sum\limits_{j=2}^{i} |A_j-A_{j-1}|\)，设 \(f_{i,1/0}\) 表示只考虑前 \(i\) 项的最小值，当前颜色与上一个颜色是否相同，讨论转移：

• \(i\) 与 \(i-1\) 同色，\(f_{i,1}=\min \{f_{i-1,0},f_{i-1,1}\}+|A_i-A_{i-1}|\)。
• \(i\) 与 \(i-1\) 不同色，\(f_{i,0}=\min\limits_{j=1}^{i-1} \{f_{j,0}+S_{i-1}-S_j+|A_i-A_{j-1}|\}\)。

上述转移原理与【CSP-S 2024 T3 染色】几乎一致。

现在有 \(O(n^2)\) 做法了，考虑优化。

同色转移可以直接 \(O(1)\) 了，不同色转移可以写成如下形式：

\[f_{i,0}\leftarrow f_{j,0}-S_j-A_{j-1}+S_{i-1}+A_i\ (A_{j-1}\leq A_i)\\ f_{i,0}\leftarrow f_{j,0}-S_j+A_{j-1}+S_{i-1}-A_i\ (A_{j-1}>A_i) \]

转移式子可分为和 \(j\) 有关与和 \(i\) 有关的两部分，有一个维度有限制，这是一个经典的数据结构优化 DP 形式，随便优化一下就 \(O(n\log n)\) 了。

提交记录

T3

原题链接

题意

现有一个环，环上有 \(n\) 个数，第 \(i\) 个数是 \(a_i\)，其中第 \(i(1 \leq i < n)\) 个和第 \(i+1\) 个相邻，第 \(n\) 个和第 \(1\) 个相邻。

每次操作你可以做以下事情之一：

1. 选取 \(i\)，设 \(l, r\) 分别为与 \(i\) 左右相邻的数，将 \(a_i\) 变为 \(\min(a_i, a_l, a_r)\)。
2. 选取 \(i\)，设 \(l, r\) 分别为与 \(i\) 左右相邻的数，将 \(a_i\) 变为 \(\max(a_i, a_l, a_r)\)。

你需要对于每个 \(k(1 \leq k \leq m)\) 求出：最少操作多少次，才能使得所有数都等于 \(k\)。

题解

一开始错误的思路

对于每个 \(k\)，把环按 \(k\) 拆成若干段计算答案，发现如果当前数的后面两个数中一个大于 \(k\)，另一个小于 \(k\)，那么需要两次操作将后面一个数字改成 \(k\)，否则只需要一次操作。

所以每个段的答案就是段长加上相邻两项关于 \(k\) 的大小关系不同的位置数，然后只需要断环成链，维护一个线段树，从小到大加数，加数时将线段树上的一位由 0 反转为 1，维护相邻不同的位置数即可。

但是真的是这样吗？

Hack：3 2 2 2 2 5 2 2 2 3（\(k=3\)），发现只需要将 \(5\) 花费一步调整为 \(2\)，然后再加上段长即可。

多造几组 Hack，发现难点在于形如 010101 交替的情况，然后我就不会了。

正解

遇到这种情况，直接从难点入手，考虑极长的 01 交替子串，发现最优策略是将 \(0\) 全部调为 \(1\)，或将 \(1\) 全部调为 \(0\)。因此长为 \(len\) 的极长 01 交替子串的贡献为 \(\frac{len}{2}\)。

因此，将上述错误思路的算贡献部分，由“相邻不同的位置数”，改为“极长 01 交替子串的长度整除 \(2\) 之和”即可。

维护的话就用线段树，类似维护区间最大子段和直接做就行了。

提交记录

QTREE 4 紫

题意

给出一棵边带权的节点数量为 \(n\) 的树，初始树上所有节点都是白色。有两种操作：

• C x，改变节点 \(x\) 的颜色，即白变黑，黑变白。

• A，询问树中最远的两个白色节点的距离，这两个白色节点可以重合（此时距离为 \(0\)）。

边权有负数。

题解

点分树。

建出点分树，利用【两点在点分树上的 lca 一定在原树两点路径上】的性质。

考虑普通 DP 求树上直径的过程，是记 \(mx_u\) 表示子树 \(u\) 内到 \(u\) 的最大距离，之后枚举 lca，找两个 \(mx_v\) 拼起来。

因此点分树上每个点维护 \(C_u\) 表示点分树子树 \(u\) 内到 \(fa_u\) 的集合。

\(P_u\) 表示 \(u\) 每个子树 \(C_v\) 最大值的集合，即 \(P_u=\max \{C_v|fa_v=u\}\)。

当 \(u\) 是白点时，还需要在 \(P_u\) 加上 \(0\)。

答案就是 \(\max\limits_{i=1}^n \max(P_u)+\operatorname{secondmax}(P_u)\)。

每个点的 \(C,P\) 各维护一个可删堆，在维护一个全局可删堆表示 \(\max(P_u)+\operatorname{secondmax}(P_u)\) 的集合，修改是简单的。

提交记录

（todo）把 SPOJ 的 QTREE4 卡常卡过。

[NOI2018] 你的名字 黑

题意

给定 \(S\)，多次询问，每次给定 \(T,l,r\)，问字符串 \(T\) 中有多少本质不同字串，满足其不是 \(S_{l\dots r}\) 的子串。

数据范围为 \(10^6\) 级别。

题解

首先先不管 \(S\)，位置不同但是本质相同的子串肯定不能算重，因此考虑【本质不同子串】套路，把 \(S\) 和所有询问串拼到一起建出 SA。

每次询问求出 \(T\) 的本质不同子串，再减去是 \(S\) 子串的部分。

现在要计算是 \(S\) 子串的部分，考虑 SA 中【双指针求 height】的套路，设 \(L_i\) 表示 \(T\) 的位置 \(i\) 的后缀中，是 \(S\) 子串的最长前缀的长度。

则有 \(L_{i+1}\geq L_i-1\)，证明是容易的。

因此只要我们能 \(O(1)\) 或 \(O(\log n)\) 判断 \(T\) 中的一段是否是 \(S\) 的子串，我们就能双指针求 \(L\)，然后就能向求本质不同子串一样容斥做了。

然后考虑对于 \(T\) 的某个位置在拼接后总串的位置 \(x\)，判定【从这个位置开始 \(len\) 个字符是否是 \(S_{l\dots r}\) 的子串】，只需要查询 \([l,r-len+1]\) 中是否有一个位置 \(y\) 满足 \(\operatorname{lcp}(x,y)\geq len\) 即可。

看到 \(\operatorname{lcp}\) 大于某个数字，因为 \(\operatorname{lcp}\) 运算在后缀排序中有单调性，所以考虑在后缀排序上做这个事情。具体地，在后缀排序中二分出一个区间 \([ll,rr]\) 满足 \(\forall i\in [ll,rr],\operatorname{lcp}(x,sa_i)\geq len\)，然后判定 \(\exist i\in [ll,rr],l\leq sa_i\leq r-len+1\) 是否成立。

判定条件是一个经典的 4-side 二位数点问题，可以主席树维护，然后就可以求出 \(L\) 了。

之后仿照【本质不同子串】的套路容斥一下即可。

略微卡常。

提交记录

模拟赛。

T1 *1700

题意

给定一个长度为 \(n\) 的数列 \(a\)，每次操作可以选择一个位置 \(i\)，满足 \(2\leq i\leq n-1\land a_{i-1}<a_i\land a_i>a_{i+1}\)，执行 \(a_i\leftarrow \min(a_{i-1},a_{i+1})-1\)，求最多进行多少次操作。

题解

直接用栈模拟，是 \(O(答案)\) 的，然后发现每次新加入一个数会消除一段连续的递增序列，然后随便维护一下就行了，复杂度 \(O(n)\)，代码量约 400b。

提交记录

T2 *2100

题意

给定一个长为 \(n\) 的序列 \(a\)，初始时对于所有 \(1\leq i\leq n\)，有 \(a_i=i\)，你可以以任意顺序执行以下两种操作若干次：

• 将序列的 \([1,a]\) 翻转。
• 将序列的 \([n-b+1,n]\) 翻转。

求有多少种可能的局面。

题解

首先拿出操作序列，发现连续进行同一种操作是没有意义的，所以操作一定是 12 交替。

然后计算重复 12 操作多少次后会回到原点。

直接利用环长 lcm 的套路就行了。

提交记录

T3 *2500

题意

给你一个包含 +，*，(，)，_ 的表达式。

将 \(1\sim m\) 随机填入 _，且同一个数只能用一次。

求表达式结果的期望。

题解

由期望的线性性质，无论 \(a,b\) 是否独立，都有 \(E(a+b)=E(a)+E(b)\)。

将第 \(i\) 个下划线视为 \(x_i\)，拆括号，得到若干个 \(x\) 相乘后相加的式子，例如 (_+_)*(_+_) 变为 x1x3+x1x4+x2x3+x2x4。

用上述式子举例，\(E(x_1x_3+x_1x_4+x_2x_3+x_2x_4)=E(x_1x_3)+E(x_1x_4)+E(x_2x_3)+E(x_2x_4)\)。

通过期望的线性性质将原式拆成了若干个独立的部分，我们只关心每个部分内部的 \(x\) 互不相同即可，而 \(E(x_1x_3),E(x_1x_4)\) 没有任何区别，因此 \(E(x_1x_3)=E(x_1x_4)=E(x_2x_3)=E(x_2x_4)\)。

所以我们算出 \(g_i\) 表示从 \(1\sim m\) 选 \(i\) 个的乘积的期望，\(f_i\) 表示拆括号后 \(i\) 个 \(x\) 乘起来的单项式个数，答案就是 \(\sum f_i\times g_i\)。

\(g\) 可以 01 背包求出，\(f\) 可以建立表达式树后树上背包求出。

提交记录

T4 *????

题意

有一个初始为 \(0\) 的整数变量 \(X\) 和一个长度为 \(n\)、初始全 \(0\) 的 01 序列，对序列进行如下操作：

• 如果序列全 \(1\)

  • 结束操作。

• 否则

  • 对于每个满足 \(1\leq i\leq n\) 的整数 \(i\)，同时执行 \(a_i=a_i\lor a_{i+1-n\times [i=n]}\lor a_{i-1+n\times [i=1]}\)。
  • 随机选择一个满足 \(1\leq i\leq n\) 的整数 \(i\)，执行 \(a_i\leftarrow 1\)。
  • 执行 \(X\leftarrow X+1\)。

求操作结束后 \(X\) 的期望值。

题解

我不会，等我会了再写。

（todo）会这道题。

P3449 [POI 2006] PAL-Palindromes 紫

题意

有 \(n\) 个回文串，将这些串两两形成 \(n^2\) 个新串，求新串中有多少个回文串。

题解

串 \(a\) 和串 \(b\) 拼接后是回文串，当且仅当 \(a+b=Rev(b)+Rev(a)\)，然后因为 \(a,b\) 本身都是回文串，所以判定条件可转化为 \(a+b=b+a\)，然后考虑字符串哈希，\(a+b=b+a\) 相当于 \(hash(a)\times base^{len_b}+hash(b)=hash(b)\times base_{len_a}+hash(a)\)。

化简得到 \(\frac{hash(a)}{base^{len_a}-1}=\frac{hash(b)}{base^{len_b}-1}\)，然后就可以随便做了。

提交记录

P3435 [POI 2006] OKR-Periods of Words 蓝

题意

求每个前缀的最长周期之和。

题解

根据 border 周期的结论，只需要求每个前缀的最短非空 border 即可。

考虑 KMP 的同时维护 \(f\) 数组，\(f_i\) 表示前缀 \(i\) 的最短非空 border。

则有：

\[f_i= \begin{cases} f_{border_i},& f_{border_i}\neq 0;\\ border_i,& \text{otherwise}. \end{cases} \]

最终答案为 \(\sum\limits_{i=1\land f_i\neq 0}^{n} i-f_i\)。

提交记录

CF17E Palisection *2900

题意

给你一个字符串 \(s\)，求 \(s\) 中有多少对相交的回文子串。

题解

看到回文子串考虑 manacher。

manacher 求出以 \(i\) 结尾的回文串个数 \(f_i\)，以 \(i\) 为开头的回文串 \(g_i\)。

正难则反，统计不相交的回文子串对数，不相交回文子串对数为 \(\sum\limits_{i=2}^n \sum\limits_{j=1}^{i-1} f_{j}\times g_i\)，前缀和一下可以做到 \(O(n)\)。

略微卡空间。

提交记录

P3546 [POI 2012] PRE-Prefixuffix 紫

题意

给你一个长度为 \(n\) 的串 \(S\)，求最大的 \(L\) 使得 \(S\) 的 \(L\) 前缀和 \(L\) 后缀循环同构。

题解

发现循环同构相当于一个串是 \(AB\)，另一个串是 \(BA\)。

然后相当于把 \(S\) 划分成 \(ABTBA\) 的形式，其中 \(A\) 是 \(S\) 的 border。

因此可以枚举 border \(A\) 的长度，然后求 \(S\) 去掉两边的 \(A\) 后 border \(B\) 的长度，相加更新答案，这样复杂度是 \(O(n^2)\) 的。

所以我们充分发扬人类智慧，只取前 \(100\) 个 border 和后 \(100\) 个 border 进行枚举，然后就 通过 了。

所以我们分析性质，每次要求的是 \(S\) 中间一段的 border，考虑假设 \(S[l:r]\) 的最长 border 是 \(x\)，那么 \(S[l+1:r-1]\) 的最长 border 一定大于 \(x-2\)，因为可以把 \(S[l:r]\) 的 border 掐头去尾，得到 \(S[l+1:r-1]\) 的一个 border。

换句话说，在一个字符串的头尾各加入一个字符，border 至多增加 \(2\)。

所以我们维护区间 border \(x\)，每次在头部和尾部增加一个字符，令 \(x\) 增加 \(2\)，然后不断减少 \(x\) 直到 \(x\) 符合条件，判断是使用字符串哈希。这部分可以类比 SA 中求 height 的步骤。

注意上文中的 border 需要满足长度不超过原串长度的一半。

提交记录

P3805 【模板】manacher 模板

提交记录

P5163 WD 与地图 黑

题意

有 \(n\) 个点，\(m\) 条边的有向图，点有点权，共有三个操作：

1 a b 删除从 \(a\) 连向 \(b\) 的边，保证这条边存在。

2 a b 表示令 \(a\) 的点权增加 \(b\)。

3 a b 求 \(a\) 城市所在 SCC 前 \(b\) 个点的点权之和。如果 SCC 中的点不足 \(b\) 个则输出该 SCC 所有点的点权总和。

题解

倒着做。

如果是双向边则可以线段树合并。

然后整体二分出对于每条边 \((u,v)\)，\(u\) 和 \(v\) 被计入同一个 SCC 的时间 \(t\)，之后将这条边视为在 \(t\) 时刻 \(u,v\) 之间加入双向边，仍然可以线段树合并。

注意整体二分的时候不应该把上述信息当成操作和询问分开处理，因为动态加边的 SCC 本身是非常难维护的，所以应该把边当成操作和询问合一的东西，然后用并查集把已经加入 SCC 的边缩到一个点中，其余边进入右侧二分结构。之后撤销后再进入左侧二分结构。

提交记录

CF1252D Find String in a Grid *3000

题意

现有一个由大写字母构成的n行m列矩阵。

定义一个 L 型字符串为，从矩阵某个位置开始，先向右走若干步，再向下走若干步，路径上字符依次连接起来组成的字符串。

再给你 \(q\) 个字符串，问对于每个字符串 \(S\)，在矩阵中有多少个 L 型字符串等于 \(S\)。

题解

对于一个 L 型串，我们在他的拐点处计入贡献，同时，每个拐点只保留一个极长的 L 型串。这样只有 \(O(n^2)\) 个有用的 L 型串。那么问题转化为把所有 L 型串拿出来和所有询问串做多模匹配。

看到多模式串匹配考虑 ACAM，把所有 L 型字符串拿出来建 ACAM 空间肯定会炸，因此对询问串建 ACAM。

然后枚举每个 L 型串，加上 L 型串的贡献，再减去不过拐点的贡献。

具体地，假设 L 型串拐点为 \((x,y)\)，则在 ACAM 上以 \(1\) 的贡献跑一遍整个 L 型串，再以 \(-1\) 的贡献跑一遍 \((x,1)\sim (x,y-1)\) 和 \((x+1,y)\sim (n,y)\) 所对应的串即可。

时间复杂度 \(O(n^3+\sum |S|)\)，空间复杂度 \(O(n^2+26\sum |S|)\)。

提交记录

SP7258 SUBLEX 紫

题意

求一个字符串本质不同排名第 \(k\) 小的子串。

题解

建立 SAM，预处理每个节点开始走能形成多少个本质不同的子串，可以建反图 DP，然后在 SAM 上沿转移边找第 \(k\) 小子串即可。

提交记录

P6727 [COCI 2015/2016 #5] OOP 紫

题意

给定 \(N\) 个单词和 \(Q\) 个模板，一个模板由一个 * 和一些小写字母组成。一个模板覆盖了一个单词当且仅当将 * 替换为某个字符串（可以为空）后，模板和单词能够完全重合。对于每个模板，求出它能够覆盖多少个单词。

题解

将模板串拆成 pre+*+suf 的形式。

一个单词能被一个模板串覆盖，当且仅当 pre 是这个单词的前缀，suf 是这个单词的后缀，且单词长度大于等于 \(|pre|+|suf|\)。

pre 是这个单词的前缀，转化成前缀字典树中这个单词在 pre 的子树内。

suf 是这个单词的后缀，转化成后缀字典树中这个单词在 suf 的子树内。

然后相当于匹配一个串受到了三维的限制：

• 前缀字典树 dfn
• 后缀字典树 dfn
• 长度

三位数点即可，可以使用树状数组套线段树维护。

提交记录

CF1975H 378QAQ and Core *3500

题意

给你一个字符串，重排字符串使得所有后缀的最大字典序最小，输出重排后的字符串字典序最大的后缀。

题解

考虑样例 bazoka，不难发现只有一个最大字符时，答案就是最大的字符。

那么从最大字符入手，设最大字符是 \(c\)，那么重排后的字符串肯定是 \((cs_1)(cs_2)(cs_3)\dots (cs_k)c\)。

容易证明 \(c\) 一定在头部和尾部。

如果确定了 \(s_1,s_2,\dots,s_k\)，就可以把重排 \((cs_1)(cs_2)(cs_3)\dots (cs_k)\) 看成一个子问题，递归解决后再加上 \(c\)。

注意每个字符串最后都要接上一个比目前大的后缀，所以比较时不是传统的字符串比大小。解决方法是递归的时候维护字符串集合实时有序。

考虑如何确定 \(s_1,s_2,\dots s_k\)。

记最大字符有 \(cnt\) 个，其余字符有 \(num\) 个。

当 \(cnt\geq num+1\) 时，那么有些 \(s\) 可能是空串，显然平均分配最优，我们让每个其余字符带 \(\lfloor \frac{cnt}{num+1} \rfloor\) 个字符，余下的字符单独进入下一层递归。

例如字符串 \(z^{14}abc\)，递归时会把原串分为 \(z^3a,z^3b,z^3c,z,z\) 进入下一层递归，最后结果再加上 \(z^3\)。

当 \(cnt<num+1\) 时，不会有空的 \(s\)。

首先注意到一个最大的后缀肯定是由最大字符 \(c\) 结尾的。那么肯定先前 \(cnt-1\) 个 \(c\) 后面接上 \(cnt-1\) 个最小的其余字符。

之后考虑什么位置可以作为最大后缀。

例如字符串 \(zzzzaabbcc\)，先把结尾 \(z\) 拿出来，然后填完一轮后变为 \(za,za,zb\)，剩余 \(b,c,c\)。

此时，只有 \(zb\) 能作为最大后缀，所以应该把 \(b,c,c\) 全部接到 \(zb\) 后面，变为 \(za,za,zbbcc\)，使 \(zb\) 尽可能晚的接到下一个 \(z\)，这样最终答案就是 \(zaabbz\)。

如果不这么做，比如你将字符串分成了 \(zab,zac,zbc\)，那么就会存在 \(zbcz\) 的后缀，字典序大于 \(zaabbz\)。

因此，从小到大填，每轮将剩余字符仅填充在目前结尾是最大的字符的字符串之后。

贴一个核心代码。

string core(vector<string> S){
	if(S.size()==0) return "";
	int num=S.size();
	string mx=S[num-1];
	while(num&&S[num-1]==mx) num--;
	int cnt=S.size()-num;
	if(cnt==1){
		return mx;
	}
	if(num+1>=cnt){
		vector<string> nxt;
		for(int i=1;i<cnt;i++){
			nxt.push_back(mx);
		}
		int now=0;
		for(int i=0;i<num;){
			for(int j=now;j<cnt-1;j++){
				nxt[j]+=S[i];
				if(j>now&&S[i]>S[i-1]) now=j;
				i++;
				if(i>=num) break;
			}
		}
		return core(nxt)+mx;
	}else{
		int k=cnt/(num+1);
		vector<string> nxt;
		string kmx="";
		for(int i=1;i<=k;i++) kmx+=mx;
		for(int i=1;i<=num;i++){
			string tmp=kmx+S[i-1];
			nxt.push_back(tmp);
		}
		for(int i=1;i<=cnt%(num+1);i++) nxt.push_back(mx);
		//要实时维护集合有序，这里顺序不能错。
		return core(nxt)+kmx;
	}
}

提交记录

qoj7773 重排 *????

题意

定义一个字符串是好串，当且仅当它本身是它的最小表示。

给定一个由小写字母组成的字符串 \(S\)，将 \(S\) 中的字母重排成一个好串，并最大化这个字符串的字典序。输出重排后的字符串。

题解

与 CF1975H 相同，划分为 \((as_1)(as_2)\dots (as_n)\) 向下递归，注意这里 \(a\) 是最小的字符。

提交记录

QOJ #6842. Popcount Words *????

题意

有无穷 01 字符串 \(S\)，第 \(i\) 项为 \(\operatorname{popcnt}(i)\bmod 2\)。

记 \(w(l,r)\) 表示 \(S_lS_{l+1}\dots S_{r}\)。

给你 \(N\) 个区间 \([l_1,r_1],[l_2,r_2],\dots,[l_n,r_n]\) 和 \(Q\) 个询问串 \(s_1,s_2\dots,s_q\)，问每个询问串在 \(w(l_1,r_1)+w(l_2,r_2)+\cdots +w(l_n,r_n)\) 的出现次数。

题解

看到多模匹配，考虑 ACAM，对询问串建立 ACAM，然后只要统计出 \(w(l_1,r_1)+w(l_2,r_2)+\cdots +w(l_n,r_n)\) 在 ACAM 转移时每个点的经过次数即可。

考虑分析无穷序列 \(S\) 的性质，套路的将其拆分为整二进制形式，拆分后具有如下好处：

1. 状态数有限
2. 满足倍增性质

具体地，记：

\[W(j,0)=w(0,2^j-1)\\ W(j,1)=w(2^j,2^{j+1}-1) \]

不难证明：

1. \(w(k2^j,k2^j+2^j-1)=W(j,k\bmod 2)\)
2. \(W(j,i)=W(j-1,i)+W(j-1,1-i)\)

由 1，可以将 \(w(l_1,r_1)+w(l_2,r_2)+\cdots +w(l_n,r_n)\) 拆分为若干个 \(W(j,i)\) 拼在一起的形式，而 \(W\) 的状态是 \(O(\sum \log {(r-l+1)})\) 的。

由 2，可以倍增算出 ACAM 上从一个点 \(u\) 做一遍 \(W(j,i)\) 后到达的点，记为 \(f_{u,j,i}\)。

之后考虑计算每个点的出现次数，已经有倍增数组 \(f\) 后，这不需要依赖任何性质，直接逆向倍增即可。可以把倍增结构类比成线段树结构，维护倍增结构的标记下传，记 \(g_{u,j,i}\) 表示从 \(u\) 开始，进行 \(W(j,i)\) 转移的次数。

初始时对于每个拆分出来的 \(W(x,y)\)，打上标记，\(g_{u,x,y}=1\)。

倒着下传标记的转移如下：

\[g_{u,j,i}\to g_{u,j-1,i}\\ g_{u,j,i}\to g_{f_{u,j-1,i},j-1,1-i} \]

最后，对于一个节点 \(u\) ，其总出现次数 \(cnt_{u}=\sum\limits_{f_{v,0,0}=u} g_{v,0,0}+\sum\limits_{f_{v,0,1}=u} g_{v,0,1}\)，也可以写成 \(g_{v,0,i}\to cnt_{f_{v,0,i}}\)。

知道每个点出现次数后在 ACAM 上统计一下 fail 树的子树和就行了。

提交记录

P5446 [THUPC 2018] 绿绿和串串

题意

给定一个非空字符串 \(S\)。

定义翻转操作为：将字符串 \(r_0 r_1 \dots r_{n-1}\) 变为 \(r_0 r_1 \dots r_{n-2} r_{n-1} r_{n-2} \dots r_1 r_0\)。

求所有满足以下条件的 \(x\)：

1. \(x \le |S|\)。
2. 存在长度为 \(x\) 的字符串 \(R\)，可以通过若干次翻转得到以 \(S\) 为前缀的字符串。

题解

注意到 \(R\) 一定是 \(S\) 的前缀，所以枚举前缀然后暴力检验即可，因为翻转 \(\log\) 次就超过 \(|S|\) 了。

检验一个串是否是回文串，使用 manacher 即可。

提交记录

2025.7

P5496 【模板】回文自动机（PAM） 模板

提交记录

P3649 [APIO2014] 回文串 紫

题意

给你一个由小写拉丁字母组成的字符串 \(s\)。我们定义 \(s\) 的一个子串的存在值为这个子串在 \(s\) 中出现的次数乘以这个子串的长度。

对于给你的这个字符串 \(s\)，求所有回文子串中的最大存在值。

题解

在回文自动机上，每加入一个字符，在新节点的 fail 树到根链上加 1，最后每个点被加 1 的次数就是所对回文串的出现次数，树上差分一下就行了。

提交记录

P4287 [SHOI2011] 双倍回文 紫

题意

称两个相同偶回文串拼起来是“双倍回文串”，求给定字符串的最长双倍回文子串。

题解

我是奶龙。

注意到双倍回文串也是回文串，于是枚举本质不同的回文串然后 manacher 检查一下就行了

提交记录

P5555 秩序魔咒 紫

题意

给定两个小写字母字符串 \(S,T\)，求：

1. 两个字符串的最长公共回文子串。

2. 本质不同的最长公共回文子串个数。

题解

我是奶龙。

把 \(S\) 和 \(T\) 拼到一起建立 PAM，中间间隔两个不同且不在字符集中的字符，这样能保证不存在跨过两个串的回文串。

考虑统计回文串出现次数的过程，然后 PAM 新加入节点时，当前节点在 fail 树到根链上的所有回文串都会在这个位置出现一次。

所以直接线段树合并记录 PAM 每个节点的出现位置集合，然后枚举节点，如果这个节点所对回文串在两个串中都有出现，则更新答案。

写完通过后才发现根本不用线段树合并，因为我们无需知道具体出现位置，只关心出现位置在哪个串即可，所以每个点额外维护两个变量表示是否在 \(S,T\) 中出现过，然后递推上去也能做。

我是奶龙。

提交记录

P4762 [CERC2014] Virus synthesis 紫

题意

你有一个空串，每次可以进行以下操作的一种：

• 在开头和末尾添加一个字符
• 将字符串翻转，设原串为 \(S\)，则新串为 \(S+\operatorname{rev}(S)\)。

求将空串变为给定串的操作次数。

字符集为 \(\{A,G,T,C\}\)。

题解

PAM 上 DP。

最后的肯定是先形成了一个回文子串，然后暴力补全剩余部分形成的。

那么假设存在长为 \(len\) 的回文子串 \(T\)，\(T\) 可以由空串 \(k\) 步形成，那么可以用 \(k+n-|T|\) 更新答案。

于是对所有本质不同的回文串 DP，即 PAM 上 DP。

首先可以归纳证明偶回文串最后一步是操作 2 一定不劣。

\(dp_i\) 表示 PAM 节点 \(i\) 所对回文串的最小操作次数。

则可以左右各去掉一个字符，在翻转前的一侧加上，\(dp_{i}+1\to dp_{ch_{i,A/G/T/C}}\)，不难发现这个转移覆盖了以下情况：

• 上一次翻转操作前，新加入的字符是本串的头或尾。

然后要把没有覆盖到的补上。

考虑上上次翻转操作，如果要做到不在头或尾新加入字符，那么上上次翻转操作形成的串一定是本串的前后缀，由于是回文串，这里只考虑后缀。

假设 \(j\) 节点是 \(i\) 节点的一个回文后缀，且 \(len_j\times 2\leq len_i\)，则 \(dp_{j}+\frac{len_i}{2}-len_j\to dp_{i}\)。

然后发现，如果 \(j\) 不是小于 \(\frac{len_i}{2}\) 的最大回文后缀，那么在添加字符的过程中，会导致最大回文后缀的最后一步不是翻转，与引理 1 矛盾。

于是只转移满足条件的最大的 \(j\) 即可。

注意也可以不做操作二，此时答案为 \(n\)，所以实现时 ans 不能赋极大值，应该赋值为 \(n\)。

提交记录

CF932G Palindrome Partition *2900

题意

将字符串划分为 \(k\) 个子串，使得第 \(i\) 个子串等于第 \(k-i+1\) 个子串。

求方案数

题解

发现这个东西很像回文串，把两个相等的子串的其中一个反转后穿插到另一个里面，会形成一个偶回文串。

例如两个 \(abcde\) 变成 \(a(e)b(d)c(c)d(b)e(a)=aebdccdbea\)。

那么构造字符串 \(t=s_{1}s_{n}s_{2}s_{n-1}\dots s_{\frac{n}{2}}s_{\frac{n}{2}+1}\)，然后统计 \(t\) 的偶回文划分计数即可。

提交记录

P3501 [POI 2010] ANT-Antisymmetry 蓝

题意

对于一个 \(0/1\) 字符串，如果将这个字符串 \(0\) 和 \(1\) 取反后，再将整个串反过来和原串一样，就称作「反对称」字符串。比如 \(00001111\) 和 \(010101\) 就是反对称的，而 \(1001\) 就不是。
现在给出一个长度为 \(n\) 的 \(0/1\) 字符串，求它有多少个子串是反对称的，注意这里相同的子串出现在不同的位置会被重复计算。

题解

manacher 的正确性依赖回文串的以下两个性质：

1. 若 \([l,r]\) 回文且 \(l+1\leq r-1\)，则 \([l+1,r-1]\) 回文。
2. 若 \([l,r],[a,b]\) 回文且 \(l\leq a\leq b\leq r\)，则 \([l+r-b,l+r-a]\) 回文。

反对称串满足以上两条性质，因此直接 manacher 即可。

注意反对称串长度必须是偶数，最后统计答案要特判。

提交记录

P9646 [SNCPC2019] Paper-cutting 紫

题意

你会得到一张大小为 \(n \times m\) 的纸， 它被划分为 \(n \times m\) 个大小为 \(1 \times 1\) 的块在。这张纸可以按以下方式折叠：

• 可以在两列之间选择一条垂直线，也可以在两行之间选择一条水平线。这条线把纸分成两面。

• 你用这条线作为对称轴，把小的一面折到大的一面上。如果纸的两面大小相等，从两边对折。

你想用这张纸做一幅剪纸杰作。首先，使用上述方法将纸张折叠几次（包括零次）。然后你用剪刀剪纸。每次剪切时，都可以从折叠的纸上剪切出一个连接的部分（即使从外面无法接触到该部分并将其扔掉。请注意，如果两个 $ 1\times 1$ 的块共享一条边，则它们是连接的。

纸张的最终外观是一个包含 \(0\) 和 \(1\) 的大小为 \(n \times m\) 的矩阵，你想知道需要使用剪刀时的最小裁剪次数。

题解

肯定是先横着翻转再竖着翻转，肯定是最后大小越小越好，证明略。

引理 1 对于一个 \(1\times x\) 的串 \(S\)，肯定是先翻转长度最小的偶回文后缀。

证明 假设 \([a,x]\)，\([b,x]\) 都是 \(S\) 的偶回文后缀，且 \(a<b\)，那么可以通过先翻转 \([b,x]\) 再翻转 \([a+\frac{x-b}{2},x-\frac{x-b}{2}]\) 达到翻转 \([a,x]\) 的效果。

同时可以在串两侧加入 \(\inf\) 个万能字符说明左侧和右侧翻折互不影响。

横着翻转和竖着翻转本质相同，只考虑横着翻转，此时行之间独立，因此每次找最大的 \(i\) 满足 \([i,m]\) 在每行都是回文后缀，然后翻转。

最多有 \(m\) 个不同的 \(i\)，每次检查对每个串使用 manacher，复杂度 \(O(行数)=O(n)\)，因此最后复杂度 \(O(nm)\)。

提交记录

P5410 【模板】扩展 KMP/exKMP（Z 函数） 模板

提交记录

CF126B. Password *1700

题意

找出最长 border 满足其在字符串中出现次数大于等于 \(3\)。

题解

求出 Z 函数，枚举 border 然后用 Z 函数检查中间是否有出现即可。

提交记录

CF432D. Prefixes and Suffixes *2000

题意

求每个 border 的出现次数。

题解

使用 Z 函数，如果 \(z_i>border_x\) 就说明 \(i\) 位置出现了这个 border。

前缀和维护即可。

提交记录

[The 2nd Universal Cup Finals L](Not Another Constructive Problem) *????

题意

给定一个无向图 \(G\)，包含 \(n\) 个顶点，顶点 \(i\) 和 \(j\) 之间有 \(c_{i,j}\) 条无向边（允许多重边）。每个顶点 \(i\) 初始有一个排列值 \(p_i\)（\(1\) 到 \(n\) 的排列），目标是通过特定操作将 \(p_i\) 转换为另一个排列 \(q_i\)。

定义生成树 \(T\) 是 yummy 的，如果存在以下操作序列：

1. 每次选择 \(T\) 中的一条边 \(e = (x, y)\)，交换 \(p_x\) 和 \(p_y\) 的值，并删除 \(e\)。
2. 经过 \(n-1\) 次操作后，所有顶点的值恰好变为目标排列 \(q\)。

任务是统计图 \(G\) 中所有 yummy 生成树的数量，结果对 \(10^9 + 7\) 取模。两个生成树不同当且仅当边集不同。

题解

对节点重标号，使得 \(p_i=i\)，之后考虑置换环。

初始时 \(p_i=i\)，每个节点自成一个环。

每次操作两个属于不同置换环的点，相当于合并两个环。由于是按照树边操作，所以同一个节点不可能被合并两次。说人话就是每次合并都会恰好合并两个环。

那么 \(n-1\) 次操作后就只有一个置换环了，所以如果 \(\{p\}\to \{q\}\) 有多余的置换环，则无解。

然后考虑倒着操作，分裂置换环，发现操作在置换环上不能交叉。同时，如果满足所有操作（即树上的边）在操作环上不交叉，则容易证明可以构造出一种方案。

然后再次根据置换环顺序重标号，问题为对【所有边要么包含要么不交】的树进行计数。

区间 DP，令 \(f_{l,r}\) 表示区间 \([l,r]\) 构成满足条件的树的方案数，令 \(g_{l,r}\) 表示区间 \([l,r]\) 【满足条件 A】的方案数，最终答案为 \(f_{1,n}\)。

条件 A 为：

1. 构成两个连通块，每个连通块都是一个满足条件的树。
2. 连通块内的编号是连续的。

初始时 \(f_{x,x}=1,g_{x,x}=0\)。

转移时，枚举 \(l\) 向后连接的最后一条边，有 \(f_{l,r}=\sum\limits_{k=l}^{r} c_{l,k}\times g_{l,k}\times f_{k,r}\)，\(g_{l,r}=f_{l+1,r}+\sum\limits_{k=l}^{r} c_{l,k}\times g_{l,k}\times g_{k,r}\)。

时间复杂度 \(O(n^3)\)。

提交记录

[USACO25JAN] Table Recovery S 蓝

题意

Bessie 有一个 \(N\times N\)（\(1\le N\le 1000\)）的加法表，其中对于所有 \(1\le r,c\le N\)，第 \(r\) 行第 \(c\) 列的方格中的整数为 \(r+c\)。

不幸的是，Elsie 得到了这张表格，并通过执行若干次以下三种类型的操作对表格进行了变换。

1. 交换两行；
2. 交换两列；
3. 选择两个同时存在于表格中的值 \(a\) 和 \(b\)，然后同时将每一个 \(a\) 更改为 \(b\)，每一个 \(b\) 更改为 \(a\)。

Elsie 总是按类型顺序执行操作；也就是说，她首先执行任意数量（可能为零）的类型 \(1\) 操作，然后是类型 \(2\) 操作，最后是类型 \(3\) 操作。

请帮助 Bessie 恢复 Elsie 在执行完所有类型 \(1\) 和 \(2\) 操作后，但在执行任意类型 \(3\) 操作之前，表格的一种可能状态。可能存在多种可能的答案，在这种情况下你应当输出字典序最小的答案。

题解

考虑出现一次的数的所对行一定是 \(2\sim n+1\) 或 \(n+1\times 2n\)。

如果已经知道了【这个数的出现次数】和【这个数是否大于等于 \(n+1\)】两个条件，那么这个数唯一确定。

因此讨论出现两次的数，哪个是 \(2\)，一共有两种情况，这两个数确定后根据上面的性质遍历这两个数所在的行，可以唯一确定每个数原来是什么。也就是说最后只有两种情况，比较这两种情况的字典序，然后输出较小的即可。

提交记录

[USACO25FEB] The Best Lineup S 绿

题意

FJ 将以以下方式构造另一条队伍 \(b\)：

• 初始时，\(b\) 为空。
• 当 \(a\) 非空时，移除 \(a\) 最前面的奶牛，并选择是否将该奶牛添加到 \(b\) 的最后。

在 FJ 构造队伍 \(b\) 之前，他可以执行以下操作至多一次：

• 选择队伍 \(a\) 中的一头奶牛，并将其移动至当前位置之前的任意位置。

求他可以达到的字典序最大的 \(b\) 的编号序列。

题解

考虑如果不进行交换，直接取【等于后缀最大值】的数字形成 \(b\) 是最优的。

然后考虑一个位置的后缀最大值和后缀次大值，理想情况一定是先最大后次大。

所以从前往后枚举，找到第一个【后缀次大值在后缀最大值后面】的位置，把次大值交换到最大值前面即可。

提交记录

CF2066D1. Club of Young Aircraft Builders (easy version) *2400

题意

对满足以下条件的长度为 \(m\) 的序列 \(a\) 计数：

• \(a_i\in [1,n]\)。
• 值为 \(n\) 的数恰好出现了 \(c\) 次，且对于任意 \(i\)，\(\sum\limits_{j=1}^{i}[a_j\geq a_i]\leq c\)。

题解

考虑从大到小填数，填到 \(i\) 时，假设已经填了 \(x\) 个比 \(i\) 大的数字，那么可以分析证明 \(i\) 填完之后的位置必须 \(\leq c\)，同时容易证明这个条件是充要的。

因此令 \(f_{i,j}\) 表示只考虑高 \(i\) 层楼，填写 \(j\) 个数的方案数。

有 \(f_{i,j}\times \binom{c}{k}\to f_{i+1,j+k}\)。

提交记录

CF2066D2. Club of Young Aircraft Builders (hard version) *2900

题意

对满足以下条件的长度为 \(m\) 的序列 \(a\) 计数：

• \(a_i\in [1,n]\)，某些位置上的数字已经确定。
• 值为 \(n\) 的数恰好出现了 \(c\) 次，且对于任意 \(i\)，\(\sum\limits_{j=1}^{i}[a_j\geq a_i]\leq c\)。

题解

由于某些位置固定，因此 D1 的做法失效了。

考虑 \(1\) 可以填的位置，显然只能填在前 \(c\) 个。

考虑 \(2\) 可以填的位置，由于 \(2\) 前面 \(\geq 2\) 的不能超过 \(c\)，因此 \(2\) 只能填在前 \(c+cnt_1\) 个。

归纳证明 \(x\) 只能填在 \(c+\sum\limits_{i=1}^{x-1} cnt_i\) 个。

然后考虑已经填的位置的贡献，可以 \(O(nm)\) 预处理出前 \(i\) 个已经确定的数中 \(\geq j\) 的数 \(ge_{i,j}\)。

此时发现一个数依赖比它小的数的状态，因此从小到大填数，令 \(f_{i,j}\) 表示

转移 \(f_{i,j}\) 时，\(i+1\) 可以填入的最大位置为 \(pos=\min(j+c,m)\)，通过 \(pos-ge_{pos,i+1}-j\) 算出空余的位置。

有 \(f_{i,j}\times \binom{pos-ge_{pos,i+1}-j}{k-C_{i+1}}\to f_{i+1,j+k}\)，其中 \(C_{x}\) 表示一开始已经确定了多少个 \(x\)。

注意判断一开始确定 \(i+1\) 的最大位置编号 \(\geq j+c\) 的情况，此时不进行转移。

提交记录

[USACO21JAN] Spaced Out S 绿

题意

给定一个矩阵，你需要选取若干个位置，满足每个 \(2\times 2\) 方格中恰好有两个被选择，求被选择位置权值之和的最大值。

题解

发现如果同时存在【横向两个连续位置都选】和【纵向两个连续位置都选】，则可以推出矛盾。都不选也是同理的。

那么最终结果要么是每行 01 交替，要么是每列 01 交替，且行列之间独立。

因此维护每行、每列的奇数位置之和、偶数位置之和，然后贪心取最大值即可。

提交记录

[USACO22JAN] Counting Haybales P 紫

题意

有一个长为 \(n\) 的数列 \(h\)，若 \(|h_{i+1}-h_{i}|\leq 1\)，可以交换 \(h_i\) 和 \(h_{i+1}\)。

问最后能得到多少种不同的序列。

题解

核心思路：把数列划分为 \(O(1)\) 个集合，满足每个集合顺序固定，然后按这个顺序 DP。

首先可以发现绝对值相差 \(\geq 2\) 的数对顺序不会改变，且由于改变相同数的位置顺序不会形成新的序列，因此默认相同数相对位置不变。

因此奇偶性相同的数字之间顺序不会改变。

按这个顺序 DP，\(dp_{i,j}\) 表示使用原序列前 \(i\) 个奇数和前 \(j\) 个偶数能组成的集合个数。

预处理一个数往前交换，只考虑奇偶性不同的数带来的限制，能交换到的最前位置 \(p\)。

设 \(odd_{x}\) 表示第 \(x\) 个奇数的位置，\(even_{x}\) 表示第 \(x\) 个偶数的位置。转移时，假设新接入一个奇数，当前已经加入了 \(i\) 个奇数、\(j\) 个偶数，那么如果 \(p_{odd_{i+1}}\leq even_{j}+1\)，则进行转移 \(f_{i,j}\to f_{i+1,j}\)。

复杂度 \(O(n^2)\)。

提交记录

P9479 [NOI2023] 桂花树 黑

题意

小 B 八年前看到的桂花树是一棵 \(n\) 个节点的树 \(T\)，保证 \(T\) 的非根结点的父亲的编号小于自己。给定整数 \(k\)，称一棵 \((n+m)\) 个节点的有根树 \(T^{\prime}\) 是繁荣的，当且仅当以下所有条件满足：

1. 对于任意满足 \(1 \le i,j \le n\) 的 \((i,j)\)，在树 \(T\) 和树 \(T^{\prime}\) 上，节点 \(i\) 和 \(j\) 的最近公共祖先编号相同。
2. 对于任意满足 \(1 \le i,j \le n + m\) 的 \((i,j)\)，在树 \(T^{\prime}\) 上，节点 \(i\) 和 \(j\) 的最近公共祖先编号不超过 \(\max(i,j)+k\)。

注意题目中所有树的节点均从 \(1\) 开始编号，且根结点编号为 \(1\)。\(T^{\prime}\) 不需要满足非根结点的父亲编号小于自己。

小 B 想知道有多少棵 \((n+m)\) 个节点的树是繁荣的，认为两棵树不同当且仅当存在某一个节点在两棵树上的父亲不同。你只输出方案数在模 \((10^9+7)\) 意义下的值。

题解

条件一等价于原树构成新树的一颗虚树。

考虑 \(k=0\) 的情况，条件二相当于每个点和比它小的点求 LCA，所得结果都不超过这个点。

因此考虑从小到大插入点（相当于去掉限制中的 \(\max\)），插入点 \(i\) 时，要么放到一个点下面，要么插到一条边中，设当前树的节点个数为 \(sz\)，一共有 \(2\times sz-1\) 种插入方法。

因此 \(k=0\) 时，答案为 \(\prod\limits_{i=n}^{n+m-1} (2i-1)\)。

考虑 \(k\neq 0\) 的一般情况，沿续刚才的思路，从小到达插入点。

此时插入一个点时，除了刚才所述的情况，还可能在一个边上加入一个空白点，然后在空白点下面方当前节点。（如图）

注意这个空白节点的意思并不是最终这里只有一个节点，加入恰好一个空白节点可以帮助我们在进行插入点时不重不漏的构造出每个最终状态。

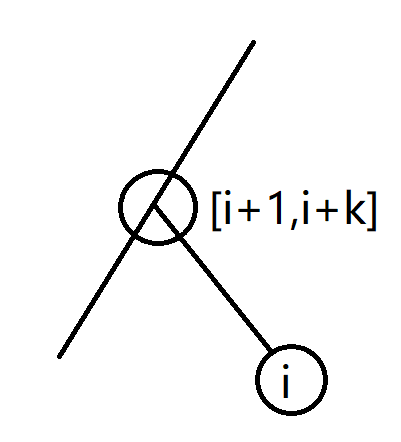
然后考虑状压 DP，\(f_{i,S}\) 表示插入 \(i\) 个点，且前 \(k\) 次操作形成的白点占用情况为 \(S\) 的方案数。

当这次操作没有形成白点或白点已经被占时 \(S\) 这一位为 \(0\)，否则 \(S\) 这一位为 \(1\)。

转移分为三种情况：

• 插到一条边中或挂到一个点下面。
• 在一个边上加入一个空白点，然后在空白点下面方当前节点。
• 填上一个空白点

注意当前树的大小不是 \(i\)，而是 \(i+\operatorname{popcount}(S)\)。

最后答案好像和树的形态没关系（雾）。

提交记录

P12030 [USACO25OPEN] OohMoo Milk G 紫

题意

给定一个数组，重复以下操作 \(d\) 次：

• 将前 \(A\) 大的数字加 \(1\)。
• 将前 \(B\) 大的数字减 \(1\)。

满足 \(A\geq B\)。

求最终数组的平方和。

题解

首先 \(B\leq A\)，所以操作 2 肯定也只能操作到前 \(A\) 个数字。

显然可以先把前 \(A\) 大中每个数字加上 \(d\)，之后进行 \(d\) 次操作 2。

于是线段树模拟，可以轻松做到 \(O(d\log n)\)。

然后发现问题其实可以转化成重复 \(d\times B\) 次【给最大值减 \(1\)】的操作，但要保证每个数被减的次数不超过 \(d\)。

注意到每个数被减的次数是单调不增的，维护一个极长的相等段，然后尝试和下一段连续段合并，同时维护最小的 \(l\) 满足 \(l\) 被减的次数 \(<d\)。

使用线段树或树状数组实现区间加和单点求和。

提交记录

P12029 [USACO25OPEN] Election Queries G 蓝

题意

维护一个数组，支持：

• 单点修改。
• 查询把数组分成两个集合，每个集合中取一个众数，两个众数之差的最大值。

题解

注意到：

• \(x,y\) 能作为两个集合的众数，当且仅当 \(cnt_x+cnt_y\geq \max\limits_{i=1}^{n} cnt_i\)。
• 不同的 \(cnt\) 只有 \(\sqrt{n}\) 个。

于是随便维护，只要保证每次遍历当前 \(cnt_x\) 不为 \(0\) 的 \(x\)，就能做到 \(O(Q\sqrt{n})\) 的复杂度。

可以使用 set 维护所有的 \(cnt\)，遍历 set 和取出 set 的最值都不带 \(\log\)。

提交记录

[ABC277Ex] Constrained Sums 紫

题意

构造一个长度为 \(n\) 的序列 \(x\)，满足下列条件：

• \(\forall i\in [1,n],\ 0\leq x_i\leq M\)。
• \(\forall i\in [1,Q],\ L_i\leq x_{a_i}+x_{b_i}\leq R_i\)。

题解

2-SAT 在赋值问题上的应用。

定义 \(n\times (m+2)\) 个变量，代表 \([x_i\geq j](1\leq i\leq n,0\leq j\leq m+1)\)。

之后考虑限制条件。

首先对于 \(x_i\geq 0\)，强制其 \(=1\)，即连边 \(\neg (x_i\geq 0)\to (x_i\geq 0)\)；对于 \(x_i\geq m+1\)，强制其 \(=0\)，连边方式同理。

其次若 \(x_i\geq j\)，则有 \(x_i\geq j-1\)；若 \(\neg (x_i\geq j)\) 则有 \(\neg (x_i\geq j+1)\)，连边方式显然。

最后考虑题目限制。

对于限制 \(L_i\leq x_{a_i}+x_{b_i}\leq R_i\)，可转化为如下限制条件：

• \((x_{a_i}\geq j)\to \neg (x_{b_i}\geq R-j+1)\)。
• \(\neg (x_{a_i}\geq j)\to (x_{b_i}\geq L-j+1)\)。

注意 \(a_i,b_i\) 对称，这里省略了两个对称的条件。

建完图跑 2-SAT 即可。

提交记录

P11844 [USACO25FEB] Friendship Editing G 紫

题意

给定一张 \(N\) 个节点的图，在一次操作中，你可以添加或删除图中的一条边。计算确保以下性质成立所需的最小操作次数：如果存在边 \((a,b)\)，则对于每头其他奶牛 \(c\)，存在边 \((a,c)\) 或者存在边 \((b,c)\)。

\(N\leq 16\)。

题解

妙妙题。

原图不好做，考虑补图，可以归纳证明补图的每个连通块都是完全图。

状压 DP，设 \(dp_{S}\) 表示只考虑集合 \(S\) 的点的最小代价。

每加入一个集合，把集合向外连接的边删掉，之后把集合内没有的边加上。

注意每条修改的边会被两个端点各算一次，因此最终答案要除以 \(2\)。

复杂度 \(O(n^2\times 2^n+3^n)\)。

提交记录

P3209 [HNOI2010] 平面图判定 紫

题意

称可以画在平面上使得任意两条无重合顶点的边不相交的图为平面图。

给定一张 \(N\) 个点 \(M\) 条边的图以及这张图的一个哈密顿回路，判断这张图是否是平面图。

\(N\leq 200,M\leq 10000\)。

题解

将哈密顿回路看成环，一条边要么被画在环内，要么被画在环外。令 \(pos_i\) 表示 \(i\) 在哈密顿回路上的位置编号。

如果两条边 \((a,b),(c,d)\)，满足线段 \([pos_a,pos_b]\) 和 \([pos_c,pos_d]\) 相交，那么 \((a,b)\)，\((c,d)\) 同时画在环内或环外时就会相交。

这相当于 \((a,b)\)，\((c,d)\) 不能同时画在环外或环内，定义 \(M\) 个变量，第 \(i\) 个变量表示第 \(i\) 条边是否画在环内。直接 2-SAT 空间复杂度为 \(O(M^2)\)，无法通过。

引理：去掉重边和自环后，\(M>3\times n-6\) 时无解。

证明：假设一张 \(N\) 个点 \(M\) 条边的图是平面图，那么将图画在平面上，把平面分成 \(F\) 个面。
每条边会恰好计入两个面中，设与面 \(f\) 相邻的面个数为 \(\operatorname{deg}(f)\)，则有 \(\sum\limits_{f} \operatorname{deg}(f)=2\times M\)。
又因为每个面至少由三个边围成，因此 \(\sum\limits_{f} \operatorname{deg}(f)\geq 3\times F\)。
由此可以得出 \(2\times M\geq 3\times F\)，代入欧拉公式 \(N-M+F=2\)，得 \(N-M+\frac{2\times M}{3}\geq 2\)，化简得 \(M\leq 3\times N-6\)。\\ \
因此 \(M>3\times n-6\) 时无解。

提交记录

P5332 [JSOI2019] 精准预测 黑

题意

火星小镇上有 \(n\) 个居民。有 \(m\) 个预测，每个预测都是如下两种形式之一：

1. \(0\ t\ x\ y\)：在 \(t\) 时刻，如果 \(x\) 是死亡状态，那么在 \(t+1\) 时刻，\(y\) 是死亡状态。（注意，当 \(x\) 在 \(t\) 时刻是生存状态时，该预测也被认为是正确的）；
2. \(1\ t\ x\ y\)：在 \(t\) 时刻，如果 \(x\) 是生存状态，那么在 \(t\) 时刻，\(y\) 是死亡状态。（注意，当 \(x\) 在 \(t\) 时刻是死亡状态时，该预测也被认为是正确的）。

注意本题是对某个时刻进行生死状态的预测，如果某个人在 \(t\) 时刻是生存状态，在 \(t+1\) 时刻是死亡状态，你可以认为是在 \(t\) 到 \(t+1\) 这段时间内发生了某个事件导致其死亡。

JYY 希望为每个火星人 \(k\) 计算：

\[\sum_{1 \leq i \leq n,\, i \neq k} \operatorname{Live}(k,i) \]

其中 \(\operatorname{Live}(i,j) = 1\) 表示编号为 \(i\) 和 \(j\) 的火星人有可能同时在第 \(\max\{t\} + 1\) 时刻处于生还状态，否则 \(\operatorname{Live}(i,j) = 0\)。

注意 \(\operatorname{Live}\) 为每一对火星人分别独立计算。火星人是不能够复活的，火星人在任何时候都可能死亡，但任意时刻观察到火星人的状态要么活着，要么死亡。

\(\max\{t\} \leq 10^6\)，\(n \leq 5 \times 10^4\)，\(m \leq 10^5\)。

题解

记 \(T = \max\{t\}\)。

令点 \((i,j)\) 表示 \(i\) 在 \(j\) 时刻活着的状态，\(\neg(i,j)\) 表示 \(i\) 在 \(j\) 时刻死掉的状态。记 \(alive(x) = (x, T+1)\)，\(dead(x) = \neg(x, T+1)\)。

考虑连边方式，和上一题差不多的考虑顺序。基本的限制是：

• 如果 \(i\) 在 \(t\) 活着，那么他在 \(t-1\) 肯定也活着；
• 如果 \(i\) 在 \(t\) 死掉了，那么他在 \(t+1\) 时刻肯定是死掉的。

因此连边：

• \((i,t) \to (i,t-1)\)
• \(\neg(i,t) \to \neg(i,t+1)\)

然后考虑题目要求：

1. 对于 \((0,t,x,y)\)，连边：\(\neg(x,t) \to \neg(y,t+1)\)，\((y,t+1) \to (x,t)\)；

2. 对于 \((1,t,x,y)\)，连边：\((x,t) \to \neg(y,t)\)，\((y,t) \to \neg(x,t)\)。

发现点的个数是 \(O(T\times n)\) 的，爆炸了。

因此考虑省掉一些没有用的点，对于每个人只保留在【题目要求】部分连边被用到的时间，这样点个数就是 \(O(n+m)\) 了。

注意到这是一个 DAG，因为：

• 连接【生】状态之间的边都是 \(t\) 大的指向 \(t\) 小的；
• 连接【死】状态之间的边都是 \(t\) 小的指向 \(t\) 大的；
• 跨越【生】【死】状态的边都是【生】指向【死】的。

所以可以不用缩点。

如果 \(\operatorname{Live}(i,j)=0\)，那么 2-SAT 图缩点后存在一条 \(alive(i) \to dead(j)\) 的边。

不难想到 \(O(n \times (n + m))\) 的暴力：对于每个点 \(p\)，从 \(p\) 开始 DFS，统计搜到的 \(dead(x)\) 个数 \(cnt\)，当 \(alive(p)\) 能到达 \(dead(p)\) 时答案为 \(0\)，否则答案为 \(n - cnt - 1\)。

注意 \(cnt\) 还要算上 \(alive(x)\) 能到达 \(dead(x)\) 这种本来就必死的人。

DAG 上的连通性问题很难继续优化了，因此考虑使用 bitset。

维护 bitset \(f_i\) 表示 \(i\) 能到达的 \(dead\) 集合，反向拓扑一遍即可。

由于空间复杂度 \(O\left(\frac{n \times (n + m)}{w}\right)\) 会炸，考虑时间换空间，把 \(f\) 值域分若干段，每段长度为 \(B\)，然后做 \(\frac{n}{B}\) 次反向拓扑然后拼起来。可以令 \(B = 2 \times 10^4\)。

将反向拓扑改成记忆化搜索实现会简单些。

提交记录

csp-s模拟测验 T3 赛道设计

题意

构造一个多边形，提供起点的坐标和 \(n\) 个拐点的坐标，坐标必须在 \(0\) 到 \(10^3\)之间，而且起点和所有拐点共 \(n+1\) 个点的坐标不能重复，不允许有线段相交。

给定一个含 L,R 的字符串，对于每个拐点，拐弯方向字符串指定。

题解

考虑有解条件，由于最后要形成闭环，开始可以提供 \(90°,0°,-90°\) 中的任意一个，因此需要满足 \(3\leq |cnt_l-cnt_r|\leq 5\)。

全是 L 或全是 R 是很好构造的。

考虑将原字符串每次删去一个 LR 或 RL，构造出全是 L 或全是 R 的基本图形，再往里面插入 LR 或 RL。

插入时，假设要在 \(pos\) 到 \(pos+1\) 个点插入 LR，记 \(pos\) 到 \(pos+1\) 的方向为 \(drc\)，将 \(pos\) 的 \(drc\) 方向上所有点全部平移 \(1000\) 格，再将 \(pos\) 的 \(L_{drc}\) 方向上所有点全部平移 \(1000\) 格，然后直接插入。

最后对点进行离散化即可。

P4637 [SHOI2011] 扫雷机器人 紫

题意

在一个直线上排列着 \(n\) 个地雷，第 \(i\) 个地雷的坐标为 \(x_i\)，爆炸威力为 \(d_i\)。若地雷 \(i\) 被引爆，则所有满足 \(|x_i - x_j| \le d_i\) 的地雷 \(j\) 也会被引爆（间接引爆可继续传播）。每次操作从未被引爆的地雷中等概率随机一个地雷进行引爆。求所有地雷都被引爆的期望操作次数。

\(n\leq 4000\)。

题解

若 \(i\) 能引爆 \(j\)，则进行连边 \(i\to j\)，最后形成一张有向图。对有向图进行 SCC 缩点，变成一个 DAG。

原问题转化为 DAG 上的问题，每个点有点权。

发现不能直接 DP，因此考虑推一些性质。

将原问题等价成：进行 \(n\) 次操作，每次随机选择一个未被选择过的点，如果被选择的点没有引爆，引爆它。求实际进行引爆的操作次数的期望。

进一步，这相当于随机一个排列，然后按顺序操作。

拆每个 SCC 的贡献，这个 SCC 被引爆当且仅当【当前 SCC 中的一个点】排到了【所有能到达当前 SCC 的点】的前面。

设第 \(i\) 个 SCC 的大小为 \(sz_i\)，能到达第 \(i\) 个 SCC 的点个数为 \(cnt_i\)（包括第 \(i\) 个 SCC 内部的点），那么上述条件发生在第 \(i\) 个 SCC 的概率为 \(\frac{sz_i}{cnt_i}\)。

这是因为我们可以只考虑能到达第 \(i\) 个 SCC 的点构成的排列，第一个元素确定后，排列的后 \(cnt_i-1\) 项方案数恒为 \((cnt_i-1)!\)，而排列的第一个元素是第 \(i\) 个 SCC 内的元素的概率为 \(\frac{sz_i}{cnt_i}\)。

使用 bitset 维护能到达每个 SCC 的集合。

复杂度为 \(O(\frac{n\times m}{w})=O(\frac{n^3}{2w})\approx 5\times 10^8\) ，实际上边数远远达不到 \(O(n^2)\)，因此可以通过，极限数据用时 \(31\) ms。

提交记录

CF1361E James and the Chase *3000

题意

给定一张 \(n\) 个点，\(m\) 条有向边的强连通图，如果一个点到其余点都只有恰好一条简单路径，则称这个点是“好点”。

如果“好点”个数不少于 \(0.2\times n\)，则输出所有“好点”，否则输出 -1。

题解

考虑如何判断一个点是否是“好点”，由于给定的图是强连通图，所以从任意一个点 DFS 都能到达所有点，考虑以这个点为根建立 DFS 树，那么这个点是“好点”当且仅当这个 DFS 树不存在前向边和横叉边。

发现一个以“好点”为根的 DFS 树只有返祖边，这是一个很好的性质，因此考虑如何从这颗 DFS 树上得出其他的“好点”。

首先因为 DFS 树没有前向边和横叉边，因此每个点到子树内的点都只有一条简单路径，一个点不是“好点”，当且仅当这个点到子树外某个点有 \(>1\) 条简单路径。

考虑每个点被返祖边覆盖的情况，由于是强连通图，每个点至少被一条返祖边覆盖。

如果一个点被两条及以上返祖边覆盖，那么容易说明，这个点到它的父节点有两条以上的简单路径，因此这个点不是“好点”。

否则，这个点被恰好一条返祖边覆盖，设这个点是 \(x\)，覆盖它的返祖边为 \(u\to v\)。

当 \(v\) 不是“好点”时，说明 \(v\) 到子树外的某个点 \(t\) 有两条简单路径，且这条路径不能经过子树 \(x\)，否则 \(x\) 就被两个返祖边覆盖了。也就是说 \(x\to v\) 的路径拼上 \(v\to t\) 的两条路径都是简单路径，\(x\) 不是“好点”。

当 \(v\) 是“好点”时，说明 \(v\) 所有点都只有一条简单路径，此时有：

• 对于 \(x\) 子树内的点，显然 \(x\) 到这些点只有一条简单路径。
• 对于 \(x\) 子树外的点，\(x\) 到这些点的唯一方法是先到 \(v\)，再从 \(v\) 到这些点，由于 \(v\) 合法，因此 \(x\) 到这些点也只有一条简单路径。

整理一个点是“好点”的条件（不含根节点）：

• 只被一条返祖边覆盖。
• 沿着返祖边走到的点是“好点”。

使用简单的树上 DP 即可求出所有“好点”。

此时还有一个遗留问题，如何找出第一个“好点”？

由于题目只要求“好点”个数大于 \(0.2\times n\) 时才需要输出，因此随机 \(100\) 次，每次选择一个点建树判断，如果随机不出来则输出 -1，复杂度 \(O(n+m)\)，\(100\) 倍常数。

提交记录

P5338 [TJOI2019] 甲苯先生的滚榜 紫

复习平衡树。

提交记录

P4146 序列终结者 紫

复习文艺平衡树。

提交记录

【模板】可持久化平衡树 模板

学习可持久化平衡树。

提交记录

CF1989F Simultaneous Coloring *3000

题意

有一个 \(n\times m\) 的空白矩阵，你可以进行任意次如下操作：

• 花费 \(0\) 代价，将某一行染成红色，或将某一列染成蓝色。该操作会覆盖原先这一 行/列 的颜色。
• 花费 \(k^2\) 代价，同时执行 \(k\) 次操作 1，并任意指定冲突位置（即被超过一个操作覆盖的格子）的颜色。

有 \(q\) 个限制，每个限制形如 \((x,y,c)\)，表示矩阵的 \((x,y)\) 位置必须染成颜色 \(c\)。

对于 \(1\leq i\leq q\) 的每个 \(i\)，计算从空白矩阵开始操作，满足限制 \(1\sim i\) 的最小代价。

\(n,m,q\leq 2\times 10^5\)。

题解

如果要求 \((i,j)\) 是红色，那么说明【对第 \(j\) 列操作】一定在【对第 \(i\) 行操作】之后，对这个限制进行图论建模，连边 \(i\to j\)。 如果要求 \((i,j)\) 是蓝色，那么连边 \(j\to i\)。

考虑如何对单次询问计算答案，SCC 缩点后，同一个 SCC 内显然是矛盾的，需要花费 SCC 大小平方的代价（大小为 \(1\) 的 SCC 代价是 \(0\)）。SCC 之间的图一定是 DAG，按照拓扑序操作即可。

那么我们要做的就是动态加入有向边，查询所有 SCC 大小的平方和减去大小为 \(1\) 的 SCC 个数。

发现如果加入的是无向边，可以直接并查集。考虑动态维护有向图连通性的套路，使用整体二分算出每条边加入 SCC 的时间，之后按照无向边计算。

注意整体二分的时候不应该把边拆成操作和询问，因为动态加边的 SCC 本身是非常难维护的，所以应该把边当成操作和询问合一的东西，然后用并查集把已经加入 SCC 的边缩到一个点中，其余边进入右侧二分结构。之后撤销后再进入左侧二分结构。

具体地，整体二分 solve(ansL,ansR,edges[]) 的流程如下：

全局实时维护可撤销并查集，如果当前二分区间为 \([ansL,ansR]\)，则并查集已经将编号在 \([1,ansL)\) 中的边加入，并把 SCC 缩成了一个点。

• 当 \(ansL=ansR\) 时记录答案并返回。
• 记 \(mid=\frac{ansL+ansR}{2}\)，将出现时间在 \(mid\) 之前的边加入缩好点的图中（即外层并查集维护的图），并对原来缩好点的图再次进行缩点，更新并查集。
• 检查所有出现时间在 \(mid\) 之前的边，将两端点在同一 SCC 内的边拿出来，进入右侧递归。
• 撤销第二步并查集的操作。
• 将剩余的边拿出来，进入左侧递归。

提交记录

P4315 月下“毛景树” 蓝

复习树链剖分。

提交记录

P3401 洛谷树 紫

题意

给定一棵树，维护两种操作：

• 1 u v，求 \(u\to v\) 的路径中【所有子路径的异或和】的算数和。
• 2 u v w，将边 \((u,v)\) 的权值改成 \(w\)，保证 \((u,v)\) 存在。

题解

虽然可以直接序列做法上树，但是有更巧的做法。

维护 \(a_u\) 表示 \(u\) 到根链的异或和，路径 \(u\to v\) 的异或和可以表示为 \(a_u\operatorname{xor} a_v\)。

拆位，设路径 \(u\to v\) 上的 \(2^w\) 位有 \(cnt1\) 个 \(1\)，\(cnt0\) 个 \(0\)，那么这一位的贡献就是 \(2^w\times cnt1\times cnt0\)。

修改时只需要将到根链翻转，使用树剖维护即可。

提交记录

P3676 小清新数据结构题 紫

题意

给定一棵树，维护两种操作：

• 1 x y，将 \(x\) 的点权改为 \(y\)，即 \(val_x\leftarrow y\)。
• 2 x，以 \(x\) 为根，求所有子树点权和的平方和，即求 \(\sum\limits_{u=1}^{n} (\sum\limits_{v\in \operatorname{subtree}(u)} val_v)^2\)。

\(n\leq 2\times 10^5\)。

题解

对于操作二，保持以 \(1\) 为根，不在 \(x\) 到根链上的点查询的仍然是以 \(1\) 为根的子树 \(x\)，在 \(x\) 到根链上的点查询的是 \(x\) 方向节点的子树补，节点 \(x\) 查询的是全局。

因此分类讨论即可，把序列维护平方和的方法用树链剖分搬到树上。

线段树上维护 \(\sum 1,\sum val,\sum sz,\sum val\times sz,\sum val^2,\sum sz^2\)。

提交记录

P5391 [Cnoi2019] 青染之心 紫

题意

Cirno 初始有一个空的物品序列，一个大小为 \(V\) 的背包，现在你有 \(q\) 个操作，分为两种：

• add x y：表示加入一种体积为 \(x\), 价值为 \(y\) 的物品到序列末尾。
• erase：表示删除序列末尾的物品。

在每个操作结束以后，你需要求出：

假设序列中的每种物品都有无穷多个，Cirno 的背包可以装下的物品最大价值和。

\(q,V\leq 2\times 10^4\)，5s，64MB。

题解

将操作视为一棵树，暴力做，发现时间可以接受，空间接受不了。

树链剖分，每个重链维护一个 DP 数组，在树上 DFS 时需要维护这个点到根链的 DP 数组，因此可以划分为不超过 \(O(\log n)\) 个重链。

维护 \(dp_{lev,x}\) 表示经过 \(lev\) 条重链，重量为 \(x\) 的最大价值。

之后处理加入物品，往下 dfs 即可。

提交记录

P5314 [Ynoi2011] ODT 黑

题意

给你一棵树，边权为 \(1\)，有点权。

需要支持两个操作：

• 1 x y z：表示把树上 \(x\) 到 \(y\) 这条简单路径的所有点点权都加上 \(z\)。
• 2 x y：表示查询与点 \(x\) 距离小于等于 \(1\) 的所有点里面的第 \(y\) 小点权。

题解

考虑每个点维护一颗平衡树表示其子节点构成的集合，直接树剖+树套树是三只 \(\log\) 的，过不去。

考虑让平衡树契合树链剖分的结构，每个点维护一颗平衡树表示其轻儿子构成的集合，这样一次路径修改只需要改 \(O(\log n)\) 个节点的平衡树，总复杂度双 \(\log\)。

提交记录

P5642 人造情感（emotion） 黑

题意

给你一颗 \(n\) 个节点的树，以及 \(m\) 条路径 \((u, v, w)\)，其中 \(w\) 可以认为是 \((u, v)\) 这题路径被标记的一个权值。一个路径集合 \(S\) 的重量 \(W(S)\) 记为：找出 \(S\) 的一个权值之和最大的子集，该子集满足任何两条路径没有公共点，这个子集的所有路径权值之和就是 \(W(S)\)。

记 \(f(u, v) = w\) 为最小的非负整数 \(w\)，使得对于给定的 \(m\) 条边组成的路径集合 \(U\)，\(W(U \cup \{(u, v, w + 1)\}) > W(U)\) 。

请你计算下式，对 \(998244353\) 取模。

\[\sum_{u=1}^n \sum_{v=1}^n f(u, v) \]

题解

Part1. 求 \(W(S)\)

考虑 DP 先求出 \(W(S)\)。

令 \(f_u\) 表示 \(u\) 子树内，\(u\) 点可用可不用的答案。

令 \(g_u\) 表示 \(u\) 子树内，\(u\) 点必须不用的答案。

令 \(c_u=g_u-f_u\)，表示将 \(u\) 空出来的代价。

考虑转移，把每个路径挂在路径的 lca 上，有：

\[g_x\leftarrow \sum\limits_{y\in son_x} f_y \\ f_x=g_x+\max(0,\max\limits_{\operatorname{lca}(u_j,v_j)=x}\{w_j+\sum\limits_{k\in \operatorname{path}(u_j,v_j)}c_k\}) \\ W(S)=f_1 \]

这部分转移需要支持单点修改，路径查询，将路径差分成到根链，之后转化为子树修改，单点查询，使用树状数组即可。

Part2. 求单个 \(F(i,j)\)

考虑加入一条边 \((u,v,w+1)\) 让独立集变大，那么要求这条边一定被选，仿照 DP 中选一条边的方式，有 \(F(i,j)=-\sum\limits_{k\in \operatorname{path}(i,j)} c_k\)。

当然，这是错的。

因为 \(c_u\) 定义中，【将 \(u\) 空出来的代价】只考虑了子树内的路径，我们还需要考虑子树外的路径，也就是说不存在一个经过 \((fa_{\operatorname{lca}(i,j)},\operatorname{lca}(i,j))\) 的路径被选择。

令 \(h_u\) 表示整棵树空出 \((fa_{u},u)\) 的答案，则空出 \((fa_{u},u)\) 的代价为 \(h_u-f_1\)，有：

\[F(i,j)=-\sum\limits_{k\in \operatorname{path}(i,j)} c_k-(h_{\operatorname{lca}(i,j)}-f_1) \]

Part3. 求 \(h\)

问题在于如何求 \(h\)，初值有 \(h_1=f_1\)，仿照求 \(W(S)\) 中【朴素转移+强制选路径转移】设计 \(h\) 的转移：

\[h_x\leftarrow h_{fa_x}+c_{fa_x} \\ h_x\leftarrow h_{\operatorname{lca}(u,v)}+w+\sum\limits_{k\in \operatorname{path}(u,v)} c_k\ \ \ ((u,v,w)\in S\land x\notin \operatorname{path}(u,v)\land fa_x\in \operatorname{path}(u,v)) \]

对于第二种转移，解释为强制选择路径 \((u,v,w)\)，这样能保证 \((x,fa_x)\) 不被选。

对于第一种转移，解释为强制去掉 \(fa_x\) 子树外经过 \((fa_{fa_x},fa_x)\) 的路径（由 \(h\) 保证）和 \(fa_x\) 子树内经过 \(fa_x\) 的路径（由 \(c\) 保证），如果去掉的路径不经过 \((x,fa_x)\) 也没关系，因为这样一定能被第二种转移覆盖到。

对于第二种转移的优化，考虑给路径上每个点打标记 \((u,x,y,z)\)，表示在节点 \(u\)，值为 \(x\)，不能下传到 \(y,z\)。

下传标记时，将标记从大到小排序遍历，每次只操作没有被下传过的子节点，保证每个点的子节点只被操作一次，这样复杂度是 \(O(标记个数)\) 的。

考虑重链剖分，每条路径上大多数标记都是 \((u,x,\operatorname{heavy\_child}_u,0)\)，其余标记不超过 \(O(\log n)\) 个。

对于 ，维护 \(t_u\) 表示 \(x\) 最大的 \((u,x,\operatorname{heavy\_child}_u,0)\)。\(t_u\) 的修改相当于树的链上取 \(\max\)，直接树剖，其余标记个数为 \(O(n\log n)\)，使用上面 \(O(标记个数)\) 的方法。

Part4. 求所有 \(F(i,j)\)

即求：

\[\sum_{i=1}^{n} \sum_{j=1}^{n} \left(-\sum\limits_{k\in \operatorname{path}(i,j)} c_k-(h_{\operatorname{lca}(i,j)}-f_1)\right) \\ =n^2\times f_1-\sum_{i=1}^{n} \sum_{j=1}^{n} h_{\operatorname{lca}(i,j)}-\sum_{i=1}^{n} \sum_{j=1}^{n} \sum\limits_{k\in \operatorname{path}(i,j)} c_k \\ n^2\times f_1-\sum_{k=1}^{n} \left(h_k\times \sum_{1\leq i,j\leq n\land \operatorname{lca}(i,j)=k} 1\right)-\sum_{k=1}^{n} \left(c_k\times \sum_{1\leq i,j\leq n\land k\in \operatorname{path}(i,j)} 1\right) \]

对于每个点 \(u\)，记有 \(p_u\) 条路径的 lca 是 \(u\)，有 \(q_u\) 条路径经过 \(u\)，则答案为：

\[n^2\times f_1-\sum_{k=1}^{n} p_k\times h_k-\sum_{k=1}^{n} q_k\times c_k \]

\(p,q\) 都是好维护的，至此本题所有问题已解决。

提交记录

QOJ #5357. 芒果冰加了空气 *????

题意

给定一颗 \(n\) 个节点的树，求对这棵树进行点分治的方案数（不要求分治中心是重心）。

\(n\leq 5000\)。

题解

考虑树上背包合并 \(u,v\) 时，合并两个点分树的过程，为了保证不重不漏，我们要保证 \(u,v\) 所在的点分树是合并后的点分树的虚树。

发现点分树上 \(u\) 不能低于 \(v\) 的儿子，因为删完 \(v\) 后 \(u\) 和 \(v\) 的儿子不连通了。

其次 \(u,v\) 是相邻的，所以 \(u,v\) 在点分树上必须是祖先关系。

然后对于点分树上 \(u\) 的父亲，由于 \(u,v\) 是祖先关系，\(u\) 的父亲和 \(u\) 是祖先关系，所以 \(u\) 的父亲和 \(v\) 是祖先关系。

之后可以归纳证明 \(u\) 在点分树上的到根链与 \(v\) 在点分树上的到根链互相具有祖先关系，即这两条链形成了一条链。

由于 \(u\) 不能低于 \(v\) 的儿子，\(v\) 同理，且 \(u,v\) 所在的点分树是合并后的点分树的虚树，因此我们确实只需要合并 \(u\) 的到根链和 \(v\) 的到根链。

设 \(u,v\) 在点分树上的到根链的节点数（即深度）分别为 \(n,m\)，这相当于合并长度分别为 \(n,m\) 的序列，逆向思考相当于从 \(n+m\) 的最终序列中选 \(n\) 个作为第一个序列，方案数为 \(\binom{n+m}{n}\)。

设 \(f_{u,i}\) 表示只考虑 \(u\) 子树内的信息，\(u\) 到点分树根节点深度为 \(i\) 的方案数。

则有 \(f_{u,i}\times f_{v,j}\times \binom{i-1+j-k}{i-1}\to f_{u,i+j-k}\)，\(O(n^3)\)。

改成填表法的式子 \(f_{u,z}\leftarrow f_{u,x}\times f_{v,y}\times \binom{z-1}{x-1}\ \ \ (x\leq z\leq x+y)\)。

即 \(f_{u,z}\leftarrow f_{u,x}\times \binom{z-1}{x-1}\times \sum\limits_{y=z-x}^{sz_v}f_{v,y}\)，后缀和优化，将 \(x\) 的范围限制在 \([z-sz_v,z]\)，复杂度为树上背包的复杂度，即 \(O(n^2)\)。

注意背包的复杂度不要写假，确保转移复杂度为 \(sz_u\times sz_v\)，而不是 \((sz_u+sz_v)\times sz_v\)。

提交记录

[AGC001C] Shorten Diameter 绿

题意

给你一棵 \(N\) 个点的无向树，你需要删除一些点，使树的直径小于等于 \(K\)，当且仅当删除某点不会对树的联通性产生影响时才可以删除。问至少删除多少点才可以满足要求。

\(n\leq 2000\)，但复杂度可以更优。

题解

设树 \(T\) 的直径为 \(D\)，有如下性质：

• 若 \(D\) 是偶数，则存在某个顶点 \(v\)，使得从 \(v\) 到其他所有顶点的距离都不超过 \(\frac{D}{2}\)。

• 若 \(D\) 是奇数，则存在某条边 \(e\)，使得从 \(e\) 到其他所有顶点的距离都不超过 \(\frac{D-1}{2}\)。

证明的话就是如果两个直径不交，则连接两个直径的端点可以发现一条更长的路径，推出矛盾。

称 \(v\) 或 \(e\) 为树的中心。

枚举删完后树的中心，删去距离大于 \(\frac{k}{2}\) 的点。

因此统计每个点距离大于 \(\frac{k}{2}\) 的点个数，使用点分治，复杂度 \(O(n\log^2 n)\)。

但是 \(O(n^2)\) 就可以过了。

提交记录

QOJ #4815. Flower's Land *????

题意

给你一颗树，点有点权，对于 \(1\leq i\leq n\) 的每个 \(i\)，求满足以下条件的连通块的点权之和最大值：

• 包含点 \(i\)。
• 大小为 \(k\)。

\(n\leq 40000,k\leq 3000\)，8s，2048MB。

题解

发现本题严格不弱于 P6326 Shopping，考虑点分治处理连通块，对于每一层，本质上是要解决这样的问题：

• 选一个包含分治中心且包含点 \(i\) 的连通块，大小为 \(k\)，权值最大化。

考虑按 dfn 转移，以分治中心为根 dfs，如果不选 \(x\)，那么就不能选 \([x,x+sz[x]-1]\) 的所有点。

令 \(f_{i,j}\) 表示 \(dfn\in [1,i)\)，选 \(j\) 个点的答案，\(g_{i,j}\) 表示 \(dfn\in [i,sz[rt]]\)，选 \(j\) 个点的答案。

则有：

\[f_{i+1,j+1}\leftarrow f_{i,j}+a_{Idfn_i} \\ f_{i+sz_{Idfn_i},j}\leftarrow f_{i,j} \\ g_{i,j}\leftarrow g_{i+1,j-1}+a_{Idfn_i} \\ g_{i,j}\leftarrow g_{i+sz_{Idfn_i},j} \]

在更新答案时，为了保证 \(i\) 被选择，需要在转移 \(g\) 的循环内更新答案，在 \(g_i\) 进行第二种转移之前使用 \(f_{i,x}+g_{i,k-x}\) 更新答案，这样 \(g\) 只考虑了 \(i\) 被选择的情况，符合题意。

提交记录

CF2101E. Kia Bakes a Cake *3100

题意

给定一个长度为 \(n\) 的二进制字符串 \(s\) 和一棵包含 \(n\) 个顶点的树 \(T\)。

一个序列 \((v_1, v_2, \ldots, v_m)\) 被称为"优美的"，当且仅当：

• 路径中每个相邻点对的距离必须至少是上一个相邻点对的两倍。
• 路径上的每个点对应的 \(s\) 都为 1。

对于每个 \(1 \le i \le n\land s_i = \mathtt{1}\) 的 \(i\)，求 \(v_1=i\) 的优美序列的最长长度。

题解

真的有 *3100 吗？

注意到答案是 \(O(\log n)\) 级别的，考虑 DP 并把序列长度计入状态，由于还要记起点，倒着 DP，令 \(f_{i,j}\) 表示已经确定序列后 \(j\) 个值，且当前在节点 \(i\)，上一个点到 \(i\) 的距离的最大值。

转移为 \(\operatorname{dist}(i,k)\to f_{k,j+1}\ \ \ (\operatorname{dist}(i,k)\leq \frac{f_{i,j}}{2})\)。

使用点分治优化转移，可以做到 \(O(n\log^3 n)\)。

最后 \(i\) 的答案为满足 \(f_{i,x}\neq 0\) 的最大的 \(x\)。

提交记录

P2500 [SDOI2012] 集合 紫

题意

给出n个点m条边的带权无向图，有3个集合A、B、C。一开始无向图中所有点都属于A集合，有如下 \(9\) 种操作：

MoveP x：表示将第x个点从所在集合中删除，并加入至 P 集合。（\(P\in \{A,B,C\}\)）

AskPQ：询问两个端点分别属于P集合和Q集合的所有边中最小的权值是多少。（\(P,Q\in \{A,B,C\}\)）

\(n<=100000,m<=500000,q<=100000\)。

题解

维护 \(6\) 个集合 \(s_{P,Q}\) 表示 \(P,Q\) 集合之间的边，然后暴力修改，发现复杂度爆炸了。

于是根据点的度数根号分治。

对于度数小于 \(\leq \sqrt{m}\) 的点按上述暴力，度数大于 \(\sqrt{m}\) 的点最多 \(\sqrt{m}\) 个，对这些点维护三个集合，表示这些点向 \(A,B,C\) 的连边。

每次修改枚举所有度数大于 \(\sqrt{m}\) 的点。最后复杂度 \(O(n\sqrt{m}\log m)\)。

提交记录

P8250 交友问题 蓝

题意

给定一张无向图，每次询问给两个点 \(u,v\)，求【与 \(u\) 距离为 \(1\) 的点】中，满足【与 \(v\) 距离 \(>1\)】的点的个数。

\(n,q\leq 2\times 10^5,m\leq 7\times 10^5\)。

题解

下文中，“\(x\) 的邻域”指距离 \(x\) 恰好为 \(1\) 的点。

根号分治。

• \(deg_u,deg_v\leq B\)
  • 暴力，在 \(v\) 和 \(v\) 的邻域打上标记，暴力枚举 \(u\) 的邻域，计算没有被标记的点个数 \(t\)，答案为 \(t\)。复杂度 \(O(q\times B)\)。
• \(deg_u\geq B\)
  • 不同的 \(u\) 只有 \(\frac{n}{B}\) 个。
  • 询问离线并去重，对于相同的 \(u\)，先在 \(u\) 的邻域打上标记，然后对于每个不同的 \(v\)，暴力枚举邻域，计算被标记的点个数 \(t\)，答案为 \(deg_u-t\)。对于相同的 \(u\)，每个不同的 \(v\) 只会被算一次，总复杂度 \(O(\sum\limits_{i=1}^{n} deg_i)=O(m)\)。
  • 一共有 \(\frac{n}{B}\) 个不同的 \(u\)，这部分总复杂度 \(O(\frac{n\times m}{B})\)。
• \(deg_v\ge B\)
  • 不同的 \(v\) 只有 \(\frac{n}{B}\) 个。
  • 询问离线并去重，对于相同的 \(v\)，先在 \(v\) 和 \(v\) 的邻域打上标记，然后对于每个不同的 \(u\)，暴力枚举邻域，计算没有被标记的点个数 \(t\)，答案为 \(t\)。对于相同的 \(v\)，每个不同的 \(u\) 只会被算一次，总复杂度 \(O(\sum\limits_{i=1}^{n} deg_i)=O(m)\)。

令 \(q\times B=\frac{n\times m}{B}\)，即 \(B=\sqrt{\frac{n\times m}{q}}\)，时间复杂度 \(O(q\sqrt{\frac{n\times m}{q}})\)。

提交记录

CF1270F. Awesome Substrings *2600

题意

给定一个 \(n\) 位二进制字符串，求满足以下条件的子串数量：

• 至少包含 \(1\) 个 \(1\)。
• 长度能被其中 \(1\) 的个数整除。

\(n\leq 2\times 10^5\)。

题解

根号分治。

转化成前缀和，答案为 \(\sum\limits_{k=1}^{n}\sum\limits_{i=1}^n\sum\limits_{j=0}^{i-1} [k\times (s_i-s_j)=i-j]=\sum\limits_{k=1}^{n}\sum\limits_{i=1}^n\sum\limits_{j=0}^{i-1} [k\times s_i-i=k\times s_j-j]\)。

当 \(k\leq \sqrt{n}\) 时暴力枚举 \(k\)，对每个 \(k\) 暴力 \(O(n)\) 计算答案，这部分复杂度位 \(O(n\sqrt{n})\)。

当 \(k>\sqrt{n}\) 时 \(1\) 的个数 \(\leq \sqrt{n}\)，因此枚举左端点和 \(1\) 的个数，确定右端点所在区间，\(O(1)\) 计算答案，这部分复杂度位 \(O(n\sqrt{n})\)。

时间复杂度 \(O(n\sqrt{n})\)。

提交记录

CF940F. Machine Learning *2600

题意

给你一个数组 \(a_i\)，支持两种操作：

1. 查询区间 \([l, r]\) 中每个数字出现次数的 \(\text{mex}\)。
2. 单点修改某一个位置的值。

\(n, Q \le 10^5\)。

题解

先离散化，然后带修莫队，本质上要维护一个集合，支持插入、删除、求 \(\text{mex}\)。

这看起来必须要带 \(\log\)，但是注意到题目求的是出现次数的 \(\text{mex}\)，而不同的出现次数只有 \(O(\sqrt{n})\) 个，因此对于每个询问暴力求即可。

提交记录

CF852I Dating *2300

题意

给定一颗树，树上节点有黑色和白色之分，点有点权，每次询问一条路径，求路径上颜色不同且点权相同的点对数量。

\(n,q\leq 10^5\)。

题解

学习树上莫队。

简单容斥，相当于 \(\sum cnt^2-\sum\limits_{白点} cnt^2-\sum\limits_{黑点} cnt^2\)。

然后树上莫队即可。

提交记录

P10590 磁力块 紫

题意

有 \(N\) 块磁石，每个磁石的性质可以用一个五元组 \((x,y,m,p,r)\) 描述，其中 \(x,y\) 表示其坐标，\(m\) 是磁石的质量，\(p\) 是磁力，\(r\) 是吸引半径。

若磁石 \(A\) 与磁石 \(B\) 的距离不大于磁石 \(A\) 的吸引半径，并且磁石 \(B\) 的质量不大于磁石 \(A\) 的磁力，那么 \(A\) 可以吸引 \(B\)。

小取酒有一块磁石 \(L\)，坐标为 \((x_0,y_0)\)，他手持磁石 \(L\) 并保持原地不动，所有可以被 \(L\) 吸引的磁石将会被吸引过来。

在每个时刻，他可以选择更换任意一块自己已经获得的磁石，在 \((x_0,y_0)\) 处吸引更多的磁石。

求小取酒最多能获得多少块磁石。

题解

分块优化 BFS。

朴素 BFS 是 \(O(n^2)\) 的。

记一个点到 \((x_0,y_0)\) 的距离为 \(dis\)，考虑我们对点 \(u\) 进行松弛时，实际上需要找出所有 \(dis\leq r_u,m\leq p_u\) 的点，这是一个二位偏序问题。

分块优化，把节点整体按 \(m\) 排序，每个块内再按 \(dis\) 排序，维护一个指针 \(l\) 表示这个块的前 \(l\) 个已经被访问。每次松弛时，找到第一个满足【块内存在一个 \(m\) 大于 \(p_u\)】的块，对于这个块暴力，对于前面的块，\(m\) 一定符合要求，因为对于每个块 \(dis\) 单增，因此每个块都可以通过移动 \(l\) 指针遍历所有满足条件的点。对于前面的每个块都进行移动指针的操作即可。

总复杂度 \(O(n\sqrt{n})\)。

提交记录

CF455D Serega and Fun *2700

题意

给定长度为 \(n (1 \le n \le 10^5)\) 的序列 \((1 \le a_i \le n)\)，共有 \(q (1 \le q \le 10^5)\) 个询问，支持两种操作：

• 1 l r 将区间 \([l, r]\) 依次向右移动一位，其中 \(a_r\) 移动到 \(a_l\)。
• 2 l r k 询问区间 \([l, r]\) 中 \(k\) 出现次数。

强制在线。

题解

一看就不是 \(polylog\) 能解决的东西，考虑分块，每个块维护一个 deque 和一个桶，移动时如果 \(l,r\) 在同一个块就暴力，否则重构 \(l,r\) 所在的两个块，然后中间的每个块的 deque 弹出最后一个元素并将其加入下一个块的第一个元素，实时维护计数桶。查询就是整块查桶、散块暴力。

提交记录

P11527 [THUPC 2025 初赛] waht 先生的法阵 紫

题意

维护一个内向森林，给定序列 \(\{a\}\)，对于每个 \(1\leq i\leq n\) 的 \(i\)，如果 \(i+\gcd(a_i,i)\leq n\)，则 \(i\) 向 \(i+\gcd(a_i,i)\leq n\) 连有向边，你需要支持：

• 给定 \(l,r,c\)，对于 \(l\leq i\leq r\) 的每个 \(i\)，\(a_i\leftarrow a_i\times c\)。
• 给定 \(x\)，求 \(x\) 的到根链节点的 \(a\) 的和，对 \(998244353\) 取模。

\(n\leq 2.5\times 10^5\)，5s。

题解

与 CF1491H Yuezheng Ling and Dynamic Tree 十分相似。

分块，维护 \(f_i\) 表示 \(i\) 的父亲，\(g_i\) 表示 \(i\) 第一次跳出块的节点标号，\(sum_i\) 表示从 \(i\) 开始跳，第一次跳出块前的权值和。

将修改拆为改 \(f\) 和改 \(a\) 两部分。先讨论改 \(f\)，对于一个 \(i\)，\(\gcd(i,a_i)\) 的个数不超过 \(i\) 的质因数个数，\(\gcd(i,a_i)\) 的总共可能出现的数字个数为 \(\sum\limits_{i=1}^{n} \operatorname{Num\_Of\_PrimeDivisers}(i)=O(埃筛复杂度)=O(n\ln \ln n)\)，因此可以均摊修改复杂度，每次进行修改时暴力重构该块。再讨论改 \(a\)，这个是简单的，记 \(tag_i\) 表示第 \(i\) 个块的 \(a\) 的全局乘法懒标记，散块暴力、整块打 \(tag\)。

设块长为 \(B\)，如果能做到均摊，修改的总时间复杂度为 \(O(B\times n\ln \ln n)\)。

查询直接整块往前跳，跳不了就一步步跳，查询的总时间复杂度为 \(O(m\times \frac{n}{B})\)。

令 \(B\times n\ln \ln n=m\times \frac{n}{B}\)，即 \(B=\sqrt{\frac{m}{\ln \ln n}}\)，总复杂度 \(O(\sqrt{\frac{m}{\ln \ln n}}\times n\ln \ln n)=O(n\sqrt{m\ln \ln n})\)，可以通过这道题。

接下来考虑如何实现修改。

对于每个 \(i\) 的每个不同质因数 \(p\)，维护 \(d_{p,i}\) 表示满足 \(\gcd(i,a_i\times p^{x+1})=\gcd(i,a_i\times p^x)\) 的最小的 \(x\)，再对于每个质数 \(p\) 维护一个 set 表示 \(d_p\) 的非零位置集合（这种方法好像叫做势能 set）。

修改时枚举 \(c\) 的质因子，利用 set 对于每个质因子枚举所有要修改的位置，进行修改并重构块。注意这里修改只改 \(f\) 并重构该块的 \(g,sum\)，不要修改 \(a\)。

一个更简单的维护方法是记 \(rd_i=\frac{i}{\gcd(i,a_i)}\)，每次修改 \(c\) 的一个质因子 \(p\) 时，在 \(rd_i\) 中移除尽可能多的 \(p\)，并贡献给 \(\gcd(i,a_i)\)，如果修改后 \(rd_i\) 中没有 \(p\) 因子，则将 \(i\) 移出 \(p\) 的 set。

最后散块的 \(a\) 暴力改，整块的 \(a\) 打 tag 即可。

查询时如果在散块操作要 pushdown。

提交记录

P6157 有趣的游戏 紫

题意

维护一颗树，点有点权，支持：

• 单点修改
• 给定 \(u,v\)，求 \(\max\limits_{x,y\in \text{path(u,v)}} \{w_x\bmod w_y\}\)，设取到最大值的两点为 \(x,y\)，还需要求出 \(\max\limits_{1\leq a,b\leq n\land|\{a,b\}\cup\{x,y\}|=4} w_a\bmod w_b\)。

题解

发现取最大值和严格次大值时最优，链上取模最大值可以树剖维护。然后全局维护一个 multiset，负责查询去掉某两个数后的最大值和次大值即可。

提交记录

P4947 PION后缀自动机 紫

题意

给定一颗 \(n\) 个节点的树，每个节点中包含一些文件。

实现三个功能，这三个功能会被调用共 \(m\) 次：

1. 计算树上 \(u,v\) 两点的距离。
2. 计算 \(u,v\) 路径中文件名为 A 的文件数量。
3. 删除 \(u,v\) 路径中所有文件名为 A 的文件，并统计被删除文件的数量。

\(n,m<=10^5,文件总数\leq 5\times 10^5\)。

题解

对每个不同文件名分开做，然后树剖实现链覆盖 \(0\)，链求和即可。

提交记录

P5556 圣剑护符 紫

题意

维护一颗 \(n\) 个节点的树，点有点权，需要支持 \(q\) 次操作。

每个操作形式如下：

1. Update x y z：将 \(x\) 到 \(y\) 的路径上的点的点权全部异或上 \(z\)。

2. Query x y：设 \(x\) 到 \(y\) 的路径上的点的点权所组成的集合为 \(S\)，判断 \(S\) 是否存在两个不同子集异或和相同。

题解

注意到当 \(\operatorname{dist}(x,y)>30\) 时，\(S\) 一定存在两个不同子集异或和相同（由线性基的插入过程可说明）。

当 \(\operatorname{dist}(x,y)\leq 30\) 时，暴力将路径上的所有点的点权插入到线性基里面判断。

用树剖维护路径异或，单点查询。

提交记录

P5138 fibonacci 黑

题意

维护一颗 \(n\) 个节点的树，支持以下操作共 \(m\) 次：

• U x k：对于 \(x\) 及其子树内的节点，若其到 \(x\) 的距离为 \(D\)，则该点点权加 \(Fib_{D+k}\)。\(Fib\) 指斐波那契数列。
• Q x y：询问路径 \(x,y\) 上所有节点的点权之和，答案对 \(10^9+7\) 取模。

\(n,m\leq 10^5\)。

题解

先写出 Fib 矩阵 \(M=\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}\)。

每个点维护两个矩阵 \(A,B\)，其中 \(A\) 固定，\(B\) 会因为修改操作改变。

记一个节点的深度为 \(dep\)，根的深度为 \(1\)，则令这个点的 \(A=M^{dep}\)。

对于子树 \(u\) 的加操作，转化为子树 \(u\) 的每个点的 \(B\) 加上 \(M^{k-dep_u+1}\)。

不难发现，一个点真正的 Fib 矩阵就是 \(A\times B\)，Fib 矩阵右下角即为这个点的点权。

使用重链剖分和 DFS 序，将树上问题转为序列问题。

序列问题是：每个下标有两个矩阵 \(A,B\)，需要支持 \(B\) 区间加，查询 \(A\times B\) 的和。

用线段树维护，线段树每个节点维护 \(Sa=\sum A\) 和 \(Sab=\sum A\times B\)，再维护一个懒标记 \(K\)。

对线段树上一个节点进行加 \(B\)，有 \(Sab\leftarrow Sab+Sa\times B\)，\(K\leftarrow K+B\)。

下传标记时，设线段树上当前节点的父节点为 \(fa\)，有 \(K\leftarrow K+K_{fa}\)，\(Sab\leftarrow Sab+Sa\times K_{fa}\)。

时间复杂度 \(O(n\log^2 n)\)，八倍常数。

提交记录

AtCoder-ddcc2020_final_C - Smaller-Suffix-Free Sequences *????

复习 SA。

提交记录

P9664 [ICPC 2021 Macao R] LCS Spanning Tree 紫

题意

给定一个有 \(n\) 个顶点的完全无向图和 \(n\) 个字符串 \(s_1, s_2, \cdots, s_n\)，连接顶点 \(i\) 和 \(j\) 的边的权重等于字符串 \(s_i\) 和 \(s_j\) 的最长公共子串（LCS）的长度。计算此图的最大生成树。

题解

两个串求最长公共子串，可以拼在一起建立 SA，然后只考虑相邻两项的 LCP（即 height）。

推广到多个串，建出 SA 后只连接后缀排序中相邻两个字符对应字符串的边，也是对的。

因为如果一条边 \((a,c)\) 在后缀排序中跨过了另一个字符串 \(b\)，那么把边改成 \((a,b)(b,c)\) 更优。

提交记录

咕咕咕。

CF1923F Shrink-Reverse *2800

题意

给你一个长度为 \(n\) 的 01 串 \(s\)，你可以进行 \(k\) 次操作。每次你可以从下面两种操作中选一种执行：

• 1. 选择两个位置 \(i \neq j\)，交换 \(s_i, s_j\)；
• 2. 将串的前导 \(0\) 清除之后翻转整个串 \(s\)。

你需要最小化至多 \(k\) 次操作后串在十进制意义下的值，对 \(10^9 + 7\) 取模并输出它。

\(2 \leq n \leq 5 \times 10^5\)，\(1 \leq k \leq n\)。

题解

发现翻转操作不会超过两次。

其次翻转肯定可以被放到最后，因为交换和翻转是独立的。

进一步我们发现反转操作不会超过一次，因为翻转两次是为了去掉后导零，然而翻转一次后已经去掉了前/后导零，因此可以把交换操作全部对称一下，然后只翻转一次。

讨论是否进行翻转：

• 不进行翻转：
  • 双指针维护第一个 \(1\) 和最后一个 \(0\) 进行交换即可。
• 进行翻转：
  • 我们需要先最小化长度，对于每个 \(i\)，找到最小的 \(R_i\) 满足 \([i,R_i]\) 有不少于 \(cnt1-k+1\) 个 \(1\) 和 \(k-1\) 个 \(0\)，这样才能把外面的 \(1\) 换到里面。
  • 其次因为要翻转，因此肯定是让 \(1\) 集中在前面，具体的，在 \([i,R_i]\) 中找到一个 \(r_i\) 满足 \([i,r_i]\) 中有 \(k-1\) 个 \(0\)，那么最后的形态肯定是 \([i,r_i]\) 全为 \(1\)，\([r_i+1,R_i]\) 保持不动。
  • 特殊的，如果 \(r_i=R_i\)，那么最后的序列全为 \(1\)。
  • 我们先选出 \([i,R_i]\) 尽可能短的一些 \(i\)，然后比较这些 \(i\) 的 \([r_i+1,R_i]\) 翻转后的字典序，注意这里比较字典序时，如果 \(A\) 是 \(B\) 的前缀，那么我们认为 \(B\) 的字典序比 \(A\) 小，因为 \([i,r_i]\) 全为 \(1\)，本质上是在 \(A,B\) 末尾都补了若干个 \(1\)。
  • 使用 SA 实现两个字符串字典序的比较函数，然后用比较函数进行排序。

提交记录

CF547E Mike and Friends *2800

题意

给定 \(n\) 个字符串 \(s_1,s_2,\dots ,s_n\)。

定义 \(\operatorname{call}(x,y)\) 表示 \(s_y\) 在 \(s_x\) 中出现的次数。

处理 \(q\) 次询问，每次给定 \(l,r,k\)，求 \(\sum\limits_{i=l}^{r} \operatorname{call}(i,k)\)。

\(n\leq 2\times 10^5,q\leq 5\times 10^5\)。

题解

建立 SA，对于 \(s_k\) 在 SA 中的第一个字符，二分出一个极长的 \(height\) 区间，满足这个区间的 \(height\) 都大于 \(\operatorname{len}(s_k)\)，记这个区间为 \([a,b]\)，那么答案就是 \(id\in [l,r]\) 且 \(rk\in [a,b]\) 的字符个数，二维数点即可。

提交记录

P4094 [HEOI2016/TJOI2016] 字符串 黑

题意

给定一个长度为 \(n\) 的字符串，\(m\) 次询问，问子串 \(s[a..b]\) 的所有子串和 \(s[c..d]\) 的最长公共前缀的长度的最大值。

\(1\le n,m\le 100,000\)。

题解

与上一题类似。建立 SA，二分答案 \(x\)，对于 \(s_c\) 在 SA 中的第一个字符，二分出一个极长的 \(height\) 区间，满足这个区间的 \(height\) 都大于 \(x\)，记这个区间为 \([rkl,rkr]\)，那么如果存在一个字符 \(id\in [a,b]\) 且 \(rk\in [rkl,rkr]\)，则答案 \(\geq x\)，在线二维数点，使用主席树维护。

提交记录

P5161 WD与数列 黑

题意

定义两个序列 \(A,B\) 是匹配的，当且仅当 \(|A|=|B|\) 且对于 \(1\le i,j\le |A|,A_i-B_i=A_j-B_j\)。即长度相同且一个数列同时加上一个数可以和另一个数列完全一样。

给定一个长度为 \(n\) 的数列，求数列中有多少对不相交的子串使得他们是匹配的。

题解

匹配的条件是长度相同且差分数组相同，统计所有长度为 \(1\) 的数列对答案的贡献，然后将原序列求差分，问题转化为求一个字符串中有多少对不相交且相等的子串。

先不考虑不相交的限制，求有多少对相等的子串，相当于求 \(\sum\limits_{i=1}^{n}\sum\limits_{j=i+1}^{n} \operatorname{lcp}(s[i\cdots n],s[j\cdots n])\)，这个问题可以建出 SA 然后求 height 的区间 \(\min\) 的和来解决。

然后考虑把相交的串减掉，考虑相交的匹配串同时删去最后一个字符也是匹配的，且删除的临界是把两个串删成相邻的匹配串（即平方字符串）。记这个临界的字符串长度为相交匹配串的临界长度。

考虑【优秀的拆分】的套路，枚举临界长度 \(p\)，之后取出点集 \(\{1,p+1,2p+1,\dots\}\)，一个临界长度的串一定经过恰好一个点，因此枚举平方字符串经过的两个相邻点，之后求这两个位置的 \(\operatorname{lcs}\) 和 \(\operatorname{lcp}\)，分别记为 \(L_a\) 和 \(L_b\)，如果 \(L_a+L_b\geq p\)，则说明这对相邻点将产生一些相交的匹配串。

具体的，令 \(k=i+p-\min(La,p)+1,w=\min(La,p)+\min(Lb,p)-p\)，则多余的贡献是首项为 \(i+Lb-k+1\)，末项为 \(i+Lb-k+1-w+1\)，公差为 \(1\) 的等差数列的和。将这个贡献减去。取 \(\min\) 的原因是不能与跨过其他相邻点的平方字符串算重。

注意差分数组的相邻在原数组上算作相交。

完结散花。

提交记录

SP1812 LCS2 - Longest Common Substring II 紫

题意

给定一些字符串，求出它们的最长公共子串。

题解

对第一个串建 SAM，然后把后面的串依次在 SAM 上做匹配，记录到达每个点的最大长度 \(p\)，然后每个点对 \(n\) 个 \(p\) 取 \(\min\)，最后取值最大的点即可。

注意，因为这是 SAM，所以到达一个点相当于匹配上了这个点 fail 树的到根链，因此父节点要对子节点取 \(\max\)，当然每个节点还需要保证值不超过这个点的 \(\text{len}\)。

提交记录

P4482 [BJWC2018] Border 的四种求法 黑

题意

给定一个长为 \(n\) 字符串 \(S\)，\(q\) 次询问，每次询问给出 \(l,r\)，求区间 \([l,r]\) 的 border。

\(n,q\leq 2\times 10^5\)。

题解

把 border 刻画为判定条件。

\([l,x]\) 是 \([l,r]\) 的 border，当且仅当 \(\operatorname{lcs}(s[1\cdots x],s[1,\cdots r])\geq x-l+1\)。

我们知道，两个前缀的 \(\operatorname{lcs}\)，是这两个前缀在 SAM 的 fail 树上的 \(\operatorname{lca}\) 的 \(\text{len}\)。

也就是说，求最大的 \(x\)，使得 \(len_{\operatorname{lca}(pos_x,pos_r)}\geq x-l+1\)。

点分治，把询问挂到 \(pos_r\) 上，在分治中心为 \(\operatorname{lca}(pos_x,pos_r)\) 时统计答案。

点分治时，确定分治中心为 \(w\)，遍历 \(w\) 向下的的每个子树，遍历到一个子树时，先考虑查询答案，设当前点为 \(t\)，则对于一个 \(pos_r=t\) 的询问 \((l,r)\)，在 \([l,r)\) 中找到一个 \(x\)，满足 \(pos_x\) 在之前的子树遍历到过，且 \(len_w\geq x-l+1\)，即 \(x\leq len_{w}+l-1\)。也就是说，我们可以找到编号在 \([l,len_{w}+l-1]\) 之间最大的 \(x\)，用 \(x-l+1\) 更新答案。

考虑如何维护，点分治遍历到一个子树时，更新完答案后，对于每个节点 \(u\)，将 \(pos_x=u\) 的 \(x\) 全部放到平衡树中，查询时在平衡树上找 \(len_{w}+l\) 的前驱即可。

但是我们还没有统计根向的路径。

对于根向路经 \((pos_x,pos_r)\)，当 \(r\) 在上 \(x\) 在下时，树上维护平衡树的启发式合并，使得树上遍历到点 \(p\) 时，所有 \(p\) 子树内的点都在平衡树里，然后对于 \(pos_r=p\) 的询问，查询 \(len_p+l\) 的前驱。

当 \(x\) 在上 \(r\) 在下时，根据 \(len_{pos_x}\geq x-l+1\)，有 \(x-len_{pos_x}\leq l-1\)，DFS 并使用线段树维护到根链的点集，线段树里下标为 \(x\) 的地方放入 \(x-len_{pos_x}\)，然后二分一个最大的 \(x\) 满足这个位置的值 \(\leq l-1\) 即可。

然后点分治没调出来，平衡树合并还被卡空间了，WA+MLE。

（todo）验证上述点分治的正确性？

---

我们发现上述方法违背了点分治的“本职工作”，我们钦定了分治中心为 \(\text{lca}\)，但点分治只保证在钦定路径经过分治中心时能够不漏的统计所有路径。

其实不用那么麻烦，我们给每条边赋一个边权，为 \(len_u-len_{fa_u}\)，然后可以用如下方式表示 \(\text{len}\)，\(len_{\operatorname{lca}(pos_x,pos_r)}\times 2=len_{pos_x}+len_{pos_r}-\operatorname{dist}(pos_x,pos_r)\)。

重新整理式子，\(len_{pos_x}+len_{pos_r}-\operatorname{dist}(pos_x,pos_r)\geq 2(x-l+1)\)，点分治时，令点 \(u\) 分治中心的边权和为 \(dis_u\)，则上述式子可进一步化简为 \(dis_{pos_r}-len_{pos_r}-2l\leq len_{pos_x}-dis_{pos_x}-2x-2\)。

这是一个二维数点问题，令一个点的属性为 \((x,y)=(x,len_{pos_x}-dis_{pos_x}-2x-2)\)，则对于一个询问 \((l,r)\)，有 \(x\in[l,r)\)，\(y\geq dis_{pos_r}-len_{pos_r}-2l\)。

然后我们发现点分治时不用扣除子树内部的贡献，因为子树内部会把 \(\text{dist}\) 算的更大。

然后直接二维数点就行了。

这种方法启示我们：可以把与 \(\text{lca}\) 相关的信息转化为与两点路径长度有关的信息，而对于路径长度，\(\operatorname{dist}(u,v)=dis_u+dis_v-2\times dis_{k}\) 在 \(k=\operatorname{lca'}(u,v)\) 时成立，其中 \(\operatorname{lca'}\) 表示将我们计算 \(dis\) 的方向作为根向的 \(\text{lca}\)，也就是说我们可以在点分治等算法中任意钦定“根”，从根开始计算 \(dis\)，利用这个式子进行一些操作。

这种方法适用于点分治计算与有根树 \(\text{lca}\) 相关的问题。

两只 \(\log\)，完结散花。

提交记录

P10780 BZOJ3028 食物 紫

学习生成函数。

提交记录

P6078 [CEOI 2004] Sweets 紫

题意

John 得到了 \(n\) 罐糖果。第 \(i\) 个糖果罐里有 \(m_{i}\) 个相同的糖果。John 决定吃掉 \(a\sim b\) 个糖果。求吃糖果的方案数。

题解

写出第 \(i\) 罐糖果的生成函数 \(\sum\limits_{j=0}^{m_i} x_j=\frac{1-x^{m_j+1}}{1-x}\)。

全部乘起来，就是 \(\left( \prod\limits_{i=1}^{n} 1-x^{m_i+1} \right)\times \frac{1}{(1-x)^{n}}\)，答案是这个式子 \(x^{a\sim b}\) 项的系数和。

\(\prod\limits_{i=1}^{n} 1-x^{m_i+1}\) 可以暴力。

\(\frac{1}{(1-x)^{n}}\) 使用牛顿二项式定理，得到 \(\sum\limits_{i\geq 0} \binom{n-1+i}{i} x^i\)。

不好直接乘，考虑暴力求完 \(\prod\limits_{i=1}^{n} 1-x^{m_i+1}\) 后，枚举每一项 \(px^k\)，这一项对答案的贡献为 \(p\) 乘上 \(\frac{1}{(1-x)^{n}}\) 的 \(x^{a-k\sim b-k}\) 项系数和，即 \(\sum\limits_{i=a-k}^{b-k} \binom{n-1+i}{i}\)。

根据 \(\binom{n-1}{m-1}+\binom{n-1}{m}=\binom{n}{m}\)，有：

\[\sum_{i=l}^{r} \binom{x+i}{i} \\ =\binom{x+l}{l-1}+\left( \sum_{i=l}^{r} \binom{x+i}{i} \right)-\binom{x+l}{l-1} \\ =\binom{x+r+1}{r}-\binom{x+l}{l-1} \]

套用这个公式，有：

\[\sum\limits_{i=a-k}^{b-k} \binom{n-1+i}{i} \\ =\binom{n+b-k}{b-k}-\binom{n-1+a-k}{a-k-1} \\ =\binom{n+b-k}{n}-\binom{n-1+a-k}{n} \]

因此枚举 \(\prod\limits_{i=1}^{n} 1-x^{m_i+1}\) 的每一项 \(px^k\)，对答案贡献为 \(p\times \left( \binom{n+b-k}{n}-\binom{n-1+a-k}{n} \right)\)。

计算组合数时，由于 \(n\) 很小，所以直接用 \(\binom{n}{m}=\frac{n^{\underline{m}}}{m!}\) 暴力计算即可。

由于模数不质，所以不能直接取模，但因为 \(m!\) 很小，所以可以计算 \(n^{\underline{m}}\bmod (2004\times m!)\)，最后在除以 \(m!\) 即为 \(\binom{n}{m}\)。

注意以下搜索边界，由于 \(\frac{1}{(1-x)^{n}}\) 的每一项次数都非负，所以搜索时系数不能超过 \(b\)。

这样比较麻烦，其实在计算 \(\binom{n}{m}\) 时把 \(n<m\) 的判成 \(0\)，也有同样的效果，因为当 \(k>b\) 时对答案贡献为 \(0\)，当 \(k>a-1\) 时对答案贡献为 \(\binom{n+b-k}{n}\)，即 \(\sum\limits_{i=0}^{b-k} \binom{n-1+i}{i}\)。

提交记录

P3978 [TJOI2015] 概率论 紫

题意

对于一棵随机生成的 \(n\) 个结点的有根二叉树（所有互相不同构的形态等概率出现），它的叶子节点数的期望是多少呢？

题解

令 \(g_{x}\) 表示大小为 \(x\) 的二叉树个数，\(f_{x}\) 表示大小为 \(x\) 的二叉树叶节点个数之和。

有：

\[g_{x}=\sum\limits_{i=0}^{n-1} g_{i}\times g_{n-i-1} f_{x}=2\times \sum\limits_{i=0}^{n-1} f_{i}\times g_{n-i+1} \]

注意特殊位置：\(f_0=0,f_1=1\)。

写出 \(g\) 的生成函数 \(G\)，\(f\) 的生成函数 \(F\)。

仿照卡特兰数列推导方式，对于 \(F\) 的式子，有 \(xF(x)\times 2G(x)+x=F(x)\)，加 \(x\) 是因为 \(f_1=1\)。

然后由于 \(G\) 是卡特兰数的生成函数，因此 \(G(x)=\frac{1-\sqrt{1-4x}}{2x}\)，所以 \(F(x)=\frac{x}{(1-4x)^{0.5}}\)。

将 \((xG)\) 求导，得到 \((xG)'=\frac{1}{(1-4x)^{0.5}}=\frac{F}{x}\)。

因此，对于 \(xG\) 中的一项 \(xg_nx^{n}\)，求导后将变为 \((xg_nx^n)'=(g_nx^{n+1})'=(n+1)g_nx^n\)，由于 \((xG)'=\frac{F}{x}\)，所以 \((n+1)g_nx^{n}=\frac{f_{n+1}x^{n+1}}{x}\)，\(f_{n+1}=(n+1)g_n\)，\(f_n=n\times g_{n-1}\)。

将卡特兰数通项公式 \(g_n=\frac{\binom{2n}{n}}{n+1}\) 带入，得 \(f_n=\frac{(2n-2)!}{(n-1)!(n-1)!}\)。

由于我们要求期望，因此最后要除以 \(g_n\)，最终答案为 \(\frac{n(n+1)}{2(2n-1)}\)。

提交记录

[ABC231G] Balls in Boxes 紫

题意

有 \(N\) 个编号为 \(1\) 到 \(N\) 的箱子。最初，第 \(i\) 个箱子中有 \(A_i\) 个球。

你需要重复进行 \(K\) 次如下操作：

• 从 \(N\) 个箱子中等概率地随机选择一个（每次操作的选择相互独立）。在选中的箱子中加入 \(1\) 个球。

\(K\) 次操作结束后，设第 \(i\) 个箱子中的球数为 \(B_i\)，则得分为所有箱子球数的乘积 \(\prod_{i=1}^{N} B_i\)。

请你计算得分的期望值，并对 \(998244353\) 取模。

题解

生成函数，推式子。

记一个数被操作了 \(p\) 次，则第 \(i\) 个盒子的生成函数是 \(F_i (x)=\sum_{p_i\geq 0} \frac{(a_i+p_i)}{p_i!}x^{p_i}\)，答案为 \(\frac{[x^k]\prod\limits_i F_i (x)\times k!}{n^k}\)。

其中 \(\frac{k!}{\prod p!}\) 是因为形成最终局面的操作方案有 \(\frac{k!}{\prod p!}\) 种。

\[F(x)=\sum_{i\geq 0} (a_i+i)\times \frac{x^i}{i!} \\ =a_i\left( \sum_{i\geq 0} \frac{x^i}{i!} \right)+\sum_{i\geq 0} i\frac{x^i}{i!} \\ =a_i e^x+xe^x \\ =(x+a_i)e^x \]

\[\prod F_i (x) \\ =e^{nx}\times \prod (x+a_i) \\ e^{nx}=\sum n^i\times \frac{x^i}{i!} \]

记 \(\prod (x+a_i)\) 的 \(x^i\) 项系数为 \(c_i\)，则答案为：

\[\frac{[x^k]\prod F_i (x)\times k!}{n^k} \\ =\sum\limits_{i=0}^{\min(n,k)} \frac{n^{k-i}}{(k-i)!}\times c_i\times \frac{k!}{n^k} \\ =\sum\limits_{i=0}^{\min(n,k)} \frac{\prod_{j=k-i+1}^{k}j}{n^i}\times c_i \]

时间复杂度 \(O(n^2)\)。

提交记录

CF891E Lust *3000

题意

你有 \(n\) 个数 \(a_1, a_2, \dots, a_n\) 要进行 \(k\) 次操作，每次随机选择一个数 \(x \in [1, n]\)，把 \(a_x\) 减一，并将答案增加除 \(a_x\) 外所有数的乘积。

求最终答案的期望，答案对 \(10^9+7\) 取模。

题解

发现原序列乘积减去新序列乘积即为答案。

与 [ABC231G] Balls in Boxes 相同。

提交记录

P2012 拯救世界2 黑

学习指数生成函数。

提交记录

P5521 [yLOI2019] 梅深不见冬 蓝

题意

给定一颗树，你要按照某个 DFS 序走遍这棵树，到达一个节点时，你可以在节点放置若干个果实。你也可以任意时刻任意地点回收某个节点的果实。（无需到达被回收节点）

你在 \(u\) 放置果实时，需要满足对于 \(u\) 的所有儿子 \(v\)，节点 \(v\) 都放置了 \(w_v\) 个果实。

对于每个节点 \(u\) 求出，想要在这个节点放置 \(w_u\) 个果实，至少需要携带多少个果实。

题解

考虑 DFS 序确定时，可以树形 DP，令 \(f_u\) 表示点 \(u\) 的答案，有：

\[f_u=\max(\max\{ans_v+\sum_{x\in son_u\land dfn_x<dfn_v} w_v\},w_u+\sum_{v\in son_u} w_v) \]

也就是说我们要给每个点子节点排序使这个值最小，邻项交换即可得出应该按 \(w-f\) 升序排序。

提交记录

CF1601D Difficult Mountain *2700

题意

\(n\) 个人相约去爬山。山的初始攀登难度为 \(d\)。每位登山者有两个属性：技巧 \(s\) 和整洁度 \(a\)。技巧为 \(s\) 的登山者能登上攀登难度为 \(p\) 的山当且仅当 \(p\leq s\)。在一位整洁度为 \(a\) 的登山者登上攀登难度为 \(p\) 的山后，山的攀登难度会变为 \(\max(p,a)\)。

请给这些登山者指定一个爬山的先后顺序，最大化登上山的人数。

\(n\leq 5\times 10^5\)。

题解

一个属性为 \((s,a)\) 的人登山成功后，如果 \(s<a\)，那么山的高度一定会变为 \(a\)，否则山的高度不确定。因此按照 \([s<a]\) 把登山的人分成两类。

对于 \(a\leq s\) 的人构成的集合，按 \(a\) 排序或者按 \(s\) 排序都行。

对于 \(s<a\) 的集合，显然按 \(a\) 排序最优，当 \(a\) 相等时顺序任意。

考虑合并两个集合。

假设 \(a_i\leq s_i,a_j>s_j\)，大力分讨。

1. \(a_i\leq s_i\leq s_j<a_j\) 显然选择 \(i\) 先。
2. \(a_i\leq s_j\leq s_i\leq a_j\) 显然选择 \(i\) 先。
3. \(a_i\leq s_j\leq a_j\leq s_i\) 谁先都一样。
4. \(s_j\leq a_i\leq s_i\leq a_j\) 谁先都只能有一人登山成功，因此我们要最小化山的高度，选 \(i\) 先。
5. \(s_j\leq a_i\leq a_j\leq s_i\) 显然选择 \(j\) 先。
6. \(s_j<a_j\leq a_i\leq s_i\) 显然选择 \(j\) 先。

注意到 \(\max(a,s)\) 取到最大值的那组肯定在后面。因此不同集合之间应该按 \(\max(a,s)\) 从小到大合并。

但是当 \(\max(a_i,s_i)=\max(a_j,s_j)\) 时，发现情况四可以有两个人登山成功了，此时要先选 \(j\)，对于其余五种情况，情况一根本不能取等，情况三、五、六的选择不改变。对于这种情况，\(s\) 小的肯定在前面，所以我们修正贪心策略，按 \(\max(a,s)\) 为第一关键字，\(s\) 为第二关键字，从小到大合并两个集合。

到这里题目已经做完了，但是我们有更简单的实现方式。其实按 \(\max(a,s)\) 为第一关键字，\(s\) 为第二关键字从小到大排序也适用于 \(s<a\)（此时第一关键字取等一定是 \(a_i=a_j\)）和 \(a\leq s\) 的两个集合内部，因此直接排序即可。

我们还要补充一个结论的证明：当前尽可能多个人登山一定不劣。发现除了情况五，我们都选择了 \(a\) 更小的先登山，这个结论是显然的。对于情况五，山的高度被提高了，如果后面存在一个人 \((a_k,s_k)\)，按照排序规则，要么 \(a_k\geq a_j\)，要么 \(s_k\geq a_j\)，前者可以不让 \(j\) 登山，换来 \(k\) 登山，但是山高增加了，不优。后者完全不影响。因此结论得证。

提交记录

CF436E Cardboard Box *2600

题意

\(n\) 个关卡，对每个关卡，你可以花 \(a_i\) 代价得到一颗星，也可以花 \(b_i\) 代价得到两颗星，也可以不玩。问获得 \(w\) 颗星最少需要多少时间。

\(n\leq 3\times 10^5\)。

题解

把题目转换成每个关卡有两种操作：

1. 花费 \(a\) 获得一颗星
2. 再花费 \(b-a\) 获得一颗星

考虑反悔贪心，增加一颗星的方式有：

1. 直接选择：选择没玩过的关卡，改选 \(a\)。
2. 直接选择：选择一个选 \(a\) 的关卡，增加 \(b-a\)。
3. 反悔：选择一个选 \(a\) 的关卡，改为不选。然后在一个没玩过的关卡选择 \(b\)。
4. 反悔：选择一个选 \(b\) 的关卡，改为选 \(a\)。然后在一个没玩过的关卡选择 \(b\)。

对于操作一，维护一个小根堆表示没玩过的关卡中 \(a\) 的集合。
对于操作二，维护一个小根堆表示选 \(a\) 的关卡中 \(b-a\) 的集合。
对于操作三，维护一个大根堆表示选 \(a\) 的关卡中 \(a\) 的集合，再维护一个小根堆表示没玩过的关卡中 \(b\) 的集合。
对于操作四，维护一个大根堆表示选 \(b\) 的关卡中 \(b-a\) 的集合，再维护一个小根堆表示没玩过的关卡中 \(b\) 的集合。

去重后总共要维护五个堆。

每个堆写成自动删除堆，即：元素写成二元组表示值和下标，操作时实时更新每个关卡的选择状态，对于一个堆，查询最值时先 pop 掉选择状态不符合要求的元素。

提交记录

P3620 [APIO/CTSC2007] 数据备份 蓝

题意

给定一个数组，两个数配对的代价是两数差的绝对值，选出 \(k\) 对不相交的匹配使得代价最小

题解

求出差分数组，即选出 \(k\) 个不相邻的位置使得代价最小。

这是经典的反悔贪心问题，解法是链表维护 01 交替的区间左右端点和改变代价，然后使用优先队列进行贪心。

提交记录

P3045 [USACO12FEB] Cow Coupons G 紫

题意

FJ 准备买一些新奶牛。市场上有 \(N\) 头奶牛，第 \(i\) 头奶牛价格为 \(P_i\)。FJ 有 \(K\) 张优惠券，使用优惠券购买第 \(i\) 头奶牛时价格会降为 \(C_i\)，当然每头奶牛只能使用一次优惠券。FJ 想知道花不超过 \(M\) 的钱最多可以买多少奶牛？

题解

反悔贪心。

新增加一头牛的方法有：

• 花费 \(P_i\) 购买。
• 花费一张券，并花费 \(C_i\) 购买。
• 将已经购买的一头牛的券撤回，并用这张券以 \(C_i\) 价格购买新的奶牛。

维护 \(P_i,C_i,P_i-C_i\) 的小根堆即可。

提交记录

P4597 序列 sequence 紫

题意

给定一个序列，每次操作可以把某个数 +1 或 −1。要求把序列变成非降数列。

题解

设计 \(dp_{i,j}\) 表示前 \(i\) 个数，\(a_i=j\) 的最小操作数。

\(dp_i\) 是凸的，使用大根堆维护拐点，如果斜率变化量是 \(2\) 就认为拐了两次，分类讨论加入一个数时斜率的变化即可。

提交记录

agc034_c Tests *????

题意

给定非负整数序列 \(\{l_n\},\{r_n\},\{b_n\},X\)，求最小的 \(s\)，使得存在非负整数序列 \(\{a_n\},\{c_n\}\)，满足 \(a_i\le X\)，\(\sum_{i=1}^n a_i=s\)，\(c_i\in[l_i,r_i]\)，且

\[\sum_{i=1}^n c_i(a_i-b_i)\ge 0 \]

所有输入均 \(\le 10^5\)。

题解

容易发现 \(c_i\) 只有 \(l_i\) 和 \(r_i\) 两种取值，并且 \(a_i\) 只有一个地方取到 \(0\) 和 \(X\) 以外的值，这个结论可以通过调整法说明。

然后二分答案，算出 \(a_i=X\) 的个数 \(t=\lfloor \frac{mid}{X} \rfloor\)，枚举取到 \(0\) 和 \(X\) 以外的值的位置，在剩余的位置中贪心选变化量最大的 \(t\) 个即可。

这个过程可以前缀和优化，复杂度 \(O(n\log^2 n)\)。

提交记录

2025.8

P4064 [JXOI2017] 加法 蓝

题意

可怜有一个长度为 \(n\) 的正整数序列 \(A\)，但是她觉得 \(A\) 中的数字太小了，这让她很不开心。

于是她选择了 \(m\) 个区间 \([l_i,r_i]\) 和两个正整数 \(a,k\)。她打算从这 \(m\) 个区间里选出恰好 \(k\) 个区间，并对每个区间执行一次区间加 \(a\) 的操作。（每个区间最多只能选择一次）。

对区间 \([l,r]\) 进行一次加 \(a\) 操作可以定义为对于所有 \(i\) ∈ \([l,r]\)，将 \(A_i\) 变成 \(A_i+a\)。现在可怜想要知道怎么选择区间才能让操作后的序列的最小值尽可能的大，即最大化 \(\min\{A_i\}\)。

题解

二分答案，然后对区间扫描线，每次选择 \(r\) 最大的区间进行操作即可。

提交记录

P3744 李彬的几何 蓝

题意

已知多边形 \(\text{P}\)，求最小的实数 D，使得存在一种点的移动方案，满足每个顶点最多移动 D 个单位距离，且移动后 \(\text{P}\) 不再是凸多边形。

题解

发现最优情况肯定是把相邻三点变成一条直线，枚举相邻三点，计算点到直线的距离即可。

提交记录

P3895 [湖南集训] Hungry Rabbit 紫

题意

兔子王国中有 \(n\) 只兔子，在接下来的 \(m\) 天中，每天恰好有 \(k\) 只兔子去觅食。

给定一张 01 表，\(a_{i,j}\) 表示兔子 \(i\) 是否能在第 \(j\) 天觅食。\(\text{1}\) 表示可以，\(\text{0}\) 表示不可以。

令 \(p_i\) 表示第 \(i\) 天出来觅食，但是第 \(i−1\) 天却没有出来觅食的兔子个数。规定 \(p_1=0\)。

要求 \(\max p_i\leq l\)，构造一个合法的方案。

\(1\leq n,m\leq 800,\)，\(1\leq k\leq n\)，\(1\leq l\leq k\)。

题解

显然存在一个最优解满足过期早的兔子比过期晚的兔子先换下，因此每次按过期时间贪心更换 \(l\) 个即可。

提交记录

P3244 [HNOI2015] 落忆枫音 紫

题意

给定一个只有 \(1\) 号点入度为 \(0\) 的 DAG，在这个 DAG 基础上加一条有向边 \((u,v)\)，求新图的外向生成树个数。

\(n,m\leq 2\times 10^5\)。

题解

首先，对于一个 DAG，其生成树个数为 \(\prod in_i\)，相当于每个点在选一个父亲，除了 \(1\) 每个点都连向拓扑序更小的点，可以证明这一定是一棵树。

我们对新图也按这种方法计算，容易发现算多的部分是“生成树”包含了一个环，且这个环上必定有一条边 \((u,v)\)。

假设存在一个环 \((v_1,v_2,\dots,v_k)\)，那么算多的部分就是 \(\frac{\prod_{i=1}^n in_i}{\prod_{i=1}^k v_i}\)。

由于所有环在 \((u,v)\)，考查 \(u\) 节点的“父亲”可以证明：我们的假生成树最多包含一个环。

所以环与环对于多算的贡献是相互独立的，也就是说我们可以对于每个环 \((v_1,v_2,\dots,v_k)\)，都将答案减去 \(\frac{\prod_{i=1}^n in_i}{\prod_{i=1}^k v_i}\)，最终得到的答案即为正确答案。

统计新图的入度，然后在原 DAG 上 DP 出所有 \((u\to v)\) 的路径 \((v_1,v_2,\dots,v_k)\) 的 \(\frac{1}{\prod_{i=1}^k v_i}\) 之和即可。

提交记录

[ARC103D] Distance Sums 紫

题意

给定一个长度为 \(N\) 的数列 \(D_1, D_2, \ldots, D_N\)。所有 \(D_i\) 的值都互不相同。构造一个具有 \(N\) 个顶点的树，满足以下条件：

• 每个顶点都标有 \(1, 2, \ldots, N\) 的编号
• 每条边都标有 \(1, 2, \ldots, N-1\) 的编号，第 \(i\) 条边连接顶点 \(u_i\) 和 \(v_i\)
• 对于每个顶点 \(i\)，从 \(i\) 到其他所有顶点的距离之和为 \(D_i\)。这里，每条边的长度都视为 \(1\)。

题解

\(D\) 互不相同启示我们从特殊点开始构造，\(D\) 最小的是重心，但是发现从重心构造做不下去，所以考虑从叶子构造。

发现 \(D\) 最大的肯定是叶子，且与 \(D\) 比它小 \(n-2\) 的点连边。

进一步，对于一个大小为 \(sz\) 的子树，记其根为 \(rt\)，则有 \(D_{fa_{rt}}=D_{rt}-n+2\times sz\)，由于 \(D\) 互不相同，所以每棵子树的 \(fa\) 确定，按 \(D\) 从大到小构造即可。

由于我们只管了 \(D\) 之间的差值而没有管具体数值，所以构造完要检验。

提交记录

CF842E Nikita and game *2800

题意

一棵树初始只有一个编号为 \(1\) 的根结点。\(n\) 次操作，每次新增一个点作为 \(p_i\) 的子结点，询问更新后有多少点可以作为树直径的端点。

题解

利用“一个点的最远点必定是直径端点”的性质可证一个点作为直径端点的时间是一个区间。

同时可以使用上述性质维护每一时刻的直径端点，二分每个点作为直径端点的时间区间即可。

提交记录

CF2108E Spruce Dispute *2600

题意

给定一棵树，你要选择相邻两点并缩成一个点，然后将点两两匹配，两点匹配的权值是两点的树上距离。

请最大化匹配权值。

\(n\leq 2\times 10^5\)，\(n\) 是奇数。

题解

树上最大匹配的套路是找出重心然后让所有匹配都跨重心，这样是最优的，每个点的贡献是其到重心的距离。

然后由于一次缩点后重心仍然是重心，所以先按不缩点计算每个点的贡献。然后计算缩每对点的变化量即可。

提交记录

CF1783G Weighed Tree Radius *2800

题意

给你一个 \(n\) 个点的树。第 \(i\) 个点的初始权值为 \(a_i\)。定义结点 \(v\) 到结点 \(u\) 的距离 \(d_v(u)\) 等于 \(v\) 和 \(u\) 之间的边的数量。

定义结点 \(v\) 到结点 \(u\) 的权值距离 \(w_v(u)=d_v(u)+a_u\)。定义结点 \(v\) 的偏心距 \(e(v)\) 是从 \(v\) 到其他结点的最大权值距离（包括\(v\)本身），即 \(e(v)=\max\limits_{1\leq u \leq n} w_v(u)\)。定义树的半径 \(r\) 是所有偏心距的最小值，即 \(r=\min\limits_{1\leq v\leq n} e(v)\)

你需要对 \(m\) 次询问进行回答，对于第 \(j\) 次询问，给出两个数 \(v_j\) 和 \(x_j\)，表示将 \(a_{v_j}\) 的值修改为 \(x_j\)。在每次询问后，输出当前该树的半径 \(r\)。

\(n\leq 3\times 10^5\)。

题解

令两个点 \(u,v\) 的距离为 \(\operatorname{dis}(u,v)+a_u+a_v\)，则答案为 \(\max a\) 和 \(\frac{直径长度}{2}\) 的最大值。

证明如下：可以把这个定义理解为每个点下挂了 \(a\) 个点的链，如果直径中点为原树上的点，那么结论显然成立，否则说明一个点的 \(a\) 已经超过直径的一半，那么答案一定大于这个点的 \(a\)，且这个点的偏心距为 \(a\)。

由于题目带修，需要使用线段树维护直径。

提交记录

[AGC018D] Tree and Hamilton Path 紫

题意

给定一棵树 \(T\)，边有边权，完全图 \(G\) 上的两点距离为两点在树 \(T\) 上的距离。

求 \(G\) 的最长哈密顿路径。

\(n\leq 10^5\)。

题解

与树上匹配那题做法相同，找出重心然后从重心出发，保证每次行走都跨越重心，如果有两个重心就在第二个重心停止，否则就在重心邻居中邻边权值最小的邻居处停止。

提交记录

QOJ 8650. Island Hopping

题意

这是一道交互题。

交互库有一棵 \(n\) 个节点的树，你可以对交互库进行形如 \(qry(x,k)\) 的询问，交互库会告诉你距离 \(x\) 第 \(k\) 小的节点编号（如有多个距离最小的点，则按第二关键字排序），你需要在 \(2n\) 次询问内确定树的形态。

题解

考虑如果我们知道每个点的度数，那么就可以通过重复【度数】次 \(qry\) 查询这个点的所有邻居，就能确定树的形态。

我们不知道每个点的度数，也就不知道我们何时才能停止调用 \(qry\)，而度数是不好求的。

让我们换一种思路，我们对一个点重复调用 \(qry\) 直到我们得到的结果是这个点的父亲。

判断相邻点的父子关系是简单的，我们可以先调用 \(qry(1,2\sim n)\) 来得出 bfs 序，然后判断一个点的bfs序是否小于另一个点。

然后我们对于每个点不断调用 \(qry\) 直到我们得到一个 bfs 序比当前小的点作为这个点的父亲。至此我们会了 \(3n\) 次调用的做法（\(n-1\) 定 bfs 序，\(2n-2\) 定每个点的父亲）

然后我们发现我们不断调用 \(qry\) 时会浪费很多信息，因此考虑把这些信息利用起来，我们按照 bfs 序从小到大进行操作，不断调用 \(qry\) 直到我们得到一个 bfs 序比当前小的点作为这个点的父亲，对于知道父亲之前的每个点 \(p\)，更新 \(fa_p=now\)，然后处理一个点时，如果这个点父亲以确定就跳过。

这样我们就做到了 \(n-1\) 次操作定每个点的父亲，总共 \(2n-2\) 次操作。

提交记录

NOIP 模拟赛 T4 tree

题意

给定一棵有 \(N\) 个节点的点带权无根树。现在，你需要选择一些互不相交（包括端点）的路径。如果你选择了 \(K\) 条路径，且覆盖的点权和为 \(S\)，你的得分即为 \(\frac{S}{K+1}\)。

另外，在选取路径之前，你必须执行一次如下操作（操作分为三个步骤）：

1. 选定一个参数 \(C\)，满足 \(C \in [0, T]\)
2. 将所有的点权 \(+C\)
3. 将所有的点权对 \(LIMIT\) 取模

其中，\(T\)、\(LIMIT\) 的值已经被给出。你的任务就是求出可能的最高得分。

要求 \(O(n^2)\)。

题解

发现只有 \(O(n)\) 个有用的 \(C\)，枚举这些 \(C\)。

然后我们要解决树上选若干不交路径，最大化 \(\frac{S}{K+1}\)。这是一个经典的分数规划问题，二分答案后将所有路径减去 \(mid\)。

然后树形 DP 检验，时间复杂度 \(O(n^2\log V)\)。

对有用的 \(C\) 以随机顺序枚举，并做最优性剪枝，那么我们进行二分的次数就是随机序列前缀 \(\max\) 的期望个数，即 \(O(\log n)\)，因此总期望复杂度 \(O(n^2+n\log^2 n)\)。

提交记录

NOIP 模拟赛 T3 circle

题意

有一个环，环上有 \(2^M\) 个位置，用 \(0 \sim 2^M - 1\) 标号。现在，\(N\) 个小朋友要在这个环上做游戏。每个小朋友一开始都占据了一个位置，之后，每隔一秒，每个小朋友都会沿顺时针移动到下一个位置上，求满足小朋友们所占据位置的编号的异或和为 \(S\) 的时刻个数。

题解

每个数都加上相同的数，要求异或和，计数。这些约束可以让我们想到数位 DP。

套路地，令 \(f_{i,j,0/1}\) 表示只考虑低 \(i\) 为，\(i\) 位向 \(i+1\) 位进位为 \(j\)，是否超过边界的方案数。

我们需要干两个事情：计算当前位异或和，计算当前位向下一位的进位。

我们需要观察到一个关键性质：进位为 \(j\) 说明只考虑低 \(i\) 位，前 \(j\) 大的数各进一位。

然后我们维护的信息类似于：前 \(i-1\) 位前 \(j\) 大中，第 \(i\) 位为 \(1\) 的数字个数。这个可以通过基数排序维护。

从高到低应该也能做。

提交记录

P3647 [APIO2014] 连珠线 紫

题意

有一个游戏称为连珠线。线是红色或蓝色的，珠子被编号为 \(1\) 到 \(n\)。这个游戏从一个珠子开始，每次会用如下方式添加一个新的珠子：

Append(w, v)：一个新的珠子 \(w\) 和一个已经添加的珠子 \(v\) 用红线连接起来。

Insert(w, u, v)：一个新的珠子 \(w\) 插入到用红线连起来的两个珠子 \(u, v\) 之间。具体过程是删去 \(u, v\) 之间红线，分别用蓝线连接 \(u, w\) 和 \(w, v\)。

给定一棵树，请对这棵树的边进行红蓝染色，满足这棵树是一个可能被得到的游戏局面，并且蓝边的权值和被最大化。输出蓝边权值和的最大值。

题解

以一开始的珠子为根，如果一颗红链之后变成了蓝链，那么可以视为一开始就加入了这条蓝链。我们发现我们每次会在树上加入一个长度为 \(1\) 的红链或长度为 \(2\) 的根向蓝链。

如果已知开始的珠子，我们只需要树形 DP 出若干根向长度为 \(2\) 的不交路径最大权值和。

但是我们不知道开始的珠子，所以换根 DP 就行了。

提交记录

CF1773G Game of Questions *2800

题意

Genie 正在参加一个问答比赛。比赛共 \(n\) 题，有 \(m\) 个参赛者（Genie 为 \(1\) 号参赛者）。

比赛的形式如下：先将 \(n\) 道题随机排序（即每个排列出现的概率都是 \(\dfrac{1}{n!}\)），然后按排列的顺序会依次问出这 \(n\) 个问题。问一个问题时，若所有人都会或所有人都不会则无事发生，否则不会的人会被淘汰。在 \(n\) 个问题都被问完之后，未被淘汰的人就都赢得胜利。

现在给出每个人是否会每道题，请求出 Genie 获胜的概率。

题解

首先需要注意到一个关键性质：重复是无关紧要的，因为重复的题目不会对场上的局面造成任何改变。

然后把问题转化成每次随机选题，令 \(f_S\) 表示场上剩余 \(S\) 时 \(1\) 的获胜概率，进行传统的概率 DP 即可。

在 DP 的时候需要处理 \(g_{S,T}\) 表示可以把场上的人从 \(S\) 淘汰到 \(T\) 的题目数量。

类比组合数，随便取一个不在 \(S\) 里面的数 \(x\)，有转移式 \(g_{S,T}=g_{S\cup x,T}+g_{S\cup x,T\cup x}\)。

卡常，需避免使用 umap 之类的工具，精细实现 \(g\) 的转移。

提交记录

CF908G New Year and Original Order *2800

题意

Let $ S(n) $ denote the number that represents the digits of $ n $ in sorted order. For example, $ S(1)=1,S(5)=5,S(50394)=3459,S(353535)=333555$ .

Given a number $ X $ , compute 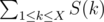modulo $ 10^{9}+7 $。

题解

横竖拆贡献，对于每个数码 \(x\ (1\leq x\leq 9)\)，\(x\) 对数字 \(k\) 的贡献计算方式如下：

• 记 \(k\) 中不小于 \(x\) 的数位个数为 \(t\)，贡献为 \(\sum\limits_{i=0}^{t-1}10^i\)，即 \(\underbrace{11\dots 1}_{t 个 1}\)。

枚举数码 \(x\)，数位 DP。

提交记录

CF1765C Card Guessing *2600

题意

考虑一副扑克牌。每张牌有 \(4\) 种花色，每种花色恰好有 \(n\) 张牌——因此，这副牌共有 \(4n\) 张牌。牌堆经过随机洗牌后，$ (4n)! $ 种可能的排列顺序每种都等概率出现。记 \(c_i\) 为牌堆中的第 \(i\) 张牌（从上到下编号）。

Monocarp 开始依次从牌堆顶抽牌。在抽每一张牌之前，他会尝试猜测这张牌的花色。Monocarp 会记住最近 \(k\) 张牌的花色，他的猜测是：在最近抽出的 \(k\) 张牌中出现次数最少的花色。也就是说，在抽第 \(i\) 张牌时，Monocarp 会猜测其花色为 \(c_{i-k}, c_{i-k+1}, \dots, c_{i-1}\) 这 \(k\) 张牌（如果 \(i \le k\)，则他会考虑所有已经抽出的牌，即 \(c_1, c_2, \dots, c_{i-1}\)）中出现次数最少的花色。如果有多个花色出现次数同为最少，他会等概率地随机选择其中之一作为猜测。

做出猜测后，Monocarp 抽出一张牌，并将其花色与自己的猜测进行比较。如果猜对了，则本次猜测正确；否则为错误。

你的任务是计算，Monocarp 抽完全部 \(4n\) 张牌后，猜对的次数的期望值。

题解

答案是每个位置猜对的概率之和。

对于一个位置，考虑卡牌怎么放置才能被猜中，当前牌需要在前 \(c=\min(i-1,k)\) 张牌中出现次数最小，组合数刻画这个方案数，然后跑一遍物品个数为 \(4\) 的 背包计算总和即可。

提交记录

AT_agc013_e Placing Squares 紫

题意

给长度为 \(n\ (n\leq 10^9)\) 的序列分段，一种方案的贡献为所有段长度的平方之积，给定 \(m\) 个地方不能作为断点，求所有方案贡献总和。

题解

将平方转化为组合意义：在区间内放置两个不同的球的方案数。

然后令 \(f_{i,0/1/2}\) 表示当前区间放了 \(0/1/2\) 个球的方案数，就可以分段矩阵乘法了。

提交记录

AT_agc030_f Permutation and Minimum 黑

题意

有一个 \(2N\) 个数的序列 \(A\)，从 1 到 \(2N\) 标号。你要把 \(1\sim 2N\) 这些数填进去，使它形成一个排列。

但是已经有一些位置强制填了特定的数了，输入时会给出。

最后令长度为 \(N\) 的序列 \(B\) 为：令 \(B_i=min\{A_{2i−1},A_{2i}\}\)。

询问所有方案中能得到的不同的 \(B\) 的数量。

\(N\leq 300\)。

题解

先把确定的位置扔掉，留下一边确定和两边都不确定的位置。

然后问题转化为将数字两两匹配，然后乘上两边都不确定位置数的阶乘来分配位置。

令 \(f_{i,j,k}\) 表示已填入 \(i\sim 2\times n\) 个数字，有 \(j\) 个不定位置的数字等待匹配，\(k\) 个确定位置的数字等待匹配。

转移时分：匹配一个位置确定的数、匹配一个位置不定的数、等待匹配三种情况讨论。

注意：位置确定的数不能互相匹配，匹配一个位置确定的数需要乘系数，因为不同位置的数显然不同。

从大到小填数的好处在于我们所填的数一但匹配，那么这个位置就确定了，不会算重。

提交记录

[ABC262Ex] Max Limited Sequence 黑

题意

求满足以下条件的长度为 \(N\) 的序列 \(A=(A_1,A_2,\cdots A_N)\) 有多少种：

• \(\forall i \in[1,N],0\leq A_i\leq M\)
• \(\forall i \in[1,Q],\max \limits_{L_i\leq j\leq R_i}A_j=X_i\)

\(N\leq 2\times 10^5\)。

题解

容易得出每个数的上界，且可以发现我们只关心每个数是否取到上界。

然后上限低的位置不会对上限高的位置和限制高的区间造成任何影响，因此上限不同的位置是独立的。

因此我们现在只需要解决 \(X\) 都相同的情况，令 \(f_{i,j}\) 表示前 \(i\) 个位置，上一个取到最大值的位置是 \(j\) 的方案数，线段树维护整体 DP 即可（转移比较特殊，也可以不用线段树）。

细节还挺多的。

提交记录

CF53E Dead Ends *2500

题意

求一张图有 \(k\) 个叶子的生成树数量。

\(n\leq 10,m\leq \binom{n}{2}\)。

题解

状压 DP，以 \(1\) 为根一层层加入节点，令 \(dp_{x,S,T}\) 表示树上节点集合是 \(S\)，最后一层节点是 \(T\)，除 \(T\) 以外有 \(x\) 个叶子。这里“除 \(T\) 以外”是因为 \(T\) 中的点还不确定是否是叶子。

转移时枚举一个 \(S\) 补集的子集将其每个节点连向 \(T\)，假设 \(T\) 中有 \(x\) 个节点没有被连接，那么会增加 \(x\) 个叶子（注意如果 \(S=T=1\) 且加入的集合大小也为 \(1\)，那么要额外加上节点 \(1\) 这个叶子）。

我们枚举 \(x\)，然后需要处理 \(g_{S,T,x}\) 表示 \(S\) 中的节点向 \(T\) 中的节点连边，且 \(T\) 中有 \(x\) 个节点被至少一个点连边的方案数。这部分可以做到 \(O(n2^n\times n2^n)=O(n^2 4^n)\)。

那么我们可以令 \(to_{S,T}\) 表示 \(S\) 中的节点向 \(T\) 中的节点连边，不做任何要求的方案数，\(to\) 可以直接把每个点的方案数乘起来，然后容斥一下可以得到 \(g_{S,T,|T|}\)。

则有 \(g_{S,T,x}=\sum\limits_{T'\subseteq T\land \operatorname{popcnt}(T')=x} g_{S,T',|T'|}\)，这部分可以做到 \(O(2^n\times 3^n)=O(6^n)\)。

有了 \(g\) 可以轻松得到 \(dp\) 的转移。

时间复杂度 \(O(6^n+n^2 4^n)\)。

提交记录

CF1789F Serval and Brain Power *2700

题意

定义一个字符串 \(T\) 是好的，当且仅当存在字符串 \(T'\) 和整数 \(k(k\geq2)\)，使得 \(T\) 可以由 \(k\) 个 \(T'\) 首尾相接得到。

例如，字符串 \(\texttt{gogogo}\) 就是好的，因为它可以由 \(3\) 个字符串 \(\texttt{go}\) 首尾相接得到；而 \(\texttt{power}\) 就不是好的。

给定仅包含小写英文字母的字符串 \(S\)。求出 \(S\) 最长的好的子序列的长度。

\(|S|\leq 80\)。

题解

对于重复次数 \(\leq 3\) 的，直接枚举断点然后求 LCS。

对于重复次数 \(\geq 4\) 的，那么单位序列长度 \(\leq 20\)，直接枚举起点然后暴力，经过合理的剪枝可以做到 \(O(5\times 2^20\times n)\)。

提交记录

P12038 [USTCPC 2025] 送温暖 紫

题意

给定一个 \(n\) 个点的树，点 \(i\) 的点权为 \(a_i\)，你需要从中选出一个连通块，使得它们的点权和模 \(M\) 的余数最大。克露丝卡尔酱想知道这个点权和模 \(M\) 的余数最大是多少。

\(n\leq 33\)。

题解

找出重心，不包含重心的情况可以暴力。

然后把重心的若干子树平均分成两半 meet in the middle。

提交记录

CF1552G A Serious Referee *3000

题意

Andrea 想出了一个他认为新颖的长度为 \(n\) 的数组排序算法。该算法的工作方式如下：

最初有一个包含 \(n\) 个整数 \(a_1,\, a_2,\, \dots,\, a_n\) 的数组。然后，执行 \(k\) 步操作。

在第 \(i\) 步中，将子序列 \(a_{j_{i,1}},\, a_{j_{i,2}},\, \dots,\, a_{j_{i,q_i}}\) 排序，数组中的其他元素保持不变。

判断 Andrea 的算法是否正确，也就是说，对于任意长度为 \(n\) 的整数数组 \(a\)，算法结束后数组 \(a\) 是否一定有序。

题解

首先发现值域是无关紧要的，能对所有数组 \(a\) 排序当且仅当能被所有 \(01\) 序列排序。

直接枚举会炸，我们每次只枚举被排过序的地方，这样的好处是我们新增一个排序操作后，这个排序操作所对应的位置一定有序，而其余被排过序的位置一定不变。因此我们每次只需要枚举 \(0\) 的个数即可。

复杂度为将 \(n\) 分为 \(k\) 份，所有份乘积的最大值乘上 \(n\)，由于极限数据下 \(3k<n\)，因此复杂度为 \(O((\frac{n}{k})^kn)\)。

提交记录

CF1601F Two Sorts *3400

题意

将 \(1\) 到 \(n\)（包含）的整数按字典序排序（将整数视为字符串）。排序后得到数组 \(a_1, a_2, \dots, a_n\)。

计算 \((\sum_{i = 1}^n ((i - a_i) \mod 998244353)) \mod 10^9 + 7\) 的值。

\(n\leq 10^{12}\)。

题解

\(n\leq 10^{12}\) 提示我们使用折半算法。

考查 \(O(n)\) 的暴力过程，在字典树上暴力搜索，求 \(\sum ((dfn_i-i)\bmod 998244353)\bmod (10^9+7)\)，这启示我们可以求 \(a_i\) 的逆排列 \(b_i\)，然后求 \(\sum b_i-i\)，可以通过折半搜索 \(i\)，然后当高 \(6\) 位固定时 \(b_i\) 与低 \(6\) 位有一定规律，可以批量计算。

直接折半搜索有很多细节，令比如固定高位还是低位位数等，如果你固定低位位数为 \(6\)，那么你发现字典序排序可能出现形如下面的情况：

\[\color{blue}{12345}\color{red}{600000}\\ 123456000000\\ 123456000001\\ \cdots\\ 123456000009\\ \color{blue}{12345}\color{red}{600001}\\ \]

然后高位确定时低位不一定连续，然后做不下去了。

如果你固定高位位数为 \(6\)，那么你无法确定低位可以拼的位数，那么你的字典序排名也是不好求的，如果硬做，你会多若干个 \(\log\) 因子。

我们回归到在字典树上搜索的方法，仿照数位 DP 减少运算次数的方法，当子树内是深度为 \(6\) 的满字典树时，就可以直接借助预处理的东西直接算了。

具体的，令 \(dfn\) 为数值不超过 \(n\) 的字典树的 \(dfs\) 序，\(dfn'\) 表示在深度为 \(6\) 的满字典树的 \(dfs\) 序，我们在深度为 \(6\) 的满字典树上搜索并计算这棵树的 \(dfn'_i-i\) 集合。

假设我们在数值不超过 \(n\) 的字典树上搜到的数是 \(x\)，要往下接一个 \(t\) 位数的 \(y\)，那么这个拼接完的数的贡献就是 \(dfn_x-x\times 10^t+dfn'_y-y\)。

对于 \(0\sim 6\) 位分别开 vector 存下来，然后在数值不超过 \(n\) 的字典树上搜索，如果当前数字 \(x\) 满足 \(x\times B+B-1\leq n\land x\times B\times 10>n\) 则说明 \(x\) 子树下的分支是深度为 \(6\) 的满字典树，那么枚举往下接的位数，然后 vector 上二分算出有多少个数需要减去 \(998244353\) 即可。

提交记录

P3881 [JLOI2008] CODES 黑

题意

给定 \(n\) 个 \(\texttt{01}\) 编码串 \(S_1,S_2,\dots,S_n\)，你的任务是寻找一个编码串 \(T\)，使得它至少可以被划分为两种不同的 \(S_i\) 的排列。\(S\) 可以重复使用。

最小化 \(T\) 的长度并构造方案。

\(n\leq 20，len\leq 20\)。

题解

考虑双序列 DP，即模拟往两个序列中填数的过程。

令 \(f_{i,S}\) 表示已经填了 \(i\) 位，多出未匹配的字符串为 \(S\) 的最小 \(T\)，这样空间爆炸。

注意到我们每次往短的序列中加上一个字符串，那么我们多出的部分必定是某个字符串的后缀。

因此令 \(f_{i,j,k}\) 表示已经填了 \(i\) 位，其中第二个序列的后 \(k\) 位没有匹配且属于 \(s_j\) 的后 \(k\) 位的最小 \(T\)，暴力转移的复杂度是 \(O(n^4(状态数)\times n(转移数)\times n^2(chkmin))=O(n^7)\)。

注意到 \(i\) 只和转移顺序有关，因为我们已经在 \(f\) 中存了当前字符串。

换句话说我们删掉第 \(i\) 维唯一的坏处是不知道转移顺序。

因此直接滚掉第 \(i\) 维，使用 dijkstra 进行转移顺序不确定的 DP 即可。

提交记录

CodeChef-SADPAIRS Chef and Sad Pairs *2925

题意

给定一张图，每个点有一个颜色。

对于每个点求：

• 删去这个与点相连的所有边后，图上颜色相同且不可达的无序点对数量。

\(n,m\leq 2\times 10^5\)。

题解

建出圆方树，不同连通块之间的贡献是好算的，相同连通块贡献相当于对每个点求圆方树上删掉这个点后两侧相同颜色数，对于每个点是不好求的，但是可以对于每个颜色建立虚树，然后在虚树上统计，一个颜色对于其所对应虚树的相邻两个节点之间的所有点贡献一样，做一个树上差分即可。

提交记录

P10674 【MX-S1-T3】电动力学 紫

题意

给定一张包含 \(n\) 个点 \(m\) 条边的简单无向连通图，点的编号为 \(1\sim n\)。

你需要求出有多少集合对 \(S,T\sube \{1,2,\dots,n\}\)，满足对于任意的 \(i\in S\)，要么 \(i\) 也 \(\in T\)，要么存在 \(x,y\in T\)（\(x\neq y\)），满足存在一条从 \(x\) 到 \(y\) 的简单路径经过 \(i\)。

注意，集合对 \(S,T\) 可以为空集。

输出答案对 \(998244353\) 取模后的结果。

题解

由于点双满足任意两点路径并集都是全集，因此将 \(T\) 看作圆方树上选若干个圆点， 记这些圆点所构成的虚树为 \(Tr\)，那么 \(S\) 就是 \(Tr\) 上所有方点邻域构成集合的子集。

那么，记 \(Tr\) 上所有方点邻域构成集合的子集大小为 \(x\)，这个 \(T\) 的贡献就是 \(2^x\)。

对 \(T\) 进行 DP，套路的，我们让方点承担计算贡献的责任，圆点只负责计数。

一个天真的想法是我们令每个方点的权值为 \(2^{deg}\) 次方然后求选若干个点所构成虚树的权值乘积和。

但是这样会算重，因为一个点可能会被相邻的多个方点计算。

那么我们考虑让一个方点的权值为 \(2^{deg-1}\)，即只计入其儿子的贡献，然后如果虚树的根节点是圆点就再 \(\times 2\)，就不会算重了。

之后就是套路的虚树计数 DP，令 \(f_{u}\) 表示 \(u\) 只考虑子树内，如果子树内有点则钦定其虚树向上延申的方案数。当 \(u\) 是圆点时，有 \(f_{u}=2\times \prod f_v\)，表示 \(u\) 可选可不选；当 \(u\) 是方点时，\(f_u=1+2^{deg_u-1}\times ((\prod f_{v})-1)\)，表示 \(u\) 不能选，乘上 \(u\) 的权值 \(2^{deg_u-1}\)，注意要单独考虑什么都不选的情况。

计算答案时，枚举虚树的 \(\text{lca}\)，如果这个点是圆点，分类讨论这个点是否选，如果是方点就必须不选，但是此时需要乘上这个方点的 \(2^{deg}\)。注意当 \(u\) 不选且要求 \(\text{lca}=u\) 是，需要保证 \(u\) 必须至少两个子树内有东西，这个需要用总方案数减去空方案和只有一个子树有东西的方案数来计算。

提交记录

CF1054F Electric Scheme *2700

题意

二维平面上铺了一些电线。每个电线可以看作一条线段，一些是水平的，另一些是竖直
的。在这些电线的交点处会迸发火花（不妨假设水平电线和竖直电线各自内部不交）。

现在电线消失了，你只知道所有 \(n\) 个火花的位置。求原来最少有多少根电线，并构造一组方案。

\(1\leq n\leq 1000\)。

题解

每个火花处放一个极小的十字，这样一定有解。

将同行或同列的相邻火花连边，如果能连上那么答案就会减一。

如果有相交的边不能同时连接，因此将边视作点，建出冲突关系图，答案就是 \(2n-最大独立集大小\)。

注意到这是一个二分图，跑二分图最大独立集即可，构造方法是跑完最大匹配后在残量网络上 DFS，找出左侧搜到的点和右侧没搜到的点，这些点就是最大独立集。下面来说明这件事。

使用最小割刻画最大独立集，最小割问题是要最小化 \(\sum\limits_{(u_i\to v_i,w_i)} w_i x_{u_i}(1-x_{v_i})\)，并强制 \(x_S=1,x_T=0\)。最大独立集问题是要最小化 \(\sum -x_u+\sum\limits_{(u_i - v_i)} +\infin x_{u_i}x_{v_i}\)。

我们发现一个 \(x\) 同号一个 \(x\) 异号，下式无法变形到上式。

一般图最大独立集是 NP 问题，但是我们只需要处理二分图，我们将二分图右部点的 \(x\) 取反，即 \(x=1\) 代表它实际在 \(T\)，\(x=0\) 代表它实际在 \(S\)，然后最大独立集的式子可以变为如下形式，因为 \(x_S=1,x_T=0\)，该式可进一步转化。

\[\sum_{u\in \text{left}} -x_u+\sum_{v\in \text{right}} -(1-x_v)+\sum\limits_{(u_i - v_i)} +\infin x_{u_i}(1-x_{v_i})\\ =\sum_{u\in \text{left}} -x_u+\sum_{v\in \text{right}} x_v+\sum\limits_{(u_i - v_i)} +\infin x_{u_i}(1-x_{v_i})-|\text{right}|\\ =\sum_{u\in \text{left}} 1\times x_S(1-x_u)+\sum_{v\in \text{right}} 1\times x_v(1-x_T)+\sum\limits_{(u_i - v_i)} (+\infin) \times x_{u_i}(1-x_{v_i})-|\text{left}|-|\text{right}| \]

根据这个式子连边，然后求出最小割，并在残量网络上搜出一个割的构造，由于我们刚才对右部点进行了取反，因此最终的独立集是左侧搜到的点和右侧没有搜到的点。

实际实现的时候在把中间的边权从 \(+\infin\) 改为 \(1\) 也是可以的，因为中间的边受两侧点的限制最多流 \(1\) 的流量。

提交记录

CF1416F Showing Off *3300

题意

给定一个 \(n\times m\) 的 LRDU 矩阵，除此之外，矩阵上每个格子还有⼀个正整数权值 \(a_{i,j}\)。

现在我们根据这些信息求出一个新矩阵 \(b\)，\(b_{i,j}\) 的值为：从 \((i,j)\) 出发开始沿着格子上写的方向走 \(10^{100}\) 步之后，经过至少一次的所有单元格的 \(a_{i,j}\) 值之和。

现在给出矩阵 \(b\)，请构造任意符合条件的字符矩形，以及 \(a\)。或者报告无解。字符矩形需满足所有边缘的方向不能指向矩形外。

\(1\leq n\times m\leq 10^5\)。

题解

我们发现如果一个点 \(u\) 旁边存在一个小于它的点 \(v\)，那么令点 \(u\) 方向指向 \(v\) 并令 \(a_u=b_u-b_v\) 即可。

我们发现如果一个点 \(u\) 旁边的所有点的 \(b\) 都大于 \(b_u\)，那么这个点往哪走都不行，因此无解。

如果两个点权值相同，那么这两个点可能在同一个环中。

特殊的，如果一个点 \(u\) 旁边不存在一个小于它的点，那么这个点必定在环中，称这样的点为“黑点”，其余点为“白点”。

注意到一个环拆成若干个二元环是不会更差的。

我们把可以在同一个环中的点连边，容易发现这构成一个二分图，我们的问题是求一个匹配方案，要求关键点都被匹配。

我们考虑求最大匹配，但是这样是错的，因为白点可能抢占黑点的匹配。

我们考虑尽可能满足白点，避免其抢占黑点匹配，使用若干个虚拟白点将两侧点的数量补到一致，然后在所有白点之间两两连边，然后跑最大匹配即可。如果存在完美匹配即有解。

让我们尝试说明这是对的：当不存在黑点都被匹配的方案时，我们只加入了白点和白点之间的边，新图也不会存在黑点都被匹配的方案，因此新图不存在最大匹配；当存在黑点都被匹配的方案时，在黑点都被匹配的情况下两侧肯定剩下数量相同的白点，那么将这些白点两两匹配后就是完美匹配，因此完美匹配存在。

白点之间两两连边在网络流中可以使用虚点优化建图。

提交记录

QOJ#3555. Chameleon's Love *????

题意

这是一道交互题。

• 共有 \(2n\) 只变色龙，其中 \(n\) 只性别为 \(X\)，另外 \(n\) 只性别为 \(Y\)。
• 每只变色龙有一个原色，原色取值范围为 \(1\sim n\)，满足：
  • 同一性别内部，所有变色龙的原色互不相同。
  • 每只变色龙恰好与一只异性变色龙的原色相同。
• 每只变色龙有一个恋慕对象，满足：
  • 恋慕对象一定是异性；
  • 一只变色龙与其恋慕对象的原色不同；
  • 每个变色龙恰好喜欢一只变色龙，且恰好被一只变色龙喜欢。
• 初始时只知道 \(n\)，其余信息全部未知。
• 允许进行如下操作（最多 \(20000\) 次）：
  • 选择一个变色龙集合 \(S\) 举办聚会。
  • 对于每只参加聚会的变色龙：
    • 如果其恋慕对象也参加了聚会，则其肤色变为恋慕对象的原色。
    • 否则，肤色保持为自己的原色。
  • 最终，你会得到聚会上肤色种类数。
• 目标：通过不超过 \(20000\) 次聚会，确定每只变色龙与哪只变色龙原色相同（即找出所有原色配对的变色龙对）。
• 数据范围：\(n \le 500\)。

部分分：

• 所有恋慕关系都是双向的。
• 允许 \(O(n^2)\) 次询问。
• 性别已知。

题解

考虑部分分一，发现双向恋慕关系在一起时会彼此互换颜色，对肤色数没有任何影响，因此直接二分即可。

因此，我们称两个点 \(a,b\) “有关”，当且仅当满足以下三条中任意一条：

• \(a\) 喜欢 \(b\) 且 \(b\) 不喜欢 \(a\)。
• \(b\) 喜欢 \(a\) 且 \(a\) 不喜欢 \(b\)。
• \(a,b\) 原色相同。

注意我们完全忽略了双向喜欢的关系。

考虑部分分二，我们让变色龙两两聚会，如果颜色数是 \(1\) 就说明两个变色龙有关。

容易发现对于每个变色龙，与其有关的变色龙有 \(1\) 或 \(3\) 个。

如果与变色龙 \(x\) 有关的变色龙只有一个，设其为 \(y\)，那么有 \(x,y\) 原色相同，我们解决了变色龙 \(x\) 的问题。

否则，设 \(a\) 喜欢 \(x\)，\(x\) 与 \(b\) 原色相同，\(x\) 喜欢 \(c\)。我们选择 \(x\) 和 \(a,b,c\) 中的两个参加聚会，如果这两个人是 \(a,b\) 那么颜色数为 \(1\)，否则为 \(2\)，因此我们可以确定哪个是 \(c\)，求出所有变色龙的 \(c\) 后就可以推出与所有变色龙的 \(b\)。

考虑部分分三。

我们令每个 \(x\) 与一些性别与 \(x\) 不同的变色龙聚会，那么肤色数 \(\neq 聚会人数\)，当且仅当里面有变色龙与 \(x\) 有关，因此分三段二分即可。

考虑正解，我们发现部分分三的做法中，不需要满足【与 \(x\) 聚会的变色龙性别都与 \(x\) 不同】，只需要满足【与 \(x\) 聚会的变色龙互相没有关系】即可。

那么增量维护，维护两个独立集 \(S1,S2\)，加入一条变色龙时在 \(S1,S2\) 上二分，之后得到与新加入变色龙有关的若干点，之后再重构独立集即可。

由于这是二分图，且 \(n\leq 500\)，因此重构独立集是简单的，直接黑白染色即可。

时间复杂度 \(O(n^2\log n)\)，询问次数 \(O(n\log n)\)。

二分时注意剪枝，不然会被卡询问次数。

提交记录

QOJ#7999. 拉丁方 / P10062 [SNOI2024] 拉丁方 黑

题意

给定一个 \(n \times n\) 的矩阵，其中左上角的 \(R \times C\) 的子矩阵已经填好。要求将矩阵补充完整，使得每行每列均为 \(1 \sim n\) 的排列。需要给出构造或判断无解。

\(1 \leq n \leq 500\)。

部分分：\(C = n\)。

题解

考虑部分分，我们建出数与列的二分图，发现这是一个二分图边染色问题，\(k\) 正则二分图边染色必定有解，因为根据 Hall 定理一定存在一组匹配，然后删去匹配后变为 \(k-1\) 正则二分图，可归纳证明。

因此对于 \(C\neq n\)，我们先填上面的数字，将拉丁方补成 \(C=n\)，只要能填出上面 \(R\times n\) 合法的解，那么下面一定有解。

对于上面 \(R\times n\) 的数字，相当于左部点为 \(n\)，右部点为 \(R\) 的二分图，要染成 \(n-C\) 种颜色，并且每条边都要被染色，每种颜色 \(R\) 个。我们发现如果存在一个点，其度数大于 \(n-C\)，那么说明染色不能办到，否则直接套用二分图边染色即可求解。

填完上面的数字后再用二分图边染色填下面的数字即可。

提交记录

QOJ#8602. Занулити пiдвiдрiзок(UkrainianOI D2T4) *????

题意

给定一个长度为 \(n\) 的数列 \(a_1, a_2, \cdots, a_n\)。

初始时变量 \(x=0\)，每一步可以进行以下两种操作之一：

1. \(x \leftarrow x + 1\)
2. 选择一个 \(1 \leq i \leq n\)，令 \(a_i \gets a_i \oplus x\)

\(q\) 次询问，每次给定区间 \([l, r]\)，求最少操作次数使得子数组 \(a[l:r]\) 中的所有元素变为 \(0\)。

\(1 \leq n, q \leq 2 \times 10^5\)，\(1 \leq a_i < 2^{60}\)，强制在线。

部分分：\(O(nq)\) 的解法。

题解

首先每个数只会被异或两次，记最后操作到的 \(x\) 为 \(mx\)，那么区间 \([l,r]\) 的答案为 \(r-l+1+(mx+\sum\limits_{i=l}^{r}[a_i>mx])=2(r-l+1)-(\sum\limits_{i=l}^{r}[a_i\leq mx]-mx)\)，我们要最大化后面减去的部分，令 \(cnt_i\) 表示区间中等于 \(i\) 的数字个数，求出 \(cnt_i-1\) 在 \(i\in [2^h,+\infin)\) 前缀和数组 \(p\)，记区间中 \(a\) 的二进制最高位为 \(2^h\)，需要满足 \(x\geq 2^h\)，那么答案为 \((r-l+1)+cnt+2^{h}-\max\limits_{mx\geq 2^h} p_{mx}\)，\(cnt\) 表示最高位是 \(2^h\) 的数的个数。

注意我们要忽略 \(2\) 的整数幂，因为它们总会被异或一次。

我们把 \(cnt_i-1\) 看成扩展 Hall 定理的形式，即 \(cnt_i\to |S|,1\to |N(S)|\)，我们构造二分图，左部点为 \(a\)，右部点为所有 \(\geq 2^h\) 的整数，左边每个 \(a\) 向右边每个比它小的数连边，那么根据扩展 Hall 定理，最小失配数就是 \(\max \{|S|-|N(S)|\}\)，即 \(\max\limits_{mx\geq 2^h} p_{mx}\)。最小失配数可以由最大匹配数得到。

对每个 \(h\) 单独拎出来 \(\text{highbit}=h\) 的 \(a\) 序列，我们要干的事情就是每次给定某个序列的某个区间，求最大匹配。

引理：一定存在一个最大匹配，使得将左侧被匹配的点从大到小排序后，这个被匹配的序列偏序所有其他的最大匹配。

证明：考虑两个不互相偏序的匹配 \(B,C\)，将所有匹配边画出，图中将形成若干链和环，然后在这张图上构造新的匹配。对于链，由于是最大匹配，因此匹配方法唯一；对于环，让字典序更优，在新图中一定能找到一个不劣于 \(B,C\) 的匹配。

对序列扫描线，需要维护单点加入，并尝试增广掉最早被加入的节点，求最大匹配。这对于一般二分图是不能低于 \(O(n^2)\) 的。

考虑反向 Hall 定理，维护被匹配的集合 \(S\)，并求出只考虑 \(S\) 的 \(cnt_i-1\) 的前缀和，如果有位置大于 \(0\) 就会失配，即 \(S\) 是非法的。

新加入一个数 \(a_x\)，线段树维护 \(cnt_i-1\) 的前缀和，将 \([a_x,\max a]\) 加 \(1\)，如果出现 \(>0\) 的位置，找出最前 \(>0\) 的位置 \(p\)，并找到满足 \(a_y\in [2^h,p]\) 的最小 \(y\)，删掉 \(a_y\) 即可。

加入一个数 \(a_x\) 时，相当于在扫描线线段树上的 \(l\leq x\) 的答案加 \(1\)，删除同理。由于强制在线，需要可持久化。

【2025/8/27 23:04】 没调完，睡觉了。

”注意我们要忽略 \(2\) 的整数幂，因为它们总会被异或一次。“的另一个原因是，我们需要让 \(cnt-1\) 的前缀最大值从 \(2^h+1\) 开始，先将 \(x\) 加到 \(2^h\)。

如果从 \(2^h\) 开始，那么实际上 \(x\) 被加到的初值是 \(2^h-1\)，那么此时如果存在完美匹配，无法判断 \(x\) 在这个方案中是否被加到了 \(2^h\) 及以上，如果没有则不符合题意，这会导致你的答案可能比正确答案少 \(1\)。

【2025/8/28 15:07】 调完了。

提交记录

2025.9

CF1310C. Au Pont Rouge *2800

题意

给定一个长度为 \(n\) 的由小写英文字母构成的字符串 \(s\)。对于每种将 \(s\) 分割成连续的 \(m\) 部分的方案，令字典序最小的子串作为元素构成的集合为 \(A\)。将集合 \(A\) 中的元素按字典序逆序排序，求第 \(k\) 个元素是什么。

数据范围：\(2 \leq n, m \leq 10^3; 1 \leq k \leq 10^{18}\)。

题解

子串数总和是可以接受的，把所有子串拿出来，排序后二分答案。

之后 DP 统计划分 \(m\) 段，最小字典序大于当前子串的方案有多少个。

直接把所有子串插到 Trie 里面，就能 \(O(1)\) 比较字典序。

每个点往后转移是一段区间，算出区间后直接 DP 即可。

提交记录

CF616F. Expensive Strings *2700

题意

给你 \(n\) 个字符串。每个字符串的成本都是 \(c_i\)。 定义定义域为字符串的函数，其中 \(\operatorname{f}(s) = \sum_{i=1}^{n} c_i \cdot p_{s, i} \cdot |s|\)，其中 \(p_{s, i}\) 为 \(s\) 在 \(t_i\) 中出现的次数，\(|s|\) 为字符串 \(s\) 的长度。求对于所有字符串，\(\operatorname{f}(s)\) 的最大值。

注意字符串 \(s\) 不一定是 \(t\) 中的某个字符串。

题解

建出 SA，相当于求一个区间，这个区间的贡献是 \(len\times (\min height)\times \sum c\)。

统计每个 \(height\) 作为最小值的答案即可。

特殊处理长度为 \(1\) 的区间。

提交记录

CF1065G. Fibonacci Suffix

题意

我们再次定义斐波那契字符串序列：

$F(0) = $ 0，$F(1) = $ 1，\(F(i) = F(i - 2) + F(i - 1)\)，其中加号表示两个字符串的连接。

我们将字符串 \(F(i)\) 的所有后缀按字典序排序后得到的序列记为 \(A(F(i))\)。例如，\(F(4)\) 为 01101，\(A(F(4))\) 为以下序列：01，01101，1，101，1101。该序列中的元素从 \(1\) 开始编号。

你的任务是输出 \(A(F(n))\) 中第 \(k\) 个元素的前 \(m\) 个字符。如果该后缀长度小于 \(m\)，则输出整个后缀。

题解

考虑把 \(A(F(n))\) 插入 01 Trie，那么可以算出子树大小后在 Trie 树上走。

现在我们需要算子树大小，假设我们当前走到位置的串是 \(ans\)，令 \(f_i\) 表示 \(F(i)\) 中前缀为 \(ans\) 的串的个数，那么子数大小就是 \(f_{n}\)

先把 \(F(14),F(15)\) 暴力算出来，这样可以发现后面的 \(F\) 在前后缀拼接的时候都是 \(F(14),F(15)\) 的某个后缀拼上某个前缀。

令 \(g_{i,j}\) 表示 \(F(i)\) 拼上 \(F(j)\) 新产生的前缀为 \(ans\) 的串的个数，则 \(f_i=f_{i-1}+f_{i-2}+g_{i-2,i-1}\)。

\(g\) 可以由上述性质得到。

提交记录

CF1536F. Omkar and Akmar *2600

题意

Alice 和 Bob 在一个 \(n\) 个格子的环上玩游戏，环上的格子编号为 \(1\sim n\)。

每一轮中，玩家可选择一个空格子填入字母 A 或 B，同时要求不能存在两个相邻的格子内的字母相同。若没有合法操作，则游戏结束，当前玩家失败。

假设 Alice 和 Bob 每局游戏两个人都按最优策略行动，问有多少种可能的不同游戏。两种游戏不同，当且仅当回合数不同，或者对于某个回合，放置的字母或单元格编号不同。答案对 \(10^9+7\) 取模。

\(n\leq 10^6\)。

题解

核心思想：枚举最后局面，计算每个最后局面对答案的贡献。

首先，两个玩家肯定是能操作就操作，因此最后局面肯定不能继续操作。

那么最后局面一定是一个 ABAB 交替的环上序列，中间穿插若干不相邻的空位。

因为这是环上 ABAB 交替的序列，所以最后填上数的位置个数必定为偶数，因此后手必胜。

当最后局面确定时，两个玩家可以随便操作。因为这相当于有若干个石子，每次操作取走恰好一个石子的简单博弈问题。

假设我们最后确定的局面有 \(i\) 个空格，那么这个局面的操作方案书就是 \((n-i)!\)。

我们枚举空格个数，然后计算满足条件的局面个数。再乘上操作方案数。

当空格个数确定时，由于要求空格不能相邻，因此考虑插板，为了方便插板，我们假设环上一开始只有 ABAB...，然后把环从第一次操作的地方断开，对于断开的链，每个位置的后面可以选择放不放空格。

因此，空格个数为 \(i\) 时，总方案数为 \(2\times n\times \binom{n-i}{i}\times (n-i-1)!\)。

乘 \(2\) 是因为 AB 可以互换，乘 \(n\) 是因为这是有标号环，需要枚举断开位置的标号。

空格个数一定与 \(n\) 奇偶相同，最后答案为 \(\sum\limits_{i=n\bmod 2}^{\lfloor \frac{n}{2}\rfloor} \left(2\times n\times \binom{n-i}{i}\times (n-i-1)!\right)\)。

提交记录

2025/9/7 NOIP 模拟赛 T4 *????

题意

求 \(n\) 个点的有标号无根树的直径之和。

\(n\leq 500\)。

题解

核心思想：以所有直径的交点/边为中心。

令 \(f_{i,j}\) 表示 \(i\) 个点编号为 \(1\sim i\)，深度不超过 \(j\) 的有标号有根树的数量。

令 \(g_{i,j}\) 表示 \(i\) 个点编号为 \(1\sim i\)，深度不超过 \(j\) 的有标号叶向森林（即 \(f\) 去掉根）数量。

如果所有直径交于一边，即直径长度为 \(2k+1\)，那么枚举两边点的个数 \(x,n-x\)，答案为 \(\sum\limits_{x=1}^{n} (f_{x,k}-f_{x,k-1})\times (f_{n-x,k}-f_{n-x,k-1})\times \binom{n}{x}\div 2\)，除以 \(2\) 的原因是交边两侧是无序的。

但是模数不质，且常数不允许我们再存一个 \(2\) 因子，我们不能除以二，考虑强制让 \(1\) 在左侧，即 \(\sum\limits_{x=1}^{n} (f_{x,k}-f_{x,k-1})\times (f_{n-x,k}-f_{n-x,k-1})\times \binom{n-1}{x-1}\)。

如果所有直径交于一点，即直径长度为 \(2k\)，那么这个点所有子树至少有 \(2\) 个深度等于 \(k\)，容斥，答案为 \(n\times \left( g_{n-1,k}-g_{n-1,k-1}-\sum\limits_{x=1}^{n-1} (f_{x,k}-f_{x,k-1})\times g_{n-1-x,k-1}\times \binom{n-1}{x} \right)\)。

考虑如何求 \(f\)，显然有 \(f_{i,j}=g_{i-1,j-1}\times i\)。

考虑如何求 \(g\)，有 \(g_{i,j}=\sum\limits_{k=1}^{i} g_{i-k,j}\times f_{k,j}\times \binom{i-1}{k-1}\)。

解释一下 \(g\) 的转移，有一个错误的想法是 \(g_{i,j}=\sum\limits_{k=1}^{i} g_{i-k,j}\times f_{k,j}\times \color{red}\binom{i}{k}\)，但是这样算，子树是有序的，因此会算重。

考虑把子树按照一定顺序排序，并有序的加入这些子树，由于我们在实时分配编号，因此考虑按子树内的最小值降序排序，然后每次强制让 \(1\) 出现在新的子树里，即 \(g_{i,j}=\sum\limits_{k=1}^{i} g_{i-k,j}\times f_{k,j}\times \binom{i-1}{k-1}\)。

初始时 \(f_{0,i}=g_{0,i}=1\)。

提交记录

CF1038F. Wrap Around *2900

题意

给定一个字符串 \(s\)，字符集为 \(\{0,1\}\)。

求有多少长度为 \(n\) 的字符串 \(t\)，满足以 \(t\) 为循环节的无限循环字符串包含 \(s\)。

\(1\le|s|\le n\le 40\)。

题解

\(s\) 在无限循环的 \(t\) 中出现，等价于 \(s\) 在 \(t^2\) 中出现。

考虑建立 KMP 自动机，在自动机上 DP。

但是直接对 \(t^2\) 的结构做 DP 会导致有后效性。

考虑 DP 为什么无法处理 \(t^2\) 的情况，因为正常 KMP 自动机上 DP 只能处理往后加入一个字符，而维护 \(t^2\) 要求我们往中间插入字符。

考虑把 DP 改成只往后加字符的情况。只往后加字符，一种想法是假设 \(t\) 在 KMP 自动机的结束状态确定，然后往后加第二个 \(t\)。

时间充裕，因此可以直接枚举 \(t\) 在自动机上最后的节点 \(p\)，令 \(f_{i,j,k}\) 表示 \(|t|=i\)，\(t\) 在自动机上走到了 \(j\)，\(t^2\) 在自动机上走到了 \(k\)，初值令 \(f_{0,0,p}=1\) 即可。

时间复杂度 \(O(n^4)\)。

提交记录

CF587F. Duff is Mad *3000

题意

给定 \(n\) 个字符串 \(s_1…s_n\)。定义 \(f_y (x)\) 表示 \(s_x\) 在 \(s_y\) 中出现的次数。

\(q\) 次询问，每次给定 \(l,r,k\)，求 \(\sum\limits_{i=l}^{r} f_k (i)\)。

\(n, q, \sum_{i=1}^n |s_i| \leq 10^5\)。

题解

*所有复杂度认为 \(n,q,|s_i|\) 同阶。

搬到 ACAM 上，发现问题可以转化为如下形式：

• 给定 \(n\) 个点集，保证点集大小之和不超过 \(10^5\)，每次询问给定 \(l,r,k\)，求编号在 \([l,r]\) 的点中，子树内含有第 \(k\) 个点集中点的个数之和。

直接做很难做，考虑反过来，变成把编号在 \([l,r]\) 的点的子树加一，然后求第 \(k\) 个点集的权值和。

然后如果点集大小为 \(1\)，就可以直接做了。

保证点集大小之和不超过 \(10^5\)，可以根号分治，点集大小不超过 \(B\) 的直接暴力，复杂度 \(O(nB\log n)\)，点集大小大于 \(B\) 的点集不超过 \(\frac{n}{B}\) 个，提前预处理每个点进行子树加对这些点集的贡献，然后维护 \(O(\frac{n}{B})\) 个 BIT 一起扫描线，复杂度 \(O(\frac{n^2}{B})\)。

令 \(nB\log n=\frac{n^2}{B}\)，即 \(B=\sqrt{\frac{n}{\log n}}\)，此时复杂度为 \(O(n\sqrt{n \log n})\)。

但是由于 \(O(\frac{n^2}{B})\) 的空间复杂度无法接受，因此最后决定令 \(B=10^{2.5}=316\)，此时当 \(n,q,|s|=100000\) 时，时间复杂度为 \(O(n\sqrt{n}\log n)\)。

提交记录

CF1400F. x-prime Substrings *2800

题意

给定一个整数 \(x\) 和一个只包含数字 \(1\) 到 \(9\) 的字符串 \(s\)。设 \(f(l, r)\) 表示子串 \(s[l..r]\) 的数字之和。

我们称子串 \(s[l_1..r_1]\) 为 \(x\)-prime，当且仅当：

• \(f(l_1, r_1) = x\)；
• 不存在 \(l_2, r_2\) 满足：
  • \(l_1 \le l_2 \le r_2 \le r_1\)；
  • \(f(l_2, r_2) \neq x\)；
  • \(x\) 能被 \(f(l_2, r_2)\) 整除。

你可以从字符串中删除一些字符。每删除一个字符，字符串会被分成两部分并直接拼接，顺序不变。

请问，最少需要删除多少个字符，才能使字符串中不存在 \(x\)-prime 子串？如果原字符串中本就不存在 \(x\)-prime 子串，则输出 \(0\)。

\(1\leq |s|\leq 1000\)，\(1\leq x\leq 20\)。

题解

考虑要求一些子串不能出现，即多模匹配，搬到 ACAM 上考虑。

\(x\leq 20\)，发现 \(x\)-prime 字符串总数不会太多，最多的时候是 \(x=19\)，此时所有 \(x\)-prime 字符串建出的 ACAM 大小为 \(4852\)。

因此暴力建出 ACAM 后跑 DP 即可，\(dp_{i,j}\) 表示前 \(i\) 个字符走到 ACAM 的 \(j\) 号点最小要删去几个字符，转移显然。

提交记录

CF2045E. Narrower Passageway *2700

题意

有一个 \(2\) 行 \(N\) 列的网格。我们用 \((r, c)\) 表示网格中第 \(r\) 行第 \(c\) 列的格子。每天会安排一个力量值为 \(P_{r, c}\) 的士兵驻守在 \((r, c)\) 位置上。

每列都有 \(50\%\) 的概率被雾气笼罩。定义连通区域 \([u, v]\)（\(u \leq v\)）为从第 \(u\) 列到第 \(v\) 列连续且无雾的列。

连通区域 \([u, v]\) 的力量可以这样计算。设 \(m_1\) 和 \(m_2\) 分别为该区域内第一行和第二行士兵力量的最大值。具体来说，对于 \(r \in \{1, 2\}\)，有 \(m_r = \max (P_{r, u}, P_{r, u + 1}, \dots, P_{r, v})\)。如果 \(m_1 = m_2\)，则该区域的力量是 \(0\)；否则，力量为 \(\min (m_1, m_2)\)。

一个工作日的总力量定义为所有连通区域力量的总和。请计算在任意一天部署的期望总力量。

\(1\leq N\leq 10^5\)。

题解

硬讨论也能做，但是有更简单的做法。

变换一下贡献计算形式，对于一个区间，令其贡献为 \(m1+m2-m1[m1=\max(m1,m2)]-m2[m2=\max(m1,m2)]\)。

所有区间 \(m1\)、\(m2\) 的和都是好求的，\(m1[m1=\max(m1,m2)]\)、\(m2[m2=\max(m1,m2)]\) 只需要在单调栈算区间时，规定当前数不小于该区间所对另一行的所有数即可。

提交记录

NOIP 模拟 T3 *????

题意

比较难以描述……

题解

建立笛卡尔树，问题转化为选 \(k\) 个叶子并删除其到根链，最大化删除点权值和。

树形DP，令 \(f_{i,j}\) 表示子树 \(i\) 内选择 \(j\) 个叶子的答案。

有 \(f_{u,j}=w_u+\max\limits_{0\leq x\leq j} \{f_{ls_u}{x}+f_{rs_u}{j-x}\}\)。

不好继续优化，考虑维护 \(f\) 的差分数组，那么贪心地，\(f_u\) 的差分数组就是把 \(f_{ls_u},f_{rs_u}\) 的差分数组从大到小归并，再把第一项加上 \(w_u\)。

贪心的正确性在于，总和一定，要让 \(f\) 最优肯定先选择增量大的叶子。

因此每个点维护一个 set 表示这个点 \(f\) 的差分数组，然后启发式合并即可。

提交记录

CF150E. Freezing with Style *3000

题意

给定一颗带边权的树，求一条边数在 \([L,R]\) 之间的路径，并使得路径上边权的中位数最大。输出一条可行路径的两个端点。

\(n\leq 10^5\)。

题解

二分答案 \(Mid\)，将 \(\geq Mid\) 的边都赋值为 \(1\)，其余边赋值为 \(-1\)，点分治求最大权值和路径检查其是否 \(\geq 0\) 即可。

点分治中需要使用单调队列代替线段树，并按照子树大小或深度从小到大遍历保证单调队列复杂度，还要进行一些必要的剪枝（找到一条 \(\geq 0\) 的路径后立即退出）。

提交记录

AT_arc072_d [ARC072F] Dam 紫

题意

你负责管理一个最多能储存 \(L\) 升水的水库。一开始，水库是空的。接下来 \(n\) 天，第 \(i\) 天早上，有 \(v\) 升 \(t_i\) ℃ 的水会流进来；每天晚上，你可以决定要放多少水，但你必须保证第二天水不会溢出。水不会蒸发，温度也和流进水之外的因素无关。\(v_1\) 升 \(t_1\) ℃ 的水与 \(v_2\) 升 \(t_2\) ℃ 的水混合后的温度为 \(\dfrac {t_1v_1+t_2v_2}{v_1+v_2}\)。对于第 \(i (i \in [1,n] \cap \mathbb N)\) 天，你需要求出最后水库是满的的情况下能达到的最高水温。不同日期的答案相互独立。

\(1 \le n \le 5 \times 10^5\)。

题解

考虑一个贪心，如果 \(i+1\) 时刻加入水的水温比 \(i\) 时刻冷，那么 \(i\) 时刻一定选择不放水，以提高 \(i+1\) 时刻的水温。即使要放水，也是先加入 \(i+1\) 时刻的水，再一起放，这样剩余水温一定不会变差。

那么，我们把所有相邻温度递减的操作合并成一个操作，重复这个过程直到操作满足温度递增。

之后，我们肯定是能放水就放水，但是要保证询问时水池内水的体积等于 \(L\)。手动模拟一下，发现被放掉的水不可能在流回来，流回来也不会更优。因此询问可以等价成：指定体积的滑动窗口，求体积乘以温度的和，单调队列即可。

提交记录

P11283 「GFOI Round 2」Turtle and Nediam 紫

题意

对一个元素互不相同的长度 \(\ge 3\) 的正整数序列 \(a\)，定义 \(a\) 的“肿胃数（nediam）”\(f(a)\) 为：

• 当 \(|a| = 3\) 时，\(f(a)\) 为 \(a\) 的中位数；
• 当 \(|a| > 3\) 时，取 \(a\) 的任意一个长度为 \(3\) 的子段 \([a_i, a_{i + 1}, a_{i + 2}]\)，记这个子段的中位数为 \(x\)，\(a\) 删掉 \(x\) 后的序列为 \(b\)，\(f(a)\) 为所有 \(b\) 中 \(f(b)\) 的最大值。

乌龟给你一个 \(1 \sim n\) 的排列 \(p_1, p_2, \ldots, p_n\) 和 \(m\) 次询问，每次询问给定 \(l, r\)，你需要求出 \([p_l, p_{l + 1}, \ldots, p_r]\) 的“肿胃数（nediam）”，即 \(f([p_l, p_{l + 1}, \ldots, p_r])\)。

\(n\leq 10^6\)，\(m\leq 5\times 10^6\)。

题解

第一反应是找次大值，但这是错的。考虑寻找最大值可能成为答案的区间，因为次大值本质上是原序列某个子区间的最大值。

先找出全局最大值 \(a_x=mx\)，显然 \(mx\) 不能成为答案，也不会被删除。并且 \(mx\) 会把数列分为两部分。

称 \([1,x)\) 为左侧序列，\((x,n]\) 为右侧序列。

只对左侧序列讨论，右侧序列与左侧序列类似。

考虑左侧序列的最大值 \(a_i\) 能否成为答案，为了验证这件事，首先要观察一些删除数的性质：

• 对于序列的子串 \(a_{l\sim r}\)，满足 \(a_p(l\leq p\leq r)\) 是最小值且 \(a_q(l\leq q\leq r)\) 是最大值，那么一定可以把该子序列删到只剩 \(a_p\) 和 \(a_q\)。证明显然。
• 对于序列的子串 \(a_{l\sim r}\)，满足 \(a_p(l\leq p\leq r)\) 是最小值且 \(a_q(l\leq q\leq r)\) 是最大值，如果最后只能保留两个数字，那么这两个数字一定是 \(a_p\) 和 \(a_q\)。证明显然。

为了方便讨论，我们记 \(a_y\) 为 \([1,x)\) 的最小值，\(a_z\) 为 \((x,n]\) 的最小值。

根据性质，为了保留 \(a_i\)，我们可以且必须先把序列删到只剩下 \(a_{i/y},a_{y/i},(a_r),a_x,a_z\)，因为 \([y,x]\) 最多保留两个，\([x,n]\) 最多保留两个。注意 \(i,y\) 顺序不确定（\(a_r\) 的定义将在 \(y<i\) 的讨论中解释）。

如果 \(y<i\)，即 \(a_y,a_i,a_r,a_x,a_z\)，\(a_r\) 表示 \([i,x]\) 的最小值，那么如果 \(a_z>a_r\)，\(a_i\) 可以成为答案，操作步骤为 \(y,i,r,x,z\to y,i,r,x\to i,r,x 或 y,i,x\)（这里用下标代替值简写）；否则为了保留 \(a_i\)， \(a_r\) 一定会被删除，\(a_r\) 被删除后无论下一步如何操作都会删掉 \(a_i\)。

如果 \(y>i\)，即 \(a_i,a_y,a_x,a_z\)，删掉 \(a_y,a_x,a_z\) 的中位数即可。

因此 \(a_i\) 能成为答案的充要条件是 \(y>i\)。

我们发现 \(y\) 把左侧区间又分为了两部分，我们记 \([1,y)\) 的最大值为 \(a_p\)，\((y,x)\) 的最大值为 \(a_q\)。

那么 \(a_p\) 一定可以作为答案，当 \(a_q<a_z\) 时 \(a_q\) 也可以成为答案。

特判 \(a_y,a_z\)，这两个数的较大值也能成为答案。

右侧是一样的，需要实现的功能是静态 RMQ，使用 ST 表即可。

upd 我们发现刚刚推理有误。Hack 1 4 2 5 6 3，答案为 \(4\)。

原因是，\((y,x)\) 中可能存在一个数，满足这个数能作为答案但不是 \((x,y)\) 的最大值。

因此正确做法是找出最靠右的 \(w\)，满足 \(a_w<a_z\)，然后用 \((y,w)\) 的最大值更新答案。

搞一个单调栈单独维护这个东西。

提交记录

P6913 [ICPC 2015 WF] Tile Cutting 紫

题意

原题面不好描述，这里省掉一步转化。

令 \(f(x)=|\{(a,b,c,d)|a,b,c,d\in \N\land ad+bc=x\}|\)，有 \(n\) 次询问，每次给定 \(l,r\)，求 \(\max\limits_{i=l}^{r} f(i)\)。

题解

记 \(d(x)\) 表示 \(x\) 的因数个数。

\[f(n)=\sum\limits_{a+b=n} d(a)\times d(b) \\ =\sum\limits_{a}\sum\limits_{x|(n-a)} d(a) \\ =\sum\limits_{x}\sum\limits_{k} d(n-kx) \]

考虑根号分治，设 \(B=\sqrt n\)。

\[f(n)=\sum\limits_{x=1}^{B} \sum\limits_{k} d(n-kx)+\sum\limits_{x=B+1}^{n} \sum\limits_{k=1}^{\frac{n}{x}} d(n-kx) \\ =\sum\limits_{x=1}^{B} \sum\limits_{i=1}^{n} d(i)\times [n\bmod x=i\bmod x]+\sum\limits_{k=1}^{\frac{n}{B}}\sum\limits_{x=B+1}^{\frac{n}{k}} d(n-kx) \]

记 \(t_{x,y}=\sum\limits_{i=1}^{n} [i\bmod x=y]\times d(i)\ \big(x,y\leq B\big)\)，\(g_{n,k}=\sum\limits_{x\geq 0} d(n-kx)\)。

\[f_{n}=\sum\limits_{x=1}^{B} t_{x,n\bmod x}+\sum\limits_{k=1}^{\frac{n}{B}} g_{n-(B+1)\times k,k} \\ g_{n,k}=g_{n-k,k}+d(n) \]

\(g\) 需要重复利用以节省空间，注意特殊处理 \(n<B\) 的情况。

我们可以在 \(O(n\sqrt n)\) 的时间复杂度内求出所有 \(f\)，之后使用 ST 表查最值即可。

提交记录

CF2013F2 Game in Tree (Hard Version) *3500

题意

Alice 和 Bob 在一棵 \(n\) 个节点的树上玩游戏，规则如下：双方轮流移动，爱丽丝先手。每位玩家在自己的回合中，必须移动到一个未被访问过（无论自己或对手）的相邻节点上。第一个无法移动的玩家输掉游戏。

爱丽丝初始位于 \(1\) 号节点，你需要对于给定简单路径 \(u\to v\)（一定不穿过 \(1\)）上的每个节点 \(c\) 判断：若 Bob 初始位于 \(c\)，谁将获胜。

玩家的初始位置也被视为访问过的节点。

\(n\leq 2\times 10^5\)。

题解

令 \(dep_{u}\) 表示 \(u\) 的深度，\(dep_{1}=0\)，\(length_{u}\) 表示 \(u\) 去掉 \(1\to c\) 的点后子树下的最大深度。

对于点 \(c\)，Alice 获胜的充要条件是：

\[\exist u,dep_{c}+\max\limits_{v\in (1\to c)\land dep_{v}>dep_{u}} \{-dep_{v}+length_{v}\}-length_{u}<dep_{u}\leq \lfloor\frac{dep_{c}}{2}\rfloor \]

对于这种复杂的式子，考虑放缩，以缩小 \(u\) 的范围。

对于一个拐点 \(u\)，它能使 Alice 获胜的必要条件是 \(dep_{u}+length_{u}-1>dep_{c}-dep_{u}-1\)。

即 \(2\times dep_{u}+length_u>dep_c\)。

由于 \(dep_c\) 是常量，\(\sum length_{u}\leq n\)，考虑根号分治。

当 \(length_{u}<B\) 时，\(dep_u\) 的范围极差为 \(O(B)\) 级别。

当 \(length_u\geq B\) 时，\(u\) 的个数时 \(O(\frac{n}{B})\) 级别。

令 \(B=\sqrt n\) 即可，时间复杂度 \(O(n\sqrt n)\)。

对路径上每个点求 \(length\) 还是有一些细节的。

对 Alice 和 Bob 分别判断，假设在他到达 \(u\) 前，两人都不往下拐，且他在 \(u\) 下拐是否可能赢。称可能赢的点为关于他的必胜点。

取离 Alice 最近的关于 Alice 必胜点和离 Bob 最近的关于 Bob 必胜点，比较一下距离即可。

提交记录

20250921 模拟赛 T1

题意

求长度为 \(n\) 值域为 \([1,m]\) 逆序对个数为偶数的序列个数模非质数 \(mod\) 的值，可以做到 \(O(\log n)\)。

题解

打表发现答案为 \(\frac{m^n+m^{\lfloor \frac{n+1}{2}\rfloor}}{2}\)。

证明：考虑把 \(12,34,56\dots\) 配对，剩一个不管他，如果存在一个配对中数不相等，那么可以构造奇数逆序对和偶数逆序对序列的映射 \(f:Odd\to Even,交换第一个不相等的配对\)。

如果不存在一个配对中数不相等，那么逆序对个数显然为偶数。

因此偶逆序对比奇逆序对序列个数多 \(m^{\lfloor \frac{n+1}{2}\rfloor}\) 个，上述式子正确。

模数不质，因此需要先模 \(2\times mod\) 再除以二。

提交记录

20250921 模拟赛 T2

题意

小 X 和小 Q 在海边捡贝壳。

小 X 把捡到的贝壳分为三类。小 Q 趁小 X 不注意，把贝壳分到了 \(n\) 个袋子里，其中第 \(i\) 个袋子中三类贝壳的数量分别为 \(x_i, y_i, z_i\)。

为了安慰小 X，小 Q 让小 X 先选 \(\frac{n}{2} + 1\) 袋贝壳走，剩下的就都归小 Q 了。

小 X 想请你帮助她，找到一种选贝壳的方案，使得她每一类贝壳都不比小 Q 拿到的少。

\(n\leq 10^5\)，可以做到 \(O(n)\)。

题解

如果 \(n\) 是奇数就补一个 \((0,0,0)\)。

按 \(x\) 排序，选 \(x\) 最大的一个，按 \(y\) 排序，再选剩下的 \(y\) 最大的一个。

然后按 \(x\) 排序后两两配对，\(23,45,67\) 中每组只要选一个就符合条件。

\(y\) 同理，建图，连边表示相邻两个至少选一个。

最终必定形成若干偶环，每个偶环有两个选择方案，选 \(z\) 和大的一个方案即可。

提交记录

20250921 模拟赛 T3

题意

给定 01 矩阵，对每个位置求这个位置翻转后全局的最大全 \(0\) 矩阵。

要求 \(O(nm)\)。

题解

对于 \(0\) 变 \(1\) 的情况，相当于要求这个点不选，那么矩形一定在这个点的四个方向外，预处理出上下左右方向的前缀答案即可。

对于 \(1\) 变 \(0\)，相当于在普通全 \(0\) 矩阵的问题上新增了一个忽视 \(1\) 的机会，对于每行单调栈维护直方图，每个柱子可以往上长，简单讨论一下即可。

求一个点靠左第二个大于它的值，可以维护链表，从小到大删数，删除前查 \(pre_{pre_i}\) 即可。

提交记录

20250921 模拟赛 T4

题意

给定一个只含字符 x、y 且长度为 \(n\) 的字符串 \(S\) 和一个长度为 \(n\) 的数组 \(c_1, c_2, \cdots, c_n\)。你需要进行若干次操作将这个字符串删除。有一个值 \(a\) 初始为 0。

每次操作如下：选中 \(1 \leq i < |S|\) 满足 \(S_i\) 是 x 且 \(S_{i+1}\) 是 y，则将 \(S_i, S_{i+1}\) 同时删除，\(i + 1\) 右侧的字符向前补空位，并给 \(a\) 加上 \(c_i\)。

求问所有操作结束后，\(a\) 的最小值是多少呢？如果不能删空 \(S\)，输出 No Solution。

\(n\leq 5000\)。

题解

判无解是简单的。

建立括号树。

记 \(t_i\) 表示第 \(i\) 个括号被删除的位置。

首先父亲的 \(t\) 必定小于儿子的 \(t\)，其次 \(t_i\leq i\)，且奇偶性与 \(i\) 相同。

上述性质必要性显然，实际上也具有充分性，证明如下：

我们找到最靠前的一个叶子，它的 \(t\) 必定是它本身的位置，“删”掉它后剩下的 \(t\) 仍然满足这个性质，可归纳证明。这里的“删”指去掉而非题目中的删除。

记 \(f_{u,i}\) 表示子树 \(u\) 内，\(t_u=i\) 的答案，后缀和优化 DP 即可。

提交记录

CF1916F. Group Division *2900

学习【耳分解与双极定向】。

提交记录

P5776 [SNOI2013] Quare 紫

题意

给定一张图，求一个边权和最小的边双连通生成图（包含所有点，但不一定包含所有边的图）。

输出最小边权和。

\(n\leq 12\)，\(m\leq 40\)。

题解

根据耳分解，令 \(f_S\) 表示点集 \(S\) 的答案，\(g_{S,i,j}\) 表示 \(S\) 构成耳且以 \(i,j\) 为端点的最小边权和，\(h_{S,i}\) 表示点集 \(S\) 向 \(i\) 连边的最小边权，则：

\[f_{S}=\min\limits_{T\subset S\land i\in S/T\land j\in {S/T}} f_{S/T}+g_{T\cup\{i,j\},i,j} \\ g_{S,i,j}=\min\limits_{k\in S\land k\neq i\land k\neq j}g_{S/\{i\},k,j}+h_{S/\{i\},i} \]

时间复杂度 \(O(n^32^n\times 3^n)\)，足以通过这道题。

但是，实际上根本不用这样转移，直接把耳分步转移，令 \(f_{S,i,j,0/1/2}\) 表示当前集合是 \(S\)，当前的耳长度 \(=1/>1/=0\)，端点分别为 \(i,j\) 的答案，注意特殊处理二元环。当耳长度为 \(0\) 时 \(i,j\) 是没有用处的。

每次转移时往 \(i\) 上加点，或者封闭这个耳。

为了避免重边，单独处理长度为 \(2\) 的开耳和闭耳。

时间复杂度 \(O(n^3 2^n)\)。

提交记录

P10809 [LMXOI Round 2] Nirvana 黑

题意

给定一张图，询问有多少组 \(x,y\ (x\leq y)\)，满足加入边 \((x,y)\) 后，新图可以定向成一个 DAG，且唯一的零入度点是 \(S\)，唯一的零出度点是 \(T\)。

若存在这样的 \((x,y)\)，选一组 \((x,y)\) 并构造方案。

若不存在，求至少删多少个点使得原图能够定向成一个 DAG，且唯一的零入度点是 \(S\)，唯一的零出度点是 \(T\)。

\(1\leq n,m\leq 5\times 10^5\)。

题解

存在 \(S\to T\) 的双极定向，当且仅当连接 \(S,T\) 后原图点双联通。

连接 \(S,T\)，相当于询问有多少种加边方案使得加完边原图是点双。

建出圆方树，连接两个点相当于将路两点径上的所有点缩成一个方点。

点双相当于只有一个双点，容易发现，当且仅当圆方树的方点排成一条链时，才存在这样的加边方案。

此时加边的方案数就是链两端方点的 \(1\) 度儿子个数之积，需要特殊处理只有一个方点（即原图本来就是点双）的情况。

如果 \(P=0\)，连接 \(S,T\) 后选出儿子数最大的方点保留即可。

否则，找一组加边方案跑双极定向即可。

注意加入一个自环并不合法，所以计算 \(P\) 时应该去掉这种情况，\(P\) 一定不为 \(1\)。

提交记录

QOJ #4805. Grammy Sorting *????

题意

给定一张图和两点 \(A,B\)，给定排列 \(p\) 为初始点权。

现在要求你进行操作，使得操作完后对于所有点 \(x\)，都存在一条路径，满足：

• 路径从 \(A\) 开始，经过 \(x\)，在 \(B\) 结束
• 路径从 \(A\) 到 \(B\) 经过的所有点权值递增。

可以进行的操作如下：

• 选择一条从A开始，任意点结束的路径，假设路径上的点权依次为 \(a_1,a_2,\dots a_k\)，将其变为 \(a_2,a_3,\dots a_1\)。

操作次数要求 \(\leq 10000\)。（实际 \(1000\) 次就够用了）

\(n\leq 1000,m\leq 2000\)。

题解

有解仅当原图存在 \(A\to B\) 的双极定向，并且定向完的 DAG 能被操作成一个满足点权和 bfs 序正相关的 DAG。

先双极定向，然后执行操作。

考虑链的情况，直接模拟插入排序即可，具体地，从后往前维护递增序列，第 \(i\) 次操作保证 \([n-i+1,n]\) 递增。

考虑 DAG，对于一般 DAG 很难做，考虑利用双极定向的性质——bfs 序后缀连通。

我们依然想链一样倒着做，考虑当前操作到了点 \(x\)，若 \(p_x< \min\limits_{x\to v} p_v\)，直接不进行操作。否则，当 \(p_A< \min\limits_{x\to v} p_v\)，把 \(p_A\) 换到 \(p_x\)；当 \(p_A> \min\limits_{x\to v} p_v\)，考虑将 \(p_x< \min\limits_{x\to v} p_v\) 换到 \(p_x\)，具体地，记 \(nxt_i\) 表示 \(i\) 后继中点权最小的，让 \(x\) 不断跳 \(nxt\) 直到 \(p_{nxt_x‘}>p_A\)，然后轮换 \(A\to x'\) 即可。

不断跳 \(nxt\) 是因为，这样轮换后，对于每个 \(bfn\) 大于 \(bfn_x\) 的点 \(y\) 依然能够保证 \(p_y< \min\limits_{y\to v} p_v\)。

显然这样构造一定有解。

提交记录

CF2151E. Limited Edition Shop *2200

题意

有一家商店，里面有 \(n\) 件从 \(1\) 到 \(n\) 编号的物品，并且每件物品只有一个副本。据你所说，这些物体
具有值 \(v_1,v_2,\dots ,v_n\)（可以为负）。

Alice 和 Bob 对物体有自己的偏好顺序（分别为 \(a_1,a_2,\dots ,a_n\) 和 \(b_1,b_2,\dots,b_n\)）。

两人一共进行 \(n\) 次购物，每次其中一人去商店购买店里目前存在的他最喜欢的商品。最后，Alice 和
Bob 有自己的物品集。

在所有 Alice 可能买到的物品集合中，\(v\) 的和最大是多少？

\(n\leq 2\times 10^5\)。

题解

这道题的关键是意识到 DP 不可能是一维的，因为在沿着 Alice 顺序转移时，必须记录 Bob 选择到哪了。

记 \(f_{i,j}\) 表示 Alice 选到了她第 \(i\) 喜欢的物品，Alice 没选的物品中在 Bob 序列最大位置为 \(j\) 的答案，大胆的推一下转移，发现转移都是区间加和单点改为前缀 \(\min\)，线段树维护整体 DP 即可。

提交记录

P2934 [USACO09JAN] Safe Travel G 蓝

题意

给定一张图，保证 \(1\) 到每个点的最短路径唯一，求对于每个点 \(i\ (2\leq i\leq n)\)，去掉 \(1\to i\) 最短路的最后一条边后，\(1\to i\) 的最短路是多少。

\(n\leq 10^5\)，\(m\leq 2\times 10^5\)。

题解

建出最短路数，点 \(u\) 的答案肯定是向下走到某点 \(v\)，找到非树边 \(u\frac{w}{} v\)，答案为 \(dis_v-dis_u+w+dis_x\)。

启发式合并维护子树内的 \(dis_{x}+w\)，每次往上爬一个点就让整个集合加上爬过的边权，维护一个全局懒标记即可。

对于一条非树边，当且仅当一个点在 \(u\) 子树内，另一个点在子树外时可用，因此到达点 \(u\) 时，需要去掉所有 \(\text{lca}\in \text{subtree}(u)\) 的非树边的贡献，用 set<pair<int,int>> 维护集合，第一维记 \(dis_x+w\)，第二维记 \(\text{lca}\) 即可。

提交记录

P5100 [JOI 2017 Final] 足球 / Soccer 紫

题意

JOI 联赛足球俱乐部俱乐部有 \(N\) 名球员，编号为 \(1\ldots N\)。

足球场可视为一个底为 \(W\) 米，高 \(H\) 米的长方形。

练习结束后，你要回收练习用的足球。开始回收时，所有球员都在足球场上，球员 \(i (1\leqslant i\leqslant N)\) 位于 \((S_i, T_i)\)，球在球员 \(1\) 脚下。你正和球员 \(N\) 一起站在 \((S_N, T_N)\)，并准备回收球。球员们把球传到 \((S_N, T_N)\) 时，你才会回收球。

你可以指挥球员，但某些操作会提升球员的疲劳度。一个球员不能同时进行多项操作。

你可以指挥控球的球员进行如下操作：

• 踢球。在东西南北四个方向中任选一个，并指定一个正整数 \(p\)，该球员将球朝指定方向踢出恰好 \(p\) 米。假定球滚动时可以穿过其他球员。该球员不会移动，且自动停止控球，疲劳度上升 \(A\times p+B\)。
• 运球。在东西南北四个方向中任选一个，该球员带球，朝指定方向移动 \(1\) 米。该球员仍然控球，疲劳度上升 \(C\)。
• 停止控球。该球员的疲劳度不改变。

你可以指挥没有控球的球员进行如下操作：

• 移动。在东西南北四个方向中任选一个，该球员朝指定方向移动 \(1\) 米，疲劳度上升 \(C\)。
• 控球。如果该球员所在的位置恰好有球，且没有其他球员控球，该球员才能控球。该球员的疲劳度不改变。

球员和球有可能跑出场外，一个位置上可能有多个球员。

求在回收球的过程中，所有球员上升的疲劳度之和的最小值。

\(1\leqslant H,W\leqslant 500, 0\leqslant A, B, C\leqslant 10^9, 2\leqslant N\leqslant 10^5, 0\leqslant S_i\leqslant H, 0\leqslant T_i\leqslant W(1\leqslant i\leqslant N), (S_1, T_1)\neq(S_N, T_N)\)。

题解

因为运球和移动代价一样，所以先把球给出去再接住不如直接带球带过去，所以一定存在最优解使得一个人只控球一次。

然后假设球在一个位置，一定是最近的人移动过去捡球，因为一个人去捡球会损失在原本位置接球的机会，而一个人只会拿球一次，所以实际上什么也没损失。

拆点，令 \(f_{i,j}\) 表示球在 \((i,j)\) 停下的答案，\(g_{i,j}\) 表示球在 \((i,j)\) 被控制的答案，\(p_{i,j}\) 表示球在 \((i,j)\) 横着飞的答案，\(q_{i,j}\) 表示球在 \((i,j)\) 竖着飞的答案，建图跑 dij 即可。

具体地，多元 bfs 求出每个点到最近球员的距离 \(dis_{i,j}\)。\(f_{i,j}\) 向 \(g_{i,j}\) 连 \(dis_{i,j}\) 的边；\(g_{i,j}\) 向四连通方向连 \(C\) 的边，向 \(p_{i,j}\) 和 \(q_{i,j}\) 连 \(B\) 的边；\(p_{i,j}\) 向 横向相邻点连 \(A\) 的边；\(q_{i,j}\) 向纵向相邻点连 \(A\) 的边。

不用区分横向的左和右、纵向的上和下，因为允许球掉头一定不会更优。

另外，直接把球员初始位置当成每次球员位置，正确的原因是，可以通过分讨证明，即使球员可以瞬移到初始点也不会更优。

提交记录

P10652 [ROI 2017] 前往大都会 (Day 1) 紫

题意

ROI 国有 \(n\) 个城市，以及 \(m\) 条铁路，每条铁路都是单向运行的，第 \(i\) 条铁路依次经过 \(v_{i,1},v_{i,2},\dots,v_{i,l_i+1}\) 号城市并停靠，其中 \(v_{i,j} \to v_{i,j+1}\) 的铁路长度是 \(t_{i,j}\)。

如果多条铁路经过 \(u\) 号城市，那么你可以在 \(u\) 号城市换乘其他铁路。（每条铁路都可以在停靠点任意上车/下车）

你需要找到一条从 \(1\) 号城市到 \(n\) 号城市的路径，这条路径需要满足其总长度最小，并且在此条件上路径上相邻两个换乘点间火车上距离的平方和最大。

起点和终点都是换乘点，题目保证有解，\(n,m\leq 10^6\)。

题解

先建出最短路 DAG，然后问题相当于在 DAG 上进行上述操作，不需要管路程最短的限制。

考虑一个铁路在 DAG 上肯定是以若干条链的形式出现，这些链相互独立，因此把这些连分割成若干条独立的铁路，下文的所有”铁路“都指分割完之后的铁路。

由于是平方和最大，因此这个问题严格不弱于斜优板子，考虑斜率优化 DP。

具体地，如果存在一条铁路同时经过 \(i,j\)，则有 \(f_{j}\leftarrow f_{i}+(dis_j-dis_i)^2\)，由于 \(a^2+b^2\leq (a+b)^2\)，转移后不换乘一定不优，因此这里并不需要要求 \(j\) 立刻换乘。

我们无法在 DAG 上维护凸包，考虑对每个铁路维护一个凸包，在 DAG 上按拓扑序 DP，每到一个点时遍历经过这个点的所有铁路，求出最大的 \(f\)，之后再用 \(f\) 更新所有铁路的凸包即可。

时间复杂度 \(O(n+m\log m)\)，瓶颈在于建最短路 DAG。

提交记录

P9734 [JOISC 2021] 逃走経路 (Escape Route) (Day2) 黑

题意

IOI 王国使用 Byou（秒）作为时间单位，将一天划分成 \(S\) Byou，分别称为时刻 \(0,1,\dotsc,S-1\)。

IOI 王国中有 \(N\) 个城市和 \(M\) 条双向道路，均从 \(0\) 开始标号。保证任两个城市之间均连通。第 \(i\) 条道路连接城市 \(A_i\) 和 \(B_i\)，需要恰好 \(L_i\) Byou 通过。每天的时刻 \(C_i\) 后，第 \(i\) 条道路将开始进行检查，直到当天结束。

JOI 组织是一个活跃在 IOI 王国中的秘密团体。出于其保密性，成员不能在道路上受到检查。如果其成员想要通过道路 \(i\)，最晚要在时刻 \(C_i-L_i\) 到达这条路的一端。道路的检查不会影响两端的城市。

现在有 \(Q\) 名 JOI 组织的成员，从 \(0\) 开始标号。第 \(j\) 名成员在某天的时刻 \(T_j\)，要从城市 \(U_j\) 出发去城市 \(V_j\)。成员可以在任意城市内停留任意长的时间。注意这名成员可能会在路上花费一天以上。

请计算每名成员花费的最短时间，精确到 Byou.

\(2 \leq N \leq 90\)，\(N-1 \leq M \leq \dfrac{N(N-1)}{2}\)，\(2 \leq S \leq 10^{15}\)，\(1 \leq Q \leq 3 \times 10^6\)，图连通。

题解

显然早出发不劣于晚出发，因此对于 \(T=0\) 的询问，直接 dijkstra 即可，但是没啥用。

复杂度 \(Q\) 的系数最多为 \(n\)，因此几乎所有东西都要预处理。

对于跨天情况，枚举到哪个城市过第一夜，假设 \(u\) 到城市过夜 \(p\)，需要满足 \(u\) 在 \(T\) 时刻出发，能到达，这部分还要预处理，令 \(f_{u,v}\) 表示 \(u\) 出发到达 \(v\) 的最晚出发时间。当然可以二分然后 dij，但是存在更聪明的做法，建出反图后直接 dij 就行了。

有了 \(f\)，自然也就能 floyd 预处理出每个点对 \((i,j)\)，\(i\) 到达 \(j\) 的最少天数 \(g_{i,j}\)。

记 \(h_{u,v}\) 表示 \(u\) 在 \(0\) 时刻到达 \(v\) 的最短时间，且强行要求不跨天。

则 \(u\) 到 \(v\) 跨天情况的答案就是 \(\min\limits_{p,q|f_{u,p}\geq T} (S-T+g_{p,q}+h_{q,v})\)，把 \(g\) 和 \(h\) 卷起来，枚举 \(p\) 即可。

然后是不跨天。

时间点太多了，考虑对于 \((u,v)\)，有用的时间点有多少个？

答案是 \(O(m)\) 个，因为对于一条路，能用的时间段肯定是一段前缀，求出 \((u,v)\) 的最短路，然后等到存在一条边断掉后再在这个时刻跑最短路，以此类推，最多有 \(m\) 条边断掉。

考虑对每个 \((u,v)\) 算出这样的 \(O(m)\) 个路径，单调栈过滤掉无用信息后，询问时直接二分。

具体地，对于每个点 \((u,v)\)，模拟上述过程，求最短路，找出第一个不能用的边 \((x,y)\)，之后断掉它，再跑最短路。

但是我们有更聪明的实现方式，枚举点对 \((u,v)\) 和边 \((x,y,l)\)，计算 \((x,y,l)\) 第一个断掉（非严格）的最短路径长度（不要求其是全局最短路），计算方法为 \(u\) 在 \(f_{u,x}\) 时刻出发到 \(x\) 的时间 \(t_0\) 加上 \(t_0+l\) 时刻从 \(y\) 出发到 \(v\) 的最短路，最短路直接 dij 就行了。这样计算保证经过这条边后这条边立刻断开，因此是正确的。

提交记录

P13065 [GCJ 2020 #2] Emacs++ 黑

题意

给定一个长为 \(n\) 的括号串，有一个光标在括号串上，在任何时刻，你可以执行以下三种操作之一来移动光标：

• 将光标向左移动一个字符。此操作耗时 \(L_i\) 秒。
• 将光标向右移动一个字符。此操作耗时 \(R_i\) 秒。
• 将光标传送到与第 \(i\) 个字符的括号匹配的括号处。此操作耗时 \(P_i\) 秒。

\(Q\) 次询问光标在 \(S_i\) 开始到达 \(E_i\) 的最短时间。

数据范围

• \(1 \leq T \leq 100\)，对于最多 9 个测试用例，\(n = 10^5\) 且 \(Q = 10^5\)，其他所有情况下，\(2 \leq n \leq 1000\) 且 \(1 \leq Q \leq 1000\)。

部分分：

• 对于所有 \(i\)，\(L_i = R_i =P_i = 1\)。

题解

史。

如果将匹配的点两两缩成一个点，那么原图是仙人掌图，考虑从这里入手。

对于部分分，直接缩点建立仙人掌，讨论一下环上距离即可。

对于一般情况，由于原图并不是真正的仙人掌，匹配点之间的连边可能同时位于多个环中，因此环上最短路完全可以从一点出环，绕一大圈后回到与之匹配的点，这样当 \(P_i\) 非常大时，可以绕开两点之间权值为 \(P_i\) 的边。

考虑圆方树常用技巧：重标边权，将 \(P_i\) 边重标为两点真实的最短路。

如果我们成功重标边权，我们可以进行类仙人掌最短路状物，唯一和仙人掌最短路不同的是，我们每个匹配点有两个状态，分别为在左侧和在右侧。因此在倍增的时候维护 \(up_{u,j,0/1,0/1}\) 表示 \(u\) 的左/右侧上跳 \(2^j\) 步到 \(2^j\) 级祖先的左/右侧。

太史了，考虑换个实现方式，具体地，我们可以把父亲作为方点，这样契合括号数的结构，更加方便。

实现的时候直接建立括号数就行了。

考虑树形 DP 重标边权。

令 \(f_{u}\) 表示子树内左侧到右侧的最短路，\(g_{u}\) 表示字数外左侧到右侧的最短路。右侧到左侧同理。

\(f_u\) 自下而上，通过儿子的 \(f\) 转移过来，再和原边权取 \(\min\)。

\(g_u\) 自上而下，通过父亲的 \(g\) 和兄弟的 \(f\) 转移，具体地就是在环上绕了一圈。

做完这些后，实现一下环上最短路，处理出 \(up_{*,0,*,*}\)，然后倍增即可，这样省掉了 tarjan 建圆方树。

提交记录

[ABC134F] Permutation Oddness 紫

题意

定义 {\(1, 2, \ldots, n\)} 的一个排列 \(p = \{p_1, p_2, \ldots, p_n\}\) 的“奇妙度”为 \(\sum_{i=1}^n |i - p_i|\)。

请你求出奇妙度等于 \(k\) 的 {\(1, 2, \ldots, n\)} 的排列的个数，并对 \(10^9+7\) 取模后输出。

\(n\leq 50\)。

题解

首先排列的两个经典套路（离散化和顺序填数）似乎都不适用。

其次置换环也不是很适用。

把原问题看成匹配问题，拆贡献，\(\sum\limits_{i=1}^n |i - p_i|=\sum\limits_{i=2}^{n} \sum\limits_{j=1}^{n} [j<i]\times [p_j\geq i]\)。

令 \(f_{i,l,r,x}\) 表示只考虑前 \(i\) 对数，左侧点有 \(l\) 个未匹配，右侧点有 \(r\) 个未匹配，奇妙度为 \(x\) 的方案数。

只考虑前 \(i\) 对数的匹配，必有 \(l=r\)，因此状态可以优化成三维 \(f_{i,j,x}\)。

转移分为：新加入的点对不匹配、互相匹配、一个匹配前面的点、两个匹配前面的点。

提交记录

AT_joisc2020_q 治療計画 (Treatment Project) 黑

题意

JOI 村庄有 \(N\) 个房屋，这 \(N\) 个房屋里的村民全部感染病毒，有 \(M\) 个治疗方案被提出，第 \(i\) 个治疗方案描述为，在第 \(T_i\) 天的晚上，编号在 \([L_i,R_i]\) 区间内的村民被治愈。

病毒还会继续传播，在某天早上，如果村民 \(i\) 被感染，那么村民 \(i+1\) 和村民 \(i-1\) 也会被感染，因为病毒威力巨大，所以被治愈的村民有可能再次被感染。

选择一些方案使得 JOI 村庄所有村民全部被治愈，一天可以进行很多方案，第 \(i\) 个方案要花费 \(C_i\)，求最小花费。

\(1 \le N,T_i,C_i \le 10^9\)，\(1 \le M \le 10^5\)，\(1 \le L_i \le R_i \le N\)。

题解

放到二维平面上考虑。

横轴是村民，纵轴是时间。

一个治疗计划相当于在二维平面上治愈了一个以 \((l,t),(r,t)\) 为底边的直角三角形，最后目的是用这些三角形把平面分割成上下两部分。

我们发现如果按区间右端点排序，把一组正确答案依次加入平面，我们覆盖的区间必定是 \([1,r_i]\)，\(r_i\) 是某个治疗计划的右端点。

考虑 DP，令 \(dp_i\) 表示覆盖 \([1,r_i]\) 的最小代价，那么有 \(dp_i+c_j\to dp_j\ (|t_i-t_j|\leq r_i-l_j+1)\)，后面的条件是要求两个三角形之间不存在空隙。

直接建图后 dij 跑 DP 的方法极其困难，考虑分析一些性质。

性质一：\(dp_i\) 的最优转移点是所有满足条件的 \(j\) 中，\(dp_j\) 最小的一个。

性质二：如果 \(i\) 能直接转移到 \(j\)，就一定不会先转移到别的点再由别的点转移到 \(j\)。

因此我们可以维护一个 \(dp\) 值的小根堆，每次使用队首元素把所有能转移到的点转移并入队，根据上述性质，这样被入队的点的 \(dp\) 值之后不会再变得更优。

因此每个点只会入队一次，使用类似势能树的 DS 暴力维护即可。

具体地，按照 \(t\) 排序建立线段树，每个点维护 \(l+t,l-t\) 的最小值，之后每次从线段树上暴力找未入队过的点入队。

上述的性质，本质上说的是只有点权没有边权的最短路可以做到每个点只入队一次，这个性质对一般图也成立。

提交记录

2025.10

圆圈排列 NOIP 模拟 T3（分析性质，刻画，计数 DP）

题意

有 \(n\) 个小朋友要在一个圆形操场上围成一圈做游戏，编号是 \(1, 2, \ldots, n\)。对于两个小朋友 \(a, b\)，如果小朋友 \(a\) 沿着操场逆时针走到小朋友 \(b\) 的距离严格小于小朋友 \(b\) 沿着操场逆时针走到小朋友 \(a\) 的距离，那么小朋友 \(a\) 在小朋友 \(b\) 的西边，小朋友 \(b\) 在小朋友 \(a\) 的东边。如果两个小朋友走的距离相等，那么这两个小朋友是对称的。

小朋友们需要按指定的规则围成一圈，并且小朋友 \(i\) 沿着操场逆时针走遇到的第一个人是小朋友 \((i \mod n) + 1\)。规则可以简化为一个 \(n \times n\) 的矩阵 \(D\)，矩阵正对角线上的元素 \(D_{ii} = *\)，其他位置上的元素 \(D_{ij}\) 是 \(W\) 和 \(E\) 的其中一个，如果 \(D_{ij} = W\)，那么小朋友 \(i\) 需要在小朋友 \(j\) 的西边，如果 \(D_{ij} = E\)，那么小朋友 \(i\) 需要在小朋友 \(j\) 的东边。

现在给定了一个矩阵 \(D\)，但是其中的一些非正对角线上的元素看不清，被替换成了 ?，你需要求出，对于将每个问号，如果将它们替换成 \(W\) 或 \(E\) 得到的所有矩阵中，有多少种矩阵可以让小朋友们按照相应的规则围成一圈。

由于答案可能很大，请输出对 \(998244353\) 取模的值。

\(n\leq 500\)。

题解

首先矩阵是反对称的，只用考虑一边。

其次，考虑尝试满足矩阵构造站立方案的过程，首先，矩阵从左到右必定是由 \(W\) 变成 \(E\)，从上到下必定是从 \(E\) 变成 \(W\)。

这说明 \(W\) 和 \(E\) 之间有一条单调的分界线。

其次，我们不能让小朋友站位超过一圈，因此不能存在 \(i<j<k\) 使得 \(D_{i,j}=D_{j,k}=E\)。

令第一行第一个 \(E\) 在 \((1,x)\)，那么分界线需要在 \(x\) 行结束，容易看出这是充要的。

枚举 \(x\)，DP 即可。

提交记录

数区间 NOIP 模拟 T4（另类 SGT 区间合并）

题意

维护一个序列，支持单点修改，全局查 \(\text{LCM}=v\) 的区间个数，\(v\) 每次询问给定。

\(n,m\leq 10^5,v\leq 10^9\)。

题解

考虑每次修改 \(x\) 时更新数 \(x\) 的贡献。

\(\text{LCM}\) 最多有 \(\log V\) 段，因此可以从 \(x\) 往前二分 \(\log V\) 段，往后二分 \(\log V\) 段，总共 \(\log V\) 个区间，暴力更新即可。

这样需要线段树维护区间 \(\text{LCM}\)，复杂度 \(\log^2 n\log^2 V\)，死翘翘。

由于区间总数是单 \(\log\) 的，考虑用线段树暴力维护，每个节点 \([l,r]\) 维护所有以 \(l\) 开始和以 \(r\) 结尾的 \(\text{LCM}\) 区间，合并是简单的，更新 \(x\) 贡献的时候在线段树上查出以 \(x\) 开头和结尾的区间即可。

最终复杂度（\(n,m\) 同阶） \(O(m\log^3 V)\)，有一个 \(\log\) 是 \(\text{LCM}\) 贡献的，因此能过。

提交记录

图 NOIP 模拟 T3（去重技巧）

题意

给定一个包含 \(n\) 个点 \(m\) 条边的简单无向连通图（无自环、重边），点编号为 \(1, 2, \ldots, n\)。

给定一个非负整数 \(k\)，保证 \(0 \leq k \leq 2\)。

你需要对于所有满足 \(0 \leq i \leq k\) 的非负整数 \(i\) 求出，有多少种从 \(m\) 条边中选出 \(n - 1 + i\) 条边的方案，满足只保留 \(n\) 个点和选出的这 \(n - 1 + i\) 条边的图依然连通。

由于答案可能很大，所以你只需要求出对 \(998244353\) 取模后的结果。

\(n\leq 17\)。

题解

直接做子集 DP，进行两种操作：

• 用一条边合并两个连通块。
• 添加一条边。

钦定每次合并进来的连通块具有最小编号，这样每次转移时，一个状态会被算重 \(|E|\) 次，\(|E|\) 是这个状态的边数。

因为可以考虑一个状态的前一个状态，发现删去任何一条边都对应恰好一个上一状态。

提交记录

蛋糕 NOIP 模拟 T3（计数，Raney 引理）

题意

对满足如下条件，下标范围为 \([0,n+1]\) 的序列计数：

• \(a_0=a_{n+1}=0\)。
• \(\sum\limits_{i=1}^{n} \max(0,a_i-a_{i-1})=m\)。

\(n,m\leq 2\times 10^5\)。

题解

求差分数组，相当于对满足如下条件的差分数组计数：

• \(\sum\limits_{i=1}^{n+1} d_i=0\)。
• \(\sum\limits_{i=1}^{n+1} \max(0,d_i)=m\)。
• \(\forall_{x\in [1,n+1]\cap \Z},\sum\limits_{i=1}^{x} d_i\geq 0\)。

考虑将原条件映射为：

• \(\sum\limits_{i=1}^{n+1} d_i=1\)。
• \(\sum\limits_{i=1}^{n+1} \max(0,d_i)=m+1\)。
• \(\forall_{x\in [1,n+1]\cap \Z},\sum\limits_{i=1}^{x} d_i>0\)。

映射方法为将第一个数 \(+1\)，容易证明这是双射。

利用 Raney 引理：和为 \(1\) 的序列恰有一个循环位移使得任意前缀和大于 \(0\)。

那么直接对满足前两个条件的序列计数，最后再除以 \(n+1\) 即可。

对前两个条件计数只需枚举非负数的个数然后组合数即可。

提交记录

等式 NOIP 模拟 T4（简单推式子）

题意

定义 \(f(a, b, m)\) 为最小的非负整数 \(x\) 使得其满足以下条件：

\[a x \equiv b \quad (\text{mod } m) \]

若不存在这样的 \(x\)，则定义 \(f(a, b, m) = 0\)。

给定正整数 \(n, a, b\)，你需要求出：

\[\sum_{i=1}^n f(a, b, i) \]

由于答案可能很大，所以你只需要求出对 \(998244353\) 取模后的结果。

题解

\(ax\equiv b \quad (\text{mod } m)\)，即 \(x=\frac{b+m\times y}{a}\)，\(y\) 取任意非负整数。

为了让 \(x\) 最小，必有 \(y=f(m,-b,a)\)。

当 \(m\bmod a\) 一样时，\(f(m,-b,a)\) 也一样，因此枚举 \(m\bmod a\)，之后对答案的贡献是一个等差数列，直接求和即可。

提交记录

P3623 [APIO2008] 免费道路 紫（Kruskal）

题意

给定一张图，边有黑色和白色之分，构造一个恰有 \(k\) 条黑边的生成树，或报告无解。

题解

普通生成树只要图连通就必定有解，我们先不加入黑边，这样图会分为若干百边连通块，把这些连通块缩成点，先用黑边跑一边 MST，这样保证剩下的图即使全选白边也是连通的，所以再在剩下的图中贪心选黑边即可。

提交记录

CF1120D. Power Tree *2500（序列转差分，树论建模）

题意

Arkady 和 Vasily 在树上玩游戏。游戏分为三个阶段。第一阶段，Arkady 购买树上的一些非空顶点集合。第二阶段，Vasily 给所有叶子节点赋一些整数。第三阶段，Arkady 可以进行若干次（也可以不进行）如下操作：选择他在第一阶段购买的某个顶点 \(v\) 和某个整数 \(x\)，然后将 \(x\) 加到 \(v\) 的子树中所有叶子的整数上。整数 \(x\) 可以是正数、负数或零。

Arkady 的目标是让所有叶子上的整数都变为零。无论 Vasily 在第二阶段如何赋值，Arkady 都要保证自己能够达成目标。请你求出 Arkady 在第一阶段至少需要支付的总费用 \(s\)，以及有多少个顶点属于至少一个最优集合（即总费用为 \(s\) 的集合），使得 Arkady 购买这些顶点后能够保证胜利。

输出最优方案的并集。

题解

相当于让每个叶子独立，这放到树上不是很好做，把它拍到 DFN 序上，相当于有 \(n\) 个区间可以买，让一些关键点独立。

考虑差分数组，这些区间能让关键点的差分数组全为 \(0\)（最后一位除外）。

假设一个区间加在差分数组上的体现是 \(i\) 加 \(1\)，\(j\) 减 \(1\)，那么在 \(i,j\) 连一条边权为 \(c\) 的边表示能花 \(c\) 块钱让 \(i\to j\) 之间实现任意数值的转移。

那么最后我们需要让所有叶子和最后一位连通，即所有叶子连通，因此跑 MST 即可。

求可能成为 MST 边的并集，只需要按边权分类，对每个边权求：如果它是在同边权的边中第一个被加入的，那它是否可能被算入 MST。这是正确的，因为根据 MST 的性质，只加入 \(\leq w\) 的边（\(w\) 取任意数），图的连通情况是确定的。

提交记录

CF888G. Xor-MST *2300（Boruvka，启发式合并）

题意

给定一个有 \(n\) 个点的完全无向图，每个点有一个权值 \(a_{i}\)，点 \(i\) 与点 \(j\) 之间的边权为 \(a_{i} \operatorname{xor} a_{j}\)。

请你计算该图的最小生成树的权值。

题解

Boruvka 算法，每次让每个连通块往外找一条最短的边连上，不断重复这个过程。

每个连通块维护一个 Trie，全局维护一个 Trie，差分一下就能找到一个点往外连接的最小边。

合并连通块时做启发式合并即可。

注意 Boruvka 必须每个连通块往外找恰好一条边，而不是每个点找一条边。

提交记录

CF1305G. Kuroni and Antihype *3500,但是这是假的 *3500（树论建模，枚举子集，另类 Kruskal）

题意

Kuroni 不擅长经济学。因此他决定创办一个名为 Antihype 的新型金融金字塔。其规则如下：

1. 你可以免费加入金字塔，并获得 \(0\) 个金币。
2. 如果你已经是 Antihype 的成员，你可以邀请你目前还不是 Antihype 成员的朋友，每邀请一位朋友，你将获得等于你年龄数目的金币。

最近有 \(n\) 个人听说了 Antihype，第 \(i\) 个人的年龄为 \(a_i\)。他们之间有些是朋友，但现在的友谊很奇怪：第 \(i\) 个人和第 \(j\) 个人是朋友，当且仅当 \(a_i \text{ AND } a_j = 0\)。

目前这 \(n\) 个人中还没有人是 Antihype 的成员。他们希望合作，以某种方式依次加入并邀请彼此，使得他们获得的金币总数最大。你能帮帮他们吗？

\(1\leq n\leq 200000,0\leq a_i\leq 200000\)。

题解

邀请与被邀请信息可以构成一棵树，

将所有 \(a_i \text{AND} a_j=0\) 的边连边 \(a_i+a_j\)，那么容易发现答案就是最大生成树权值 \(-\sum a_i+\) 若干个连通块的 max。

为每个值建立一个虚点，虚点 \(v\) 下挂 \(a_i=v\) 的 \(i\)，对虚点枚举超集建 \(v \text{AND} v'=0\) 的边，边数是 \(O({3}^{\log_2 n})\) 的，之后跑 Kruskal 即可。

直接 Kruskal 会 TLE，考虑在 \(\text{AND}=0\) 时，加法实际上是或运算，枚举边权后再枚举边权子集即可。

问题是我们这么做图不一定连通，而且答案最后的减 \(\max\) 会让连边不一定优，因此需要加一个 \(0\) 的虚点，即 \(a_{n+1}=0\)，然后就能正常做了。

实现方面，按值缩点，维护 \(cnt\) 表示这个值的连通块个数。

提交记录

ARC096 E - Everything on It *3100（二项式反演（容斥），集合划分计数，分类计数）

题意

有 \(n\) 部电影，她计划要每天和优太看几部。但他们作为具有精致电影品味的人，有如下几点要求：

• 她一天不能多次看同一部电影，也不能存在两天看的电影集合相同。
• 每部电影都要至少看两次！
• 可以存在某一天不看电影

每天的顺序不计，或是一天内看电影的顺序不计。我们只关心对于每个电影集合，是否存在一天恰好看了这些电影。

求在这样情况下不同的计划数有多少种，对质数 \(p\) 取模。

\(2\leq n\leq 3000\)。

题解

第一步容易想到容斥，钦定一些电影出现次数小于 \(2\)，然后通过类似二项式反演的式子计算答案。

假设钦定了 \(k\) 个电影出现次数小于 \(2\)，不妨设是 \(1\sim k\)。

考虑分类计数，把集合分为不包含 \(1\sim k\) 和包含 \(1\sim k\) 的两类。

对于不包含 \(1\sim k\) 的集合，\(k+1\sim n\) 的数随便选，结果为 \(2^{2^{n-k}}\)。

对于包含 \(1\sim k\) 的集合，枚举这样的集合个数 \(i\)，对于一个固定的 \(i\)，结果为 \(S(k,i)\times (2^{n-k})^i\)，其中 \(S(k,i)\) 表示把 \(k\) 个不同的球放入 \(i\) 个相同盒子，球可以不使用的方案数。\((2^{n-k})^i\) 表示把每个含 \(1\sim k\) 的集合并上一个 \(k+1\sim n\) 的集合。

\(S\) 的推导类似斯特林数，\(S_{i,j}=S_{i-1,j-1}+S_{i-1,j}*j+S_{i-1,j}\)，最后一项表示把当前球扔掉，前面是第二类斯特林数的转移。

提交记录

你、组乐队了吧 NOIP 模拟T4（l-r 平面扫描线，历史和线段树）

题意

Sumimi 有两个 \(1, 2, \cdots, N\) 的排列 \(S\) 和 \(M\)。

当一个区间 \([l, r] (1 \leq l \leq r \leq N)\) 满足如下条件时，真奈会觉得自己的心意能够与小初产生共鸣。因此我们称这样的区间是 「两位一体」 的：

\[\min_{l \leq x \leq r} S_x = \min_{l \leq x \leq r} M_x \land \max_{l \leq x \leq r} S_x = \max_{l \leq x \leq r} M_x \]

但是作为当红偶像，计划的变动是当然会有的。真奈一共有 \(q\) 天的计划，每天的计划是一个 \([1, N]\) 的子区间 \([L, R]\)。

对于每一天，真奈想知道在当天计划 \([L, R]\) 的限制下，究竟有多少 \([L, R]\) 的子区间 \([l, r]\) 是 「两位一体」 的呢？

题解

考虑放到 l-r 平面上，\(\min=i\) 的区间构成一个矩形，从这里入手。

那么对 \(S,M\) 分别算出 \(2\times n\) 个矩阵，表示区间在 \(S,M\) 的 \(\min / \max\) 为 \(i\) 的矩形，之后历史和线段树扫描线维护被覆盖两次的位置。

我在实现的时候把值反了过来，求的是 \(0\) 的个数，但是这不重要，因为都是最值计数。

最值计数的历史和线段树，维护的 \(histag\) 含义应为将所有子节点 \(\min\) 等于当前节点 \(\min\) 的节点计入历史和，而不是将 \(\min=0\) 的点计入，因为 \(\min\) 会发生修改。

这样写无需关心加法和计入历史和的标签顺序问题，也避免了先写矩阵再拆矩阵的麻烦。

提交记录

P11673 [USACO25JAN] Median Heap G 蓝（重标数值，树形 DP）

题意

Farmer John 有一棵包含 \(N\) 个结点的二叉树，结点编号从 \(1\) 到 \(N\)（\(1 \leq N < 2\cdot 10^5\)，\(N\) 为奇数）。对于 \(i>1\)，结点 \(i\) 的父结点为 \(\lfloor i/2\rfloor\)。每个结点都有一个初始整数值 \(a_i\)，以及将初始值修改为任意其他整数值的代价 \(c_i\)（\(0\le a_i,c_i\le 10^9\)）。

定义近似中位数为：从最后一个结点 \(N\) 开始向前执行。在算法的每一步，如果一个结点不是它和它的两个结点的中位数，他就交换当前结点和值为中位数的子结点的值。在这个算法结束时，结点 \(1\)（根结点）上的值即为近似中位数。

有 \(Q\) 次独立的询问，每次询问给定 \(m\)，求近似中位数等于 \(m\) 所需要的最小总代价。

题解

首先对于单次询问，有显然的 \(O(nV)\) DP，但是我们最后复杂度不能带 \(V\)。

考虑重标数值，由于我们只要求最终值等于 \(m\)，中位数也只关心最后的数是否等于 \(m\)，因此我们 DP 的时候只用关心当前点权和 \(m\) 的相对大小。

因此令 \(f_{i,0/1/2}\) 表示 \(i\) 子树内，结果小于/等于/大于 \(m\) 的最小代价。

我们 DP 的时候只用关心当前点权和 \(m\) 的相对大小，也能说明一个点被修改时，它的值一定改变了 \(</=/>m\) 的状态。

因为我们要处理多次询问，考虑让 DP 式子优美一些，令 \(w_{i,0/1/2}\) 表示将 \(i\) 改到 \(</=/>m\) 的最小代价，则 \(f_{i,Mid(i,j,k)}\leftarrow f_{ls,i}+f_{rs,j}+w_{i,k}\)。

注意到 \(w_{i,*}\) 只有两种取值且随 \(m\) 增长单调，因此进行询问离线，每次暴力修改所有改变的 \(w\)，对修改的每个点的到根链更新 \(f\) 即可，由于题目给的二叉树深度是 \(O(\log n)\) 的，因此复杂度正确。

提交记录

P11676 [USACO25JAN] DFS Order P 蓝（树形结构的区间 DP）

题意

Bessie 有一个无向简单图，结点编号为 \(1\dots N\)（\(2\le N\le 750\)）。给定图的初始状态以及修改每条边状态的代价。具体地说，对于每对满足 \(1\le i<j\le N\) 的结点 \((i,j)\)，给定一个整数 \(a_{i,j}\)（\(0<|a_{i,j}|\le 1000\)），其中

• 如果 \(a_{i,j}>0\)，则边 \((i,j)\) 当前不在图中，可以以代价 \(a_{i,j}\) 添加。
• 如果 \(a_{i,j}<0\)，则边 \((i,j)\) 当前在图中，可以以代价 \(-a_{i,j}\) 移除。

求使得 \([1,2\dots,N]\) 成为一个可能的 DFS 序的最小总代价。

题解

刚看到题没啥思路，点开标签，看到区间 DP 就会了。

DFS 树中，一个子树的编号一定是连续区间，因此可以区间 DP。

首先把 \(a_{i,j}<0\) 的边都删掉，然后令选择这些边的代价是 \(a_{i,j}\)，这样问题转化为边的代价有正有负，选一个树加上所有负边权的返祖边，让边权和最小。

考虑区间 DP 出 dfs 树，然后把负边权返祖边加上。

考虑常见的树形结构区间 DP 的套路，令 \(f_{l,r}\) 表示区间 \([l,r]\)，DFS 序可以为 \([l,l+1,\dots,r]\)，\(l\) 为根的答案。

转移时枚举 \(l\) 的儿子节点 \(k_1,k_2,\dots,k_x\)，要求 \(k_1=l+1\)，此时返祖边必定有一端点是 \(l\)，记 \(s_{i,j}=\sum\limits_{k=1}^{j} [a_{i,k}<0]a_{i,k}\)，有 \(f_{l,r}\leftarrow \sum\limits_{i=1}^{x} f_{k_i,k_{i+1}-1}+a_{l,k_i}+s_{l,k_{i+1}-1}-s_{l,k_i-1}-[a_{l,k_i}<0]a_{l,k_i}\)。最后减的那项是因为 \(a_{l,k_i}\) 不能算重。

枚举 \(k_1,k_2,\dots,k_x\) 的过程本质上是区间划分 DP，因此倒着枚举 \(l\)，对每个 \(l\) 做一遍区间划分 DP 即可。

提交记录

P12031 [USACO25OPEN] Forklift Certified P 蓝（递归实现拓扑排序，二维数点转一维序列）

题意

农夫约翰（Farmer John）需要从一个旧仓库中清理 \(N\)（\(1 \le N \le 10^5\)）个箱子，这些箱子被标记为 \(1\) 到 \(N\)。

这些箱子可以被建模为二维平面上的轴对齐矩形，其中 \(+x\) 方向是东，\(+y\) 方向是北。箱子 \(i\) 的西南角坐标为 \((x_{i1}, y_{i1})\)，东北角坐标为 \((x_{i2}, y_{i2})\)。所有坐标都是范围 \([1, 2N]\) 内的整数，并且来自不同矩形的任意两个角都不会共享相同的 \(x\) 或 \(y\) 坐标。所有箱子都有非零面积，且没有两个箱子相交。

农夫约翰计划每次从仓库的西南入口处移除一个箱子。然而，由于叉车的物理限制，他只有在没有其他箱子的任何部分位于该箱子东北角的南方和西方时，才能移除该箱子。

下面显示了一个 \(N = 4\) 的示例。要移除箱子 4，阴影区域内不能有任何其他箱子。箱子 2 和 3 阻止了箱子 4 被移除，但箱子 1 不会。

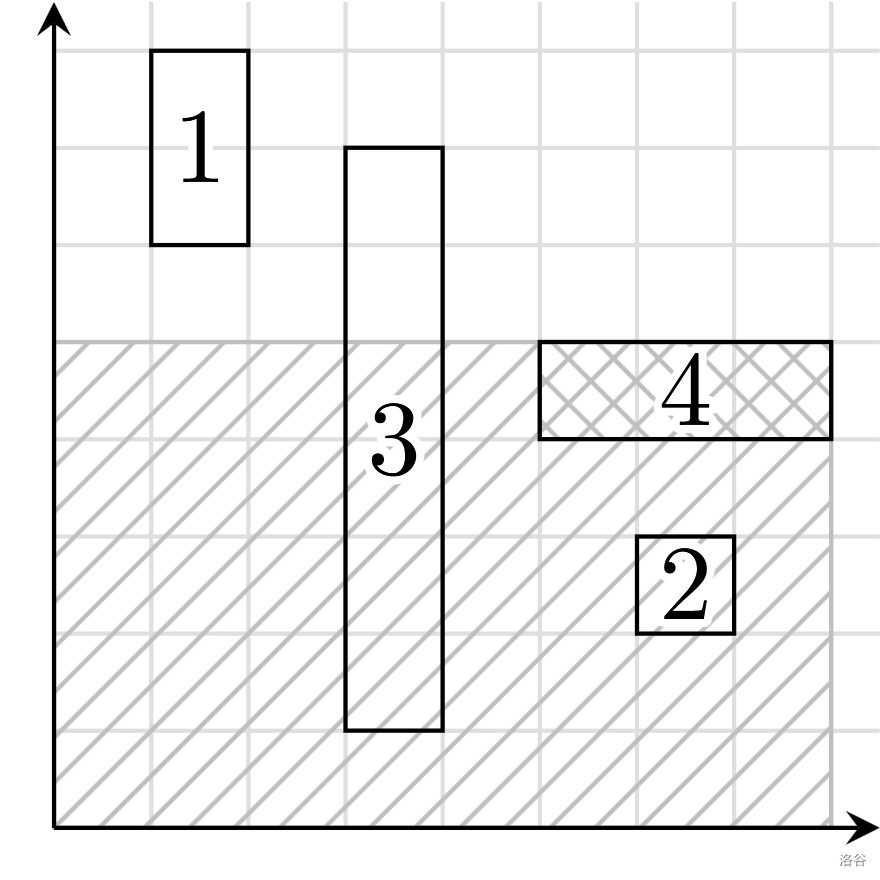
帮助农夫约翰决定如何移除所有箱子！您的代码应根据整数标志 \(M\) 在两种不同的模式下运行：

• 模式 1（\(M = 1\)）：生成一个 \(1, \dots, N\) 的排列，指定一个有效的箱子移除顺序。如果存在多个有效的顺序，则输出任意一个。可以证明这样的顺序总是存在的。
• 模式 2（\(M = 2\)）：对于每个 \(k = 1, \dots, N\)，如果农夫约翰可以在箱子 \(1, \dots, k-1\) 都已被移除的情况下移除箱子 \(k\)，则输出 1，否则输出 0。

题解

第二问是好做的。

第一问，相当于对箱子拓扑排序。

建图是困难的，考虑拓扑排序的另一种实现方法：在反图上每次选择任意一条出边，递归下去。

因此我们只需要动态查询挡住一个箱子的任意一个箱子。

可以 bit 套 set 做到 \(O(n\log^2 n)\)。

由于 \(x,y\) 各不相同，因此可以二维转一维，将 \(x\) 视为下标，\(y\) 视为值，即 \(a_x=y\)，有一个点在 \((x,y)\) 的右下方，当且仅当 \(\min\limits_{i\in [1,x-1]} a_i < y\)。线段树维护即可。

这启示我们拓扑排序问题不需要真正建图，只要我们能快速找到一个点的任意一个前驱，就能实现拓扑排序。

提交记录

P11847 [USACO25FEB] True or False Test P 紫（决策单调性）

题意

Bessie 正在参加一场 \(N\) 道判断题的考试（\(1\le N\le 2\cdot 10^5\)）。对于第 \(i\) 道题目，如果她答对了将获得 \(a_i\) 分，如果答错了将失去 \(b_i\) 分，如果不回答则分数不变（\(0<a_i,b_i\le 10^9\)）。

因为 Bessie 是一头聪明的牛，她知道所有的答案，但她担心 Elsie（主考官）会在测试后追溯性地更改至多 \(k\) 道题目，使得 Bessie 无法答对这些题目。

给定 \(Q\)（\(1\le Q\le N+1\)）个 \(k\) 的候选值（\(0\le k\le N\)），求对于每一个 \(k\)，Bessie 在回答至少 \(k\) 道题目的前提下可以保证的分数。

题解

按 \(a_i+b_i\) 升序排序，相当于选一个分界线，使得分界线下面选 \(k\) 个 \(-b_i\)，分界线上面全选 \(a_i\)。

发现分界线不一定具有单峰性质，因此考虑更一般化的性质——决策单调性。注意到 \(k\) 增大的时候分界线不能往下。因为如果分界线往下会更优，那 \(k\) 小的时候分界线往下也会更优，不符合最优性。

因此 \(k\) 越大，分界线越往前，分治即可。

提交记录

AT_arc154_d [ARC154D] A + B > C ? 蓝（Adhoc，擂台算法，排序）

题意

PCT 君有一个 $ (1,2,\dots,N) $ 的排列 $ (P_1,P_2,\dots,P_N) $。你只知道 $ N $ 的值。

你可以向 PCT 君最多询问 $ 25000 $ 次以下的问题：

• 指定满足 $ 1\le i,j,k\le N $ 的整数三元组 $ (i,j,k) $，询问 $ P_i+P_j>P_k $ 是否成立。

请你求出 $ P_1,P_2,\dots,P_N $ 的全部值。

$ 1\le N\le 2000 $，交互库不自适应，但是自适应也能做。

题解

首先，\(1+1\) 不大于除 \(1\) 以外的任何数，所以可以 \(O(n^2)\) 次询问找到 \(1\)。

考虑优化，若 \(A_i+A_i<A_j\)，则 \(A_j\neq 1\)，若 \(A_i+A_i>A_j\)，则 \(A_i\neq 1\)，因此我们每次询问都能排除一个数，因此可以用类似擂台算法 \(O(n)\) 找出 \(1\) 的位置。

找出 \(1\) 的位置后，固定 \(A_i=1\)，则条件转化为 \(P_j\geq P_k\)，归并排序即可。

提交记录

P12032 [USACO25OPEN] Lazy Sort P 紫（简单分析性质，组合数 DP）

题意

称一个序列是好的，当且仅当它能通过这种方式正确排序。

函数 LazySort(数组 a):
    n = 数组 a 的长度
    
    对于 t 从 1 到 1e100 执行:
        对于 i 从 1 到 n-1 执行:
            如果 a[i] > a[i+1] 则:
                a[i] = a[i] - 1
                a[i+1] = a[i+1] + 1

规定序列长度为 \(n\)，有 \(Q\) 个位置固定，即有 \(Q\) 个限制 \((c,v)\)，第 \(i\) 个限制为 \(a_{c_i}=v_i\)。

对好的序列计数。

题解

分析性质，发现好序列一定能被分成若干段，每段极差不超过 \(1\)，每段的最大值递增，第一个数一定是这一段的最大值。

令 \(f_{i,0/1}\) 表示前 \(i\) 个数，第 \(i\) 个数是当前段最小值 \(+0/1\) 的方案数。

分 \(Q\) 段转移，先算 \(c_{i-1}\) 和 \(c_i\) 在同一段的情况。

之后，分类讨论 \(c_i\) 是不是一个段的开头，中间枚举有多少段，然后插板法分段，再乘上 \(2^{长度-段数}\) 转移。

提交记录

乘积 NOIP 模拟 T1（折半，双指针）

题意

令质数 \(P = 10^7 + 19\)，给定一个长度为 \(n\) 的整数序列 \(a\) 和一个整数 \(k \in [0, P-1]\)，保证 \(\forall i \in [1, n]\)，\(a_i\) 在 \([1, P-1]\) 之间等概率随机。

有 \(q\) 次询问，每次询问给定区间 \([l, r]\)，问是否存在 \(l \leq t_1 \leq t_2 \leq t_3 \leq t_4 \leq r\)，使得

\[a_{t_1} \times a_{t_2} \times a_{t_3} \times a_{t_4} \equiv k \pmod{P} \]

若存在，则输出 \(1\)；若不存在，则输出 \(0\)。

题解

注意到区间的期望长度是 \(O(^4\sqrt {p})\) 的，但是区间长度的 \(\max\) 大概是 \(O(\sqrt p)\)，所以不能设阈值暴力。

考虑双指针，维护两个数相乘的桶，每次更新桶的时候 meet in the middle 计算四个数相乘等于 \(k\) 的数量，就可以双指针了。

提交记录

简单环 NOIP 模拟 T2（模拟费用流）

题意

点 \(u\) 具有一个权重：\(\alpha_u\)。初始时，对于所有的 \(u\)，\(\alpha_u = 0\)。

对于从 \(u\) 连向 \(v\)、边权为 \(w\) 的边，你可以：

• 花费 \(w\) 的代价，使得 \(\alpha_u\) 减一，\(\alpha_v\) 加一；
• 花费 \(w\) 的代价，使得 \(\alpha_u\) 加一，\(\alpha_v\) 减一。

一个局面是合法的，当且仅当：

1. 能从初始局面（所有 \(\alpha_u = 0\)）经过一系列上述操作后达到该局面；
2. 对于所有的 \(u\)，都有 \(|\alpha_u| \le C\)（\(|\cdot|\) 表示绝对值）。

小 G 给出 \(q\) 组询问，每次询问给定一个 \(\alpha\)，求所有关于 \(\alpha\) 合法的局面中代价的最大值。

如果最大值可以无穷大，答案为 \(0\)；否则答案为代价最大值对 \(998244353\) 取模的值。

题解

根据 \(q,c\) 的范围判断出 \(q,c\) 没啥用，进一步，这个问题的答案相当于 \(x=1\) 的答案，再乘上 \(x\)。

先写费用流，删去费用为 \(0\) 的增广路，发现本质上是选若干个端点不交的路径，使得绝对值长度之和最大。

考虑模拟费用流，求出前缀和，然后考查一条路径的贡献，发现本质上就是两个位置前缀和的差。

因此也不用什么高深的技巧了，把前缀和排序，答案就是前缀和数组后半截的和减去前半截的和。

提交记录

P11845 [USACO25FEB] Min Max Subarrays P 紫（暴力）

题意

给定一个长为 \(N\) 的整数数组 \(a_1,a_2,\dots,a_N\)（\(2\le N \le 10^6\)，\(1\le a_i\le N\))。输出所有 \(N(N+1)/2\) 个 \(a\) 的连续子数组的以下子问题的答案之和。

给定一个非空整数列表，交替执行以下操作（从第一个操作开始）直到列表大小恰好为一。

1. 将列表内的两个相邻整数替换为它们的较小值。
2. 将列表内的两个相邻整数替换为它们的较大值。

求最终余下的整数的最大可能值。

题解

傻逼题，看到操作先猜测长度是奇数取最大值，偶数取次大值，这显然是答案上界。

模拟发现 \(n\) 大的时候总能取到上界。

当 \(n\) 是大于 \(3\) 的奇数时，答案总取到最大值，因为只需要确保每次操作二用在最大值上即可。

当 \(n\) 为偶数时，有如下情况可以取到次大值：

• 把序列分成三块，最大值和次大值中间、最大值一侧、次大值一侧。
• 存在一侧至少有三个数。

这是因为，如果有一块的数字个数 \(\geq 3\)，我们可以把其余两块消成大小 \(\leq 1\)，之后用这一块攒出两个操作二把剩下的数消掉。

注意到 \(n>8\) 都满足上述条件，进一步，因为 \(n=8\) 时的唯一情况是 \(a_3,a_6\) 取最大或次大，模拟一下发现是可以取到次小值的。

只有 \(n\leq 6\) 时答案取不到上界，对 \(n\leq 6\) 的情况暴力即可。

提交记录

[ARC107D] Number of Multisets *2100（计数 DP，刻画）

题意

给定正整数 \(N,\ K\)。有多少种有理数的多重集合满足以下所有条件？

• 多重集合的元素个数为 \(N\)，元素的总和为 \(K\)。
• 多重集合的元素只能取 \(1,\ \frac{1}{2},\ \frac{1}{4},\ \frac{1}{8},\ \dots\)，即只能是 \(\frac{1}{2^i}\ (i = 0,1,\dots)\) 之一。

答案可能很大，请输出对 \(998244353\) 取模的结果。

\(1\leq K\leq N\leq 3000\)

题解

考虑初始时所有数都是一，然后我们不断选择数分裂。

令 \(f_{i,j}\) 表示当前有 \(i\) 个数，有 \(j\) 个数是最大值的方案数。

为了避免重复，每次只让最大值分裂。

有转移方程 \(f_{i,j}\to f_{i+k,2\times k}\ \ (1\leq k\leq j)\)。

斜向差分优化即可。

提交记录

[ARC107F] Sum of Abs *3100（网络流最小割，最大权闭合子图）

题意

给定一个 \(n\) 个点 \(m\) 条边的无向图，每个点有权值 \(a_i\) 和 \(b_i\)。

定义一个连通块的权值为其中所有点的 \(b_i\) 之和的绝对值。

可以删去任意个点，删去点 \(i\) 的代价为 \(a_i\)。

求：总权值（所有连通块权值之和）减去总代价（删点代价之和）的最大值。

题解

由一般图上删掉若干个点这个操作，可以推断这是流题了，除了网络流以外其余算法处理不了这个操作。

发现同一个连通块内点的贡献要么都是 \(b_i\)，要么都是 \(-b_i\)。因此考虑最大权闭合子图的套路，先设定理想情况，所有 \(b_i>0\) 做正贡献，所有 \(b_i<0\) 做负贡献。

令理想的总权值为 \(\sum |b_i|\)。

如果 \(b_i>0\) 做负贡献，或 \(b_i<0\) 做正贡献，那么总权值会减小 \(2|b_i|\)。

如果删去一个点，总权值减小 \(a_i+|b_i|\)。

然后，如果 \(b_i>0\)，向 \(S\) 连 \(b_i\) 边，如果 \(b_i<0\)，向 \(T\) 连 \(-b_i\) 边。

拆点刻画删点操作，入点和出点连上 \(a_i+|b_i|\) 的边，之后连上原图边，边权为 \(+\infin\)，答案为理想权值减去最小割。

最大权闭合子图套路：先假定理想贡献情况，再计算每个点不做理想贡献的损失，以损失为边权向源/汇连边，再按照点贡献之间的关系进行连边。答案为理想权值减去最小割。

提交记录

P11677 [USACO25JAN] Shock Wave P 黑（分析性质，分析总变化次数，可删堆思想）

题意

Bessie 有 \(N\)（\(2 \leq N \leq 10^5\)）块砖块排开在面前，分别需要至少 \(p_0,p_1,\dots,p_{N-1}\) 的力量才能击破（\(0 \leq p_i \leq 10^{18}\)）。

Bessie 可以通过击打特定的砖块来施加力量，如果她选择击打砖块 \(x\) 一次，对所有在 \([0,N-1]\) 范围内的整数 \(i\)，它将对砖块 \(i\) 施加 \(|i-x|\) 的力量。

请求出击破所有砖块所需要的最少击打次数。

题解

首先各种 DP 都没有任何前途。

考虑分析性质减少不必要的操作，对于一个操作 \(i\)，肯定不能断言它能够被其他操作替代，考虑分析两个操作 \(i,j\)，发现将操作 \(i,j\) 替换为操作 \(1,n\) 一定更优。

因此我们最后肯定是先操作若干次 \(1\)，再操作若干次 \(n\)，最后操作一次 \(m\ (2\leq m\leq n-1)\)。

考虑二分只操作 \(1,n\) 的最小操作次数 \(ans\)，然后检查 \(ans-1\) 是否可行。

设 \(1\) 操作了 \(a\) 次，\(n\) 操作了 \(b\) 次，不妨设 \(2i\leq n\)（\(2i>n\) 同理），有如下式子：

\[p_i\leq a(i-1)+b(n-i) \]

强行提取 \(ans\) 的表达式 \(a+b\)。

\[p_i\leq (a+b)(i-1)+b(n-2i+1) \\ b\geq \frac{p_i-(a+b)(i-1)}{n-2i+1} \]

当 \(2i>n\) 时，同理可得：

\[a\geq \frac{p_i-(a+b)(n-i)}{2i-n+1} \]

因此，只需满足 \(\max \frac{p_i-(a+b)(i-1)}{n-2i+1}+\frac{p_i-(a+b)(n-i)}{2i-n+1}\leq a+b\) 即可。

因此我们可以轻松求得 \(ans\)，检查 \(ans-1\) 时，我们的式子又多出了一部分。（\(2i>n\) 的情况略）

\[\exist 2\leq m\leq n-1,\max \frac{p_i-(a+b)(i-1)-|m-i|}{n-2i+1}\leq a+b \]

我们希望对所有 \(m\) 维护一坨式子的最大值。

考虑这个式子的变化次数，\(\frac{|m-i|}{n-2i+1}\) 只会变化不超过 \(\frac{n}{n-2i+1}\) 次，因此总变化量是调和级数的。

实现方面，我们只关心最大的 \(\frac{p_i-(a+b)(i-1)-|m-i|}{n-2i+1}\)，考虑让最大值递减，利用可删堆的思想，每次保证最大值更新即可。由于 \(a,b\geq 0\)，我们不用处理任何式子是负数的情况。

必须要满足最大值递减才能保证优先队列做法正确，而 \(m\) 增加时只保证 \(i<m\) 的最大值递减，因此需要先从小到大枚举 \(m\)，再从大到小枚举 \(m\)，做两遍。

做两遍的时候需要控制优先队列中只保留 \(i>m\) 或 \(i<m\) 的数，因为多余的数可能无法更新到其本身的最大值，影响答案。

复杂度 \(O(T(n\log V+n\log^2n))\)。

提交记录

P11678 [USACO25JAN] Watering the Plants P 黑（SlopeTrick）

题意

Bessie 的花园中有 \(N\) 株植物，从左到右编号为 \(1\) 到 \(N\)（\(2\leq N\leq 5\cdot 10^5\)）。Bessie 知道植物 \(i\) 至少需要 \(w_i\)（\(0\leq w_i \leq 10^6\)）单位的水。

Bessie 有一个十分古怪的灌溉系统，包含 \(N-1\) 条水渠，编号为 \(1\) 到 \(N-1\)。每条水渠 \(i\) 有一个相关的单位费用 \(c_i\)（\(1\le c_i\le 10^6\)），Bessie 可以支付费用 \(c_i k\) 来为植物 \(i\) 和 \(i+1\) 各提供 \(k\) 单位的水，其中 \(k\) 是一个非负整数。

Bessie 很忙，可能没有时间使用所有的水渠。对于每一个 \(2\leq i \leq N\)，计算仅使用前 \(i-1\) 条水渠灌溉植物 \(1\) 到 \(i\) 所需要的最小费用。

题解

以下的 \(p\) 表示 \(w\)。

首先有一个显然的 DP，\(f_{i,j}\) 表示使用了 \(1\sim {i-1}\) 水渠，\(i\) 植物有 \(j\) 单位的水的最小代价。

则：

\[f_{i,j}=\min_{k\geq p_{i-1}-j} f_{i-1,k}+c_{i-1}\times j \]

进行后缀和优化，令 \(sf\) 表示 \(f\) 的后缀 \(\min\)。

\[f_{i,j}=sf_{i-1,p_{i-1}-j}+c_{i-1}\times j \]

整体 DP，这相当于，每次把 \(f\) 在 \([0,p_{i-1}]\) 翻转，加上斜率为 \(c_{i-1}\) 的直线，再进行后缀 \(\text{chkmin}\)。

维护差分数组 \(t\)，下标范围为 \([0,\max p]\)。

翻转 \(f\) 相当于将 \(t_0\) 设为 \(\sum\limits_{i=0}^{\max p} t\)，然后将 \(t_{1\sim p_{i-1}}\) 翻转并取相反数，并将 \(t_{p_{i-1}+1\sim \max p}\) 推平为 \(0\)。

加上斜率 \(c_{i-1}\) 的直线，相当于 \(t_{1\sim \max p}\) 加 \(c_{i-1}\)。

考虑平衡树。

\(\text{chkmin}\)，发现如果此时存在谷点，谷点处 \(t\) 的正负性改变，因此平衡树上二分出谷点，再推平即可。可以做到 \(O(n\log V)\)。

注意要特殊处理第一个植物，可以通过在序列最前面添加虚拟的 \(0\) 代价植物和 \(+\infin\) 代价水渠处理。

提交记录

AT_arc190_b *2200

题意

有 \(N\times N\) 矩形，定义 \(K\) 阶 L 型为宽和高都是 \(K\) 的 L 型，显然使用 \(1\sim N\) 阶 L 型各一个可以将 \(N\times N\) 的矩形覆盖。

给定 \(a,b\)，有 \(q\) 次询问，每次询问给出 \(k\)，求 \((a,b)\) 被 \(k\) 阶 L 型覆盖的前提下，使用 \(1\sim N\) 阶 L 型各一个将 \(N\times N\) 的矩形覆盖的方案数。

题解

首先每次填入最大的 L 型，发现填法较为唯一，只能填边上，有四种情况。

每次放入一个 L 型，都会将矩形缩小一圈。

\((a,b)\) 被 \(k\) 阶矩形覆盖，需满足在 \(n-k+1\) 次缩小后，\((a,b)\) 位于边缘。

设使得 \((a,b)\) 满足上述条件的 \(n-k+1\) 次缩小的方案数为 \(cnt\)，其中 \((a,b)\) 在矩形一角的方案数为 \(cnt'\)，则这次询问的答案为 \(cnt\times (1+[k\neq 1])\times 4^{k-1}+cnt'\times [k\neq 1]\times 4^{k-1}\)。

考虑分析缩小操作，假设当前矩阵为 \([l_x,r_x],[l_y,r_y]\)，缩小会分别将两个区间缩小 \(1\)，可以缩左边也可以缩右边。不难发现对两个区间的操作是独立的。

设 \(n-k+1\) 次后的矩阵为 \([1+A,n-B],[1+C,n-D]\ \ (A+B=C+D=n-k+1)\)，当 \(A,B,C,D\) 固定时，方案数为 \(\binom{A+B}{A}\binom{C+D}{C}\)。

在角上：分讨 \((a,b)\) 在哪一角，可以求得一侧 \(A,B,C,D\) 的值，组合数即可。

在边上：分讨 \((a,b)\) 在哪一边，可以求得 \(A,C\) 其中之一的值，另一个值是一个范围，以 \(1+A=a\) 为例，\(A=a-1,B=n-k-a+2,n-k+b< C< b-1\)，答案为 \(\binom{A+B}{A}\times \sum\limits_{C} \binom{n-k+1}{C}\)，每次 \(k\) 增大的时候增量维护 \(\sum\limits_{C}\binom{n-k+1}{C}\)。

代码咕咕咕。

模拟赛因为 T1 没对拍，大样例和手造样例都缺一种情况导致爆零，警钟长鸣。

P11675 [USACO25JAN] Photo Op G 紫（分析性质，分类讨论）

题意

Bessie 目前站在 xy 平面上 \((X,0)\) 处，她想要前往 \((0,Y)\)（\(1\le X,Y\le 10^6\)）。不幸的是，\(N\)（\(1 \leq N \leq 3 \cdot 10^5\)）头其他奶牛决定在 \(x\) 轴上摆姿势。更具体地说，奶牛 \(i\) 将位于 \((x_i,0)\)，她的摄影师位于 \((0,y_i)\)（\(1 \leq x_i,y_i \leq 10^6\)），准备拍摄她的照片。他们将在时刻 \(s_i\)（\(1 \leq s_i < T\)）开始摆姿势，并且他们会保持姿势很长时间（他们必须拍出完美的照片）。这里，\(1\le T\le N+1\)。

Bessie 知道每头奶牛的摄影安排，她将选择最短欧几里得距离到达目的地，而不穿越任何摄影师与其对应的奶牛之间的视线（她的路径将由一条或多条线段组成）。

如果 Bessie 在时刻 \(t\) 出发，她将需要避开所有在时刻 \(s_i \le t\) 开始摆姿势的摄影师-奶牛对的视线，此外令她到达最终目的地的距离为 \(d_t\)。求从 \(0\) 到 \(T-1\) 的每一个整数 \(t\) 的 \(\lfloor d_t\rfloor\) 的值。Bessie 可以从摄影师或者奶牛的位置经过，这样不算穿越视线。

题解

看到这道题的第一反应是我可以 bit 求出每个线段端点往 \(Y\) 轴走的位置区间，但是从左/右侧找第一个能往上走的点是错误的，答案的式子也不是简单的线性式子，因此我们无法动态维护答案。

我们分析两个线段交叉的情况，发现我们不能从中间穿过，换句话说，我们可以把相交的线视作一条粗线段。

显然，粗线段和粗线段还可以继续合并成更粗的线段。

所以我们可以使用 set 维护粗线段，这样所有线段之间不交，枚举相邻线段计算答案即可。

然后我们每次修改集合只会改变 \(O(1)\) 对相邻关系，使用 multiset 维护答案集合，动态修改即可。

插入 \((0,0)\) 和 \((+\infin,+\infin)\) 线段以避免边界的麻烦。

提交记录

[AGC008F] Black Radius 黑（去重技巧）

题意

Snuke 君有一棵 \(n\) 个节点的全白的树，其中有一些节点他喜欢，有一些节点他不喜欢。他会选择一个他喜欢的节点 \(x\)，然后选择一个距离 \(d\)，然后将所有与 \(x\) 距离不超过 \(d\) 的节点都染成黑色，恰好操作一次，问有多少种可能的染色后状态。

两个状态不同当且仅当存在一个节点，它在两个状态中不同色。

部分分（1300pts/1900pts）：Snuke 君喜欢所有节点。

题解

令 \(f(u,d)\) 表示 \(u\) 的 \(d\) 邻域，本题难点在于处理重复，考虑对于一个集合，只让最小的 \(d\) 计入贡献，即 \(f(u,d)\) 能被计入贡献当且仅当不存在 \(f(v,d+x)=f(u,d)\ \ (x\gt 0)\)。

这样做稍微有点问题，因为如果 \(f(u,d)=f(v,d)\)，这样也会计重，讨论 \(f(u,d)=f(v,d)\)，发现只有在 \(f(u,d)=[1,n]\cap \Z\) 时出现，因此我们特殊处理全集即可。

注意到重复关系具有单调性，若 \(f(u,d)=f(v,d')\) 则 \(f(u,d+1)=f(v,d'+1)\)，因此只需要求出所有点最大的 \(d\) 然后求和即可。

考虑部分分，先把所有点的 \(d\) 最大值设成这个点到最远点的距离 \(-1\)，然后考虑点 \(u\) 的最大 \(d\)，记 \(u\) 为根时，其中一子节点为 \(v\)，子树 \(v\) 深度为 \(h_v\)，\(u\) 刨去 \(v\) 的最大深度为 \(h_u\)，当 \(h_v < h_u\) 时始终有 \(f(v,d')\neq f(u,d)\ \ (d'<d)\)，否则有 \(f(u,h_u+2)=f(v,h_u+1)\)，更新 \(u\) 的最大 \(d\) 为 \(h_u+1\)。

把上面的话翻译成人话就是 \(u\) 的最大 \(d\) 为 \(u\) 刨去深度最大的子树后深度 \(+1\)。

考虑正解，此时对于每个 \(u\) 存在一个最小 \(d=d_{\min}\)，当 \(d<d_{\min}\) 时不存在一个 Snuke 君喜欢的节点 \(x\) 使得 \(f(x,d')=f(u,d)\)。

当 \(x\) 是 Snuke 君喜欢的节点时，\(d_{\min}=0\)。否则我们仿照刚刚的思路找出最深子树 \(v\)，记其余子树最大深度为 \(t\)，\(v\) 中最靠上的 Snuke 喜欢的节点为 \(x\)，则 \(f(x,dep_{x}+t)=f(u,2\times dep_{x}+t)\)，那么 \(u\) 此处不应该被计算（因为 \(dep_x+t<2dep_x+t\)）。对于其余子树，如果子树内有 Snuke 喜欢的节点，则其贡献为子树的最大深度 \(+1\)。

显然上面的 \(2\times dep_x+t\) 相比于下面的子树深度 \(+1\) 必定不优，因此上面的话翻译成人话就是：记含有 Snuke 君喜欢的节点的子树中，深度最小的子树为 \(w\)，则 \(d_{\min}\) 等于子树 \(w\) 的深度 \(+1\)。

最大 \(d\) 同理，记 \(u\) 最大深度的子树为 \(v\)，如果 \(v\) 内存在一个 Snuke 喜欢的节点，设这个节点为 \(x\)，记 \(x\) 与 \(u\) 的深度为 \(dep_x\)，次大子树深度为 \(t\)，则 \(d_{u\max}=2dep_x+t-1\)。

我在玩原神，实际上 \(f(u,d)\) 被记录不一定保证 \(u\) 是 Snuke 喜欢的节点。本质上是我们对于每个合法的集合，选择使 \(d\) 最小的中心点 \(u\)，将 \(f(u,d)\) 计入答案。

所以 \(u\) 的最大 \(d\) 就是 \(u\) 子树次大深度 \(+1\)，和部分分结论一致。

如果某个 \(f(u,x)\) 能被 \(f(v,y)(y<x)\) 替代，那么有 \(d_{u\min}\geq x\)，即 \(f(u,x)\) 存在，那么 \(f(v,y)=f(u,d)\) 也存在，即 \(d_{v\min}\geq y\)，逻辑是自洽的。

换根即可。

提交记录

CF1657E. Star MST *2200（计数 DP）

题意

如果一个无向图满足以下条件，则称其为“美丽图”：所有与顶点 \(1\) 相连的边的权值之和，等于该图的最小生成树（MST）的权值。

请计算恰好有 \(n\) 个顶点、边权值从 \(1\) 到 \(k\) 的所有完全美丽图的数量。由于答案可能很大，请输出对 \(998244353\) 取模后的结果。

\(2 \le n \le 250\)，\(1 \le k \le 250\)。

题解

一道 *2200，但是想的时间还挺久的。

考虑模拟 Kruskal 的过程，并在同边权下优先选择与 \(1\) 向邻的边，如果存在一条边比所有没选的与 \(1\) 相邻的边都要小，且加上这条边不会成环，那么这张图就不合法。

假设 \(l\sim r\) 中与 \(1\) 相邻的边都是 \(x\)，那么 \(l\sim r\) 之间的边的取值范围是 \([x,k]\)。

令 \(f_{i,j}\) 表示 \(i\) 个点（含 \(1\)），最大边权为 \(j\) 的方案数，从小到大分配 \(2\sim n\) 与 \(1\) 相连的边权。

转移时枚举边权为 \(j+1\) 且与 \(1\) 相邻的边数，式子比较简单，不写了。

显然这样不会算重，因为对于一个状态，其前驱状态唯一。

提交记录

P12033 [USACO25OPEN] Package Pickup P 黑（线段树维护矩阵 DP）

题意

农夫约翰（Farmer John）按照以下奇怪的方式在数轴上分布了奶牛和包裹：

• 农夫约翰选择一个数字 \(M\)（\(1 \le M \le 10^{18}\)）。
• 农夫约翰选择 \(N\)（\(1 \le N \le 2 \cdot 10^4\)）个区间 \([L_i, R_i]\) 来分布奶牛（\(1 \le L_i \le R_i \le 10^{18}\)）。然后他在位置 \(L_i, L_i + M, L_i + 2M, \dots, R_i\) 放置奶牛。保证 \(R_i - L_i\) 是 \(M\) 的倍数。
• 农夫约翰选择 \(P\)（\(1 \le P \le 2 \cdot 10^4\)）个区间 \([A_j, B_j]\) 来分布包裹（\(1 \le A_j \le B_j \le 10^{18}\)）。然后他在位置 \(A_j, A_j + M, A_j + 2M, \dots, B_j\) 放置包裹。保证 \(B_j - A_j\) 是 \(M\) 的倍数。

一旦奶牛和包裹分布完毕，农夫约翰想知道奶牛们捡起所有包裹需要多长时间。每一秒，农夫约翰可以用他方便的对讲机（walkie talkie）向一头奶牛发出指令，让其从当前位置向左或向右移动一个单位。如果一头奶牛移动到包裹所在的位置，它就能捡起该包裹。农夫约翰想知道，奶牛们捡起所有包裹所需的最少时间（以秒为单位）。

注意 \(M\) 是给定的。

题解

#define 草 包裹。

考虑暴力怎么做，贪心显然能做，但是没啥优化空间，考虑 DP。

显然奶牛不会在没有东西的地方掉头，考虑把奶牛和草的坐标排序，然后按照坐标顺序 DP。

将相邻的位置之间视为一个段，容易发现每个段只会被经过 \(0,1,2\) 次，令 \(d_i\) 表示第 \(i\) 段经过的次数，将问题转化为求一个符合条件的 \(d\) 使其加权和最小。

考虑分析 \(d\) 的充要条件，充要条件如下：

• 草旁边至少有一个位置非 \(0\)。
• 如果这个位置有一头牛，则两侧不能为 \(11\) 或 \(22\)。
• 如果这个位置有两头及以上牛，则不做任何限制。
• 所有非 \(0\) 段至少连接一头牛。

令 \(f_{i,1/2/3/4/5}\) 表示第 \(i\) 个位置，不考虑第 \(i\) 个位置是啥（这个限定是为了方便后面矩阵的边界处理），如下状态的答案。

1. 上一段是 \(1\)，未连接牛。
2. 上一段是 \(2\)，未连接牛。
3. 上一段是 \(1\)，已连接牛。
4. 上一段是 \(2\)，已连接牛。
5. 上一段是 \(0\)。

转移显然。

考虑使用 \((\min,+)\) 矩阵维护 DP，注意到 \(M\) 是给定的，考虑将数轴划分为若干周期，即 \([0,M),[M,2M),[2M,3M)\dots\)，当加入 \((l,r)\) 时，相当于修改了 \(l,r\) 中间的周期。

套路地扫描线，使用线段树维护一个周期的信息，具体地，将操作坐标离散化，线段树维护 \([0,M)\) 中所有操作涉及到的坐标，每个节点 \([x,y]\) 维护第 \(x\) 个坐标转移到第 \(y\) 个坐标的矩阵，以及最右侧坐标是一头牛还是两头牛还是草，并插入 \(0,M\) 为哨兵节点。还需要维护全 \(0\) 前缀长度和全 \(0\) 后缀长度来合并区间。

合并区间大概是算出中间长度 \(dis\)，通过左侧区间最后一个非空坐标的状态（草/一头牛/两头牛）构造出中间转移一步的矩阵，之后将左侧矩阵、中间矩阵、右侧矩阵乘起来合并。

扫描线时，假设本次操作坐标为 \(x\)，上一次操作坐标为 \(y\)，则当 \(\lfloor\frac{x}{m}\rfloor\neq \lfloor\frac{y}{m}\rfloor\) 时，操作中间跨过了不少于 \(1\) 个周期，应该统计答案，从线段树根节点查询这个周期的转移矩阵，把答案乘上转移矩阵的 \(\lfloor\frac{x}{m}\rfloor-\lfloor\frac{y}{m}\rfloor\) 次方。

更新答案的过程和线段树合并区间的过程是一样的，可以将答案初值设成 \((\min,+)\) 单位矩阵，此时最后一行与 DP 初值恰好吻合，因此最后直接使用答案矩阵的最后一行作为 DP 数组即可，注意需要特判最后位置是牛还是草，因为我们 DP 时没有考虑最后一位。

提交记录

P8096 [USACO22JAN] Drought G 蓝（计数 DP）

题意

FJ 的 \(N\) 头奶牛（\(1 \leq N \leq 100\)）排成一行，队伍中的第 \(i\) 头奶牛的饥饿度为一个非负整数 \(h_i\)。FJ 可以选择两头相邻的奶牛 \(i\) 和 \(i+1\)，令她们的饥饿度各减少 1。

FJ 想让他的奶牛饥饿度全部相同且非负。尽管他不知道他的奶牛们具体的饥饿度，他知道每一头奶牛的饥饿度上界；具体地说，第 \(i\) 头奶牛的饥饿度 \(h_i\) 至多为 \(H_i\)（\(0\le H_i\le 1000\)）。

计算符合上述上界的 \(N\) 元组 \([h_1,h_2,\ldots,h_N]\) 的数量，使得 FJ 有可能达到他的目标，答案对 \(10^9+7\) 取模。

题解

第一反应是观察性质，直接在原序列上操作很难发现有用的性质，考虑转为差分序列后分析性质。

转为差分数组后可以发现将差分分为奇数下标和偶数下标，性质和差分数组的和有关，具体地，操作一次相当于把 \(d_i\) 的一个 \(1\) 转移到 \(d_{i+1}\)，但是奇数下标差分数组的和是 \(O(nV)\) 级别的，无法 DP。

但是刚才的思考并不是没有用处的，因为我们可以通过差分数组证明，\(n\) 是奇数时，对于任意有解的序列，最后的值是唯一的，且等于 \(\sum_{i=2w+1\land i\leq n,w\in \N} d_i-d_{i-1}\)，\(n\) 为偶数时，不难注意到对于任意有解的序列，假设其能够操作到 \(k\)，那么最后一定能够操作到 \(0\)（在两两配对各执行 \(k\) 次操作即可）。

回到原序列上，\(n\) 是偶数时，考虑按位 DP 填数，\(f_{i,j}\) 表示 \(1\sim i\) 中 \(1\sim i-1\) 已经满足，且 \(i\) 操作了 \(j\) 次的方案数，目标是最后操作到 \(0\)，转移显然，前缀和优化可以做到时间复杂度 \(O(nV)\)。

对于 \(n\) 是奇数的情况，需要额外枚举最后操作到的数，时间复杂度 \(O(nV^2)\)。

提交记录

CF724F. Uniformly Branched Trees *2700（计数 DP，去重技巧）

题意

给定三个数 \(n,d,mod\)，对满足如下条件的无根树计数，同构的树算作一棵：

• 有 \(n\) 个点，除了叶子以外所有点的度数都为 \(d\)。

\(n\leq 1000\)，\(d\leq 10\)，\(10^8\leq mod\leq 10^9\)。

题解

无根树去重技巧：钦定重心为根。

无序卷积去重技巧，加入 \(x\) 个重量为 \(y\) 物品，方案数为 \(\binom{f_y+x-1}{x}\)。

令 \(f_i\) 表示 \(i\) 个节点，根的度数是 \(d-1\)，其余点度数为 \(d\) 的方案数，\(f_i\) 可以卷积得到。

卷积时如果两颗或多颗子树大小相同，则需要去重，具体地，加入 \(x\) 个大小为 \(y\) 的子树，方案数为 \(\binom{f_y+x-1}{x}\)。

再将 \(f_{1\sim \frac{n}{2}}\) 卷积得到根是重心的答案。

当 \(n\) 是奇数时已经做完了。

\(n\) 是偶数时，有两个重心且两边不一样的情况会被算重两次，因此将答案减去 \(\binom{f_{\frac{n}{2}}}{2}-f_{\frac{n}{2}}\) 即可。

提交记录

P11846 [USACO25FEB] Transforming Pairs P 黑（二维平面，分类讨论，meet-in-the-middle）

题意

回答 \(Q\)（\(1\le Q\le 10^5\)）个独立查询，每个查询的形式如下：

给定四个整数 \(a\)，\(b\)，\(c\)，\(d\)（\(-10^{18}\le a,b,c,d\le 10^{18}\)）。在一次操作中，你可以执行 \(a\mathrel{+}=b\)，或 \(b\mathrel{+}=a\)。求将 \((a,b)\) 转变为 \((c,d)\) 所需要的最小操作次数，或者如果不可能完成，输出 \(-1\)。

弱化版：\(a,b\geq 0\)。

题解

对于弱化版，考虑正难则反，发现每一步是唯一的，辗转相除即可。

记 \(a,b,c,d\) 的答案为 \(\text{ans}(a,b,c,d)\)。

注意到：\(\text{ans}(a,b,c,d)=\text{ans}(-a,-b,-c,-d)=\text{ans}(b,a,d,c)=\text{ans}(c,-d,a,-b)\)。

因此所有不能归约到 \(a,b,c,d\geq 0\) 的情况，都能归约到 \(ac<0\land bd<0\) 或 \(a,c,d>0\land b<0\)。前者显然无解，考虑后者。

分析性质，\((a,b)\) 必定有一个时刻进行竖直方向移动，离开象限后进入第一象限，之后变为平凡情况。

对于不离开象限的情况，\((a,b)\) 的下一个状态唯一。画出 \((a,b)\) 不离开象限的路径图，发现图由若干个横线和竖线构成。

我们需要保证我们跳到第一象限的点能够到达。

分析从下面路径往上跳的性质，发现肯定是下面在横向行走时往上跳，往上跳的轨迹是一个斜率为 \(1\) 的线，这些线与上面的若干线段形成交点。

线段个数是 \(\log V\) 级别的，暴力枚举上面和下面的线进行 meet in the middle 即可，需要一些模拟的细节。

我们不需要考虑上面的竖线，因为根本不会和竖线相交，逆向考虑，如果相交那么这个竖线下一步会直接下来，因此交点必定是拐点，只考虑横线也能覆盖这个点。

提交记录

P3349 [ZJOI2016] 小星星 紫（计数 DP，去重技巧，容斥原理，子问题划分技巧）

题意

给定一颗 \(n\) 个点的树，又给定一张 \(n\) 个点的图，需要将树中的 \(n\) 个点与图中的 \(n\) 个点一一对应，使得所有树中存在的边在图中能够找到与之对应的边。问对应方案数。

\(n\leq 17\)。

题解

没有任何思路，感觉怎样都要记录阶乘级状态。

考虑从树结构入手，把给定的树的 \(1\) 号点定为根，树为我们提供了一个子问题划分的结构。

令 \(f_{i,j,S}\) 表示图上 \(i\) 对应树上 \(j\)，原树子树 \(j\) 内的点对应到了图上集合 \(S\) 的方案数。

直接转移需要枚举子集，复杂度爆炸。

有一个处理排列（即编号不重复）的容斥技巧，枚举 \([1,n]\cap \Z\) 的子集 \(S\)，记不要求编号不重复，且只考虑原图 \(S\) 子集内的点的方案数为 \(g_S\)，则 \(ans=\sum\limits_{S\in [1,n]\cap \Z} g_S\times (-1)^{n-|S|}\)。根据容斥原理的基本公式 \(\sum\limits_{i=0}^n \binom{n}{i}(-1)^i=[n=0]\) 即可得证。

令 \(f_{i,j}\) 表示图上 \(i\) 对应树上 \(j\)，且原树子树 \(j\) 内已完成映射，不要求编号不重复的方案数，枚举 \([1,n]\cap \Z\) 的子集进行 DP，最后再容斥一下就做完了。

---

这种去重方法有一个名字叫做子集反演，具体内容如下：

记 \(f(S)\) 表示恰好使用 \(S\) 的答案（\(n\) 个点映射恰好使用了 \(S\) 中所有点），\(g(S)\) 表示至多使用 \(S\) 的答案（\(n\) 个点映射使用了 \(S\) 中的一些点），则有：

\[f(S)=\sum_{T\subseteq S}(-1)^{|S|-|T|}\times g(T) \]

提交记录

P8273 [USACO22OPEN] Pair Programming G 蓝（计数 DP，去重技巧）

题意

一个程序由一系列指令组成，每条指令都具有以下形式之一：

• \(\times pri_d\)，其中 \(d\) 是一个 \([0,9]\) 范围内的一位数，\(pri_d\) 表示第 \(d-1\) 大的质数，并规定 \(pri_0=0\)，\(pri_1=1\)。
• \(+s\)，其中 \(s\) 是一个表示变量名称的字符串。一个程序中出现的所有的变量名均不相同。

程序执行的结果定义对表达式 \(0\) 依次应用每条指令后得到的表达式。例如，执行程序 \([\times 3,+x,+y,\times 2,+z]\) 得到的结果是表达式 \((0\times 3+x+y)\times 2+z=2 \times x+2\times y+z\)。不同的程序执行后可能会得到相同的表达式；例如，执行 \([+w,\times 0,+y,+x,\times 2,+z,\times 1]\) 也会得到表达式 \(2\times x+2\times y+z\)。

Bessie 和 Elsie 各有一个 \(N\)（\(1\le N\le 2000\)）条指令的程序。他们将交错这些程序的指令以制造一个 \(2N\) 条指令的新程序。

计算执行 Bessie 和 Elsie 的交错程序可能得到的不同表达式的数量，对 \(10^9+7\) 取模。

题解

直接对最终形成的表达式计数是不现实的。

先考虑一些特殊情况和细节，首先 \(\times 1\) 可以删除。

对于 \(\times 0\)，不知道咋特殊处理，考虑直接带着 \(0\) DP。

本题难点肯定在于去重，考虑分析操作序列性质，我们在钦定当前操作和下一步操作不同时（加变乘或乘变加），在结果不为 \(0\) 的前提下一定不会算重。

于是令 \(f_{i,j,0}\) 表示 Bessie 前 \(i\) 个指令和 Elsie 前 \(j\) 个指令，以 $+/\times $ 结尾且结果不为 \(0\) 方案数，\(g_{i,j}\) 表示 Bessie 前 \(i\) 个指令和 Elsie 前 \(j\) 个指令，结果为 \(0\) 是否可能。分段转移即可。

咕咕咕。

P4778 Counting swaps 紫（置换环，打表）

题意

给定一个排列 \(p_1, \ldots, p_n\)，它是数字 \(1\) 到 \(n\) 的一个排列。在每一步中，你可以选择两个数字 \(x < y\) 并交换 \(p_x\) 和 \(p_y\)。

设 \(m\) 为将给定排列排序所需的最小交换次数。计算恰好用 \(m\) 次交换来排序给定排列的不同序列的数量。由于这个数量可能很大，计算它对 \(10^9 + 9\) 取模的结果。

\(1 \leq n \leq 10^5\)。

题解

唐氏打表题，考虑置换环，每个置换环独立，每次操作相当于把一个置换环分成两个置换环。

令 \(f_i\) 表示大小为 \(i\) 的置换环方案数，则：

\[f_i=\frac{i\times \sum\limits_{j=1}^{i-1} f_j\times f_{i-j}\times \binom{i-2}{j-1}}{2} \]

含义是枚举操作的数对，除二是因为每个数对会算重两次。

不知道如何优化，打表发现 \(f_i=i^{i-2}\)，然后就愉快的 AC 了。

考虑证明，通过式子不难想到无根树个数，定义 \(g_i\) 表示大小为 \(i\) 的无根树数量，根据 prufer 序列的性质，有 \(g_i=i^{i-2}\)。

考虑另一种求 \(g\) 的方法，为了去重，我们以重心为根进行 DP 求出 \(g\)。

则有：

\[g_i=i\times \sum\limits_{j=1}^{\lfloor \frac{i}{2} \rfloor} f_j\times f_{i-j}\times \binom{i-2}{j-1} \\ g_i\leftarrow g_i-\frac{i}{2}\times g_{\frac{i}{2}}^2\ \ (i \bmod 2=0) \]

含义是，在大小为 \(i-j\) 的基础上加入大小为 \(j\) 的子树，强制钦定除根外的最小值在新加入的子树内，并分配编号，枚举 \(g_{i-j}\) 中在这次转移后变为重心的点的最终编号（可以直接枚举最终编号的原因是，分配完编号后最终编号和之前的编号一一对应），去重双重心树。

发现 \(g=f\)，证毕。

提交记录

P14256 平局（draw） 黑（DP 套最优化）

题意

• 有 \(n\) 个人在石头剪刀布，每个人只会出固定的手势。你每次可以让相邻两个人石头剪刀布决斗，输的人被删除，如果平局就随便删除一个。求过程中的最多平局数。

现在你知道每个人分别是否可能出石头、剪刀、布，请对所有可能的出手方案求以上问题的答案之和。\(n≤3000\)。

题解

考场上写了 \(O(3^n\times n)\) 的暴力但是不知道为啥写挂了，于是淘汰了正确结论，然后交了个 \(O(3^n\times n^3)\) 就遗憾离场了 。

首先区间 DP 是没法放到 DP 套 DP 里面的。

考虑序列确定怎么做。

容易分析一些性质想到用栈模拟，但是想不清楚具体在干什么。

考虑把序列转化为类似括号的结构来操作，具体地，我们不关心手势具体是啥，只关心谁赢谁。

我们维护一个 \(b\) 序列表示将手势记作 \(0,1,2\) 后的差分序列，\(1\) 表示前赢后，\(-1\) 表示后赢前，\(0\) 表示平局。

显然可以先消去 \(0\)，考虑产生 \(0\) 的方案。

1. 对于 \(1,-1\) 子串，可以产生一个 \(0\) 并消失。
2. 对于 \(-1,1\) 子串，没有贡献。
3. 对于 \(1,1,1\) 或 \(-1,-1,-1\) 子串，可以产生一个 \(0\) 并消失，注意这种操作必定不优于操作一。

那么看前两个操作就可以想到把 \(1\) 视为 \((\)，\(-1\) 视为 \()\)，用栈模拟括号匹配，然后

此时我们可以直接设计 DP \(f_{i,j,k}\) 表示 \(1\sim i\) 位，栈里面有 \(j\) 个左，\(k\) 个右括号的方案数。

此时我们记录栈里面右括号个数仅仅是为了方便做操作三，考虑操作三的本质是什么，本质上是先把 \(-1,-1,-1\) 变为 \(1,-1\) 再匹配。

那么我们在对栈进行操作的时候，遇到两个 \(-1\) 直接把它变成 \(1\) 即可，这样栈中最多有一个 \()\)，且必定在栈底，\(f_{i,j,0/1,k},g_{i,j,0/1,k}\) 表示原数组 \(1\sim i\) 位，栈中有 \(j\) 个 \((\)，\(0/1\) 个 \()\)，\(a_i=k\)（记录这个方便求 \(b\)） 的答案/方案数。

按找上述过程 DP 即可。

提交记录

NOIP 模拟 T4（DP 套 DP，统计答案技巧）

题意

在一条数轴上有 \(n\) 台计算机，第 \(i\) 台计算机位于 \(x = a_i\) 处。
有两种窃取数据的方式：

• 花费 \(1\) 秒窃取长度为 \(20\) 的区间内的所有计算机数据；
• 花费 \(3\) 秒窃取长度为 \(75\) 的区间内的所有计算机数据。

注意：区间可以重叠，同一个位置可以被多次窃取。

每台计算机可能存放绝密文件，也可能没有，用 \(1/0/?\) 表示。对于所有可能的情况，计算最少花费时间的总和，并对 \(10^9 + 7\) 取模。

\(n\leq 1000\)。

题解

对最优化问题求和，不难想到 DP 套最优化或者 DP 套 DP。

本题的内层问题只能 DP，因此考虑后者。

考虑序列固定时如何求答案，令 \(f_{i}\) 表示处理 \(1\sim i\) 的最小花费，从第一个位置大于 \(a_i-20\) 和 \(a_i-75\) 的地方转移过来。

我们的转移“跨度”较大，如果要把这个 DP 当作内层 DP，那么我们需要记录一个位置大于 \(a_i-75\) 到现在的所有 DP 值。

考虑互换 DP 状态与值，令 \(f_{i,j}\) 表示 \(1\sim i\) 花 \(j\) 元是否可行，我们的目的是实现 \(f_i\to f_{i+1}\) 的唯一转移（不能有取 \(\max\)），因此将“是否可行”转为“最大向后延伸长度 \(+1\)（为 \(0\) 表示不能覆盖到 \(i\)）”，就能按位转移了。

记 \(j_0\) 为最小的 \(j\) 满足 \(f_{i,j}>0\)，则只有 \(f_{i,j_0},f_{i,j_0+1},f_{i,j_0+2}\) 有用，因为 \(f_{i,j_0+3}\) 一定不比在 \(f_{i,j_0}\) 的情况再在下一个 \(1\) 位置加上 \(75\) 区间优。

这样容易发现 \(f\) 的转移是唯一的。\(f\) 的缺陷是我们要么存储 \(j_0\)，要么动态累计答案。

设计外层 DP，令 \(g_{i,j_0,x,y,z}\) 表示处理了 \(1\sim i\) 位，\(x=f_{i,j_0},y=f_{i,j_0+1},z=f_{i,j_0+2}\) 的方案数。

此时状态爆炸了，我们记录 \(j_0\) 是为了统计答案，考虑将答案拆贡献到每一步转移，具体地，设 \(g_{i,x,y,z}\) 表示处理了 \(1\sim i\) 位，\(x=f_{i,j_0},y=f_{i,j_0+1},z=f_{i,j_0+2}\) 的方案数，\(j_0\) 未知，转移本质上是在 DAG 上走，边权就是答案的增加量，答案就是所有路径的长度和。

这个 DAG 的性质是任意点到 \(n\) 的路径条数固定（为这个点后面的问号个数），当发生转移 \(g_{i,x,y,z}\to g_{i+1,nx,ny,nz}\) 时，若 \(x-(a_{i+1}-a_{i})\leq 0\)，则答案会变大 \(1\)，此时 \(ans\leftarrow ans+g_{i,x,y,z}\times 2^{cnt_{i+2}}\)，其中 \(cnt_x\) 表示 \(x\sim n\) 的问号个数。

Longest Array Deconstruction *2100（DP 状态设计）

题意

Chanek 先生给你一个从 \(1\) 到 \(n\) 编号的序列 \(a\)。定义 \(f(a)\) 为满足 \(a_i = i\) 的下标 \(i\) 的个数。

你可以从当前序列中选择一个元素并将其移除，然后将剩下的元素拼接在一起。例如，如果你从序列 \([4, 2, 3, 1]\) 中移除第 \(3\) 个元素，得到的新序列为 \([4, 2, 1]\)。

你希望通过移除若干个元素（可以为零），使得 \(f(a)\) 最大。请你求出可以得到的最大的 \(f(a)\)。

题解

哎不知道为啥没想到。

朴素的 DP 是令 \(f_{i,j}\) 表示以 \(a_i\) 结尾，选择了 \(j\) 个的方案数。

仿照【CSP-S 2024 染色】，强制钦定状态每步转移都有新贡献，重新设计状态，\(f_i\) 表示 \(1\sim i\) 选了 \(a_i\) 个数的答案。

转移是 \(f_{i}\to f_{j}(j>i\land a_j-a_i\leq j-i)\)，随便优化。

代码太简单了不写了。

NOIP 模拟 T1（行列二分图转化）

警示：\((x,y)\to (x\times V+y)\bmod p\) 是错误的，根据抽屉原理和多模哈希的实现，多少个模数冲突概率都很大。

题意

小 Y 现在正在模拟赛，但是一题不会。事已至此，他拿出了祖传棋盘。

这是一个 \(n\times n\) 的棋盘，每个格子上都有一个硬币，每个硬币只能是正或反。每次操作选择一个位置 \((i,j)\)，然后将与这枚硬币在同一行或同一列的硬币全部翻面，需要注意的是，选择的这枚硬币不会翻面。

小 Y 很快将所有硬币翻成了正面，作为他的同桌，你自然不能落下。小 Y 会告诉你初始时棋盘上反面朝上的 \(k\) 枚硬币的位置。你希望求出将所有硬币翻成正面朝上的最小操作次数来薄纱小 Y。不过小 Y 的记性并不是很好，所以他给出的局面可能无解，如果无解，请告诉他 No Solution!。

题解

完全没往二分图上考虑/kel。

记有 \(a\) 个行被翻转，\(b\) 个列被翻转，则最终答案为 \(\min (a,b)\)。

特殊地，当 \(a,b\) 奇偶性不同是无解。

建立行列二分图，要求连边的点状态不同，没有连边的点状态相同。

这样确定第一行后所有列的状态就确定了，所有行的状态也确定了。

所以一共就有两种情况，模拟和判断是否符合题意都是简单的。

提交记录

NOIP 模拟 T2（树形 DP，另类换根）

题意

小 W 初始有一棵以 \(1\) 为根的树，并且此时有一个虚拟结点 \(0\) 向 \(1\) 连了一条边（初始 \(1\) 的父亲为 \(0\)）。他很喜欢变化这棵树的形态，于是他定义一次操作如下：

• 选择两个不为 \(0\) 且不同的点 \(u, v\)，满足 \(u\) 是 \(v\) 的祖先。先将 \(v\) 与其父亲断开，再将 \(v\) 连向 \(u\) 的父亲作为新的父亲，最后将 \(u\) 与其父亲断开。此时将 \(u\) 所在连通块删除。

对于操作过程中，我们定义 \(0\) 的唯一一个儿子为当前树的根，所有结点的父亲都是相对于这个根来说的。

经过任意次操作后（可以不进行操作），小 W 对最后不同的树十分感兴趣（这里定义两棵树不同为确定根有标号的情况下不同构）。将所有最后不同的树放入集合 \(S\)，小 W 需要你对于每个结点 \(x\) 计算出：

\[cnt_x = \sum_{T \in S}[x \in T] \]

当然这个值可能很大，小 W 只需要你输出其对 \(998244353\) 取模后的结果。

\(n\leq 10^6\)。

题解

首先推出 DP 计算一号点的答案，令 \(f_u\) 表示只考虑子树 \(u\) 内，\(u\) 不进行操作也不被操作删除的方案数。则有 \(f_u=\prod_{v\in \text{son}_u}\left (\sum\limits_{x\in \text{subtree}(v)}{f_x}\right )\)。

维护 \(g_u=\sum\limits_{x\in \text{subtree}(u)}{f_x}\)，即可 \(O(n)\) 计算。

计算其他点的答案相当于要求某个点不被操作删除，因此将这个点到根连的 \(g\) 减去其他子树的 \(f\) 的和即可，暴力可以过掉所有树高不是很高的点。

刚才的操作无法被拆贡献，祖孙关系确定也没法换根，然后赛时就不会了。

对于祖先关系确定的问题，可以使用自上而下的 DP 代替换根。

令 \(h_u\) 表示 \(u\) 以及 \(u\) 子树外，不考虑 \(u\) 子树内的操作且 \(u\) 不被操作删除的方案数。

第 \(i\) 个点的答案为 \(f_i\times h_i\)。

枚举 \(u\) 替换掉了哪个点，易得 \(h_u=\sum\limits_{v\in \text{Path}(1,fa_u)} h_v\times \left ( \sum\limits_{x\in \text{son}_v\land x\notin \text{Path}(v,u)}g_x \right )\)。

可以轻松做到 \(O(n)\)，本质上式子和换根的差别应该是不大的，都是子树内刨去和 \(v\) 相连的点的贡献。

提交记录

NOIP 模拟 T3（随机游走 Trick，势能函数）

题意

给定一个字符串 \(S\)。

你有一个打字机。这个打字机打出的第一个字符一定是 \(S\) 的第一位，之后打出的所有字符的概率分布只和它打出的上一个字符有关，并且按照如下规则进行：

• 将字符串 \(S\) 首尾相接连成一个环，记录下每种字符的下一个字符的种类和出现次数；
• 那么，如果它打出的上一个字符是 \(i\)，此时它接下来打出字符 \(j\) 的概率为 \(\frac{cnt2_{i,j}}{cnt1_i}\)。
• 其中，\(cnt1_i\) 为字符 \(i\) 在 \(S\) 中的出现次数，\(cnt2_{i,j}\) 为顺序拼接字符 \(i,j\) 得到的子串在环状的 \(S\) 中的出现次数。

每个新打出的字符会接在上一个打出的字符的后面。

当 \(S\) 首次成为打字机打出字符串的子串时，记录下当前打字机打出的字符总数。求这个总数的期望值模 \(998244353\) 的结果。

\(|S|\leq 3\times 10^5\)。

题解

显然这相当于在 KMP 自动机上随机游走。

对于图上随机游走问题，设 \(f_u\) 表示 \(u\) 到目标节点的期望步数，令 \(f_n=0\)，答案为 \(f_1+1\)，转移为 \(f_u=\sum (1+f_v)\times p_{u\to v}\)。

注意到等式右侧概率和相同，因此我们把 \(f\) 集体加上某个值，仍然满足转移。

对于本题，需要额外设 \(f_{0,c}\) 表示没有匹配且当前字符是 \(c\)，走到最后的期望步数。

不妨设 \(f_1=0\),答案为 \(-f_n+1\)。

则可以高斯消元算出 \(f_{0,c}\)

正序递推可以得到 \(f_{i}=f_{i+1}\times \alpha+\beta\)，即 \(f_{i+1}=\frac{f_i-\beta}{\alpha}\)。

提交记录

NOIP 模拟 T4（树剖，重链剖分拓展）

题意

给你一棵以 \(1\) 为根的树，每个点有点权，你需要完成 \(Q\) 次操作，操作分为 \(3\) 种：

1. 给定三个非负整数 \(u,v,w\) ，表示你需要将 \(u,v\) 之间的简单路径上的每一个节点 \(x\) 的点权加上 \(fib_{dis+w}\) ，即斐波那契数列的第 \(dis+w\) 位，其中 \(dis\) 表示节点 \(x\) 到 \(lca(u,v)\) 路径上的边数。
2. 给定两个整数 \(u,v\) ，你需要回答 \(u,v\) 之间的简单路径上的点权和。
3. 给定两个整数 \(u,k\) ，你需要回答在所有与 \(u\) 距离不超过 \(1\) 的节点中，点权对 \(10^9+7\) 取模后，第 \(k\) 小的点权是多少（保证有解）。

答案对 \(10^9+7\) 取模。

\(w\leq 2\times 10^5,n,Q\leq3\times 10^5\)。

题解

为了解决 \(1\) 邻域查询，可以重剖后使用平衡树维护轻儿子。

剩余的部分就是 《fibonacci》的套路。

可以矩阵差分，也可以用公式 \(Fib_{n+m}=Fib_{n+1}Fib_{m}+Fib_{n}Fib_{m+1}\)。

由于 \(w\leq 2\times 10^5\)，不需要矩阵。

提交记录

[AGC022E] Median Replace 紫（DFA 上 DP（DP 套最优化），构建 DFA）

题意

由 \(0\) 和 \(1\) 组成的奇数长度 \(N\) 的字符串 \(X\)，如果满足以下条件，则是美丽的：

• 可以进行 \(\frac{N-1}{2}\) 次如下操作，使得最终字符串唯一的字符为 \(1\)。
  • 选择 \(X\) 中连续的 \(3\) 个比特，并用它们的中位数替换这三个比特。例如，对 00110 的中间 \(3\) 个比特应用该操作后，字符串变为 010。

太一有一个由 0、1、? 组成的字符串。他想知道，将每个 ? 替换为 0 或 1，能够得到美丽字符串的方法数。请输出该方法数对 \(10^{9}+7\) 取模的结果。

题解

对于确定序列，判定时，使用栈结构模拟消除 \(000,011,101,110\)，最后剩的如果全是 \(1\) 就是”美丽的“。

然后发现这样消除没有什么性质。

考虑将一些子串打包，来制造一些性质，具体地，如果栈底是 \(11\)，则序列必定有解，直接结束，如果栈底是 \(01\)，那么直接把 \(01\) 删掉，因为不管后面的数是多少，都和 \(01\) 无关（即 \(011=1,010=0\)），且就算 \(01\) 的 \(1\) 和后面操作，也会变成 \(1\)，\(01\) 结构不变。

但是 \(10\) 似乎不满足这个性质，因为 \(10001=1\)，而消掉 \(10\) 后会错。原因是 \(10\) 结尾的 \(0\) 可以和后面的 \(0\) 操作，将 \(10\) 后面的值由 \(0\) 变成 \(1\)，而 \(01\) 没有这个问题。

那么我们的逻辑就是：

• 加入的数是 \(1\)。
  • 如果栈中有恰好一个 \(1\)，计入答案。
  • 如果栈顶是 \(0\) 且栈只有一个元素，弹栈。
  • 否则将 \(1\) 入栈。
• 加入的数是 \(0\)。
  • 如果栈顶有超过两个 \(0\)，弹栈。
  • 否则将 \(0\) 入栈。

不难发现，栈中最多有两个 \(1\) 和两个 \(0\)。

考虑 DP 套最优化，令 \(f_{i,0/1/2,0/1/2}\) 表示只考虑原序列前 \(i\) 位，栈中有 \(0/1\) 个 \(1\) 和 \(0/1/2\) 个 \(0\) 的方案数，按照上述栈模拟方式 DP 即可。

---

推出这种 DP 的另一种方式是 Brzozowski 导数，大概方法是推出前缀恒等式，然后不断搜索直到状态形成闭包。

对于本题，初始状态为 \(\empty\)。

对于任意后缀 \(t\)，都有：

• \(01t=t\)，上述已经说明
• \(001t=0t\)，因为为了消掉 \(00\)，\(001\) 的 \(1\) 必须消失。

\(\empty\)：

• \(+0=0\)
• \(+1=1\)

\(0\)：

• \(+0=00\)
• \(+0=01=\empty\)

\(1\)：

• \(+0=10\)
• \(+1=11\)

\(00\)：

• \(+0=000=0\)
• \(+1=001=0\)

......

以此类推，得到 \(\empty,0,1,00,11,10,100,110,1100\)。

考虑接受状态，由于 \(n\) 是奇数，因此最后 DFA 状态的串长度肯定是奇数，当 DFA 状态为 \(1,110\) 时最后状态为 \(1\)。

为了实现方便，我们把 \(11+1\) 视为 \(11\)，这样会改变长度奇偶，因此将 \(1100\) 和 \(11\) 也作为接收状态。

提交记录

CF1582F2 Korney Korneevich and XOR (hard version) *2400（基础算法）

题意

给一个长度为 \(n\) 的序列 \(a_1,a_2,\dots,a_n\) ，寻找在 \(a\) 的所有递增子序列（可以为空）的异或和中出现的数。

题解

注意到 \(i<j\land a_i=a_j\) 时，以 \(j\) 位置结尾的异或和集合包含以 \(i\) 位置结尾的异或和集合，考虑按值操作。

\(V=5000\) 引导 \(O(V^2)\)，令 \(dp_{i,j}\) 表示结尾值为 \(i\)，且异或和为 \(j\) 的最靠前结尾。

从小到大枚举结尾值 \(i\) 和异或值 \(j\) 转移，转移时，记 \(a_i=x\) 的 \(i\) 集合为 \(pos_i\)，则在 \(pos_{i}\) 找到第一个大于 \(dp_{i'(i'<i),j^i}\) 的位置转移到 \(dp_{i,j}\)。

将 \(dp\) 压成一维方便实现。

提交记录

（DAG 计数，竞赛图，连通性）

题意

有 \(n\) 支队伍参加每场比赛。每支队伍有一个实力值 \(a_i\)。每两支队伍 \(i < j\) 恰好互相比赛一次。队伍 \(i\) 获胜的概率为 \(\frac{a_i}{a_i + a_j}\)，队伍 \(j\) 获胜的概率为 \(\frac{a_j}{a_i + a_j}\)。

如果一支队伍直接或间接击败了所有其他队伍，则称其为“胜者”。如果存在一系列队伍 \(c_1, c_2, \dots, c_k\)，使得 \(c_1 = a\)，\(c_k = b\)，并且对于所有 \(i\) 从 \(1\) 到 \(k-1\)，队伍 \(c_i\) 击败了队伍 \(c_{i+1}\)，则称队伍 \(a\) 直接或间接击败了队伍 \(b\)。注意，可能出现队伍 \(a\) 击败了队伍 \(b\)，同时队伍 \(b\) 也击败了队伍 \(a\) 的情况。

求本次比赛中胜者数量的期望值，\(n\leq 14\)。

题解

一开始想了一些奇奇怪怪的东西，没有用竞赛图的性质。

竞赛图缩点之后一定是一个链，我们要求的就是第一个 SCC 的期望大小。

考虑枚举一个 SCC，只需要要求这个 SCC 内与这个 SCC 外的边都是内向外的，那么这个 SCC 就是第一个 SCC，且这样不会算重。

现在我们只需要知道对于任意集合 \(S\)，它构成 SCC 的概率。

考虑模仿主旋律，记 \(f_S\) 表示 \(S\) 构成 \(SCC\) 的概率，\(g_S\) 表示 \(S\) 不是 SCC 的概率。

则 \(g_S\) 一定是若干个 SCC 拼成的 DAG，并且根据竞赛图性质，这个 DAG 是一条链。

因此：

\[g_S=\sum\limits_{T\subset S\land T\neq \emptyset} f_T\times (f_{S/T}+g_{S/T})\times E(T,S/T) \\ f_S=1-g_S \]

其中 \(E(x,y)\) 表示将 \(x\) 的所有边都指向 \(y\) 的概率，需要先维护 \(Ev_{i,S},Evi_{i,S}\) 表示点 \(i\) 到集合 \(S\) 的正反向概率，再增量维护。

有了 \(f\) 就做完了。

提交记录

CF1554E You *2600（计数，构造映射，观察答案）

题意

给你一个 \(n\) 个点的树，可以通过以下方式生成一个长度为 \(n\) 的序列 \(a\)：

• 每次在树中选取一个未被标记的节点 \(u\)，令 \(a_u\) 等于与节点 \(u\) 相邻的未被标记的节点个数，然后将节点 \(u\) 标记。

对于每一个整数 \(k\in[1,n]\)，输出符合以下条件的序列 \(a\) 的数量模 \(998244353\) 的值：

• 序列 \(a\) 可以由给定的树通过上述方式生成；
• \(\gcd(a_1,a_2,\cdots,a_n)=k\)。

\(n\leq 3\times 10^5\)。

题解

咦？计数题你告诉我答案不超过 \(1\)？

一开始想了一些套路的东西，但好像都没有啥用。

首先注意到 \(\sum a_i=n-1\)，然后就不会了。

或许可以通过暴力等手段发现（？），\(k>1\) 时答案为 \(0\) 或一，总答案为 \(2^{n-1}\)。

将原问题等价为给每个点赋一个权值，这些权值构成排列，一个点的 \(a\) 就是周围权值大于这个点的点个数。

进一步我们发现我们只关心权值的大小关系，图中的大小关系一共有 \(n-1\) 对，因此总方案数为 \(2^{n-1}\)。

考虑 \(k>1\) 时构造方案的过程，首先叶子节点必定比父亲小。

令 \(f_u\) 表示 \(u\) 是否比父亲后删除，则有：

• 当 \((\sum f_v)\bmod k=0\) 时，\(f_u=1\)。
• 当 \((\sum f_v)\bmod k=k-1\) 时，\(f_u=0\)。
• 否则无解。

因此 \(k>1\) 时答案是唯一的，之后再把 \(a\) 序列拿出来看一下 \(\gcd\) 是不是真正的 \(k\) 即可。

我们发现我们只需要枚举质数，然后计入最后 \(a\) 的 \(\gcd\) 的贡献即可。

并且只需要枚举 \(n-1\) 的因数，因为 \(\sum a_i=n-1\)。

时间复杂度 \(O(n\log n)\)。

提交记录

CF1263F Economic Difficulties *2400（DP，树论）

题意

给你两棵树，结点分别是 \(1,\dots A\) 与 \(1,\dots B\)，然后给了 \(N\) 台设备，并且 \(A\) 树和 \(B\) 树的叶子结点（两棵树的叶子节点数量相同）都是链接电机的。

求最多可以删掉几条边，使得每个电机都能连到任意一棵（或两棵）树的根节点（\(1\) 号点）。

题解

为什么要使用了网络流？为什么要使用了网络流？为什么要使用了网络流？

首先我们转换一下问题，相当于求最小保留边数。

假设我们钦定了一个集合被上面的电网连接，那么对答案就是这些点到根链的并集大小。

而这道题恰好保证的叶子 DFS 序递增，根据虚树结论，新加入一个点 \(i\) 时，记上一个同侧点为 \(j\)，则保留边数增加了 \(dep_{i}-dep_{\text{lca}(i,j)}\)。可以增量维护贡献。

令 \(dp_{i,j,1/2}\) 表示处理了 \(1\sim i\)，上一个与当前点不同侧的点是 \(j\) 的最小保留边数，简单 DP 即可，复杂度 \(O(n^2\log n)\)，使用线性 LCA 算法可以做到 \(O(n^2)\)。

现在这个 DP 形式与【CSP-S 2024 染色】十分相似，也许可以优化到 \(O(n\log n)\) 或 \(O(n)\)，但我不会。

提交记录

CF383E Vowels *2700（SOSDP）

题意

有一本包含 \(n\) 个“三字词”的词典。一个三字词是由第一个 \(24\) 个英文字母（\(a\) 到 \(x\)）中任意三个小写字母组成的序列（正好 \(3\) 个）。她规定其中一些字母为元音，其他的则为辅音。整个语言基于一个简单规则：只要单词中至少包含一个元音，该单词就是正确的。

Iahubina 想知道对所有可能的元音集合（共有 \(2^{24}\) 种），每种集合中正确单词数的平方的 \(xor\) 总和。请帮助 Iahub 求出这个数字。

题解

看到题解第一行高维前缀和就会了，咋回事呢。

首先平方后异或无任何特殊性质，因此需要求出对于所有集合 \(S\)，元音为 \(S\) 的单词个数。

令 \(f_S\) 表示集合 \(S\) 的答案，第一反应是构造 \(f_S\to f_{S\cup \{x\}}\) 的转移，但发现行不通。

集合包含关系，考虑高维前缀和，将三字词容斥拆成七个贡献在跑 SOSDP 就做完了。

提交记录

CF348D *2500（格路计数，类反射容斥）

题意

有一个 \(n\times m\) 的网格图，有一些位置有障碍物，不能通行。

有两只乌龟从 \((1,1)\) 出发前往 \((n,m)\)，两条路径除起点和终点外点不相交。

对行走方案计数，认为两只乌龟相同。

\(n,m\leq 3000\)。

题解

首先一条路径只能 DP，所以两条路径要么是 DP 优化，要么是容斥状物。

我们发现如果 DP 出两条路径，状态信息量是 \(O(n^3)\)（认为 \(n,m\) 同阶）的，非常不能优化。

考虑容斥，第一反应是枚举第一个或最后一个相交的点，对一侧不做要求，对另一侧要求不交。

但是发现这样会把原问题切分成子问题，子问题仍然无法快速解决，复杂度退化至 \(O(n^4)\)，然后我就不会了。

考虑格路计数中对最后一个交点操作的套路，将最后一个交点往后的两条路径翻转之后终点互换，构造不合法方案与某个规模相同问题答案的映射。

首先要确定不同的起点和终点，可以发现本题的第一步和最后一步固定，令 \(f(a,b,c,d)\) 表示 \((a,b)\) 走到 \((c,d)\) 的单个路径条数，总方案数可以转化为 \(f(1,2,n-1,m)\times f(2,1,n,m-1)\)。

考虑将最后一个交点后的坐标翻转，则不合法方案数为 \(f(1,2,n,m-1)\times f(2,1,n-1,m)\)。

容易证明这个转化是正确的，即 \(f(1,2,n,m-1)\times f(2,1,n-1,m)\) 与不合法方案构成双射。

提交记录

(VP)CF2159B Rectangles *????（基础算法）

题意

给定一个二进制网格 \(G\)，其尺寸为 \(n \times m\)。

我们将一个矩形定义为元组 \((u,d,l,r)\)，需满足以下条件：

• \(1 \le u < d \le n\)；
• \(1 \le l < r \le m\)；
• 单元格 \((u,l)\)、\((u,r)\)、\((d,l)\)、\((d,r)\) 均为 \(1\)。

矩形 \((u,d,l,r)\) 的面积定义为 \((d-u+1) \cdot (r-l+1)\)。

对于每个单元格 \((i,j)\)，请找到所有满足 \(u \le i \le d\) 且 \(l \le j \le r\) 的矩形 \((u,d,l,r)\) 中面积的最小值，如果不存在这样的矩形，则输出 \(0\)。

\(n\times m\leq 250000\)。

题解

提交记录

[xinyoudui模拟赛]

(VP) [AGC001D] Arrays and Palindrome *????（构造）

题意

高桥くん的母亲在高桥生日的时候送了他 \(a, b\) 两个数列。因为 \(a, b\) 满足了如下的所有性质， 所以他非常高兴：

• \(a\) 数列的数字总和是 \(N\)；
• \(b\) 数列的数字总和是 \(N\)；
• \(a, b\) 中包含的数都是正整数；
• 满足以下两个条件的数列， 所有元素必定是相同的。
  • 最开始的 \(a_1\) 个元素, 接下来的 \(a_2\) 个元素，更后面的 \(a_3\) 个，等等，都是回文；
  • 最开始的 \(b_1\) 个元素, 接下来的 \(b_2\) 个元素，更后面的 \(b_3\) 个，等等，都是回文。

但是有一天，高桥把把数列 \(a\) 和 \(b\) 都弄丢了， 幸运的是，他知道数列 \(a\) 是另一个长度为 \(M\) 的序列 \(A\) 的排列。

为了让他再一次高兴起来， 他妈妈决定给他另一对数列使其满足如上性质。

\(1≤N≤10^5\)，\(1≤M≤100\)，\(1≤A_i≤10^5\)。

题解

手模一下发现有三个奇数时无解。

又发现若干个偶数可以交错拼接。

因此分讨一下就构造完了。

所以为什么我做了 50min 呢？

提交记录

[AGC001E] BBQ Hard *????（组合意义）

题意

给定 \(n\) 和 \(n\) 个数对 \((a_i,b_i)\)，求：

\[\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n\dbinom{a_i+a_j+b_i+b_j}{a_i+a_j} \]

\(n\leq 2\times 10^5\)，\(1\leq a_i,b_i\leq 2000\)

题解

不知道咋优化，考虑组合意义。

\(\dbinom{a_i+a_j+b_i+b_j}{a_i+a_j}\) 相当于从 \((0,0)\) 到 \((a_i+a_j,b_i+b_j)\) 的路径条数。

将 \(i\) 和 \(j\) 分开，相当于 \((-a_i,-b_i)\) 到 \((a_j,b_j)\) 的路径条数。

直接按 \(1\leq i,j\leq n\) 算，相当于点对之间路径条数和，DP 后修一下式子中 \(i=j\) 的边界即可。

提交记录

重做了种树、染色、括号序列。

CF1111E. Tree *2500（DFS 序上 DP）

题意

给定一棵有 \(n\) 个节点的树，以及 \(q\) 个询问。

每个询问以三个整数 \(k\)、\(m\) 和 \(r\) 开头，接着是树上的 \(k\) 个节点 \(a_1, a_2, \ldots, a_k\)。对于每个询问，假设树以 \(r\) 为根。我们需要将给定的 \(k\) 个节点分成最多 \(m\) 个组，满足以下条件：

• 每个节点恰好属于一个组，每个组至少有一个节点。
• 在任意一个组内，不能存在两个不同的节点，使得其中一个节点是另一个节点的祖先（无论是直接还是间接的祖先）。

你需要输出每个询问的方案数，对 \(10^9+7\) 取模。

题解

点集询问考虑建立虚树。

建立虚树后跑计数 DP，由于我们要考虑祖孙关系，直接自下而上合并不能优于 \(O(nm^2)\)，考虑按 DFS 序 DP，令 \(f_{i,j}\) 表示考虑 DFS 序在 \([1,i]\) 的点，分 \(j\) 组。

则 \(f_{i,j}\leftarrow f_{i-1,j-1}+f_{i-1,j}\times (j-dep_i)\)，表示新开一组或分为之前的任意一组。

这样我们只需要知道有多少颜色和当前点冲突（即 \(j-dep_i\)），而无需进行复杂的树形背包合并。

提交记录

P7077 [CSP-S 2020] 函数调用 蓝

题意

某数据库应用程序提供了若干函数用以维护数据。已知这些函数的功能可分为三类：

1. 将数据中的指定元素加上一个值；
2. 将数据中的每一个元素乘以一个相同值；
3. 依次执行若干次函数调用，保证不会出现递归（即不会直接或间接地调用本身）。

在使用该数据库应用时，用户可一次性输入要调用的函数序列（一个函数可能被调用多次），在依次执行完序列中的函数后，系统中的数据被加以更新。为了计算出正确数据，小 A 查阅了软件的文档，了解到每个函数的具体功能信息，现在他想请你根据这些信息帮他计算出更新后的数据应该是多少。

\(0 \le a_i \le 10^4\)，\(T_j \in \{1,2,3\}\)，\(1 \le P_j \le n\)，\(0 \le V_j \le 10^4\)，\(1 \le g^{(j)}_k \le m\)，\(1 \le f_i \le m\)。

题解

函数调用关系是一个 DAG，使用虚拟节点依次调用 \(f_1,f_2\dots f_Q\) 可将原问题转化为 \(Q=1\) 的问题。

一开始想的是维护每个数 \(\times p+q\) 的标签，后来发现对每个数维护较为困难，因此考虑对最终的操作序列入手。

具体地，我们希望可以对于求出所有 \(+\) 操作，它后面所有乘操作的乘积和，即对于每个 \(1\) 类函数 \(x\)，记操作序列为 \(op\)，求 \(\sum\limits_{id_i=x}\sum\limits_{j=i}^{opcnt} op_i(v)[op_i(type)=2]\)。

考虑拓扑排序，记 \(g_u\) 表示完整调用函数 \(u\) 的操作序列的乘积，\(h_u\) 表示操作序列中完整调用 \(u\) 后（不含 \(u\)）的乘积和，转移较为自然，正序倒序分别做一遍拓扑即可。

提交记录

赛前打板子。。。

2025.11

NOIP 模拟T3（环上 DP，矩阵乘法，二进制分段倍增）

题意

小 \(*\) 有一个 o。

o 可以视为一个 \(n+1\) 个点的无向图，编号从 \(0\) 到 \(n\)。对于每个 \(i\in[0,n)\)，有一条 \(i\) 和 \((i+1)\bmod n\) 之间的边。

小 \(*\) 非常嘟嘟，她把所有 \(\operatorname{popcount}(i)\) 是奇数的 \(i\) 连了一条和点 \(n\) 之间的边。

小 \(*\) 想让你告诉她，有多少断掉一些边的方式（可以不断边），使得她的 o 还是连通的。由于答案可能很大，你需要对 \(10^9+7\) 取模。

题解

断边相当于把环分为若干段，每一段连接中心，记 \(f_{i,0/1}\) 表示当前段是否断边的方案数。

矩阵乘法，用二进制的性质倍增。

细节忘了。

NOIP 模拟 T4（二分图染色）

题意

小 \(*\) 有一条地铁线路。

有 \(n\) 个嘟嘟要乘坐地铁。第 \(i\) 个嘟嘟会在第 \(l_i\) 站上车，第 \(r_i\) 站下车（\(l_i<r_i\)）。

为了方便，我们假定有 \(2n\) 个地铁站，且 \(l_i,r_i\) 互不相同。

小 \(*\) 很坏，所以只有两班地铁。地铁非常拥挤，所以只有最后上车的嘟嘟才能下车，也就是每班地铁是一个栈。

请你帮每个嘟嘟决定一下上哪班地铁，使得每个嘟嘟都能够成功在目标车站下车。为了方便，数据保证有解。

题解

《平面图判定》加强版，考虑二分图染色，每次找出任意一条通向未访问的边染色，可以用数据结构实现。

细节忘了。

P11057 诈骗题 蓝（二分图建模）

题意

定义 \(f(n,m)\) 为下列问题的答案。

考虑一个 \(n\times m\) 黑白网格图，初始全是白色的。每次操作如下：

• 选择一个白格子 \((x,y)\)，将其所在行全染黑，这个操作叫 \((x,y,\text{R})\)。
• 选择一个白格子 \((x,y)\)，将其所在列全染黑，这个操作叫 \((x,y,\text{C})\)。

假设最多能操作 \(k\) 次。问：

• 对于所有操作 \(k\) 次的方案，有多少种本质不同的 操作集合 。操作集合是一个大小为 \(k\) 的集合，代表操作过的 \(k\) 种操作。（注意，顺序不同但操作集合相同的 \(2\) 种方案只会被计算 \(1\) 次）

称两个操作集合 \(A, B\) 本质不同，当且仅当存在某种操作 \(opt\)，满足 \([opt \in A] + [opt \in B] = 1\)。

现在给定 \(n,m\)，请你对于所有 \(1\le i\le n,\ 1\le j\le m\) 求出 \(f(i,j)\) 的取值，取模 \(998244353\)。

保证 \(1\le n,m\le 5000\)。

题解

注意到 \(k=n+m-1\)，最后一步是删掉一个 \(1\times 1\) 的矩阵。

建立行列二分图，对于操作 \((x,y)\)，如果第 \(y\) 行被删除则连边 \(x\to y\)，否则 \(y\to x\)，显然每个点只能有一个入度。

操作后我们会得到一个外向树。

容易发现所有外向树和操作集合构成双射，因此答案为 \(K_{n,m}\) 的有根生成树个数，这是一个经典结论，答案为 \((n+m)\times n^{m-1}\times m^{n-1}\)。

提交记录

P11056 Fire and Big 蓝（博弈论，打表）

题意

小 F 要和其他人玩游戏，但他不想输，所以来找你帮他研究策略。

有 \(m\) 个石子，小 F 和小 B 轮流取石子，小 F 先开始取，不能取的人输。

给定正整数 \(n\)，每次取石子的个数 \(k\)（\(k\) 是正整数） 必须满足如下两个条件之一：

• \(k\) 是 \(n\) 的倍数。
• \(k\) 是 \(<n\) 的完全平方数。

他们要玩 \(T\) 局游戏，不过每一局游戏的 \(n\) 不变，只有石子个数 \(m\) 会变。

对于每一局，假设两人足够聪明，问谁有必胜策略。

对于所有数据，保证 \(1\le T,n\le 5\times 10^5\)，\(1\le m\le 10^9\)。

题解

打个表发现后手必胜个数极少。

发现如果把模 \(n\) 相同的数看作一个等价类，每个类里面只能有一个后手必胜，这是显然的。

因此直接往后递推，遇到后手必败就更新后 \(\sqrt n\) 个状态，这样总状态数 \(O(n\sqrt n)\)，可以接受。

提交记录

[AGC002E] Candy Piles 紫（二维平面，博弈论）

题意

桌子上有 \(N\) 堆糖果。每堆糖果有 \(a_i\) 颗糖果。

Snuke 和 Ciel 正在玩游戏。他们轮流走。Snuke 先走。在每个回合中，当前玩家必须执行以下两个操作之一：

• 选择剩余糖果数量最多的一堆，然后吃掉那堆糖果中的所有糖果。
• 从仍有糖果剩余的每堆中吃一颗糖果。

吃了桌上最后一块糖的玩家输掉了比赛。确定如果两个玩家都以最佳方式玩游戏，哪个玩家会赢。

\(N\leq 10^5\)。

题解

将糖果从大到小排序，放到二维平面上考虑，在二维平面上有一个直方图，每次往上或往右，走到边界算输。

关键结论：在网格图上，不考虑边界问题的情况下，\((x,y)\) 和 \((x+1,y+1)\) 的胜负态一样。证明是简单的，反证法即可导出矛盾。

因此直接从 \((0,0)\) 走到最后一个不是边界的点，然后先手现在要么往右要么往上，之后操作方案唯一，判一下奇偶性即可。

提交记录

[AGC002F] Leftmost Ball 紫（计数）

题意

Snuke 喜欢彩色球。他共有 \(N\times K\) 个球，其中包含 \(N\) 种他最喜欢的颜色，每种颜色各有 \(K\) 个。颜色编号为 \(1\) 至 \(N\)。

他将所有球从左到右排成一行，顺序任意。然后，对于每种颜色，他会将该颜色最左侧的球重新涂为颜色 \(0\)（这是一种不同于原有 \(N\) 种颜色的新颜色）。

涂色完成后，球的颜色序列可能有多少种不同的排列方式？请将答案对 \(10^9+7\) 取模。

\(1\leq N,K\leq 2000\)。

题解

白球对其他球的限制是：任意后缀（或前缀）的白球个数大于等于颜色种类数。

只限制后缀也能保证正确性，因此从后往前 DP，并且需要把白球个数和颜色种类数计入状态。

具体地，我们钦定 \(i\) 第二次出现的位置小于 \(i+1\) 第二次出现的位置。

令 \(dp_{i,j}\) 表示填入了 \(i\sim n\) 的数字，填入了 \(j\) 个白球的方案数，每次钦定填入的第一个球在最前面以避免重复。

转移是简单的。

似乎也可以正着做。

提交记录

[AGC001F] Wide Swap 黑

题意

给定一个长度为 \(N\) 的数列 \(P_1\ldots P_N\)，该数列是 \(1\sim N\) 的一个排列。

你可以对该数列进行如下操作任意次：

• 选择整数 \(i, j\)，满足 \(1 \leq i < j \leq N\)。
• 交换 \(P_i\) 和 \(P_j\) 的值。
• 但必须满足 \(j - i \geq K\) 且 \(|P_i - P_j| = 1\)。

请你求出通过上述操作能够得到的字典序最小的数列。

\(2\leq N\leq 500000\)。

题解

下标差大于 \(K\) 且值相邻不好处理，这种情况可以考虑将排列转为逆排列，变为交换相邻且值相差超过 \(K\) 的值。

从前往后扫，再从后往前冒泡，即可做到 \(O(N^2)\)。

使用平衡树模拟冒泡过程，二分一个位置能冒泡到哪，可以做到单 \(\log\)，但是比较麻烦。

这个东西是冒泡排序形式，考虑使用高级排序算法进行优化。

首先冒泡的条件是 \(q_{i-1}\geq q_i+k\)，因为交换顺序对显然不优，使用归并排序，记录归并第一段的后缀 \(\min\) 即可判断是否可以进行归并。

另一个做法是按照值域连边然后拓扑排序，通过分析边之间的支配关系将边数缩小到 \(O(N)\)。

提交记录

P9818 游戏王 紫（knapsack 技巧）

题意

给出一个长为 \(n\) 的序列 \(\{S_n\}\)，其中 \(S_i\) 为多个二元组 \((s_{i,j},m_{i,j})\) 构成的可重集。有 \(q\) 次询问，每次给定 \(l,r\)，你需要从 \(S_l,S_{l+1},\cdots,S_r\) 的每个集合中分别选出 \(0\) 个或 \(1\) 个二元组。记选出的 \(k\) 个二元组为 \((s'_i,m'_i),1\le i\le k\)，则你需要在保证 \(\prod_{i=1}^km'_i\le v\) 的基础上，最大化 \(\sum_{i=1}^k s'_i\)。

对于所有数据，保证 \(1\le n,tot\le 10^5\)，\(1\le q\le 2\times 10^5\)，\(1\le m_{i,j}\le v\le 10^5\)，\(1\le s_{i,j}\le 10^4\)，\(1\le l\le r\le n\)。

题解

直接 DP 是不弱于背包的，无法优化。

Hint：对于乘积小于某个数的背包，可以整除分块做到 \(O(\sqrt V)\) 状态。

具体地，将 \(\frac{V}{\prod m}\) 计入状态，因为 \(\frac{\frac{x}{y}}{z}=\frac{x}{yz}\)，因此状态是可合并的。

前缀和优化后可以 \(O(\sqrt V)\) 的求出一个位置的值，用类似猫树的结构分治即可。

提交记录

NOIP 模拟 T3（计数，随机选数转排列，树上 DP）

题意

考虑这样的一个算法：

给定树 \(T\)，初始时图上所有节点均为白色，计数器 \(c = 0\)。不断进行下列操作直到 \(T\) 上不存在白色点：

• 从树上所有白色点中随机选择一个点 \(u\)，将 \(u\) 以及与其有边直接相连的所有白色点 \(v\) 全部染黑，并令 \(c \leftarrow c + 1\)。

最后返回 \(c\) 作为答案。

林尼想知道，对于给定的树 \(T\)，算法的正确率是多少，即有多大概率使得算法返回的答案确实为原图的最大独立集大小。

你只需要输出概率对 \(10 ^ 9 + 7\) 取模的结果。

记 \(n\) 为树的大小，\(n\leq 5000\)。

部分分：最大独立集唯一。

题解

首先按照经典套路，将白点选数改成随机一个排列，按排列选数，然后跳过不合法的选择。

这样最终方案和排列构成双射，至此我们完成了概率转计数。

考虑部分分，分析排列性质，首先考虑限制所有独立集的点都被选，但是发现这样不好限制。

考虑限制所有不在独立集的点都不被选，由于是独立集，所以这样限制也是充要的。

记排列的逆为 \(rk\)，独立集为 \(S\)。一个不是 \(S\) 的点 \(u\) 不被选，当且仅当存在一个邻域 \(v\)，\(rk_v<rk_u\)，且 \(v\in S\)，这样我们就得到了充要条件。

记 \(f_{u,i,0/1}\) 表示子树 \(u\) 内，离散化后的 \(rk_u=i\)，且如果 \(u\notin S\)，是否有 \(u\) 的儿子 \(v\)，满足 \(v\in S\land rk_v<rk_u\)。

转移时如果 \(u\in S\)，则直接合并 \(f_{v,x,1}\)，对于 \(f_{v,x,0}\)，我们需要做的问题如下：

• 合并两个数列，第一个序列的第 \(x\) 个位置在第二个序列的第 \(y\) 个位置前。

转移时进行树上背包：

\[f_{u,i+k,1}'=f_{u,i,1}\times f_{v,j,0}\times \binom{i+k-1}{k}\times \binom{sz_u-i+sz_v-k}{sz_u-i}(j> k) \]

如果 \(u\notin S\)，大致同理，当第三维由 \(0\) 变 \(1\) 时做上面的转移，只是把 \(>\) 改为 \(\leq\)。

可以前缀和优化做到 \(O(n^2)\)。

考虑正解。

类似 DP of DP，先使用最大独立集 DP（\(g_{u,0/1}\) 表示 \(u\) 子树 \(u\) 是否选择）建立出最优转移 DAG，然后在 \(f\) 后加一维表示 \(u\) 是否属于 \(S\)，只进行 DAG 上边的转移即可。

我们无需显式建立 DAG，只需要在往上做独立集 DP 时只转移最优情况即可。

NOIP 模拟 T4（构造，杨表）

题意

给定一个数 \(n \geq 3\)，你需要构造一颗树，其中每个点有正整数点权，满足：

• 对于任意一个 \(k \in [1,n]\)，满足存在一条点数 \(> 1\) 的链，使得链上点的 \(\gcd = k\)。

由于一些原因，你希望树的点数与权值尽可能小。具体来说，每个点有一个限制 \(X,Y\)，你需要保证你构造的树的点数 \(\leq X\)，且你构造的树的点权 \(\max \leq Y\)，你通过这个点。

\(n\leq 2500,X=n,Y=11000\)。

部分分：\(X=\frac{3n}{2}\)。

题解

考虑部分分，先构造一个 \(2n\) 个点的方案，然后把互成倍数的点合并到一条链上。

现在我们只用到了 \(2\)，考虑继续用 \(3\)。我们引入一个科技：

• 有一个表格叫做杨表，其中 \((x,y)\) 位置的值时 \(2^x\times 3^y\times a\)，\(a\) 是与 \(6\) 互质的任意数。

这个表格的性质是任意一条链的 \(\gcd\) 是其横纵坐标 \(\min\) 所对应的点，因此我们枚举 \(a\) 建立杨表，把杨表中大于 \(n\) 的数所围成的路径连接起来，构成一条链，就实现了 \(X=n+w\)，\(w\) 是极小的常数（这个是暴力验证的）

然后开始发癫，把两个大于 \(\frac{n}{2}\) 的值单独处理，不使用杨表，对于两个大于 \(\frac{n}{2}\) 且与 \(6\) 互质的数 \(x,y\)，构造 \(x-\text{lcm}(x,y)-y\) 的链，即可省去一个点，可以通过。

事实上只需要配对一组 \(x,y\) 就能过了，😓。

P7013 [CERC2013] History course 黑（数据结构优化贪心，Hall 定理，单调性）

题意

你需要按某种顺序为一系列重要历史事件安排讲座，每个讲座对应一个事件。每个事件持续一段时间区间 \([a_i, b_i]\)。如果两个事件的时间区间有公共点，则称这两个事件是相关的。为了方便起见，安排相关事件的讲座时应尽量靠近。此外，对于不相关的事件，讲座应按照事件发生的顺序进行（如果事件 A 先于不相关事件 \(B\) 发生，那么 A 的讲座应先于 B 的讲座）。找到最小的整数 \(k \ge 0\) 和一个讲座顺序，使得任何两个相关事件的讲座之间的间隔最多为 \(k\)（讲座编号 \(i\) 和 \(j\) 之间的间隔被认为是 \(|i−j|\)）。

\(n\leq 50000\)。

题解

先二分答案，然后尝试构造。

一个 \(k=mid\) 的方案的合法判据是，对于任意区间 \(i\)，若 \(i\) 填入第 \(j\) 个位置，与其相交的区间填入位置 \(\leq j+mid\)。

我们不好处理相交，但是题目有一个神秘要求：相离的区间 \(l\) 小的排前面。我们发现这个限制对答案没有任何影响，但是可以给我们一些提示。

具体地，我们考虑弱化相交条件，将 \(l'<r\land r'>l\) 弱化为 \(l'<r\)，这样由于题目的神秘要求，判据仍然成立。

做到这，大致思路就出来了，按 \(r\) 贪心从小到大填入，同时维护每个区间的最大位置。

具体地，令 \(f_i\) 表示第 \(i\) 个区间的最大位置，初始时 \(f_i=n\)。按照课程顺序填入区间，填入第 \(i\) 个区间 \([l,r]\) 时将与其相交的区间的 \(f\) 对 \(i+mid\) 取 \(\min\)。

这是我们注意到：将区间按 \(l\) 排序后，\(f\) 为前缀 \(chkmin\)，且由于 \(i+mid\) 递增，每个 \(f\) 只会被 \(chkmin\) 一次，十分优美。

当然区间不能随便填，显然我们的 \(f\) 限制对当前局面是必要的，当我们不知道限制的时候，先考虑对于一个 \(f\) 如何判无解。

一个显然的思路是，将 \(i\) 与 \(1\sim f_i\) 连边，转为二分图最大匹配，之后用 Hall 定理作为判据。

具体地，令 \(s_i=\sum\limits_{x} [f_x=i]\)，并且规定已经填入的区间的 \(f\) 值为 \(0\)。

记 \(use(l,r)\) 表示当前位置 \([l,r]\) 中已经有区间占用的位置个数。如果存在 \([l,r]\) 满足 \(\sum\limits_{i=l}^{r} s_i< r-l+1-use(l,r)\)，则无解，我们需要在贪心时尽可能避免这种情况。

记 \(c(l,r)=r-l+1-use(l,r)-\sum\limits_{j=l}^{r} s_j\)。

具体地，利用增量构造的思想，假设无解判据中 \(l=1\sim i\) 的情况已经满足，且我们在填入 \(i\) 时只能避免上述无解判据中 \(l=i+1\) 的情况，且对于任意 \(r\)，我们有能力保持 \(c(i,r)\) 不变。构造方式是选一个 \(f\in [i,r]\) 的区间填入当前位置。

因此我们声称，只有存在一个 \(r\) 满足 \(c(i,r)=0\) 时我们才需要对操作进行限制，要不然我们完全不用着急，只需要等待其变为 \(0\) 后让其保持即可。

具体地，我们找出最小的 \(r\) 满足 \(c(i,r)=0\)，然后在 \(f\in [i,r]\) 的点中找到 \(r\) 最小的填入当前位置。

进一步把 \(f\in [i,r]\) 改为 \(f\leq r\)，因为填到 \(i\) 时必有 \(f_x\geq i\ \ (x\geq i)\)，否则不符合“最后位置”的定义。

由于 \(i+mid\) 递增，每个 \(f\) 只会被 \(chkmin\) 一次，因此我们可以双指针维护 \(f\)，并实时维护 \(s\)，并且在线段树上的一个原区间 \([l,r]\) 维护 \(c(l,r)\) 和 \(\min_{l\leq i\leq r} c(l,i)\)，这一部分是容易的。

我们再维护一颗线段树维护一个区间内 \(r\) 最小的区间编号。

我们二分出最前的 \(r\) 满足 \(c(i,r)=0\)，然后在 \(f\leq r\) 的区间中找到 \(r\) 最小的区间填入，最后更新 \(f\) 和维护 \(cost\) 的线段树。

我们额外维护 \(g_i\) 表示 \(\max\limits_{x} f_x=i\)，以实现 \(f\) 值域和区间编号的转化。

提交记录

P8147 [JRKSJ R4] Salieri 黑（ACAM，树上差分，虚树）

题意

给出 \(n\) 个字符串 \(s_i\)，每个字符串有一个权值 \(v_i\)。\(m\) 次询问每次给出一个字符串 \(S\) 和一个常数 \(k\)。设 \(cnt_i\) 为 \(s_i\) 在 \(S\) 中的出现次数，求 \(cnt_i\times v_i\) 第 \(k\) 大的值。

对于 \(100\%\) 的数据，\(1\le n,m\le10^5\)，\(\sum |S|,\sum s_i\leq 5\times10^5\)。

\(s\) 和 \(S\) 中只会出现 \(\texttt a,\texttt b,\texttt c,\texttt d\) 四种字符，\(v_i\le10^3\)，\(k\le n\)。

题解

死因：认为 \(s_i\) 的每个位置在 ACAM 上都有贡献。

该复习一下 ACAM 了。

多模匹配，有两种思路：ACAM 和 SA(M)。

考虑 SA，可以将问题转化为：

• 给定一个长为 \(O(L)\) 的序列，每个位置有一个值和一个颜色，颜色范围为 \([1,n]\)，多次询问一个区间 \([l,r]\)，记 \(sum_x\) 表示区间内颜色为 \(x\) 的位置的值的和，求 \(sum\) 序列的第 \(k\) 大。

这个东西的信息量是平方的，问了 GPT 得知复杂度下界为 \(O(n^{1+\epsilon})\)，所以这个做法似了。

Hint：通过 ACAM 将一个字符串转为只有一个点有贡献，可以解决很多棘手的多模匹配问题。

考虑 ACAM，如果用 \(S\) 建立 ACAM，会转化为和上述问题类似的问题，这里不再赘述。

用 \(s_i\) 建立 ACAM，记 \(p_i\) 表示 \(s_i\) 的结束位置，把 \(S\) 在 ACAM 上跑一遍得到点集 \(T\)，\(s_i\) 在 \(S\) 中出现，当且仅当存在 \(x\in T\)，\(x\in \text{subtree}(p_i)\)。这样，每个 \(s_i\) 提供的有用位置恰好是 \(1\) 个，比上面的问题优美很多，而且信息量是对的。

对 fail 树树剖，对 \(T\) 上每个点实现到根链加，可以将问题转化为：

• 维护一个序列，每个位置有一个值 \(v_i\) 和一个值 \(t_i\)，实现区间 \(t_i\) 加，全局求 \(v_i\times t_i\) 的第 \(k\) 大，询问在查询后。

先二分答案，转化问求 \(v_i\times t_i\geq mid\) 的位置个数，由于区间加一共 \(O(|S|\log S)\) 次，因此不同的 \(t\) 一共 \(O(|S|\log S)\) 个，之后对一段相同的 \(t\)，用主席树查 \(v_i\geq \lceil \frac{mid}{t} \rceil\) 的个数即可，维护到根连主席树，每次二分有 \(O(|S|\log S)\) 次主席树查询，一共三 \(\log\)，无法通过。

你发现你学树剖学傻了，重新分析 \(T\) 的到根连加法，发现 \(T\) 的点构成一颗虚树，虚树上只有 \(O(|S|)\) 条边，于是复杂度双 \(\log\)，因为 \(v\leq 10^3\)，不用担心主席树常数和空间问题，做完了。

提交记录

P13559 【MX-X15-T6】翻树树 蓝（构造）

题意

小 G 有一棵 \(n\) 个节点的树，节点的编号为 \(1 \sim n\)。每个节点的颜色可以是黑或者白，初始所有节点都为白色。

小 G 和小 C 还各有一个集合，分别称作 \(S\) 和 \(T\)。\(S\) 为所有节点的度数组成的集合，而初始时 \(T = \varnothing\)。

小 C 可以进行若干次操作。在每次操作中，他可以翻转树上的一个节点的颜色（黑变白、白变黑）。随后，他会计算 \(k\) 为树中两端点不同色的边数，然后将 \(k\) 插入至集合 \(T\) 中。

小 G 指定了一个整数 \(m\)，满足 \(m \geq 2\lceil\sqrt{n}\rceil\)。如果小 C 使用了超过 \(m\) 次操作，小 G 就会生气。小 C 被要求在小 G 不生气的情况下让 \(T \supseteq S\)，可他并不会解决这个问题。你能帮他构造一组方案吗？

题解

Hint：叶子个数 \(\geq\) 节点度数最大值。

考虑暴力，最多有 \(\sqrt {2n}\) 个不同的度数，每个度数找一个点翻两次，次数为 \(2\sqrt {2n}\)。

考虑更多的暴力，把所有叶子翻一次，次数为 \(\max\limits_{1\leq i\leq n} deg_i\)

考虑使用翻转叶子来平衡，具体地，设定阈值 \(B\)，度数大于 \(B\) 的点翻两次，再翻 \(B\) 个叶子。

证明：

能使得操作次数最大的 \(S=\{1,3,5,\dots B-1,B,B+2,B+4,\dots,B+2k\}\)，这样保证 \(B\) 是最优的，解 \(\sum_{i\in S} (i-1)\leq n-2\)（\(n-2\) 是因为至少有两个叶子，去重后和只会变小），得到 \(B+2k\) 的最大值 \(\leq 2\lceil\sqrt{n}\rceil\)。

提交记录

CF1466H Finding satisfactory solutions *3300

题意

有 \(n\) 个人，第 \(i\) 个人初始的时候手上有物品 \(i\)。

他们之间可以交换物品，每个人恰好拿到一个物品。而每个人有对物品的偏好，第 \(i\) 个人的偏好用排列 \(\{s_{i,n}\}\) 来表示。第 \(i\) 个人相较物品 \(y\) 更喜欢物品 \(x\)，当且仅当在排列 \(\{s_{i,n}\}\) 中 \(x\) 在 \(y\) 之前。

对于一个物品交换的排列 \(p\)，表示第 \(i\) 个物品最后到了 \(p_i\) 的手上。对于一个非空的，人的子集 \(S\)，如果子集内部的人，使用子集内所有人初始手上的物品进行交换，可以达到以下结果：

1. 不存在一个人 \(x \in S\)，在子集内交换后得到物品 \(y \in S\)，且第 \(x\) 个人比起 \(y\) 更喜欢 \(p_x\)。

2. 至少存在一个人 \(x \in S\)，在子集内交换后得到物品 \(y \in S\)，且第 \(x\) 个人比起 \(p_x\) 更喜欢 \(y\)。

则称这样一个子集 \(S\) 是“不稳定”的。一个物品交换的排列 \(p\) 是“稳定”的，当且仅当不存在一个“不稳定”的子集。

现给出一个物品交换的排列 \(p\)，求有多少种 \(\{\{s_{1,n}\},\{s_{2,n}\}\cdots,\{s_{n,n}\}\}\) 使得 \(p\) 是“稳定的”。

可以证明，对于一组 \(\{\{s_{1,n}\},\{s_{2,n}\}\cdots,\{s_{n,n}\}\}\)，恰好存在一个 \(p\) 是“稳定”的。

\(1 \leq n \leq 40\)。

题解

一开始读题读成选出的集合必须封闭，白做了 1.5h。

考虑题目给出的判据。

• 使用子集内所有人初始手上的物品进行交换，说明交换后的集合是一个若干个置换环的并。
• 不存在一个人 \(x \in S\)，在子集内交换后得到物品 \(y \in S\)，且第 \(x\) 个人比起 \(y\) 更喜欢 \(p_x\)。至少存在一个人 \(x \in S\)，在子集内交换后得到物品 \(y \in S\)，且第 \(x\) 个人比起 \(p_x\) 更喜欢 \(y\)。以某种方式重排置换环后，不会存在每个人都不劣的情况。

题目说：可以证明，对于一组 \(\{\{s_{1,n}\},\{s_{2,n}\}\cdots,\{s_{n,n}\}\}\)，恰好存在一个 \(p\) 是“稳定”的，我们尝试证明这一点。

考虑模拟题目的调整法，先令 \(i\to s_{i,1}\)，然后调整。

此时，置换图是一个基环内向树森林，对于一个环，如果令 \(S\) 为这个环上的点，则这些点只有一种方案，即当前的最优方案，因此这个环已经确定。

将环删去，剩余点如果指向环，则把边指向 \(s_{i,2}\)，然后递归下去即可。

这样我们每一步都是固定且最优的，连环一起被删除的边就是最终的 \(p\)，证毕

考虑被删除的边满足的性质，若 \(j\) 在 \(\{s_i\}\) 中排名比 \(p_i\) 靠前，则必有 \(i\to p_i\) 被删除。

分析被删除的边的性质，显然被删除的边不能成环，具体地：

连白色边 \(i\to p_i\)，连黑色边 \(i\to j\ \ (rk(s_i)_j<rk(s_i)_{p_i})\)，则每个环中不能有黑边。

必要性显然，充分性可以通过构造 \(p\) 的方法证明，只要黑边都不在环内则黑边必定被删。

感性理解就是选择红色集合重排。

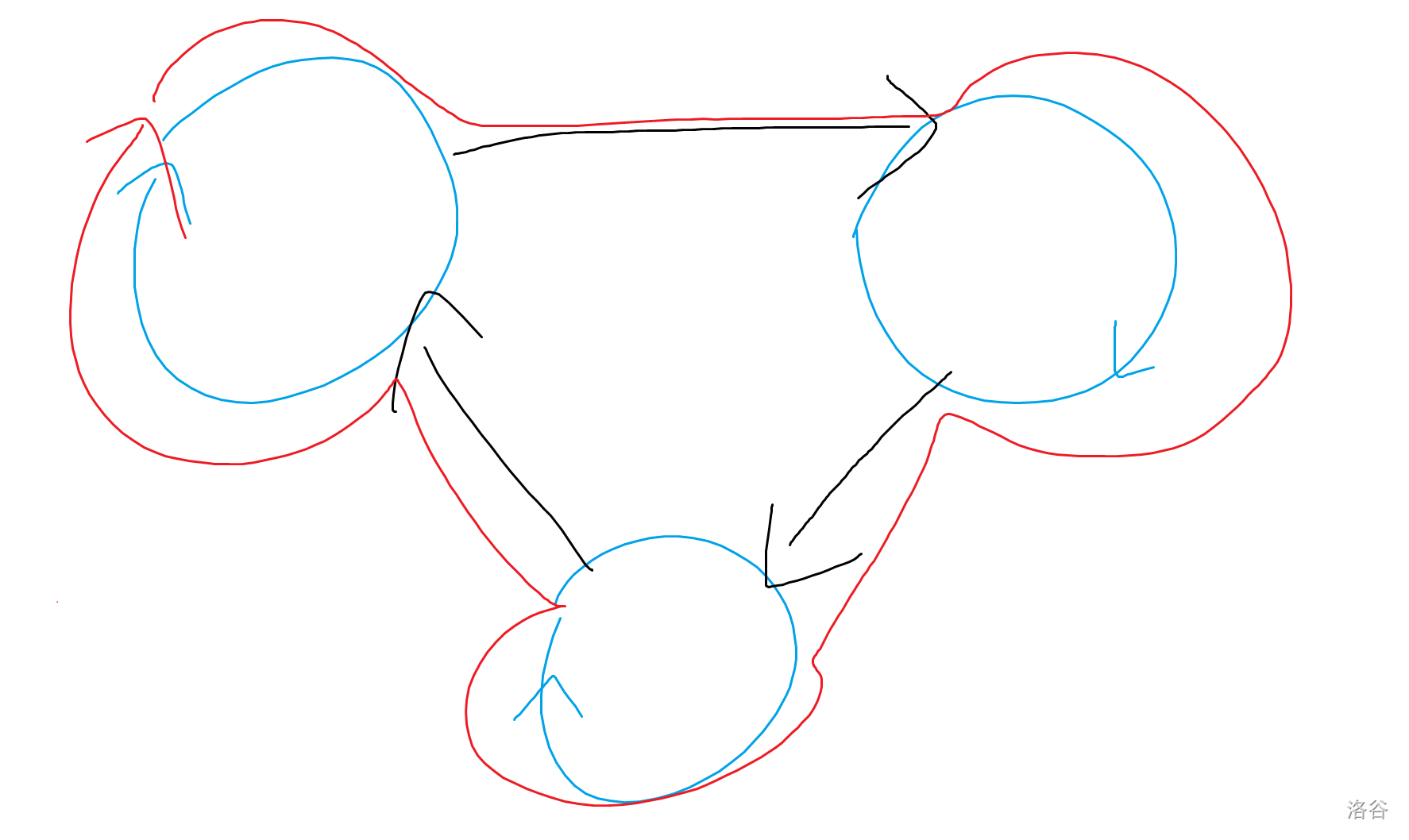
将置换环缩点，黑边连成若干个 DAG，考虑 DAG DP。

先考虑对于一个 DAG 如何统计答案。

我们并不关心黑边的顺序，如果 \(i\) 连出了 \(deg_i\) 条黑边，则对答案的贡献就是 \((deg_i)!(n-deg_i-1)!\)。

令 \(dp_S\) 表示集合 \(S\) 连成 DAG 的答案，\(E(X,Y)\) 表示集合 \(X\) 向集合 \(Y\) 的所有边方式的答案之和，则有：

\[dp_S=\sum_{T\subsetneq S} dp_T\times E(S-T,T)\times (-1)^{|S-T|-1} \]

DAG 计数只能指数级 DP，这个 DP 没有任何优化前途，但是由于我们对置换环缩点，因此这个 DP 的状态数看起来不多。

现在我们需要求 \(E(X,Y)\)，从对答案贡献来看，每个点是独立的，即 \(E(X,Y)=E(\{x\},Y)^{|X|}\ \ (x\notin Y)\)。

单点连向 \(Y\) 的贡献，可以枚举这个点的 \(deg\)，即 \(\sum\limits_{i=0}^{|Y|} \binom{|Y|}{i}i!(n-i-1)!\)。记其为 \(g(|Y|)\)。

受求 \(E(X,Y)\) 过程的启发，我们不关心点的编号，只关心环的大小。将 DP 状态 \(S\) 改为每个大小的环出现了几次，爆搜总状态数，发现最多只有 \(1440\) 种状态，状态的平方都是可接受的，无需任何优化。

则：

\[dp_S=\sum_{in(T,S)} dp_T\times X(S,T)\times g(sz_T)^{sz_S-sz_T}\times (-1)^{loop_S-loop_T-1} \]

其中，\(sz_S\) 表示 \(S\) 中原图上的点数，\(loop_S\) 表示 \(S\) 中缩点后的点数，即置换环数。\(in(T,S)\) 表示 \(S\) 包含 \(T\)，\(X(S,T)\) 表示从 \(S\) 中选出状态为 \(T\) 的子集的方案数。

提交记录

CF1770F Koxia and Sequence *3100（观察性质，容斥，Lucas 定理，范德蒙德卷积，拆位技巧）

题意

Mari 有三个整数 \(n\)、\(x\) 和 \(y\)。

如果一个长度为 \(n\) 的非负整数数组 \(a\) 满足以下条件，则称其为“好数组”：

• \(a_1 + a_2 + \ldots + a_n = x\)；
• \(a_1 \mid a_2 \mid \ldots \mid a_n = y\)。

一个好数组的得分定义为 \(a_1 \oplus a_2 \oplus \ldots \oplus a_n\)。

Koxia 想让你求出所有好数组得分的总异或值。

题解

看到这道题首先思考题目限制条件，\(y\) 的第 \(i\) 位为 \(0\) 表示不用填入数字，为 \(1\) 表示要填入一个数字。

题目还要求和为 \(n\)，有两个思路，一个是对按位或为 \(y\) 容斥，一个是数位 DP。

感觉容斥不好做，考虑数位 DP，按位分配，令 \(f_{i,j}\) 表示只考虑低 \(i\) 位，向 \(i+1\) 位进位为 \(j\) 的所有数组异或和，\(g\) 表示方案数，有转移

\[f_{i+1,\frac{j+x}{2}}\leftarrow f_{i,j}+ (g_{i,j}\times x\times \binom{n}{x}\bmod 2) \]

复杂度 \(O(y^2\log n)\)，不可接受。

根据 Lucas 定理有：

\[f_{i+1,\frac{j+x}{2}}\leftarrow f_{i,j}\times [x\bmod 2=1\land x\subseteq n\land g_{i,j}\bmod 2=1] \]

感觉还是没法优化呜呜。

看题解，怎么真是容斥，怎么第一步就错了/ll。

---

每个位置是独立的，因此对于每个位置，其等于任意值的情况都相等，因此 \(n\) 是偶数时答案为 \(0\)，\(n\) 是奇数时答案为所有序列 \(a_1\) 的异或和。

需要意识到：

• 要直接处理和为 \(n\) 且异或和为 \(y\) 必须数位 DP。
• 数位 DP 复杂度至少 \(O(y^2)\)。

我们不能直接维护两个信息，考虑对异或和为 \(y\) 容斥。

记 \(ans(y')\) 表示钦定 \(\forall_{i} ,a_i\subseteq y'\) 的答案，子集反演，此时容斥系数要么为 \(1\) 要么为 \(-1\)，对异或和都有贡献。

因此答案直接异或起来就是对的，为

\[\bigoplus\limits_{y'\subseteq y} ans(y') \]

拆位求 \(a_1\)，规定 \(a\) 的某一位必选并提前去掉这一位，\(a_1\) 的第 \(i\) 为贡献为：

\[\bigoplus_{\sum a=x-2^i}[a_1\subseteq y'-2^i][a_2\subseteq y']\dots[a_n\subseteq y'] \]

根据上面数位 DP 用到的 Lucas 定理，我们知道 \([x\subseteq y]=\binom{y}{x}\bmod 2\)。

上式的 \(\sum a\) 固定，如果逆用 Lucas 定理，可以套用范德蒙德卷积公式。

\[\bigoplus_{\sum a=x-2^i}[a_1\subseteq y'-2^i][a_2\subseteq y']\dots[a_n\subseteq y'] \\ =\left (\sum_{\sum a=x-2^i}\binom{y'-2^i}{a_1}\binom{y'}{a_2}\dots\binom{y'}{a_n}\right ) \bmod 2 \\ =\binom{ny'-2^i}{x-2^i}\bmod 2 \\ =[x-2^i\subseteq ny'-2^i] \]

枚举 \(i,y'\)，时间复杂度 \(O(y\log y)\)。

提交记录

P3665 [USACO17OPEN] Switch Grass P 紫（MST）

题意

给定一张图，每个点有一个颜色，实现数据结构维护：

• 颜色单点修改。
• 全局查询异色边边权最小值。

题解

根号分治是没有前途的。

Hint：如果 \(a\) 和 \(b\) 颜色不同，则中间必有一条边是异色边，选边权最小的异色边贡献到答案。

所以异色边的支配关系满足最小瓶颈路的支配关系，只需保留在 MST 上的 \(n-1\) 条边，然后就随便做了。

这道题启示我们可以使用 MST 很好的刻画边的支配关系。

（不小心把 mid>=pos 打成 mid>=l 了，我是奶龙。

提交记录

有另一个优美的做法，建立 Kruskal 重构树，对于一个虚点，当以下条件满足时，他可能成为答案：

• 两侧子树内颜色相同
• 两侧子树间颜色不同

且不满足第一个条件不会让答案边优。

因此子树内任何一个点的颜色都能代表整个子树，把 Kruskal 重构树建为链，具体地，在连边时将链头和链尾连接，链上找边权最小的异色边即可。

暴力维护的复杂度就是对的。

P13004 [GCJ 2022 Finals] Schrödinger and Pavlov 紫（计数转期望，模拟）

题意

给定 \(n\) 个节点，已知每个节点上的状态是「确定有猫」「确定没有猫」「不确定是否有猫」三种状态之一。

对于节点 \(i\)，它唯一的一条出边为 \(i \to a_i (i \neq a_i)\)。

现在遍历节点 \(i = 1, 2, \cdots, n\)，若节点 \(i\) 有猫，且节点 \(a_i\) 无猫，则位于节点 \(i\) 的猫移动到节点 \(a_i\)。同一只猫在整个过程中可能会多次移动。

设初始有 \(k\) 个位置的状态为「不确定是否有猫」，则对于所有节点，有 \(2^k\) 种可能的初始猫分布的状态。

求遍历完后，节点 \(n\) 有猫的可能初始状态数量。对 \(10^9 + 7\) 取模。

\(1 \leq a_i \leq n \leq 5000\)，多测，\(\sum n\leq 6170000\)。

题解

第一反应是考虑基环树上 DP，发现根本做不了。

考虑计数转期望，令 \(f_i\) 表示 \(i\) 有猫的概率，直接按题意模拟过程。

当然，这是错的，因为有环，环上点概率不独立，无法相乘。

因为这是基环树，有两种处理方法：

• 断一条边。
• 环上 DP。

无论如何都需要规定一个起始点。

考虑枚举第一步，断开环上编号最小的点的出边 \(x\to a_x\)，枚举 \(x,a_x\in \{0,1\}\) 四种状态，就做完了。

断开最小的点的出边是因为，先执行第一步后剩余的图构成 DAG，对于未转移到的点，点之间概率是独立的。

还有一个更“符合直觉”的想法是断开编号最小的入边，但是这样是没有任何道理的，因为模拟到最后边的两侧不独立且无法被直接规定为有猫/无猫。

简单来说，每次执行操作 \(i\) 时，需要保证要么 \(a_i\) 这个点状态完全确定，要么 \(a_i\) 这个点状态完全不确定（即概率为 \(\frac{1}{2}\)）。

具体地，在模拟到 \(x\) 时，乘上 \(x\) 和 \(a_x\) 处于被规定状态的概率，并将 \(x,a_x\) 修改为我们规定的状态。

注意我们规定的是执行 \(x\) 时的状态，因此规定 \(x\) 有猫并不代表它在初始状态可能有猫。

复杂度 \(O(Tn)\)。

这道题启示我们：

• 概率 DP 时破环成链也是正确的，即转移成环时可以枚举第一步的状态。
• 在转移构成一条链的概率 DP 中可以任意选择一个 DP 状态并固定其值为 \(p\)，并对最后算出的结果乘上它值为 \(p\) 的概率计入答案。

提交记录

NOIP 模拟 T1 （Ad-hoc，构造）

题意

小 M 马上要闯一个传送阵，这个传送阵由 \(K+1\) 排房间组成，每排有 \(N\) 个房间。第 \(i(i \le K)\) 排房间与第 \(i+1\) 排房间间有传送门连接，其中对于 \(\forall i \le K\) 都存在一个长为 \(N\) 的排列 \(P_i\) 满足第 \(i\) 行第 \(j\) 个房间与第 \(i+1\) 行第 \(P_{i,j}\) 个房间间有传送阵连接，在闯关过程中可以将排列 \(P_i\) 变为 \({P_i}^{-1}\)，也就是让第 \(i\) 行第 \(P_{i,j}\) 个房间与第 \(i+1\) 行第 \(j\) 个房间连接。

小 M 初始在第 \(1\) 行的某个房间，每次只能向编号更大的行走，一直要走到第 \(K+1\) 行的某个房间。

现在你并不知道他初始会在哪个房间，目标在哪个房间，请你设计这 \(K\) 个排列，使无论初始在哪个房间，目标在个房间，小 M 都可能完成闯关。

题解

倍增 shift，发现只能过 \(n\) 是奇数，因为 \(n\) 是偶数奇偶性不对。

考虑分治，难点在于合并区间，合并条件是每一个点既能到这一侧又能到另一侧。

Hint：遇到这种问题，尝试考虑特殊情况和小情况，用小数据情况拼成大数据情况。

每次从两边各拿出两个点，发现这四个点可以合并。

边界情况是每次从两边各拿出三个点，此时一个排列做不到，新加一个排列即可。

选三个点的情况是两个 \(n=6\) 的排列，可以暴搜也可以手搓，手搓方法是第一个排列满足 \(4\) 个点，第二个排列满足 \(4\) 个点，保证每个点被满足至少一次。

NOIP 模拟 T2（位运算）

题意

给定一个正整数 \(k\) 和一个长为 \(n\) 的数组 \(\left \{ a \right \}\)，保证对于 \(\forall 1 \le i \le n\)，都有 \(0 \leq a_i < 2^{k}\)，且对于 \(\forall 1 \le i < n\)，都有 \(a_i \le a_{i+1}\)。

定义如下函数：

\[c(n,x) = \max\limits _{i=0}^{x} (n \oplus i) \\ f(n,x) = \max\limits _{i=1}^{n} c(a_i,x) \\ g(n,x) = \sum\limits _{i=1}^{n} \left [ c(a_i,x)=f(n,x) \right ] \]

你需要求出 \(\sum \limits _{x=0}^{2^{k}-1} f(n,x)\) 和 \(\sum \limits _{x=0}^{2^{k}-1} g(n,x)\) 的值，答案对 \(2^{64}\) 取模。

题解

首先放 Trie 树上模拟一下即可发现只有 \(a_n\) 能取到最大值。

所以第一问直接令 \(x \oplus a_n=2^k-1\)。

考虑按位递推，令 \(f_i\) 表示只考虑 \(a_n\) 低 \(i\) 位的值，容易得到递推式。

考虑求 \(\sum g\)。

显然，如果 \(a_i\) 能取到最大值，则比 \(a_i\) 大的数字也能取到最大值。

设当前最大值为 \(ans\)，则 \(x\oplus a_i=ans\)，由前缀最大性质，易证 \(x\subseteq ans\)，则若要使 \(a_i\) 最小，必有 \(a_i=ans\oplus x\)。

枚举 \(x\) 从高到低第一个和 \(a_n\) 相同的位置。

如果这个位置的值是 \(0\)，无法确定 \(ans\)，我们把问题缩小到了子问题，但是贡献计算涉及到值平移，因此我们似乎啥也没干。

如果这一位是 \(1\)，则 \(ans\) 的后若干位都是 \(1\) 很好做。

因此我们打破套路，枚举第一位相同且为 \(1\) 的位置。

对于前面的位置，\(a_n\) 这一位为 \(0\) 时 \(x\) 任意，\(a_n\) 这一位为 \(1\) 时 \(x\) 这一位为 \(0\)，否则与“第一个相同且为 \(1\) 的位置”矛盾，记前面位置的方案数为 \(2^{cnt0}\)。

则 \(ans\) 低位取全 \(1\)，\(x\) 低位任取，根据异或的经典双射结论，\(ans\oplus x=000\dots 000\sim 011\dots 111\) 。

则令 \(l=\min ans\oplus x,r=\max ans\oplus x\)，贡献为 \(2^{cnt0}\times \sum\limits_{i=l}^{r} \sum\limits_{j}[a_j\geq i]\)，随便拆一下贡献就行了。

要处理 \(a_n\) 和 \(x\) 每一位都不同的情况，这种情况很好处理。

NOIP 模拟 T3（多项式奇偶分离，（多项式）状压 DP）

题意

给定一个所有系数都 \(\in \{0,1\}\) 的 \(n-1\) 次多项式 \(P\)，求 \(P^{k}\) 中有多少项的系数为奇数。

\(n\leq 20\)，\(k\leq 10^{16}\)。

题解

考虑快速幂，有两个方向：

• 计算 \(f^{2^k}\)，卷积。
• 通过 \(f^{i}\) 递推到 \(f^{2i}\) 和 \(f^{2i+1}\)。

第一个方向的卷积不保证项数，倒闭。

考虑第二个方向，根据模二性质，有：

\[f^{2i} (x)=f^{i}(x^2) \\ f^{2i+1} (x)=f^{i}(x^2)f(x) \]

考虑 DP，我们无法处理第二个式子后面的 \(f(x)\)。

正常 DP 思路，把不能处理的东西记到状态里，记 \(dp_{i,g}\) 表示 \(k\) 的高 \(i\) 位的 \(f^{?}(x)\) 乘上 \(g(x)\) 的 \(\text{popcnt}\)，\(g\) 是一个多项式（额好像记多项式为状态不是很正常，但确实能做）。

推式子。

\[f^{2i}(x)g(x)=f^{i}(x^2)g(x) \]

由于是 \(popcnt\)，\(f(x^2)\) 与 \(f(x)\) 等价，考虑将 \(g\) 奇偶分离，将式子写成 \(f(x^2)\) 的形式。

\[f^{2i}(x)g(x)=f^{i}(x^2)g(x)=f^{i}(x^2)[F(x^2)+xG(x^2)]\equiv f^{i}(x)F(x)+xf^{i}(x)G(x) \]

奇偶项相加互不干扰，即 \(dp_{i,g}\leftarrow dp_{i-1,F}+dp_{i-1,G}\)，其中 \(F,G\) 是 \(g\) 奇偶分离后的两个多项式。

\(f^{2i+1}\) 同理，每次奇偶拆分会将项数除以二，因此 \(g\) 的项数不超过 \(n\)，状压存 \(g\) 即可。

需要预处理所有 \(g\) 所拆成的 \(F\) 和 \(G\)。

提交记录（qoj原题）。

NOIP 模拟 T4（树剖处理树上邻域）

题意

给定一棵 \(n\) 个节点的无根树，边有边权，定义两点的距离为两点之间路径上的边权和。

初始树上有若干关键点，每个关键点 \(p_i\) 有安全系数 \(k_i\) 代表其 \(k_{i}\) 邻域内的点为安全点。即对于 \(\forall dis(u,p_i)\le k_i\)，\(u\) 为安全点。

令 \(m\) 为当前最大关键点编号，给出 \(q\) 次操作，每次操作根据 \(opt\) 分为三种：

• \(opt=1\)，令 \(m\) 为 \(m+1\)，加入一个新的关键点在点 \(p_m\) 处，其安全系数为 \(k_m\)。
• \(opt=2\)，删除编号为 \(x_i\) 的关键点，数据保证关键点 \(x_i\) 存在。
• \(opt=3\)，询问 \(u_i,v_i\) 两点间路径是否都是安全点。

\(n\leq 500000\)，4s，512MB。

题解

可能有点分树做法但我不会。

暴力：将每个关键点赋值 \(-k_i\)，跑 dij，安全点即 \(dis\leq 0\) 的点。

考虑维护每个点的 \(a=-dis\) 值，表示第 \(i\) 个点还能往外扩 \(a_i\) 个单位长度。

考虑树剖，修改时暴力在每个链上做性质 A。查询单 \(\log\)，修改复杂度爆炸。

当然我们不需要 \(a\) 的全部信息，我们只需要修改垂直于这个重链的位置的 \(a\)，然后在查询时查 \(\max_{i\in \text{chain}} \{a_i-|dep_i-dep_u|\}\)。

换一种思路，修改在当前重链上做性质 A，查询枚举重链，查询复杂度爆炸。

考虑平衡，设修改点为 \(u\)，查询点为 \(v\)，对于 \(u\) 扩展到 \(v\) 的过程，有 \(\text{path}(u,v)=\text{path}(u,\text{lca}(u,v))+\text{path}(\text{lca}(u,v),v)\)。

考虑一半查询管一半修改管，具体地，每次对 \(u\) 到根连的重链做性质 B，在垂直点 \(x\) 打上 \(k-(dep_x-dep_u)\) 的标记，查询时查 \(v\) 的到根连上的重链。

每个重链开一个线段树，拆绝对值维护 \(\max_{i\in \text{chain}} \{a_i-|dep_i-dep_u|\}\) 即可。

具体地每个点维护一个 set 表示当前这个点的 \(a\) 的标记，更新标记时从 set 中查最大值更新线段树。

查询路径时对每个重链找到这条链最下面一个【没有被经过当前重链上的修改覆盖的点】进行检验即可，因为此时没有被覆盖的点只能被上面的点覆盖，所以选最下面一个点是最紧的。

所以还要开一颗线段树维护操作到根连对途径重链的覆盖情况。

三 \(\log\)，但是能过。

NOIP 模拟 T2（最短路）

题意

isj2OO9 是著名的网络探险家，负责在复杂的数字城市网络中导航。这个网络由 \(n\) 个节点和 \(m\) 条有向边组成。每条边 \(i\) 都有特定的通行成本 \(w_i\)，且 \(w_i\) 为非负值。

最近，网络中出现了一些新的安全协议：对于第 \(i\) 条边，存在 \(k_i\) 条边 \(t_{i,1\sim k_i}\)，不能在经过这些边后立刻走第 \(i\) 条边。

isj2OO9 的任务是从起点节点 \(1\) 出发，找到到达所有其他节点的最短路径，同时遵守这些限制。如果某个节点无法到达，isj2OO9 将标记为 -1，表示该节点不可访问。

现在，请你帮助 isj2OO9 解决这个问题：给定图 \(G\) 和限制条件，计算从节点 \(1\) 到所有点的最短路径。

题解

我是奶龙。

点权最短路中每个点只会被松弛一次，特殊图上复杂度可以和实际边数无关。

因此把边看成点暴力松弛即可，即使边数高达 \(m^2\)，松弛时间复杂度也是对的。

NOIP 模拟 T3/P11802 【MX-X9-T6】『GROI-R3』Graph（分析性质，计数 DP，分步转移）

题意

特工 isj2OO9 奉命潜入一个秘密组织的内部通信网络。

该网络由 \(n\) 个节点（编号为 \(1 \sim n\)）组成，每个节点代表一个通信终端。

由于组织的安全协议，每个终端的入度和出度均不超过 \(1\)，这意味着网络由若干条链和环构成，甚至可能存在孤立节点（即入度和出度均为 \(0\) 的终端）。

isj2OO9 的任务是重构该网络，通过增加若干条边，使得网络满足以下条件：

• 每个节点的入度和出度恰好为 \(1\)（即网络由若干不相交的环组成）。
• 如果两个非孤立节点在重构后的网络中位于同一连通块（定义为准无向连通块，即忽略边方向后的连通分量），那么它们在原网络中也必须位于同一连通块。
• 存在一张有向图 \(G\)，满足其每个点出度恰好为 \(1\)，且使得重构后的网络上存在边 \((u,v)\) 当且仅当在 \(G\) 上从 \(u\) 走恰好 \(k\) 步后可以到达 \(v\)。

isj2OO9 需要计算所有可能的加边方案数，以便评估任务的成功概率。由于结果可能很大，请输出答案对 \(998244353\) 取模的值。

要求小常数 \(O(n^3)\)。

题解

模拟赛赛时认为 \(\gcd\) 必须等于 \(1\)，爆零了/ll。

看来考试时要把发现结论的依据写一写（周期结论）。

首先由题意，\(G\) 上任意一个点能走到他自己，因此 \(G\) 是若干环的并。

得到 \(\gcd=1\) 的错误结论是由于周期结论的直觉，让我们仔细想想这个结论能带给我们什么信息。

对于 \(G\) 上一个长为 \(len\) 的环，我们从一个点出发，每次走 \(k\) 步，能得到 \(\gcd(k,len)\) 个长为 \(\frac{len}{\gcd(k,len)}\) 的环。

因此，我们还可以选择把若干个相同长度的环在 \(G\) 中拼在一起。

具体地，用若干个长度为 \(i\) 的环拼成长为 \(i\times t\) 的大环，则有：

\[\frac{it}{\gcd(k,len)}=i \\ t=\gcd(k,it) \\ \gcd(\frac{k}{t},i)=1 \]

因此，设 \(cntloop_i\) 表示环长为 \(i\) 的环数，找到最小的 \(t\) 使得 \(\gcd(\frac{k}{t},i)=1\)，则 \(t|cntloop_i\)。这个条件是充要的。

考虑计数 DP。

按链 id DP要记录每个环长的 \(cnt\)，不可接受。

因此考虑按需要记录的值 DP，这样的好处是我们可以在进行 \(i\to i+1\) 的转移时顺便判断 \(i\) 是否合法。

令 \(f_{i,j,k}\) 表示当前处理长度 \(i\)，长度为 \(i\) 的链有 \(j\) 个，有 \(k\) 个剩余孤点（记录长度 \(\leq j\) 的链个数不容易保证不重不漏，因此选择 \(=\) 的定义）。

有一个技巧：我们可以把没有闭合的链各加上一个孤点，以保证 \(i\) 增加时链长 \(=i\) 的定义。

然而 \(w\) 个孤点在环上的贡献为 \(w!\)，这要求了我们不能实时计算这个贡献，只能在最后计算。

具体地，我们在转移时不区分孤点，最后乘上孤点个数的阶乘，根据组合意义，这个方法在不存在全是孤点组成的环时正确。

在孤点成环时，我们发现是阶乘和圆排列的区别。

具体地，对于一个 \(x\)，设长为 \(x\) 的全孤点环为 \(y\) 个，则我们多算了 \(x^y y!\) 倍，因为我们要：

• 除掉圆排列的循环。
• 当孤点都相同时，这些环没有顺序之分，除掉【最后乘上孤点个数的阶乘】对这些环顺序的错误贡献。

我们尝试用分步的思想来推导 DP 转移方程。

• 加入原图上的长为 \(i\) 的链，这一步是模拟题意。\(f_{i,j,k}\to f'_{i,j+cntlink_i,k}\)（\(cntlink_i\) 指原图上长为 \(i\) 的链个数）。

• 求出最小的 \(t\) 使得 \(\gcd(\frac{k}{t},i)=1\)，加入一些环，满足长为 \(i\) 的总环数是 \(t\) 的倍数，形成环有如下两种方式：

  • 选出若干孤点构成环。
  • 将已有的链闭合形成环。

  即枚举 \(c,l\)，\(\frac{f'_{i,j,k}\binom{j}{l}}{i^c c!}\to f''_{i,j-l,k-ic}\)，转移条件是 \((cntloop_i+l+c)\bmod t=0\)。

• 把没有闭合的链加上一个孤点，\(f''_{i,j,k}\to f_{i+1,j,k-j}\)。

记孤点个数为 \(cnt1\)，答案即为 \(f_{n+1,0,0}\times cnt1!\)。

分析复杂度，有 \(ij\leq n,ic\leq k\leq n,l\leq j\)。

\(ij,ic,il\) 各贡献 \(\sum \frac{n}{i}\)，\(k\) 贡献 \(n\)。

总复杂度 \(O(n\sum\frac{n^3}{i^3})=O(n^4\sum\frac{1}{i^3})=O(n^4)\)。

在推导时，我们发现没有转移条件时完全可以把【选出若干孤点构成环】和【将已有的链闭合形成环】分步转移做到 \(O(n^3)\)。

把条件改成 \(-cntloop_i-l=c\pmod t\) 仍然可以分步转移，枚举 \(cntloop_i+l\bmod t\) 的值做若干遍即可。

\(O(n^3)\) 卡卡就过 \(n=1000\) 了（逃。

模拟赛 T4 差点没会 \(O(nq)\) 呜呜呜。

这启示我们最优化问题可以将若干上界取 \(\min\)，并证明至少取到一个上界。

P8179 「EZEC-11」Tyres 紫（悬浮点函数贪心，DP，类根号分治）

题意

有 \(n\) 套轮胎，滴叉需要用这些轮胎跑 \(m\) 圈。

使用第 \(i\) 套轮胎跑的第 \(j\) 圈（对每套轮胎单独计数）需要 \(a_i+b_i(j-1)^2\) 秒。在本题中，你不需要担心爆胎，安全车，红旗或者不同的比赛策略。

滴叉需要进入维修站来更换轮胎，所消耗的时间为 \(t\) 秒。特别地，滴叉使用的第一套轮胎不需要进站更换。

你需要最小化总时间，总时间等于每圈的时间之和加上进站所花费的时间。

\(1\leq n,b_i\leq 500\)，\(0\leq t\leq 500\)，\(1\leq m\leq 2 \times 10^5\)，\(1\leq a_i\leq 10^9\)。

题解

首先一个轮胎不会被更换又被换回来。

首先 \(t=0\) 可以用堆贪心，因为函数是凹的。

其次我会 DP，\(dp_{i,j}\) 表示前 \(i\) 个轮胎，跑了 \(j\) 圈，决策单调性优化后可以做到 \(O(n^2m\log m)\) 无法通过。

但是我不会这道题。

---

考虑贪心的本质，对若干凹函数做多重背包的最优化可以贪心。

对于每个下凸函数 \(f_i\)，令 \(f_{i,0}\leftarrow f_{i,0}+t\)，这样只会破坏前 \(\lceil \sqrt{t} \rceil\) 项的凸性。

因此对于前 \(\sqrt{t}\) 项 DP，然后默认前 \(\sqrt{t}\) 项 全选，后面直接贪心。

这样正确的原因是对于一个实际没有选择的函数 \(f\)，选 \(\sqrt{t}\) 到 \(x+\sqrt{t}\) 项不优于选 \(1\) 到 \(x+1\) 项，因为第 \(\sqrt{t}\) 项的函数值已经 \(>f(1)\)。

另一种说法是一个轮胎如果不选择 \(\sqrt{t}\) 前面则一定不会选择 \(\sqrt{t}\) 项后面。

也可以理解成分组背包。

大概思路就是拼接然后证明不连续一定不优，这种方法适用于有悬浮点的函数最优化。

提交记录

P10681 [COTS 2024] 奇偶矩阵 Tablica 紫（行列二分图，容斥）

题意

考虑只包含 \(0\) 和 \(1\) 的 \(N\times M\) 矩阵 \(A\)。

我们称满足以下条件的矩阵是好的：

• \(\forall 1\le i\le N\)，\(\displaystyle \sum_{j=1}^M A_{i,j}\in \{1,2\}\)；
• \(\forall 1\le j\le M\)，\(\displaystyle \sum_{i=1}^N A_{i,j}\in \{1,2\}\)。

求出 \(N\) 行 \(M\) 列的好的矩阵的数量，对 \((10^9+7)\) 取模。

\(1\le N,M\le 3\, 000\)。

题解

把 \(01\) 矩阵视为行列二分图，相当于要求每个点度数为 \(1\) 或 \(2\)。

枚举左侧二度点个数 \(x\)，相当于把 \(n+x\) 个球放入 \(m\) 个盒子，球有些相同有些不同，盒子都不同，盒子中有 \(1\sim 2\) 个球。

先假设所有球都相同令 \(g_{i,j}\) 表示 \(i\) 个球 \(j\) 个盒子的方案数，转移仿照斯特林数。

\[g_{i,j}=\binom{i}{1}g_{i-1,j-1}+\binom{i}{2}g_{i-2,j-1} \]

由于一个点连出的两条边相同，因此以 \(\frac{g_{n+x,m}}{2^{x}}\) 作为答案。

由于可能有重边（在度数为 \(2\) 的点同时指向一个点时发生），因此枚举（钦定）重边个数 \(i\)，容斥一下。

一开始我的做法是枚举重边个数然后合并重边为一条边作为子问题，但是这是错的，因为重边调用子问题后仍然会有重边的重边。

这启示我们容斥的时候被钦定的东西不能继续违反条件，即钦定要完全确定一个东西的状态。

其次被钦定的东西是为了去重，因此计算贡献时必须与正常情况无异，即钦定的重边也要除以二（即使算出来不是整数）。

钦定 \(i\) 条重边，系数为 \((-1)^i\binom{n}{i}\binom{m}{i}i!\frac{1}{2^i}\)，枚举剩余 \(j\) 个不做要求的二度点。

本质上就是把钦定的点按正确贡献算完后容斥掉，而不是钦定后看成一个新问题或子问题。

\(O(n^2)\)。

提交记录

CF2068D Morse Code *3100（DP 贡献计算技巧，分步转移）

题意

在莫尔斯电码中，字母表中的每个字符被分配一个由点（.）和划（-）组成的序列，且没有序列是另一个序列的前缀。传输字符串时，各字符对应的序列按顺序发送。划的传输时间是点的两倍。

你的字母表包含 \(n\) 个字符，其中第 \(i\) 个字符在你的语言中出现频率为 \(f_i\)。你的任务是设计一个莫尔斯电码编码方案，为每个字符分配点划序列，以最小化单个字符的期望传输时间。即你需要最小化 \(f_1t_1 + f_2t_2 + \cdots + f_nt_n\)，其中 \(t_i\) 是传输第 \(i\) 个字符序列所需的时间。

\(n\leq 200\)。

题解

感觉还是对 DP 过程中算贡献和分布转移的理解不是很深刻。

对二叉树形态 DP，由于节点放置不连续，显然要按深度 DP。

\(f_{i,j,k,l}\) 表示 \(i\) 个叶子，\(j\) 个最大深度的叶子，\(k\) 个次大深度的叶子，最大深度是 \(l\)，可以做到 \(O(n^5)\)。

我尝试了在转移时算贡献，但是没有成功，因为最终排名不确定。

事实上，DP 过程中算贡献和分布转移本质上是让每个点实时有贡献，并且固定一些点停止贡献。

对于扩展深度为 \(2\) 的点，我们并不用管，因为我们每次只会把点的最浅深度集体下移 \(1\)，且点只有在作为最浅深度时才会被固定。

因此这个点的实际深度就是这个点（这个点不存在时我们认为这个点的祖先就是这个点）在状态里的时间 \(-1\)。

令 \(f_{i,j,k}\) 表示固定了 \(i\) 个叶子不再扩展，在未固定的叶子中有 \(j\) 个最大深度、\(k\) 个次大深度的叶子。

则要么固定一个次大深度的叶子，要么把次大深度的叶子全部扩展。

\[f_{i,j,k}\to f_{i+1,j,k-1} \\ f_{i,j,k}+w\to f_{i,k,j+k} \]

\(w\) 表示 \(p\) 的第 \(i+1\sim n\) 大的和，答案为 \(f_{n,0,0}\)，构造方案是简单的。

\(O(n^3)\)。

double 要加上 \(0.5\) 再转为 int 啊啊啊。

提交记录

CF1792F1 Graph Coloring (easy version) *2700（补图性质，计数 DP）

题意

给定一个有 $ n $ 个顶点的无向完全图。完全图是指任意两个顶点之间都有一条边相连。你需要将图中的每条边涂成红色或蓝色（每条边只能涂一种颜色）。

你需要对图进行涂色，使得：

• 至少存在一条红色边；
• 至少存在一条蓝色边；
• 对于每一个满足 $ |S| \ge 2 $ 的顶点集合 $ S \(，\) S $ 要么是红连通的，要么是蓝连通的，但不能同时两者都是。

请计算有多少种不同的涂色方案，并将答案对 $ 998244353 $ 取模后输出。

题解

红蓝互为补图，因此红蓝都不连通的情况不存在。

第一反应是对红蓝都连通的情况容斥，但是发现这样根本做不了。

不妨转化为有一个颜色不连通，对恰有一种颜色不连通的情况计数，此时另一种颜色必定连通。

令 \(f_i\) 表示 \(i\) 个点，每个子集满足蓝色不连通的方案数，枚举与 \(1\) 相连极大的蓝色连通块 \(S\)，保证跨过 \(S\) 和 \([1,i]/S\) 的集合中不存在红蓝都连通的集合，这个连通块需要满足红色不连通，用“极大”保证不重。

由于是"极大连通块"，所以两个集合之间的连边方案是固定的，只能是红色边。

恰好，这样的连边方式满足【跨过 \(S\) 和 \([1,i]/S\) 的集合中不存在红蓝都连通的集合】，因此逻辑以一种很奇怪的方式自洽了。

由于对称性，红色不连通方案数 \(=\) 蓝色不连通方案数。

则 \(f_i=\sum\limits_{j=1}^{n-1}\binom{i-1}{j-1}\times f_{j}\times (2f_{n-j}-[n-j=1])\)。

乘二是因为当集合有边时可以任意交换红蓝。

提交记录

CF1610G AmShZ Wins a Bet *3300（贪心，trie+hash，DP）

题意

给定一个字符串 \(S\)，每次可以删去一个 \(()\) 子序列，求能得到的最小字典序字符串。

\(1\leq |S|\leq 3\times 10^5\)

题解

删除字符的字典序最优化只有后缀的局部最优等于整体最优。

首先删除一个左括号时，贪心地，肯定删除最前的右括号。

并且我们可以把删去一个左括号等价为删除这个左括号连续段中最后一个左括号。

那么我们可以把题目中的子序列改为子串。

那么我们删去一个左括号时，一定会删除后面极短的合法括号串。

删一个合法括号串后变为子问题，考虑 DP，令 \(f_i\) 表示 \([1,i]\) 的答案，记 \(lst_i\) 表示第 \(i\) 个字符向前极短的括号串为 \([lst_i,i]\)（若 \(S_i=(\) 则 \(lst_i=-1\)）。

在 \(S_i=(\) 时转移是唯一的。

在 \(S_i=)\) 时有：

\[f_{i}=\min(f_{lst_i-1},f_{i-1}+S_i) \]

把所有 \(f\) 放到 trie 上，相当于动态加叶子的 trie，可以求 \(\text{lca}\) 快速比较字典序。

但是，这是错的。

因为我们对前缀进行 DP 时，局部最优不等于整体最优，比如 \((((()))))\)，则应该不删任何东西，但是我们会令 \(f_8=\emptyset\)，\(f_9=)\)。

本质上是我们删完前缀的后缀时不知道后面拼接的是啥，后面拼的字符可能影响最优性，局部最优不等于整体最优。

考虑对后缀 DP，则：

\[f_{i}=\min(f_{nxt_i+1},S_i+f_{i+1}) \]

需要在反 trie 上加叶子，那么在反 trie 上倍增倍增维护哈希即可。

后缀 DP 的好处是删完后缀的前缀时知道后面拼什么，而前面拼什么不影响后缀串的最优性，因此是正确的。

提交记录

CF251E Tree and Table *3000（子问题划分，分类讨论）

题意

小 Petya 非常喜欢树。最近他的妈妈送了他一棵有 \(2n\) 个节点的树。Petya 立刻决定把这棵树放在一个由 2 行 \(n\) 列组成的矩形桌子上，使得满足以下条件：

1. 表格的每一个单元格恰好对应树的一个节点，反之每个树节点也恰好对应表格的一个格子。
2. 如果两个树节点之间有一条边，那么它们在表格中对应的两个格子必须有公共边。

现在，Petya 想知道有多少种不同的方式可以将他的树放到桌子上。输出对 \(10^{9}+7\) 取模后的结果。

题解

注意到树的度数不超过 \(4\)。

当树是一条链时，分类讨论，一定是从某点开始走到头，拐回来走一段之后开始走折线，简单讨论后发现答案是 \(2(n^2-n+2)\)，注意链可以翻转，翻转后算不同的方案。

对于一般情况，先放入一个三度点，设其为树根。

当根存在一个儿子是叶子时，两侧被划分为了两个子问题，否则枚举儿子放在哪边，也是两个子问题。

容易发现我们有两种不同的子问题：

• 矩形左上（或左下）有一个点，要用这个点的子树铺成一个矩形。
• 矩形左上和左下各有一个点，要用这两个点的子树铺成一个矩形。

设第一种为 \(F(u)\)，第二种为 \(G(u,v)\)。

先讨论 \(F(x)\)（假设 \(x\) 在左上）。

• 如果 \(x\) 没有儿子，则无解。

• 如果 \(sz_x=2\)，答案为 \(1\)。

• 如果 \(x\) 有两个儿子，则枚举两个儿子是怎么放置的，设放在下面的为 \(u\)，右边的为 \(v\)。

  • 当 \(u\) 的儿子个数为 \(0\)，答案加上 \(F(v)\)。
  • 否则，\(u\) 的儿子个数必为 \(1\)，答案加上 \(G(v,son_u)\)。

• 如果 \(x\) 有一个儿子：

  • 若子树 \(x\) 为一条链，答案为 \(\frac{sz_{x}}{2}\)。
  • 若 \(son_x\) 放在下面，答案加上 \(F(son_{son_x})\)。
  • 否则找到最浅的有两个儿子的点，设其为 \(y\)，一直直走直到遇到这个点停止，枚举哪个点向下拐。
    • 如果向下拐的点（设其为 \(z=son_{y,0}\)）有一个儿子，判断一下它能不能把第二行的前缀填满，如果可以，答案加上 \(F(son_{y,1})\)。
    • 否则，枚举一下哪个儿子（设其为 \(son_{z,0}\)）能把第二行的前缀填满，如果可以，答案加上的 \(G(son_{y,1},son_{z,1})\)。

再讨论 \(G(x,y)\)。

• 如果 \(x,y\) 没有儿子，答案为 \(1\)。
• 如果 \(x,y\) 各有一个儿子，答案为 \(G(son_x,son_y)\)。
• 否则，设 \(x\) 有一个儿子，答案为 \(F(son_x)\)。

复杂度看似 \(O(n^2)\)，但是提交后直接过了。

因为 \(G(u,v)\) 被调用时，两个点的深度差不超过 \(1\)，每次 \(G\) 往后转移只有一个后继，而这颗树每层节点个数是 \(O(1)\) 的（似乎最多 \(6\)），因此 \(G\) 的总状态是 \(O(n)\) 的。

提交记录

P6898 [ICPC 2014 WF] Metal Processing Plant（2-SAT，生成树性质）

题意

有一个无向完全图，\(i,j\) 的边权为 \(d(i,j)\ \ (0\leq d(i,j)\leq 10^9)\)。

令 \(D(S)=\max_{i,j\in S} d(i,j)\)。

将图划分为两个子集 \(A\) 和 \(B\)，使 \(D(A) + D(B)\) 最小。输出这个最小值。

\(1\leq n\leq 200\)。

题解

枚举 \(D(A)\) 双指针 \(D(B)\)，使用 2-SAT 检验即可做到 \(O(n^4)\)。

考虑 \(D(A)\) 对点选法造成的限制，将所有大于 \(D(A)\) 的边加入表示如果加入一条边后形成偶环，则这条边本身不提供任何信息，如果是奇环，则直接不合法。

因此建立最大生成树，只有树边加入时是有用的，枚举树边，二分 \(D(B)\) 即可做到 \(O(n^3\log n)\)。

提交记录

CF618F Double Knapsack *3000（弱化条件）

题意

给定两个多重集 \(A\) 和 \(B\)，每个多重集中恰好有 \(n\) 个整数，每个整数都在 \(1\) 到 \(n\) 之间（包含 \(1\) 和 \(n\)）。

你需要找到 \(A\) 的一个非空子集和 \(B\) 的一个非空子集，使得这两个子集中元素的和相等。子集内可以包含重复元素。

构造方案或报告无解。

题解

子序列选数的一个套路是重排后弱化为选子段。

但实际上本题不用重排。

样例均未报告无解，想想为什么必定有解。

由于值域和长度相同且为 \(n\)，考虑模 \(n+1\)，假设 \(\sum a>\sum b\)，对 \(b\) 的每个前缀 \(0\leq i\leq n\) 找到 \(a\) 最小的前缀 \(j\) 使得 \(\sum_{x\leq i} a_x>\sum_{y\leq j} b_y\)，显然二者之差在 \([0,n]\) 之间，如果是 \(0\) 就做完了，否则根据抽屉原理差必定会撞一次，取上一次撞的位置到当前位置的子段，也做完了。

提交记录

NOIP 模拟 T3（整体思想，整体算贡献，分析性质）

题意

ChiFAN 构建了一棵树形分流器 \(T\)，其是一棵有 \(2 \times n - 1\) 个节点，以 \(1\) 为根的二叉树，其恰有 \(n-1\) 个有两个儿子的节点与 \(n\) 个没有儿子的叶子节点。

分流器 \(T\) 的每个非叶子节点 \(u\) 上有一个参数为 \(a_u,t_u\) 的分流装置，记点 \(u\) 的左儿子为 \(son_{u,0}\) 右儿子为 \(son_{u,1}\)，当点 \(u\) 收到一个大小为 \(x\) 的物品时，假若 \(x\) 大于等于 \(a_u\) 则会将物品分发到节点 \(son_{u,t_u}\) 上，否则会分发到节点 \(son_{u,(t_u+1) \bmod 2}\) 上。

你可以任意地修改每个节点的 \(t_u\) 以及有代价地修改每个点的 \(a_u\)，具体而言如果点 \(u\) 的 \(a_u\) 最终被修改为 \(a'_u\)，你需要付出 \((a_u-a'_u)^2\) 的代价。你需要保证 \(a'_u\) 是整数。

记 \(f(u,l,r)\) 表示最小花费多少的修改代价（你可以修改 \(a,t\) 的取值，请注意你可以无代价地决定 \(t\) 的取值），才能使得修改后依次往点 \(u\) 分发大小为 \(l,l+1,\dots,r\) 的物品，最终不会有两个不同的物品被分发到同一个叶子节点上。

初始时所有非叶子节点 \(u\) 的 \(a_u = 0\)。

现在有 \(q\) 次操作，第 \(i\) 次操作给出 \(u_i,y_i,v_i,l_{i,1},r_{i,1},l_{i,2},r_{i,2}\)，你需要将 \(a_{u_i} \gets y_i\) 后回答 \(f(v_i,l_{i,1},r_{i,1})-f(v_i,l_{i,2},r_{i,2})\) 的值（保证 \(r_{i,1}-l_{i,1}+1=r_{i,2}-l_{i,2}+1\) 并且等于 \(v_i\) 子树内叶子数量）。

操作之间不互相独立，也就是一个操作产生的修改会影响后面的操作。

\(1\leq n\leq 10^6\)。

题解

直接 DP 后发现是二次函数错位取 \(\min\)，不可做。

考虑整体算贡献，将子树内若干 \(a\) 拿出来，不难发现他们的值互不相同，不妨设 \(a_i=l+p_i\)，\(p\) 是我们定义的 \(1\sim r-l\) 的排列，答案为 \(\sum (a_i-l-p_i)\)，拆出来 \(p\) 和 \(l\) 无关，所以策略和 \(l\) 的值没有关系，拆出来随便维护一下就行了。

注意平方拆出来要乘以二。

NOIP 模拟 T1（实际是 T2 难度）（序列转差分）

题意

有一个 \(n\) 的字符串 \(a\) 和一个参数 \(k\)，\(a\) 的每一个位置都印有一个字符 o 或者 x 。你可以任意次数的对字符串 \(a\) 进行如下两种操作之一（也可以不操作）：

1. 选择一个长度为 \(k\) 的区间 \([l,r]\) 。将字符串中第 \(l\) 个到第 \(r\) 个位置（下标从 \(1\) 开始，下同）的字符取反。即 o 变成 x ，x 变成 o 。

2. 选择一个长度为 \(k\) 的区间 \([l,r]\) 。如果字符串中第 \(l\) 个到第 \(r\) 个位置的字符全部是一样的，就可以删除它们，然后剩余字符拼接起来。

字符串 \(a\) 某些位置变成了 ? ，表示这个位置既可以是 o 也可以是 x。

有多少个字符串 \(b\) 可能被 \(a\) 通过上述两种操作表示出来？\(b\) 可以是空串。输出答案对 \(10^9+7\) 取模后的结果。

部分分：没有 ?。

题解

考虑部分分。

维护差分数组 \(b\)，对于没有问号的情况，\(b\) 存在一个模 \(k\) 等价类，每个等价类只需保证异或和，在没有删除操作时容易计数。

有删除时，删除一个子段会让所有等价类的异或和都改变，因此删除是本质没有影响的，对 \(m=n+1-pk\) 计数即可，注意 \(b\) 的长度是 \(n+1\)，因此不能把 \(b\) 删空。

对于问号，其作用是合并两个等价类，即限制了 \(i\bmod k\) 和 \((i+1)\bmod k\) 的等价类的异或和，那么本质上是等价类合并，使用并查集维护，原先的每个等价类方案数是 \(1\)，现在每个等价类的内部方案数为 \(2^{连通块大小-1}\)，乘上刚刚算的东西即可。

问题是我们是否能把序列删到长为 \((n+1)\bmod k\)，那么我们本质上要求 \(b_1=b_2=\dots=0\)，但是不对最后 \(n\bmod k\) 项做要求。

这些等价类中第 \(1\sim (n\bmod k)+1\) 项可以任意取，其余项不能任取，维护 \(rsz\) 表示等价类代表元中去掉编号为 \(0\) 和 \((n\bmod k)+2\sim k-1\) 的大小，这部分对答案的贡献为 \(+\prod 2^{rsz-1}\)，注意当等价类连通块异或和不为 \(0\) 且 \(rsz=0\) 时这部分无解。

AT_agc020_f [AGC020F] Arcs on a Circle 黑（状压 DP，实数处理技巧，DP 转移处理）

题意

有一个长度为 \(C\) 的圆周，在这个圆周上放置 \(N\) 条圆弧。第 \(i\) 条圆弧的长度为 \(L_i\)。

每条圆弧 \(i\) 都被独立地、以均匀概率，随机地放在圆周上的某个位置。也就是说，从圆周上的一个随机点出发，以该点为起点，出现一个长度为 \(L_i\) 的圆弧。

这些圆弧的放置是相互独立的。例如，圆弧之间可以有重叠、交叉，甚至可以包含其他圆弧。

问：圆周上的所有点都至少被一条圆弧覆盖的概率是多少？圆弧的两端也算作被覆盖。

\(L_i\leq C\leq 50\)，\(N\leq \color{red}{6}\)。

题解

小数处理技巧：暴力枚举 \(N\) 个数小数部分的排名。

枚举完把小数部分离散化一下变为 \(NC\) 个点，状压 DP 即可。

注意要先让最长的线段放置，要不然可能存在线段绕环大半圈后回来的情况，此时 DP 有后效性。

DP 时按照线段的左端点为顺序转移，避免计重。

提交记录

P9523 [JOIST 2022] 复制粘贴 3 / Copy and Paste 3 紫（区间 DP，简化转移，操作后置，调和级数）

题意

你可以执行如下几种操作来输入某个字符串，设 \(X\) 为屏幕上的字符串，\(Y\) 为剪切板中的字符串，初始均为空串：

• 操作 A：输入字符 \(c\)，即将 \(X\) 更新为 \(X+c\)。
• 操作 B：选择所有字符并剪切，即将 \(Y\) 更新为 \(X\)，并将 \(X\) 置为空串。
• 操作 C：将剪切板中的字符串粘贴到当前字符串末尾，即将 \(X\) 更新为 \(X+Y\)。

使用一次操作 A,B,C 分别要花费 \(A,B,C\) 单位时间。

计算出输入一个长度为 \(N\) 的字符串 \(S\) 最少需要花费多少时间。

\(1\leq N\leq 2500\)。

题解

这个操作看起来就很符合区间 DP 的形式。

令 \(dp_{l,r}\) 表示 \([l,r]\) 的生成代价，一个区间形如 \(??? [Y] ??? [Y] ?? [Y] ???\)，即若干个字符加上若干个剪切板字符串。

转移时枚举第一个 \([Y]\) 的位置可以做到 \(O(n^4)\)，考虑简化转移，要求转移到的区间末尾是 \([Y]\)，再用区间扩展转移实现往后加 \(?\)，可以做到 \(O(n^3)\)。

我们的贡献和字符串 \(Y\) 在 \([l,r]\) 的出现次数有关，考虑反过来刷表，枚举出现次数以做到调和级数的复杂度。

\[dp_{l,r}+B+C(\text{occur}(s[x:r],s[l:r]))+A(r-x+1-\text{occur}(s[x:r],s[l:r])\times (r-l+1))\to dp_{x,r}\ \ (x\leq l) \\ dp_{l,r}\to dp_{l,r+1} \]

我们发现我们还要处理 \([x,r]\) 开头 \(?\) 段，可以上数据结构做到双 \(\log\)，但是无法通过。

Hint：将操作 A 后置，即允许在字符串开头添加字符。

即 \(dp_{l,r}\to dp_{l-1,r}\)，这相当于把操作 A 在操作序列中插入到了头部。

这样我们只需要枚举 \(O(n\ln n)\) 个 \(x\)，复杂度 \(O(n^2\ln n)\)。

后置操作 A 本质上就是我们新加入了一个操作 D 是在串前加入字符，然后发现和原问题等价。

实际写的时候写的是 \(dp_{l,r}\to dp_{l,x}\ \ (x>r)\)，总之是等价的。

提交记录

P14412 [JOISC 2015] AAQQZ 紫（分类讨论）

题意

给定一个长为 \(n\) 的数组，选择一个区间 \([l,r]\) 进行排序，最大化排序后最长回文子串的长度。

\(1\leq n\leq 3000\)。

题解

首先令答案对原串最长回文子串和众数个数取 \(\max\)，这两种情况是平凡的。

之后有两种情况：

• 回文中心在排序区间外。
• 回文中心在排序区间的开头（或结尾）极长相等连续段内（例如 \(443322\color{red}1\color{blue}1\color{red}1223344\)）

对于第一种情况，设排序区间在右，枚举回文中心，向两侧扩展后枚举排序区间，当然你可以平衡树维护哈希，但是有简单做法：对左侧最长不升子序列开桶，由于排序后区间是上升的，所以可以维护值域指针 \(ptr\) 表示匹配到了哪个值，最后判断能否向外扩展即可。

对于第二种情况，枚举回文中心不好做，考虑枚举排序区间起点 \(l\)，对以 \(l-1\) 结尾的最长不升子序列开桶，此时往后枚举 \(r\)，当遇到 \(<a_{l-1}\) 的数时开始记贡献，匹配方式与第一种情况相同，唯一区别是不匹配最小值。

\(O(n^2)\)。

提交记录

P14424 [JOISC 2014] 邮戳收集 / Collecting Stamps 紫（贡献后置，状态简化）

题意

有 \(n + 2\) 个车站从西到东顺次标号为 \(0, \ldots, n + 1\)。有两班电车经过所有车站，方向分别为从西向东和从东向西。乘坐两种电车移动 1 站的耗时都是 \(T\) 秒。

车站 \(1, \ldots, n\) 在两列电车间的月台上设有邮戳台，每个车站的电车到邮戳台之间只能步行，步行消耗的时间分别为 \(U_i, V_i, D_i, E_i\)，如图：

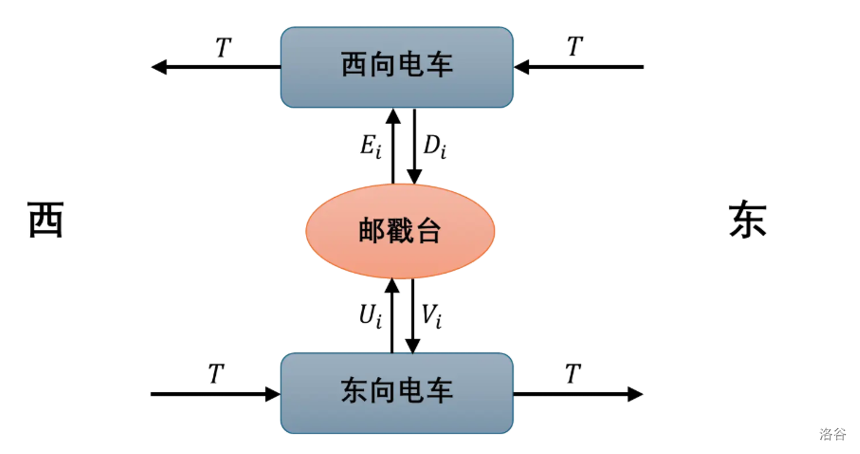
你一开始在东向电车上，位于 \(0\) 号车站，你想要在所有邮戳台各盖至少一次邮戳，最终到达 \(n + 1\) 号车站。\(0\) 号车站和 \(n + 1\) 号车站分别只能在开始和结束时经过一次，其它车站可以经过任意多次，每个邮戳台也可以经过任意多次。问你需要花费的最短时间。

\(1\leq N\leq 3000\)，\(85\%\) 数据满足 \(N\leq 100\)。

题解

经过一个邮戳台有四种方式：

1. \(u+e\)。
2. \(d+v\)。
3. \(u+v\)。
4. \(e+d\)。

考虑在东向电车行走的路线，可以跳过若干邮戳台不走，其余走 \(u+v\)，或者走 \(u+e\) 上去，把没走的邮戳台挑若干个走 \(e+d\)，挑一个走 \(d+v\) 下去。

注意 \(u+e\) 和 \(d+v\) 可能被走多次。

将 \(e+d\) 和 \(d+v\) 的贡献后置，在转移时加上额外贡献，令 \(f_{i,j,k}\) 表示到了站台 \(i\)，有 \(j\) 个邮戳台被指定走 \(d+e\)，\(k\) 个邮戳台被指定走 \(d+v\)，转移时加上 \(2T(j+k)\) 的贡献，枚举当前有 \(k_1\) 个 \(u+e\) 和前面匹配，\(k_2\) 个 \(d+v\) 和后面匹配。可以做到 \(O(\text{poly}(n))\)。

简化状态，由于在上面只能往左走，因此只有存在没有匹配的 \(d+v\) 时才能匹配存在未匹配的 \(d+e\)，另一方面，我们做 \(u+e\) 和 \(d+v\) 的匹配时实际上顺便把 \(d+e\) 走了，可以把向上和向下理解称括号匹配，当存在未匹配的左括号时可以选择 \(d+e\)。

令 \(dp_{i,j}\) 表示到了站台 \(i\)，有 \(j\) 个未匹配的 \(d+v\) 的最小代价。

转移时，可以选择 \(u+v\)，当 \(j>0\) 时可以选择 \(d+e\)。枚举这个站台有 \(k1\) 个 \(u+e\) 和前面匹配，\(k2\) 个 \(d+v\) 和后面匹配，转移到 \(dp_{i+1,j-k1}\) 或 \(dp_{i+1,j+k2}\)。

前缀和优化可以做到 \(O(n^2)\)。

提交记录

P10433 [JOIST 2024] 棋盘游戏 / Board Game 黑（函数（计算几何），凸包，阈值分治）

题意

给定一个 \(N\) 点 \(M\) 边的无向连通图，无自环。点分为白点和黑点。图上有 \(K\) 个人，每个人初始在点 \(V_i\) 上。

设一个人当前在点 \(x\)，他的一次行动将执行如下操作：

1. 选择 \(x\) 的一个邻点 \(v\)（必须选），走到 \(v\)，并花费 1 的代价。
2. 若 \(v\) 是白点，继续重复 1. 步骤。否则结束这次行动。

现在 \(K\) 个人按标号 \(1, 2, \cdots, K\) 依次进行一次行动，第 \(K\) 个人行动完成再轮到第 1 个人行动。对于所有 \(T = 1, 2, \cdots, N\)，询问使标号为 1 的人到达 \(T\)（中途经过也可以），所有人的总花费最少是多少。

\(2 \leq N, M, K \leq 5 \times 10^4\)。

部分分 \(K\leq 100\)。

题解

首先 \(1\) 和 \(2\sim K\) 的行动是分开的，先考虑 \(2\sim K\)。

记 \(S(v,i)\) 表示 \(v\) 走 \(i\) 轮的最小代价，\(2\sim K\) 有两种行动方式：

1. 在黑点跳出在跳回，代价为 \(2\)。
2. 在相邻黑点反复跳，代价为 \(1\)。

第一种短期内更优，第二种长期内更优。

为了到达相邻黑点，必须先经过若干不相邻的黑点，这些黑点之间的距离都不小于 \(2\)。

把两种方式画成关于轮数的函数，第一种是一条直线，第二种是前面一堆斜率超过 \(2\) 的直线，后面拼上斜率为 \(1\) 的直线。

即使有多种方式到达相邻黑点，每种方式的轮数和代价各不相同，但最后只有一个方式会被采用，即截距最小的方案。

求截距最小即求路径长度减去黑点个数最小，\(01\) bfs 即可。

我们把 \(S_v(i)\) 求和得到一轮 \(2\sim K\) 的总代价 \(S(i)\)。

现在考虑 \(1\) 的行动方案，每个行动方案都有轮数 \(c\) 和代价 \(dis\)，则答案 \(ans=\min(dis+S(c-1))\)，减一是因为 \(1\) 到达这个点后立刻停止。

由于轮数每增加 \(1\) 代价增加至少 \(K-1\)，部分分的 \(K\leq 10\) 提示 \(K\) 小时有简单做法，因此考虑根号（阈值）分治。

当 \(K>B\) 时，最优轮数最多比最小轮数大 \(\frac{N}{K}\)，分层图 bfs 一下即可求出每个轮数的 \(dis\)，这部分复杂度 \(O(\frac{N^2}{K})\)。

当 \(K\leq B\) 时，\(S(i)\) 函数最多 \(K\) 段，每次变化都代表一个人的 \(S\) 斜率由 \(2\) 变为 \(1\)，枚举在哪一段，把这一段视作一条直线，这样每个黑点贡献相同，dij 即可，复杂度 \(O(KN\log N)\)。

令 \(\frac{N^2}{B}=BN\log N\)，即 \(B=\sqrt{\frac{N}{\log N}}\) 时，复杂度取到 \(O(N\sqrt{N\log N})\)。

其实最难的是发现两种方案有一个临界，这启示我们可以尝试把贡献形式刻画成函数，以发现较好的性质。

P14382 [JOISC 2017] 开荒者 / Cultivation 黑（单调队列，双指针，简化枚举）

题意

给定一个 \(R \times C\) 的 01 矩阵，设为 \(F\)。其只有 \(n\) 个格子为 1，其它均为 0。你可以执行若干次操作，一次操作形如：

1. 选取四个方向（\(U/D/L/R\)）中的一个，设 \(G\) 为 \(F\) 的每个格子向此方向平移一格形成的矩阵；
2. 更新 \(F' \leftarrow F \lor G\)，其中 \(\lor\) 定义为对每个格子取 \(OR\)。

求使得 \(F\) 全为 1 所需要的最小操作次数。

\(1 \leq n \leq 300\)， \(1 \leq R, C \leq 10^9\)。

题解

记移动次数分别为 \(u,d,l,r\)。

枚举每个点的 \(l\) 和 \(r\)，计算 \(u,d\) 的下界即可做到 \(O(R^2n^2)\)。

每一个竖线对 \(u,d,u+d\) 各有一个限制。具体地，把所有跨竖线的点按 \(y\) 排序，则要求：

• \(u+d\geq \max(y_{i+1}-y_{i})\)；
• \(u\geq \min(y_i)\)；
• \(d\geq C-\max(y_i)\)。

考虑只枚举 \(l+r\)，通过移动矩形来求 \(u,d\) 的最松限制，具体地，枚举 \(r\) 并令 \(l=0\)，之后将矩形向右移动 \(r\) 格，每移动一格更新一次答案。

每移动一格会加入一个竖线，再删除一个竖线，使用单调队列维护竖线，每个竖线暴力计算限制，一共 \(O(n)\) 种竖线，可以做到 \(O(Rn^2)\)。

不难发现，对于一个竖线，扫到的点的 \(x\) 是一个区间，我们预处理每个区间的限制，每次加入竖线时双指针找到区间查表，即可做到 \(O(n^3+Rn)\)。

考虑简化枚举，由于限制是二元的，考虑对每个二元组统计其限制情况，只枚举以下的 \(r\)：

• \(0\)。
• \(r=x_j-x_i\ (x_j\geq x_i)\)，即 \(i\) 和 \(j\) 是否存在一个时刻会产生限制。
• \(r=R+x_j-x_i\ (x_j\geq x_i)\)，表示 \([x_i,x_i+r]\) 和 \([x_j,x_j+r]\) 的限制中，\([x_i,x_j)\) 和 \([x_i+r,x_j+r)\) 能否同时进入矩形边框。

[CSP-S 2025] replace 紫（Trie，二维数点）

题意

给定 \(n\) 个字符串二元组，第 \(i\) (\(1 \leq i \leq n\)) 个字符串二元组为 \((s_{i,1}, s_{i,2})\)，满足 \(|s_{i,1}| = |s_{i,2}|\)，其中 \(|s|\) 表示字符串 \(s\) 的长度。

对于字符串 \(s\)，定义 \(s\) 的替换如下：

• 对于 \(s\) 的某个子串 \(y\)，若存在 \(1 \leq i \leq n\) 满足 \(y = s_{i,1}\)，则将 \(y\) 替换为 \(y' = s_{i,2}\)。具体地，设 \(s = x + y + z\)，其中 \(x\) 和 \(z\) 可以为空，“+” 表示字符串拼接，则 \(s\) 的替换将得到字符串 \(s' = x + y' + z\)。

小 W 提出了 \(q\) 个问题，第 \(j\) (\(1 \leq j \leq q\)) 个问题会给定两个不同的字符串 \(t_{j,1}, t_{j,2}\)，她想知道有多少种字符串 \(t_{j,1}\) 的替换能够得到字符串 \(t_{j,2}\)。两种 \(s\) 的替换不同当且仅当子串 \(y\) 的位置不同或用于替换的二元组 \((s_{i,1}, s_{i,2})\) 不同，即 \(x, z\) 不同或 \(i\) 不同。你需要回答小 W 提出的所有问题。

题解

补坑。

赛时由于被 T1 狙杀导致没时间写了，最后把相同部分替换为 # 后没想到 trie，想了个 ACAM 做法根本不可写。

把相同部分替换为 # 后相当于 \(s\) 串的前面是 \(t\) 的前面的后缀，\(s\) 串的后面是 \(t\) 的后面的前缀，对每个不同的 # 开 trie 后二维数点即可。

提交记录

[CSP-S 2025] employ 紫（贡献后置，匹配型 DP）

题意

小 Z 可以选择一个 \(1 \sim n\) 的排列 \(p\)，然后在第 \(i\) (\(1 \leq i \leq n\)) 天通知编号为 \(p_i\) 的人前来面试。

第 \(i\) (\(1 \leq i \leq n\)) 天的面试题的难度为 \(s_i \in \{0,1\}\)，其中 \(s_i = 0\) 表示没有人能够做出；\(s_i = 1\) 表示所有人都能做出。如果面试者没有做出面试题，则会拒绝，否则会录用。

编号为 \(i\) (\(1 \leq i \leq n\)) 的人若在他之前已经有不少于 \(c_i\) 人被拒绝或放弃参加面试，则他也将放弃参加面试。

小 Z 想知道一共有多少种面试的顺序 \(p\) 能够让他们录用至少 \(m\) 人。求能够录用至少 \(m\) 人的排列 \(p\) 的数量对 \(998244353\) 取模。

\(1\leq n\leq 500\)。

题解

会了贡献后置但是不会推式子，要练组合数学了。

首先这是一个匹配问题，具体匹配方案如下：

• 当这个点值为 \(1\)，且有人被录取时，匹配一个 \(c\) 大于【之前失败人数】的人。
• 当这个点值为 \(1\)，且无人被录取时，匹配一个 \(c\) 小于等于【之前失败人数】的人。
• 当这个点值为 \(0\) 时，匹配任意一个人。

匹配问题考虑 DP + 贡献后置，按 \(c\) 的值 DP，令 \(f_{i,j,k}\) 表示 \([1,i]\) 拒绝 \(j\) 个人，匹配了 \(k\) 个 \(c>j\) 的人的方案数。

\(j\) 既代表当前拒绝的人数，也代表 \(c\) 匹配到的值，在本题中可以合并成一维状态。

记 \(cnt_i=\sum\limits_x [c_x=i],pre_i=\sum\limits_{x=1}^{i} cnt_x\)。

\(\sum [s_i=1]\leq 18\) 的部分分启示我们暴力枚举每个点的状态：

• \(s_i=1\)，实际有人录取，则有：$$f_{i,j,k}\to f_{i+1,j,k+1}$$

\(\tiny{\text{以上是我自己会的部分 qwq}}\)。

• \(s_i=1\)，实际无人录取，有一个 \(\leq j\) 的 \(c\) 与当前位匹配，有 \(j\to j+1\)，那么我们要枚举 \(c=j+1\) 的有多少和前面匹配，则有：$$\sum\limits_{w=1}^{\min(k,cnt_{j+1})} f_{i,j,k}\binom{k}{w}\binom{cnt_{j+1}}{w}w!(pre_j-(i-k))\to f_{i+1,j,k-w}$$

• \(s_i=1\)，有 \(j\to j+1\)，那么我们要枚举 \(c=j+1\) 的有多少和前面匹配，并且我们要讨论与这个位置匹配的人的 \(c\) 是否 \(>j+1\)。

  • 当 \(c>j+1\) 时：$$\sum\limits_{w=1}^{\min(k,cnt_{j+1})} f_{i,j,k}\binom{k}{w}\binom{cnt_{j+1}}{w}w!\to f_{i+1,j+1,k-w+1}$$
  • 当 \(c\leq j+1\) 时：$$\sum\limits_{w=1}^{\min(k,cnt_{j+1})} f_{i,j,k}\binom{k}{w}\binom{cnt_{j+1}}{w}w!(pre_{j+1}-(i-(k-w)))\to f_{i+1,j+1,k-w}$$

讨论到这里，我们发现已经没有必要枚举每个点状态了，直接转移所有可能的情况就做完了。

注意统计答案时必须要求 \(k=n-pre_j\)。

提交记录

P4859 已经没有什么好害怕的了 紫（二项式反演，匹配型 DP）

题意

将 \(a\) 数组与 \(b\) 数组匹配使得 \(a>b\) 恰好比 \(b>a\) 的对数大 \(k\) 对，求方案数。

\(1\leq n\leq 2000\)。

题解

令 \(t=\frac{n-k}{2}\)。

二项式反演，钦定 \(i\) 个 \(a>b\)，其余不管的方案数为 \(g_i\)，则 \(ans=\sum\limits_{i=t}^{n} \binom{i}{t}(-1)^{i-t}g_i\)。

匹配型 DP 求出 \(g_i\)，具体地令 \(f_{i,j}\) 表示 \(b[1\sim i]\) 中有 \(j\) 个匹配了比他小的 \(a\) 的方案数，限制由严到松，因此转移是容易的。

最后 \(g_i=f_{n,i}\times \color{red}(n-i)!\)，不要忘了这个系数，表示其余的匹配任意。

提交记录

NOIP 模拟 T2/utpc2022_f（冒泡排序扩展）

题意

给定长为 \(N\) 的排列 \(P\) 和一个参数 \(K\)，求：

for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= N - i - K + 2; j++) {
        if (is_sorted(P[j], P[j + 1], ..., P[j + K - 1])) {
            sort(P[j], P[j + 1], ..., P[j + K - 1]) ... (1)
        }
    }
}

执行以下伪代码表示的算法时，（1）的公式执行几次？

部分分：\(\forall_{i\leq K},P_i=i\)。

题解

\(k=2\) 是逆序对个数。

冒泡排序的经典转化是记 \(b_i=\sum\limits_{j=1}^{i-1}[a_j<a_i]\)，然后分析 \(b\) 的变化。

发现我们在维护排序区间时，区间排序前的前 \(k-1\) 个位置是当前前缀的最大值。

考虑部分分，此时每次挪动排序区间，\([i-k,i-1]\to [i-k+1,i]\) 时，发现只会改变 \(b_i\)，且此时 \([i-k+1,i-1]\) 已经有序，因此这次排序会让 \(b_i\) 变为 \(\min(0,b_i-k+1)\)，可以直接求得答案为 \(\sum\limits_{i=1}^{n} \lceil \frac{b_i}{k-1}\rceil\)。

否则，可能存在一些点在 \([1,k]\) 一起排好的情况，特判一下，如果 \(i\) 的 \(b\) 值在减到 \(0\) 的前一次，\(i\) 的位置到了 \([1,k]\)，那么它可能和其他数共用一次排序，这部分也是好处理的。

注意 \(i\) 在 \(t\) 次操作后（\(t<\lceil \frac{b_i}{k-1}\rceil\)）的位置为 \(i-t\times (k-1)\) 而不是和 \(a_i\) 相关的式子，因为此时比 \(a_i\) 小的数不一定排在 \(a_i\) 前面。

提交记录

NOIP 模拟 T3（整除分块，容斥，信息复用）

题意

称函数 \(f: \mathbb Z ^ + \to \mathbb Z\) 为积性函数，当且仅当：

• \(f(1) = 1\)。
• \(\forall \gcd(x, y) = 1, f(xy) = f(x) f(y)\)。

可以证明，如果我们对所有素数 \(p\)，正整数 \(k\) 知道了 \(f(p ^ k)\) 的值，就可以唯一确定函数 \(f\)。

给定积性函数 \(g\) 和序列 \(a_1, a_2, \cdots, a_n\)，初始时满足 \(\forall x, g(x) = 1\)。

你需要维护这个积性函数，并支持以下两种操作：

1. 给定参数 \(p, k, x\)，表示将 \(g(p ^ k)\) 的取值修改为 \(x\)。
2. 查询 \(\sum _ {xy \le n} g(x) a_y\)，由于答案可能很大，你只需输出其对 \(2 ^ {64}\) 取模的结果。

题解

赛时干了一些没有道理的事情，对 \(a\) 整除分块，然后啥也不会。

显然难点在于维护 \(g\) 而不是 \(a\)，对 \(g\) 整除分块，记 \(g\) 的前缀和为 \(G\)，答案为 \(\sum\limits_{i=1}^{n} a_iG(\lfloor \frac{n}{i}\rfloor)\)。

只需要维护 \(O(\sqrt{n})\) 个 \(G\)，考虑每次修改暴力重构。

当我们修改 \(g\) 时，需要把修改视为 \(g\leftarrow g+\Delta\) 而不是 \(g\leftarrow x\)，因为后者的修改式子涉及除法。

当我们修改 \(g_{p^k}\) 时，对于一个 \(G(i)\) 的影响是 \(G(i)\leftarrow G(i)+\Delta\sum\limits_{j\bmod p\neq 0,j\leq \lfloor \frac{i}{p^k}\rfloor} g_j\)。

令 \(S_p(i)=\sum\limits_{j\bmod p\neq 0,j\leq i} g(i)\)，则 \(G(i)\leftarrow G(i)+\Delta S_p(\lfloor \frac{i}{p^k}\rfloor)\)，我们也只需要维护 \(O(\sqrt{n})\) 个 \(S\)。由于每个修改的 \(p\) 固定，以下简记 \(S_p\) 为 \(S\)。

由于 \(\lfloor \frac{i}{p^k}\rfloor=\lfloor \frac{\lfloor \frac{n}{t}\rfloor}{p^k}\rfloor=\lfloor \frac{n}{tp^k}\rfloor\)，因此状态数是 \(O(\sqrt {n})\) 的。

对于 \(S\)，考虑容斥， \(S(i)=G(i)-\sum\limits_{x} g(p^x)S(\lfloor\frac{i}{p^x}\rfloor)\)，复杂度 \(O(Q\sqrt {n}\log n)\)。

这个式子很难优化了。

记整除分块能取到的位置为关键点，考虑复用 \(S\) 的信息，由上一个关键点递推出当前关键点。

记上一个关键点的位置为 \(i'\)，则 \(S(i)\leftarrow S(i')+G(i)-G(i')-\sum\limits_{x}(S(\lfloor\frac{i}{p^x}\rfloor)-S(\lfloor\frac{i'}{p^x}\rfloor))g(p^x)\)，枚举到 \(\lfloor\frac{i}{p^x}\rfloor=\lfloor\frac{i'}{p^x}\rfloor\) 时停止，这样复杂度不高于 \(O(Q\sqrt {n}\log n)\)。

注意算 \(S\) 时用到的是修改前的 \(G\)。

复杂度 \(O(Q(\sum\limits_{i=2}^{n} \log(\lfloor \frac{n}{i-1} \rfloor-\lfloor \frac{n}{i} \rfloor))\)，并定义 \(\log 0=0\)。

有经典结论 \(\sum\limits_{i=2}^{n} \log(\lfloor \frac{n}{i-1} \rfloor-\lfloor \frac{n}{i} \rfloor)=O(\sqrt {n})\)，因此复杂度 \(O(Q\sqrt {n})\)。

NOIP 模拟 T4/P9104 [PA 2020] Królewski bal（二分图最大匹配，贪心，调整法）

题意

用矩形若干异或的形式给出一个 \(n\times n\) 的 \(01\) 矩阵，把 \(0\) 看做左部点，\(1\) 看做右部点，如果两个不同值的点在同一行或同一列则连一条边。

有 \(q\) 次修改，每次反转矩阵中一个位置的值，你需要实时维护这个二分图的最大匹配。

\(1\leq n,q\leq 3\times 10^5\)。

题解

最大匹配肯定是不能直接维护的，有两种思路：

1. 维护 \(cnt_{0}-\max\{|S|-|N(S)|\}\)。
2. 维护 \(n^2-\max |S_{独立集}|\)。

实际上联立一下发现两个式子可以化为 \(\max |S_{独立集}|=cnt_1+\max\{|S|-|N(S)|\}\)，这个式子本身可以用调整法说明，即上述两个思路的式子等价，因此我们无需纠结到底用哪个。

考虑维护最大独立集大小，假设我们选择的若干个 \(0\)，那么可以选择与这些 \(0\) 不同行且不同列的的 \(1\)，并且必定全选。

那么贪心地，我们肯定选择若干行和列，并且将这些行和列的交点上的 \(0\) 全选，不在这些行列交点的 \(1\) 全选。

记我们选择的行编号集合为 \(S\)，列编号集合为 \(T\)，同时计算 \(S\) 和 \(T\) 是不好做的，考虑使用调整法求最大独立集。

固定 \(T\) 为全集，删掉若干个 \(t\in T\)。

令第 \(i\) 行的 \(0\) 个数为 \(a_i\)，第 \(i\) 列的 \(1\) 个数为 \(b_i\)，扫描线求得 \(a\) 和 \(b\)。

初始时，最大独立集为 \(\sum\limits_{i\in S} a_i\)。

删掉一个 \(t\)，会删除第 \(t\) 列中行编号在 \(S\) 内的 \(0\)，加上行编号不在 \(S\) 内的 \(1\)。

独立集大小的变化量为列内的 \(S\) 外的 \(1\) 个数减去 \(S\) 内的 \(0\) 个数，即 \(S\) 外 \(1\) 的个数减去 \(|S|\) 再加上 \(S\) 中 \(1\) 的个数，即 \(b_i-|S|\)。

我们发现调整时每列独立，且变化量只与 \(|S|\) 有关。

贪心地，我们枚举 \(|S|\)，选择前 \(|S|\) 大的 \(a\)，之后求 \(\sum \max(0,b_i-|S|)\)。

那么我们可以轻松得到 \(O(nq)\) 的做法。

写一下最大独立集大小的式子，先把 \(a\) 从大到小排序。

\[\max |S_{独立集}|=\max\limits_{x=0}^{n} \{sa_x+\sum\limits_{i=1}^{n} \max(0,b_i-x)\} \\ \max |S_{独立集}|=\max\limits_{x=0}^{n} \{sa_x+\sum\limits_{i=1}^{n} [b_i\geq x]b_i-x\sum\limits_{i=1}^{n} [b_i\geq x]1\} \]

我们发现这个东西可以用线段树维护，具体地令 \(f(x)=sa_x+\sum\limits_{i=1}^{n} [b_i\geq x]b_i-x\sum\limits_{i=1}^{n} [b_i\geq x]1\)，开一颗线段树维护 \(f\)，每次会把 \(a\) 的某一位和 \(b\) 的某一位加减 \(1\)，每次修改实现 \(a\) 的单点加减，实时维护 \(a\) 有序并维护 \(a\) 的前缀和，\(b\) 的修改也是好维护的。

提交记录

二分边界无解时返回的数要符合定义，返回 \(0,n+1\) 而不是 \(1,n\)，写错调了好久（记得 CSP-S 2023 T2 也是这么死的）。

[AGC010F] Tree Game 蓝（博弈论，换根 DP）

题意

有一棵包含 \(N\) 个顶点的树，顶点编号为 \(1\) 到 \(N\)。此外，第 \(i\) 条边连接了顶点 \(a_i\) 和顶点 \(b_i\)。

现在，每个顶点 \(i\) 上放有 \(A_i\) 个石子。高桥君和青木君打算用这棵树进行游戏。

首先，高桥君选择一个顶点，并将棋子放在该顶点上。之后，从高桥君开始，双方轮流进行以下操作：

• 从当前棋子所在的顶点取走一个石子。
• 然后选择一个与当前顶点相邻的顶点，将棋子移动到该顶点。

如果当前棋子所在的顶点没有石子可取，则无法进行操作，该玩家判负。请你求出所有高桥君可以选择并保证获胜的初始顶点编号，并按升序输出。

\(1\leq N\leq \color{red}10^6\)。

标红的原因是原题是 \(3000\)，但是可以做到 \(O(N)\)。

题解

肯定要考虑树上 DP，令 \(f_i\) 表示子树 \(i\) 内，\(i\) 开始是否先手必胜，通过换根求答案。

对于叶子节点，先手无法行走，\(f=0\)。

对于树上的一个节点。

• 如果其叶子节点全部是先手必胜态，那么走到叶子后另一方可以控制节点不出子树，因此这个点先手必败。
• 否则，当前先手必定前往一个先手必败的子树，此时另一方必定不进入子树，即另一方会走回来。也就是说，情况退化为菊花。

对于菊花，是简单的，设菊花根为 \(u\)，叶子中 \(A\) 的最小值为 \(A_{\min}\)，当 \(A_{\min}<A_{u}\) 时先手必胜，否则先手必败。

博弈论限定范围时，只需要考虑先手在最优情况下能否限制后手不走出范围，无需考虑后手尝试走出范围的 case。

提交记录

[AGC025E] Walking on a Tree 黑（构造，欧拉回路）

题意

高桥君计划在树上进行 \(M\) 次散步。第 \(i\) 次散步将按以下方式进行：

• 给定两个顶点 \(u_i\) 和 \(v_i\)。从顶点 \(u_i\) 移动到顶点 \(v_i\)，或者从顶点 \(v_i\) 移动到顶点 \(u_i\)，且同一条边不会被重复经过。

此外，第 \(i\) 次散步的乐趣定义如下：

• 在第 \(i\) 次散步中经过的边中，满足以下任一条件的边的数量：
  • 本次散步中首次经过的边；
  • 之前曾经经过但仅以相反方向经过的边。

高桥君希望通过为每次散步选择方向，使得 \(M\) 次散步的总乐趣最大化。计算最大总乐趣，并构造方案。

\(1\leq N\leq \color{red}10^6\)。

标红的原因是原题是 \(2000\)，但是可以做到 \(O(N\log N)\)。

题解

事实上欧拉路径可以视作添加一条边的欧拉回路，构造时要求：“每条边只经过一次”或“出入度不超过 \(1\)，考虑欧拉回路。

我们希望一条边的两个方向都被经过。如果能实现，则答案取到上界 \(\sum \min(cnt_i,2)\)，其中 \(cnt_i\) 表示第 \(i\) 条边被经过的次数。

手玩一下发现本质上是在 \(u_i - v_i\) 的图上走，每条边只经过一次。一个想法是欧拉回路，假如我们规定每条边在两个方向经过的次数相同，则我们可以把图建出来，对每个连通块跑欧拉回路。

当存在欧拉回路时就做完了，否则，\(u-v\) 图存在若干点的度数是奇数，这些点的个数为偶数个。

实际上每条边正反经过的次数相同这个条件过于严格，例如当 \(M=1\) 时一定无法满足。

我们发现限制每条边经过正反次数的绝对值之差 \(\leq 1\) 也能满足条件，仍然考虑欧拉回路，添加一些边使得每个点的度数都是偶数。

只要满足这些添加的边在树上无（边）交集，即不存在两个边覆盖同一条树边，则这个方案就是合法的。

由于度数为奇数的点个数为偶数，自下而上两两配对，可以归纳证明一定有解，且容易构造加边方案。

提交记录

P8326 [COCI 2021/2022 #5] Fliper 紫（欧拉回路，构造，二分图染色）

题意

现有一个包含 \(n\) 块挡板的旧弹球机。

游戏在二维平面内进行，其中每块挡板与坐标轴所夹锐角总为 \(45^\circ\)，长度为 \(1\) 个单位。挡板用其中心坐标 \((x_i,y_i)\) 和字符 / 或 \ 来表示。小球在碰到挡板后，其运动方向将会旋转 \(90^\circ\)。注意，挡板的两面都可使小球的运动方向发生偏转。

不难发现，当小球处于弹球机中时，它只有两种结局：

• 沿着某一方向一直运动下去而不碰到挡板
• 处于若干个挡板的循环之中

在翻新弹球机的过程中，有四种颜色的染料可供选择。现要将弹球机中的每个挡板进行染色，使得每一个循环内经过每一种颜色的次数相同且为偶数。

请给出一种符合题意的染色方式，或证明这样的染色方式不存在。如果不存在，输出 -1。

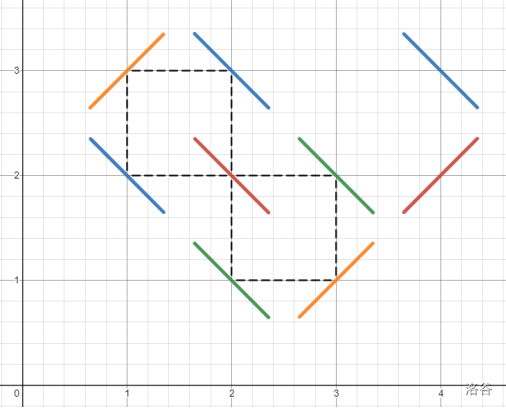
题解

对一个点出边染色/要求出入度相差小于等于 \(1\)，可以考虑欧拉回路。

默认环长是八的倍数，只需要求四个颜色都相等。

首先将挡板正反两侧拆成两个点，建图，先考虑两种颜色怎么做，首先不能二分图染色，因为一个挡板两侧点可能位于二分图不同侧。

直接做不好做，我们观察性质发现每个点的度数 \(\leq 2\)，所以拆点后原图形成若干环和链。

链是不受限制的，先考虑环。

现在我们有 \(n\) 对点，要求每对点颜色相同，考虑点边互换/对偶思想，将环视作点，如果两个点颜色相同则连一条边，本质上我们要对边染色，使得每个点的出边中黑白色相等，跑一个欧拉回路就行了。

现在我们要考虑的是四色，由于默认环一定是八的倍数，所以每个点黑色出边一定是四的倍数。

因此我们把黑色出边的导出子图拿出来在跑欧拉回路，必定有解，白边导出子图同理。

也就是说环长是八的倍数确定有解，现在我们要考虑链，我们把链首尾相接成一个环然后当作环处理，把所有连向链的边都指向这个环，

注意虚点上要连接一些自环满足虚点的度是八的倍数（其实四的倍数就行，因为只需要求虚点的欧拉回路有解就行）。

提交记录

[AGC067D] Unique Matching 黑（唯一匹配增广路性质，DAG 容斥，子问题划分技巧）

题意

定义 \(n\) 个区间是好的，当且仅当：

• \(1 \leq l_i \leq r_i \leq N\)。
• 存在唯一的 \(N\) 阶排列 \(x_1,x_2,\cdots,x_N\)，使得 \(x_i \in \left[ l_i , r_i\right]\)

给定整数 \(N\)、素数 \(P\)。求有多少组 \(\left[l_1,r_1\right],\left[l_2,r_2\right],\cdots,\left[l_N,r_N\right]\) 是好的。答案对 \(P\) 取模。

\(2\leq N\leq 5000\)。

题解

DAG 容斥不只局限于 \(n\leq 15\)，\(m\leq \frac{n(n-1)}{2}\)。

将匹配二分图建出，完美匹配唯一的充要条件是增广路无环。可以通过反证法证明。

现在问题是匹配边不固定，由于区间之间没有区别，不妨设第 \(i\) 个区间匹配数字 \(i\)，最后答案乘上 \(N!\)。

增广路是未匹配边和匹配边交替的路，匹配边即 \(i\leftarrow [l_i,r_i]\)，我们套路的把 \([l_i,r_i]\) 和 \(i\) 缩为一个点，则剩余边即 \(i\to [l_x,r_x]/\{i\}\quad (1\leq x\leq n)\)，要求剩余边组成的图无环。

这样不好处理，我们不妨换一下二分图两侧边的方向，\(i\to [l_i,r_i]\)，这样将 \([l_i,r_i]\) 视作一个点后，未匹配边形如 \(i\to [l_i,r_i]/\{i\}\)。

有向图无环考虑 DAG 容斥，每次加入一些 \(0\) 度点，要求 \(0\) 度即要求不存在其他区间包含这个点。

令 \(f_i\) 表示考虑 \(i\) 个点的方案数，转移时枚举零度点个数 \(j\)，直接从 \(f_{i-j}\) 转移是不好限制的。

我们发现这 \(j\) 个零度点把 \(i\) 个点的序列划分成了若干个不交的段，从这些段转移即可。

具体地：

\[f_i=\sum\limits_{j=1}^{i} \sum\limits_{1\leq v_1<v_2<\dots<v_j\leq i} (-1)^{j+1} \left( (v_1)(i-v_j+1)\prod\limits_{k=2}^{j} (v_k-v_{k-1})^2 \right) f_{v_1-1}f_{i-v_j}\prod\limits_{k=2}^{j} f_{v_k-v_{k-1}-1} \]

式子的含义表示分配区间端点并乘上 \(j+1\) 个独立子问题的 \(f\)。

枚举 \(v\) 的过程相当于序列划分 DP，直接预处理 \(g_{i,j}\) 是 \(O(n^3)\) 的，我们按照传统序列划分方法，设 \(g_i\) 表示 \([1,i]\)，选若干个 \(v\) 且最后一个 \(v=i\) 的带权和（包括 \(-1\) 容斥系数），即可做到 \(O(n^2)\)。

具体地：

\[g_i=if_{i-1}-\sum\limits_{j=1}^{i-1} (i-j)^2 g_j f_{i-j-1} \\ f_i=\sum\limits_{j=1}^{i} (i-j+1) g_j f_{i-j} \]

答案为 \(n!f_n\)。

提交记录

P4099 [HEOI2013] SAO（树上 DP）

题意

给定一个 \(n-1\) 条边 \(n\) 个点的弱连通 DAG，求拓扑序个数，\(1\leq n\leq 1000\)。

题解

DP，令 \(f_{i,j}\) 表示子树 \(i\) 内 \(i\) 的排名是 \(j\) 的方案数，转移时类似《NOIP 模拟 T3（树上 DP）》。

提交记录

P7213 [JOISC 2020] 最古の遺跡 3（分析性质，贡献后置，子问题划分）

题意

你发现了一行古代石柱的废墟及一份古代文献。古代文献上的记载如下：

• 刚建造完成的时候，有 \(2\times N\) 个石柱，对于 \(1\le k\le N\) 均有两个石柱高度为 \(k\)，同时记第 \(i\) 个石柱的高度为 \(h_i\)。
• 会发生 \(N\) 次地震，每次地震会使一些石柱的高度 \(-1\)，其他石柱高度不变。
• 石柱 \(i\) 地震时高度不变，当且仅当 \(h_i\ge 1\) 并且对于 \(j>i\) 都要有 \(h_i\not=h_j\)
• \(N\) 次地震后，恰好只剩下了 \(N\) 个石柱。

现在有仅存的 \(N\) 个石柱的位置 \(A_1,A_2,\ldots,A_N\)，他想让你求出，最初 \(2\times N\) 个石柱高度的修建方案数 \(\bmod~10^9+7\) 的值。

\(1\leq N\leq 600\)，四秒时限。

题解

令 \(b_i\) 表示第 \(i\) 个石柱最后的高度，根据题意有且仅有 \(b_{A_i}\neq 0\)。

考虑如何从 \(h\) 求 \(b\)，首先我们发现最后 \(b\) 会变成一个排列，因为每次都会固定 \(1\sim N\) 恰一个数不动。排列继续进行操作不会受任何影响，所以进行 \(N\) 次操作等价于不断进行操作。

模拟一下发现每个时刻相同高度的石柱最多有两个，且下一步前面的石柱高度会减一。

一个石柱从不变到减少的状态转变，当且仅当：

• 后面某个石柱上一步减少到了这个高度，之后由于相同高度的石柱最多有两个，因此后面的石柱被固定，前面的石柱开始减少。
• 石柱减少到某个位置，后面不存在高度相同的石柱，石柱被固定。

容易发现，高度为 \(i\) 的石柱位置会不断前移，严谨的说：

• 一个后缀中如果出现了高度为 \(i\) 的石柱，则这个后缀在接下来的时间里必定含有高度为 \(i\) 的石柱。
• 反之，一个后缀中没有出现高度为 \(i\) 的石柱，则这个后缀在之前也没有出现过高度为 \(i\) 的石柱。

从后往前考虑，如果 \(i\) 后面的 \(b\) 出现了 \(1\sim h_i\) 的所有整数，那么 \(b_i=0\)，否则，记 \(x\) 表示满足以下条件的最大整数：

• \(x\in[1,h_i]\)。
• 不存在 \(b_j=x\land j>i\)。

那么 \(b_i=x\)，因为上述条件表示 \(i\) 后面高度为 \(x\) 的石柱从未出现过，那么 \(i\) 必定变为高度为 \(x\) 的石柱。

现在我们知道了 \(N\) 个 \(b\neq 0\) 的位置，我们需要对 \(h\) 计数。

但是我们不知道如何根据 \(b\) 求 \(h\) 的方案数，所以直接对 \(b\) 的排列进行计数的方法是没有前途的。

考虑直接对 \(h\) DP，模拟 \(b\) 的生成方式，具体地令 \(f_{i,j}\) 表示 \([i,n]\) 中，\(b\) 出现了 \(1\sim n\) 的所有整数，所对应 \(h\) 的方案数。

我们要干的事情是对 \(h\) 进行匹配计数，\(1\sim N\) 的每个数可以被匹配两次，我们记 \(cnt0_i\) 表示 \(1\sim i\) 中 \(b=0\) 的位置个数。

核心思想：贡献前置、不同高度之间的独立性。

为了计算可以填数的数量，我们把两个相同的 \(i\) 视作本质不同的数字，最后除以 \(2^n\)。

讨论 \(b_i\)：

• 当 \(b_i=0\) 时，\(h_i\leq j\)，\(f_{i,j}\leftarrow f_{i+1,j}\times (2j-(j+cnt0_{n}-cnt0_{i}))\)，表示匹配一个 \(\leq j\) 的数，\(\leq j\) 的中 \(j\) 个数已经被用掉并且 \(b\neq 0\)、\(cnt0_{n}-cnt0_{i}\) 个数被用掉且 \(b=0\)。由于 \(j\) 在从后往前的模拟中递增，限制由紧到松，因此转移逻辑自洽。
• 当 \(b_i\neq 0\) 时：
  • 当 \(b_i>j+1\) 时，考虑延迟贡献这一部分，先不管，\(f_{i,j}\leftarrow f_{i+1,j}\)。
  • 当 \(b_i=j+1\) 时，如果 \([j+2,k]\) 在后面都出现过且 \(k+1\) 没有出现过，则 \(f_{i,k}\leftarrow f_{i+1,j}\)。在这里，我们需要处理之前 \(h_i>j+1\) 所带来的贡献。有 \(j+1\leq b_i\leq k\)。
    • 枚举 \(k\)，计算 \([j+2,k]\) 都出现的方案数，这部分与之前的状态独立，因此可以直接乘起来。
    • 记 \(suf_1=(n-i)-(cnt0_n-cnt0_i)\)，我们需要在 \(j-suf_1\) 个数中选 \(k-j-1\) 个数，要求这 \(k-j-1\) 个数排成连续段，则有 \(f_{i,k}\leftarrow f_{i+1,j}\binom{suf_1-j}{k-j-1}(2(k-j+1)-(k-j-1))g_{k-j-1}\)，其中 \(g_i\) 表示 \(i\) 个数最后形成的 \(b\) 排成连续段的方案数。容易发现在这次转移后所有未确定的石柱高度都 \(>k\)，所以这些石柱不会对当前 \(k-j-1\) 个数排成连续段造成任何影响，即 \(g\) 完全独立。

考虑如何求 \(g_i\)。考虑类似区间 DP 的子问题划分结构，枚举最后一个被固定的石柱的高度，\(g_{i}=\sum\limits_{j=1}^{i} g_{j-1}g_{i-j}\binom{i-1}{j-1}(2(i-j+1)-(i-j))\)。

时间复杂度 \(O(N^3)\)，常数极小可以通过。

启示：

1. 当 DP 遇到无法处理的 case 时（通常是对另一种转移有后效性），不管这个贡献，放到受影响的转移 case 中后置处理。
2. 不知道如何拆分子问题时，可以考查个别数，例如如果把第一个/最后一个满足某条件的元素拿走会怎么样。

提交记录

NOIP 模拟 T3

题意

汤圆的世界可以被看作是一棵以 \(1\) 为根的有根树，节点编号 \(1\sim n\)，每个点的父亲编号小于自己。

雨一共会下 \(m\) 个时刻，它的扩散规律如下所述：

• 在第 \(1\) 时刻开始时，节点 \(1\) 会被淋湿。
• 在第 \(2\sim m\) 时刻开始时，每个在前一时刻自己或父亲是湿的的节点会被淋湿。

在第 \(i\) 时刻结束前，汤圆会把以 \(a_i\) 为根的子树擦干，此时它们不再是湿的。
由于汤圆的能力不是无限的，他并不能把根节点擦干，并且也不是每个时刻他会擦干一棵子树。

形式化地说，序列 \(a\) 中没有 \(1\)，并且可能存在 \(0\)。对于 \(a_i=0\)，在 \(i\) 时刻汤圆什么都不会做。

现在汤圆想要知道，对于每个 \(1\sim n\) 的节点，在这 \(m\) 个时刻中它在多少时刻结束时是湿的。

\(1\leq n\leq 1000000\)。

题解

崭新的维护方式。

对于一个点维护一个数组 \(b_i\)，\(b_{i,x}\) 表示点 \(i\) 在 \(x\) 时刻是否是湿的。

考虑一个点在 \(t\) 时刻处于湿状态的充要条件，点 \(i\) 在 \(t\) 时刻湿，需要同时满足：

• \(a_{t}\neq i\)
• \(b_{fa_i,t-1}=1\)
• \(b_{fa_i,t}=1\)

因此 \(b\) 从父亲转移进儿子时，会删除每个 \(1\) 连续段头部的 \(1\)，也即将每个 \(0\) 连续段扩展 \(1\)。

每个 \(0\) 的贡献是一个关于深度的一次函数。

dfs 维护，具体地维护一个 set 表示当前点 \(b\) 的每个 \(0\) 开始段，只维护由“擦干操作”产生的初始 \(0\)，加入时的操作时 set 维护相邻信息的经典套路，一段信息对应到深度线段树上是区间加等差数列，也是好维护的。

撤销时直接暴力撤销即可。

提交记录

CF995F Cowmpany Cowmpensation *2700（容斥，子集反演（二项式反演））

题意

给定一棵树，给树上每个点赋一个 \([1,D]\) 的值，使得父亲的值大于等于儿子的值。输出方案数对 \(10^9+7\) 取模后的结果。

\(1\leq n\leq 3000\)。

题解

一开始想了两个思路，一个是把 \(=\) 合并之后转拓扑序计数，一个是树上背包维护这个点在子树的相对排名，前者状态就是 \(n^3\) 的，后者状态 \(O(n^2)\) 转移 \(O(n)\)，且转移系数不弱于组合数，不可优化。

回归原本的思路，我们希望记录树上使用了 \(k\) 个值的方案数，为了避免计重需要维护相对排名，即出现 \([1,k]\) 的每个值的方案数，最后乘上 \(\binom{D}{k}\)。

要求出现每个值，可以考虑容斥（子集反演），对于 \([1,k]\) 的每个子集算出至多使用子集中的数的方案数，之后容斥。

显然方案数只和子集大小有关，因此容斥是容易的，具体地记 \(f_i\) 表示子树 \(i\) 内至多只用 \([1,i]\) 且根节点的值为 \(i\) 的方案数，\(f\) 可以树上 DP 求出，\(g_i\) 表示整棵树恰好使用 \([1,i]\) 的方案数，则有：

\[g_{i}=\sum\limits_{j=0}^{i} (-1)^j\binom{i}{j}f_{1,i-j} \\ ans=\sum\limits_{i=1}^{n} \binom{D}{i}g_i \]

也可以理解成钦定 \(j\) 个数不出现然后做二项式反演。

类似的题还有【ZJOI 小星星】。

提交记录

CF1895F Fancy Arrays（区间有交容斥，差分数列性质）

题意

给定 \(n\)、\(x\) 和 \(k\)，对满足以下条件的长度为 \(n\) 的非负整数数组 \(a\) 计数，对 \(10^9+7\) 取模：

• 数组中至少出现了 \(x, x+1, \ldots, x+k-1\) 中的某一个数；
• 数组中相邻元素的差的绝对值不超过 \(k\)（即对于每个 \(i \in [2, n]\)，都有 \(|a_i - a_{i-1}| \le k\)）。

题解

首先肯定要容斥，如果使用总方案数减去不合法方案数，那么实际上是无穷减无穷的容斥，并不可做。

考虑 \(x\sim x+k-1\) 的数有什么性质，显然我们不可能跨过这个区间，即我们记区间最小值为 \(mn\)，最大值为 \(mx\)，则合法序列的充要条件是 \([mn,mx]\cap [x,x+k-1]\neq \emptyset\)。

令 \(L=x,R=x+k-1\)，对区间有交进行容斥，与 \([L,R1]\) 相交的区间等于 \(l\leq R\) 的区间减去 \(r<L\) 的区间。

后者直接矩阵快速幂即可，前者限制最小值，考虑对差分序列计数，由于最小值加差分序列必定能唯一确定原序列，因此这部分答案可以直接算，为 \((x+k)(2k+1)^{n-1}\)。

事实上差分序列加任意位置（不只局限于 \(a_1\)）的值都能唯一确定原序列。

提交记录

[ARC195D] Swap and Erase（分析性质）

题意

1. 交换操作：设操作前 $ A $ 的长度为 $ K $。选择满足 $ 1 \leq i \leq K - 1 $ 的整数 $ i $，交换 $ A $ 的第 $ i $ 项和第 $ (i+1) $ 项。
2. 删除操作：设操作前 $ A $ 的长度为 $ K $。选择满足 $ 1 \leq i \leq K $ 且 $ A $ 的前 $ i $ 项全部相等的整数 $ i $，删除 $ A $ 的前 $ i $ 项。

请求出将 $ A $ 变为空数列所需的最小总操作次数，\(1\leq N\leq 2\times 10^5\)。

题解

被蓝题击败了，怎么回事呢？

各种 DP 直接做都行不通，考虑分析性质。

答案是交换次数加上相同值连续段个数。

分析性质没有思路时，不妨先考虑特殊情况。

如果只允许交换一个数，段数最多减少 \(2\)，欲使答案减少，这个数被交换次数最多不超过 \(1\)。

假设最优解形态存在一个数被交换多次，先把这个数调回原位，之后只调整这个数必定能得到最优解，而只有一个数能交换的情况就是上述分析的情况。

存在多个数被交换多次可以按上述方法调整证明。

因此直接 DP 即可。\(dp_{i,0/1}\) 表示 \([1,i]\)，\(i\) 是否和前面数交换的答案。

提交记录

[ARC195E] Random Tree Distance

题意

给定一个整数列 \(A = (A_2, A_3, \ldots, A_N)\)。对于每个满足 \(1 \leq P_i \leq i-1\)（\(2 \leq i \leq N\)）的整数序列 \(P = (P_2, P_3, \ldots, P_N)\)，定义以顶点 \(1\) 为根的 \(N\) 顶点带权树 \(T(P)\) 如下：

• 对于每个 \(i\)（\(2 \leq i \leq N\)），顶点 \(i\) 的父节点为 \(P_i\)，且连接 \(i\) 与 \(P_i\) 的边权值为 \(A_i\)。

现需处理 \(Q\) 个查询。第 \(i\) 个查询形式如下：

• 给定两个整数 \(u_i, v_i\)（\(1 \leq u_i < v_i \leq N\)），求所有可能的 \((N-1)!\) 种 \(P\) 序列对应的树 \(T(P)\) 中，顶点 \(u_i\) 与 \(v_i\) 之间距离的总和对 \(998244353\) 取模后的结果。

题解

首先枚举 \(\text{lca}\) 肯定不可行，考虑使用期望的线性性质把答案拆为 \(\mathbb{E}(dep_{u})+\mathbb{E}(dep_{v})-2\mathbb{E}(\text{lca}(u,v))\)。

设 \(f_i\) 表示 \(\mathbb{E}(dep_{i})\)，则有：

\[f_i=A_i+\frac{1}{i-1}\sum\limits_{j=1}^{i-1} f_{j} \]

问题是如何求 \(\text{lca}\) 深度的期望，直接 DP 的话状态是二维的。

一个 naive 的尝试是枚举 \(\text{lca}\) 计算，并统计所有 \(v\) 到根连的概率和。如果这么做，你会发现概率由编号在 \((u,v)\) 和 \((1,u)\) 的点贡献，且两部分贡献独立，具体地假设选的点集是 \(S\)，那么贡献为 \(\sum\limits_{i\in S} \frac{1}{i-1}\)。由于这个方法没有前途（其实就是我用这个方法没推出来（逃））因此不做展开。

由于两部分贡献互相独立，因此设 \(t\) 表示 \(v\) 到根连第一个 \(\leq u\) 的值，则 \(t\) 在 \([1,u]\) 中均匀独立，即 \(\mathbb{E}(dep_{\text{lca}(u,v)})=\frac{1}{u}\sum\limits_{i=1}^{u}\mathbb{E}(dep_{\text{lca}(u,i)})\)。

到这里还是不好推，我们发现式子右侧和 \(v\) 无关，为了减少状态量，我们先进行如下转化：\(\mathbb{E}(dep_{\text{lca}(u,v)})=\mathbb{E}(dep_{\text{lca}(u,u+1)})\)。

令 \(g_u=\mathbb{E}(dep_{\text{lca}(u,u+1)})\)，考虑递推，枚举 \(u+1\) 的父亲，可得：

\[g_u=\frac{f_{u}}{u}+\frac{1}{u}\sum\limits_{i=1}^{u-1} \mathbb{E}(dep_{\text{lca}(i,u)}) \]

沿用刚刚的结论，得到：

\[g_u=\frac{f_{u}}{u}+\frac{1}{u}\sum\limits_{i=1}^{u-1} \mathbb{E}(dep_{\text{lca}(i,i+1)}) \\ g_u=\frac{f_{u}}{u}+\frac{1}{u}\sum\limits_{i=1}^{u-1} g_i \]

提交记录

MX-NOIP 模拟 T3（排列 DP，状态设计优化）

题意

求出有多少个 \(1 \sim n\) 的排列 \(a_1, \ldots, a_n\) 满足以下条件：

对于每个下标 \(i\)（\(1 \le i \le n\)），

0. \(a_i < \min_{j < i} a_j\) 或
1. \(a_i > \max_{j < i} a_j\) 或
2. \(a_i < \min_{j > i} a_j\) 或
3. \(a_i > \max_{j > i} a_j\)。

对每个下标 \(i\)，其满足四种情况中的哪一种由输入给出。答案对 \(998244353\) 取模。约定 \(0\) 个数的 \(\min\) 为 \(+\infty\)，\(0\) 个数的 \(\max\) 为 \(-\infty\)。

\(1\leq n\leq 5000\)。

题解

VP 获得 \(70\) 分，怎么回事呢。

永远不要忘记排列 DP 的两种状态维护方法——绝对大小和相对大小。

按值域 DP 没有什么前途，考虑按位置 DP，假设 \([1,i]\) 已确定，注意到 \(op_{i+1}=2/3\) 时第 \(i+1\) 位填法有且仅有一种，且为当前未出现数字中最小/最大的一个，记 \(f_{i,j,k}\) 表示 \([1,i]\) 中最小值为 \(j\) 最大值为 \(k\) 即可 \(O(n^3)\)，如果只记录最小值可以做到 \(O(n^2)\) 并通过特殊性质 BC。

考虑特殊性质 A，不难发现答案恰好为 \(1\)，原因是每一位与前面数字的相对大小固定，现在我们获得了 \(70\) 分。

我们刚刚设计状态时维护的是前面数字绝对大小的信息，考虑换一个思路，维护相对大小。

容易发现对于任意前缀，把 \(op\in \{0,1\}\) 的位置拿出来，它们的相对大小固定。

考虑此时插入一个 \(op=2\) 的数字，那么此时后面的数都必须大于这个数，因此相对大小比这个数小的位置就废掉了，这些数的绝对大小在此刻已经确定。

\(op=3\) 同理，因此令 \(f_{i,j}\) 表示 \([1,i]\) 中有 \(j\) 个数字绝对大小未确定的方案数。

对于 \(op_{i+1}=0/1\)，\(f_{i,j}\to f_{i+1,j+1}\)。

对于 \(op_{i+1}=2/3\)，\(f_{i,j}\to f_{i+1,x}\ (0\leq x\leq j)\)。

但是这样是有漏洞的，如果 \(op\) 出现 \(31\) 或 \(20\) 子序列，我们的 DP 会默认 \(op=1/2\) 的位置可以填入数字，实际上是不行的，不难发现当且仅当出现这种情况时无解，直接特判输出 \(0\) 即可。

另一种思路是，对 \(O(n^3)\) 的 DP 式子优化，发现转移只和 \([j=1],[k=n],k-j+1\) 有关，可以直接优化。

MX-NOIP 模拟 T4（DP 套最优化）

题意

在最后一个暑假，羽未在绘画日记留下了这么一个题目：

给定一个 \(B\)（\(B \ge 2\)）进制的正整数 \(N\)，你可以进行操作：

• 选定两个相邻的、且和不超过 \(B-1\) 的两个数码。删除它们，并在原位置插入它们的和。

求在有限次操作内，\(N\) 能变成的最小可能值。

记上面问题的答案是 \(f_B(N)\)。

给定正整数 \(B\)和两个 \(B\) 进制下的正整数 \(L,R\)，求 \(\sum_{i=L}^R f_B(i)\)，对 \(998244353\) 取模。

多测，令 \(n_R\) 表示 \(R\) 在 \(B\) 进制下的长度。保证 \(\sum B\cdot n_R\leq 10^7\)。

题解

考虑 \(L=R\) 怎么做，我们希望让位数最小的前提下字典序最小，从后往前用栈合并即可，原序列必定被分割成若干段，每段合并成一个数，最后一个分割线往左移动必定更优，可通过调整法证明。

DP 套最优化，先做 B 性质，\(f_{i,j,k}\) 表示低 \(i\) 位，栈顶元素是 \(j\)，栈大小是 \(k\) 的答案之和，同时记 \(g\) 表示其方案数。

发现最优化合并方向和增量维护数字的方向相反，不会优化 \(k\)，寄。

将 \(g\) 的定义修改为 \(\sum B^k\) 之和，由于栈顶元素会变，因此不把栈顶元素贡献计入状态。

\[f_{i,j}=\left (\sum\limits_{j+k\geq B} f_{i-1,k}+g_{i-1,k}\times k\right )+\left (\sum\limits_{k\leq j} f_{i-1,k}\right ) \\ g_{i,j}=\left (B\sum\limits_{j+k\geq B} g_{i-1,k}\right )+\left (\sum\limits_{k\leq j} g_{i-1,k}\right ) \]

对于一般情况，加一个是否超出数位限制的 \(0/1\) 状态就做完了。

这启示我们维护方案数的 DP 数组不只局限于维护方案数，实际上这个数组可以维护任何独立状态的系数和。

提交记录

CF2165C Binary Wine 蓝（堆优化贪心）

题意

给定 $ n $ 个整数 $ a_1,a_2,\ldots,a_n $，范围在 $ [0,2^{30}) $ 内。

你可以花费 $ 1 $ 枚硬币将任意 $ a_i $ 增加 $ 1 $。你可以执行此操作任意多次。

你需要解决 $ q $ 个查询；对于每个查询，你会得到一个整数 $ c $，范围也在 $ [0,2^{30}) $ 内。你希望存在一个长度为 $ n $ 的序列 $ b $，满足以下性质：

• 对于每个 $ 1\le i\le n $，有 $ 0\le b_i\le a_i $。
• $ b_1\oplus b_2\oplus\ldots\oplus b_n=c $。

请计算你需要花费的最少硬币数量，使得存在一个合适的 \(b\)。

询问间独立，\(n\leq 5\times 10^5\)，\(q\leq 5\times 10^4\)。

题解

显然是取后 \(30\) 个数随便搞搞的题，但是为什么我没过呢。

本质上是让每个数匹配若干位使得浪费最少，从高位到低位考虑，设当前位为 \(k\)，假设目前最大数 \(\geq 2^{k}\)，那么可以直接匹配，否则，将这个数减去这一位的值。

赛时并没有使用堆模拟，直接扫了两遍显然是不对的，用堆模拟一下就对了。

提交记录

QOJ401. 因子统计（阶乘分解质因数，前缀和）

题意

你有 \(q\) 组询问，每组询问你需要计算出组合数 \(\binom{n}{m}\) 的因子数量，对 \(p=10^9+7\) 取模。

\(n\leq 10^6\)，\(q\leq 5\times 10^5\)，2s。

题解

有结论：

\[\sum\limits_{i\leq n}\frac{1}{\ln i}=O(\frac{n}{\ln n}) \]

因子数量相当于所有质因子指数加一的乘积，考虑对每个质数求出这个质数的指数，可以阶乘分解质因数，单个 \(p\) 复杂度为 \(O(\log_p n)\)。

对于 \(p\leq \sqrt{n}\)，\(p\) 的贡献为 \(\lfloor\frac{n}{p}\rfloor -\lfloor\frac{m}{p}\rfloor -\lfloor\frac{n-m}{p}\rfloor\)，可以直接计算，对于 \(p\leq \sqrt{n}\)，直接暴力的复杂度是 \(O(\frac{1}{\ln n}\times \sum\limits_{i\leq \sqrt{n}}\frac{\ln n}{\ln i})=O(\sum\limits_{i\leq \sqrt{n}}\frac{1}{\ln i})=O(\frac{\sqrt n}{\ln n})\)。

对于 \(p>\sqrt{n}\)，容易发现 \(\lfloor\frac{n}{p}\rfloor -\lfloor\frac{m}{p}\rfloor -\lfloor\frac{n-m}{p}\rfloor\leq 1\)，若有 \(k\) 个 \(p\) 的贡献不为 \(0\)，则这部分总贡献为 \(2^k\)。

直接算是 \(O(\sqrt n)\) 的，整除分块不可优化，考虑预处理，枚举每个 \(p\)，维护 \(sum_i=\sum\limits_{p} \lfloor\frac{i}{p}\rfloor\)，一个 \(p\) 对 \(sum\) 差分数组的贡献是 \(\frac{\max n}{p}\) 的，只枚举 \(>\sqrt n\) 的 \(p\)，这部分可以 \(O(\max n)\)。

提交记录

QOJ14419. Maximum Segment Sum（反射容斥）

题意

Calculate the number of sequences of \(−1\) and \(1\) of length \(n\) with maximum subsegment sum k. Solve this task for all \(k\) from \(0\) to \(n\), and print the answers modulo \(998 244 353\). The empty subsegment is considered too.

\(n\leq 5\times 10^5\).

题解

反射不只用于容斥。

先简单容斥，改成最大子段和 \(\leq k\) 的序列个数。

考虑格路计数，直接格路计数不好做，考虑求最大子段和的过程。

令 \(cur=0\)，每次遇到一个数，令 \(cur\leftarrow \max(0,cur+a_i)\)。

这反映到格路上是不能跨过 \(y=k\)，往下走要对 \(0\) 取 \(\max\)。

对 \(0\) 取 \(\max\) 其实是不好做的，但实际上这相当于把路径关于 \(y=-\frac{1}{2}\) 反射。即将路径第一次被 \(chkmin\) 视作穿过 \(y=-\frac{1}{2}\)，之后全部取反。

因此原问题转化为不能跨过 \(y=k\) 和 \(y=-k-1\)，双限制格路计数可以在 \(O(\frac{n}{k})\) 的复杂度解决单次询问，总复杂度 \(O(n\ln n)\)。

提交记录

NOIP 模拟 T3（树上 DP，拆贡献）

题意

有一颗树，每条边长度为 \(1\)，移动代价为 \(w_i\)。

A 国初始选择了 \(m\) 座城市，并在这些城市上各建造一座军营，其中第 \(i\) 座军营建造在城市 \(a_i\)。

A 国每次可以选择第 \(i\) 条边，将一座位于城市 \(u_i\) 的军营，移到城市 \(v_i\) 或将一座位于城市 \(v_i\) 的军营，移到城市 \(u_i\)，要求移到的城市这次移动前没有建造军营。此外，这次移动军营的代价是为 \(w_i\)。

A 国希望制定一个移动军营的方案，使得最终每个点到其最近的军营距离 \(\leq k\)。

\(1\leq m,k\leq n\leq 5000\)，\(m,k\leq 100\)。

题解

直接维护移动过程是不好做的，先做链的部分分，发现将 \(a\) 排序后，如果最终局面固定，记 \(f_{i,j}\) 表示第 \(i\) 个位置放置第 \(j\) 个军营的答案，单调队列优化即可做到 \(O(nm)\)。

考虑如何简单的完成链的部分分，考虑按军营单步转移，判断这个位置放不放军营的依据是是否存在之前的军营能覆盖到这里。

令 \(f_{i,j}\) 表示前 \(i\) 个军营，往后覆盖到 \(j\) 的答案，转移用填表法，使用后缀和优化。

从链的做法受到启发，考虑正解，拆每条边的贡献以计算总贡献。

设计树上 DP，我们只关心当前子树的军营个数和能往外覆盖多少个点，令 \(f_{u,i,j}\) 表示子树 \(u\) 内有 \(i\) 个军营，能往子树外覆盖 \(j\) 个点。

若 \(j<0\) 说明存在一个和子树根深度差 \(-(j+1)\) 的点未被覆盖。

转移枚举当前点是否放置军营，第二维是树上背包，第三维可以前缀和优化，时空复杂度 \(O(nmk)\)。（其实可以把空间复杂度做到 \(O(n+mk)\)）。

具体地，初值有 \(u\) 点放置或不放置两种情：

\[f_{u,0,-1}=f_{u,1,k}=0 \]

转移有：

\[y'\leftarrow y-1 \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,\max(j,y')}\quad (j,y'\geq 0) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,j}\quad (j\geq 0,y'< 0,j\geq -(y'+1)) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,y'}\quad (j\geq 0,y'< 0,j <-(y'+1)) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,y'}\quad (j< 0,y'\geq 0,y'\geq -(j+1)) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,j}\quad (j< 0,y'\geq 0,y'< -(j+1)) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,\min(j,y-1)}\quad (j,y'< 0) \]

整理。

\[f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,j}\quad (j\geq y-1\geq 0) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,j}\quad (j\geq 0,y-1< 0,y-1\geq -j-1) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,j}\quad (j\leq y-1< 0) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,j}\quad (j<0,y-1\geq 0,y-1<-j-1) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,y-1}\quad (y-1\geq j\geq 0) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,y-1}\quad (y-1\geq 0,0>j\geq -y'-1) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,y-1}\quad (y-1\leq j< 0) \\ f_{u,i,j}+f_{v,x,y}+w|cnt_v-x|\to f_{u,i+x,y-1}\quad (y-1< 0,0\leq j<-y'-1) \]

前缀和优化即可。

提交记录

NOIP 模拟 T2（随机化，二分答案）

题意

Hmr 发现了一个宝石装置，并对其进行了研究：

这个装置由 \(n\) 颗宝石组成，依次编号为 \(1,2,\dots,n\)。

这些宝石之间由总计 \(m\) 条路径连接。其中第 \(i\) 条路径可以由 \((u_i,v_i,a_i,b_i,x_i)\) 五个参数组成，代表着，在第 \(u_i\) 个宝石被激活之后，这条路径将会开始运作，在 \(a_ix_i+b_i\) 单位时间后，\(v_i\) 也将会被激活。其中 \(u_i,v_i,a_i,b_i\) 是固定的，\(x_i\) 可以由 Hmr 设置成任意非负实数。

Hmr 可以在 \(0\) 时刻主动使用魔力激活任意一个节点 \(S\)，然后宝石装置将会通过路径激活其他的宝石。如果一个宝石在不超过 \(V_i\) 时刻激活了，那么称这个宝石是有效的。

如果有效的宝石数量不小于 \(K\)，那么这个装置将会开始工作，并释放出 \(\min\limits_{i=1}^mx_i\) 的能量。求这个装置最多可以释放多少能量。

题解

赛时建反图加剪枝，然后发现没有优化前途。

注意到每个点是独立的，因此对每个点分别二分答案，取 \(\max\)。

以随即顺序枚举每个点，这样加最优化剪枝后，期望下只用做 \(O(\log n)\) 次二分，因为随机序列的前缀严格最大值期望为 \(O(\sqrt n)\)。

NOIP 模拟 T1（DP 状态简化）

题意

现在有一根长度为 \(n\) 的 Pocky，其中从左往右数第 \(i\) 单位长度 Pocky 的美味值为 \(a_i\)。现在 Mdk 和 Hmr 决定吃掉这根 Pocky，Mdk 从左往右吃，Hmr 从右往左吃。

• Mdk 先开始吃，她会从左侧吃 \(1\) 或 \(2\) 单位长度的 Pocky。
• 接下来，如果上一个人吃了 \(k\) 单位的 Pocky，则下一个人可以吃 \(k\) 或 \(k+1\)（如果剩余长度 \(\ge k+1\)）单位的 Pocky。
• 如果剩下的 Pocky 长度小于 \(k\)，则这个游戏将会停止。

双方都想要最大化自己吃掉的 Pocky 的美味值减掉对方吃掉的 Pocky 的美味值，问在双方都使用最优策略的情况下，Mdk 吃掉的 Pocky 的美味值减去 Hmr 吃掉的 Pocky 的美味值将会是多少？

\(n\leq 4000\)，1s，256MB。

题解

\(O(n^2\sqrt n)\) 的 DP 是平凡的。

分析一下发现状态数不是很多。赛时分析了区间长度，发现没有进展。

分析两侧的差值，发现两侧取数个数差值不超过 \(k\)，因此总状态数为 \(O(nk^2)=O(n^2)\)。

NOIP 模拟 T3（根号平衡，扫描线）

题意

维护长为 \(n\) 的静态序列，\(Q\) 次询问求一个区间 \(L,R\) 的每个子区间的第 \(c\) 大和。

\(c\) 每次询问相同，\(n\leq 1.5\times 10^5\)，\(Q\leq 2\times 10^5\)，\(c\leq 50\)。

部分分：\(c\leq 5\)。

题解

首先找出 \(nc\) 个矩形，跑历史和扫描线可以获得部分分。

考虑将矩形加法视作对下标贡献的一次函数，可以减小常数。

具体地每个点维护三个值 \(x,k,b\)，扫描线移动时，修改时对区间的 \(k\) 和 \(b\) 做加操作，查询时求前缀和的前缀和，推一下式子需要维护 \(\sum k_i,\sum b_i,\sum ik_i,\sum ib_i\)。

修改总复杂度 \(O(nc\log n)\)，查询总复杂度 \(O(Q\log n)\)，考虑根号平衡，用 \(O(1)\) 修改 \(O(\sqrt n)\) 查询的分块实现上述数据结构，即可做到 \(O(nc+Q\sqrt{n})\)。

NOIP 模拟 T4/CF1060G Balls and Pockets *3400（平衡树）

题意

Mdk 发现了一个可数无穷长的队列，其中队列从左往右数第 \(i\) 个元素初始编号为 \(i\)。

Mdk 想要对序列进行 \(d\) 次操作，每一次操作描述如下：

她会同时删掉队列中的 \(n\) 个元素，它们分别是从左往右数的第 \(a_1,a_2,\dots,a_n\) 个元素，空缺的位置将由右侧的元素来补齐。

Mdk 想要知道最后某几个位置的元素的编号，但是她现在并没有时间，所以她希望你来告诉她。她会给你 \(Q\) 个位置 \(x_i\)，希望你能够回答 \(d\) 次操作之后，从左往右数第 \(i\) 个数的编号是多少。

\(n,Q\leq 5\times 10^5\)，\(1\leq a_i,d\leq 10^{12}\)。

题解

二分答案正序模拟可以获得 \(70\) 分。

发现二分继续优化唯一途径是整体二分，而答案值域为 \(O(nd)\)，不可优化。

考虑正序模拟，可以把序列划分为若干段，第 \(i\) 段进行倒序模拟一轮后会加上 \(i-1\)。

还是不好优化，考虑这些区间有什么性质。

跳段问题考虑先把询问跳到第一个跨过当前段的位置，以缩减信息规模。

这样做完后，每个点在所处段（记为第 \(id\) 个段）的第 \([1,id-2]\) 个位置，记这些点再跳到下一个段的次数是 \(v\)，容易发现，由于这些点下标差严格小于 \(id\)，所以不同点 \(v\) 的极差不超过 \(1\)，且取值单调，把点按位置分为两部分 \(A,B\)，进一步的，经过一轮模拟后，\(A,B\) 点的大小关系交换。

考虑直接使用文艺平衡树维护这个操作，具体地我们需要实现按值分裂，子树加减，找出 \(<0\) 的位置。

前两个操作是平凡的，找出 \(<0\) 的位置可以维护子树 \(\min\) 后直接暴力，和势能线段树复杂度分析本质相同，总复杂度 \(O((n+Q)\log (n+Q))\)。

提交记录

CF2157E Adjusting Drones *2300（模拟，序列并查集）

题意

你管理着一支由 \(n\) 架无人机组成的机队，这些无人机的能量值分别为 \(a_1, \ldots, a_n\)。同时，给定一个正整数 \(k\)，表示最多允许多少架无人机拥有相同的能量值。

为了防止过载，无人机队会自动进行能量平衡操作。具体来说，只要存在某个特定的能量值在所有无人机中出现严格超过 \(k\) 次，就会按照如下步骤进行能量平衡操作：

• 首先，如果一架无人机 \(i\) 满足它的能量值 \(a_i\) 在它之前已经出现过（即存在某个 \(j < i\) 使得 \(a_j = a_i\)），则标记它；
• 然后，对每架被标记的无人机，将其能量值增加 \(1\)；
• 最后，清除所有标记。

如果仍然存在某个特定的能量值在所有无人机中出现严格超过 \(k\) 次，上述过程就会再次执行，直到任何特定的能量值在所有无人机中出现都不超过 \(k\) 次。

题解

赛时把模拟过程看成了序列循环，寄。看来以后分析性质需要理解一下，而不是只找规律。

首先这道题只和 \(cnt\) 有关，\(cnt\) 非零连续段为 \(1\) 是好做的，第一反应是模拟 \(n\) 次后直接做。

分析模拟时的性质，一个 \(cnt\) 会往后移，遇到 \(0\) 时减一。

使用序列并查集维护每个位置下一个 \(0\) 在哪，即可模拟。

进一步发现模拟复杂度严格不大于 \(\sum cnt=n\)，因此不需要模拟 \(n\) 次后做，直接二分后模拟即可。

提交记录

[NOIP2023] 双序列拓展（Ad-hoc，递归分治，子问题划分）

题解

先转为二维平面问题，思考特殊性质，发现能到达 \(x=n-1\) 或 \(y=m-1\) 就合法。

推广，找出 \(x\) 的全局最小值，如果其大于 \(y\) 的全局最小值，则无解，否则可以将平面分为两部分。

由于只能向右或向下，考虑同理找 \(y\) 的全局最大值，这样可以将矩形分为四部分，递归左上和右下即可。

递归内部只用将矩形分为两部分往下递归即可，因为只要求到达边界。

提交记录

[CSP-S 2019] Emiya 家今天的饭

题解

被 CSP-S2025T1 创飞，所以来做这个题。

注意到超过 \(\lfloor \frac{n}{2}\rfloor\) 的食材只有一个，随便容斥一下即可。

提交记录

[NOIP2024] 树的遍历（计数，去重技巧）

题解

容易发现，链的答案为 \(1\)，\(k=1\) 时的答案为 \(\prod (deg_i-1)!\)，表示可以任意决定儿子边的访问顺序。

考虑菊花，此时生成树是一个链，且关键边必定是链头或链尾部，在链尾算贡献，答案为 \(\prod\limits_{i=1}^{k} (n-2)!-(i-1)(n-3)!\)。

对于一般情况，考虑选取代表元计数，首先要搞清楚一个生成树可能的起始边都有哪些。

若父边是可能的起始边，则其子边中，有且只有最后一个遍历的子边符合条件。

同时这里的父子关系是不重要的，所以知道一个符合条件的起始边，就能推出一个叶子到叶子的链。

对于链上的点有顺序限制，链上点贡献为 \(\prod (deg_i-2)!\)，其余点为 \(\prod (deg_i-1)!\)（令 \((-1)!=1\)）。

把链上点点权视为 \((deg_i-1)^{-1}\)，这个问题是可 DP 的，时间复杂度 \(O(n)\)。

提交记录

[NOIP2021] 方差（观察性质，DP）

题解

推式子略去（逃。

操作转为交换差分数组，打表发现差分数组单谷。

证明大概是推式子后发现影响差分数组 \(d\) 分布的式子形如 \((\sum id_i)(\sum (n-i)d_i)\)，可以打表说明。

写出答案的式子：

\[n\sum_i a_i^2 - (\sum_i a_i)^2 \]

发现平方项难处理，考虑将式子的后半部分放入状态，另一部分放入状态的值，即：记 \(f_{i,x}\) 表示 \(\sum_i a_i=x\) 的最小 \(\sum_i a_i^2\)。

则有填左侧和填右侧两种转移。

\[f_{i,x}+2d_i x+id_i^2\to f_{i+1,x+id_i} \\ f_{i,x}+s_i^2\to f_{i+1,x+s_i} \]

\(O(n^2V)\)，有 \(88\) 分。

发现 \(d=0\) 时啥也不干因此实际复杂度是 \(O(\min(n,a)nV)\)。

提交记录

NOIP 模拟 T1（异或，位运算）

题意

小 \(\delta\) 喜欢异或。因此，他想到了这样一个问题：给定非负整数 \(l,r\)，满足 \(l \le r\)。你需要告诉他，对于所有 \(l \le l' \le r' \le r\)，\(\bigoplus\limits_{i=l'}^{r'} i\) 的结果的种类数。多测，\(T\leq 10^3\)，\(1\leq l,r\leq 10^{18}\)。

题解

先转化为前缀异或，然后发现前缀异或满足模 \(4\) 性质，第 \(4k\sim (4k+3)\) 的前缀异或和分别为 \(4k,1,4k+3,0\)。

考虑从中选数异或，对于 \(4k,4k+3\)，其右移两位后是一个区间，其余情况也可以拆为 \(O(1)\) 个区间。

即我们需要处理的问题是 \([l1,r1],[l2,r2]\) 两个区间的异或卷积，最后取并。

处理方法是把区间拆为若干个形如 \([n2^k,(n+1)2^k)\) 的区间，\(O(log^2 V)\) 分别做。

两个形如 \([n2^k,(n+1)2^k)\) 的区间做异或卷积的方法是简单的，具体地答案一定是一个区间，其中后 \(\max(k1,k2)\) 位任意，前面固定。

最后区间取交即可，复杂度 \(O(T\log^2 V)\)。

NOIP 模拟 T3（分类讨论）

题意

给定一张有向图，你需要添加恰好一条有向边（可以是自环，可以与图中边重合），使得所有从 \(1\) 开始的极长路径都经过 \(n\)。

极长路径指中点没有出边的路径或无限长的路径（比如重复走环）。

\(n\leq 5\times 10^4\)，3s，512MB。

题解

分类讨论，首先把 \(n\) 的出边删除以减少分讨情况数量。

当 \(u\) 能到达两个 \(0\) 出度为 \(0\) 且不为 \(n\) 的点，无解。

当 \(u\) 能到达一个非 \(n\) \(0\) 出度点 \(x\)，则加边的 \(u=x\)，\(v\) 需要满足不在环中、不能到达环或不是 \(n\) 的 \(0\) 出度点、能到达 \(n\)。

当 \(u\) 能到达零个非 \(n\) \(0\) 出度点时，加边 \(u,v\) 需要满足：

• 当 \(1\) 不能到 \(u\) 或 \(u=n\)，随便加。
• 否则 \(1\) 能到 \(u\)，则 \(v\) 需要满足不在环中、不能到达环或不是 \(n\) 的 \(0\) 出度点、能到达 \(n\)。

bitset 即可。

2025.12

考完 NOIp 咕咕咕了一周，所以是从 12.8 开始的。

NOIP 2025 T2 清仓售卖（判定型计数，分段分讨）

题意略。

题解

先做 \(m=2\)，可以算不合法方案，分讨即可，具体地不合法当且仅当买到了 \(a_y\)，\(w_y=1\)，且存在 \(z,x\)，\(w_z=2\land w_x=1\land a_x+a_y<a_z\)。

对于一般情况，不合法当且仅当在购买过程中 \(m\) 剩余 \(1\) 时可以反悔掉之前的一个 \(1\)，买当前的 \(2\)。

具体地，我们要对按性价比降序排序后，\(w\) 构成如下结构的方案计数：

\[\underbrace{\dots{\color{red}1}22\dots2}_{\sum w=m-1}{\color{aqua}2}2\dots22{\color{orange}1}\dots \]

其中红色是 \(y\)，蓝色是 \(z\)，橙色是 \(x\)，满足 \(a_x+a_y<a_z\)。

这个结构直接的保证了不重不漏，直接枚举 \(x,y,z\)，由于按性价比排序后的序列不确定，在原价上考虑，将原价升序排序。

我们发现，我们把原序列分为了 \(4\) 段，括起来的数字表示不存在于序列中的数。

\[\underbrace{\dots}_{1} a_x\underbrace{\dots(\frac{a_z}{2})\dots}_{2} a_y\underbrace{\dots}_{3} a_z\underbrace{\dots(2a_y-0.5)\dots}_{4} \]

第 \(1\) 段无论如何也不会被买，随便定价，贡献 \(2^{len_1}\)。

第 \(2\) 段如果填 \(1\)，那么它会在性价比排序时排到 \(y\) 后面、\(x\) 前面，与结构中 \(y,x\) 之间都是 \(2\) 的性质不符。所以第 \(2\) 段必须全为 \(2\)。

第 \(3\) 段如果填 \(1\)，那么会在 \(z\) 之前买，如果填 \(2\)，会在 \(z\) 之后买。

第 \(4\) 段无论填啥都要在 \(z\) 之前买。

那么我们要让第 \(3\) 段 \(1\) 的个数 \(+\) 第 \(4\) 段 \(w\) 的和 \(+w_y=m-1\)。

由于 \(w_y=1\)，条件就是第 \(3\) 段 \(1\) 的个数 \(+\) 第 \(4\) 段 \(w\) 的和 \(=m-2\)。

这是一个简单的组合问题，答案为 \(\binom{m-len_4}{len_3+len_4}\)，复杂度 \(O(n^3)\)。

发现 \(x\) 的取值是一个前缀且贡献独立，所以可以双指针求 \(x\) 然后两部分贡献相乘，复杂度 \(O(n^2)\)。

提交记录

NOIP 2025 T3 树的价值（树上 DP，链剖结构，DP 形式化描述）

题意

题意略。

题解

考虑 \(O(\text{poly}(n))\) 做法，令 \(f_{u,i,j}\) 表示子树 \(u\) 内 \(\text{mex}=i\)，有 \(j\) 个空闲点的最大价值。

直接转移 \(O(n^4)\) 或 \(O(n^5)\)，转移时第二维有取 \(\max\) 操作，枚举子树 \(\text{mex}\) 的 \(\max\)，进行前缀和优化可以做到 \(O(n^3)\)。

令子树 \(i\) 内的 \(\text{mex}\) 为 \(b_i\)，DP 合并子树 \(v\) 时，有两种情况：

1. 使用 \(u\)，并继承 \(b_v\)，即 \(f'_{u,x+1,j+y}\leftarrow f_{u,i,j+1}+f_{v,x,y}+x+1\)。
2. \(u\) 做空闲点，并继承 \(b_v\)，即 \(f'_{u,x,j+y}\leftarrow f_{u,i,j}+f_{v,x,y}+x\)。
3. 啥也不管，即 \(f'_{u,i,j+y}\leftarrow f_{u,i,j}+f_{v,x,y}+x\)。

最后枚举一下用几个空闲点。

考查 DP 转移结构，即尝试使用 DP 转移构造最优解的方案，发现每个点必定是选择了一个子节点，继承了这个点的 \(b\)，不妨设 \(u\) 继承了 \(b_{sson_u}\)。

这形成了一个链剖结构，记点 \(i\) 的链头为 \(tp_i\)，考查一个点 \(x\)，如果 \(b_x\) 的值 \(+1\)，那么对于 \(x\sim tp_x\) 的点，它们的 \(b\) 都会 \(+1\)。

考虑先确定链剖结构，再考虑一个链剖结构能取到的最大答案是什么。

增量构造思想，初始时，每个点都是空闲点。

一个点 \(u\) 作为空闲点可以给一个祖先 \(x\) 的 \([tp_x,x]\) 的 \(b\) 增加 \(1\)，在转移时“使用 \(u\)”可以视作贡献给 \([tp_u,u]\)。

那么，点 \(u\) 的贡献就是 \(u\) 到根链上最长同链连续段长度。

形式化的，令 \(d_1=1\)，对于一个 \(u\)，选择一个 \(sson_u\in \text{son}_u\)，\(d_{sson_u}=d_u+1\)，对于其余的 \(v\in \text{son}_u\land v\neq sson_u\)，\(d_v=1\)。

则 \(ans=\sum\limits_{u=1}^{n}\left(\max\limits_{x\in \text{anc}_u} d_x\right)\)，我们需要确定一个 \(d\) 的生成方案使得 \(ans\) 取到最大值。

后面就比较套路了。

树上 DP，我们关心一个点的 \(d\)，但是显然不能从上往下转移，令 \(f_{u,i,j}\) 表示子树 \(u\) 内，假设 \(d_u=i\) 且祖先 \(\max d=j\) 的答案，可以 \(O(nm^2)\)。

分段转移，令 \(f_{u,i}\) 表示 \(u\) 子树内 \(tp_u=u\)，假设 \(d_u=i\) 的答案。

设 \(u\) 所在链长为 \(len_u\)，枚举 \(len_u\) 可以做到 \(O(nm^2)\)。

若 \(len_u>i\)，则 \(f\) 的转移在下标上是等差数列，不好优化。

为了优化，我们考虑在 \(len_u>i\) 时从 \(dep_u+i-1\) 处截断，具体地令 \(g_{u,i}\) 表示 \(u\) 子树内 \(tp_u\) 不一定等于 \(u\)，假设 \(d_u=i\) 且 \(d_u\) 取到祖先最大 \(d\) 的答案。

有转移：

\[f_{u,i}=\max_{v\in \text{leaf}(u)\land dep_v-dep_u+1 < i} \left (i(dep_v-dep_u+1)+\sum_{j\in \text{path}(v,u)}\sum_{k\in \text{son}(j)\land k\notin \text{path}(v,u)} f_{k,i}\right ) \\ f_{u,i}=\max_{v\in \text{subtree}(u)\land dep_v-dep_u+1 = i}\left (g_{v,i}+i(dep_v-dep_u)+\sum_{j\in \text{path}(fa_v,u)}\sum_{k\in \text{son}(j)\land k\notin \text{path}(fa_v,u)} f_{k,i}\right ) \\ g_{u,i}=i+\left(\sum_{v\in \text{son}(u)}f_{v,i}\right)+\max_{v\in \text{son}(u)} \left( g_{v,i+1}-f_{v,i}\right) \]

第一个转移式可以放缩，去掉 \(dep_v-dep_u+1<i\)，答案一定不会更优。

\[f_{u,i}=\max_{v\in \text{leaf}(u)} \left (i(dep_v-dep_u+1)+\sum_{j\in \text{path}(v,u)}\sum_{k\in \text{son}(j)\land k\notin \text{path}(v,u)} f_{k,i}\right ) \\ f_{u,i}=i(i-1)+\max_{v\in \text{subtree}(u)\land dep_v = i+dep_u-1}\left (g_{v,i}+\sum_{j\in \text{path}(fa_v,u)}\sum_{k\in \text{son}(j)\land k\notin \text{path}(fa_v,u)} f_{k,i}\right ) \\ g_{u,i}=i+\left(\sum_{v\in \text{son}(u)}f_{v,i}\right)+\max_{v\in \text{son}(u)} \left( g_{v,i+1}-f_{v,i}\right) \]

第三个式子直接做，第二个式子暴力枚举 \(u,i,v\)，复杂度 \(O(\sum sz)=O(nm)\)，使用 bit 维护链上权值和可以做到 \(O(nm\log n)\)。

对于第一个式子，对每个 \(i\) 维护子树内所有叶子转移到根的 \(\sum_{j\in \text{path}(v,u)}\sum_{k\in \text{son}(j)\land k\notin \text{path}(v,u)} f_{k,i}+i(dep_v+1)\) 的最小值 \(mxf_i\)，可以增量维护，转移直接 \(f_{u,i}=mxf_i-i\times dep_u\)，这部分复杂度 \(O(\sum sz)=O(nm)\)。

总复杂度 \(O(nm\log n)\)，瓶颈在于 BIT。

注意到第二个式子转移时 \(i\leq \frac{m}{2}\)，否则不存在一个合法的 \(v\)，进行这个卡常后可以通过。

提交记录

省选模拟 T1（构造）

题意

给定一张无向连通图，删去一条简单路径，使得图分为若干个连通块，且存在一个将这些连通块划分为两个集合的方案使得两个集合内的连通块大小之和相等。

部分分：\(m=n-1\)。

\(n,m\leq 2\times 10^5\)。

题解

考虑部分分，从树上任意一个点开始走，此时图会裂成若干个连通块，考虑往大的连通块走（设其为 \(v\)），实时维护两个集合的 \(\Delta\)，其余连通块经过 \(+-\) 组合能做到绝对值 \(\leq sz_v\)，若 \(|\Delta|=sz_v\) 就做完了。否则向 \(v\) 递归，设 \(v\) 的最大子树为 \(w\)，则 \(\text{son}_u/\{w\}\) 中的子树与 \(\Delta\) 必定能再次通过 \(+-\) 组合做到新的 \(|\Delta'|\leq sz_w\)，递归下去就做完了。

考虑正解，根据部分分提示建立 DFS 树，发现如果从根开始走，返祖边没有任何影响，直接按树的方法做即可。

提交记录

QOJ. 2806/省选模拟 T2（生日悖论）

题意

给定一个随机数生成器 \(f\)，给定种子 \(s1,s2,s3,s4\)，\(f\) 可看做 \([0,2^n-1]\to [0,2^n-1]\) 的一个函数，你需要找到 \(1\leq c1,c2,c3,c4\leq 10^8\)，使得 \(f^{c1}(s1)\oplus f^{c2}(s2)\oplus f^{c3}(s3)\oplus f^{c4}(s4)=0\)，保证有解。

\(1\leq n\leq 50\)。

题解

先 meet in the middle，拆成 \(f^{c1}(s1)\oplus f^{c2}(s2)= f^{c3}(s3)\oplus f^{c4}(s4)\)，考虑生日悖论，设 \(B=2\times 2^{\frac{n}{4}}\)，枚举 \(c1,c2,c3,c4\in [1,B]\)，则我们构造了一个两边大小为 \(4\times 2^{\frac{n}{2}}\) 的集合，根据生日悖论，碰撞概率极大，由于需要哈希表无法通过，可以通过 \(n\leq 40\)（\(60\) 分）。

充分发扬人类智慧，令 \(B=2\times 2^{\frac{n}{3}}\)，\(m=\frac{n}{3}\)。假设 \(c1,c2,c3,c4\in [1,B]\)，\(2^{m}|f^{c1}(s1)\oplus f^{c2}(s2)\)，\(2^m|f^{c3}(s3)\oplus f^{c4}(s4)\)，枚举满足条件的 \(\{c1,c2\}\) 和 \(\{c3,c4\}\)，由于每个 \(c1\) 期望和一个 \(c2\) 在后 \(m\) 位碰撞，因此 \(\{c1,c2\}\) 总期望对数为 \(B\)，那么 \(\{c1,c2,c3,c4\}\) 的总对数为 \(B^2\)，此时可能的非 \(0\) 位只能在前 \(2m\) 位出现，相当于在 \([0,2^{2m}-1]\) 随机 \(B^2=4\times 2^{2m}\) 个数有 \(0\)，这个事件的期望次数为 \(4\)，则不发生的概率为 \(e^{-4^2}\)，可以忽略不计。

提交记录

省选模拟 T3（栈思想，匹配，复杂 DP，图论建模）

题意

（样例 \(1\) 输出 \(2\)）

\(1\leq n\leq 2\times 10^5\)。

部分分 \(a_i>0\)。

题解

Hint：DP 想不清楚时可以考虑建图并简化转移边。

\(a_i>0\) 是好做的，枚举 \(i,j\)，在 \([1,i]\) 往左移动，\((i,j)\) 用样例一的方法原地消失，\([j,n]\) 往右移动，贡献是好算的，容易优化到 \(O(n)\)。

考虑一般情况，将每个方块从左到右从下到上标号，一个非零段肯定存在两个分界点 \(i,j\)，\([1,i]\) 块往左，\((i,j)\) 块往右，\([j,sz]\) 块往右。

据此对每个 \(0\) 段 DP，但是细节多、不好优化。

考虑建图以理解 DP 过程，类似《切糕》，在每个块间设置一个点，空位向后枚举匹配到哪个点，连接一条有向边，贡献是好算的，要求匹配的空位一定足够。

设原点 \(S\) 表示开头的无限个空位，\(T\) 表示结尾的无限个空位。

对于原地消失的贡献，将块 \(i\to i+1\) 连接边权为 \(2\) 的边。

对于 \(i,i+1\) 不在同一列，有边 \(i\to i+1\)，边权为 \(0\)。

现在边数为 \(O(nV)\)。

考虑分析性质以优化，边分为三类：

1. \(S,T\) 连向中间点。
2. 空位连向中间点。
3. \(i\to i+1\)。

对于第 \(1\) 类，根据 \(a_i>0\) 的结论，\(S,T\) 必定匹配整段，这部分边数可以优化为 \(O(n)\)。

推广，空位在位置足够的情况下匹配整段，这部分边数也是 \(O(n)\)，用单调栈快速找到连边位置。

最后对于 \(i\to i+1\)，只保留之前 \(O(n)\) 条边的端点进行缩边即可。

复杂度 \(O(n)\)，显然这是 DAG，可以 \(O(n)\) 求得 \(S\to T\) 的最短路。

总复杂度 \(O(n\log n)\)，瓶颈在于建图。精细实现也许可以做到 \(O(n)\)。

注意由于空位不能同时匹配左侧和右侧，因此需要将空位拆成出、入点，匹配前面连向入点、匹配后面连向出点，最后出点向入点连接边权为 \(0\) 的有向边。

提交记录

NOIP2025 T4 序列询问（序列分治，倍增分块）

题意

题意略。

题解

处理区间，特殊性质 \(L\geq \frac{n}{2}\) 保证了区间一定跨过整个序列的中点，据此考虑分治，处理跨 \(mid\) 的区间，直接 \(\text{chkmax}\) 是不好做的，考虑按分治结构以 \(mid\) 分左右两部分 \(\text{chkmax}\)。

设分治区间为 \([l',r']\)，枚举左端点 \(l\in [l',mid]\)，则 \(r\) 是一个区间，可以查到这些区间的最大权值 \(x\)，并对 \(i\in [l,mid]\) 进行 \(\text{chkmax}\)，右侧同理，这样分治复杂度为 \(O(nq\log n)\)。

考虑剪枝，当 \(r'-l'+1<L\) 时 break，这样分治的复杂度如下：

\[T(n)= \left\{\begin{matrix} 2T(\frac{n}{2})+\min(R,\frac{n}{2})\quad (n \geq L) \\ 0\quad (n < L) \end{matrix}\right. \]

这个复杂度看起来并非简单的 \(T(n)=n\log n\)。分治树分析复杂度，可得：

\[T(n)=\sum_{i=0}^{\log \frac{n}{L}} 2^i \min(\frac{n}{2^{i+1}},R) \\ T(n)=\sum_{i=0}^{\log \frac{n}{L}} \min(\frac{n}{2},2^i R) \]

当 \(R\geq \frac{n}{2}\) 时，\(T(n)=n\log \frac{n}{L}\)。

当 \(L\leq R<\frac{n}{2}\) 时，分治下半部分取到 \(\frac{n}{2}\)，上半部分取到 \(R\)，\(T(n)=O(\left (\sum\limits_{i=0}^{\log \frac{n}{R}} 2^iR\right )+\left (\sum\limits_{i=\log \frac{n}{R}}^{\log \frac{n}{L}} \frac{n}{2}\right ))=O(n+n\log \frac{R}{L})\)。

当 \(R\leq 2L\) 时 \(T(n)=n\)，考虑倍增分块，将询问拆为一个 \([L,2^i]\)、若干个 \([2^j,2^{j+1})\)、和一个 \([2^k,R]\)，这样每个区间都满足 \(R\leq 2L\)。\([2^j,2^{j+1})\) 可以预处理每个 \(j\) 的区间，复杂度 \(O(n\log^2 n)\)。对于 \([L,2^i]\)、\([2^k,R]\)，每次询问暴力做，复杂度 \(O(qn)\)。

总复杂度 \((qn+n\log^2 n)\)。

提交记录

P9877 [EC Final 2021] Vacation 黑（定长分块）

题意

给定 \(n\) 和长为 \(n\) 的序列 \(\{a\}\)，再给定一个常数 \(c\)。

维护序列，执行 \(m\) 个操作：

• \(1~x~y\)，\(a_x\leftarrow y\)。
• \(2~l~r\)，求：\(\max\left(\max\limits_{l \leq l' \leq r' \leq r\atop r'-l'+1\leq c} ~~ \left(\sum_{i=l'} ^{r'} a_i\right), 0\right)\)。

\(1\leq n,m\leq 2\times 10^5\)。

题解

这是一道定长分块的模板题。

原问题不弱于最大子段和，当 \(r-l+1\leq c\) 时直接做最大子段和，开一颗线段树即可。

以下默认 \(r-l+1>c\)，考虑定长分块的套路，将序列分为若干个长为 \(c\) 的段，每一段维护 \(res,Lres,Rres\) 三个和最大子段和有关的信息，表示段内答案，前缀最大值和后缀最大值。

开 \(\frac{n}{c}\) 个线段树维护每块答案，同时需要处理跨块答案，即对于两个相邻快 \(\text{blk}_1,\text{blk}_2\)，我们需要求 \(\max\limits_{i\in \text{blk}_1\land j\in \text{blk}_2\land j-i+1\leq c} Rres_{i}+Lres_{j}\)。

将 \(\text{blk}_2\) 的 \(Lres\) 向前平移 \(c\) 格，换言之，令 \(Lres'_j=Lres_{j+c}\)。

则我们要维护的信息是 \(\max\limits_{j< i} Rres_i+Lres'_j\)，这个是可维护的，具体地在线段树上维护段内的 \(Tres=\max\limits_{j< i} Rres_i+Lres'_j\)，以及段内 \(Rmax=\max Rres\) 和 \(Lmax=\max Lres'\)，合并区间时使用 \(Rmax_{rson_p}+Lmax_{lson_p}\) 更新 \(Tres_p\) 即可。

注意我们需要令 \(Rres\) 为整段的后缀和，所以实现是需要处理一些细节。

对块间开一颗线段树维护跨块的信息。

对询问 \([l,r]\)，\(l',r'\) 不跨块的情况是简单的，讨论跨块情况。

若 \(r-l+1\leq 2c\)，先问一遍 \([l,l+c-1],[r-c+1,r]\)，在问一下 \(l'\in [l,r-c]\) 的跨块情况即可。

若 \(r-l+1>2c\)，记 \(L\) 表示 \(l\) 所在块的右端点，\(R\) 表示 \(r\) 所在块的左端点。先用维护块间信息的线段树查询 \([L+1,R-1]\) 之间块的答案，再查 \(l'\in [l,L]\) 的跨块答案和 \(r'\in [R,r]\) 的跨块答案，最后拼上 \([l,l+c-1],[r-c+1,r]\) 的答案。

由于我不想写两个 qry，所以可以把 \(r'\in [R,r]\) 的跨块答案改为 \(l'\in [R-c,r-c]\) 跨块的答案与 \([r-c+1,r]\) 的答案的 \(\max\)。

大常数 \(O(n\log n)\)。

提交记录

CF1781F. Bracket Insertion *2700（子问题划分，括号序列，计数 DP）

题意

Vika 喜欢玩括号序列。今天她想用如下算法生成一个新的括号序列。起初，Vika 的序列是一个空字符串，然后她会重复以下操作 \(n\) 次：

• 在当前括号序列中的某个位置等概率地插入新的括号。如果当前序列长度为 \(k\)，那么有 \(k+1\) 个插入位置。以概率 \(p\) 选择字符串 "()"，或者以概率 \(1-p\) 选择字符串 ")("，并将其插入到选定的位置。括号序列的长度会增加 \(2\)。

求 Vika 最终得到的括号序列是合法括号序列的概率，对 \(998\,244\,353\) 取模，\(n\leq 500\)。

题解

括号序列的几种处理方式（摘自《dp 题方法总汇》）：

1. 按下标 DP，记录多余的 (。
2. 拆第一层括号。
3. 拆第一对括号。
4. 视作折线进行容斥（格路计数）。

---

对于本题，合法的充要条件是每次 )( 都填入的前缀和 \(\geq 1\) 的位置，但是直接 DP 需要记录前缀和 \(=x\) 的位置个数，状态是指数级的。

如果不按照时间 DP，根本没法算概率，转为方案数，再除以 \(\prod\limits_{i=1}^{n} (2i-1)\)。

讨论最后加入的括号是不好做的，考虑拆第一个加入的括号，\(()\) 将序列分为了前缀和以 \(0,1,0\) 开始的三段，\()(\) 则为 \(0,-1,0\)。

记 \(f_{i,j}\) 表示还能操作 \(i\) 次，以前缀和 \(j\) 开始的方案数。

则：

\[f_{n,x}\leftarrow p\sum_{i=0}^{n-1}\sum_{j=i}^{n-1} f_{i,x}\times f_{j-i,x+1}\times f_{n-j-1,x}\times \binom{j}{i}\binom{n-1}{j} \\ f_{n,x}\leftarrow (1-p)\sum_{i=0}^{n-1}\sum_{j=i}^{n-1} f_{i,x}\times f_{j-i,x-1}\times f_{n-j-1,x}\times \binom{j}{i}\binom{n-1}{j} \]

简单优化一下（只讨论第一个式子）：

\[p\sum_{j=0}^{n-1}f_{n-j-1,x}\binom{n-1}{j}\sum_{i=0}^{j} f_{i,x} f_{j-i,x+1} \binom{j}{i} \]

记 \(g_{n,x}=\sum\limits_{i=0}^{n}f_{i,x}f_{n-i,x+1}\binom{n}{i}\)，则 \(f_{n,x}\leftarrow p\sum\limits_{j=0}^{n-1}f_{n-j-1,x}\binom{n-1}{j}g_{j,x}\)。

同理记 \(h_{n,x}=\sum\limits_{i=0}^{n}f_{i,x}f_{n-i,x-1}\binom{n}{i}\)，则 \(f_{n,x}\leftarrow (1-p)\sum\limits_{j=0}^{n-1}f_{n-j-1,x}\binom{n-1}{j}h_{j,x}\)。

提交记录

P13999 [eJOI 2025] Collecting Diamonds 蓝（后缀排序，周期性质）

题意

题解

将 \(N\) 连向 \(0\sim N-1\)，边权为 \(0\)，默认从 \(N\) 开始。保留最大出边，后缀排序，但是不知道 \(2^j\) 步后到哪里。

但事实上完全没有必要倍增后缀排序，每次进行步长为 \(1\) 的后缀排序，看起来复杂度 \(O(KN\log N)\)。我们发现最后一定会走到环，即在 \(N\) 步之内进入周期。直觉上我们只用模拟 \(O(N)\) 轮。

考虑证明，记在后缀排序中 \(rk\) 数组不同值个数为 \(cnt\)，则 \(cnt\) 随排序次数单调不降，且 \(cnt\leq n\)。

若一步后 \(cnt\) 不变，则后缀排序可以直接结束，否则 \(cnt\) 至少加 \(1\)。因此只用进行 \(n\) 轮后缀排序。

最后可得每个点的字典序最大出边，倍增即可。

提交记录

P14000 [eJOI 2025] Grid 黄（绝对值处理技巧）

题意

Simona 将从一个 \(N \times M\) 的网格 \(A\) 的格子 \((0, 0)\) 出发，这个网格填充了正整数。她必须到达格子 \((N-1, M-1)\)。为此，她可以重复进行如下移动：从当前位置 \((x, y)\) 移动到任意 \((x + d, y)\) 或 \((x, y + d)\)，其中 \(d > 0\)。每次移动时，她将获得奖励硬币 \(|A_{x,y} - A_{x',y'}| - C\)，其中 \((x', y')\) 是她的新位置，\(C\) 是游戏开始前固定的常数代价。注意，如果表达式 \(|A_{x,y} - A_{x',y'}| - C\) 的结果为负数，Simona 将失去硬币。注意游戏结束时她可能拥有负数硬币。

请帮助 Simona 确定她最多可以获得多少硬币。

其中，\(|a| = a\) 若 \(a \geq 0\)，否则 \(|a| = -a\)。

• \(1 \leq N, M\)
• \(N \cdot M \leq 500000\)
• \(1 \leq A_{i,j} \leq 1000000\)，对所有 \(0 \leq i < N, 0 \leq j < M\)
• \(0 \leq C \leq 1000000\)

时限 \(0.3\) s。

题解

带 \(\log\) 是简单的，发现不限制上界不会更优，因此可以去 \(\log\)。

提交记录

P14001 [eJOI 2025] Prison 紫（通信）

题意

每天，Alice 想要向 Bob 发送一个介于 \(0\) 与 \(N-1\) 之间的数字。午餐时 Alice 会得到三张餐巾，并在每张餐巾上写一个 \(0\) 到 \(M-1\) 的数字（允许重复）。接着，他们的敌人 Charly 会销毁其中一张餐巾，并把剩下两张的顺序打乱。最后，Bob 会找到仅存的两张餐巾并读取上面的数字。他必须准确解码出 Alice 最初想要发送的数字。\(M\) 固定。Alice 与 Bob 可以自由选择尽可能大的 \(N\)。请通过为二人各自实现策略，尽力最大化 \(N\) 的取值（\(N\geq N^*\) 即可获得满分）。

子任务	分值	\(M\)	\(N^*\)
1	10	700	82017
2	10	1100	202217
3	10	1500	375751
4	10	1900	602617
5	10	2300	882817
6	10	2700	1216351
7	10	3100	1603217
8	10	3500	2043417
9	10	3900	2536951
10	10	4300	3083817

题解

考虑我们需要已知两个数确定更多的信息，不妨令 \(x+y+z=m\)，只保留这些数对，可以获得 \(40\) 分左右。

\(x+y+z=m\) 比较浪费，令 \(x+y+z\bmod m=0\)，算出来的上界刚好等于题目上界，获得 \(100\) 分。

提交记录

P9970 [THUPC 2024 初赛] 套娃 紫（mex 性质）

题意

给定一个序列 \(a_1,\dots,a_n\)，对于每个 \(1\leq k\leq n\)，我们按照如下方式定义 \(b_k\)：

• 对于 \(a\) 的所有长为 \(k\) 的子区间，求出这个子区间构成的数集的 \(\operatorname{mex}\)。
• 对于求出的所有 \(\operatorname{mex}\)，求出这个数集自己的 \(\operatorname{mex}\)，记为 \(b_k\)。

请你求出序列 \(b\)。

题解

有一个经典结论：对于每个 \(1\leq x\leq n\) 的 \(x\)，极小的 \(\text{mex}=x\) 区间总数只有 \(O(n)\) 个，换言之，\(\text{mex}\) 在平面上形成了 \(O(n)\) 个值相同的矩形。

证明如下：

只考虑 \(a_l>a_r\) 的区间，最后将所求区间个数乘二即可。
假设 \([l,r]\) 是极小的 \(\text{mex}=x\) 的区间，\([l,r']\) 是极小的 \(\text{mex}=y\) 的区间，\(r'>r,a_l>a_r,a_l>a_{r'}\)。
由 \(\text{mex}\) 的单调性，有 \(y>x>a_l>a_{r'}\)，\(x>a_{r'}\) 说明 \([l,r]\) 的 \(\text{mex}>a_{r'}\)，即 \(a_{r'}\) 在 \([l,r]\) 中出现过，因此从 \([l,r']\) 中删去 \(a_{r'}\) 不会影响 \(\text{mex}\)，与假设矛盾。
因此每个 \(l\) 只有恰一个 \(r\) 满足 \(a_l>a_r\) 且 \([l,r]\) 是极小的 \(\text{mex}=x\) 的区间。总共有最多 \(2n\) 个极小的 \(\text{mex}=x\) 的区间。

只要求出这些区间，就可以求出对应矩形，然后扫描线即可。

求矩形是简单的，对于一个 \(\text{mex}=x\) 的极小区间 \([l,r]\)，记 \(lst_{l,x}=i,nxt_{r,x}=j\)，则矩形为 \([i+1,l],[r,j-1]\)。

我们发现，得知任何一个矩形边界的点，就可以二分出极小区间，考虑增量构造的思想，对于 \(\text{mex}=x\) 的极小区间 \([l,r]\)，记 \(lst_{l,x}=i,nxt_{r,x}=j\)，则 \([i,r],[l,j]\) 必定在 \(\text{mex}=x\) 的矩形边界，二分即可求出新的极小区间。写一个在线区间求 \(\text{mex}\) 即可完成上述操作，\(O(n\log^2 n)\)。

但实际上没有必要二分，直接取 \([i,r],[l,j]\) 也是对的，原因是，记 \([i,r'] (r'<r)\) 为实际上二分到的区间，则 \(\text{mex}(i+1,r')=x,\text{mex}(i+1,r'-1)\neq x\)，因此必定存在另一个 \(\text{mex}=x\) 的极小区间 \([l',r'] (l'\geq i+1)\)，此时 \([l',r']\) 使用【直接取 \([i,r],[l,j]\)】的方法可以覆盖到 \([i,r']\)，因此我们不会漏算任何东西，\(O(n\log n)\)。

提交记录

[ARC058E] 和風いろはちゃん *2473（暴力，字符串匹配）

题意

给定一个长度为 \(N\) 的数列 \(a_0, a_1, \ldots, a_{N-1}\)，其中每个元素的取值范围为 \(1\) 到 \(10\)。这样的数列共有 \(10^N\) 种可能。请问，其中包含 XYZ 的数列有多少种？

这里，包含 XYZ 被定义如下：

• 存在 \(0 \leq x < y < z < w \leq N\)，使得
  • \(a_x + a_{x+1} + \cdots + a_{y-1} = X\)
  • \(a_y + a_{y+1} + \cdots + a_{z-1} = Y\)
  • \(a_z + a_{z+1} + \cdots + a_{w-1} = Z\)

请输出包含 XYZ 的数列个数，对 \(10^9+7\) 取模。

\(N\leq 40\)，\(X,Z\leq 5\)，\(Y\leq 7\)。

题解

鉴定为做计数做傻了，尝试了容斥、DP、组合，发现都没有办法处理两个子序列有重合部分且都是 XYZ 子串的情况，计算不满足条件的串又不知道怎么限制，然后就倒闭了。

实际上这是一个字符串匹配计数，暴搜出所有 \(XYZ\) 子串后丢到 ACAM 上就做完了。

计算不满足条件的串也是可行的，因为 \(X,Y,Z\) 都很小，从前往后 DP，状压前 \(17\) 位中和为 \(t\) 的后缀是否出现即可。

启示：思维要打开，不要只按套路做题，当发现题目中某个值范围很小时，可以考虑朴素的暴力。

提交记录

CF888F Connecting Vertices *2500（区间 DP）

题意

有一张 \(n\) 个点的图，这些点以正多边形的形式排列在平面上。

对满足【树边在平面中除端点外不交】的生成树计数，对 \(10^9+7\) 取模。

\(1\leq n\leq 500\)。

题解

区间 DP，进行连边，只要保证连通且无环即可。

令 \(f_{l,r,0/1}\) 表示 \([l,r]\) 区间，\(l,r\) 是否连通的方案数，转移枚举 \(l\) 连向的点 \(k\)，将其拆为两个子问题 \([l,k],[k,r]\)。当 \(l,r\) 连通时还有一种情况是 \(l\) 没有出边，此时从 \(f_{l+1,r,0}\) 转移。

也可以理解为“拆第一对括号”。

提交记录

CF622F The Sum of the k-th Powers（拉插模板）

\(\sum\limits_{i=1}^{n} i^k\) 是一个关于 \(n\) 的 \(k+1\) 次多项式，选 \(k+2\) 个点拉插即可。

提交记录

QOJ 7649. 序列（计数 DP）

题意

称一个序列 \((a_1,a_2,\cdots,a_n)\) 是避免 120 模式的，当且仅当不存在 \(1\leq i<j<k\leq n\) 使得 \(a_k<a_i<a_j\)。

给定质数 \(P\)。\(q\) 次询问，每次给定 \(n,m\)，求有多少个长度为 \(n\) 的、值域在 \([0,m]\) 内的整数序列 \(a\) 是避免 120 模式的，结果对 \(P\) 取模。

\(n\leq 100,m\leq 10^9\)。

题意

解法：令 \(f_{i,j,k}\) 表示长为 \(i\)，所有顺序对(i,j)（a_i<a_j）中 \(a_i\) 的最大值相对大小为 \(j\)，共有 \(k\) 个值不相同的数。

则枚举 \(a_{i+1}\) 的相对大小转移。

1. \(a_{i+1}\) 与相对大小为 \(x\) 的数值相同：\(f_{i,j,k}\to f_{i+1,max(j,x-1),k}\)。

2. \(a_{i+1}\) 在相对大小为 \(x\) 的数与相对大小为 \(x+1\) 的数之间：\(f_{i,j,k}\to f_{i+1,max(j,x),k+1}\)。

上述两种情况需要保证 \(x\geq j\)。

答案为 \(f_{n,*,cnt}\times \binom{m+1}{cnt}\)。

随便优化一下可以做到 \(O(n^3+qn)\)。

提交记录

还有一种方法是拎出最大值 DP，令 \(f_{i,j}\) 表示长为 \(i\)，值域 \([1,j]\) 的方案数，记 \(g_{i,j}\) 表示最大值恰好等于 \(j\)，用于优化。DP 可以做到 \(O(n^2m^2)\)，发现当 \(m\leq n+1\) 时，大小关系本质不同的序列不会变多，因此答案是 \(\sum\limits_{i=1}^{n} \binom{m+1}{i} g_i\) 的形式，\(g_i\) 表示有 \(i\) 种数字的序列个数。

\(\binom{m+1}{i}\) 是一个关于 \(m\) 的 \(i\) 次多项式，因此答案是关于 \(m\) 的 \(n\) 次多项式，拉插即可。可以做到 \(O(n^4+qn)\)。

P10009 [集训队互测 2022] 线段树 黑（根号重构，序列分块，操作分块）

题意

给定一个长度为 \(n\) 的序列 \(a_1,a_2,\cdots a_n\)。你需要进行共 \(q\) 次下面两种操作：

• 1 l r：将 \(a_{l\sim r}\) 替换为它的异或差分。形式化地说，令 \(b_i := a_i \text{ xor } a_{i-1}\)（\(l<i\leq r\)），然后对于每个 \(l<i\leq r\)，将 \(a_i\) 替换为 \(b_i\)。

• 2 pos：查询 \(a_{pos}\) 的值。

操作执行完后，你还需要回答最终的 \(a\) 序列。

特殊性质 D：操作 \(1\) 满足 \(l=1\)，\(r=n\)。

特殊性质 E：没有操作 \(2\)。

题解

考虑 DE 怎么做，一次操作相当于进行错位异或，手玩一下发现和杨辉三角的转移一致。

即进行 \(k\) 次操作后，\(a_i=\bigoplus\limits_{0\leq j\leq i,\binom{k}{j}\bmod 2=1} a_{i-j}\)，根据 Lucas 定理，\(\binom{k}{j}\bmod 2=[j\subseteq k]\)，暴力枚举子集应该是能过的。

考虑更聪明的做法，对 \(q\) 二进制分解，当 \(k\) 是二的整数次幂时对 \(i\) 产生贡献的点只有 \(O(1)\) 个，总复杂度可以做到 \(O(n\log q)\)。

对于性质 D，考虑根号重构。

当静态问题可做且一次修改对一个询问的影响为 \(O(1)\) 时，可以根号重构。

显然取 \(B=\sqrt{n}\) 时一次修改对一个询问的影响并非 \(O(1)\)。

不妨取 \(B=2^{\log \sqrt{n}}\)，即可满足上述条件，复杂度 \(O(q\sqrt n)\)。

一般情况考虑沿用刚才的思想，先对序列进行分块然后根号重构（序列分块+操作分块）。

若每 \(\sqrt{n}\) 次操作重构，则每个块的修改只和上一个块的原始值有关（这是也根号重构的主要目的）。

根号重构，即默认 \(q\leq B\)，每次修改对 \(4\) 个块产生影响（即两个散块和两个散块的后继），暴力重构散块，整块打 tag。

查询枚举子集即可。

重构直接 pushdown 所有标记，pushdown 时将 \(tag\) 二进制分解可以做到 \(O(\log n)\)。

但是这样有点问题，因为本块对下一个块有影响，所以不能随意 pushdown。

考虑按块处理，每 \(B\) 个询问一组，每组询问从后往前遍历每个块处理，由于一个块依赖于上一个块，因此需要将 \(i,i+1\) 块同时拿出来处理，并更新第 \(i\) 个块的结果。

即，第 \(i\) 次把 \(n-i+1,n-i\) 块拿出来，正确维护第 \(n-i+1\) 块的信息，不完全正确的维护第 \(n-i\) 块的信息，保证“不正确”部分不会对第 \(n-i+1\) 块产生影响。

提交记录

CF913E Logical Expression *2400（最短路辅助 DP）

题意

给定一个由其长为 \(8\) 的真值表定义的三变量布尔函数。你需要找到一个等价于该函数的最短表达式。表达式可以包含以下内容：

• 与运算符号（'&'，ASCII 码 38）
• 或运算符号（'|'，ASCII 码 124）
• 非运算符号（'!'，ASCII 码 33）
• 变量 x、y 和 z（ASCII 码 120-122）
• 括号（'('，ASCII 码 40，和 ')'，ASCII 码 41）

如果存在长度最短的多个表达式，你应当输出字典序最小的那一个。

例如 (y|z)&x，将 \(x,y,z\) 的取值按 \((4x+2y+z)_2\) 升序排序，对应真值表为 00000111。

题解

考虑状压 DP，状态是真值表，值是整个表达式。

每次加入 |(expr)，&(expr)，|x/y/z，&x/y/z，|!x/y/z，&!x/y/z，还需要实现给自己加括号。

简化转移，每次给自己加 ()、!()，或加入 |expr，&expr。

发现这样没有办法处理 $| 的优先级，把优先级丢到状态里，定义 \(dp_0\) 为最外层是 () 和 ! 的表达式（或单个 \(xyz\)），\(dp_{1}\) 为最外层是 & 的表达式，\(dp_2\) 为最外层是 | 的表达式。

则 \(dp_{0/1/2}\) 加入 () 或 !() 时转移到 \(dp_0\)。\(dp_i\) 不能用 &| 连接 \(dp_j(j>i)\)。

转移有后效性，因此使用 dijkstra 完成转移即可。

由于转移边也有后效性，因此 dijkstra 一次不够。原因是短表达式接长表达式时，长表达式未被计算。

事实上两次 dij 就能通过。

一次 dijkstra 能保证长度正确，第二次松弛修正字典序。用归纳的思想，长为 \(1,2\) 的表达式字典序显然是对的，对于正确的长度 \(\leq i+1\) 的表达式，第二次松弛会把长度 \(\leq i+1\) 的正确表达式拼接得到长为 \(i+2,i+3\) 的正确表达式。因此两次 dij 足够。

提交记录

CF1097G Vladislav and a Great Legend *3000（斯特林拆幂）

题意

给你一棵有 \(n\) 个节点的树 \(T\)，\(n\) 个节点编号为 \(1\) 到 \(n\)。

对于 \(T\) 中每个非空的顶点的集合 \(X\)，令 \(f(X)\) 为包含 \(X\) 中每个节点的最小连通子树的最小边数，即虚树的大小。

再给你一个整数 \(k\)。你需要计算对于每一个顶点的集合 \(X\)，\((f(X))^k\) 之和，即：

\[\sum_{X\subseteq\{1,2,\dots,n\},X\neq\varnothing}(f(X))^k \]

\(1\leq n\leq 10^5\)，\(1\leq k\leq 200\)。

题解

\(O(nk^2)\) 的 DP 是容易的。

有一个技巧叫做斯特林拆幂，可以把单点加入 \(O(n)\)、无信息合并、有组合意义的 \(k\) 次方和优化至 \(O(nk)\)（传统做法是对每个 \(1\leq i\leq k\) 维护 \(i\) 次方和，复杂度 \(O(nk^2)\)）。

树上背包虽然不是单点加入，但是复杂度是 \(O(nV)\) 的，可以视作单点加入。

具体地，有公式：

\[i^k=\sum\limits_{j=0}^{i}\binom{i}{j}\begin{Bmatrix}k\\j\end{Bmatrix}j! \]

对于本题，即求：

\[\sum_{X\subseteq\{1,2,\dots,n\},X\neq\varnothing} \sum\limits_{j=0}^{f(X)}\binom{f(X)}{j}\begin{Bmatrix}k\\j\end{Bmatrix}j! \]

令 \(dp_{u,i,0/1}\) 表示 \(u\) 子树内，\(u\) 内是否有点，从 \(X\) 的生成虚树内选 \(i\) 条边的方案数。

然后就是经典的虚树结构背包，规定每个选的点的虚树边向上延申到根，然后枚举虚树 \(\text{lca}\) 统计答案，复杂度 \(O(nk)\)。

提交记录

P6620 [省选联考 2020 A 卷] 组合数问题 紫（斯特林拆幂，下降幂多项式）

题意

众所周知，小葱同学擅长计算，尤其擅长计算组合数。小葱现在希望你计算

\[\left(\sum_{k=0}^{n}f(k)\times x^k\times \binom{n}{k}\right)\bmod p \]

的值。其中 \(n\), \(x\), \(p\) 为给定的整数，\(f(k)\) 为给定的一个 \(m\) 次多项式 \(f(k) = a_0 + a_1k + a_2k^2 + \cdots + a_mk^m\)。\(\binom{n}{k}\) 为组合数，其值为 \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\)。

\(1\le n, x, p \le 10^9, 0\le a_i\le 10^9, 0\le m \le \min(n,1000)\)。

题解

有公式：

\[k^{\underline{i}}\binom{n}{k}=n^{\underline{i}}\binom{n-i}{k-i} \]

之后下降幂项和 \(k\) 无关，可以提出。

根据斯特林拆幂，可以将普通多项式转为下降幂多项式。

\[\sum_{k=0}^{n}f(k)\times x^k\times \binom{n}{k} \\ =\sum_{k=0}^{n}\sum_{i=0}^{m}a_i k^i x^k \binom{n}{k} \\ =\sum_{k=0}^{n}\sum_{i=0}^{m}a_i \sum\limits_{j=0}^{\min(k,i)}\begin{Bmatrix}i\\j\end{Bmatrix}k^{\underline{j}} x^k \binom{n}{k} \\ =\sum_{k=0}^{n}\sum_{i=0}^{m}a_i \sum\limits_{j=0}^{\min(k,i)}\begin{Bmatrix}i\\j\end{Bmatrix} x^k n^{\underline{j}}\binom{n-j}{k-j} \\ =\sum_{i=0}^{m}a_i \sum\limits_{j=0}^{i}\begin{Bmatrix}i\\j\end{Bmatrix} n^{\underline{j}}\sum_{k=j}^{n}x^k \binom{n-j}{k-j} \]

我们需要快速求 \(\sum_{k=j}^{n}x^k \binom{n-j}{k-j}\)，当然可以尝试对 \(x^k\) 拆幂，但是拆完是两个 \(\sum\) 里面带斯特林数，一看就不能做。

事实上这部分是简单的：

\[\sum_{k=j}^{n}x^k \binom{n-j}{k-j} \\ =\sum_{k=0}^{n-j}x^{k+j} \binom{n-j}{k} \\ =x^j \sum_{k=0}^{n-j}x^k \binom{n-j}{k} \\ =x^j (x+1)^{n-j} \]

因此最终答案为：

\[\sum_{i=0}^{m}a_i \sum\limits_{j=0}^{i}\begin{Bmatrix}i\\j\end{Bmatrix} n^{\underline{j}}x^j(x+1)^{n-j} \]

提交记录

[ARC076F] Exhausted? *2800（扩展 Hall 定理）

题意

给定一张 \(n+m\) 个点的二分图，第 \(i\) 个左部点点向第 \([1,L_i]\cup[R_i,M]\) 个右部点连边，求最小失配数。

\(1\leq n,m\leq 2\times 10^5\)，直接前后缀优化建图无法通过。

题解

找了个不知道叫啥的 AI 模型，秒出做法，到底是怎么做到的 /kk。

考虑 ex-hall 定理，答案等于 \(\max (|S|-N(S))\)，注意到 \(N(S)\) 一定是一段前缀加上一段后缀，考虑将其转为区间形式，即：

\[ans=\max (S-|\bigcup_{i\in S}[1,L_i]\cup[R_i,M]|)=\max (S-m+|\bigcap_{i=1}^{n}[L_i+1,R_i-1]|) \]

问题转化为我们需要选择 \(|S|\) 个区间使 \(|S|+|\bigcap\limits_{(L,R)\in S}[L,R]|\) 最大化。

枚举交集左端点 \(l\)，此时对于每个 \(L\leq l\) 的区间 \([L,R]\)，当交集右端点 \(r\in [l,R]\) 时产生 \(1\) 的贡献，扫描线即可。

提交记录

还有一个做法是按 \(l\) 排序后尽可能用左侧椅子，悔贪。由于不会证明所以咕咕咕。

P12493 [集训队互测 2024] 子集和 黑（猫树分治，矩形差分）

题意

有 \(n\) 个物品，物品 \(i\) 有两个属性 \(a_i,b_i\)。对于一个物品集合 \(S\)，定义 \(f(S)\) 是如下问题的答案：

对于每个物品 \(i\in S\)，选择 \(0,a_i,b_i\) 三个数中的一个，使得所有物品选择的数之和是 \(m\) 的倍数的方案数。

定义物品集合 \(S=\{1,2,\dots,n\}\)。有 \(q\) 次询问，每次给定四个正整数 \(1\le l_1\le r_1<l_2\le r_2\le n\)，求：

\[\sum_{l_1\le i\le r_1} \sum_{l_2\le j\le r_2} f(S\setminus \{i,j\}). \]

答案对 \(10^9+7\) 取模。

部分分 \(l1=r1,l2=r2\)，高达 \(5\) 分。

\(n\leq 10000\)，\(m\leq 200\)，\(q\leq 10^6\)。

题解

考虑 \(l1=r1,l2=r2\) 怎么做，假如只有 \(l1,r1\)，可以做缺一分治，但是现在有两个数。

我们不能涉及任何和 \(q\) 有关的背包合并，否则复杂度 \(O(qm^2)\) 不可接受。其次，循环卷积不能撤销。

但是查询两个背包合并后某个点的值可以做到 \(O(m)\)。

考虑猫树分治，询问离线挂在 \([L,M],[M+1,R]\) 上，维护序列前后缀背包 \(pre,suf\)。

将 \([L,M]\) 以 \(pre_{L-1}\) 为初值做缺一分治，\([M+1,R]\) 同理，可以做到 \(O(nm\log^2 n+qm)\)。

推广，还是猫树分治，问题是我们要查两个区间，不一定存在 \([L,M],[M+1,R]\) 使得区间被分在两侧。如果两个区间不被分在两侧，分治结构完全失效。

考虑差分，本题询问本质上是矩形求和，将其差分为 2-side 矩形，变为形如 \([1,l],[r,n]\) 的询问。

设 \(l\in [L,M],r\in [M+1,R]\)，维护 \(pre_{V,0/1}\) 表示前缀是否有数已经不选的背包，\(suf\) 同理。

对于 \(l\)，处理没选物品不在 \([L,M]\) 的情况，\(pre_{V,1}\) 卷上 \([L,M]\) 即可，\(r\) 同理，这部分是简单的。

没选物品在 \([L,M]\) 的情况，还是以 \(pre_{L-1,0}\) 为初值缺一分治，若到达叶子节点 \(x\)，对于 \(l\geq x\) 的询问都有贡献，在次位置记录背包，然后做前缀和即可，前缀和方法就是背包对位相加。

\([M+1,R]\) 同理。

最后还是两个背包合并，查询 \(0\) 处点值，时间复杂度 \(O(nm\log^2 n+qm)\)，空间 \(O(nm)\)。

提交记录

P4609 [FJOI2016] 建筑师 紫（第一类斯特林数，斯特林卷积，组合意义）

题意

求前缀最大值个数为 \(A\)，后缀最大值个数为 \(B\) 的 \(1\sim N\) 排列个数，多测，\(T=2\times 10^5\)。

\(1\leq N\leq 50000\)，\(1\leq A,B\leq 100\)。

题解

拎出最大值，左右独立，令 \(f_{i,j}\) 表示长为 \(i\) 有 \(j\) 个前缀 \(\max\) 的方案数，维护相对大小，插入法 DP，\(f_{i,j}=f_{i-1,j-1}+(i-1)f_{i-1,j}\)。

后缀和前缀本质相同，因此：

\[ans=\sum_{i=1}^{n} f_{i-1,A-1}f_{n-i,B-1}\binom{n-1}{n-i} \]

复杂度 \(O(TN)\)，无法接受。

观察到 \(f\) 是第一类斯特林数，考虑组合意义，相当于每个前缀 \(\max\) 到下一个前缀 \(\max\) 之间的位置可以随便排，则相当于将 \(i\) 个数分为 \(j\) 个原排列。

拎出最大值，其余数总共构成 \(A+B-2\) 个原排列，左侧 \(A-1\) 个、右侧 \(B-1\) 个。

因此答案为 \(f_{n-1,A+B-2}\binom{A+B-2}{A-1}\)。

提交记录

方法二：

\[ans=\sum_{i=1}^{n} f_{i-1,A-1}f_{n-i,B-1}\binom{n-1}{i-1} \\ =\sum\limits_{k=0}^{n-1}\binom{n-1}{k}f_{k,A-1}f_{n-k-1,B-1} \]

有斯特林卷积恒等式：

\[\sum_{k=0}^{m}\binom{m}{k}f_{k,r}f_{m-k,s}=\binom{r+s}{s}f_{m,r+s} \]

根据第一类斯特林数的组合意义很好理解，最后化简和上面式子是一样的。

P4827 [集训队互测 2011] Crash 的文明世界 黑（斯特林拆幂，换根 DP）

题意

给定一颗 \(n\) 个点的树，再给定常数 \(k\)，对每个点 \(i\)，求。

\[\left (\sum_{j = 1}^{n}{\rm dist}(i, j) ^ k\right) \bmod\ 10007 \]

\(1\le n\le 5\times 10^4\)，\(1\le k\le 150\)。

题解

\(k=1\) 可以换根，\(k\geq 2\) 可以维护 \(1\sim k\) 次方和，利用二项式定理换根，做到 \(O(nk^2)\)。

考虑斯特林拆幂，本质上需要对每个 \(w\leq k\)，求 \(\sum \binom{\text{dist}(i,j)}{w}\)。

照样换根，\(f_{u,i}\) 表示 \(u\) 子树内每个路径选出 \(i\) 个点的方案数，则有：

\[f_{u,i}=\sum_{v\in \text{son}(u)} (f_{v,i}+f_{v,i-1}) \]

换根，\(O(nk)\)。

提交记录

CF1806D DSU Master *2500（分析性质，mex）

题意

给定一个整数 \(n\) 和一个长度为 \(n-1\) 的数组 \(a\)，其中每个元素都是 \(0\) 或 \(1\)。

我们定义一个长度为 \(m-1\)（\(m \leq n\)）的排列 \(p\) 的值如下：

令 \(G\) 为一个有 \(m\) 个顶点的图，顶点编号为 \(1\) 到 \(m\)，初始时没有任何边。对于每个 \(i\) 从 \(1\) 到 \(m-1\)，执行以下操作：

• 设 \(u\) 和 \(v\) 分别为仅有入边的弱连通分量中包含顶点 \(p_i\) 和 \(p_i+1\) 的（唯一）顶点；
• 如果 \(a_{p_i}=0\)，则在图 \(G\) 中添加一条从顶点 \(v\) 指向 \(u\) 的有向边；否则（即 \(a_{p_i}=1\)），添加一条从 \(u\) 指向 \(v\) 的有向边。

注意，每一步操作后，可以证明 \(G\) 的每个弱连通分量都恰好有一个仅有入边的顶点。排列 \(p\) 的值定义为 \(G\) 中顶点 \(1\) 的入边数。

对于每个 \(k\) 从 \(1\) 到 \(n-1\)，求所有长度为 \(k\) 的排列的值之和（共 \(k!\) 个排列）。由于答案可能很大，只需输出对 \(998\,244\,353\) 取模的结果。

当 \(n=3\)，\(a=[0,1]\) 且 \(p=[1,2]\) 时的操作示意图。

题解

看了题解的前三个字母（\(\text{mex}\)）就会了，怎么回事呢？

先不要关心边的方向，先考虑连通性，排列中的一个值的作用是合并 \(i,i+1\) 所在的连通块，那么 \(1\) 的连通性改变，当且仅当 \(1\sim i-1\) 都连通，也就是说 \(p_i\) 是 \(p_1\sim p_{i-1}\) 中最小未出现的正整数。此时当 \(a_{p_i}=0\) 且贡献未中断时，对答案造成贡献，\(a_{p_i}=1\) 时贡献中断。

对 \(\text{mex}\) DP 的常见套路是按位 DP，记录当前 \(\text{mex}\)，贡献延迟计算。

但是本题不能这么干，复杂度不允许。

对每个 \(k\) 求答案，启示我们按值插入，一个数作为 \(\text{mex}\)，当且仅当被插入在最后。

这么做与常见套路的区别是，只保证了存在一个数是 \(\text{mex}\)，而没有保证位置（保证了值，但是对于本题不重要）。

那么记 \(f_{i,0/1}\) 表示值域 \([1,i]\)，贡献是否中断的答案，\(g\) 为其对应的方案数，转移是容易的。

提交记录

启示：不知道怎么算贡献时，可以考虑单个元素产生贡献的条件并分析性质。

另一种做法是 \(f_{i}\) 表示 \([1,i]\) 且 \(i\) 产生贡献的答案，则有 \(f_{i}=\sum\limits_{j<i} f_j\binom{i-2}{i-j-1}(i-j-1)!\)，拆阶乘后可以将 \(i,j\) 分离，做到线性。

CF1437F Emotional Fishermen *2600（排列 DP）

题意

给定长为 \(n\) 的序列 \(a\)，对满足如下条件，长为 \(n\) 的排列 \(p\) 计数：

\[\forall_{2\leq x\leq n},a_{p_x}\geq 2\max_{i=1}^{x-1} a_{p_i}\lor 2a_{p_x}\leq \max_{i=1}^{x-1} a_{p_i} \]

答案对 \(998244353\) 取模。\(1\leq n\leq 5000\)。

题解

拎出前缀最大值，只有 \(\log V\) 个，但是分析下好像没啥用。

将 \(a\) 升序排序，对前缀最大值 DP，记 \(\leq \frac{a_i}{2}\) 的数字个数为 \(lim_i\)，考虑上一个前缀最大值是 \(i\)，这个前缀最大值是 \(j\)，则我们需要分配 \(lim_i-lim_j-1\) 个数的位置，因为这些数要被填入到 \(i\) 后，而我们是从前往后 DP，所以不能维护相对位置，考虑直接维护绝对位置，目前一共有 \(n-lim_i-1\) 个位置可用，因此有 \(f_i=\sum\limits_{2a_j\leq a_i} f_{j}\binom{n-lim_i-1}{lim_i-lim_j-1}(lim_i-lim_j-1)!\)。

\(O(n^2)\) 通过。（？）

提交记录

不怼，把组合数拆成阶乘，发现转移式为 \(f_i=\sum\limits_{2a_j\leq a_i} f_{j}\frac{(n-lim_j-2)!}{(n-lim_i-1)!}\)，可以轻松做到线性，这个懒得写了（逃）。

CF725F *2900（贪心，调整法）

题意

共有 \(n\) 堆照片。每一堆里正好有两张照片。在每一轮，玩家只能从某一堆的顶部拿走一张照片。

每一张照片用两个非负整数 $ a $ 和 $ b $ 表示，分别表示该照片对 Alice 和 Bonnie 的幸福值分别为 $ a $ 和 $ b $。

玩家可以选择跳过，而不是拿照片。当所有照片都被取走或连续两位玩家都跳过时，游戏结束。

玩家的目标是最大化自己与对方之间幸福值的差距。假设两位玩家都采取最优策略，求最终 Alice 的幸福值减去 Bonnie 的幸福值的最大可能差值。若最优情况下 Alice 的幸福值为 \(x\)，Bonnie 的为 \(y\)，输出 \(x-y\)。

题解

分析什么时候会跳过不选。显然堆大小为 \(1\) 不会跳过。

堆大小为 \(2\)，当且仅当 \(a_1\land b_2\land a_2\land b_1\) 时会跳过。

否则当 \(a_1>b_2\)，A 选会更优，因此 A 和 B 会抢着选，其余同理。

确定不会跳过的堆，假设所有堆都归 A，之后调整，记 \(v=a+b\)，B 的目标是最大化选择的 \(\sum v\)。

如果 \(v_1<v_2\)，A 肯定不选 \(v_1\)，此时 \(B\) 为了最大化 \(\sum v\)，在没得选时肯定选 \(v_1\)，然后 A 选择 \(v_2\)。

如果 \(v_1=v_2\)，AB 肯定各选一个。

如果 \(v_1>v_2\)，A 直接贪就是对的。

唉怎么 WA 了？

原因是 \(v_1<v_2\) 的部分不能假设 B 选上面，B 可以一直跳过。如果不被选那么一开始的【假设未被跳过的堆都归 A】就是错的。

此时，如果 \(a_1>b_2\)，A 选，否则 B 选，由于过滤了被跳过的堆，且 \(v_1<v_2\)，恰好一个条件满足。

并且 \(v_1<v_2\) 与 \(v_1>v_2\) 独立，因为当存在 \(v_1>v_2\) 的 \(v\) 更大时 A 肯定选这些，否则 A 选了 \(v_1<v_2\) 的 \(v_1\) 后 B 肯定立马选 \(v_2\)，B 选了同理，所以不会出现【A 连选两个 \(v_1<v_2\)，B 去连选两个 \(v_1>v_2\)】的情况。

提交记录

AT_jsc2019_qual_f Candy Retribution 黑（组合数学，容斥）

题意

请计算满足以下条件的长度为 \(N\) 的非负整数序列 \(A_1,\ A_2,\ ...,\ A_N\) 的方案数。

• \(L \leq A_1 + A_2 + ... + A_N \leq R\)
• 将 \(N\) 个元素降序排列后，第 \(M\) 个和第 \(M+1\) 个元素相等。

答案可能非常大，请输出对 \(10^9+7\) 取模的结果。

题解

先转为 \(\leq R\) 和 \(\leq L-1\)。

由于是序列，不能对排序后的东西计数（？）。

考虑按值填入，要求 \(M,M+1\) 在同一层，可以设计 DP，\(dp_{i,j,k}\) 表示 \(i\) 个数，和为 \(j\)，当前值为 \(k\)。则有 \(f_{i,j,k}\to f_{i+1,j+k,k}\)，\(f_{i,j,k}\to f_{i+1,j,k-1}\)。显然优化不了。

考虑组合，把 \(M,M+1\) 拎出来，需要枚举一堆东西，然后转成所有数大于/小于某个数的个数，因为枚举的数太多还是做不了。

---

哦不怼，排序后的东西乘上可重集排列数就是原序列。

设排序后的序列为 \(b\)，由于 \(b_M=b_{M+1}=x\)，且可能存在其他值等于 \(x\)，前 \(M\) 个和后 \(N_M\) 个并非完全独立（因为要乘可重集排列数），这并不好做（可能得到一坨有 \(\geq 4\) 个 \(\sum\) 的式子），考虑容斥，对 \(b_M>b_{M+1}\) 计数。

枚举 \(v=b_M\)，即要求前 \(M-1\) 个数字 \(\geq v\)，后 \(N-M\) 个数字 \(\leq v-1\)。

不能枚举前 \(M\) 个数字的和 \(x\)，不然复杂度爆炸。

我们绕不开的问题是，和不超过 \(x\)，长为 \(n\) 的非负整数序列个数是多少？

引入第 \(n+1\) 项，答案为 \(\binom{n+x}{x}\)，也就是说总方案数为 \(\binom{N+R}{R}\)。

考虑一起算，一个长为 \(N\) 的序列，有 \(M\) 个数字 \(\geq v\)，\(N-M\) 个数字 \(\leq v-1\)，和不超过 \(R\)，一个数字 \(=v\)。

不能把 \(=v\) 的数刨去，因为可能有多个 \(=v\) 的数，与刚才一个道理。

不妨去掉 \(=v\) 的限制，记其为 \(f(N,M,v,v-1)\)，则 \(ans=\binom{N+R}{R}-\sum_{v=0}^{R} (f(N,M,v,v-1)-f(N,M,v+1,v-1))\)。

\(f(N,M,v_1,v_2)\) 表示长为 \(N\) 的序列，有 \(M\) 个数 \(\geq v_1\)，\(N-M\) 个数 \(\leq v_2\) 的方案数。

标准二反，钦定本来该 \(\leq v_2\) 的 \(k\) 个数字 \(\geq v_2+1\)，分配 \(\geq v_1\) 的位置，分配钦定点的标号、插板。

\[f(N,M,v_1,v_2)=\sum_{k=0}^{N-M} (-1)^k\binom{N}{M}\binom{N-M}{k}\binom{R-(v_2+1)k-v_1M+N}{N} \]

由 \(R-(v_2+1)k-v_1M+N\geq 0\)，复杂度调和级数。

提交记录

启示：可以把 \(=\) 容斥成 \(>\) 避免多个 \(=\) 带来的重复，简单容斥或把 \(=\) 变为 \(\geq v-\geq v+1\)。

P7044 「MCOI-03」括号（简单组合，序列分治）

题意

定义一个括号串的 \(0\) 级偏值为将该括号串修改为 合法括号串 需要的最小操作数。一次操作你可以在一个位置 添加 一个括号或者 删除 一个位置的括号。

定义一个括号串的 \(i\ (i>0)\) 级偏值为该串 所有子串 的 \(i-1\) 级偏值之和。

求长度为 \(N\) 的括号串 \(S\) 的 \(K\) 级偏值，对 \(998244353\) 取模。

对于 \(100\%\) 的数据，\(1 \le N,K \le 10^6\)。

题解

对于一个子串，一个经典的转化是合并匹配的括号串，保留形如 \(\text{)))(((}\) 的串，\(\text{)))(((}\) 可以用二元组 \(\{a,b\}\) 表示，答案即为 \(a+b\)。

先考虑 \(k=1\)，求所有子串的权值和，考虑序列分治，问题在于合并子串，\(\{a,b\}\) 和 \(\{c,d\}\) 合并后会变成 \(\{a+\max(0,c-b),d+\max(0,b-c)\}\)，只关心 \(b,c\) 的大小关系，左侧贡献为 \(a+b\) 或 \(a-b\)，右侧同理，答案即为贡献两两相加的和。由于 \(b,c\) 的值不超过串长，使用桶排可以做到 \(O(n\log n)\)。

对于 \(k>1\)，一个子串 \([l,r]\) 的贡献是：

\[\sum\limits_{1\leq l_{k-1}\leq l_k\leq \cdots\leq l_1\leq l\leq r\leq r_1\leq \cdots\leq r_{k-1}\leq n} ans(l,r) \\ =ans(l,r)\binom{k+l-2}{l-1}\binom{n-r+k-1}{n-r} \]

记 \(f(l)=\binom{k+l-2}{l-1},g(r)=\binom{n-r+k-1}{n-r}\)。

继续分治，本质上要求的是 \(\sum\limits_{L\leq l\leq M<r\leq R} ans(l,r)f(l)g(r)\)，分治时将贡献拆为两部分加和，设其为 \(x,y\)，即求 \(\sum\limits_{L\leq l\leq M<r\leq R} (x+y)f(l)g(r)\)，简单推导可得 \(\sum (x+y)f(l)g(r)=(f(l)\sum yg(r))+(g(r)\sum xf(l))\)，分治时维护 \(\sum f(l),\sum xf(l),\sum g(r),\sum yg(r)\) 即可。

提交记录

事实上对于一个左括号 \(i\) 和一个与之匹配的右括号 \(j\)，\(i\) 产生贡献的充要条件就是 \(l\in [1,i]\land r\in [i,j]\)。

因此可以线性，鉴定为学 DS 学的。

CF1363F Rotating Substrings *2600（排列刻画，计数 DP，分析性质，mex）

题意

给定两个长度为 \(n\) 的字符串 \(s\) 和 \(t\)，均由小写拉丁字母组成。你需要将 \(s\) 变为 \(t\)。

你可以对 \(s\) 执行如下操作任意次：

• 选择 \(s\) 的任意一个子串，并将其顺时针旋转一次。也就是说，如果选中的子串是 \(s[l,l+1,\ldots,r]\)，那么它会变为 \(s[r,l,l+1,\ldots,r-1]\)。\(s\) 的其他字符保持不变。例如，对区间 \([2,4]\) 进行旋转，字符串 "abcde" 会变为 "adbce"。

请你求出将 \(s\) 变为 \(t\) 所需的最少操作次数，或者判断是否无法实现。

\(1\leq n \leq 2000\)。

题解

判无解是简单的。

考虑 \(t\) 的每一位是从 \(s\) 的哪里得来的，这构成一个排列，我们每次可以对排列进行逆时针旋转，最后变为 \(p_i=i\) 的排列。

分析以下发现，当 \(p_i\) 前面 \(1\sim p_i-1\) 都出现时，\(p_i\) 不用被旋转到后面去，否则 \(p_i\) 一定会被旋转到后面去。

另一个 \(p_i\) 的条件是 \(t_{p_i}=s_i\)。

按位 DP 维护 \(\text{mex}\) 的经典套路，\(f_{i,j}\) 表示前 \(i\) 个数字，\(1\sim j\) 都出现的答案。

当这一位是 \(\text{mex}\) 时，\(f_{i,j}\to f_{i+1,j+1\sim i+1}\)，同时检查 \(t_{j+1}=s_i\)。

当这一位不是 \(\text{mex}\) 时，\(f_{i,j}+1\to f_{i+1,j}\)。

但问题是 \(f_{i,j}\) 可能不合法，因为我们没有对空闲点进行限制，\([1,i]\) 能出现 \(1\sim j\) 的所有数，当且仅当 \(s_{1\sim j}\in t_{1\sim i}\)，特判一下，如果不满足这个条件，将 \(f_{i,j}\) 置为 \(+\inf\) 即可。

复杂度 \(O(n^2|\Sigma|)\)。

显然包含关系存在单调性可以双指针，但是懒得写了，反正能过。

提交记录

额。做复杂了？

事实上不用转排列，求 \(s\) 和 \(t\) 的 LCS，但是第 \(i\) 位满足这一位对应 \(s\) 的前缀包含于这一位对应 \(t\) 的前缀，这样这一位就不用动。直接 DP 即可。

P6831 [IOI 2020] 嘉年华奖券 紫（贪心，调整法）

题意

共有 \(n\) 种颜色的奖券，每种颜色的奖券有 \(m\) 张，第 \(i\) 种颜色对应的第 \(j\) 张奖券上印的数字为 \(x[i][j]\)。

一次奖券游戏要进行 \(k\) 轮，轮次的序号从 \(0\) 到 \(k-1\)。每一轮按照下面的方式进行：

• 首先，Ringo 从每种颜色的奖券中各选出一张奖券，形成一个 \(n\) 张奖券的集合。
• 接下来，游戏负责人选择一个整数 \(b\)。
• 对于上述集合中每一个奖券上的数字 \(a[i](0\le i \le n-1)\)，游戏负责人会计算 \(a[i]\) 和 \(b\) 的差的绝对值。让 \(S\) 代表这 \(n\) 个差的绝对值之和。
• 所得到的数字 \(S\) 就是 Ringo 本轮能够获得的奖励数额。
• 一轮游戏结束后，本轮集合中的奖券全部被丢弃，不会在未来的轮次所使用。

当 \(k\) 轮游戏结束后，Ringo 会丢弃口袋中的所有奖券。

在每一轮，游戏负责人都会选择一个能够最小化当前轮次游戏奖励的整数 \(b\)。

设计每轮游戏中的奖券分配方案，使得 \(k\) 轮游戏中获得的总体奖励数额之和最大，构造方案。

\(1\leq n,m\leq 1500\)。

题解

考虑 \(k=1\) 怎么做，显然一轮游戏的答案是前 \(\frac{n}{2}\) 大减去后 \(\frac{n}{2}\) 大，因此先选每行最大值，然后按 \(\max+\min\) 将 \(\frac{n}{2}\) 个数调整为最小值即可。

推广，先选出每行的前 \(k\) 大值，然后第 \(i\) 大值可以调整为第 \(i\) 小值，总共调整 \(\frac{nk}{2}\) 次即可。

构造方案的话，每次选未被选择，被调整做负贡献的数最多的 \(\frac{n}{2}\) 列进行匹配，正贡献同理。

不会出现一次游戏和为负数的情况，因为这样不优，因此只要找到匹配方案，就一定是合法的方案。

提交记录

QOJ15877. 回响形态/THUPC. B（正反拼接）

题意

给定一个长为 \(n\) 的串 \(s\)。称子串 \(s[i\ldots j]\) 的中心是 \(\frac{i+j}{2}\)。

现在你要回答 \(q\) 次询问，每次询问给出一个 \(k\)，问所有中心为 \(\frac{k}{2}\) 的子串的 border 个数之和。

要求 \(O(nq)\)。

题解

刻画子串相等的一个套路是将字符串按如下方式拼接：

\[s_1s_ns_2s_{n-1}s_3s_{n-2}\cdots \]

此时一个以反串结尾的偶回文串 \([l,r]\) 与原串里中心为 \(\frac{n-1}{2}\) 的相等子串对唯一对应。

对于本题，当两个子串相等时，对两个子串中心产生贡献，因此把串拿出来按照上述方法拼接，manacher 即可。

注意当回文串不在中心位置时会计重两次，要去重。

提交记录

还有一个比较自然的做法是从中间往两边扫描线，每次 border 至多增加 \(2\)，考虑增量维护的过程，本质上每次加入新的 border 长度为 \(1\) 或 \(2\)，其余都是扩张之前的 border，对新加入的 border 做一个 LCS/LCP，使用 SA 维护。

QOJ15876. Asian Soul/THUPC. A（重链剖分）

题意

给定一颗节点编号 \(1, 2, \cdots, n\) 的树，其中根节点的编号为 1，再给定序列 \(\{a\}\)

你要回答 \(q\) 次询问。每一组询问给出 \(l, r, u\)，需要你求出 \(\max_{l \leq k \leq r} LCA(a_k, u)\)。

\(1\leq n,q\leq 5\times 10^5\)。

题解

\(\max\) 是不可差分的，因此直接在 \(a\) 上不太能做。

考虑哪些点可能成为点 \(u\) 的 LCA，首先这些点在点 \(u\) 的到根链上。

到根链查询不妨先重剖一下，到根链转为若干重链的前缀，每个前缀中，如果存在一个 \(a_{l\sim r}\) 的点，其在重链前缀中某个点 \(x\) 的轻子树中，那么 \(x\) 可能成为答案，由于轻子数大小总和为 \(O(n\log n)\)，这部分直接遍历轻子树即可，复杂度 \(O(n\log^2 n)\)。

还有一个情况是对于每次往上跳新到达一个重链，此时查询范围变为了一个子树刨去另一个子树，可以拍到 DFN 序上变为二维偏序，总复杂度 \(O(n\log^2 n)\)。

启示：

1. 到根链信息可以考虑重剖，重剖后转为若干个重链的前缀，通常是容易处理的。
2. 轻子树大小之和为 \(O(n\log n)\)。

提交记录

省选模拟 T1

比较简单但是把 \(>m\) 读成 \(\geq m\) 挂了 \(5\) 分，记录一下（逃）。

省选模拟 T2（矩形容斥，线段树二分）

题意

对 \((1,1,1)\leq (a,b,c)\leq (A,B,C)\) 的满足 \(\forall_i,a>a_i\)、\(\forall_i,b>b_i\)、\(\forall_i,c>c_i\) 中至少两个的 \((a,b,c)\) 计数。

\(1\leq n,A,B,C\leq 7\times 10^5\)。

题解

唐氏题，但是没切，怎么回事呢？

一开始转为矩形加矩形最大值个数，意识到不可做后去写 T3，会来写完 \(O(n^2)\)，

\(O(n^2)\) 是枚举一段前缀，满足这些前缀的 \(a\)，然后对于后缀，\(b,c\) 的取值是一个矩形，对于前缀再枚举满足的 \(b\)，取交集。

考虑正解，还是枚举 \(a\)，然后需要做的是前缀要求 \(b>b_i\lor c>c_i\)，后缀是 \(b>b_i\land c>c_i\)。

容斥前缀要求，改为 \(b\leq b_i\land c\leq c_i\)，然后是前缀矩形并与一个矩形取交，都是同个方向的 2-side，直接 SGT 维护 \(\max\) 即可。

提交记录

*省选模拟 T3（简化状态）

一开始只打算打暴力，听说 ysz 秒了后自己立马就会了，看来每题要至少留 30min 思考正解。

\(O(n^2)\) 的 DP 显然，考虑每次只舍弃长的一段，设 \(lst_i\) 为上一个区间和为 \(0\) 的区间的最大左端点，在加一个转移是转移到 \(dp_{\min(i,j),\min(i,j)}\)，这样复杂度是对的。

注意如果 \(i=j\)，两边都要往前跳。

原因是转移到 \(dp_{\min(i,j),\min(i,j)}\) 与 \(dp_{i,j}\) 直接跳长的有相当一部分状态重合，具体地只有 \(O(1)\) 个状态不重合。

因此在过滤 \(i=j\) 的状态后，每个状态的后继唯一，复杂度 \(O(N)\)。

（todo）严谨证明。

QOJ15884. My Mayday（子问题划分，二进制拆位比较）

题意

两人读取到了一段记录了 \(N\) 个二进制数的日志，个数是一个长度为 \(M\) 的二进制整数，部分二进制位未知，用 . 表示。已知这 \(N\) 个二进制数单调不降，对所有情况计数。

\(N,M\leq 200\)，由于正解复杂度比较奇怪，可以视作 \({\color{red}16}\) 秒时限。

题解

赛时认为这题是《划艇》，但应该是本质不同的，因为中间会有 \(O(V)\) 个断点。

按下标 DP 似乎做不了，考虑用二进制的结构拆位，必定存在一个分割点，前面数的第一位是 \(0\)，后面数的第一位是 \(1\)。

那么令 \(dp_{i,l,r}\) 表示所有数前 \(i\) 位已经确定，当前在区间 \([l,r]\) 的方案数，转移枚举分割点即可。

\(O(N^3M)\)，但是能过。

启示：在见到与之前做过的题“类似”的题时不要局限于套路，任何题都应先分析题目本身的性质。

提交记录

QOJ15886. 集合（序列 nxt 树性质）

题意

滑姬酱有两个大小分别为 \(n\)、\(m\) 的集合 \(A\)、\(B\)，它们的元素均为区间 \([0, L]\) 中的整数，且 \(0\) 与 \(L\) 均包含在这两个集合中。

现在她想找到一个最小的集合 \(C\)，满足以下条件：

• \(0, L\in C\)；
• 将 \(A\cap C\) 中的元素按从小到大排序后，任意相邻两项之差不超过 \(a\)；
• 将 \(B\cap C\) 中的元素按从小到大排序后，任意相邻两项之差不超过 \(b\)。

输出集合 C 的大小，无解输出 -1。

\(2\leq n,m\leq 10^6\)。

题解

把两个数列相等的位置拿出来 DP，\(dp_{i}=\min\limits_{j}\{ dp_j+cost(j,i)\}\)，\(cost(j,i)\) 表示 \(j,i\) 之间（含）至少选多少个数字使得满足题意。

令 \(nxtA_i\) 表示最小的满足和 \(A_i\) 的差不超过 \(a\) 的下标，\(nxt_B\) 同理，则求 \(cost\) 可以倍增单 \(\log\)，总共 \(O(n^2\log n)\)，这个信息不能合并不能增量维护，因此直接做是不好做的。

我们需要考虑更优美的刻画方式，按 \(nxt\) 连边变为树，我们有性质：

• 树边没有包含关系。

据此分析一下，可以得出，\(0\leq cost(l,r)-(dep_l-dep_r)\leq 1\)。

具体地记 \(l,r\) 的 LCA 为 \(x\)，当 \(x\) 的 \(l\) 所在方向的儿子编号更小时，\(cost(l,r)-(dep_l-dep_r)=1\)，记 \(d(l,r)=cost(l,r)-(dep_l-dep_r)\)。

使用 DFN 刻画这个性质，先搜儿子编号小的子树，则 \(d(l,r)=[dfn_l< dfn_r]\)，很可做。

有 DP：\(dp_{i}\leftarrow dp_{j}+depA_{j}-depA_{i}+depB_{j}-depB_{i}+dA(i,j)+dB(i,j)-1\)。

即 \(dp_i+depA_{i}+depB_{i}\leftarrow dp_{j}+depA_{j}+depB_{j}+dA(i,j)+dB(i,j)-1\)，记 \(f_i=dp_i+depA_i+depB_i\)，对 \(f\) DP。

\(f_i=\min(f_j+[dfnA_j<dfnA_i]+[dfnB_j<dfnB_i]-1)\)。

双 \(\log\) 显然，发现 \(f\) 最多减少 \(1\) 且只由目前最小 \(f\) 和次小 \(f\) 贡献，因此对于最小值和次小值拿出来维护一个不带权的 2-side 数据结构即可，将一维看做下标，使用 sgt 维护 \(\max\)，\(O(n\log n)\)。

提交记录

另一个做法是令 \(f_{i,j}\) 表示两边选到哪里，发现 \(f\) 值构成竖线，直接大力 DS 维护。

P3206 [HNOI2010] 城市建设 紫（MST 性质，时间轴分治）

题意

\(q\) 次修改，每次修改一条边的边权，动态维护 MST。要求 \(\text{polylog}\)。

题解

MST 有很好的性质。

引理 1：以任意顺序做任意边集的 Kruskal，得到图的连通性相同。

证明 1：显然。

引理 2：边集 \(E_1\) 做 Kruskal 时，记 \(M\) 为实际使用的边，那么边集 \(E_1\cup E_2\) 做 Kruskal 与边集 \(M\cup E_2\) 做 Kruskal 结果相同。

证明 2：参考 CSP-S 2025 T2。

引理 3：边集 \(E_1\cup E_2\) 做 Kruskal，且先加入 \(E_2\) 的边，如果此时 \(E_1\) 中被使用的边为 \(N\)，那么以边权顺序做 Kruskal 时 \(N\) 中的边全部会被使用，且 \(N\in M\)（\(M\) 的定义见【引理 2】）。

证明 3：显然。

引理 4：对任意 \(E_1,E_2\)，沿用前两个引理定义 \(E_1\) 的 \(N,M\) 集合，则有 \(|M|-|N|\leq |E_2|\)。

证明 4：\(M-N\) 集合中的边表示不确定的边，这些边要根据 \(E_2\) 的情况决定是否加入。换言之，如果不考虑边权，任意 \(S\in (M-N)\) 都可能出现在生成树中。不考虑边权，不妨先加入所有 \(M-N\) 中的边，在加入 \(E_2\) 的边并反悔（类似次小生成树板子），每加入一条边时最多反悔掉一个在 \(M-N\) 中的边，且在所有 \(E_2\) 的边都被使用时，\(M-N\) 中的边必定全部不出现在 MST 中。因此 \(|M-N|\leq E_2\)。

引理推广 1：对于边集 \(E_1,E_2\) 做 Kruskal，Kruskal 内的复杂度可降至 \(O(|E_2|\log |E_2|)\)，方法是先转为 \(M,E_2\) 的 Kruskal，再把 \(N\) 中的边提前加入，然后拿 \(M-N\) 和 \(E_2\) 做 Kruskal。

引理推广 2：考虑对边集 \(E\) 做 Kruskal 的另一个方法，令 \(E_1,E_2\) 为 \(E\) 的一个划分，保留 \(E_1\) 的 \(M-N\) 集合 \(E'\)，并将 \(E_1-M\) 的边舍弃、\(N\) 的边直接加入图，令 \(E\leftarrow E'\cup E_2\)，并不断重复此过程，当 \(|E|=1\) 时判断边能否加入。复杂度 \(T(n)=T(2\min(a,n-a))+n\)。

以下 \(N,M\) 与引理中 \(N,M\) 定义相同。\(E_1\) 表示边权固定的集合，\(E_2\) 表示边权会被修改的集合。

考虑按时间轴分治，如果直接线段树分治需要维护动态加边的 MST，需要 LCT，比较麻烦。

对于分治区间 \([L,R]\)，\(|E_2|\leq R-L+1\)，使用引理推广 1，核心思想是每次更新 \(E_1\) 的 \(M-N\) 集合使得做 Kruskal 的复杂度正确。

具体地，初始将没有被修改过的边加入 \(E_1\)，使用可撤销并查集维护分治区间外，已经加入边集合 \(N\) 的图 \(G\)。

设当前分治区间为 \([L,mid]\cup [mid+1,R]\)，将 \([mid+1,R]\) 中被修改，且没有在 \([L,mid]\) 被修改的边加入 \(E_1\)，更新 \(N\)、重构 \(M-N\)、更新图 \(G\)，并递归进入 \([L,mid]\)。

然后恢复 \(E_1\)、\(N\)、\(M-N\)、\(G\)，执行 \([L,mid]\) 的修改操作，将 \([L,mid]\) 中被修改，且没有在 \([mid+1,R]\) 被修改的边加入 \(E_1\)，更新 \(N\)、重构 \(M-N\)、更新图 \(G\)，并递归进入 \([mid+1,R]\)。最后恢复 \(E_1\)、\(N\)、\(M-N\)、\(G\)。

当 \(L=R\) 时，\(|E_2|=1\)，\(|M-N|\leq 1\)，在图 \(G\) 中按边权顺序加入这两条边，记录答案即可。

不难发现分治的过程正是引理推广 2 的过程。

分治中需要在可撤销并查集上跑 Kruskal，因此复杂度 \(O(n\log^2 n)\)。

提交记录

CF710F String Set Queries *2400（二进制分组，在线 SGT）

题意

你需要对一个字符串集合 \(D\) 处理 \(m\) 个查询。每个查询有三种类型之一：

1. 向集合 \(D\) 中添加一个字符串 \(s\)。保证字符串 \(s\) 之前没有被添加过。
2. 从集合 \(D\) 中删除一个字符串 \(s\)。保证字符串 \(s\) 当前在集合 \(D\) 中。
3. 给定字符串 \(s\)，求集合 \(D\) 中所有字符串在 \(s\) 中出现的次数总和。如果集合 \(D\) 中的某个字符串 \(p\) 在 \(s\) 中出现了多次，则应计入所有出现次数。

强制在线。

题解

对于有结合律、不支持快速合并（否则可以直接用 SGT 维护）的强制在线信息，可以使用二进制分组。

方法是动态维护一个 SGT，假设当前有 \(x\) 个操作，那么用 \(O(\log x)\) 个 DS 维护最近 \(2^0,2^1,2^2,\dots\) 的操作信息，维护一个栈，每次操作将一个新的大小为 \(1\) 的 DS 加入栈，当栈顶两个 DS 大小相同时合并两个 DS，暴力重构即可，不难发现复杂度是对的，因为每个点只会被合并 \(O(n\log n)\) 次。

不难发现这个过程本质上就是线段树。

对于本题，出现次数显然有结合律，维护 \(O(n\log n)\) 个 ACAM 即可，\(O(n\log^2 n)\)。

需要垃圾回收节省空间，注意当 ACAM 根节点儿子为 \(0\) 时需要修改儿子为自己。

提交记录

P3309 [SDOI2014] 向量集 紫（二进制分组，SGT 维护凸包）

题意

维护一个向量集合，在线支持以下操作：

• A x y：加入向量 \((x,y)\)；
• Q x y l r：询问第 \(l\) 个到第 \(r\) 个加入的向量与向量 \((x,y)\) 的点积的最大值。

集合初始时为空。\(1 \le N \le 4 \times 10^5\)。

题解

\(ans=x\cdot x_0+y\cdot y_0\)，即 \(\frac{ans}{y_0}=x\cdot \frac{x_0}{y_0}+y\)。离线直接线段树维护上凸壳，即可。

凸包合并是 \(O(n)\) 的，不能直接做，考虑二进制分组，每组维护一个 SGT，就行了。

二进制的分租本质上是动态构建 SGT，因此具体实现直接在一颗线段树上做，可以合并时就 pushup 即可。

代码严格弱于下一题，不写了。

QOJ191. 【集训队互测2016】Unknown（二进制分组，撤销技巧——SGT 每层延迟构建）

题意

维护一个向量栈，在线支持以下操作：

• 1 x y：加入向量 \((x,y)\)；
• 2：删除末尾元素
• 3 l r x y：询问 \((x,y)\) 与第 \(l\) 个到第 \(r\) 个加入的向量的叉积的最大值。

询问的 \(x> 0\)。

集合初始时为空。\(1 \le N \le 5\times 10^5\)。

题解

\(ans=x_0\cdot y-y_0\cdot x\)，即 \(\frac{ans}{x_0}=x\cdot -\frac{y_0}{x_0}+y\)。如果没有操作二直接线段树维护上凸壳即可。

难点在于处理撤销，这里给出一个厉害的 Trick：

每次加入相当于线段树每层对应位置加一个点，正常方法是当加满点时建立凸包，我们对这个方法进行修改，保留最后一个加满点的区间不建立凸包，查询时直接往下递归，只会进行 \(O(1)\) 次双侧递归和 \(O(\log)\) 次单侧递归，查询需要二分答案，复杂度为 \(O(m\log^2 m)\)。

也就是说，包含没满的点，每层保证两个点不建立凸包，当这个节点满时建立上一个点的凸包。

撤销直接暴力，考虑一个建立凸包的线段树节点 \(x\)，他被重构，需要加入位置回撤整整一个与其长度相同，没有满的区间。重构复杂度带排序的 \(\log\)，因此复杂度每层均摊 \(O(m\log m)\)，总复杂度 \(O(m\log^2 m)\)。

翻了翻题解，没有发现线性空间的写法（upd：问了 le0n，确实能线性空间，但是方法只是卡空间，没有特别技巧），就这样吧。

提交记录（MLE）

P5904 [POI 2014] HOT-Hotels 加强版（长剖优化 DP）

学习长剖优化 DP。

每个长链开 vector。

如果是 \(i\leftarrow i-1\)，继承位置为 \(i+(dep_u-dep_{top})\)；如果是 \(i\leftarrow i+1\)，继承位置为 \(i-(dep_u-dep_{top})+mxlen_{top}\)。后者需要两倍空间。

提交记录

P8376 [APIO2022] 排列 紫（随机化）

题意

构造一个长不超过 \(1.5\log_2 k\) 的排列，使得其上升子序列个数恰好为 \(k\)。

\(k\leq 10^{18}\)。

题解

考虑插入法，枚举当前位的排名，贪心插入可以获得 \(91.3\) 分。

贪心不一定正确，考虑随机化，当满足条件时有 \(\frac{1}{B}\) 的概率不插入，跑 \(1000\) 次，取 \(B=\frac{1}{8}\) 时表现较好，可以通过。

提交记录

[ARC086E] Smuggling Marbles（长剖优化 DP）

学习长剖优化 DP*2，计数转概率后 DP 是容易的。

提交记录

P10641 BZOJ3252 攻略 蓝（闵和）

题意

树上选 \(k\) 个叶子，最大化到根链并集的点权和。

题解

对于 \(\min +\) 的卷积，可以使用闵和优化，即归并差分数组。

前提是上凸。

提交记录

*P8375 [APIO2022] 游戏 黑（动态序列分治，线段树）

题意

你有一张 \(n\) 个点的有向图，初始时对于每个节点 \(i\)（\(0 \le i \le k - 2\)），都有边 \((i, i + 1)\)。

支持 \(m\) 次加边操作，每次加边判断是否会发生以下情况：

存在一个满足如下条件的星球序列 \(w[0], w[1],\dots , w[t]\) 时发生：

• \(1 \le t\)。
• \(0 \le w[0] \le k - 1\)。
• \(w[t] = w[0]\)。
• 对于每个 \(i\)（\(0 \le i \le t - 1\)），存在边 \((w[i], w[i + 1])\)。

加边操作强制在线，你需要实现一个 add_edge(u,v) 交互函数。

\(n,m,k\leq 5\times 10^5\)。

题解

考虑按 \([0,k-1]\) 的序列分治，相当于要维护一个动态分治结构，即线段树。

维护能到 \([L,mid]\) 的点 \(T\) 和能到 \((mid,R]\) 的点 \(S\)，若 \(S\cap T\neq \emptyset\)，返回 \(1\)。

问题是同层之间有多个块，如果对于每个块都维护 \(S,T\)，复杂度爆炸。

我们发现，对于每个点，只需要维护他能到编号最小的点和能到他编号最大的点。

这里给出一个技巧（准确的来说是一个优秀的实现方式），将同层的块一起维护，并过滤掉可能影响正确性的边。

即分治结构为：

\[TTTTSSSS \\ TTSSTTSS \\ TSTSTSTS \]

过滤掉第三层形如 \((2,3)\) 等会影响正确性的边。

还是按线段树的方式理解，加入边 \(u,v\) 时，讨论当前层 \(u,v\) 的关系：

1. \(u\in S\land v\in T\)，返回 \(1\)。
2. \(u\in S\or v\in T\) 向下递归，此时肯定会向
3. \(u\in S\land v\notin S\)，更新 \(v\in S\)，复杂度均摊。
4. \(v\in T\land u\notin T\)，更新 \(u\in T\)，复杂度均摊。

因此写一个按层搜索，维护每个边被下放到的层（即这个层之前，边不会影响正确性），一旦出现点的松弛，就将被松弛的边下放，因为此时 \(u,v\) 属于同一侧的 \(S\) 或 \(T\)。

现在说明 \((u,v)\) 不会跨块，我们发现只有 \(u,v\) 属于同一侧的 \(S\) 或 \(T\) 时边会被下放，且仍然保证最小/最大编号的性质，因此正确性被保证。

提交记录

P14230 不连续子串 / subseq 紫（子序列自动机 DP）

题意

你需要求出有多少正整数序列对 \((b_{1\dots l_1},c_{1\dots l_2})\)，满足存在两个序列 \(p_{1\dots l_1},q_{1\dots l_2}\) 使得：

• \(1\le p_1<p_2<\dots<p_{l_1}\le n\)；
• \(\forall i\in[1,l_1],b_i=a_{p_i}\)；
• \(1\le q_1<q_2<\dots<q_{l_2}\le l_1\)；
• \(\forall i\in[1,l_2],c_i=b_{q_i}\)。

将答案对 \(10^9+7\) 取模。

\(1\le n\le 8000\)，\(1\le a_i\le n\)。

题解

考虑子序列自动机的思想，每次 \(i\to j\) 的转移时要求 \(i,j\) 之间没有等于 \(j\) 的数字。

现在有两层，对于 \(q_i,q_{i+1}\)，要求之间在 \(p\) 中的数字中，没有 \(=a_{q_{i+1}}\) 的数字。

由于限制和后一个数有关，考虑倒着 DP，\(f_{i,j}\) 表示当前外层为 \(i\) 内层为 \(j\) 的方案数，使用过滤不合法状态的技巧，将 \(f_{i,j}(i\neq j\land a_i=a_j)\) 置零即可，剩下的转移可以在 \(i\) 这一维做前缀和优化，复杂度 \(O(n^2)\)。

提交记录

CF1656H Equal LCM Subsets *3200（构造，”剥洋葱“构造技巧，辗转相除均摊）

题意

给定两个正整数集合 \(A\) 和 \(B\)。你需要找到两个非空子集 \(S_A \subseteq A\)，\(S_B \subseteq B\)，使得 \(S_A\) 中所有元素的 LCM 等于 \(S_B\) 中所有元素的 LCM。

\(|A|,|B|\leq 1000\)，值域为 \(4\times 10^{36}\)，无法分解质因数。

题解

肯定是先考虑能分解质因数该怎么做，开始做的时候考虑的是增量构造，然后没有会任何东西。

有一个类似于”剥洋葱“的构造技巧，先加入全集，不断删去任何情况都无法满足条件的元素，直到没有元素可以删除为止。

设”任何情况都无法满足条件“为性质 \(P\)，这种方法适用需要满足：

• 当所有元素都不满足性质 \(P\) 时，方案合法。
• 当元素 \(x\) 满足性质 \(P\) 时，删去任意不包含 \(x\) 的子集后，\(x\) 仍然满足性质 \(P\)。

质因数分解后 LCM 是因子指数对位取 \(\max\)，当 \(x\in A\) 的因子 \(p\) 的指数 \(k\) 比 \(B\) 中因子 \(p\) 的最大指数 \(\max k\) 还要大，那么称 \(x\) 满足性质 \(P_A\)，同理定义 \(P_B\)。

容易证明 \(P_A,P_B\) 符合上述条件。

重复 \(n+m\) 次，每次枚举元素并暴力检查，删去满足性质 \(P_A\) 或 \(P_B\) 的元素，复杂度 \(O((n+m)^2\log (n+m))\)，\(\log\) 的原因是最大值可以动态维护。

现在不能质因数分解，我们需要另一种刻画 \(P_A\) 的方式，求 \(\text{lcm}\) 不容易因为值域过大，但是求 \(\gcd\) 是容易的。

\(x\) 满足性质 A 当且仅当 \(\gcd(x,\text{lcm}(B))<x\)，我们有恒等式：

\[\gcd (x,\operatorname{lcm}(y_1,y_2,\dots,y_n))=\operatorname{lcm}(\gcd (x,y_1),\gcd (x,y_2),\dots,\gcd (x,y_n)) \]

因此判定条件相当于 \(\operatorname{lcm}(\gcd(x,b_i))<x\)，每个点开一颗线段树维护 \(\text{lcm}\) 即可。

当然这一步有很多转化方式，也可以转为 \(\gcd (\frac{x}{\gcd(x,b_i)})>1\)。

复杂度是 \(O((n+m)^2\log n\log V)\) 的，但是每次修改是删除，所以可以记录辗转相除步骤，做到势能均摊 \(O((n+m)^2\log n+(n+m)\log n\log V)\)（线段树每层 \(\log V\)）。

具体地每次修改都是将一个位置改为 \(1\)，修改后的 \(\text{lcm}\) 是前一次的因数，我们有公式：

\[\gcd(a,b)=v \\ \gcd(a,\frac{b}{k})=\gcd(v,\frac{b}{k}) \]

可以对 \(a\) 势能分析，不会有任何重复的辗转相除。

\(\gcd\) 的复杂度为 \(O(1+\log (\frac{\min(a,b)}{\gcd(a,b)}))\)（感谢 cxy 大佬指出）。

提交记录

P6109 [Ynoi2009] rprmq1（猫树分治，历史最值）

题意

有一个 \(n \times n\) 的矩阵 \(a\)，初始全是 \(0\)，有 \(m\) 次修改操作和 \(q\) 次查询操作，先进行所有修改操作，然后进行所有查询操作。

一次修改操作会给出 \(l_1,l_2,r_1,r_2,x\)，代表把所有满足 \(l_1 \le i \le r_1\) 且 \(l_2 \le j \le r_2\) 的 \(a_{i,j}\) 元素加上一个值 \(x\)。

一次查询操作会给出 \(l_1,l_2,r_1,r_2\)，代表查询所有满足 \(l_1 \le i \le r_1\) 且 \(l_2 \le j \le r_2\) 的 \(a_{i,j}\) 元素的最大值。

\(1\leq n,m\leq 5\times 10^4\)，\(1\leq q \leq 5\times 10^5\)，\(1\leq x\leq 2147483647\)，\(1\leq l_1\leq r_1\leq n\)，\(1\leq l_2\leq r_2\leq n\)。

题解

考虑先分治掉一维，最大值支持合并，直接猫树分治，对询问，在 \(L\leq l_1\leq M<M+1\leq r_1\leq R\) 时处理。

对于已知的 4-side 矩形加和同方向 3-side 矩形 \(\max\)，可以使用扫描线解决，只需维护区间加减区间历史最值，可以线段树维护。

显然对修改不能只在 \(L\leq l_1\leq M<M+1\leq r_1\leq R\) 时处理，考虑将修改视作 SGT 上的区间修。

具体地，对于修改，只将其放在与 \([l_1,r_1]\)有交但不被 \([l_1,r_1]\) 包含的猫树节点上。在向被其包含的子区间递归时，不在扫描线线段树上执行撤销操作。

具体地，猫树分治的流程如下：

0. 实时维护当前区间 \(L,R\) 和涉及到的修改集合 \(Opt\)，记 \(M=\lfloor\frac{L+R}{2} \rfloor\)。
1. 自 \(M\) 到 \(L\) 扫描线处理挂在当前点询问的左半部分。
2. 撤销 \(Opt\) 中不包含 \([L,M]\) 的修改在扫描线中执行的操作。
3. 拿出与 \([L,M]\) 有交但不包含 \([L,M]\) 的操作集合 \(Opt_l\)，递归解决 \((L,M,Opt_l)\)。
4. 撤销第 \(2\) 步扫描线中执行的所有操作。
5. 自 \(M\) 到 \(R\) 扫描线处理挂在当前点询问的右半部分。
6. 撤销 \(Opt\) 中不包含 \([M+1,R]\) 的修改在扫描线中执行的操作。
7. 拿出与 \([M+1,R]\) 有交但不包含 \([M+1,R]\) 的操作集合 \(Opt_r\)，递归解决 \((M+1,R,Opt_r)\)。
8. 撤销第 \(5\) 步扫描线中执行的所有操作。

撤销需要存下所有执行的操作，空间复杂度 \(O(m\log^2n)\)。

分析复杂度，每个询问贡献一个 \(\log\)，每个修改会被执行 \(\log\) 次扫描线，总共 \(O(m\log^2 n+q\log n)\)。

由于不想写撤销，因此写了另一个做法。

修改本质上是平面直角坐标系的两个直线，权值为 \(v,-v\)。

分治 \([L,R]\) 时，扫描 \([L,mid]\) 加入 sgt，然后递归 \([mid+1,R]\)，解决 \([L,mid]\) 时在 \(mid\) 处将历史 \(\max\) 改为当前 \(\max\)，然后往回正常扫描线即可。

提交记录

CF1666K Kingdom Partition *3200（最小割的理性理解方法）

题意

将无向图分为 A 区、B 区和 C 区。城镇 \(a\) 必须位于 A 区，城镇 \(b\) 必须位于 B 区。

Adrian 和 Beatrice 面临一个问题。当他们选择了城镇之后，他们将需要支付道路修复的费用。他们所需承担的长度为 \(l\) 的道路修复费用取决于它连接的城镇：

• 对于连接 A 区内的两个城镇之间的道路，Adrian 需要支付 \(2\cdot l\) 金币的费用。
• 对于连接 B 区内的两个城镇之间的道路，Beatrice 需要支付 \(2\cdot l\) 金币的费用。
• 对于连接 A 区和 C 区之间的城镇的道路，Adrian 需要支付 \(l\) 金币的费用。
• 对于连接 B 区和 C 区之间的城镇的道路，Beatrice 需要支付 \(l\) 金币的费用。

Adrian 和 Beatrice 希望尽量减少在道路修复上的总花费。找到他们将王国分割成三个区域的最便宜的方式。

\(2\le n\le 1000;0 \le m\le 2000\)。

题解

最小割用于解决如下式子的最小化问题：

\[\sum_{(u,v,w)\in E} wx_u(1-x_v)+\sum_{(i,t1_i)\in A} t1_i(1-x_i)+\sum_{(i,t2_i)\in B} t2_ix_i \]

肯定是要往这上面靠。式子中不能出现 \(x_ux_v\)（二分图除外，因为可以将一部点取反）。

二元变量不能刻画该限制，考虑令 \(x_{u,A},x_{u,B}\) 表示 \(u\) 是否在集合 \(A,B\) 里，要求 \(x_{u,A},x_{u,B}\) 不同时为 \(1\)，用 \(1-x_{u,A}-x_{u,B}\) 表示 \(u\) 是否在 C 中。

但问题是最小割无法处理两个变量不同时为 \(1\) 的问题，这个问题严格强于一般图最大独立集。

考虑不做这个要求，设 \(x_{u,A}=x_{u,B}=1\) 的点为 D 类点，这种点的贡献为 A+B-C，那么我们发现 D 与 A,B 的连边贡献与 C 与 A,B 连边贡献相同，且 C,D 之间有 \(2w\) 的贡献，因此最后答案一定不会同时出现 C 和 D，否则将所有 D 调整为 C 必定更优。因此最后我们将所有 D 类点改为 C 类点输出即可。

贡献为：

\[2wx_{u,A}x_{v,A}+2wx_{u,B}x_{v,B} \\+w_{u,A}(1-w_{v,A}-x_{v,B})+w_{v,A}(1-w_{u,A}-x_{u,B}) \\+w_{u,B}(1-w_{v,A}-x_{v,B})+w_{v,B}(1-w_{u,A}-x_{u,B}) \\ =wx_{u,A}(1-x_{v,B})+wx_{u,B}(1-x_{v,A})+wx_{v,A}(1-x_{u,B})+wx_{v,B}(1-x_{u,A}) \]

照着式子连边即可。

要求 \(x_{a,A}=x_{b,B}=1\)，可以视作最小化 \(+\infin x_S(1-x_{a,A})+\infin x_S(1-x_{a,A})\)，要求 \(x_{a,B}=x_{b,A}=0\) 同理。

提交记录

启示：有些看起来是错的东西实际上是对的，要仔细分析一下。

CF1799G Count Voting *2600（容斥，多重集合排列数）

题意

有 \(n\) 个人将参与投票。每个人恰好有一票。

第 \(i\) 个人属于团队 \(t_i\)（\(1 \leq t_i \leq n\)），其中 \(t_i = t_j\) 表示第 \(i\) 个人和第 \(j\) 个人属于同一个团队。根据规则，每个人必须投票给不同团队的人。注意，这也意味着每个人不能投票给自己。

每个人都知道自己希望获得的票数 \(c_i\)。有多少种可能的投票方式，使得每个人都能获得期望的票数？对 \(998\,244\,353\) 取模。

\(n\leq 200\)，可以 \(O(n^2)\)。

题解

钦定 \(k\) 个人投票给自己组，记 \(k_i\) 表示第 \(i\) 人收到自己组票数，方案数为 \(\binom{n-k}{c_1-k_1,c_2-k_2,\dots}\times \prod 每组方案\)，一组方案同理也是一个多重集组合数，还要乘上一个 \(\binom{sz}{\sum k}\) 分配投给自己组的人。

对着式子 DP 可以做到 \(O(n^2)\)。

提交记录

P7386 「EZEC-6」0-1 Trie 紫（组合数学）

题意

现在 tlx 有 \(n\) 个 \(\mathbf{1}\) 和 \(m\) 个 \(\mathbf{0}\)，你需要把它们排列，但要保证任意的 \(\mathbf{1}\) 互不相邻且第一个位置是 \(\mathbf{0}\)、最后一个位置是 \(\mathbf{1}\)，现在把所有可以构造出的串放到一棵 0-1 Trie 上，需要多少个节点？

对 \(18888913\)（质数）取模。

多测，\(T\leq 2\times 10^6\)，\(n,m\leq 5\times 10^{18}\)。

题解

一开始尝试的方法：

\(n\leftarrow n-1,m\leftarrow m-1\)。\(n=m\) 是简单的，只考虑 \(m>n\)。

\[ans=2\binom{m}{n}+\sum_{i=1}^{n+m}\sum_{c1=0}^{\min(\frac{i}{2},n)} \binom{i-c_1}{c_1} \\ =2\binom{m}{n}+\sum_{i=1}^{2n+1} Fib_i+\sum_{i=2n+2}^{n+m}\sum_{c_1=0}^{n}\binom{i-c_1}{c_1} \\ =2\binom{m}{n}+\sum_{i=1}^{2n+1} Fib_i+\sum_{c_1=0}^{n}\sum_{i=2n+2}^{n+m}\binom{i-c_1}{c_1} \]

最后 \(\sum_{c_1=0}^{n}\sum_{i=2n+2}^{n+m}\binom{i-c_1}{c_1}\) 式子无法优化。

遇到这种情况，换思路是必要的。

---

我们要求的是所有可能成为答案前缀的串的个数。

将 \(01\) 捆绑。

先考虑一般情况，答案是 \(\sum_{i=0}^{cnt_{01}} \sum_{j=0}^{cnt_0} \binom{i+j}{i}\)。

对内层求和，再求和，可以得到 \(\binom{cnt_{01}+cnt_{0}+2}{cnt_{0}+1}-1\)。

需要减去末尾不是 \(01\) 的方案数 \(\binom{cnt_{01}+cnt_{0}-1}{cnt_{01}}\)。

前缀需要给末尾留一个 \(01\)，因此有 \(\sum_{i=0}^{cnt_{0}-1} \binom{i+cnt_{01}}{i}\) 种方案是不合法的，减去 \(\binom{cnt_{0}+cnt_{01}}{cnt_{01}+1}\)。

当且仅当 \(0\) 用完时，前缀末尾的 \(0\) 可能是 \(01\) 的一半（“仅当”保证不重），这部分推导过程与上面同理，为 \(\sum_{i=0}^{cnt_{01}-1} \binom{cnt_{0}+i}{cnt_{0}}=\binom{cnt_{0}+cnt_{01}}{cnt_{0}+1}\)。

需要减去空串。

答案为 \(\binom{cnt_{01}+cnt_{0}+2}{cnt_{0}+1}-\binom{cnt_{01}+cnt_{0}-1}{cnt_{01}}-\binom{cnt_{0}+cnt_{01}}{cnt_{01}+1}+\binom{cnt_{0}+cnt_{01}}{cnt_{0}+1}-2\)。

提交记录

这种题目的一个技巧是打表，如果发现 \(ans(n,m)-ans(n,m-1)\) 是关于 \(m\) 的多项式，那么答案一定不含 \(Fib\)，通常是组合数。

当你发现自己在试图解决一个纯数学计算难题（如“求变限组合数倒数和的封闭形式”），而不是在解决算法逻辑问题时，通常就是方向错了。只有当 3 种以上的不同建模方式都指向同一个难解算式时，才硬着头皮推导。（by Gemini）

[AGC007F] Shik and Copying String（贪心，队列）

题意

Shikk 的工作是复制。有一天，Shikk 从他的上司那里拿到了一个由小写英文字母组成的长度为 \(N\) 的字符串 \(S_{0}\)（假设这天是第 \(0\) 天）。这之后第 \(i\) 天的工作是把 \(S_{i-1}\) 复制到 \(S_{i}\)。下文中的 \(S_{i}[j]\) 表示字符串 \(S_{i}\) 的第 \(j\) 个字母。

Shikk 还不怎么习惯这个工作。每天，当 Shikk 从第一个字母开始按顺序复制字符串时，他有可能会写下和刚刚写下的字母相同的字母，而不是本来应该写下的字母。也就是说，\(S_{i}[j]\) 要么与 \(S_{i-1}[j]\) 相同，要么与 \(S_{i}[j-1]\) 相同。（特别地，字符串开头的字母不可能出错。也就是说，\(S_{i}[1]\) 必然与 \(S_{i-1}[1]\) 相同。）

输入两个字符串 \(S_{0}\) 和 \(T\)，请求出使得 \(S_{i}\) 有可能与 \(T\) 相同的最小的整数 \(i\)。如果这样的 \(i\) 不存在，请输出 \(-1\)。

\(1\le N\le 10 ^ 6\)。

题解

一开始的思路是贪心匹配然后建造依赖链，但是是假的，随便拍一下应该能 Hack：

5
abaab
aabba

ans=2

---

模拟一组样例：

\[a\text{b}aab \\ a\text{bb}aa \\ aa\text{bb}a \]

再模拟：

\[abcdefgh \\ aaccddff \\ aaaccdff \]

我们发现每个字符的轨迹是一个只能向右或向下的路径。而冲突链默认先向下后向右，导致错误。

我们保持贪心匹配的思路不变，从后往前维护当前拐点最深深度，贪心地让拐点先向右后向下。

我们发现拐点从后往前变化的逻辑是删去若干个个后缀、位置集体 \(-1\)，深度集体 \(+1\)，可以队列维护。

提交记录

P13954 [ICPC 2023 Nanjing R] 红黑树（长剖优化 DP，单调队列）

题意

有一棵 \(n\) 个节点的有根树，节点编号从 \(1\) 到 \(n\)，其中节点 \(1\) 为根。每个节点都有一个颜色， 要么是红色，要么是黑色。

称一个节点是好的，若每一条以该节点为起点，以该节点任意一个后代叶子节点为终点的简单路径中，都包含相同数量的黑色节点。称一棵树是完美的，若树中每个节点都是好的。

令 \(R_k\) 表示以节点 \(k\) 为根的子树。对于每个 \(1 \le k \le n\)，回答以下询问：如果您可以任意选择一些节点并改变它们的颜色，至少需要选择几个节点才能让 \(R_k\) 变得完美。

\(2\leq n\leq 10^6\)。

题解

容易得到关于高度的 DP 式，\(f_{u,x}\) 表示 \(u\) 子树内到根黑点个数为 \(x\) 的方案数，那么：

\[f_{u,x}=\min(\sum f_{v,x}+[col_u=B],\sum f_{v,x-1}+[col_u!=B]) \]

不能直接长剖优化，因为要处理相邻位取 \(\min\)。

分析 DP 范围，注意到 \(x\) 不超过最浅子树高度，因此对于儿子个数 \(\geq 2\) 的暴力做即可。

对于儿子个数 \(=1\)，先不管。

用到 \(f_v\) 是，从 \(v\) 往下找第一个儿子个数 \(\neq 1\) 的点 \(x\)，那么：\(f_{v,i}=\min(f_{v,t}+|t+cnt_1-i|)\)，其中 \(cnt_1\) 是 \(x\) 到 \(v\) 上路径的点个数。

注意需要要求 \(i-d\leq t\leq i\)，其中 \(d\) 表示 \(x\) 到 \(v\) 的深度（我一开始没有注意这个 qwq）。

拆完绝对值可以 ST 表维护。

提交记录

CF526G Spiders Evil Plan *3300

题意

给定一颗 \(n\) 个点的树，\(q\) 次询问，每次问选择 \(y\) 条路径，要求路径并包含 \(x\) 的最大路径并权值和是多少。强制在线。

\(1\leq n,q\leq 10^5\)

题解

考虑 \(x\) 固定怎么做。

我们知道，以 \(x\) 为根选 \(y\) 条到根链是一个经典的贪心问题，每次选择变化量最大的链即可，证明的话，可以写一个闵和优化 DP，写完后发现流程与贪心一致。

现在我们选择的时路径，那么以 \(x\) 为根，选 \(2y\) 条到根链，即为原问题答案（？）。

当选的到根链都在 \(x\) 的同一个子树内时，会爆。

因此撤销最后一个选的，再补上不在 \(x\) 子树内最大的即可。

考虑多次询问，强制在线，要么答案是关于 \(x,y\) 可以 \(O(1)\) 或 \(O(\log)\) 求的式子，要么是可持久化扫描线的结构。

考虑后者，发现 \(x\) 第一个选的到根链是直径端点，且不会被撤销，因此以直径端点为根做权值长剖，记录每个时刻的答案。

还是需要处理都在 \(x\) 一个子树内，于是我写了？！？！主席树！？！？

由于以 \(x\) 为根，往上跳，链的排名递减。因此这种情况肯定是选择的点都在 \(x\) 子树外。

撤销由于并不是简单的贡献相减，贪心有问题。

分两种情况：

1. 替换掉最后一个，正常贪。
2. 替换掉 \(x\) 到根链上排名最大的链。

两个情况分别对应两个 case 的最优解。

---

写了 5.5k，因为判断前缀是否有 \(x\) 子树中的点写了主席树，发现有个地方细节假了还要写倍增，于是弃疗了。

看到粉兔只写了 2k，有点想/tuu。

重构。

你发现以直径端点为根，一个点往上跳，所在长链的排名是递减的。

因此 \(x\) 子树内有没有选，可以直接用 \(x\) 所在长链有没有选判断。

处理替换掉最后一个、另一选择是替换掉 \(x\) 到根链排名最大的长链。

封装两棵树为一个结构体。

启示：重复结构尽量封装，在不是题目重点的 case 上慎用大 DS。

提交记录

省选模拟 T1（条件概率，随机抽样对称性质）

题意

略

题解

额，有两个知识点不会，现学了下。

DP，本质上，需要求在前 \(i\) 个球中有 \(j\) 个红球时，下一个是红球的概率。

根据贝叶斯公式（知识点 \(1\)），原来有 \(k\) 个红球的后验权重为 \(w_k=p_k\binom{k}{j}\binom{n-k}{i-j}\)。

后验概率为 \(P_k=\frac{w_k}{\sum w}\)。

那么下一个是红球的概率为 \(\sum P_k\frac{k-j}{n-i}\)。

等于 \(\frac{\sum p_k\binom{k}{j}\binom{n-k}{i-j}(k-j)}{\sum p_k\binom{k}{j}\binom{n-k}{i-j}}\times \frac{1}{n-i}\)。

\(k-j\) 融入组合数。

\((k-j)\binom{k}{j}=\binom{k}{j+1}(j+1)\)。

\(Pr_{i,j}=\frac{j+1}{n-i}\frac{\sum p_k\binom{k}{j+1}\binom{n-k}{i-j}}{\sum p_k\binom{k}{j}\binom{n-k}{i-j}}\)。

额没啥用。。。

根据不放回抽样对称性（知识点 \(2\)），前 \(i\) 个球中有 \(j\) 个红球时，\(i+1\) 和 \(i+2\) 位置的红球概率一样。

那么可以列出方程 \(Pr_{i,j}=Pr_{i,j}Pr_{i+1,j+1}+(1-Pr_{i,j})Pr_{i+1,j}\)。

变形（/bianxing），\(Pr_{i,j}=\frac{Pr_{i+1,j}}{1-Pr_{i+1,j+1}+Pr_{i+1,j}}\)。

分母有 \(0\) 必死，但我不会其他方法了。

---

设事件 \(A\) 表示前 \(i\) 次抽中了 \(j\) 个红球，事件 \(B\) 表示前 \(i+1\) 次抽中了 \(j+1\) 次红球。

\(P(A的前提下发生B)=\frac{P(A 且 B)}{P(A)}=\frac{P(B 的前提下发生 A)P(B)}{P(A)}\)。

那么我们绕不开的是 \(P(A)\)，即前 \(i\) 个球中有 \(j\) 个红球的概率。

记其为 \(P_{i,j}\)，\(P_{n,k}=p_k\)。

考查所有长为 \(i+1\) 的抽样序列，不放回抽样时，每个位置被抽中的概率是相等的，因此对于 \(P_{i+1,x}\)，最后一个位置是红球的概率是 \(\frac{x}{i+1}\)。

因此 \(P_{i,j}=P_{i+1,j+1}\times \frac{j+1}{i+1}+P_{i+1,j}\times \frac{i+1-j}{i+1}\)。

那么 \(P(B)=P_{i+1,j+1}\)，\(P(B 的前提下发生 A)=\frac{j+1}{i+1}\)，\(Pr_{i,j}=\frac{P_{i+1,j+1}\times \frac{j+1}{i+1}}{P_{i,j}}\)。

另一个方法是概率后置到最终状态，递推求方案数，但是精度不知道有没有保证。

提交记录

省选模拟 T2

题意

现在有一个长为 \(n\) 的字符串 \(a\) 和一个大小为 \(m\) 的字符串集合 \(\{s_i\}\)，小 T 需要先选出 \(a\) 的一个连续子串 \(S\)。

接着，小 M 可以对串 \(S\) 做若干次以下操作：

1. 选择一个 \(1 \leq i \leq m\)，将串 \(S\) 变为 \(S\) 与 \(s_i\) 顺次连接的字符串，即 \(S \leftarrow S + s_i\)；
2. 选择一个 \(k > 1\)，将串 \(S\) 变为 \(S\) 复制 \(k\) 份后顺次连接的字符串，即 \(S \leftarrow S + S + \cdots + S\)，其中右面的 \(S\) 有 \(k\) 个；
3. 选择一个 \(1 \leq i \leq m\)，再选择串 \(S\) 的一个子序列，若选出的子串经过任意重排后与 \(s_i\) 相同，那么将串 \(S\) 中的这个子串删去，也就是将串 \(S\) 中未被删去的字符顺次连接。

下面给一个例子：
\(S = aababa\), \(m = 2\), \(s_1 = bbaa\), \(s_2 = aaab\)。
\(aababa \rightarrow ba \rightarrow baba \rightarrow \text{空串}\)。

求能被消除到空串的连续子串个数。

题解

不难发现字符串没用，有用的是每个字符的出现次数。

三个操作相当于将 \(\{s_i\}\) 进行任意的线性变换，得到 \(S\)，并且是有理数变换，考查 \(aaa\to aaaaaa\to aaaaaaaaa\to aaaaaaaaaaaa\to aaaaaaaa\to aaaa\to \emptyset\)，相当于 \(aaaa=aaa\times \frac{4}{3}\)。

在 \(\mathbb{F}_{10^{18}+3}^{26}\) 上做线性基，现在要求子串计数，乍一看是不好做的。

考虑线性基的 RREF 化，即将每个有主元的列消到只剩主元一个 \(1\)，这样，一个 \(26\) 维向量 \(cnt\) 丢到线性基里可以表示为 \(cnt-\sum cnt_i\times base_i\)，这个记其为 \(f\) 变换，变换是线性的，即 \(f(a+b)=f(a)+f(b)\)，那么 \([l,r]\) 符合条件当且仅当 \(f(cnt[1,r]-cnt[1,l-1])=f(cnt[1,r])-f(cnt[1,l-1])=\mathbf{0}\)，因此每个前缀在线性基里跑一遍，维护一个向量哈希即可。

预处理每个字符对应的 \(-base_i\) 值，前缀的 \(f\) 可以增量维护，复杂度 \(O(m|\Sigma|^2+|\Sigma|^3+n|\Sigma|)\)。

提交记录

省选模拟 T3（平面整点个数转化，对称贡献处理技巧，整除差分处理技巧）

题意

多次询问，每次给出 \(n\)，求：

\[\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{k=i+1}^{n} \left\lfloor \frac{ij}{k} \right\rfloor \]

对 \(P\) 取模的值。

\(T\leq 10^6\)，\(n\leq 10^7\)。

题解

限制 \(k>i\) 后不能直接算因子数。

答案是 \(\sum\limits_{k>i}\sum\limits_{j} \lfloor\frac{i}{k}\cdot j \rfloor\)，可以转化为斜率 \(\frac{i}{k}\) 直线下整点个数。

考虑每个点的贡献，发现贡献点集合与被贡献点集合一致，也就是说贡献是对称的，将所有点按极角排序，极角小的贡献到极角大的。

对于极角相等的点可能有重复贡献，因此将极角相等的点缩为等价类，记其为 \(a_i\)，则答案为 \(\sum\limits_{j\geq i}a_ia_j=\frac{(\sum a)^2+\sum a^2}{2}\)。

算 \(\sum a^2\)，按照互质的点对 \((i,j)\) 分类，枚举 \(j\)，答案为 \(-n^2+\sum\limits_{1\leq j\leq n} \phi(j)\lfloor\frac{n}{j} \rfloor^2\)，\(-n^2\) 是因为 \(j=1\) 不合法。

整除分块，\(O(T\sqrt n)\)。

对于整除，除了分块，另一个处理技巧是差分，令 \(f(n)=\sum\limits_{1\leq j\leq n} \phi(j)\lfloor\frac{n}{j} \rfloor^2\)，\(g(n)=f(n)-f(n-1)\)。当 \(d|n\) 时 \(\lfloor\frac{n}{d}\rfloor\) 会变大 \(1\)。

因此 \(g(n)=\sum\limits_{d|n}\phi(d)(2\cdot\frac{n}{d}-1)\)，记 \(h(n)=\sum\limits_{d|n}\phi(d)\frac{n}{d}\)，\(h(d)\) 为两个积性函数狄利克雷卷积，为积性函数，可以 \(O(n)\)。

因此总复杂度为 \(O(\max n+T)\)。

提交记录

CF1060F Shrinking Tree *2900（期望转排列，分析性质，树上 DP）

题意

给定一棵 \(T\)，有 \(n\) 个顶点，编号为 \(1\) 到 \(n\)。我们对 \(T\) 进行如下操作：当 \(T\) 中顶点数大于 \(1\) 时，重复以下步骤：

• 等概率随机选择 \(T\) 的一条边；
• 收缩所选边：若该边连接顶点 \(v\) 和 \(u\)，则删除 \(v\) 和 \(u\)，新建一个顶点，并使其与所有原本与 \(v\) 或 \(u\) 相邻的顶点相连。新顶点的编号等概率地取 \(v\) 或 \(u\) 的编号。

当操作结束时，\(T\) 只剩下一个顶点，其编号为 \(1, 2, \ldots, n\) 中的某一个。对于每一个编号，求该编号最终成为唯一顶点编号的概率。

\(1\leq n\leq \color{red}{300}\)，原题是 \(50\) 但可以做到 \(O(n^3)\)。

题解

先把随机选边转为排列，考虑固定排列怎么做。

设 \(rt\) 被缩的次数为 \(c\)，那么 \(rt\) 被保留的概率就是 \(\frac{1}{2^c}\)。

分析 \(rt\) 被缩的次数，发现当一个边是到根链最大值时，这个边会有贡献。

那么我们设 \(f_{i,j}\) 表示 \(i\) 子树内（含 \(i\) 的父边）有 \(j\) 个到根 \(\max\) 的方案数。

为了方便转移，还要再记录 \(k\) 表示钦定 \(i\) 到根链（不含 \(i\) 的父边）在子树中的排名。

即 \(f_{i,j,k}\) 表示子树 \(i\) 内有 \(j\) 个到根 \(\max\)，钦定 \(i\) 到根链 \(\max\) 在子树中比 \(k\) 个边大的方案数。

转移时，由于子树状态对 \(i\) 的父边有约束，先合并子树，最后枚举 \(i\) 父边的值。

合并是简单的树上背包，系数是组合数。

枚举 \(i\) 父边的相对排名，当 \(i< k+1\) 时，\(f_{i,j,k}\to f_{i,j,k+1}\)；当 \(i=k+1\) 时新增一个到根链 \(\max\)，\(f_{i,j,k}\to f_{i,j+1,k'}(k'<k+1)\)。

需要枚举根，做 2D 背包，复杂度 \(O(n^5)\)。

最后答案是 \(\sum \frac{f_{rt,j,0}\frac{1}{2^j}}{(n-1)!}\)，\(\frac{1}{2^j}\) 仅与 \(j\) 状态有关且可以增量维护，考虑将 \(\frac{1}{2^j}\) 计入状态，令 \(f_{i,k}\) 表示 \(i\) 子树钦定 \(i\) 到根链比子树中 \(k\) 个边大的所有情况的 \(\frac{1}{2^j}\) 之和，\(f_{i,j,k}\to f_{i,j+1,k'}\) 改为 \(f_{i,k}\cdot \frac{1}{2}\to f_{i,k'}\)，可以做到 \(O(n^3)\)。

提交记录

P5912 [POI 2004] JAS 黑（贪心，树论）

题意

求一颗树 \(\max dep\) 最小的点分树的 \(\max dep\)。

\(1\leq n\leq \color{red}{500000}\)，原题是 \(50000\)，因为当时评测机较慢。

题解

对树形结构要有非常深刻的理解。

引理 1：一个生成树是点分树，当且仅当对于任意点对 \(i,j\)，\(i,j\) 在点分树上的 \(\text{lca}\) 位于原树上 \(i,j\) 的简单路径上。

证明 1：点分树基本性质，略。

引理 2：对于一个树 \(T_1\)，当给定另一个树 \(T_2\) \(dep\) 序列，\(\forall_{i,j,dep_i=dep_j}\)，任取满足 \(dpe_k<dep_i\land k\in \text{pathT1(i,j)}\) 的 \(k\) 作为 \(\text{lcaT2(i,j)}\)，都存在满足条件的 \(T_2\)。

证明 2：从 \(dep\) 最小的点 \(i\) 开始，删除点 \(i\) 并递归子树，模拟建立点分树的过程即证。

本题的最优化目标是点分树上的 \(\max dep\)，考虑刻画 \(dep\) 序列的合法条件。

引理 3：\(dep\) 序列合法，当且仅当对于任意满足 \(i\neq j\land dep_i=dep_j\) 的 \(i,j\)，都存在一个在 \((i,j)\) 路径上的 \(k\)，满足 \(dep_k<dep_i\)。

必要性：若存在 \(i,j\) 不满足条件则 \(i,j\) 在点分树上的 \(\text{lca}\) 不在 \(i,j\) 的简单路径上，与引理 1 矛盾。

充分性：对于这样的 \(i,j\)，随意指定 \(i,j\) 路径上 \(dep\) 比 \(i,j\) 大的任意一个满足 \(dep_k<dep_i\) 的 \(k\) 作为 \(\text{lca}\)，根据引理 2，存在一颗树满足条件，且根据引理 1 这个树是点分树。

那么我们将原问题转化为形式化问题，对满足条件的 \(dep\) 赋值使得 \(\max dep\) 最小。

显然 \(\max dep\leq \log_2 n+O(1)\)，可以考虑和值域相关的做法。

由于要处理路径，考虑类似树上 DP 自下而上增量维护答案，假设当前在子树 \(u\)，我们只需要决策 \(dep_u\) 的值，我们发现：

• 只有满足 \(dep_v\leq \min\limits_{x\in \text{path}(u,v)} dep_x\) 的点 \(v\) 是重要的。

记满足上述条件的 \(dep_v\) 集合为 \(S\)，假设当前在 \(u\)，合并子树，当我们合并 \(v\) 至 \(u\) 时，记同时出现在 \(S_u,S_v\) 的最小 \(dep\) 为 \(dep_{\min}\)，那么 \(dep_u<dep_{\min}\)，且 \(\forall_{v\in \text{son}(u)},dep_u\notin S_v\)。

我们发现 \(S\) 中的重复元素是没有用的，因此可以去重后状压维护。

我们发现每次不一定让 \(dep_u\) 等于满足条件的最小 \(dep\)，会被样例 Hack。

写一下代码，发现直接原因是 \(dep_u<dep_{\min}\) 根本没用，且会导致无解发生。

我们需要找到一个方法使得无论如何不能出现无解，本质原因是，我们维护的 \(dep\) 是相对的 \(dep\)，在出现上述“无解”时，需要实现的是将之前的所有 \(dep\) 加一，并将答案加一。

也许上 DS 维护是可行的，但是有更巧妙的方法。不妨令 \(dep\to ans-dep+1\)，这样，新增一个最大的 \(dep\) 就能代替刚才的操作。

那么上述分析中所有大于小于号取反，我们记同时出现在 \(S_u,S_v\) 的最大 \(dep\) 为 \(dep_{\max}\)，那么 \(dep_u>dep_{\max}\)，且 \(\forall_{v\in \text{son}(u)},dep_u\notin S_v\)。

引理 4：对于 \(S\) 中每个值，其对应的节点是唯一的，即我们无需对 \(S\) 去重，因为 \(S\) 本身不重。

证明 4：按照上述过程归纳即证。

猜测我们每次选择满足条件的最小值赋给 \(dep_u\)，最后求得即为正确答案。

证明：当子树 \(u\) 内的某个 \(dep\) 减少 \(1\)（记其为 \(dep_v\)），且子树 \(u\) 内部合法时，讨论 \(S\) 的变化情况，如果我们说明 \(S\) 对上面的限制不会更严格，就证完了。

1. \(dep_v\notin S\)，说明 \(v\) 到 \(u\) 存在 \(dep>dep_v\) 的点（记其为 \(k\)），那么 \(dep_v\) 减一后仍然不会在 \(S\) 中，\(v\) 子树内的点会受限于 \(k\)，是否在 \(S\) 的状态不会改变。

2. \(dep_v\in S\)，对于子树 \(v\) 内的点，所有 \(=dep_v\) 的点距离 \(v\) 都存在一个 \(k\) 满足 \(dep_k>dep_v\)。因此这些点不会加入 \(S\)。

   2.1. 当 \(v\) 的到根链存在 \(dep_k=dep_v\)，\(dep_v\) 从 \(S\) 中移除，更优。

   2.2. 没有这样的 \(k\)，那么 \(S\) 会变为 \(S-\{dep_v\}+\{dep_{v}-1\}\)。讨论 \(S\) 之后的限制，可能出现如下看起来更劣的情况：

   • 导致 \(dep_{v}-1\) 不能出现在 \(S\) 的祖先中，但是 \(dep_{v}\) 可以。

   这对最大 \(dep\) 没有影响，且对之后的 \(S\) 集合，可以发现 \(dep_v-1\) 在下 \(dep_v\) 在上不比 \(dep_v\) 在下 \(dep_v-1\) 在上优。

提交记录

[AGC064D] Red and Blue Chips（分析性质，计数）

题意

你有 \(N\) 个字符串，初始情况下每个字符串只有一个字符，是 \(\texttt{R}\) 或 \(\texttt{B}\)，保证第 \(N\) 个字符串是 \(\texttt{B}\)。

你需要对每个 \(i=1,2,\cdots ,n-1\) 执行以下操作：

• 选择一个整数 \(j\) 使得 \(i< j\le n\)，且第 \(j\) 个字符串的最后一个字符是 \(\texttt{B}\)，然后把第 \(i\) 个字符串整体拼接在第 \(j\) 个字符串的前面。

问最后可以得到多少种本质不同的第 \(N\) 个字符串，对 \(998244353\) 取模。

\(1\leq N\leq 300\)。

题解

思路是考虑一个目标串能不能被表示出。

分析性质，想不清楚的东西先从特殊情况考虑，然后推广。

考察目标串 \(T\) 开头极长全 \(\texttt{R}\) 前缀 \(X\) 与给定串 \(S\) 去掉最后一个 \(\texttt{B}\) 后极长全 \(\texttt{R}\) 后缀 \(Y\)，发现 \(Y\) 的字符肯定都去了 \(X\)，因此 \(|X|\geq |Y|\)。

先扣除前缀的 \(|Y|\) 个 \(R\)，然后继续分析。

由于拼接过来长度 \(>1\) 的字符一定以 \(\texttt{B}\) 结尾，考察最后一个这样的串。

即，将 \(T\) 从某个 \(\texttt{B}\) 处断开（\(\texttt{B}\) 在断点前），将 \(\texttt{B}\) 串移回到原始位置，考察断开后独立出来的 \(\texttt{R}\)，即 \(RRRBRRRB|{\color{red}RRR}B\cdots\) 中标红部分，其中部分的 \(\texttt{R}\) 需要填入如图（原串）的标绿部分：

\[\cdots BRRBRRRBB{\color{green}RRR}{\color{blue}B}{\color{green}RRR}BRRRB \]

其中，蓝色位置表示断点前的原始位置。要保证 \(\texttt{R}\) 能填满。

解释一下，因为蓝色的 \(\texttt{B}\) 前面肯定是由其前面的 \(\texttt{B/R}\) 拼接来的，因此这些 \(\texttt{R}\) 有两个可能：

1. 由标红的 \(\texttt{R}\) 填入。
2. 由一开始的 \(\texttt{R}\) 的多余部分填入。

所以我们要求【这一段的 \(\texttt{R}\) 个数】不超过【开头的 \(\texttt{R}\) 加上分裂出的 \(\texttt{R}\) 个数】。

因此，贪心地，我们将原始位置设为最靠后的之前未使用的 \(\texttt{B}\)，并分裂出 \(\texttt{R}\) 个数最多的一段。

整理判据，为【\(S\) 后两段 \(\texttt{R}\) 的个数】不超过【\(T\) 前缀 \(\texttt{R}\) 的个数 \(+\) \(T\) 最大极长 \(\texttt{R}\) 段中 \(\texttt{R}\) 的个数】。

归纳，根据上述过程以此类推，可以得出：

【\(S\) 后三段 \(\texttt{R}\) 的个数】不超过【\(T\) 前缀 \(\texttt{R}\) 的个数 \(+\) \(T\) 前两大极长 \(\texttt{R}\) 段中 \(\texttt{R}\) 的个数和】。

\(\cdots\)。

【\(S\) 后 \(k\) 段 \(\texttt{R}\) 的个数】不超过【\(T\) 前缀 \(\texttt{R}\) 的个数 \(+\) \(T\) 前 \(k-1\) 大极长 \(\texttt{R}\) 段中 \(\texttt{R}\) 的个数和】。

那么对 \(T\) 中 \(\texttt{R}\) 段进行 DP，假设长度为 \(x\) 的段由 \(c_x\) 个，那么贡献为 \(\frac{(\sum c_x)!}{c_x!}\)。

对这个式子 DP 一下即可。枚举新填入的段数是调和级数的，复杂度 \(O(n^3\ln n)\)。

提交记录

省选模拟 T2（连通块刻画，换维）

题意

略。

题解

直接在线做比较困难，考虑离线下来维护时间维度，连通块个数刻画为 \(n\) 减去和父亲合并的点的个数。

记 \(t_i\) 表示 \(i\) 与父亲合并的时间，则 \(i\) 时刻的答案为 \(n-\sum_x [t_x\leq i]\)。

\(t_i\) 相当于到根链区间查 \(\min\)，可以用 multiset 维护。

提交记录

省选模拟 T3（树上莫队，根号平衡）

题意

略。

题解

查路径 \(cnt\)，考虑树上莫队，本质上要查询 \(cnt\) 区间等于某个数的个数，使用平衡树维护 \(ccnt\) 可以做到 \(O(n\sqrt{n}\log n)\)。

由于修改操作与查询操作不平衡，考虑根号平衡，使用 \(O(1)-O(\sqrt n)\) 的分块维护 \(cnt\) 数组即可。

不能维护 \(ccnt\) 的原因是分块不支持动态开点，空间会爆。

提交记录

[ARC169D] Add to Make a Permutation（贪心，调整法）

题意

给定一个长度为 \(N\) 的整数序列 \(A=(A_1,A_2,\cdots,A_N)\)。\(A\) 的每个元素都是 \(0\) 到 \(N-1\) 之间的整数。

你可以进行如下操作任意次（包括 \(0\) 次）：

• 从 \(A\) 中恰好选出 \(M\) 个元素，将选中的每个元素的值加 \(1\)。如果加 \(1\) 后某个元素的值变成了 \(N\)，则将其值变为 \(0\)。

你的目标是将 \(A\) 变成 $ (0,1,\cdots,N-1) $ 的一个排列。请判断目标是否可以达成，如果可以，输出所需的最小操作次数；否则输出 \(-1\)。

\(2\leq N\leq 250000\)。

题解

设每个数操作次数为 \(c_i\)，\(b_i=a_i+c_i\)。

刻画满足题意的条件。

1. \(b_i\geq a_i\)。
2. \(\max \{b_i-a_i\}\leq \frac{\sum (b_i-a_i)}{m}\)。
3. \(b_i\bmod m\) 互不相同。
4. \(\sum (b_i-a_i)\bmod m=0\)。

将 \(a\) 升序排序，容易发现 \(b\) 递增一定不劣。

猜测 \(b\) 构成公差为 \(1\) 的等差数列。

证明：若 \(b_n-b_1>n-1\)，同时令 \(b_1\leftarrow b_n-n,b_n\leftarrow b_1+n\)，发现上述条件变得更容易满足，因此 \(b_n-b_1\leq n-1\)。又因为 \(b\) 递增，因此 \(b\) 构成公差为 \(1\) 的等差数列。

枚举 \(b_1\) 按条件模拟即可。

提交记录

P14135 【MX-X22-T6】「TPOI-4F」Miserable EXperience（差分转化，贪心，长链剖分）

题意

给定一棵有根树，每个点有点权，你每次可以对这棵树进行如下两种操作之一：

1. 任选点 \(x\)，将 \(x\) 子树内所有点的点权减一。
2. 任选整数 \(d\)，将所有深度为 \(d\) 的点点权减一。

对于每个点 \(u\)，输出将 \(u\) 子树内所有点操作为 0 的最少操作次数。如果无法操作到全 0，输出 \(-1\)。

\(1 \leq n \leq 10^6, \quad 0 \leq a_i \leq 10^9\)。期望复杂度 \(O(n)\)。

题解

先转为树上差分，令 \(d_i=a_i-a_{fa}\)，则操作一相当于单点减，操作二相当于一层减，下一层加。

咕咕咕。

提交记录

[ARC128F] Game against Robot（贪心，拆贡献技巧——转 01 序列，格路计数）

题意

A 和 B 要在一个长为 \(n\) 的序列 \(x_i\) 上进行游戏，A,B 将进行如下操作 \(\frac{n}{2}\) 轮：

• A 从 \(x_i\) 中剩下的数中选一个，并将其删除。
• B 删去 \(x_i\) 剩下的数中下标最小的数。

保证 \(n\) 是偶数。A 希望最大化他删除的数之和，定义这个最大的和是这个序列的「分数」。

现在给定一个数组 \(a_i\)，求出对它任意进行下标重排后得到的 \(n!\) 种序列的分数之和，对 998244353 取模。

• \(1 \leq N \leq 10^6\)
• \(N\) 是偶数
• \(1 \leq A_i \leq 10^9\)

题解

考虑如何对固定序列求答案，显然最后 A 肯定选择 \(\frac{n}{2}\) 个数，按 \(x\) 重排后，设第 \(i\) 个数下标为 \(id_i\)，则有 \(id_i\geq 2i-1\)，因为有 B 的删除操作。

经典的从后往前贪心，从后往前扫，每次入队后两个并去出一个最大值。

对于堆上的贪心问题，满足判定条件只和相对大小有关，结果只和总和有关，可以考虑 \(01\) 序列拆贡献。具体地，\(x=\sum\limits_{v\leq x} 1\)，因此我们枚举 \(v\)，将 \(\geq v\) 的数设为 \(1\)，其余数设为 \(0\) 跑一遍贪心，将所有结果加起来即为答案。

我们发现我们只需要维护当前下标和 \(1\) 的个数，状态是有限的。

将 \(a\) 降序排序，序列 \(a\) 将 \(1\) 的个数分为 \(n\) 段，具体地设 \(f(i)\) 表示有 \(i\) 个 \(1\) 的方案数，那么答案为：

\[\sum\limits_{i=1}^{n} (a_{i+1}-a_i)i!(n-i)!f(i) \]

考虑如何求 \(f(i)\)，两个两个看，一段可能有 \(0,1,2\) 个 \(1\)，记当前段 \(1\) 的个数为 \(k_i\)，那么堆中 \(1\) 的个数 \(cnt1\) 变为 \(\max(cnt1+k_i-1,0)\)。

转为格路计数，可以向右上、右、右下走，向右走方案为 \(\times 2\)。

对 \(0\) 取 \(\max\)，要么对 \(y=-0.5\) 反射，要么枚举被取 \(\max\) 的个数，然后去掉限制。前者无法确定最后的中点，且答案和被取 \(\max\) 的次数有关，考虑后者。

设被取 \(\max\) 的 \(m\) 次，去掉限制后相当于全局最小值恰好为 \(-m\)，去掉反射后中点为 \((\frac{n}{2},c-\frac{n}{2})\)。对答案的贡献倍数是 \(\frac{n}{2}-m\)，表示有 \(m\) 次没有取到 \(1\)。

令 \(g(n,t,m)\) 表示 \((0,0)\) 到 \((n,t)\)，全局最小值为 \(m\) 的方案数，\(h(n,t)=\sum\limits_{m\in \mathbb{R}} g(n,t,m)\)。

则 \(g(n,t,m)=(h(n,t)-h(n,2(m-1)-t))-(h(n,t)-h(n,2m-t))\)，这一步是标准的反射容斥。

从 GF 的角度考虑，\(h(n,t)=[x^t](x+2+x^{-1})=[x^{t+n}](x+1)^{2n}=\binom{2n}{t+n}\)。

剩余的就是推式子环节。

\(f(c)=\sum\limits_{m\leq \min(0,c-\frac{2}{n})} (m+\frac{n}{2})(\binom{n}{n-c+2m}\binom{n}{n-c+2m-2})\)。

简单列项即可做到 \(O(1)\)，令 \(p=-\min(0,c-\frac{2}{n})\)，\(f(c)=(\frac{n}{2}-p)\binom{n}{c+2p}-\sum\limits_{m\geq p+1}\binom{n}{c+2m}\)。

预处理组合数奇偶项前缀和，可以除排序外 \(O(n)\)。

提交记录

CF2152H2 Victorious Coloring（贪心，Kruskal 重构树，状态支配关系——保留 O(n) 个有用状态，slopetrick）

题意

给定一棵有 \(n\) 个顶点的树，每个顶点编号为 \(1\) 到 \(n\)。每条边都被赋予一个正整数权值 \(w_1, w_2, \ldots, w_{n-1}\)。

一种“胜利染色”指的是将所有顶点染成红色或黄色两种颜色，其中必须至少有一个顶点染成红色。

设对每个顶点分配了一个非负整数权值 \(x_1, x_2, \ldots, x_n\)。胜利染色的代价被定义为：所有红色顶点权值之和，加上所有异色边的权值之和。定义 \(f([x_1, x_2, \ldots, x_n])\) 为所有胜利染色下可能的最小代价。

\(q\) 个询问，每次询问给定一个整数 \(l\)，求一组非负整数顶点权值 \([x_1, x_2, \ldots, x_n]\)，使得 \(f([x_1, x_2, \ldots, x_n]) \ge l\) 且顶点权值总和 \(\sum_{i=1}^n x_i\) 最小，你需要输出相应的最小总顶点权值。

\(1 \le n,q \le 250\,000\)。

题解

先考虑怎么求 \(f\)，可以树上 DP，但是继续做是 DP of DP，状态和值域有关没有前途。

分析性质，不难发现红色构成连通块，直观上考虑红色连通块的生成过程，相当于从一个点拓展。

但是拓展需要有决策，比较嘟嘟。

记一个连通块内部边集为 \(E_1\)，内向外的边集为 \(E_2\)，发现若存在 \(e_1\in E_1,e_2\in E_2,w_{e_2}\geq w_{e_1}\)，则直接删去 \(e_1\) 边向 \(e_2\) 方向的连通块一定更优。

因此有 \(\max_{w_{e_2}}<\min_{w_{e_1}}\)，本质上是 Kruskal 重构树做的事情，可以建立重构树求出 \(O(n)\) 个连通块，每个子树对应一个连通块。

DP，令 \(c_i\) 表示 \(i\) 子树只算边集的 \(f\) 值，\(dp_i\) 表示 \(i\) 子树内的答案，\(dp_{i}=\max(dp_{ls}_dp_{rs},l-c_u)\)。

SlopeTrick，使用左偏树维护拐点，由于 \(\text{chkmax}\) 的直线斜率为 \(1\)，所以被 \(\text{chkmax}\) 的是一段前缀，直接暴力弹堆就是对的，注意交点可能不是整数，要特殊处理。

提交记录

[CEOI 2025] Equal Mex（根号分治，mex 区间性质，nxt 树性质）

题意

一个整数数组 \(a[0], a[1], a[2], \ldots, a[m - 1]\) 的美丽值定义为：满足以下条件的正整数 \(k\) 的个数——你可以将该数组划分为 \(k\) 个互不重叠的子数组（即连续元素的序列），使得：

1. 每个元素恰好属于一个子数组；
2. 所有子数组具有相同的 \(\text{mex}\)。

给定一个整数数组 \(v[0], v[1], \ldots, v[n - 1]\)，以及 \(q\) 个询问，每个询问的形式为 \((l_i, r_i)\)，对于每个询问，你需要求出数组 \(v[l_i - 1], v[l_i ], \ldots, v[r_i - 1]\) 的美丽值。

\(1 \leq n,q \leq 600000\)，\(1 \leq v[i] \leq 400000\)，\(5\) 秒时限。

题解

显然每个区间的 \(\text{mex}\) 等于整个区间的 \(\text{mex}\)，且符合条件的 \(k\) 是连续的。

先求出每个区间的 \(\text{mex}\)，然后暴力跳可以 \(O(n^2)\)。

根号分治，\(\text{mex}=i\) 的区间长度至少为 \(i-1\)，对于 \(\text{mex}>B\) 的暴力跳，相当于查询 \(nxt\) 数组的前缀 \(\max\)，对于 \(\text{mex}\leq B\) 的倍增，可以做到 \(O(n\sqrt n\log n)\)。

考虑如何去 \(\log\)，对于 \(\text{mex}>B\)，\(nxt\) 数组前缀 \(\max\) 可以扫描线然后根号平衡；对于 \(\text{mex}\leq B\)，对每个 \(\text{mex}\) 建出一棵树，\(i\) 连向它应该跳到的位置，注意到树边不存在严格包含关系，因此有 \(dis(l,r)=dep(l)-dep(r)+O(1)\)，\(O(1)\) 部分很好处理。

因此最终复杂度 \(O(n\sqrt n)\)。

提交记录

---

还有一个做法是找出 \(O(n)\) 个极小 \(\text{mex}\) 区间然后对每个 \(\text{mex}\) 直接离散化并倍增。

[CEOI 2025] Splits（分析性质，计数，DP）

题意

对于一个长度为 \(n\) 的排列 \(p = p[0], p[1], p[2], \ldots, p[n - 1]\)，我们定义分割排列为一个排列 \(q\)，它可以通过以下过程得到：

1. 选择两个数集 \(A = i_1, i_2, \ldots, i_k\)，\(B = j_1, j_2, \ldots, j_l\)，满足 \(A \cap B = \emptyset\)、\(A \cup B = \{0, 1, 2, \ldots, n - 1\}\)、\(i_1 < i_2 < \ldots < i_k\)、\(j_1 < j_2 < \ldots < j_l\)。
2. 将 \(q\) 定义为 \(q = p[i_1]\, p[i_2] \ldots p[i_k]\, p[j_1]\, p[j_2] \ldots p[j_l]\)。

进一步，我们定义 \(S(p)\) 为排列 \(p\) 的所有分割排列的集合。

现在，给定一个整数 \(n\) 和一个集合 \(T\)，其中包含 \(m\) 个长度为 \(n\) 的排列。要求统计有多少个长度为 \(n\) 的排列 \(p\) 满足 \(T \subseteq S(p)\)。对 \(998\,244\,353\) 取模。

\(1 \leq n \leq 300\)，\(1 \leq m \leq 300\)。

题解

分析性质，不难发现，\(p\) 的前缀在 \(T\) 中的排列 \(t\) 构成一段前缀和一段区间。

仔细分析发现状态数不是很多，直接对第一个串 DP，并暴力检查其他串，令 \(f_{i,k,j}\) 表示匹配了第一个串的 \([1,i]\cup [k,j]\) 的方案数。

但是有一个问题，其他串的两个区间可能合并，导致我们不知道到底是一串前缀还是一串前缀加一个区间。

回看【状态数不多】的事实，考虑暴搜出所有区间的 \(k\)（即区间起始点），直觉告诉我们状态数是对的。

暴搜时对每个串贪心匹配避免重复。

证明一下，把所有排列丢到 Trie 树上，分两个情况。

1. 当前排列是所有串的 LCP，那么此时一旦跳出排列前缀，所有区间立刻确定区间开头。这部分有跳到的位置和跳出时的位置两维状态，\(O(n^2)\)。
2. 其余情况，其他排列把下一步限制到只有两个元素，因此任意位置跳出的方案数为 \(2\)，一共有 \(O(Trie 节点个数)=O(nm)\) 个状态，这部分状态量 \(O(nm)\)。

因此暴搜后，对每个 \(1\) 起始的 \(k\)，将所有 \(f_{i,k,j}\) 加一一起 DP，复杂度就是对的。

还需要快速检查，排列 \(t_i\) 的合法条件是新填入的数 \(x\) 的前驱在 \(p_1\) 中已经填入，即位于 \([1,i]\cup [k,j]\)，维护 \(cnt_{i,j}\) 表示 \(i\) 的前驱在 \(p_1\) 中位置是 \(j\) 的排列数，可以轻松做到 \(O(1)\)。

提交记录

[CEOI 2025] theseus（启发式合并思想）

题意

通信题。

程序一：给定一张图和终点 \(t\)\你需要给边定向

程序二：给定点 \(u\) 和其出边，返回一条出边的目的地点 \(v\)。

你需要做到不断调用程序二在图上行走，使得任意一个点都能到达 \(d\)，且步数不超过最短路 \(+O(\log n)\)。

\(n\leq 10000\)。

题解

给边打标记的作用是给边定向，具体地当 \(u<v\land (u,v) \text{is\ black}\) 时边的方向为 \(u\to v\)，否则为 \(v\to u\)。

考虑按到 \(t\) 的距离 \(dep\) 分层，跨层边都是层级大的连向层级小的。

对于同层边，我们希望造出 \(O(\log n)\) 的额外代价，考虑启发式合并的思想，给每个点赋一个权重 \(sz\)，确保：

1. 每次进行一次同层行走，\(sz\) 至少乘以二。
2. 跨层时 \(sz\) 只增不减，且 \(\max sz\leq n\)。

我们先明确行走策略，图无特殊性质，因此每次直接往最小编号的点行走。

显然不能出现环，因此本质上我们维护了一颗内向树，不妨令 \(sz\) 为子树大小。

从低下往上做，同层内令 \(sz\) 小的点连向 \(sz\) 大的点，然后设 \(x\) 点连出编号最小值为 \(t\)，为了满足条件一和二，令 \(sz_t\leftarrow sz_t+sz_x\)。

正确性显然。

提交记录

「PMOI-4」排列变换 蓝（排列独立性，拆贡献）

题意

给定常数 \(k\)。对于一个长度为 \(n\) 的排列 \(a\)，定义

\[f(a)=\{\max_{1 \le i \le k} \{a_i\},\max_{2 \le i \le k+1} \{a_i\},\cdots,\max_{n-k+1 \le i \le n} \{a_i\}\} \]

对于一个长度为 \(n\) 的序列 \(a\)，定义其权值 \(w(a)\) 为 \(a\) 中不同的数的个数。

现在，\(\text{ducati}\) 想知道，对于所有长度为 \(n\) 的排列 \(p\)，它们的 \(w(f(p))\) 之和。

题解

排列具有良好的独立性，因此拆每个长为 \(k+1\) 的子段贡献，当第一个或最后一个为最大值时，这个位置造成 \(1\) 的 \(\max\) 改变量。式子是简单的。

提交记录

CF1523E. Crypto Lights *2600（期望拆贡献）

题意

为了监控加密货币的汇率，交易员 William 发明了一种神奇的装置，由 \(n\) 个灯按一排排列而成。该装置的工作方式如下：

最初，William 装置上的所有灯都是关闭的。在每一轮开始时，装置会以均匀分布的方式随机选择一个尚未点亮的灯并将其点亮，告诉 William 应该投资哪种加密货币。在本轮操作后，如果任意 \(k\) 个连续的灯中有超过一个被点亮，则装置停止工作。

William 不喜欢不确定性，因此他希望你计算装置停止工作后被点亮的灯的期望数量。

\(2\leq T(n+k)\leq 2\times 10^6\)。

题解

期望等于每一步的概率和，拆贡献为达到每一步的概率，本质上要求的问题是 \(n\) 个里面选 \(x\) 个，相邻两个差 \(>k\) 的方案数，可以 \(k\) 组捆绑然后组合数，式子是 \(\binom{n-xk+x+k-1}{x}\)。

提交记录

P4694 [PA 2013] Raper 紫（wqs 二分，模拟费用流）

题意

你需要生产 \(k\) 张光盘。每张光盘都要经过两道工序：先在 A 工厂进行挤压，再送到 B 工厂涂上反光层。

你知道每天 A、B 工厂分别加工一张光盘的花费。你现在有 \(n\) 天时间，每天可以先送一张光盘到 A 工厂（或者不送），然后再送一张已经在 A 工厂加工过的光盘到 B 工厂（或者不送），每家工厂一天只能对一张光盘进行操作，同一张光盘在一天内生产出来是允许的。我们假定将未加工的或半成品的光盘保存起来不需要费用。

求生产出 \(k\) 张光盘的最小花费。

\(1 \leqslant k \leqslant n \leqslant 5 \times 10^5\)，\(1 \leqslant a_i, b_i \leqslant 10^9\)。

题解

去掉 \(k\) 是费用流板子，能用费用流描述的问题具有凸性，因此 WQS 二分，然后模拟费用流即可。

注意由于是 WQS 二分，在增量相同的情况下需要先匹配后反悔。

提交记录

P5896 [IOI 2016] aliens 黑（WQS 二分，四边形不等式证明凸性）

题意

\(m\times m\) 的网格内，有 \(n\) 个关键点，用不超过 \(k\) 个端点 \(x,y\) 相等的正方形覆盖这些点，使得正方形并的面积最小。

\(1\leq k\leq n\leq 10^5\)，\(1\leq m\leq 10^6\)。

题解

首先把点放于一侧，过滤掉被偏序的点，有 DP：\(f_{i,j}\) 表示覆盖编号为 \([1,i]\) 的点，使用 \(j\) 个正方形的最小代价，可以得出一个 \(O(n^2k)\) 的 DP，斜率优化可以做到 \(O(nk)\)。

具体地，\(f_{i,j}<-f_{t-1,j-1}+(y_{i}-x_{t}+1)^2-c_t\)，\(c_t\) 表示 \(t\) 和 \(t-1\) 的重复部分。

令 \(w(l,r)=(y_r-x_l+1)^2\)，可以发现对于 \(a<b<c<d\)，\(x,y\) 递增时满足四边形不等式（交叉小于包含），即 \(w(a,c)+w(b,d)\leq w(a,d)+w(b,c)\)，因此 \(f\) 具有凸性，下凸且初始极值为 \(n\)，WQS 二分即可。

需要注意转移时在保证最优性的前提下尽可能多分段。

提交记录

P4027 [NOI2007] 货币兑换 紫（CDQ 分治，斜率优化）

题意

经典题，略。

题解

分析一下发现，必然存在一种最优的买卖方案满足：每次买进操作使用完所有的人民币，每次卖出操作卖出所有的金券（事实上题目给了这个 Hint）。

令 \(f_i\) 表示第 \(i\) 天买入后的价值最大值，记 \(cntA_i\) 表示第 \(i\) 天买入的 A 券数，\(cntB_i\) 同理，有 \(cntA_i=\frac{f_jr_j}{a_jr_j+b_j}\)，\(cntB_i=\frac{f_j}{a_jr_j+b_j}\)。

转移是 \(f_i=\max(f_{i-1},b_i\max_j \{cntA_i+\frac{b_i}{a_i}cntB_i\})\)，是一个两维都没有单调性的斜优转移，可以 CDQ 分治，具体地分治时递归左侧，然后建出左侧凸包，处理跨 \(mid\) 的转移。

启示：式子复杂时可以根据实际含义换元。

提交记录

CF713C Sonya and Problem Without a Legend（SlopeTrick）

题意

给你一个包含 \(n\) 个正整数的数组。每次操作你可以选择任意一个元素，将其增加或减少 \(1\)。你的目标是通过最少的操作次数，将数组变成严格递增的，即每个元素都严格大于前一个元素。

\(1\leq n\leq 3000\)，\(1\leq a_i\leq 10^9\)。

题解

SlopeTrick，使用优先队列维护拐点的差分，每个数减去 \(i\) 变为要求非严格递增，然后操作变为前缀 \(\text{chkmin}\) 前后缀斜率加。

提交记录

[APIO2016] 烟花表演（SlopeTrick）

题意

修改边权使得根到每个叶子的距离相等，并让修改量最小。

\(1\leq n\leq 3\times 10^5\)，\(1\leq V\leq 10^9\)。

题解

咕咕咕。

提交记录

P11459 [USACO24DEC] It's Mooin' Time P

题意

每个长度为 \(3\) 的区间有一定价值，对每个整数 \(k\leq \frac{n}{3}\)，求选出 \(k\) 个不相交区间的最小价值。

\(n\leq 3\times 10^5\)。

题解

咕咕咕。

卡常卡到 0:28，生气了。

提交记录

CF1534G A New Beginning *3300（切比雪夫距离转曼哈顿距离，SlopeTrick，对顶堆）

题意

Annie 的花园是一个无限的二维平面。她有 \(n\) 个土豆要种，第 \(i\) 个土豆必须种在 \((x_i, y_i)\)。Annie 从点 \((0, 0)\) 出发，每走一步可以向右或向上移动一单位（即 \(x\) 或 \(y\) 坐标分别加 \(1\)）。在她行走的任意点 \((X, Y)\)，她可以用土豆枪在任意位置种下土豆，在 \((x, y)\) 处种土豆需要消耗 \(\max(|X-x|, |Y-y|)\) 单位的能量。请你计算种下所有土豆所需的最小总能量。

注意，Annie 可以在任意位置种下任意数量的土豆。

\(1 \leq n \leq 800\,000\)。

题解

将切比雪夫距离转为曼哈顿距离，坐标不除以二，最后将答案除以二，这样每次行走是 \(x+1,y-1\) 或 \(x+1,y+1\)。分析一下发现一个土豆 \((x,y)\) 肯定在当前 \(X=x\) 时种植。

由于坐标没有除以二，因此我们实际上可以执行 \(x+0.5,y+0.5\) 的操作，无需限制 \(x+y\) 奇偶性。

然后将 \(x\) 排序，离散化后，可以得到一个朴素的 DP，\(f_{i,j}\) 表示 \(x=x_i,y=j\) 的最小值，则 \(f_{i,j}=|j-y|+\min\limits_{j+|x_i-x_{i-1}|\leq t\leq j+|x_i-x_{i-1}|} f_{i-1,t}\)。

SlopeTrick，先处理取 \(\min\)，套路地从斜率为 \(0\) 段入手，发现区间取 \(\min\) 相当于两侧拉长，即左侧断点位置集体减，右侧集体加。

可以平衡树但是没有必要，考虑使用对顶堆，左堆维护斜率 \(\leq 0\) 的部分，右堆维护斜率 \(\geq 0\) 的部分，两个操作通过懒标记实现，插入 \(|j-y|\) 时需要调整两个堆使得分解点斜率为 \(0\)。

我们无需将初始斜率设为 \(+\inf\)，因为所有土豆都在合法位置内，跳出合法位置的情况一定不优。

提交记录

CF280E Sequence Transformation *3000（SlopeTrick，求导）

题意

给定一个非递减序列 \(x_1, x_2, ..., x_n\)，其中 \(1 \le x_1 \le x_2 \le ... \le x_n \le q\)。你还有两个整数 \(a\) 和 \(b\)，满足 \(a \le b\) 且 \(a \cdot (n-1) < q\)。

你的任务是将序列 \(x_1, x_2, ..., x_n\) 转换为序列 \(y_1, y_2, ..., y_n\)，满足 \(1 \le y_i \le q\) 且 \(a \le y_{i+1} - y_i \le b\)。该变换的代价为下式：\(\sum\limits_{i=1}^{n} (y_i-x_i)^2\)。你的目标是选择一种 \(y\) 的方案，使变换代价最小。

\(1\leq n\leq 6000\)，\(1\leq q,a,b\leq 10^9\)。

题解

形式化推导可以帮助我们想清楚很多问题。

令 \(f_{i,j}\) 表示前 \(i\) 个数，当前 \(y_i=j\) 的最小值，则：

\[f_{i,j}=\min\limits_{j-b\leq t\leq j-a} f_{i-1,t}+(j-x_i)^2 \]

显然 \(f_{i}(j)\) 是凸的，且是在实数域上连续的，拿出最低点 \(u\) 讨论。

\[j-b\leq u\leq j-a\quad f_{i}(j)=f_{i-1}(u)+(x-j)^2 \\ j-a < u\quad f_{i}(j)=f_{i-1}(j-a)+(x-j)^2 \\ u < j-b\quad f_{i}(j)=f_{i-1}(j-b)+(x-j)^2 \]

平方不好做，考虑求导，由于是连续函数，直接导是没有问题的。

\[j-b\leq u\leq j-a\quad f_{i}(j)'=2x-2j \\ j-a < u\quad f_{i}(j)'=f_{i-1}(j-a)'+2x-2j \\ u < j-b\quad f_{i}(j)'=f_{i-1}(j-b)'+2x-2j \]

SlopeTrick，\(f'\) 每次加入的是一次函数，且恒单调递增，维护 \(f'\) 的每一段的斜率，维护每个时刻的三段划分点，可以构造方案，之后根据方案计算答案即可。

暴力维护，复杂度 \(O(n^2)\)。

提交记录

AI 告诉我的经验：在 SlopeTrick 代码中及时 assert 自己不是很确定的集合公式推导，并对拍 \(n\leq 5\) 的小数据和频发触发公式的数据（如果能造出来）。

CF856C Eleventh Birthday *2400（排列 DP，插入法）

题意

有 \(n\) 张写有数字的卡片，第 \(i\) 张卡片上写着数字 \(a_{i}\)。将这些卡片排成一排，以得到一个更大的数字。

已知一共有 \(n!\) 种排列方式。问有多少种排卡片的方法，连接成的大数字能够被 \(11\) 整除，对 \(998244353\) 取模。

\(1 \leq n \leq 2000\)。

题解

整除 \(11\) 的充要条件是奇数位和偶数位的和相等，因此本质上每个数字有两个我们关心的量：

1. 长度的奇偶性。
2. 偶数位减去奇数位

一个 Naive 的想法是 DP 出每个数的贡献情况然后组合计数，组合奇数类似于将数字插入序列，但是发现组合计数不太能做，因为长度为奇数的数字会影响后面的数字。

受组合计数的思路启发，考虑使用插入法 DP，但是不能对原序列做，考虑我们已经确定了奇长度数序列，那么此时偶长度数字就可以正常插入。

奇偶分开做，奇长度数序列 DP 时使用预定法，预定每个数的奇偶贡献情况，由于必定有一半的奇长度数做奇贡献，因此令 \(f_{i,j,0\sim 10}\) 表示前 \(i\) 个数有 \(j\) 个数做奇贡献的方案数，最后乘上两个阶乘分配顺序。

偶长度数在 \(f\) 的基础上做，维护 \(g_{i,j,0\sim 10}\) 表示前 \(i\) 个数有 \(j\) 个插入位置可以做奇贡献的方案数，复杂度 \(O(n^2)\)，\(11\) 倍常数。

CF1784D Wooden Spoon *2400（组合数学，DP，信息复用，对关键点 DP）

题意

有 \(2^n\) 名选手，编号为 \(1\) 到 \(2^n\) 的不同整数，正在进行一场单败淘汰赛。比赛的对阵表是一棵高度为 \(n\) 的满二叉树，共有 \(2^n\) 个叶子节点。

每当两名选手在一场比赛中相遇时，编号较小的选手总是获胜。最终的冠军是连续赢下 \(n\) 场比赛的选手。

有一个虚拟安慰奖“木勺奖”（Wooden Spoon），它会颁发给满足以下 \(n\) 个条件的选手：

• 他们在第一场比赛中输掉了；
• 打败他们的选手在第二场比赛中输掉了；
• 打败那位选手的选手在第三场比赛中输掉了；
• \(\ldots\)；
• 上一条件中被打败的选手在决赛中输掉了。

可以证明，总是恰好有一名选手满足这些条件。

考虑所有可能的 $ (2^n)! $ 种选手排列方式。对于每位选手，求出在多少种排列下他们会获得“木勺奖”，并将这些数对 \(998\,244\,353\) 取模后输出。

\(1 \le n \le 20\)。

题解

卡了很久，实际上不算难。

一开始的想法是自底向上合并，但是遇到了一些问题：

1. 如果维护相对大小，无法刻画节点 \(x\) 的值与其他点的大小关系。
2. 如果维护绝对大小，需要维护根节点的值，复杂度不允许。

仔细分析一下发现，充要条件是 \(x\) 的到根链递减。

把 \(x\) 的到根链拿出来 DP，假设这些点分别是 \(t_n=1,t_{n-1},\dots,t_1,t_0=x\)。

将其余贡献用组合数计算，需要分配 \(t\) 子树内的点编号、分配子树内的点顺序、分配子树间顺序，\(t\) 子树编号合法的充要条件为编号最小值是 \(t\)。

限制由紧到松，一个 \(t\) 序列的贡献为：

\[2^n\times \left (\prod_{i=0}^{n-1} (2^{i})!\right ) \times \prod_{i=0}^{n} \binom{n-t_i-i-\sum_{j=0}^{i-1} \max(0,2^{i-1}-1)}{\max(0,2^{i-1}-1)} \]

对这个式子 DP，但是不能从后往前 DP，要不然要枚举 \(x\)，考虑从前往后 DP，这样可以复用一些信息，做到 \(O(n2^n)\)。

提交记录

CF1439D INOI Final Contests *3100（排列 DP，子问题划分技巧，观察解的形态）

题意

今天是 INOI 决赛。比赛教室是一排共有 \(n\) 台电脑的房间。所有电脑从左到右依次编号为 \(1\) 到 \(n\)。有 \(m\) 位参赛者，编号为 \(1\) 到 \(m\)。

我们有一个长度为 \(m\) 的数组 \(a\)，其中 \(a_i\)（\(1 \leq a_i \leq n\)）表示第 \(i\) 位参赛者想要坐在第 \(a_i\) 号电脑后面。

另外，还有一个长度为 \(m\) 的数组 \(b\)，由字符 'L' 和 'R' 组成。\(b_i\) 表示第 \(i\) 位参赛者进入房间的方向。'L' 表示该参赛者从第 \(1\) 号电脑的左侧进入房间，并从左向右行进；'R' 表示该参赛者从第 \(n\) 号电脑的右侧进入房间，并从右向左行进。

参赛者按照 \(1\) 到 \(m\) 的顺序依次进入房间。第 \(i\) 位参赛者按照 \(b_i\) 的方向进入，并试图坐在第 \(a_i\) 号电脑后面。如果该电脑已被占用，他会沿着自己的方向继续前进，直到找到第一个空闲的电脑，然后坐下。如果他没有找到任何空闲的电脑，他会感到沮丧并放弃比赛。

第 \(i\) 位参赛者的“疯狂值”定义为他分配到的电脑（\(a_i\)）与他实际坐下的电脑之间的距离。电脑 \(i\) 和 \(j\) 之间的距离为 \(|i-j|\)。

数组 \(a\) 中的值可以相同。总共有 \(n^m \cdot 2^m\) 种可能的数组对 \((a, b)\)。

请考虑所有不会有参赛者放弃比赛的数组对 \((a, b)\)。对于每一种情况，计算所有参赛者的疯狂值之和。请你求出所有这些情况的疯狂值总和。答案对 \(p\) 取模。

\(1 \leq m \leq n \leq 500, 10^8 \leq p \leq 10^9 + 9\)。

题解

一开始的想法是固定 \(a\) 拆每一位的贡献，但是并不好做，原因是分析性质后发现是一个类似任意位置开始后第一个未出现的数的东西，而且还要判断是否有座位。

观察解的形态，发现座位被分为了若干段，每段内部的 \(a\) 的值也在内部，因此可以先考虑 \(n=m\)，最后再卷起来。

类似《ruins 3》最后一步的子问题划分技巧，枚举最后一个数插入的位置，之后序列被分为两个子问题，即记 \(f_n\) 表示 \(n=m\) 的答案，则有：

\[f_{n}=\sum_{i=1}^{n} f_{i-1}f_{n-i}\binom{n-1}{i-1}(n+1) \]

\(n+1\) 的意思是枚举第 \(n\) 位的 \(a,b\)，当 \(a_n=i\) 时 \(b\) 有两种情况，其余有一种情况。

权值和同理可求，注意因为是权值和，所以卷积时是 \((+,+)\) 卷积，式子应该形如 \(f(x)g(y)+f(y)g(x)\) 而不是 \(g(x)g(y)\)。

之后是区间划分 DP，系数是关于 \(m\) 的组合数，关于 \(m\) 的组合数已经维护了绝对大小，因此无需再乘上合并序列的组合数。

[AGC049E] Increment Decrement *3496

题意

有两个操作：

1. 单点修改：选一个位置 \(+1\) 或 \(-1\)，花费 \(1\)。
2. 区间修改：选一个区间 \([l,r]\)，区间内所有数 \(+1\) 或 \(-1\)，花费 \(C\)。

初始全 \(0\) 序列，变成目标序列的最小化费称作该目标序列的代价。

给定 \(n,C,K\) 和 \(n\) 个序列 \(B_i\)，每个长度为 \(K\)。

一个长为 \(n\) 的序列 \(A\) 满足 \(A_i\in \{B_{i,1},B_{i,2},\dots,B_{i,K}\}\)。

求所有 \(K^n\) 种 \(A\) 序列的“代价”之和，对 \(10^9+7\) 取模。

\(1\leq C\leq N\leq 50\)，\(1\leq K\leq 50\)，\(1\leq B_{i,j}\leq 10^9\)。

题解

咕。

CF963E Circles of Waiting *3100（随机游走，高斯消元技巧，带状矩阵）

题意

有一个棋子被放置在带有坐标系的平面上的点 \((0,0)\)。

每秒钟，棋子会随机移动一次。如果棋子当前在点 \((x,y)\)，那么它有概率 \(p_{1}\) 移动到点 \((x-1,y)\)，有概率 \(p_{2}\) 移动到点 \((x,y-1)\)，有概率 \(p_{3}\) 移动到点 \((x+1,y)\)，有概率 \(p_{4}\) 移动到点 \((x,y+1)\)。保证 \(p_{1}+p_{2}+p_{3}+p_{4}=1\)。每次移动都是独立的。

请你求出棋子离开原点距离大于 \(R\)（即满足 \(x^2+y^2>R^2\)）所需的期望时间。

\(0\leq R\leq 50\)。

题解

直接高斯消元复杂度为 \(O(n^6)\)，不可接受。

列出矩阵后是带状矩阵，带宽不超过 \(R\)，因此可以做到 \(O(R^4)\)，注意带状矩阵不使用高斯-约旦消元法，因为会破坏带状性质，普通高斯消元可行的原因是消元顺序是顺着带宽的。

核心思想就是只操作带状内的数，每次选主元交换行可能导致带宽乘 \(2\)，因此要往右侧消两倍带宽列，回代时也要回代两倍带宽行。

提交记录

CF24D Broken robot *2400（随机游走，高斯消元技巧）

题意

有一个 \(n\) 行 \(m\) 列的矩阵，现在有一个机器人在 \((x,y)\)，它每一步等概率向左，右，下走或原地不动，但不能走出矩阵，问走到最后一行期望的步数。

\(1\le n,m\le 10^3\)，\(1\le x\le n\)，\(1\le y\le m\)。

题解

咦？读错题但是过了。

一开始没发现能原地不动，于是拍了个 DP 上去，发现自底向上按行消元，每行的 DP 方程可以表示为 \(f_{x,y}=\alpha f_{x,y-1}+\beta f_{x,y+1}+c\)。手动模拟带状矩阵消元即可。

唉怎么和答案差 \(n-x\)？不管了加上 \(n-x\) 先交一发，过了？？

实际上，当随机游走模型满足如下条件时，可以忽略“原地不动”，最后加上最短路长度除以 \(C\)。

• 可以给每个点赋一个权值 \(w\)，使得不存在边 \((u,v)\) 满足 \(w_v<w_u\lor w_v>w_u+1\)，且对于任意节点 \(u\)，存在 \(C\) 条边 \((u,v)\) 使得 \(w_v=w_u+1\)。

证明先咕咕咕。

提交记录

P6030 [SDOI2012] 走迷宫 紫（随机游走，高斯消元）

题意

求 \(n\) 个点 \(m\) 条边的有向图中，从 \(s\) 随机游走到 \(t\) 的步数期望值。

\(1\leq n\leq 10^4\)，\(0\leq m \leq 10^6\)，保证强连通分量的大小不超过 \(\boldsymbol{100}\)。

2s。

题解

按题目提示缩点，和上一题一样倒着做，每个 SCC 内部跑高斯消元，最坏复杂度对应的计算量约为 \(10^8\)，可以通过。

提交记录

GYM100591D（高斯消元写入矩阵乘法，DDP 思想）

题意

给定 \(N\) 个点以及 \(P\) 条单向道路 \(A_i\to B_i\)，每个道路的权重为 \(R_i\)。

有 \(D\) 个询问，询问分三类：

1. 给定 \(x,y,z\)，加入边 \((x,y)\)，权重为 \(z\)。
2. 给定 \(x,y\)，删除边 \((x,y)\)，保证边存在。
3. 给定 \(x,y\)，求 \(x\) 随机游走能到达 \(y\) 的概率。

\(1\leq N\leq 50000\)，\(1\leq D\leq 20000\)，\(1\leq P\leq 10^5\)，\(1\leq R,z\leq 5\)。

有 \(T\) 组数据，\(T\leq 20\)。

对任意边 \((u,v)\)，都满足 \(0\leq \lfloor \frac{v}{4}\rfloor - \lfloor \frac{u}{4}\rfloor\leq 1\)。

题解

图的形态满足按 \(\bmod 4\) 分组后形成一条链。

一开始的想法是线段树分治，但是意识到动态加边没有显著比删边简单，于是放弃这个思路。

考虑静态、单次询问，设 \(f_i\) 表示 \(i\) 到 \(y\) 的概率。则有：

\[f_{i}=\sum_{j\in \text{out}(i)} P_{i,j}f_j \\ f_y=1 \]

矩阵带宽较小，可以 \(O(n)\) 高斯消元，但是不能直接推广。

先令 \(f_y=1\)，然后按块逆向倒推，每个块内高斯消元。

考虑静态、多次询问，高斯消元本质是线性变换，因此可以类比动态 DP，矩阵维护，具体地，每一步过程如下：

1. 对于每个跨块边 \((u,v)\)，将上一个块内 \(f_u\) 所在行的方程右侧 \(+f_v\)，此时矩阵满足对角线全为 \(1\)，其余位置只有最后一位有值。我们将这个状态记为四维向量 \((w_1,w_2,w_3,w_4)\) 表示矩阵最后的值是什么
2. 对于每个块内部边，高斯消元，本质上是对 \((w_1,w_2,w_3,w_4)\) 进行了一个线性变换，变为 \((g_1,g_2,g_3,g_4)\)，这四个数就是这一块对应的 \(f\)。

设当前块的 \(f\) 为 \(h=(h_1,h_2,h_3,h_4)\)、上一个块的 \(f\) 为 \(g=(g_1,g_2,g_3,g_4)\)，那么倒推时，第一步是求出中间量 \(w=(w_1,w_2,w_3,w_4)\)，这一步相当于对 \(h\) 线性变换，记作矩阵 \(T\)，则 \(w=h\times T\)。

第二步，设上一个块的高斯消元矩阵为 \(F\)，则 \(g=w\times F=h\times T\times F\)。

设 \(x\) 所在块为 \(L\)，\(y\) 所在块为 \(R\)，那么初始令 \(s=(s_1,s_2,s_3,s_4)\)，将 \(y\) 对应的位置置 \(1\)，其余位置置 \(0\)。暂时无视 \(y\) 的出边，强制令 \(y\) 的位置为 \(1\)，对块内做一次高斯消元得到 \(s'\)，计算 \(ans=s'\times T_{R-1}\times F_{R-1}\times T_{R-2}\times \cdots \times F_{L+1}\times T_{L}\times F_{L}\)。

注意查询 \([L,R]\) 的时候不能用 \(F_R\)，因为 \(F_R\) 没有把节点 \(y\) 视作吸收态。

将矩阵乘法搬到线段树上维护即可。

考虑带修、多次询问，如果修改的是块内边，暴力重构所在块的 \(F,T\)，如果是块间边 \((u,v)\)，暴力重构 \(u\) 所在块的 \(F\) 和 \(T\)，\(F,T\) 都要重构的原因是 \(u\) 块内的随机游走概率改变。

复杂度 \(O((N+D)\log N)\)，\(64\) 倍常数。

求 \(F\) 还是比较复杂的，本质上 \(F\) 要干的事情是，将如下矩阵：

\[\begin{pmatrix} 1 & ? & ? & ? & w_1 \\ ? & 1 & ? & ? & w_2 \\ ? & ? & 1 & ? & w_3 \\ ? & ? & ? & 1 & w_4 \\ \end{pmatrix} \]

进行线性变换后得到：

\[\begin{pmatrix} 1 & 0 & 0 & 0 & v_1 \\ 0 & 1 & 0 & 0 & v_2 \\ 0 & 0 & 1 & 0 & v_3 \\ 0 & 0 & 0 & 1 & v_4 \\ \end{pmatrix} \]

其中我们知道 ? 中的数字，求能将 \(w\in \R^4\) 变换为 \(v\in \R^4\) 的矩阵。

那么，求上面带问号矩阵的逆就行了，根据逆矩阵的定义，\(v=Inv\times w\)，这样上面矩阵乘上逆会变为下面的单位矩阵。

如果使用行向量，需要将逆转置（\((a\times b)^T=a^T\times b^T\)）。

注意，矩阵可能没有逆，需要只保留能到达下一个连通块的点消元，否则这些点是自由元，矩阵不满秩的时候没有逆。

不可到后面 SCC 的点为自由元的原因是，这个点等于的东西也不可到后面的 SCC，将这些点的 \(f\) 集体加一个值仍然满足方程，没有固定解。

提交记录

P5505 [JSOI2011] 分特产 蓝（组合数学）

题意

JYY 想知道，把 \(m\) 种特产分给 \(n\) 个同学，一共有多少种不同的分法？每个同学都必须至少分得一个特产，第 \(i\) 种特产有 \(a_i\) 种。

同学之间不同。

\(1\leq n,m,a_i\leq 1000\)。

题解

P14804 [CCPC 2024 哈尔滨站] 一个朴素的字符串问题 黑（优秀的拆分 Trick，SA，贪心）

题意

有一个 \(2\) 行 \(n\) 列的字符表格，每个单元格内有一个小写字母。你可以选择任意一个位置作为起点，然后走若干步，每一步只能向右或向下，最后停在任意一个单元格中。将经过的单元格中的字符按顺序拼接在一起，可以形成一个字符串。

定义一个字符串 \(S\) 是双重串，当且仅当存在非空字符串 \(T\) 满足 \(S = TT\)。如 \(\texttt{aa}\)，\(\texttt{xyzxyz}\) 都是双重串，而 \(\texttt{a}\)，\(\texttt{xyzyz}\) 不是双重串。

对于给定的字符表格，请求出你可以获得的最长的双重串的长度。

\(1\leq n\leq 2\times 10^5\)。

题解

死因：没有意识到 \(n=1\) 是优秀的拆分。

不难发现当起点和串中点确定时，贪心匹配一定不劣。

本问题不弱于优秀的拆分，套用其套路，枚举答案长度，转化为求可以往下走的 \(\text{lcp}\)，还是贪心匹配，SA 即可。

优秀的拆分需要要求分割点中间的长度恰好为枚举的 \(len\)，因此需要将 \(s2\) 向后平移一位。

提交记录

P10801 [CEOI 2024] 海战 紫（模拟，链表，多路归并）

咕咕咕。

提交记录

P10802 [CEOI 2024] 核酸检测（最优交互方案 DP）

咕咕咕。

提交记录

P10803 [CEOI 2024] 文本编辑器（最短路，分析性质，分析最优解结构）

咕咕咕。

提交记录

P14805 [CCPC 2024 哈尔滨站] 弹珠赛跑 紫（撤销背包）

题意

\(x\) 轴负半轴有 \(n\) 个起跑点位，第 \(i\) 个点位的坐标为 \(x_i\)。总共有 \(m\) 个弹珠，其中 \(m\) 是奇数，第 \(i\) 个弹珠的移动速度为 \(v_i\)。在一场比赛中，每一个弹珠都会等概率地随机选择一个起跑点位，不同的弹珠可以选到相同的点位。比赛开始时，所有弹珠同时出发，向 \(x\) 正半轴方向一直移动。令 \(c_i\) 为第 \(i\) 个弹珠选择的起跑点位编号，不难得出在时间为 \(t\) 时第 \(i\) 个弹珠的坐标为 \(x_{c_i} + v_i \cdot t\)。

你想知道这 \(m\) 个弹珠的所有坐标的中位数恰好在原点（即 \(x = 0\)）的时间点。由于赛跑还没开始，弹珠的起跑点位还没有确定，所以你想知道这个答案的数学期望。对 \(10^9+7\) 取模。

\(1\leq n\leq 500\)。

题解

我是奶龙，一开始看成位置不能重复，推出来带组合数的 DP，完全不能优化。

想了想发现没有任何能刻画中位数的式子，故枚举取到中位数的球的编号和位置，设这个球到达 \(0\) 的时间为 \(t\)，其余球需要满足一半到达 \(0\) 的时间不超过 \(t\)（如果存在相等的 \(t\) 需要随意固定一个偏序关系）。

设第 \(i\) 个球有 \(cnt_i\) 个位置满足【时间不超过 \(t\)】的限制，那么直接进行背包可以做到 \(O(n^2)\)，总共 \(O(n^4)\)。

考虑动态维护，按时间顺序枚举中位数，这样每次会修改恰好一个点的 \(cnt\)，做背包撤销即可，复杂度 \(O(n^3)\)。

提交记录